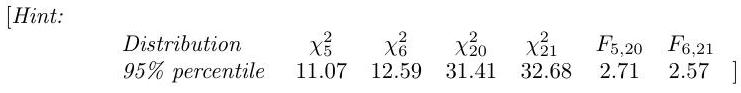Part IB, 2003, Paper 1

Analysis II

• 1.I.1F

  Analysis II | Part IB, 2003

  Let $E$ be a subset of $\mathbb{R}^{n}$. Prove that the following conditions on $E$ are equivalent:

  (i) $E$ is closed and bounded.

  (ii) $E$ has the Bolzano-Weierstrass property (i.e., every sequence in $E$ has a subsequence convergent to a point of $E$ ).

  (iii) Every continuous real-valued function on $E$ is bounded.

  [The Bolzano-Weierstrass property for bounded closed intervals in $\mathbb{R}^{1}$ may be assumed.]

  comment

• 1.II.10F

  Analysis II | Part IB, 2003

  Explain briefly what is meant by a metric space, and by a Cauchy sequence in a metric space.

  A function $d: X \times X \rightarrow \mathbb{R}$ is called a pseudometric on $X$ if it satisfies all the conditions for a metric except the requirement that $d(x, y)=0$ implies $x=y$. If $d$ is a pseudometric on $X$, show that the binary relation $R$ on $X$ defined by $x R y \Leftrightarrow d(x, y)=0$ is an equivalence relation, and that the function $d$ induces a metric on the set $X / R$ of equivalence classes.

  Now let $(X, d)$ be a metric space. If $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are Cauchy sequences in $X$, show that the sequence whose $n$th term is $d\left(x_{n}, y_{n}\right)$ is a Cauchy sequence of real numbers. Deduce that the function $\bar{d}$ defined by

  $$\bar{d}\left(\left(x_{n}\right),\left(y_{n}\right)\right)=\lim _{n \rightarrow \infty} d\left(x_{n}, y_{n}\right)$$

  is a pseudometric on the set $C$ of all Cauchy sequences in $X$. Show also that there is an isometric embedding (that is, a distance-preserving mapping) $X \rightarrow C / R$, where $R$ is the equivalence relation on $C$ induced by the pseudometric $\bar{d}$ as in the previous paragraph. Under what conditions on $X$ is $X \rightarrow C / R$ bijective? Justify your answer.

  comment

Complex Methods

• 1.I.7B

  Complex Methods | Part IB, 2003

  Let $u(x, y)$ and $v(x, y)$ be a pair of conjugate harmonic functions in a domain $D$.

  Prove that

  $$U(x, y)=e^{-2 u v} \cos \left(u^{2}-v^{2}\right) \quad \text { and } \quad V(x, y)=e^{-2 u v} \sin \left(u^{2}-v^{2}\right)$$

  also form a pair of conjugate harmonic functions in $D$.

  comment

• 1.II.16B

  Complex Methods | Part IB, 2003

  Sketch the region $A$ which is the intersection of the discs

  $$D_{0}=\{z \in \mathbb{C}:|z|<1\} \quad \text { and } \quad D_{1}=\{z \in \mathbb{C}:|z-(1+i)|<1\} .$$

  Find a conformal mapping that maps $A$ onto the right half-plane $H=\{z \in \mathbb{C}: \operatorname{Re} z>0\}$. Also find a conformal mapping that maps $A$ onto $D_{0}$.

  [Hint: You may find it useful to consider maps of the form $w(z)=\frac{a z+b}{c z+d}$.]

  comment

Fluid Dynamics

• 1.I.6C

  Fluid Dynamics | Part IB, 2003

  An unsteady fluid flow has velocity field given in Cartesian coordinates $(x, y, z)$ by $\mathbf{u}=(1, x t, 0)$, where $t$ denotes time. Dye is released into the fluid from the origin continuously. Find the position at time $t$ of the dye particle that was released at time $s$ and hence show that the dye streak lies along the curve

  $$y=\frac{1}{2} t x^{2}-\frac{1}{6} x^{3}$$

  comment

• 1.II.15C

  Fluid Dynamics | Part IB, 2003

  Starting from the Euler equations for incompressible, inviscid flow

  $$\rho \frac{D \mathbf{u}}{D t}=-\nabla p, \quad \nabla \cdot \mathbf{u}=0$$

  derive the vorticity equation governing the evolution of the vorticity $\boldsymbol{\omega}=\nabla \times \mathbf{u}$.

  Consider the flow

  $$\mathbf{u}=\beta(-x,-y, 2 z)+\Omega(t)(-y, x, 0)$$

  in Cartesian coordinates $(x, y, z)$, where $t$ is time and $\beta$ is a constant. Compute the vorticity and show that it evolves in time according to

  $$\boldsymbol{\omega}=\omega_{0} \mathrm{e}^{2 \beta t} \mathbf{k}$$

  where $\omega_{0}$ is the initial magnitude of the vorticity and $\mathbf{k}$ is a unit vector in the $z$-direction.

  Show that the material curve $C(t)$ that takes the form

  $$x^{2}+y^{2}=1 \quad \text { and } \quad z=1$$

  at $t=0$ is given later by

  $$x^{2}+y^{2}=a^{2}(t) \quad \text { and } \quad z=\frac{1}{a^{2}(t)},$$

  where the function $a(t)$ is to be determined.

  Calculate the circulation of $\mathbf{u}$ around $C$ and state how this illustrates Kelvin's circulation theorem.

  comment

Geometry

• 1.I.4F

  Geometry | Part IB, 2003

  Describe the geodesics (that is, hyperbolic straight lines) in either the disc model or the half-plane model of the hyperbolic plane. Explain what is meant by the statements that two hyperbolic lines are parallel, and that they are ultraparallel.

  Show that two hyperbolic lines $l$ and $l^{\prime}$ have a unique common perpendicular if and only if they are ultraparallel.

  [You may assume standard results about the group of isometries of whichever model of the hyperbolic plane you use.]

  comment

• 1.II.13F

  Geometry | Part IB, 2003

  Write down the Riemannian metric in the half-plane model of the hyperbolic plane. Show that Möbius transformations mapping the upper half-plane to itself are isometries of this model.

  Calculate the hyperbolic distance from $i b$ to $i c$, where $b$ and $c$ are positive real numbers. Assuming that the hyperbolic circle with centre $i b$ and radius $r$ is a Euclidean circle, find its Euclidean centre and radius.

  Suppose that $a$ and $b$ are positive real numbers for which the points $i b$ and $a+i b$ of the upper half-plane are such that the hyperbolic distance between them coincides with the Euclidean distance. Obtain an expression for $b$ as a function of $a$. Hence show that, for any $b$ with $0<b<1$, there is a unique positive value of $a$ such that the hyperbolic distance between $i b$ and $a+i b$ coincides with the Euclidean distance.

  comment

Linear Mathematics

• 1.I $. 5 \mathrm{E} \quad$

  Linear Mathematics | Part IB, 2003

  Let $V$ be the subset of $\mathbb{R}^{5}$ consisting of all quintuples $\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ such that

  $$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=0$$

  and

  $$a_{1}+2 a_{2}+3 a_{3}+4 a_{4}+5 a_{5}=0$$

  Prove that $V$ is a subspace of $\mathbb{R}^{5}$. Solve the above equations for $a_{1}$ and $a_{2}$ in terms of $a_{3}, a_{4}$ and $a_{5}$. Hence, exhibit a basis for $V$, explaining carefully why the vectors you give form a basis.

  comment

• 1.II.14E

  Linear Mathematics | Part IB, 2003

  (a) Let $U, U^{\prime}$ be subspaces of a finite-dimensional vector space $V$. Prove that $\operatorname{dim}\left(U+U^{\prime}\right)=\operatorname{dim} U+\operatorname{dim} U^{\prime}-\operatorname{dim}\left(U \cap U^{\prime}\right) .$

  (b) Let $V$ and $W$ be finite-dimensional vector spaces and let $\alpha$ and $\beta$ be linear maps from $V$ to $W$. Prove that

  $$\operatorname{rank}(\alpha+\beta) \leqslant \operatorname{rank} \alpha+\operatorname{rank} \beta$$

  (c) Deduce from this result that

  $$\operatorname{rank}(\alpha+\beta) \geqslant|\operatorname{rank} \alpha-\operatorname{rank} \beta|$$

  (d) Let $V=W=\mathbb{R}^{n}$ and suppose that $1 \leqslant r \leqslant s \leqslant n$. Exhibit linear maps $\alpha, \beta: V \rightarrow W$ such that $\operatorname{rank} \alpha=r, \operatorname{rank} \beta=s$ and $\operatorname{rank}(\alpha+\beta)=s-r$. Suppose that $r+s \geqslant n$. Exhibit linear maps $\alpha, \beta: V \rightarrow W$ such that $\operatorname{rank} \alpha=r, \operatorname{rank} \beta=s$ and $\operatorname{rank}(\alpha+\beta)=n$.

  comment

Methods

• 1.I.2D

  Methods | Part IB, 2003

  Fermat's principle of optics states that the path of a light ray connecting two points will be such that the travel time $t$ is a minimum. If the speed of light varies continuously in a medium and is a function $c(y)$ of the distance from the boundary $y=0$, show that the path of a light ray is given by the solution to

  $$c(y) y^{\prime \prime}+c^{\prime}(y)\left(1+y^{\prime 2}\right)=0$$

  where $y^{\prime}=\frac{d y}{d x}$, etc. Show that the path of a light ray in a medium where the speed of light $c$ is a constant is a straight line. Also find the path from $(0,0)$ to $(1,0)$ if $c(y)=y$, and sketch it.

  comment

• 1.II.11D

  Methods | Part IB, 2003

  (a) Determine the Green's function $G(x, \xi)$ for the operator $\frac{d^{2}}{d x^{2}}+k^{2}$ on $[0, \pi]$ with Dirichlet boundary conditions by solving the boundary value problem

  $$\frac{d^{2} G}{d x^{2}}+k^{2} G=\delta(x-\xi), \quad G(0)=0, G(\pi)=0$$

  when $k$ is not an integer.

  (b) Use the method of Green's functions to solve the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=f(x), \quad y(0)=a, y(\pi)=b$$

  when $k$ is not an integer.

  comment

Quadratic Mathematics

• 1.I.8G

  Quadratic Mathematics | Part IB, 2003

  Let $U$ and $V$ be finite-dimensional vector spaces. Suppose that $b$ and $c$ are bilinear forms on $U \times V$ and that $b$ is non-degenerate. Show that there exist linear endomorphisms $S$ of $U$ and $T$ of $V$ such that $c(x, y)=b(S(x), y)=b(x, T(y))$ for all $(x, y) \in U \times V$.

  comment

• 1.II.17G

  Quadratic Mathematics | Part IB, 2003

  (a) Suppose $p$ is an odd prime and $a$ an integer coprime to $p$. Define the Legendre symbol $\left(\frac{a}{p}\right)$ and state Euler's criterion.

  (b) Compute $\left(\frac{-1}{p}\right)$ and prove that

  $$\left(\frac{a b}{p}\right)=\left(\frac{a}{p}\right)\left(\frac{b}{p}\right)$$

  whenever $a$ and $b$ are coprime to $p$.

  (c) Let $n$ be any integer such that $1 \leqslant n \leqslant p-2$. Let $m$ be the unique integer such that $1 \leqslant m \leqslant p-2$ and $m n \equiv 1(\bmod p)$. Prove that

  $$\left(\frac{n(n+1)}{p}\right)=\left(\frac{1+m}{p}\right)$$

  (d) Find

  $$\sum_{n=1}^{p-2}\left(\frac{n(n+1)}{p}\right)$$

  comment

Quantum Mechanics

• 1.I $. 9 \mathrm{~A} \quad$

  Quantum Mechanics | Part IB, 2003

  A particle of mass $m$ is confined inside a one-dimensional box of length $a$. Determine the possible energy eigenvalues.

  comment

• 1.II.18A

  Quantum Mechanics | Part IB, 2003

  What is the significance of the expectation value

  $$\langle Q\rangle=\int \psi^{*}(x) Q \psi(x) d x$$

  of an observable $Q$ in the normalized state $\psi(x)$ ? Let $Q$ and $P$ be two observables. By considering the norm of $(Q+i \lambda P) \psi$ for real values of $\lambda$, show that

  $$\left\langle Q^{2}\right\rangle\left\langle P^{2}\right\rangle \geqslant \frac{1}{4}|\langle[Q, P]\rangle|^{2}$$

  The uncertainty $\Delta Q$ of $Q$ in the state $\psi(x)$ is defined as

  $$(\Delta Q)^{2}=\left\langle(Q-\langle Q\rangle)^{2}\right\rangle .$$

  Deduce the generalized uncertainty relation,

  $$\Delta Q \Delta P \geqslant \frac{1}{2}|\langle[Q, P]\rangle| .$$

  A particle of mass $m$ moves in one dimension under the influence of the potential $\frac{1}{2} m \omega^{2} x^{2}$. By considering the commutator $[x, p]$, show that the expectation value of the Hamiltonian satisfies

  $$\langle H\rangle \geqslant \frac{1}{2} \hbar \omega .$$

  comment

Statistics

• 1.II.12H

  Statistics | Part IB, 2003

  Suppose that six observations $X_{1}, \ldots, X_{6}$ are selected at random from a normal distribution for which both the mean $\mu_{X}$ and the variance $\sigma_{X}^{2}$ are unknown, and it is found that $S_{X X}=\sum_{i=1}^{6}\left(x_{i}-\bar{x}\right)^{2}=30$, where $\bar{x}=\frac{1}{6} \sum_{i=1}^{6} x_{i}$. Suppose also that 21 observations $Y_{1}, \ldots, Y_{21}$ are selected at random from another normal distribution for which both the mean $\mu_{Y}$ and the variance $\sigma_{Y}^{2}$ are unknown, and it is found that $S_{Y Y}=40$. Derive carefully the likelihood ratio test of the hypothesis $H_{0}: \sigma_{X}^{2}=\sigma_{Y}^{2}$ against $H_{1}: \sigma_{X}^{2}>\sigma_{Y}^{2}$ and apply it to the data above at the $0.05$ level.

  

  comment