Part II, 2017

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2017

  Let $k$ be an algebraically closed field.

  (a) Let $X$ and $Y$ be varieties defined over $k$. Given a function $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of varieties.

  (b) If $X$ is an affine variety, show that the coordinate ring $A(X)$ coincides with the ring of regular functions on $X$. [Hint: You may assume a form of the Hilbert Nullstellensatz.]

  (c) Now suppose $X$ and $Y$ are affine varieties. Show that if $X$ and $Y$ are isomorphic, then there is an isomorphism of $k$-algebras $A(X) \cong A(Y)$.

  (d) Show that $Z\left(x^{2}-y^{3}\right) \subseteq \mathbb{A}^{2}$ is not isomorphic to $\mathbb{A}^{1}$.

  comment

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2017

  Let $k$ be an algebraically closed field of any characteristic.

  (a) Define what it means for a variety $X$ to be non-singular at a point $P \in X$.

  (b) Let $X \subseteq \mathbb{P}^{n}$ be a hypersurface $Z(f)$ for $f \in k\left[x_{0}, \ldots, x_{n}\right]$ an irreducible homogeneous polynomial. Show that the set of singular points of $X$ is $Z(I)$, where $I \subseteq$ $k\left[x_{0}, \ldots, x_{n}\right]$ is the ideal generated by $\partial f / \partial x_{0}, \ldots, \partial f / \partial x_{n} .$

  (c) Consider the projective plane curve corresponding to the affine curve in $\mathbb{A}^{2}$ given by the equation

  $$x^{4}+x^{2} y^{2}+y^{2}+1=0 .$$

  Find the singular points of this projective curve if char $k \neq 2$. What goes wrong if char $k=2$ ?

  comment

• Paper 3, Section II, I

  Algebraic Geometry | Part II, 2017

  (a) Define what it means to give a rational map between algebraic varieties. Define a birational map.

  (b) Let

  $$X=Z\left(y^{2}-x^{2}(x-1)\right) \subseteq \mathbb{A}^{2}$$

  Define a birational map from $X$ to $\mathbb{A}^{1}$. [Hint: Consider lines through the origin.]

  (c) Let $Y \subseteq \mathbb{A}^{3}$ be the surface given by the equation

  $$x_{1}^{2} x_{2}+x_{2}^{2} x_{3}+x_{3}^{2} x_{1}=0 .$$

  Consider the blow-up $X \subseteq \mathbb{A}^{3} \times \mathbb{P}^{2}$ of $\mathbb{A}^{3}$ at the origin, i.e. the subvariety of $\mathbb{A}^{3} \times \mathbb{P}^{2}$ defined by the equations $x_{i} y_{j}=x_{j} y_{i}$ for $1 \leqslant i<j \leqslant 3$, with $y_{1}, y_{2}, y_{3}$ coordinates on $\mathbb{P}^{2}$. Let $\varphi: X \rightarrow \mathbb{A}^{3}$ be the projection and $E=\varphi^{-1}(0)$. Recall that the proper transform $\tilde{Y}$ of $Y$ is the closure of $\varphi^{-1}(Y) \backslash E$ in $X$. Give equations for $\tilde{Y}$, and describe the fibres of the morphism $\left.\varphi\right|_{\widetilde{Y}}: \widetilde{Y} \rightarrow Y$.

  comment

• Paper 4, Section II, I

  Algebraic Geometry | Part II, 2017

  (a) Let $X$ and $Y$ be non-singular projective curves over a field $k$ and let $\varphi: X \rightarrow Y$ be a non-constant morphism. Define the ramification degree $e_{P}$ of $\varphi$ at a point $P \in X$.

  (b) Suppose char $k \neq 2$. Let $X=Z(f)$ be the plane cubic with $f=x_{0} x_{2}^{2}-x_{1}^{3}+x_{0}^{2} x_{1}$, and let $Y=\mathbb{P}^{1}$. Explain how the projection

  $$\left(x_{0}: x_{1}: x_{2}\right) \mapsto\left(x_{0}: x_{1}\right)$$

  defines a morphism $\varphi: X \rightarrow Y$. Determine the degree of $\varphi$ and the ramification degrees $e_{P}$ for all $P \in X$.

  (c) Let $X$ be a non-singular projective curve and let $P \in X$. Show that there is a non-constant rational function on $X$ which is regular on $X \backslash\{P\}$.

  comment

Algebraic Topology

• Paper 1, Section II, I

  Algebraic Topology | Part II, 2017

  Let $X$ be a topological space and let $x_{0}$ and $x_{1}$ be points of $X$.

  (a) Explain how a path $u:[0,1] \rightarrow X$ from $x_{0}$ to $x_{1}$ defines a map $u_{\sharp}: \pi_{1}\left(X, x_{0}\right) \rightarrow$ $\pi_{1}\left(X, x_{1}\right)$.

  (b) Prove that $u_{\sharp}$ is an isomorphism of groups.

  (c) Let $\alpha, \beta:\left(S^{1}, 1\right) \rightarrow\left(X, x_{0}\right)$ be based loops in $X$. Suppose that $\alpha, \beta$ are homotopic as unbased maps, i.e. the homotopy is not assumed to respect basepoints. Show that the corresponding elements of $\pi_{1}\left(X, x_{0}\right)$ are conjugate.

  (d) Take $X$ to be the 2-torus $S^{1} \times S^{1}$. If $\alpha, \beta$ are homotopic as unbased loops as in part (c), then exhibit a based homotopy between them. Interpret this fact algebraically.

  (e) Exhibit a pair of elements in the fundamental group of $S^{1} \vee S^{1}$ which are homotopic as unbased loops but not as based loops. Justify your answer.

  comment

• Paper 2, Section II, I

  Algebraic Topology | Part II, 2017

  (a) (i) Define the push-out of the following diagram of groups.

  

  When is a push-out a free product with amalgamation?

  (ii) State the Seifert-van Kampen theorem.

  (b) Let $X=\mathbb{R} P^{2} \vee S^{1}$ (recalling that $\mathbb{R} P^{2}$ is the real projective plane), and let $x \in X$.

  (i) Compute the fundamental group $\pi_{1}(X, x)$ of the space $X$.

  (ii) Show that there is a surjective homomorphism $\phi: \pi_{1}(X, x) \rightarrow S_{3}$, where $S_{3}$ is the symmetric group on three elements.

  (c) Let $\widehat{X} \rightarrow X$ be the covering space corresponding to the kernel of $\phi$.

  (i) Draw $\widehat{X}$and justify your answer carefully.

  (ii) Does $\widehat{X}$retract to a graph? Justify your answer briefly.

  (iii) Does $\widehat{X}$deformation retract to a graph? Justify your answer briefly.

  comment

• Paper 3, Section II, I

  Algebraic Topology | Part II, 2017

  The $n$-torus is the product of $n$ circles:

  $$T^{n}=\underbrace{S^{1} \times \ldots \times S^{1}}_{n \text { times }} .$$

  For all $n \geqslant 1$ and $0 \leqslant k \leqslant n$, compute $H_{k}\left(T^{n}\right)$.

  [You may assume that relevant spaces are triangulable, but you should state carefully any version of any theorem that you use.]

  comment

• Paper 4, Section II, I

  Algebraic Topology | Part II, 2017

  Recall that $\mathbb{R} P^{n}$ is real projective $n$-space, the quotient of $S^{n}$ obtained by identifying antipodal points. Consider the standard embedding of $S^{n}$ as the unit sphere in $\mathbb{R}^{n+1}$.

  (a) For $n$ odd, show that there exists a continuous map $f: S^{n} \rightarrow S^{n}$ such that $f(x)$ is orthogonal to $x$, for all $x \in S^{n}$.

  (b) Exhibit a triangulation of $\mathbb{R} P^{n}$.

  (c) Describe the map $H_{n}\left(S^{n}\right) \rightarrow H_{n}\left(S^{n}\right)$ induced by the antipodal map, justifying your answer.

  (d) Show that, for $n$ even, there is no continuous map $f: S^{n} \rightarrow S^{n}$ such that $f(x)$ is orthogonal to $x$ for all $x \in S^{n}$.

  comment

Analysis of Functions

• Paper 1, Section II, $22 F$

  Analysis of Functions | Part II, 2017

  Consider a sequence $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$ of measurable functions converging pointwise to a function $f: \mathbb{R} \rightarrow \mathbb{R}$. The Lebesgue measure is denoted by $\lambda$.

  (a) Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Define for $k, n \geqslant 1$ the sets

  $$E_{n}^{(k)}:=\bigcap_{m \geqslant n}\left\{x \in A|| f_{m}(x)-f(x) \mid \leqslant \frac{1}{k}\right\}$$

  Prove that for any $k, n \geqslant 1$, one has $E_{n}^{(k)} \subset E_{n+1}^{(k)}$ and $E_{n}^{(k+1)} \subset E_{n}^{(k)}$. Prove that for any $k \geqslant 1, A=\cup_{n \geqslant 1} E_{n}^{(k)}$.

  (b) Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Prove that for any $\varepsilon>0$, there is a Borel set $A_{\varepsilon} \subset A$ for which $\lambda\left(A \backslash A_{\varepsilon}\right) \leqslant \varepsilon$ and such that $f_{n}$ converges to $f$ uniformly on $A_{\varepsilon}$ as $n \rightarrow+\infty$. Is the latter still true when $\lambda(A)=+\infty$ ?

  (c) Assume additionally that $f_{n} \in L^{p}(\mathbb{R})$ for some $p \in(1,+\infty]$, and there exists an $M \geqslant 0$ for which $\left\|f_{n}\right\|_{L^{p}(\mathbb{R})} \leqslant M$ for all $n \geqslant 1$. Prove that $f \in L^{p}(\mathbb{R})$.

  (d) Let $f_{n}$ and $f$ be as in part (c). Consider a Borel set $A \subset \mathbb{R}$ with finite Lebesgue measure $\lambda(A)<+\infty$. Prove that $f_{n}, f$ are integrable on $A$ and $\int_{A} f_{n} d \lambda \rightarrow \int_{A} f d \lambda$ as $n \rightarrow \infty$. Deduce that $f_{n}$ converges weakly to $f$ in $L^{p}(\mathbb{R})$ when $p<+\infty$. Does the convergence have to be strong?

  comment

• Paper 3, Section II, F

  Analysis of Functions | Part II, 2017

  Denote by $C_{0}\left(\mathbb{R}^{n}\right)$ the space of continuous complex-valued functions on $\mathbb{R}^{n}$ converging to zero at infinity. Denote by $\mathcal{F} f(\xi)=\int_{\mathbb{R}^{n}} e^{-2 i \pi x \cdot \xi} f(x) d x$ the Fourier transform of $f \in L^{1}\left(\mathbb{R}^{n}\right)$.

  (i) Prove that the image of $L^{1}\left(\mathbb{R}^{n}\right)$ under $\mathcal{F}$ is included and dense in $C_{0}\left(\mathbb{R}^{n}\right)$, and that $\mathcal{F}: L^{1}\left(\mathbb{R}^{n}\right) \rightarrow C_{0}\left(\mathbb{R}^{n}\right)$ is injective. [Fourier inversion can be used without proof when properly stated.]

  (ii) Calculate the Fourier transform of $\chi_{[a, b]}$, the characteristic function of $[a, b] \subset \mathbb{R}$.

  (iii) Prove that $g_{n}:=\chi_{[-n, n]} * \chi_{[-1,1]}$ belongs to $C_{0}(\mathbb{R})$ and is the Fourier transform of a function $h_{n} \in L^{1}(\mathbb{R})$, which you should determine.

  (iv) Using the functions $h_{n}, g_{n}$ and the open mapping theorem, deduce that the Fourier transform is not surjective from $L^{1}(\mathbb{R})$ to $C_{0}(\mathbb{R})$.

  comment

• Paper 4, Section II, $22 F$

  Analysis of Functions | Part II, 2017

  Consider $\mathbb{R}^{n}$ with the Lebesgue measure. Denote by $\mathcal{F} f(\xi)=\int_{\mathbb{R}^{n}} e^{-2 i \pi x \cdot \xi} f(x) d x$ the Fourier transform of $f \in L^{1}\left(\mathbb{R}^{n}\right)$ and by $\hat{f}$ the Fourier-Plancherel transform of $f \in L^{2}\left(\mathbb{R}^{n}\right)$. Let $\chi_{R}(\xi):=\left(1-\frac{|\xi|}{R}\right) \chi_{|\xi| \leqslant R}$ for $R>0$ and define for $s \in \mathbb{R}_{+}$

  $$H^{s}\left(\mathbb{R}^{n}\right):=\left\{f \in L^{2}\left(\mathbb{R}^{n}\right) \mid\left(1+|\cdot|^{2}\right)^{s / 2} \hat{f}(\cdot) \in L^{2}\left(\mathbb{R}^{n}\right)\right\}$$

  (i) Prove that $H^{s}\left(\mathbb{R}^{n}\right)$ is a vector subspace of $L^{2}\left(\mathbb{R}^{n}\right)$, and is a Hilbert space for the inner product $\langle f, g\rangle:=\int_{\mathbb{R}^{n}}\left(1+|\xi|^{2}\right)^{s} \hat{f}(\xi) \overline{\hat{g}(\xi)} d \xi$, where $\bar{z}$ denotes the complex conjugate of $z \in \mathbb{C}$.

  (ii) Construct a function $f \in H^{s}(\mathbb{R}), s \in(0,1 / 2)$, that is not almost everywhere equal to a continuous function.

  (iii) For $f \in L^{1}\left(\mathbb{R}^{n}\right)$, prove that $F_{R}: x \mapsto \int_{\mathbb{R}^{n}} \mathcal{F} f(\xi) \chi_{R}(\xi) e^{2 i \pi x \cdot \xi} d \xi$ is a well-defined function and that $F_{R} \in L^{1}\left(\mathbb{R}^{n}\right)$ converges to $f$ in $L^{1}\left(\mathbb{R}^{n}\right)$ as $R \rightarrow+\infty$.

  [Hint: Prove that $F_{R}=K_{R} * f$ where $K_{R}$ is an approximation of the unit as $R \rightarrow+\infty .]$

  (iv) Deduce that if $f \in L^{1}\left(\mathbb{R}^{n}\right)$ and $\left(1+|\cdot|^{2}\right)^{s / 2} \mathcal{F} f(\cdot) \in L^{2}\left(\mathbb{R}^{n}\right)$ then $f \in H^{s}\left(\mathbb{R}^{n}\right)$.

  [Hint: Prove that: (1) there is a sequence $R_{k} \rightarrow+\infty$ such that $K_{R_{k}} * f$ converges to $f$ almost everywhere; (2) $K_{R} * f$ is uniformly bounded in $L^{2}\left(\mathbb{R}^{n}\right)$ as $R \rightarrow+\infty$.]

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  A one-dimensional lattice has $N$ sites with lattice spacing $a$. In the tight-binding approximation, the Hamiltonian describing a single electron is given by

  $$H=E_{0} \sum_{n}|n\rangle\langle n|-J \sum_{n}(|n\rangle\langle n+1|+| n+1\rangle\langle n|)$$

  where $|n\rangle$ is the normalised state of the electron localised on the $n^{\text {th }}$lattice site. Using periodic boundary conditions $|N+1\rangle \equiv|1\rangle$, solve for the spectrum of this Hamiltonian to derive the dispersion relation

  $$E(k)=E_{0}-2 J \cos (k a)$$

  Define the Brillouin zone. Determine the number of states in the Brillouin zone.

  Calculate the velocity $v$ and effective mass $m^{\star}$ of the particle. For which values of $k$ is the effective mass negative?

  In the semi-classical approximation, derive an expression for the time-dependence of the position of the electron in a constant electric field.

  Describe how the concepts of metals and insulators arise in the model above.

  comment

• Paper 2, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  Give an account of the variational method for establishing an upper bound on the ground-state energy of a Hamiltonian $H$ with a discrete spectrum $H|n\rangle=E_{n}|n\rangle$, where $E_{n} \leqslant E_{n+1}, n=0,1,2 \ldots$

  A particle of mass $m$ moves in the three-dimensional potential

  $$V(r)=-\frac{A e^{-\mu r}}{r}$$

  where $A, \mu>0$ are constants and $r$ is the distance to the origin. Using the normalised variational wavefunction

  $$\psi(r)=\sqrt{\frac{\alpha^{3}}{\pi}} e^{-\alpha r}$$

  show that the expected energy is given by

  $$E(\alpha)=\frac{\hbar^{2} \alpha^{2}}{2 m}-\frac{4 A \alpha^{3}}{(\mu+2 \alpha)^{2}}$$

  Explain why there is necessarily a bound state when $\mu<A m / \hbar^{2}$. What can you say about the existence of a bound state when $\mu \geqslant A m / \hbar^{2}$ ?

  [Hint: The Laplacian in spherical polar coordinates is

  $$\left.\nabla^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \phi^{2}}\right]$$

  comment

• Paper 3, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  A particle of mass $m$ and charge $q$ moving in a uniform magnetic field $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}=$ $(0,0, B)$ is described by the Hamiltonian

  $$H=\frac{1}{2 m}(\mathbf{p}-q \mathbf{A})^{2}$$

  where $\mathbf{p}$ is the canonical momentum, which obeys $\left[x_{i}, p_{j}\right]=i \hbar \delta_{i j}$. The mechanical momentum is defined as $\boldsymbol{\pi}=\mathbf{p}-q \mathbf{A}$. Show that

  $$\left[\pi_{x}, \pi_{y}\right]=i q \hbar B$$

  Define

  $$a=\frac{1}{\sqrt{2 q \hbar B}}\left(\pi_{x}+i \pi_{y}\right) \quad \text { and } \quad a^{\dagger}=\frac{1}{\sqrt{2 q \hbar B}}\left(\pi_{x}-i \pi_{y}\right) \text {. }$$

  Derive the commutation relation obeyed by $a$ and $a^{\dagger}$. Write the Hamiltonian in terms of $a$ and $a^{\dagger}$ and hence solve for the spectrum.

  In symmetric gauge, states in the lowest Landau level with $k_{z}=0$ have wavefunctions

  $$\psi(x, y)=(x+i y)^{M} e^{-q B r^{2} / 4 \hbar}$$

  where $r^{2}=x^{2}+y^{2}$ and $M$ is a positive integer. By considering the profiles of these wavefunctions, estimate how many lowest Landau level states can fit in a disc of radius $R$.

  comment

• Paper 4, Section II, C

  Applications of Quantum Mechanics | Part II, 2017

  (a) In one dimension, a particle of mass $m$ is scattered by a potential $V(x)$ where $V(x) \rightarrow 0$ as $|x| \rightarrow \infty$. For wavenumber $k>0$, the incoming $(\mathcal{I})$ and outgoing $(\mathcal{O})$ asymptotic plane wave states with positive $(+)$ and negative $(-)$ parity are given by

  $$\begin{array}{rr} \mathcal{I}_{+}(x)=e^{-i k|x|}, & \mathcal{I}_{-}(x)=\operatorname{sign}(x) e^{-i k|x|} \\ \mathcal{O}_{+}(x)=e^{+i k|x|}, & \mathcal{O}_{-}(x)=-\operatorname{sign}(x) e^{+i k|x|} \end{array}$$

  (i) Explain how this basis may be used to define the $S$-matrix,

  $$\mathcal{S}^{P}=\left(\begin{array}{cc} S_{++} & S_{+-} \\ S_{-+} & S_{--} \end{array}\right)$$

  (ii) For what choice of potential would you expect $S_{+-}=S_{-+}=0$ ? Why?

  (b) The potential $V(x)$ is given by

  $$V(x)=V_{0}[\delta(x-a)+\delta(x+a)]$$

  with $V_{0}$ a constant.

  (i) Show that

  $$S_{--}(k)=e^{-2 i k a}\left[\frac{\left(2 k-i U_{0}\right) e^{i k a}+i U_{0} e^{-i k a}}{\left(2 k+i U_{0}\right) e^{-i k a}-i U_{0} e^{i k a}}\right]$$

  where $U_{0}=2 m V_{0} / \hbar^{2}$. Verify that $\left|S_{--}\right|^{2}=1$. Explain the physical meaning of this result.

  (ii) For $V_{0}<0$, by considering the poles or zeros of $S_{--}(k)$, show that there exists one bound state of negative parity if $a U_{0}<-1$.

  (iii) For $V_{0}>0$ and $a U_{0} \gg 1$, show that $S_{--}(k)$ has a pole at

  $$k a=\pi+\alpha-i \gamma$$

  where $\alpha$ and $\gamma$ are real and

  $$\alpha=-\frac{\pi}{a U_{0}}+O\left(\frac{1}{\left(a U_{0}\right)^{2}}\right) \quad \text { and } \quad \gamma=\left(\frac{\pi}{a U_{0}}\right)^{2}+O\left(\frac{1}{\left(a U_{0}\right)^{3}}\right)$$

  Explain the physical significance of this result.

  comment

Applied Probability

• Paper 1, Section II, $27 \mathrm{~K}$

  Applied Probability | Part II, 2017

  (a) Define a continuous time Markov chain $X$ with infinitesimal generator $Q$ and jump chain $Y$.

  (b) Let $i$ be a transient state of a continuous-time Markov chain $X$ with $X(0)=i$. Show that the time spent in state $i$ has an exponential distribution and explicitly state its parameter.

  [You may use the fact that if $S \sim \operatorname{Exp}(\lambda)$, then $\mathbb{E}\left[e^{\theta S}\right]=\lambda /(\lambda-\theta)$ for $\theta<\lambda$.]

  (c) Let $X$ be an asymmetric random walk in continuous time on the non-negative integers with reflection at 0 , so that

  $$q_{i, j}= \begin{cases}\lambda & \text { if } \quad j=i+1, i \geqslant 0 \\ \mu & \text { if } \quad j=i-1, i \geqslant 1\end{cases}$$

  Suppose that $X(0)=0$ and $\lambda>\mu$. Show that for all $r \geqslant 1$, the total time $T_{r}$ spent in state $r$ is exponentially distributed with parameter $\lambda-\mu$.

  Assume now that $X(0)$ has some general distribution with probability generating function $G$. Find the expected amount of time spent at 0 in terms of $G$.

  comment

• Paper 2, Section II, K

  Applied Probability | Part II, 2017

  (a) Give the definition of a Poisson process on $\mathbb{R}_{+}$. Let $X$ be a Poisson process on $\mathbb{R}_{+}$. Show that conditional on $\left\{X_{t}=n\right\}$, the jump times $J_{1}, \ldots, J_{n}$ have joint density function

  $$f\left(t_{1}, \ldots, t_{n}\right)=\frac{n !}{t^{n}} \mathbf{1}\left(0 \leqslant t_{1} \leqslant \ldots \leqslant t_{n} \leqslant t\right)$$

  where $\boldsymbol{I}(A)$ is the indicator of the set $A$.

  (b) Let $N$ be a Poisson process on $\mathbb{R}_{+}$with intensity $\lambda$ and jump times $\left\{J_{k}\right\}$. If $g: \mathbb{R}_{+} \rightarrow \mathbb{R}$ is a real function, we define for all $t>0$

  $$\mathcal{R}(g)[0, t]=\left\{g\left(J_{k}\right): k \in \mathbb{N}, J_{k} \leqslant t\right\}$$

  Show that for all $t>0$ the following is true

  $$\mathbb{P}(0 \in \mathcal{R}(g)[0, t])=1-\exp \left(-\lambda \int_{0}^{t} \mathbf{I}(g(s)=0) d s\right)$$

  comment

• Paper 3, Section II, K

  Applied Probability | Part II, 2017

  (a) Define the Moran model and Kingman's $n$-coalescent. Define Kingman's infinite coalescent.

  Show that Kingman's infinite coalescent comes down from infinity. In other words, with probability one, the number of blocks of $\Pi_{t}$ is finite at any time $t>0$.

  (b) Give the definition of a renewal process.

  Let $\left(X_{i}\right)$ denote the sequence of inter-arrival times of the renewal process $N$. Suppose that $\mathbb{E}\left[X_{1}\right]>0$.

  Prove that $\mathbb{P}(N(t) \rightarrow \infty$ as $t \rightarrow \infty)=1$.

  Prove that $\mathbb{E}\left[e^{\theta N(t)}\right]<\infty$ for some strictly positive $\theta$.

  [Hint: Consider the renewal process with inter-arrival times $X_{k}^{\prime}=\varepsilon \mathbf{1}\left(X_{k} \geqslant \varepsilon\right)$ for some suitable $\varepsilon>0$.]

  comment

• Paper 4, Section II, $26 K$

  Applied Probability | Part II, 2017

  (a) Give the definition of an $M / M / 1$ queue. Prove that if $\lambda$ is the arrival rate and $\mu$ the service rate and $\lambda<\mu$, then the length of the queue is a positive recurrent Markov chain. What is the equilibrium distribution?

  If the queue is in equilibrium and a customer arrives at some time $t$, what is the distribution of the waiting time (time spent waiting in the queue plus service time)?

  (b) We now modify the above queue: on completion of service a customer leaves with probability $\delta$, or goes to the back of the queue with probability $1-\delta$. Find the distribution of the total time a customer spends being served.

  Hence show that equilibrium is possible if $\lambda<\delta \mu$ and find the stationary distribution.

  Show that, in equilibrium, the departure process is Poisson.

  [You may use relevant theorems provided you state them clearly.]

  comment

Asymptotic Methods

• Paper 2, Section II, E

  Asymptotic Methods | Part II, 2017

  Consider the function

  $$f_{\nu}(x) \equiv \frac{1}{2 \pi} \int_{C} \exp [-i x \sin z+i \nu z] d z$$

  where the contour $C$ is the boundary of the half-strip $\{z:-\pi<\operatorname{Re} z<\pi$ and $\operatorname{Im} z>0\}$, taken anti-clockwise.

  Use integration by parts and the method of stationary phase to:

  (i) Obtain the leading term for $f_{\nu}(x)$ coming from the vertical lines $z=\pm \pi+i y(0<$ $y<+\infty)$ for large $x>0$.

  (ii) Show that the leading term in the asymptotic expansion of the function $f_{\nu}(x)$ for large positive $x$ is

  $$\sqrt{\frac{2}{\pi x}} \cos \left(x-\frac{1}{2} \nu \pi-\frac{\pi}{4}\right)$$

  and obtain an estimate for the remainder as $O\left(x^{-a}\right)$ for some $a$ to be determined.

  comment

• Paper 3, Section II, E

  Asymptotic Methods | Part II, 2017

  Consider the integral representation for the modified Bessel function

  $$I_{0}(x)=\frac{1}{2 \pi i} \oint_{C} t^{-1} \exp \left[\frac{i x}{2}\left(t-\frac{1}{t}\right)\right] d t$$

  where $C$ is a simple closed contour containing the origin, taken anti-clockwise.

  Use the method of steepest descent to determine the full asymptotic expansion of $I_{0}(x)$ for large real positive $x .$

  comment

• Paper 4, Section II, E

  Asymptotic Methods | Part II, 2017

  Consider solutions to the equation

  $$\frac{d^{2} y}{d x^{2}}=\left(\frac{1}{4}+\frac{\mu^{2}-\frac{1}{4}}{x^{2}}\right) y$$

  of the form

  $$y(x)=\exp \left[S_{0}(x)+S_{1}(x)+S_{2}(x)+\ldots\right]$$

  with the assumption that, for large positive $x$, the function $S_{j}(x)$ is small compared to $S_{j-1}(x)$ for all $j=1,2 \ldots$

  Obtain equations for the $S_{j}(x), j=0,1,2 \ldots$, which are formally equivalent to ( $)$. Solve explicitly for $S_{0}$ and $S_{1}$. Show that it is consistent to assume that $S_{j}(x)=c_{j} x^{-(j-1)}$ for some constants $c_{j}$. Give a recursion relation for the $c_{j}$.

  Deduce that there exist two linearly independent solutions to $(\star)$ with asymptotic expansions as $x \rightarrow+\infty$ of the form

  $$y_{\pm}(x) \sim e^{\pm x / 2}\left(1+\sum_{j=1}^{\infty} A_{j}^{\pm} x^{-j}\right)$$

  Determine a recursion relation for the $A_{j}^{\pm}$. Compute $A_{1}^{\pm}$and $A_{2}^{\pm}$.

  comment

Automata and Formal Languages

• Paper 1, Section I, $4 \mathrm{H}$

  Automata and Formal Languages | Part II, 2017

  (a) Prove that every regular language is also a context-free language (CFL).

  (b) Show that, for any fixed $n>0$, the set of regular expressions over the alphabet $\left\{a_{1}, \ldots, a_{n}\right\}$ is a CFL, but not a regular language.

  comment

• Paper 1, Section II, $11 H$

  Automata and Formal Languages | Part II, 2017

  (a) Give an encoding to integers of all deterministic finite-state automata (DFAs). [Here the alphabet of each such DFA is always taken from the set $\{0,1, \ldots\}$, and the states for each such DFA are always taken from the set $\left.\left\{q_{0}, q_{1}, \ldots\right\} .\right]$

  (b) Show that the set of codes for which the corresponding DFA $D_{n}$ accepts a finite language is recursive. Moreover, if the language $\mathcal{L}\left(D_{n}\right)$ is finite, show that we can compute its size $\left|\mathcal{L}\left(D_{n}\right)\right|$ from $n$.

  comment

• Paper 2, Section I, $4 \mathrm{H}$

  Automata and Formal Languages | Part II, 2017

  (a) Give explicit examples, with justification, of a language over some finite alphabet $\Sigma$ which is:

  (i) context-free, but not regular;

  (ii) recursive, but not context-free.

  (b) Give explicit examples, with justification, of a subset of $\mathbb{N}$ which is:

  (i) recursively enumerable, but not recursive;

  (ii) neither recursively enumerable, nor having recursively enumerable complement in $\mathbb{N}$.

  comment

• Paper 3, Section I, 4H

  Automata and Formal Languages | Part II, 2017

  (a) Define what it means for a context-free grammar (CFG) to be in Chomsky normal form (CNF). Give an example, with justification, of a context-free language (CFL) which is not defined by any CFG in CNF.

  (b) Show that the intersection of two CFLs need not be a CFL.

  (c) Let $L$ be a CFL over an alphabet $\Sigma$. Show that $\Sigma^{*} \backslash L$ need not be a CFL.

  comment

• Paper 3, Section II, $11 \mathrm{H}$ Automata and formal languages

  Automata and Formal Languages | Part II, 2017

  (a) Given $A, B \subseteq \mathbb{N}$, define a many-one reduction of $A$ to $B$. Show that if $B$ is recursively enumerable (r.e.) and $A \leqslant_{m} B$ then $A$ is also recursively enumerable.

  (b) State the $s-m-n$ theorem, and use it to prove that a set $X \subseteq \mathbb{N}$ is r.e. if and only if $X \leqslant_{m} \mathbb{K}$.

  (c) Consider the sets of integers $P, Q \subseteq \mathbb{N}$ defined via

  $$\begin{aligned} &P:=\left\{n \in \mathbb{N} \mid n \text { codes a program and } W_{n} \text { is finite }\right\} \\ &Q:=\left\{n \in \mathbb{N} \mid n \text { codes a program and } W_{n} \text { is recursive }\right\} \end{aligned}$$

  Show that $P \leqslant \leqslant_{m} Q$.

  comment

• Paper 4, Section I, $4 \mathrm{H}$

  Automata and Formal Languages | Part II, 2017

  (a) Describe the process for converting a deterministic finite-state automaton $D$ into a regular expression $R$ defining the same language, $\mathcal{L}(D)=\mathcal{L}(R)$. [You need only outline the steps, without proof, but you should clearly define all terminology you introduce.]

  (b) Consider the language $L$ over the alphabet $\{0,1\}$ defined via

  $$L:=\left\{w 01^{n} \mid w \in\{0,1\}^{*}, n \in \mathbb{K}\right\} \cup\{1\}^{*} .$$

  Show that $L$ satisfies the pumping lemma for regular languages but is not a regular language itself.

  comment

Classical Dynamics

• Paper 1, Section I, E

  Classical Dynamics | Part II, 2017

  Consider a Lagrangian system with Lagrangian $L\left(x_{A}, \dot{x}_{A}, t\right)$, where $A=1, \ldots, 3 N$, and constraints

  $$f_{\alpha}\left(x_{A}, t\right)=0, \quad \alpha=1, \ldots, 3 N-n .$$

  Use the method of Lagrange multipliers to show that this is equivalent to a system with Lagrangian $\mathcal{L}\left(q_{i}, \dot{q}_{i}, t\right) \equiv L\left(x_{A}\left(q_{i}, t\right), \dot{x}_{A}\left(q_{i}, \dot{q}_{i}, t\right), t\right)$, where $i=1, \ldots, n$, and $q_{i}$ are coordinates on the surface of constraints.

  Consider a bead of unit mass in $\mathbb{R}^{2}$ constrained to move (with no potential) on a wire given by an equation $y=f(x)$, where $(x, y)$ are Cartesian coordinates. Show that the Euler-Lagrange equations take the form

  $$\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial \dot{x}}=\frac{\partial \mathcal{L}}{\partial x}$$

  for some $\mathcal{L}=\mathcal{L}(x, \dot{x})$ which should be specified. Find one first integral of the EulerLagrange equations, and thus show that

  $$t=F(x)$$

  where $F(x)$ should be given in the form of an integral.

  [Hint: You may assume that the Euler-Lagrange equations hold in all coordinate systems.]

  comment

• Paper 2, Section I, E

  Classical Dynamics | Part II, 2017

  Derive the Lagrange equations from the principle of stationary action

  $$S[q]=\int_{t_{0}}^{t_{1}} \mathcal{L}\left(q_{i}(t), \dot{q}_{i}(t), t\right) d t, \quad \delta S=0$$

  where the end points $q_{i}\left(t_{0}\right)$ and $q_{i}\left(t_{1}\right)$ are fixed.

  Let $\phi$ and $\mathbf{A}$ be a scalar and a vector, respectively, depending on $\mathbf{r}=(x, y, z)$. Consider the Lagrangian

  $$\mathcal{L}=\frac{m \dot{\mathbf{r}}^{2}}{2}-(\phi-\dot{\mathbf{r}} \cdot \mathbf{A})$$

  and show that the resulting Euler-Lagrange equations are invariant under the transformations

  $$\phi \rightarrow \phi+\alpha \frac{\partial F}{\partial t}, \quad \mathbf{A} \rightarrow \mathbf{A}+\nabla F,$$

  where $F=F(\mathbf{r}, t)$ is an arbitrary function, and $\alpha$ is a constant which should be determined.

  comment

• Paper 2, Section II, E

  Classical Dynamics | Part II, 2017

  Show that an object's inertia tensor about a point displaced from the centre of mass by a vector $\mathbf{c}$ is given by

  $$\left(I_{\mathbf{c}}\right)_{a b}=\left(I_{0}\right)_{a b}+M\left(|\mathbf{c}|^{2} \delta_{a b}-c_{a} c_{b}\right),$$

  where $M$ is the total mass of the object, and $\left(I_{0}\right)_{a b}$ is the inertia tensor about the centre of mass.

  Find the inertia tensor of a cube of uniform density, with edge of length $L$, about one of its vertices.

  comment

• Paper 3, Section I, E

  Classical Dynamics | Part II, 2017

  Define an integrable system with $2 n$-dimensional phase space. Define angle-action variables.

  Consider a two-dimensional phase space with the Hamiltonian

  $$H=\frac{p^{2}}{2 m}+\frac{1}{2} q^{2 k}$$

  where $k$ is a positive integer and the mass $m=m(t)$ changes slowly in time. Use the fact that the action is an adiabatic invariant to show that the energy varies in time as $m^{c}$, where $c$ is a constant which should be found.

  comment

• Paper 4, Section I, E

  Classical Dynamics | Part II, 2017

  Consider the Poisson bracket structure on $\mathbb{R}^{3}$ given by

  $$\{x, y\}=z, \quad\{y, z\}=x, \quad\{z, x\}=y$$

  and show that $\left\{f, \rho^{2}\right\}=0$, where $\rho^{2}=x^{2}+y^{2}+z^{2}$ and $f: \mathbb{R}^{3} \rightarrow \mathbb{R}$ is any polynomial function on $\mathbb{R}^{3}$.

  Let $H=\left(A x^{2}+B y^{2}+C z^{2}\right) / 2$, where $A, B, C$ are positive constants. Find the explicit form of Hamilton's equations

  $$\dot{\mathbf{r}}=\{\mathbf{r}, H\}, \quad \text { where } \quad \mathbf{r}=(x, y, z)$$

  Find a condition on $A, B, C$ such that the oscillation described by

  $$x=1+\alpha(t), \quad y=\beta(t), \quad z=\gamma(t)$$

  is linearly unstable, where $\alpha(t), \beta(t), \gamma(t)$ are small.

  comment

• Paper 4, Section II, $14 \mathrm{E}$

  Classical Dynamics | Part II, 2017

  Explain how geodesics of a Riemannian metric

  $$g=g_{a b}\left(x^{c}\right) d x^{a} d x^{b}$$

  arise from the kinetic Lagrangian

  $$\mathcal{L}=\frac{1}{2} g_{a b}\left(x^{c}\right) \dot{x}^{a} \dot{x}^{b}$$

  where $a, b=1, \ldots, n$.

  Find geodesics of the metric on the upper half plane

  $$\Sigma=\left\{(x, y) \in \mathbb{R}^{2}, y>0\right\}$$

  with the metric

  $$g=\frac{d x^{2}+d y^{2}}{y^{2}}$$

  and sketch the geodesic containing the points $(2,3)$ and $(10,3)$.

  [Hint: Consider $d y / d x .]$

  comment

Coding and Cryptography

• Paper 1, Section I, G

  Coding and Cryptography | Part II, 2017

  Let $C$ be a binary code of length $n$. Define the following decoding rules: (i) ideal observer, (ii) maximum likelihood, (iii) minimum distance.

  Let $p$ denote the probability that a digit is mistransmitted and suppose $p<1 / 2$. Prove that maximum likelihood and minimum distance decoding agree.

  Suppose codewords 000 and 111 are sent with probabilities $4 / 5$ and $1 / 5$ respectively with error probability $p=1 / 4$. If we receive 110 , how should it be decoded according to the three decoding rules above?

  comment

• Paper 1, Section II, G

  Coding and Cryptography | Part II, 2017

  Let $C$ be a binary linear code. Explain what it means for $C$ to have length $n$ and $\operatorname{rank} k$. Explain what it means for a codeword of $C$ to have weight $j$.

  Suppose $C$ has length $n$, rank $k$, and $A_{j}$ codewords of weight $j$. The weight enumerator polynomial of $C$ is given by

  $$W_{C}(s, t)=\sum_{j=0}^{n} A_{j} s^{j} t^{n-j}$$

  What is $W_{C}(1,1) ?$ Prove that $W_{C}(s, t)=W_{C}(t, s)$ if and only if $W_{C}(1,0)=1$.

  Define the dual code $C^{\perp}$ of $C$.

  (i) Let $\mathbf{y} \in \mathbb{F}_{2}^{n}$. Show that

  $$\sum_{\mathbf{x} \in C}(-1)^{\mathbf{x} \cdot \mathbf{y}}= \begin{cases}2^{k}, & \text { if } \mathbf{y} \in C^{\perp} \\ 0, & \text { otherwise }\end{cases}$$

  (ii) Extend the definition of weight to give a weight $w(\mathbf{y})$ for $\mathbf{y} \in \mathbb{F}_{2}^{n}$. Suppose that for $t$ real and all $\mathbf{x} \in C$

  $$\sum_{\mathbf{y} \in \mathbb{F}_{2}^{n}} t^{w(\mathbf{y})}(-1)^{\mathbf{x} \cdot \mathbf{y}}=(1-t)^{w(\mathbf{x})}(1+t)^{n-w(\mathbf{x})}$$

  For $s$ real, by evaluating

  $$\sum_{\mathbf{x} \in C}\left(\sum_{\mathbf{y} \in \mathbb{F}_{2}^{n}}(-1)^{\mathbf{x} \cdot \mathbf{y}}\left(\frac{s}{t}\right)^{w(\mathbf{y})}\right)$$

  in two different ways, show that

  $$W_{C^{\perp}}(s, t)=2^{-k} W_{C}(t-s, t+s) .$$

  comment

• Paper 2, Section I, G

  Coding and Cryptography | Part II, 2017

  Prove that a decipherable code with prescribed word lengths exists if and only if there is a prefix-free code with the same word lengths.

  comment

• Paper 2, Section II, G

  Coding and Cryptography | Part II, 2017

  Define the entropy, $H(X)$, of a random variable $X$. State and prove Gibbs' inequality.

  Hence, or otherwise, show that $H\left(p_{1}, p_{2}, p_{3}\right) \leqslant H\left(p_{1}, 1-p_{1}\right)+\left(1-p_{1}\right)$ and determine when equality occurs.

  Show that the Discrete Memoryless Channel with channel matrix

  $$\left(\begin{array}{ccc} 1-\alpha-\beta & \alpha & \beta \\ \alpha & 1-\alpha-\beta & \beta \end{array}\right)$$

  has capacity $C=(1-\beta)(1-\log (1-\beta))+(1-\alpha-\beta) \log (1-\alpha-\beta)+\alpha \log \alpha$.

  comment

• Paper 3, Section I, G

  Coding and Cryptography | Part II, 2017

  Find and describe all binary cyclic codes of length 7 . Pair each code with its dual code. Justify your answer.

  comment

• Paper 4, Section I, G

  Coding and Cryptography | Part II, 2017

  Describe the RSA system with public key $(N, e)$ and private key $d$.

  Give a simple example of how the system is vulnerable to a homomorphism attack.

  Describe the El-Gamal signature scheme and explain how this can defeat a homomorphism attack.

  comment

Cosmology

• Paper 1, Section I, C

  Cosmology | Part II, 2017

  In a homogeneous and isotropic universe, describe the relative displacement $\mathbf{r}(t)$ of two galaxies in terms of a scale factor $a(t)$. Show how the relative velocity $\mathbf{v}(t)$ of these galaxies is given by the relation $\mathbf{v}(t)=H(t) \mathbf{r}(t)$, where you should specify $H(t)$ in terms of $a(t)$.

  From special relativity, the Doppler shift of light emitted by a particle moving away radially with speed $v$ can be approximated by

  $$\frac{\lambda_{0}}{\lambda_{\mathrm{e}}}=\sqrt{\frac{1+v / c}{1-v / c}}=1+\frac{v}{c}+\mathcal{O}\left(\frac{v^{2}}{c^{2}}\right)$$

  where $\lambda_{e}$ is the wavelength of emitted light and $\lambda_{0}$ is the observed wavelength. For the observed light from distant galaxies in a homogeneous and isotropic expanding universe, show that the redshift defined by $1+z \equiv \lambda_{0} / \lambda_{\mathrm{e}}$ is given by

  $$1+z=\frac{a\left(t_{0}\right)}{a\left(t_{\mathrm{e}}\right)}$$

  where $t_{\mathrm{e}}$ is the time of emission and $t_{0}$ is the observation time.

  comment

• Paper 1, Section II, C

  Cosmology | Part II, 2017

  The evolution of a flat $(k=0)$ homogeneous and isotropic universe with scale factor $a(t)$, mass density $\rho(t)$ and pressure $P(t)$ obeys the Friedmann and energy conservation equations

  $$\begin{array}{r} H^{2}(t)=\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho+\frac{\Lambda c^{2}}{3} \\ \dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+P / c^{2}\right) \end{array}$$

  where $H(t)$ is the Hubble parameter (observed today $t=t_{0}$ with value $H_{0}=H\left(t_{0}\right)$ ) and $\Lambda>0$ is the cosmological constant.

  Use these two equations to derive the acceleration equation

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)+\frac{\Lambda c^{2}}{3}$$

  For pressure-free matter $\left(\rho=\rho_{\mathrm{M}}\right.$ and $\left.P_{\mathrm{M}}=0\right)$, solve the energy conservation equation to show that the Friedmann and acceleration equations can be re-expressed as

  $$\begin{gathered} H=H_{0} \sqrt{\frac{\Omega_{\mathrm{M}}}{a^{3}}+\Omega_{\Lambda}} \\ \frac{\ddot{a}}{a}=-\frac{H_{0}^{2}}{2}\left[\frac{\Omega_{\mathrm{M}}}{a^{3}}-2 \Omega_{\Lambda}\right] \end{gathered}$$

  where we have taken $a\left(t_{0}\right)=1$ and we have defined the relative densities today $\left(t=t_{0}\right)$ as

  $$\Omega_{\mathrm{M}}=\frac{8 \pi G}{3 H_{0}^{2}} \rho_{\mathrm{M}}\left(t_{0}\right) \quad \text { and } \quad \Omega_{\Lambda}=\frac{\Lambda c^{2}}{3 H_{0}^{2}}$$

  Solve the Friedmann equation and show that the scale factor can be expressed as

  $$a(t)=\left(\frac{\Omega_{\mathrm{M}}}{\Omega_{\Lambda}}\right)^{1 / 3} \sinh ^{2 / 3}\left(\frac{3}{2} \sqrt{\Omega_{\Lambda}} H_{0} t\right)$$

  Find an expression for the time $\bar{t}$ at which the matter density $\rho_{\mathrm{M}}$ and the effective density caused by the cosmological constant $\Lambda$ are equal. (You need not evaluate this explicitly.)

  comment

• Paper 2, Section I, C

  Cosmology | Part II, 2017

  In a homogeneous and isotropic universe $(\Lambda=0)$, the acceleration equation for the scale factor $a(t)$ is given by

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right),$$

  where $\rho(t)$ is the mass density and $P(t)$ is the pressure.

  If the matter content of the universe obeys the strong energy condition $\rho+3 P / c^{2} \geqslant 0$, show that the acceleration equation can be rewritten as $\dot{H}+H^{2} \leqslant 0$, with Hubble parameter $H(t)=\dot{a} / a$. Show that

  $$H \geqslant \frac{1}{H_{0}^{-1}+t-t_{0}}$$

  where $H_{0}=H\left(t_{0}\right)$ is the measured value today at $t=t_{0}$. Hence, or otherwise, show that

  $$a(t) \leqslant 1+H_{0}\left(t-t_{0}\right)$$

  Use this inequality to find an upper bound on the age of the universe.

  comment

• Paper 3, Section I, C

  Cosmology | Part II, 2017

  (a) In the early universe electrons, protons and neutral hydrogen are in thermal equilibrium and interact via,

  $$e^{-}+p^{+} \leftrightharpoons H+\gamma$$

  The non-relativistic number density of particles in thermal equlibrium is

  $$n_{i}=g_{i}\left(\frac{2 \pi m_{i} k T}{h^{2}}\right)^{\frac{3}{2}} \exp \left(\frac{\mu_{i}-m_{i} c^{2}}{k T}\right)$$

  where, for each species $i, g_{i}$ is the number of degrees of freedom, $m_{i}$ is its mass, and $\mu_{i}$ is its chemical potential. [You may assume $g_{e}=g_{p}=2$ and $g_{H}=4$.]

  Stating any assumptions required, use these expressions to derive the Saha equation which governs the relative abundances of electrons, protons and hydrogen,

  $$\frac{n_{e} n_{p}}{n_{H}}=\left(\frac{2 \pi m_{e} k T}{h^{2}}\right)^{\frac{3}{2}} \exp \left(-\frac{I}{k T}\right)$$

  where $I$ is the binding energy of hydrogen, which should be defined.

  (b) Naively, we might expect that the majority of electrons and protons combine to form neutral hydrogen once the temperature drops below the binding energy, i.e. $k T \lesssim I$. In fact recombination does not happen until a much lower temperature, when $k T \approx 0.03 I$. Briefly explain why this is.

  [Hint: It may help to consider the relative abundances of particles in the early universe.]

  comment

• Paper 3, Section II, C

  Cosmology | Part II, 2017

  (a) The scalar moment of inertia for a system of $N$ particles is given by

  $$I=\sum_{i=1}^{N} m_{i} \mathbf{r}_{i} \cdot \mathbf{r}_{i}$$

  where $m_{i}$ is the particle's mass and $\mathbf{r}_{i}$ is a vector giving the particle's position. Show that, for non-relativistic particles,

  $$\frac{1}{2} \frac{d^{2} I}{d t^{2}}=2 K+\sum_{i=1}^{N} \mathbf{F}_{i} \cdot \mathbf{r}_{i}$$

  where $K$ is the total kinetic energy of the system and $\mathbf{F}_{i}$ is the total force on particle

  Assume that any two particles $i$ and $j$ interact gravitationally with potential energy

  $$V_{i j}=-\frac{G m_{i} m_{j}}{\left|\mathbf{r}_{i}-\mathbf{r}_{j}\right|}$$

  Show that

  $$\sum_{i=1}^{N} \mathbf{F}_{i} \cdot \mathbf{r}_{i}=V$$

  where $V$ is the total potential energy of the system. Use the above to prove the virial theorem.

  (b) Consider an approximately spherical overdensity of stationary non-interacting massive particles with initial constant density $\rho_{i}$ and initial radius $R_{i}$. Assuming the system evolves until it reaches a stable virial equilibrium, what will the final $\rho$ and $R$ be in terms of their initial values? Would this virial solution be stable if our particles were baryonic rather than non-interacting? Explain your answer.

  comment

• Paper 4, Section I, C

  Cosmology | Part II, 2017

  (a) By considering a spherically symmetric star in hydrostatic equilibrium derive the pressure support equation

  $$\frac{d P}{d r}=-\frac{G M(r) \rho}{r^{2}},$$

  where $r$ is the radial distance from the centre of the star, $M(r)$ is the stellar mass contained inside that radius, and $P(r)$ and $\rho(r)$ are the pressure and density at radius $r$ respectively.

  (b) Propose, and briefly justify, boundary conditions for this differential equation, both at the centre of the star $r=0$, and at the stellar surface $r=R$.

  Suppose that $P=K \rho^{2}$ for some $K>0$. Show that the density satisfies the linear differential equation

  $$\frac{1}{x^{2}} \frac{\partial}{\partial x}\left(x^{2} \frac{\partial \rho}{\partial x}\right)=-\rho$$

  where $x=\alpha r$, for some constant $\alpha$, is a rescaled radial coordinate. Find $\alpha$.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2017

  Define what it means for a subset $X \subset \mathbb{R}^{N}$ to be a manifold.

  For manifolds $X$ and $Y$, state what it means for a map $f: X \rightarrow Y$ to be smooth. For such a smooth map, and $x \in X$, define the differential map $d f_{x}$.

  What does it mean for $y \in Y$ to be a regular value of $f$ ? Give an example of a map $f: X \rightarrow Y$ and a $y \in Y$ which is not a regular value of $f$.

  Show that the set $S L_{n}(\mathbb{R})$ of $n \times n$ real-valued matrices with determinant 1 can naturally be viewed as a manifold $S L_{n}(\mathbb{R}) \subset \mathbb{R}^{n^{2}}$. What is its dimension? Show that matrix multiplication $f: S L_{n}(\mathbb{R}) \times S L_{n}(\mathbb{R}) \rightarrow S L_{n}(\mathbb{R})$, defined by $f(A, B)=A B$, is smooth. [Standard theorems may be used without proof if carefully stated.] Describe the tangent space of $S L_{n}(\mathbb{R})$ at the identity $I \in S L_{n}(\mathbb{R})$ as a subspace of $\mathbb{R}^{n^{2}}$.

  Show that if $n \geqslant 2$ then the set of real-valued matrices with determinant 0 , viewed as a subset of $\mathbb{R}^{n^{2}}$, is not a manifold.

  comment

• Paper 2, Section II, I

  Differential Geometry | Part II, 2017

  Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a regular smooth curve. Define the curvature $k$ and torsion $\tau$ of $\alpha$ and derive the Frenet formulae. Give the assumption which must hold for torsion to be well-defined, and state the Fundamental Theorem for curves in $\mathbb{R}^{3}$.

  Let $\alpha$ be as above and $\tilde{\alpha}: I \rightarrow \mathbb{R}^{3}$ be another regular smooth curve with curvature $\tilde{k}$ and torsion $\tilde{\tau}$. Suppose $\tilde{k}(s)=k(s) \neq 0$ and $\tilde{\tau}(s)=\tau(s)$ for all $s \in I$, and that there exists a non-empty open subinterval $J \subset I$ such that $\left.\tilde{\alpha}\right|_{J}=\left.\alpha\right|_{J}$. Show that $\tilde{\alpha}=\alpha$.

  Now let $S \subset \mathbb{R}^{3}$ be an oriented surface and let $\alpha: I \rightarrow S \subset \mathbb{R}^{3}$ be a regular smooth curve contained in $S$. Define normal curvature and geodesic curvature. When is $\alpha$ a geodesic? Give an example of a surface $S$ and a geodesic $\alpha$ whose normal curvature vanishes identically. Must such a surface $S$ contain a piece of a plane? Can such a geodesic be a simple closed curve? Justify your answers.

  Show that if $\alpha$ is a geodesic and the Gaussian curvature of $S$ satisfies $K \geqslant 0$, then we have the inequality $k(s) \leqslant 2|H(\alpha(s))|$, where $H$ denotes the mean curvature of $S$ and $k$ the curvature of $\alpha$. Give an example where this inequality is sharp.

  comment

• Paper 3, Section II, I

  Differential Geometry | Part II, 2017

  Let $S \subset \mathbb{R}^{N}$ be a manifold and let $\alpha:[a, b] \rightarrow S \subset \mathbb{R}^{N}$ be a smooth regular curve on $S$. Define the total length $L(\alpha)$ and the arc length parameter $s$. Show that $\alpha$ can be reparametrized by arc length.

  Let $S \subset \mathbb{R}^{3}$ denote a regular surface, let $p, q \in S$ be distinct points and let $\alpha:[a, b] \rightarrow S$ be a smooth regular curve such that $\alpha(a)=p, \alpha(b)=q$. We say that $\alpha$ is length minimising if for all smooth regular curves $\tilde{\alpha}:[a, b] \rightarrow S$ with $\tilde{\alpha}(a)=p, \tilde{\alpha}(b)=q$, we have $L(\tilde{\alpha}) \geqslant L(\alpha)$. By deriving a formula for the derivative of the energy functional corresponding to a variation of $\alpha$, show that a length minimising curve is necessarily a geodesic. [You may use the following fact: given a smooth vector field $V(t)$ along $\alpha$ with $V(a)=V(b)=0$, there exists a variation $\alpha(s, t)$ of $\alpha$ such that $\left.\left.\partial_{s} \alpha(s, t)\right|_{s=0}=V(t) .\right]$

  Let $\mathbb{S}^{2} \subset \mathbb{R}^{3}$ denote the unit sphere and let $S$ denote the surface $\mathbb{S}^{2} \backslash(0,0,1)$. For which pairs of points $p, q \in S$ does there exist a length minimising smooth regular curve $\alpha:[a, b] \rightarrow S$ with $\alpha(a)=p$ and $\alpha(b)=q$ ? Justify your answer.

  comment

• Paper 4, Section II, I

  Differential Geometry | Part II, 2017

  Let $S \subset \mathbb{R}^{3}$ be a surface and $p \in S$. Define the exponential map exp $p$ and compute its differential $\left.d \exp _{p}\right|_{0}$. Deduce that $\exp _{p}$ is a local diffeomorphism.

  Give an example of a surface $S$ and a point $p \in S$ for which the exponential map $\exp _{p}$ fails to be defined globally on $T_{p} S$. Can this failure be remedied by extending the surface? In other words, for any such $S$, is there always a surface $S \subset \widehat{S} \subset \mathbb{R}^{3}$ such that the exponential map $\widehat{\exp }_{p}$ defined with respect to $\widehat{S}$is globally defined on $T_{p} S=T_{p} \widehat{S}$?

  State the version of the Gauss-Bonnet theorem with boundary term for a surface $S \subset \mathbb{R}^{3}$ and a closed disc $D \subset S$ whose boundary $\partial D$ can be parametrized as a smooth closed curve in $S$.

  Let $S \subset \mathbb{R}^{3}$ be a flat surface, i.e. $K=0$. Can there exist a closed disc $D \subset S$, whose boundary $\partial D$ can be parametrized as a smooth closed curve, and a surface $\tilde{S} \subset \mathbb{R}^{3}$ such that all of the following hold:

  (i) $(S \backslash D) \cup \partial D \subset \tilde{S}$;

  (ii) letting $\tilde{D}$ be $(\tilde{S} \backslash(S \backslash D)) \cup \partial D$, we have that $\tilde{D}$ is a closed disc in $\tilde{S}$ with boundary $\partial \tilde{D}=\partial D$

  (iii) the Gaussian curvature $\tilde{K}$ of $\tilde{S}$ satisfies $\tilde{K} \geqslant 0$, and there exists a $p \in \tilde{S}$ such that $\tilde{K}(p)>0$ ?

  Justify your answer.

  comment

Dynamical Systems

• Paper 1, Section II, A

  Dynamical Systems | Part II, 2017

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=-x+x^{3}+\beta x y^{2} \\ &\dot{y}=-y+\beta x^{2} y+y^{3} \end{aligned}$$

  where $\beta>-1$ is a constant.

  (a) Find the fixed points of the system, and classify them for $\beta \neq 1$.

  Sketch the phase plane for each of the cases (i) $\beta=\frac{1}{2}$ (ii) $\beta=2$ and (iii) $\beta=1$.

  (b) Given $\beta>2$, show that the domain of stability of the origin includes the union over $k \in \mathbb{R}$ of the regions

  $$x^{2}+k^{2} y^{2}<\frac{4 k^{2}\left(1+k^{2}\right)(\beta-1)}{\beta^{2}\left(1+k^{2}\right)^{2}-4 k^{2}} .$$

  By considering $k \gg 1$, or otherwise, show that more information is obtained from the union over $k$ than considering only the case $k=1$.

  $\left[\right.$ Hint: If $B>A, C$ then $\left.\max _{u \in[0,1]}\left\{A u^{2}+2 B u(1-u)+C(1-u)^{2}\right\}=\frac{B^{2}-A C}{2 B-A-C} \cdot\right]$

  comment

• Paper 2, Section II, A

  Dynamical Systems | Part II, 2017

  (a) State Liapunov's first theorem and La Salle's invariance principle. Use these results to show that the fixed point at the origin of the system

  $$\ddot{x}+k \dot{x}+\sin ^{3} x=0, \quad k>0,$$

  is asymptotically stable.

  (b) State the Poincaré-Bendixson theorem. Show that the forced damped pendulum

  $$\dot{\theta}=p, \quad \dot{p}=-k p-\sin \theta+F, \quad k>0,$$

  with $F>1$, has a periodic orbit that encircles the cylindrical phase space $(\theta, p) \in \mathbb{R}[\bmod 2 \pi] \times \mathbb{R}$, and that it is unique.

  [You may assume that the Poincaré-Bendixson theorem also holds on a cylinder, and comment, without proof, on the use of any other standard results.]

  (c) Now consider $(*)$ for $F, k=O(\epsilon)$, where $\epsilon \ll 1$. Use the energy-balance method to show that there is a homoclinic orbit in $p \geqslant 0$ if $F=F_{h}(k)$, where $F_{h} \approx 4 k / \pi>0$.

  Explain briefly why there is no homoclinic orbit in $p \leqslant 0$ for $F>0$.

  comment

• Paper 3, Section II, A

  Dynamical Systems | Part II, 2017

  State, without proof, the centre manifold theorem. Show that the fixed point at the origin of the system

  $$\begin{aligned} &\dot{x}=y-x+a x^{3} \\ &\dot{y}=r x-y-y z \\ &\dot{z}=x y-z \end{aligned}$$

  where $a \neq 1$ is a constant, is nonhyperbolic at $r=1$. What are the dimensions of the linear stable and (non-extended) centre subspaces at this point?

  Make the substitutions $2 u=x+y, 2 v=x-y$ and $\mu=r-1$ and derive the resultant equations for $\dot{u}, \dot{v}$ and $\dot{z}$.

  The extended centre manifold is given by

  $$v=V(u, \mu), \quad z=Z(u, \mu),$$

  where $V$ and $Z$ can be expanded as power series about $u=\mu=0$. What is known about $V$ and $Z$ from the centre manifold theorem? Assuming that $\mu=O\left(u^{2}\right)$, determine $Z$ to $O\left(u^{2}\right)$ and $V$ to $O\left(u^{3}\right)$. Hence obtain the evolution equation on the centre manifold correct to $O\left(u^{3}\right)$, and identify the type of bifurcation distinguishing between the cases $a>1$ and $a<1$.

  If now $a=1$, assume that $\mu=O\left(u^{4}\right)$ and extend your calculations of $Z$ to $O\left(u^{4}\right)$ and of the dynamics on the centre manifold to $O\left(u^{5}\right)$. Hence sketch the bifurcation diagram in the neighbourhood of $u=\mu=0$.

  comment

• Paper 4, Section II, A

  Dynamical Systems | Part II, 2017

  Consider the one-dimensional map $F: \mathbb{R} \rightarrow \mathbb{R}$ defined by

  $$x_{i+1}=F\left(x_{i} ; \mu\right)=x_{i}\left(a x_{i}^{2}+b x_{i}+\mu\right),$$

  where $a$ and $b$ are constants, $\mu$ is a parameter and $a \neq 0$.

  (a) Find the fixed points of $F$ and determine the linear stability of $x=0$. Hence show that there are bifurcations at $\mu=1$, at $\mu=-1$ and, if $b \neq 0$, at $\mu=1+b^{2} /(4 a)$.

  Sketch the bifurcation diagram for each of the cases:

  $$\text { (i) } a>b=0, \quad \text { (ii) } a, b>0 \text { and (iii) } a, b<0 \text {. }$$

  In each case show the locus and stability of the fixed points in the $(\mu, x)$-plane, and state the type of each bifurcation. [Assume that there are no further bifurcations in the region sketched.]

  (b) For the case $F(x)=x\left(\mu-x^{2}\right)$ (i.e. $\left.a=-1, b=0\right)$, you may assume that

  $$F^{2}(x)=x+x\left(\mu-1-x^{2}\right)\left(\mu+1-x^{2}\right)\left(1-\mu x^{2}+x^{4}\right) .$$

  Show that there are at most three 2-cycles and determine when they exist. By considering $F^{\prime}\left(x_{i}\right) F^{\prime}\left(x_{i+1}\right)$, or otherwise, show further that one 2-cycle is always unstable when it exists and that the others are unstable when $\mu>\sqrt{5}$. Sketch the bifurcation diagram showing the locus and stability of the fixed points and 2-cycles. State briefly what you would expect to occur for $\mu>\sqrt{5}$.

  comment

Electrodynamics

• Paper 1, Section II, 35D

  Electrodynamics | Part II, 2017

  In some inertial reference frame $S$, there is a uniform electric field $\mathbf{E}$ directed along the positive $y$-direction and a uniform magnetic field $\mathbf{B}$ directed along the positive $z$ direction. The magnitudes of the fields are $E$ and $B$, respectively, with $E<c B$. Show that it is possible to find a reference frame in which the electric field vanishes, and determine the relative speed $\beta c$ of the two frames and the magnitude of the magnetic field in the new frame.

  [Hint: You may assume that under a standard Lorentz boost with speed $v=\beta$ c along the $x$-direction, the electric and magnetic field components transform as

  $$\left(\begin{array}{c} E_{x}^{\prime} \\ E_{y}^{\prime} \\ E_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} E_{x} \\ \gamma(\beta)\left(E_{y}-v B_{z}\right) \\ \gamma(\beta)\left(E_{z}+v B_{y}\right) \end{array}\right) \quad a n d \quad\left(\begin{array}{c} B_{x}^{\prime} \\ B_{y}^{\prime} \\ B_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} B_{x} \\ \gamma(\beta)\left(B_{y}+v E_{z} / c^{2}\right) \\ \gamma(\beta)\left(B_{z}-v E_{y} / c^{2}\right) \end{array}\right),$$

  where the Lorentz factor $\gamma(\beta)=\left(1-\beta^{2}\right)^{-1 / 2}$.]

  A point particle of mass $m$ and charge $q$ moves relativistically under the influence of the fields $\mathbf{E}$ and $\mathbf{B}$. The motion is in the plane $z=0$. By considering the motion in the reference frame in which the electric field vanishes, or otherwise, show that, with a suitable choice of origin, the worldline of the particle has components in the frame $S$ of the form

  $$\begin{aligned} &c t(\tau)=\gamma(u / c) \gamma(\beta)\left[c \tau+\frac{\beta u}{\omega} \sin \omega \tau\right] \\ &x(\tau)=\gamma(u / c) \gamma(\beta)\left[\beta c \tau+\frac{u}{\omega} \sin \omega \tau\right] \\ &y(\tau)=\frac{u \gamma(u / c)}{\omega} \cos \omega \tau \end{aligned}$$

  Here, $u$ is a constant speed with Lorentz factor $\gamma(u / c), \tau$ is the particle's proper time, and $\omega$ is a frequency that you should determine.

  Using dimensionless coordinates,

  $$\tilde{x}=\frac{\omega}{u \gamma(u / c)} x \quad \text { and } \quad \tilde{y}=\frac{\omega}{u \gamma(u / c)} y$$

  sketch the trajectory of the particle in the $(\tilde{x}, \tilde{y})$-plane in the limiting cases $2 \pi \beta \ll u / c$ and $2 \pi \beta \gg u / c$.

  comment

• Paper 3, Section II, D

  Electrodynamics | Part II, 2017

  By considering the force per unit volume $\mathbf{f}=\rho \mathbf{E}+\mathbf{J} \times \mathbf{B}$ on a charge density $\rho$ and current density $\mathbf{J}$ due to an electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$, show that

  $$\frac{\partial g_{i}}{\partial t}+\frac{\partial \sigma_{i j}}{\partial x_{j}}=-f_{i}$$

  where $\mathbf{g}=\epsilon_{0} \mathbf{E} \times \mathbf{B}$ and the symmetric tensor $\sigma_{i j}$ should be specified.

  Give the physical interpretation of $\mathbf{g}$ and $\sigma_{i j}$ and explain how $\sigma_{i j}$ can be used to calculate the net electromagnetic force exerted on the charges and currents within some region of space in static situations.

  The plane $x=0$ carries a uniform charge $\sigma$ per unit area and a current $K$ per unit length along the $z$-direction. The plane $x=d$ carries the opposite charge and current. Show that between these planes

  $$\sigma_{i j}=\frac{\sigma^{2}}{2 \epsilon_{0}}\left(\begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)+\frac{\mu_{0} K^{2}}{2}\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right)$$

  and $\sigma_{i j}=0$ for $x<0$ and $x>d$.

  Use $(*)$ to find the electromagnetic force per unit area exerted on the charges and currents in the $x=0$ plane. Show that your result agrees with direct calculation of the force per unit area based on the Lorentz force law.

  If the current $K$ is due to the motion of the charge $\sigma$ with speed $v$, is it possible for the force between the planes to be repulsive?

  comment

• Paper 4, Section II, D

  Electrodynamics | Part II, 2017

  A dielectric material has a real, frequency-independent relative permittivity $\epsilon_{r}$ with $\left|\epsilon_{r}-1\right| \ll 1$. In this case, the macroscopic polarization that develops when the dielectric is placed in an external electric field $\mathbf{E}_{\text {ext }}(t, \mathbf{x})$ is $\mathbf{P}(t, \mathbf{x}) \approx \epsilon_{0}\left(\epsilon_{r}-1\right) \mathbf{E}_{\text {ext }}(t, \mathbf{x})$. Explain briefly why the associated bound current density is

  $$\mathbf{J}_{\text {bound }}(t, \mathbf{x}) \approx \epsilon_{0}\left(\epsilon_{r}-1\right) \frac{\partial \mathbf{E}_{\text {ext }}(t, \mathbf{x})}{\partial t}$$

  [You should ignore any magnetic response of the dielectric.]

  A sphere of such a dielectric, with radius $a$, is centred on $\mathbf{x}=0$. The sphere scatters an incident plane electromagnetic wave with electric field

  $$\mathbf{E}(t, \mathbf{x})=\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}$$

  where $\omega=c|\mathbf{k}|$ and $\mathbf{E}_{0}$ is a constant vector. Working in the Lorenz gauge, show that at large distances $r=|\mathbf{x}|$, for which both $r \gg a$ and $k a^{2} / r \ll 2 \pi$, the magnetic vector potential $\mathbf{A}_{\text {scatt }}(t, \mathbf{x})$ of the scattered radiation is

  $$\mathbf{A}_{\mathrm{scatt}}(t, \mathbf{x}) \approx-i \omega \mathbf{E}_{0} \frac{e^{i(k r-\omega t)}}{r} \frac{\left(\epsilon_{r}-1\right)}{4 \pi c^{2}} \int_{\left|\mathbf{x}^{\prime}\right| \leqslant a} e^{i \mathbf{q} \cdot \mathbf{x}^{\prime}} d^{3} \mathbf{x}^{\prime}$$

  where $\mathbf{q}=\mathbf{k}-k \hat{\mathbf{x}}$ with $\hat{\mathbf{x}}=\mathbf{x} / r$.

  In the far-field, where $k r \gg 1$, the electric and magnetic fields of the scattered radiation are given by

  $$\begin{aligned} &\mathbf{E}_{\text {scatt }}(t, \mathbf{x}) \approx-i \omega \hat{\mathbf{x}} \times\left[\hat{\mathbf{x}} \times \mathbf{A}_{\text {scatt }}(t, \mathbf{x})\right] \\ &\mathbf{B}_{\text {scatt }}(t, \mathbf{x}) \approx i k \hat{\mathbf{x}} \times \mathbf{A}_{\text {scatt }}(t, \mathbf{x}) \end{aligned}$$

  By calculating the Poynting vector of the scattered and incident radiation, show that the ratio of the time-averaged power scattered per unit solid angle to the time-averaged incident power per unit area (i.e. the differential cross-section) is

  $$\frac{d \sigma}{d \Omega}=\left(\epsilon_{r}-1\right)^{2} k^{4}\left(\frac{\sin (q a)-q a \cos (q a)}{q^{3}}\right)^{2}\left|\hat{\mathbf{x}} \times \hat{\mathbf{E}}_{0}\right|^{2}$$

  where $\hat{\mathbf{E}}_{0}=\mathbf{E}_{0} /\left|\mathbf{E}_{0}\right|$ and $q=|\mathbf{q}|$.

  [You may assume that, in the Lorenz gauge, the retarded potential due to a localised current distribution is

  $$\mathbf{A}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} d^{3} \mathbf{x}^{\prime},$$

  where the retarded time $\left.t_{\text {ret }}=t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right| / c .\right]$

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2017

  Fluid of density $\rho$ and dynamic viscosity $\mu$ occupies the region $y>0$ in Cartesian coordinates $(x, y, z)$. A semi-infinite, dense array of cilia occupy the half plane $y=0$, $x>0$ and apply a stress in the $x$-direction on the adjacent fluid, working at a constant and uniform rate $\rho P$ per unit area, which causes the fluid to move with steady velocity $\mathbf{u}=(u(x, y), v(x, y), 0)$. Give a careful physical explanation of the boundary condition

  $$\left.u \frac{\partial u}{\partial y}\right|_{y=0}=-\frac{P}{\nu} \quad \text { for } \quad x>0$$

  paying particular attention to signs, where $\nu$ is the kinematic viscosity of the fluid. Why would you expect the fluid motion to be confined to a thin region near $y=0$ for sufficiently large values of $x$ ?

  Write down the viscous-boundary-layer equations governing the thin region of fluid motion. Show that the flow can be approximated by a stream function

  $$\psi(x, y)=U(x) \delta(x) f(\eta), \quad \text { where } \quad \eta=\frac{y}{\delta(x)}$$

  Determine the functions $U(x)$ and $\delta(x)$. Show that the dimensionless function $f(\eta)$ satisfies

  $$f^{\prime \prime \prime}=\frac{1}{5} f^{\prime 2}-\frac{3}{5} f f^{\prime \prime}$$

  What boundary conditions must be satisfied by $f(\eta)$ ? By considering how the volume flux varies with downstream location $x$, or otherwise, determine (with justification) the sign of the transverse flow $v$.

  comment

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2017

  A cylinder of radius $a$ falls at speed $U$ without rotating through viscous fluid adjacent to a vertical plane wall, with its axis horizontal and parallel to the wall. The distance between the cylinder and the wall is $h_{0} \ll a$. Use lubrication theory in a frame of reference moving with the cylinder to determine that the two-dimensional volume flux between the cylinder and the wall is

  $$q=\frac{2 h_{0} U}{3}$$

  upwards, relative to the cylinder.

  Determine an expression for the viscous shear stress on the cylinder. Use this to calculate the viscous force and hence the torque on the cylinder. If the cylinder is free to rotate, what does your result say about the sense of rotation of the cylinder?

  [Hint: You may quote the following integrals:

  $$\left.\int_{-\infty}^{\infty} \frac{d t}{1+t^{2}}=\pi, \quad \int_{-\infty}^{\infty} \frac{d t}{\left(1+t^{2}\right)^{2}}=\frac{\pi}{2}, \quad \int_{-\infty}^{\infty} \frac{d t}{\left(1+t^{2}\right)^{3}}=\frac{3 \pi}{8}\right]$$

  comment

• Paper 3, Section II, B

  Fluid Dynamics II | Part II, 2017

  A spherical bubble of radius a moves with velocity $\mathbf{U}$ through a viscous fluid that is at rest far from the bubble. The pressure and velocity fields outside the bubble are given by

  $$p=\mu \frac{a}{r^{3}} \mathbf{U} \cdot \mathbf{x} \quad \text { and } \quad \mathbf{u}=\frac{a}{2 r} \mathbf{U}+\frac{a}{2 r^{3}}(\mathbf{U} \cdot \mathbf{x}) \mathbf{x}$$

  respectively, where $\mu$ is the dynamic viscosity of the fluid, $\mathbf{x}$ is the position vector from the centre of the bubble and $r=|\mathbf{x}|$. Using suffix notation, or otherwise, show that these fields satisfy the Stokes equations.

  Obtain an expression for the stress tensor for the fluid outside the bubble and show that the velocity field above also satisfies all the appropriate boundary conditions.

  Compute the drag force on the bubble.

  [Hint: You may use

  $$\int_{S} n_{i} n_{j} d S=\frac{4}{3} \pi a^{2} \delta_{i j}$$

  where the integral is taken over the surface of a sphere of radius a and $\mathbf{n}$ is the outward unit normal to the surface.]

  comment

• Paper 4, Section II, B

  Fluid Dynamics II | Part II, 2017

  A horizontal layer of inviscid fluid of density $\rho_{1}$ occupying $0<y<h$ flows with velocity $(U, 0)$ above a horizontal layer of inviscid fluid of density $\rho_{2}>\rho_{1}$ occupying $-h<y<0$ and flowing with velocity $(-U, 0)$, in Cartesian coordinates $(x, y)$. There are rigid boundaries at $y=\pm h$. The interface between the two layers is perturbed to position $y=\operatorname{Re}\left(A e^{i k x+\sigma t}\right)$.

  Write down the full set of equations and boundary conditions governing this flow. Derive the linearised boundary conditions appropriate in the limit $A \rightarrow 0$. Solve the linearised equations to show that the perturbation to the interface grows exponentially in time if

  $$U^{2}>\frac{\rho_{2}^{2}-\rho_{1}^{2}}{\rho_{1} \rho_{2}} \frac{g}{4 k} \tanh k h .$$

  Sketch the right-hand side of this inequality as a function of $k$. Thereby deduce the minimum value of $U$ that makes the system unstable for all wavelengths.

  comment

Further Complex Methods

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2017

  Calculate the value of the integral

  $$P \int_{-\infty}^{\infty} \frac{e^{-i x}}{x^{n}} d x$$

  where $P$ stands for Principal Value and $n$ is a positive integer.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2017

  The Riemann zeta function is defined by

  $$\zeta_{R}(s)=\sum_{n=1}^{\infty} n^{-s}$$

  for $\operatorname{Re}(s)>1$.

  Show that

  $$\zeta_{R}(s)=\frac{1}{\Gamma(s)} \int_{0}^{\infty} \frac{t^{s-1}}{e^{t}-1} d t$$

  Let $I(s)$ be defined by

  $$I(s)=\frac{\Gamma(1-s)}{2 \pi i} \int_{C} \frac{t^{s-1}}{e^{-t}-1} d t$$

  where $C$ is the Hankel contour.

  Show that $I(s)$ provides an analytic continuation of $\zeta_{R}(s)$ for a range of $s$ which should be determined.

  Hence evaluate $\zeta_{R}(-1)$.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2017

  Euler's formula for the Gamma function is

  $$\Gamma(z)=\frac{1}{z} \prod_{n=1}^{\infty}\left(1+\frac{1}{n}\right)^{z}\left(1+\frac{z}{n}\right)^{-1}$$

  Use Euler's formula to show

  $$\frac{\Gamma(2 z)}{2^{2 z} \Gamma(z) \Gamma\left(z+\frac{1}{2}\right)}=C$$

  where $C$ is a constant.

  Evaluate $C$.

  [Hint: You may use $\Gamma(z) \Gamma(1-z)=\pi / \sin (\pi z) .]$

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2017

  The hypergeometric equation is represented by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & 1 & \infty \\ 0 & 0 & a \\ 1-c & c-a-b & b \end{array}\right\}$$

  and has solution $y_{0}(z)=F(a, b, c ; z)$.

  Functions $y_{1}(z)$ and $y_{2}(z)$ are defined by

  $$y_{1}(z)=F(a, b, a+b+1-c ; 1-z)$$

  and

  $$y_{2}(z)=(1-z)^{c-a-b} F(c-a, c-b, c-a-b+1 ; 1-z),$$

  where $c-a-b$ is not an integer.

  Show that $y_{1}(z)$ and $y_{2}(z)$ obey the hypergeometric equation $(*)$.

  Explain why $y_{0}(z)$ can be written in the form

  $$y_{0}(z)=A y_{1}(z)+B y_{2}(z)$$

  where $A$ and $B$ are independent of $z$ but depend on $a, b$ and $c$.

  Suppose that

  $$F(a, b, c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  with $\operatorname{Re}(c)>\operatorname{Re}(b)>0$ and $|\arg (1-z)|<\pi$. Find expressions for $A$ and $B$.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2017

  Find all the singular points of the differential equation

  $$z \frac{d^{2} y}{d z^{2}}+(2-z) \frac{d y}{d z}-y=0$$

  and determine whether they are regular or irregular singular points.

  By writing $y(z)=f(z) / z$, find two linearly independent solutions to this equation.

  Comment on the relationship of your solutions to the nature of the singular points of the original differential equation.

  comment

• Paper 4, Section I, $7 \mathbf{E} \quad$

  Further Complex Methods | Part II, 2017

  Consider the differential equation

  $$z \frac{d^{2} y}{d z^{2}}-2 \frac{d y}{d z}+z y=0$$

  Laplace's method finds a solution of this differential equation by writing $y(z)$ in the form

  $$y(z)=\int_{C} e^{z t} f(t) d t$$

  where $C$ is a closed contour.

  Determine $f(t)$. Hence find two linearly independent real solutions of $(\star)$ for $z$ real.

  comment

Galois Theory

• Paper 1, Section II, I

  Galois Theory | Part II, 2017

  (a) Let $K$ be a field and let $f(t) \in K[t]$. What does it mean for a field extension $L$ of $K$ to be a splitting field for $f(t)$ over $K$ ?

  Show that the splitting field for $f(t)$ over $K$ is unique up to isomorphism.

  (b) Find the Galois groups over the rationals $\mathbb{Q}$ for the following polynomials: (i) $t^{4}+2 t+2$. (ii) $t^{5}-t-1$.

  comment

• Paper 2, Section II, I

  Galois Theory | Part II, 2017

  (a) Define what it means for a finite field extension $L$ of a field $K$ to be separable. Show that $L$ is of the form $K(\alpha)$ for some $\alpha \in L$.

  (b) Let $p$ and $q$ be distinct prime numbers. Let $L=\mathbb{Q}(\sqrt{p}, \sqrt{-q})$. Express $L$ in the form $\mathbb{Q}(\alpha)$ and find the minimal polynomial of $\alpha$ over $\mathbb{Q}$.

  (c) Give an example of a field extension $K \leqslant L$ of finite degree, where $L$ is not of the form $K(\alpha)$. Justify your answer.

  comment

• Paper 3, Section II, I

  Galois Theory | Part II, 2017

  (a) Let $F$ be a finite field of characteristic $p$. Show that $F$ is a finite Galois extension of the field $F_{p}$ of $p$ elements, and that the Galois group of $F$ over $F_{p}$ is cyclic.

  (b) Find the Galois groups of the following polynomials:

  (i) $t^{4}+1$ over $F_{3}$.

  (ii) $t^{3}-t-2$ over $F_{5}$.

  (iii) $t^{4}-1$ over $F_{7}$.

  comment

• Paper 4, Section II, I

  Galois Theory | Part II, 2017

  (a) State the Fundamental Theorem of Galois Theory.

  (b) What does it mean for an extension $L$ of $\mathbb{Q}$ to be cyclotomic? Show that a cyclotomic extension $L$ of $\mathbb{Q}$ is a Galois extension and prove that its Galois group is Abelian.

  (c) What is the Galois group $G$ of $\mathbb{Q}(\eta)$ over $\mathbb{Q}$, where $\eta$ is a primitive 7 th root of unity? Identify the intermediate subfields $M$, with $\mathbb{Q} \leqslant M \leqslant \mathbb{Q}(\eta)$, in terms of $\eta$, and identify subgroups of $G$ to which they correspond. Justify your answers.

  comment

General Relativity

• Paper 1, Section II, D

  General Relativity | Part II, 2017

  A static black hole in a five-dimensional spacetime is described by the metric

  $$d s^{2}=-\left(1-\frac{\mu}{r^{2}}\right) d t^{2}+\left(1-\frac{\mu}{r^{2}}\right)^{-1} d r^{2}+r^{2}\left[d \psi^{2}+\sin ^{2} \psi\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  where $\mu>0$ is a constant.

  A geodesic lies in the plane $\theta=\psi=\pi / 2$ and has affine parameter $\lambda$. Show that

  $$E=\left(1-\frac{\mu}{r^{2}}\right) \frac{d t}{d \lambda} \quad \text { and } \quad L=r^{2} \frac{d \phi}{d \lambda}$$

  are both constants of motion. Write down a third constant of motion.

  Show that timelike and null geodesics satisfy the equation

  $$\frac{1}{2}\left(\frac{d r}{d \lambda}\right)^{2}+V(r)=\frac{1}{2} E^{2}$$

  for some potential $V(r)$ which you should determine.

  Circular geodesics satisfy the equation $V^{\prime}(r)=0$. Calculate the values of $r$ for which circular null geodesics exist and for which circular timelike geodesics exist. Which are stable and which are unstable? Briefly describe how this compares to circular geodesics in the four-dimensional Schwarzschild geometry.

  comment

• Paper 2, Section II, D

  General Relativity | Part II, 2017

  (a) The Friedmann-Robertson-Walker metric is given by

  $$d s^{2}=-d t^{2}+a^{2}(t)\left[\frac{d r^{2}}{1-k r^{2}}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  where $k=-1,0,+1$ and $a(t)$ is the scale factor.

  For $k=+1$, show that this metric can be written in the form

  $$d s^{2}=-d t^{2}+\gamma_{i j} d x^{i} d x^{j}=-d t^{2}+a^{2}(t)\left[d \chi^{2}+\sin ^{2} \chi\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)\right]$$

  Calculate the equatorial circumference $(\theta=\pi / 2)$ of the submanifold defined by constant $t$ and $\chi$.

  Calculate the proper volume, defined by $\int \sqrt{\operatorname{det} \gamma} d^{3} x$, of the hypersurface defined by constant $t$.

  (b) The Friedmann equations are

  $$\begin{aligned} &3\left(\frac{\dot{a}^{2}+k}{a^{2}}\right)-\Lambda=8 \pi \rho, \\ &\frac{2 a \ddot{a}+\dot{a}^{2}+k}{a^{2}}-\Lambda=-8 \pi P, \end{aligned}$$

  where $\rho(t)$ is the energy density, $P(t)$ is the pressure, $\Lambda$ is the cosmological constant and dot denotes $d / d t$.

  The Einstein static universe has vanishing pressure, $P(t)=0$. Determine $a, k$ and $\Lambda$ as a function of the density $\rho$.

  The Einstein static universe with $a=a_{0}$ and $\rho=\rho_{0}$ is perturbed by radiation such that

  $$a=a_{0}+\delta a(t), \quad \rho=\rho_{0}+\delta \rho(t), \quad P=\frac{1}{3} \delta \rho(t)$$

  where $\delta a \ll a_{0}$ and $\delta \rho \ll \rho_{0}$. Show that the Einstein static universe is unstable to this perturbation.

  comment

• Paper 3, Section II, D

  General Relativity | Part II, 2017

  Let $\mathcal{M}$ be a two-dimensional manifold with metric $\boldsymbol{g}$ of signature $-+$.

  (i) Let $p \in \mathcal{M}$. Use normal coordinates at the point $p$ to show that one can choose two null vectors $\mathbf{V}, \mathbf{W}$ that form a basis of the vector space $\mathcal{T}_{p}(\mathcal{M})$.

  (ii) Consider the interval $I \subset \mathbb{R}$. Let $\gamma: I \rightarrow \mathcal{M}$ be a null curve through $p$ and $\mathbf{U} \neq 0$ be the tangent vector to $\gamma$ at $p$. Show that the vector $\mathbf{U}$ is either parallel to $\mathbf{V}$ or parallel to $\mathbf{W}$.

  (iii) Show that every null curve in $\mathcal{M}$ is a null geodesic.

  [Hint: You may wish to consider the acceleration $a^{\alpha}=U^{\beta} \nabla_{\beta} U^{\alpha}$.]

  (iv) By providing an example, show that not every null curve in four-dimensional Minkowski spacetime is a null geodesic.

  comment

• Paper 4, Section II, D

  General Relativity | Part II, 2017

  (a) In the transverse traceless gauge, a plane gravitational wave propagating in the $z$ direction is described by a perturbation $h_{\alpha \beta}$ of the Minkowski metric $\eta_{\alpha \beta}=$ $\operatorname{diag}(-1,1,1,1)$ in Cartesian coordinates $x^{\alpha}=(t, x, y, z)$, where

  $$h_{\alpha \beta}=H_{\alpha \beta} e^{i k_{\mu} x^{\mu}}, \quad \text { where } \quad k^{\mu}=\omega(1,0,0,1)$$

  and $H_{\alpha \beta}$ is a constant matrix. Spacetime indices in this question are raised or lowered with the Minkowski metric.

  The energy-momentum tensor of a gravitational wave is defined to be

  $$\tau_{\mu \nu}=\frac{1}{32 \pi}\left(\partial_{\mu} h^{\alpha \beta}\right)\left(\partial_{\nu} h_{\alpha \beta}\right)$$

  Show that $\partial^{\nu} \tau_{\mu \nu}=\frac{1}{2} \partial_{\mu} \tau_{\nu}^{\nu}$ and hence, or otherwise, show that energy and momentum are conserved.

  (b) A point mass $m$ undergoes harmonic motion along the $z$-axis with frequency $\omega$ and amplitude $L$. Compute the energy flux emitted in gravitational radiation.

  [Hint: The quadrupole formula for time-averaged energy flux radiated in gravitational waves is

  \left\langle\frac{d E}{d t}\right\rangle=\frac{1}{5}\left\langle\dddot{Q}_{i j} \dddot{Q}_{i j}\right\rangle

  where $Q_{i j}$ is the reduced quadrupole tensor.]

  comment

Graph Theory

• Paper 1, Section II, H

  Graph Theory | Part II, 2017

  Let $G$ be a graph of order $n \geqslant 3$ satisfying $\delta(G) \geqslant \frac{n}{2}$. Show that $G$ is Hamiltonian.

  Give an example of a planar graph $G$, with $\chi(G)=4$, that is Hamiltonian, and also an example of a planar graph $G$, with $\chi(G)=4$, that is not Hamiltonian.

  Let $G$ be a planar graph with the property that the boundary of the unbounded face is a Hamilton cycle of $G$. Prove that $\chi(G) \leqslant 3$.

  comment

• Paper 2, Section II, H

  Graph Theory | Part II, 2017

  State and prove Hall's theorem about matchings in bipartite graphs.

  Let $A=\left(a_{i j}\right)$ be an $n \times n$ matrix, with all entries non-negative reals, such that every row sum and every column sum is 1. By applying Hall's theorem, show that there is a permutation $\sigma$ of $\{1, \ldots, n\}$ such that $a_{i \sigma(i)}>0$ for all $i$.

  comment

• Paper 3, Section II, H

  Graph Theory | Part II, 2017

  Define the Ramsey numbers $R(s, t)$ for integers $s, t \geqslant 2$. Show that $R(s, t)$ exists for all $s, t \geqslant 2$. Show also that $R(s, s) \leqslant 4^{s}$ for all $s \geqslant 2$.

  Let $t \geqslant 2$ be fixed. Give a red-blue colouring of the edges of $K_{2 t-2}$ for which there is no red $K_{t}$ and no blue odd cycle. Show, however, that for any red-blue colouring of the edges of $K_{2 t-1}$ there must exist either a red $K_{t}$ or a blue odd cycle.

  comment

• Paper 4, Section II, H

  Graph Theory | Part II, 2017

  Let $G$ be a graph of maximum degree $\Delta$. Show the following:

  (i) Every eigenvalue $\lambda$ of $G$ satisfies $|\lambda| \leqslant \Delta$.

  (ii) If $G$ is regular then $\Delta$ is an eigenvalue.

  (iii) If $G$ is regular and connected then the multiplicity of $\Delta$ as an eigenvalue is 1 .

  (iv) If $G$ is regular and not connected then the multiplicity of $\Delta$ as an eigenvalue is greater than 1 .

  Let $A$ be the adjacency matrix of the Petersen graph. Explain why $A^{2}+A-2 I=J$, where $I$ is the identity matrix and $J$ is the all-1 matrix. Find, with multiplicities, the eigenvalues of the Petersen graph.

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2017

  Define a Lie point symmetry of the first order ordinary differential equation $\Delta[t, \mathbf{x}, \dot{\mathbf{x}}]=$ 0. Describe such a Lie point symmetry in terms of the vector field that generates it.

  Consider the $2 n$-dimensional Hamiltonian system $(M, H)$ governed by the differential equation

  $$\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} t}=J \frac{\partial H}{\partial \mathbf{x}}$$

  Define the Poisson bracket $\{\cdot, \cdot\}$. For smooth functions $f, g: M \rightarrow \mathbf{R}$ show that the associated Hamiltonian vector fields $V_{f}, V_{g}$ satisfy

  $$\left[V_{f}, V_{g}\right]=-V_{\{f, g\}} .$$

  If $F: M \rightarrow \mathbf{R}$ is a first integral of $(M, H)$, show that the Hamiltonian vector field $V_{F}$ generates a Lie point symmetry of $(\star)$. Prove the converse is also true if $(\star)$ has a fixed point, i.e. a solution of the form $\mathbf{x}(t)=\mathbf{x}_{0}$.

  comment

• Paper 2, Section II, A

  Integrable Systems | Part II, 2017

  Let $U$ and $V$ be non-singular $N \times N$ matrices depending on $(x, t, \lambda)$ which are periodic in $x$ with period $2 \pi$. Consider the associated linear problem

  $$\Psi_{x}=U \Psi, \quad \Psi_{t}=V \Psi$$

  for the vector $\Psi=\Psi(x, t ; \lambda)$. On the assumption that these equations are compatible, derive the zero curvature equation for $(U, V)$.

  Let $W=W(x, t, \lambda)$ denote the $N \times N$ matrix satisfying

  $$W_{x}=U W, \quad W(0, t, \lambda)=I_{N}$$

  where $I_{N}$ is the $N \times N$ identity matrix. You should assume $W$ is unique. By considering $\left(W_{t}-V W\right)_{x}$, show that the matrix $w(t, \lambda)=W(2 \pi, t, \lambda)$ satisfies the Lax equation

  $$w_{t}=[v, w], \quad v(t, \lambda) \equiv V(2 \pi, t, \lambda)$$

  Deduce that $\left\{\operatorname{tr}\left(w^{k}\right)\right\}_{k \geqslant 1}$ are first integrals.

  By considering the matrices

  $$\frac{1}{2 \mathrm{i} \lambda}\left[\begin{array}{cc} \cos u & -\mathrm{i} \sin u \\ \mathrm{i} \sin u & -\cos u \end{array}\right], \quad \frac{\mathrm{i}}{2}\left[\begin{array}{cc} 2 \lambda & u_{x} \\ u_{x} & -2 \lambda \end{array}\right]$$

  show that the periodic Sine-Gordon equation $u_{x t}=\sin u$ has infinitely many first integrals. [You need not prove anything about independence.]

  comment

• Paper 3, Section II, A

  Integrable Systems | Part II, 2017

  Let $u=u(x, t)$ be a smooth solution to the $\mathrm{KdV}$ equation

  $$u_{t}+u_{x x x}-6 u u_{x}=0$$

  which decays rapidly as $|x| \rightarrow \infty$ and let $L=-\partial_{x}^{2}+u$ be the associated Schrödinger operator. You may assume $L$ and $A=4 \partial_{x}^{3}-3\left(u \partial_{x}+\partial_{x} u\right)$ constitute a Lax pair for KdV.

  Consider a solution to $L \varphi=k^{2} \varphi$ which has the asymptotic form

  $$\varphi(x, k, t)= \begin{cases}e^{-\mathrm{i} k x}, & \text { as } x \rightarrow-\infty \\ a(k, t) e^{-\mathrm{i} k x}+b(k, t) e^{\mathrm{i} k x}, & \text { as } x \rightarrow+\infty\end{cases}$$

  Find evolution equations for $a$ and $b$. Deduce that $a(k, t)$ is $t$-independent.

  By writing $\varphi$ in the form

  $$\varphi(x, k, t)=\exp \left[-\mathrm{i} k x+\int_{-\infty}^{x} S(y, k, t) \mathrm{d} y\right], \quad S(x, k, t)=\sum_{n=1}^{\infty} \frac{S_{n}(x, t)}{(2 \mathrm{i} k)^{n}}$$

  show that

  $$a(k, t)=\exp \left[\int_{-\infty}^{\infty} S(x, k, t) \mathrm{d} x\right]$$

  Deduce that $\left\{\int_{-\infty}^{\infty} S_{n}(x, t) \mathrm{d} x\right\}_{n=1}^{\infty}$ are first integrals of KdV.

  By writing a differential equation for $S=X+\mathrm{i} Y$ (with $X, Y$ real), show that these first integrals are trivial when $n$ is even.

  comment

Linear Analysis

• Paper 1, Section II, F

  Linear Analysis | Part II, 2017

  Let $X$ be a normed vector space over the real numbers.

  (a) Define the dual space $X^{*}$ of $X$ and prove that $X^{*}$ is a Banach space. [You may use without proof that $X^{*}$ is a vector space.]

  (b) The Hahn-Banach theorem states the following. Let $X$ be a real vector space, and let $p: X \rightarrow \mathbb{R}$ be sublinear, i.e., $p(x+y) \leqslant p(x)+p(y)$ and $p(\lambda x)=\lambda p(x)$ for all $x, y \in X$ and all $\lambda>0$. Let $Y \subset X$ be a linear subspace, and let $g: Y \rightarrow \mathbb{R}$ be linear and satisfy $g(y) \leqslant p(y)$ for all $y \in Y$. Then there exists a linear functional $f: X \rightarrow \mathbb{R}$ such that $f(x) \leqslant p(x)$ for all $x \in X$ and $\left.f\right|_{Y}=g$.

  Using the Hahn-Banach theorem, prove that for any non-zero $x_{0} \in X$ there exists $f \in X^{*}$ such that $f\left(x_{0}\right)=\left\|x_{0}\right\|$ and $\|f\|=1$.

  (c) Show that $X$ can be embedded isometrically into a Banach space, i.e. find a Banach space $Y$ and a linear map $\Phi: X \rightarrow Y$ with $\|\Phi(x)\|=\|x\|$ for all $x \in X$.

  comment

• Paper 2, Section II, F

  Linear Analysis | Part II, 2017

  (a) Let $X$ be a normed vector space and $Y \subset X$ a closed subspace with $Y \neq X$. Show that $Y$ is nowhere dense in $X$.

  (b) State any version of the Baire Category theorem.

  (c) Let $X$ be an infinite-dimensional Banach space. Show that $X$ cannot have a countable algebraic basis, i.e. there is no countable subset $\left(x_{k}\right)_{k \in \mathbb{N}} \subset X$ such that every $x \in X$ can be written as a finite linear combination of elements of $\left(x_{k}\right)$.

  comment

• Paper 3, Section II, F

  Linear Analysis | Part II, 2017

  Let $K$ be a non-empty compact Hausdorff space and let $C(K)$ be the space of real-valued continuous functions on $K$.

  (i) State the real version of the Stone-Weierstrass theorem.

  (ii) Let $A$ be a closed subalgebra of $C(K)$. Prove that $f \in A$ and $g \in A$ implies that $m \in A$ where the function $m: K \rightarrow \mathbb{R}$ is defined by $m(x)=\max \{f(x), g(x)\}$. [You may use without proof that $f \in A$ implies $|f| \in A$.]

  (iii) Prove that $K$ is normal and state Urysohn's Lemma.

  (iv) For any $x \in K$, define $\delta_{x} \in C(K)^{*}$ by $\delta_{x}(f)=f(x)$ for $f \in C(K)$. Justifying your answer carefully, find

  $$\inf _{x \neq y}\left\|\delta_{x}-\delta_{y}\right\| .$$

  comment

• Paper 4, Section II, F

  Linear Analysis | Part II, 2017

  Let $H$ be a complex Hilbert space with inner product $(\cdot, \cdot)$ and let $T: H \rightarrow H$ be a bounded linear map.

  (i) Define the spectrum $\sigma(T)$, the point spectrum $\sigma_{p}(T)$, the continuous spectrum $\sigma_{c}(T)$, and the residual spectrum $\sigma_{r}(T)$.

  (ii) Show that $T^{*} T$ is self-adjoint and that $\sigma\left(T^{*} T\right) \subset[0, \infty)$. Show that if $T$ is compact then so is $T^{*} T$.

  (iii) Assume that $T$ is compact. Prove that $T$ has a singular value decomposition: for $N<\infty$ or $N=\infty$, there exist orthonormal systems $\left(u_{i}\right)_{i=1}^{N} \subset H$ and $\left(v_{i}\right)_{i=1}^{N} \subset H$ and $\left(\lambda_{i}\right)_{i=1}^{N} \subset[0, \infty)$ such that, for any $x \in H$,

  $$T x=\sum_{i=1}^{N} \lambda_{i}\left(u_{i}, x\right) v_{i}$$

  [You may use the spectral theorem for compact self-adjoint linear operators.]

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2017

  State the Completeness Theorem for Propositional Logic.

  [You do not need to give definitions of the various terms involved.]

  State the Compactness Theorem and the Decidability Theorem, and deduce them from the Completeness Theorem.

  A set $S$ of propositions is called finitary if there exists a finite set $T$ of propositions such that $\{t: S \vdash t\}=\{t: T \vdash t\}$. Give examples to show that an infinite set of propositions may or may not be finitary.

  Now let $A$ and $B$ be sets of propositions such that every valuation is a model of exactly one of $A$ and $B$. Show that there exist finite subsets $A^{\prime}$ of $A$ and $B^{\prime}$ of $B$ with $A^{\prime} \cup B^{\prime} \models \perp$, and deduce that $A$ and $B$ are finitary.

  comment

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2017

  Give the inductive and synthetic definitions of ordinal addition, and prove that they are equivalent.

  Which of the following are always true for ordinals $\alpha, \beta$ and $\gamma$ and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha+\beta=\beta+\alpha$

  (ii) $(\alpha+\beta) \gamma=\alpha \gamma+\beta \gamma$

  (iii) $\alpha(\beta+\gamma)=\alpha \beta+\alpha \gamma$

  (iv) If $\alpha \beta=\beta \alpha$ then $\alpha^{2} \beta^{2}=\beta^{2} \alpha^{2}$

  (v) If $\alpha^{2} \beta^{2}=\beta^{2} \alpha^{2}$ then $\alpha \beta=\beta \alpha$

  [In parts (iv) and (v) you may assume without proof that ordinal multiplication is associative.]

  comment

• Paper 3, Section II, H

  Logic and Set Theory | Part II, 2017

  State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Indicate clearly where in your proof you have made use of the Axiom of Choice.

  Show that $\mathbb{R}$ has a basis as a vector space over $\mathbb{Q}$.

  Let $V$ be a vector space over $\mathbb{Q}$. Show that all bases of $V$ have the same cardinality.

  [Hint: How does the cardinality of $V$ relate to the cardinality of a given basis?]

  comment

• Paper 4, Section II, H

  Logic and Set Theory | Part II, 2017

  Prove that every set has a transitive closure. [If you apply the Axiom of Replacement to a function-class $F$, you must explain clearly why $F$ is indeed a function-class.]

  State the Axiom of Foundation and the Principle of $\epsilon$-Induction, and show that they are equivalent (in the presence of the other axioms of $\mathrm{ZFC}$ ).

  State the $\epsilon$-Recursion Theorem.

  Sets $C_{\alpha}$ are defined for each ordinal $\alpha$ by recursion, as follows: $C_{0}=\emptyset, C_{\alpha+1}$ is the set of all countable subsets of $C_{\alpha}$, and $C_{\lambda}=\cup_{\alpha<\lambda} C_{\alpha}$ for $\lambda$ a non-zero limit. Does there exist an $\alpha$ with $C_{\alpha+1}=C_{\alpha}$ ? Justify your answer.

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2017

  A model of insect dispersal and growth in one spatial dimension is given by

  $$\frac{\partial N}{\partial t}=D \frac{\partial}{\partial x}\left(N^{2} \frac{\partial N}{\partial x}\right)+\alpha N, \quad N(x, 0)=N_{0} \delta(x),$$

  where $\alpha, D$ and $N_{0}$ are constants, $D>0$, and $\alpha$ may be positive or negative.

  By setting $N(x, t)=R(x, \tau) e^{\alpha t}$, where $\tau(t)$ is some time-like variable satisfying $\tau(0)=0$, show that a suitable choice of $\tau$ yields

  $$R_{\tau}=\left(R^{2} R_{x}\right)_{x}, \quad R(x, 0)=N_{0} \delta(x)$$

  where subscript denotes differentiation with respect to $x$ or $\tau$.

  Consider a similarity solution of the form $R(x, \tau)=F(\xi) / \tau^{\frac{1}{4}}$ where $\xi=x / \tau^{\frac{1}{4}}$. Show that $F$ must satisfy

  $$-\frac{1}{4}(F \xi)^{\prime}=\left(F^{2} F^{\prime}\right)^{\prime} \quad \text { and } \quad \int_{-\infty}^{+\infty} F(\xi) d \xi=N_{0}$$

  [You may use the fact that these are solved by

  $$F(\xi)= \begin{cases}\frac{1}{2} \sqrt{\xi_{0}^{2}-\xi^{2}} & \text { for }|\xi|<\xi_{0} \\ 0 & \text { otherwise }\end{cases}$$

  where $\left.\xi_{0}=\sqrt{4 N_{0} / \pi} .\right]$

  For $\alpha<0$, what is the maximum distance from the origin that insects ever reach? Give your answer in terms of $D, \alpha$ and $N_{0}$.

  comment

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2017

  A bacterial nutrient uptake model is represented by the reaction system

  $$\begin{array}{rll} 2 S+E & \stackrel{k_{1}}{\longrightarrow} & C \\ C & \stackrel{k_{2}}{\longrightarrow} 2 S+E \\ C \stackrel{k_{3}}{\longrightarrow} & E+2 P \end{array}$$

  where the $k_{i}$ are rate constants. Let $s, e, c$ and $p$ represent the concentrations of $S, E, C$ and $P$ respectively. Initially $s=s_{0}, e=e_{0}, c=0$ and $p=0$. Write down the governing differential equation system for the concentrations.

  Either by using the differential equations or directly from the reaction system above, find two invariant quantities. Use these to simplify the system to

  $$\begin{aligned} \dot{s} &=-2 k_{1} s^{2}\left(e_{0}-c\right)+2 k_{2} c \\ \dot{c} &=k_{1} s^{2}\left(e_{0}-c\right)-\left(k_{2}+k_{3}\right) c . \end{aligned}$$

  By setting $u=s / s_{0}$ and $v=c / e_{0}$ and rescaling time, show that the system can be written as

  $$\begin{aligned} u^{\prime} &=-2 u^{2}(1-v)+2(\mu-\lambda) v \\ \epsilon v^{\prime} &=\quad u^{2}(1-v)-\mu v \end{aligned}$$

  where $\epsilon=e_{0} / s_{0}$ and $\mu$ and $\lambda$ should be given. Give the initial conditions for $u$ and $v$.

  [Hint: Note that $2 X$ is equivalent to $X+X$ in reaction systems.]

  comment

• Paper 3, Section I, B

  Mathematical Biology | Part II, 2017

  A stochastic birth-death process has a master equation given by

  $$\frac{d p(n, t)}{d t}=\lambda[p(n-1, t)-p(n, t)]+\beta[(n+1) p(n+1, t)-n p(n, t)]$$

  where $p(n, t)$ is the probability that there are $n$ individuals in the population at time $t$ for $n=0,1,2, \ldots$ and $p(n, t)=0$ for $n<0$.

  Give the corresponding Fokker-Planck equation for this system.

  Use this Fokker-Planck equation to find expressions for $\frac{d}{d t}\langle x\rangle$ and $\frac{d}{d t}\left\langle x^{2}\right\rangle$.

  [Hint: The general form for a Fokker-Planck equation in $P(x, t)$ is

  $$\frac{\partial P}{\partial t}=-\frac{\partial}{\partial x}(A P)+\frac{1}{2} \frac{\partial^{2}}{\partial x^{2}}(B P)$$

  You may use this general form, stating how $A(x)$ and $B(x)$ are constructed. Alternatively, you may derive a Fokker-Plank equation directly by working from the master equation.]

  comment

• Paper 3, Section II, B

  Mathematical Biology | Part II, 2017

  In a discrete-time model, adults and larvae of a population at time $n$ are represented by $a_{n}$ and $b_{n}$ respectively. The model is represented by the equations

  $$\begin{aligned} a_{n+1} &=(1-k) a_{n}+\frac{b_{n}}{1+a_{n}} \\ b_{n+1} &=\mu a_{n} \end{aligned}$$

  You may assume that $k \in(0,1)$ and $\mu>0$. Give an explanation of what each of the terms represents, and hence give a description of the population model.

  By combining the equations to describe the dynamics purely in terms of the adults, find all equilibria of the system. Show that the equilibrium with the population absent $(a=0)$ is unstable exactly when there exists an equilibrium with the population present $(a>0)$.

  Give the condition on $\mu$ and $k$ for the equilibrium with $a>0$ to be stable, and sketch the corresponding region in the $(k, \mu)$ plane.

  What happens to the population close to the boundaries of this region?

  If this model was modified to include stochastic effects, briefly describe qualitatively the likely dynamics near the boundaries of the region found above.

  comment

• Paper 4, Section I, B

  Mathematical Biology | Part II, 2017

  Consider an epidemic model with host demographics (natural births and deaths).

  The system is given by

  $$\begin{aligned} &\frac{d S}{d t}=-\beta I S-\mu S+\mu N \\ &\frac{d I}{d t}=+\beta I S-\nu I-\mu I \end{aligned}$$

  where $S(t)$ are the susceptibles, $I(t)$ are the infecteds, $N$ is the total population size and the parameters $\beta, \mu$ and $\nu$ are positive. The basic reproduction ratio is defined as $R_{0}=\beta N /(\mu+\nu) .$

  Show that the system has an endemic equilibrium (where the disease is present) for $R_{0}>1$. Show that the endemic equilibrium is stable.

  Interpret the meaning of the case $\nu \gg \mu$ and show that in this case the approximate period of (decaying) oscillation around the endemic equilibrium is given by

  $$T=\frac{2 \pi}{\sqrt{\mu \nu\left(R_{0}-1\right)}}$$

  Suppose now a vaccine is introduced which is given to some proportion of the population at birth, but not enough to eradicate the disease. What will be the effect on the period of (decaying) oscillations?

  comment

• Paper 4, Section II, B

  Mathematical Biology | Part II, 2017

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} &\frac{\partial u}{\partial t}=u(c+u-v)+\frac{\partial^{2} u}{\partial x^{2}} \\ &\frac{\partial v}{\partial t}=v(a u-b v)+d \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  where $a, b, c, d>0$.

  Find and sketch the range of $a, b$ for which the spatially homogeneous system has a stable stationary solution with $u>0$ and $v>0$.

  Considering spatial perturbations of the form $\cos (k x)$ about the solution found above, find conditions for the system to be unstable. Sketch this region in the $(a, b)$-plane for fixed $d$ (for a value of $d$ such that the region is non-empty).

  Show that $k_{c}$, the critical wavenumber at the onset of the instability, is given by

  $$k_{c}=\sqrt{\frac{2 a c}{d-a}}$$

  comment

Number Fields

• Paper 1, Section II, H

  Number Fields | Part II, 2017

  Let $\mathcal{O}_{L}$ be the ring of integers in a number field $L$, and let $\mathfrak{a} \leqslant \mathcal{O}_{L}$ be a non-zero ideal of $\mathcal{O}_{L}$.

  (a) Show that $\mathfrak{a} \cap \mathbb{Z} \neq\{0\}$.

  (b) Show that $\mathcal{O}_{L} / \mathfrak{a}$ is a finite abelian group.

  (c) Show that if $x \in L$ has $x \mathfrak{a} \subseteq \mathfrak{a}$, then $x \in \mathcal{O}_{L}$.

  (d) Suppose $[L: \mathbb{Q}]=2$, and $\mathfrak{a}=\langle b, \alpha\rangle$, with $b \in \mathbb{Z}$ and $\alpha \in \mathcal{O}_{L}$. Show that $\langle b, \alpha\rangle\langle b, \bar{\alpha}\rangle$ is principal.

  [You may assume that $\mathfrak{a}$ has an integral basis.]

  comment

• Paper 2, Section II, 18H

  Number Fields | Part II, 2017

  (a) Let $L$ be a number field, $\mathcal{O}_{L}$ the ring of integers in $L, \mathcal{O}_{L}^{*}$ the units in $\mathcal{O}_{L}, r$ the number of real embeddings of $L$, and $s$ the number of pairs of complex embeddings of $L$.

  Define a group homomorphism $\mathcal{O}_{L}^{*} \rightarrow \mathbb{R}^{r+s-1}$ with finite kernel, and prove that the image is a discrete subgroup of $\mathbb{R}^{r+s-1}$.

  (b) Let $K=\mathbb{Q}(\sqrt{d})$ where $d>1$ is a square-free integer. What is the structure of the group of units of $K$ ? Show that if $d$ is divisible by a prime $p \equiv 3(\bmod 4)$ then every unit of $K$ has norm $+1$. Find an example of $K$ with a unit of norm $-1$.

  comment

• Paper 4, Section II, H

  Number Fields | Part II, 2017

  (a) Write down $\mathcal{O}_{K}$, when $K=\mathbb{Q}(\sqrt{\delta})$, and $\delta \equiv 2$ or $3(\bmod 4)$. [You need not prove your answer.]

  Let $L=\mathbb{Q}(\sqrt{2}, \sqrt{\delta})$, where $\delta \equiv 3(\bmod 4)$ is a square-free integer. Find an integral basis of $\mathcal{O}_{L} \cdot$ [Hint: Begin by considering the relative traces $t r_{L / K}$, for $K$ a quadratic subfield of $L .]$

  (b) Compute the ideal class group of $\mathbb{Q}(\sqrt{-14})$.

  comment

Number Theory

• Paper 1, Section $I$, G

  Number Theory | Part II, 2017

  Define the Legendre symbol $\left(\frac{a}{p}\right)$.

  State Gauss' lemma and use it to compute $\left(\frac{2}{p}\right)$ where $p$ is an odd prime.

  Show that if $m \geqslant 4$ is a power of 2 , and $p$ is a prime dividing $2^{m}+1$, then $p \equiv 1(\bmod 4 m)$.

  comment

• Paper 2, Section I, G

  Number Theory | Part II, 2017

  State and prove Legendre's formula for $\pi(x)$. Use it to compute $\pi(42)$.

  comment

• Paper 3, Section I, G

  Number Theory | Part II, 2017

  Explain what is meant by an Euler pseudoprime and a strong pseudoprime. Show that 65 is an Euler pseudoprime to the base $b$ if and only if $b^{2} \equiv \pm 1(\bmod 65)$. How many such bases are there? Show that the bases for which 65 is a strong pseudoprime do not form a subgroup of $(\mathbb{Z} / 65 \mathbb{Z})^{\times}$.

  comment

• Paper 3, Section II, G

  Number Theory | Part II, 2017

  Let $d$ be a positive integer which is not a square. Assume that the continued fraction expansion of $\sqrt{d}$ takes the form $\left[a_{0}, \overline{a_{1}, a_{2}, \ldots, a_{m}}\right]$.

  (a) Define the convergents $p_{n} / q_{n}$, and show that $p_{n}$ and $q_{n}$ are coprime.

  (b) The complete quotients $\theta_{n}$ may be written in the form $\left(\sqrt{d}+r_{n}\right) / s_{n}$, where $r_{n}$ and $s_{n}$ are rational numbers. Use the relation

  $$\sqrt{d}=\frac{\theta_{n} p_{n-1}+p_{n-2}}{\theta_{n} q_{n-1}+q_{n-2}}$$

  to find formulae for $r_{n}$ and $s_{n}$ in terms of the $p$ 's and $q$ 's. Deduce that $r_{n}$ and $s_{n}$ are integers.

  (c) Prove that Pell's equation $x^{2}-d y^{2}=1$ has infinitely many solutions in integers $x$ and $y$.

  (d) Find integers $x$ and $y$ satisfying $x^{2}-67 y^{2}=-2$.

  comment

• Paper 4, Section I, G

  Number Theory | Part II, 2017

  Show that, for $x \geqslant 2$ a real number,

  $$\prod_{\substack{p \leqslant x \\ p \text { is prime }}}\left(1-\frac{1}{p}\right)^{-1}>\log x$$

  Hence prove that

  $$\sum_{\substack{p \leqslant x, p \text { is prime }}} \frac{1}{p}>\log \log x+c,$$

  where $c$ is a constant you should make explicit.

  comment

• Paper 4, Section II, 10G

  Number Theory | Part II, 2017

  (a) State Dirichlet's theorem on primes in arithmetic progression.

  (b) Let $d$ be the discriminant of a binary quadratic form, and let $p$ be an odd prime. Show that $p$ is represented by some binary quadratic form of discriminant $d$ if and only if $x^{2} \equiv d(\bmod p)$ is soluble.

  (c) Let $f(x, y)=x^{2}+15 y^{2}$ and $g(x, y)=3 x^{2}+5 y^{2}$. Show that $f$ and $g$ each represent infinitely many primes. Are there any primes represented by both $f$ and $g$ ?

  comment

Numerical Analysis

• Paper 1, Section II, A

  Numerical Analysis | Part II, 2017

  State the Householder-John theorem and explain how it can be used in designing iterative methods for solving a system of linear equations $A \mathbf{x}=\mathbf{b}$. [You may quote other relevant theorems if needed.]

  Consider the following iterative scheme for solving $A \mathbf{x}=\mathbf{b}$. Let $A=L+D+U$, where $D$ is the diagonal part of $A$, and $L$ and $U$ are the strictly lower and upper triangular parts of $A$, respectively. Then, with some starting vector $\mathbf{x}^{(0)}$, the scheme is as follows:

  $$(D+\omega L) \mathbf{x}^{(k+1)}=[(1-\omega) D-\omega U] \mathbf{x}^{(k)}+\omega \mathbf{b} .$$

  Prove that if $A$ is a symmetric positive definite matrix and $\omega \in(0,2)$, then, for any $\mathbf{x}^{(0)}$, the above iteration converges to the solution of the system $A \mathbf{x}=\mathbf{b}$.

  Which method corresponds to the case $\omega=1 ?$

  comment

• Paper 2, Section II, A

  Numerical Analysis | Part II, 2017

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1]$, equipped with the zero Dirichlet boundary conditions on $\partial \Omega$, is discretized with the nine-point formula:

  $$\begin{aligned} \Gamma_{9}\left[u_{i, j}\right]:=&-\frac{10}{3} u_{i, j}+\frac{2}{3}\left(u_{i+1, j}+u_{i-1, j}+u_{i, j+1}+u_{i, j-1}\right) \\ &+\frac{1}{6}\left(u_{i+1, j+1}+u_{i+1, j-1}+u_{i-1, j+1}+u_{i-1, j-1}\right)=h^{2} f_{i, j} \end{aligned}$$

  where $1 \leqslant i, j \leqslant m, u_{i, j} \approx u(i h, j h)$, and $(i h, j h)$ are the grid points with $h=\frac{1}{m+1}$.

  (i) Find the order of the local truncation error $\eta_{i, j}$ of the approximation.

  (ii) Prove that the order of the truncation error is smaller if $f$ satisfies the Laplace equation $\nabla^{2} f=0$.

  (iii) Show that the modified nine-point scheme

  $$\begin{aligned} \Gamma_{9}\left[u_{i, j}\right] &=h^{2} f_{i, j}+\frac{1}{12} h^{2} \Gamma_{5}\left[f_{i, j}\right] \\ &:=h^{2} f_{i, j}+\frac{1}{12} h^{2}\left(f_{i+1, j}+f_{i-1, j}+f_{i, j+1}+f_{i, j-1}-4 f_{i, j}\right) \end{aligned}$$

  has a truncation error of the same order as in part (ii).

  (iv) Let $\left(u_{i, j}\right)_{i, j=1}^{m}$ be a solution to the $m^{2} \times m^{2}$ system of linear equations $A \mathbf{u}=\mathbf{b}$ arising from the modified nine-point scheme in part (iii). Further, let $u(x, y)$ be the exact solution and let $e_{i, j}:=u_{i, j}-u(i h, j h)$ be the error of approximation at grid points. Prove that there exists a constant $c$ such that

  $$\|\mathbf{e}\|_{2}:=\left[\sum_{i, j=1}^{m}\left|e_{i, j}\right|^{2}\right]^{1 / 2}<c h^{3}, \quad h \rightarrow 0$$

  [Hint: The nine-point discretization of $\nabla^{2} u$ can be written as

  $$\Gamma_{9}[u]=\left(\Gamma_{5}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u=\left(\Delta_{x}^{2}+\Delta_{y}^{2}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u$$

  where $\Gamma_{5}[u]=\left(\Delta_{x}^{2}+\Delta_{y}^{2}\right) u$ is the five-point discretization and

  $$\left.\begin{array}{l} \Delta_{x}^{2} u(x, y):=u(x-h, y)-2 u(x, y)+u(x+h, y) \\ \Delta_{y}^{2} u(x, y):=u(x, y-h)-2 u(x, y)+u(x, y+h) \end{array}\right]$$

  [Hint: The matrix A of the nine-point scheme is symmetric, with the eigenvalues

  $$\lambda_{k, \ell}=-4 \sin ^{2} \frac{k \pi h}{2}-4 \sin ^{2} \frac{\ell \pi h}{2}+\frac{8}{3} \sin ^{2} \frac{k \pi h}{2} \sin ^{2} \frac{\ell \pi h}{2}, \quad 1 \leqslant k, \ell \leqslant m$$

  comment

• Paper 3, Section II, A

  Numerical Analysis | Part II, 2017

  Let $A$ be a real symmetric $n \times n$ matrix with real and distinct eigenvalues $0=\lambda_{1}<\cdots<\lambda_{n-1}=1<\lambda_{n}$ and a corresponding orthogonal basis of normalized real eigenvectors $\left(\mathbf{w}_{i}\right)_{i=1}^{n}$.

  To estimate the eigenvector $\mathbf{w}_{n}$ of $A$ whose eigenvalue is $\lambda_{n}$, the power method with shifts is employed which has the following form:

  $$\mathbf{y}=\left(A-s_{k} I\right) \mathbf{x}^{(k)}, \quad \mathbf{x}^{(k+1)}=\mathbf{y} /\|\mathbf{y}\|, \quad s_{k} \in \mathbb{R}, \quad k=0,1,2, \ldots$$

  Three versions of this method are considered:

  (i) no shift: $s_{k} \equiv 0$;

  (ii) single shift: $s_{k} \equiv \frac{1}{2}$;

  (iii) double shift: $s_{2 \ell} \equiv s_{0}=\frac{1}{4}(2+\sqrt{2}), s_{2 \ell+1} \equiv s_{1}=\frac{1}{4}(2-\sqrt{2})$.

  Assume that $\lambda_{n}=1+\epsilon$, where $\epsilon>0$ is very small, so that the terms $\mathcal{O}\left(\epsilon^{2}\right)$ are negligible, and that $\mathbf{x}^{(0)}$ contains substantial components of all the eigenvectors.

  By considering the approximation after $2 m$ iterations in the form

  $$\mathbf{x}^{(2 m)}=\pm \mathbf{w}_{n}+\mathcal{O}\left(\rho^{2 m}\right) \quad(m \rightarrow \infty)$$

  find $\rho$ as a function of $\epsilon$ for each of the three versions of the method.

  Compare the convergence rates of the three versions of the method, with reference to the number of iterations needed to achieve a prescribed accuracy.

  comment

• Paper 4, Section II, A

  Numerical Analysis | Part II, 2017

  (a) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant x \leqslant 1, \quad 0 \leqslant t \leqslant T$$

  is approximated by the Crank-Nicolson scheme

  $$u_{m}^{n+1}-\frac{1}{2} \mu\left(u_{m-1}^{n+1}-2 u_{m}^{n+1}+u_{m+1}^{n+1}\right)=u_{m}^{n}+\frac{1}{2} \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)$$

  with $m=1, \ldots, M$. Here $\mu=k / h^{2}, k=\Delta t, h=\Delta x=\frac{1}{M+1}$, and $u_{m}^{n}$ is an approximation to $u(m h, n k)$. Assuming that $u(0, t)=u(1, t) \stackrel{M+1}{=} 0$, show that the above scheme can be written in the form

  $$B \mathbf{u}^{n+1}=C \mathbf{u}^{n}, \quad 0 \leqslant n \leqslant T / k-1$$

  where $\mathbf{u}^{n}=\left[u_{1}^{n}, \ldots, u_{M}^{n}\right]^{T}$ and the real matrices $B$ and $C$ should be found. Using matrix analysis, find the range of $\mu>0$ for which the scheme is stable.

  [Hint: All Toeplitz symmetric tridiagonal (TST) matrices have the same set of orthogonal eigenvectors, and a TST matrix with the elements $a_{i, i}=a$ and $a_{i, i \pm 1}=b$ has the eigenvalues $\lambda_{k}=a+2 b \cos \frac{\pi k}{M+1}$. ]

  (b) The wave equation

  $$\frac{\partial^{2} u}{\partial t^{2}}=\frac{\partial^{2} u}{\partial x^{2}}, \quad x \in \mathbb{R}, \quad t \geqslant 0$$

  with given initial conditions for $u$ and $\partial u / \partial t$, is approximated by the scheme

  $$u_{m}^{n+1}-2 u_{m}^{n}+u_{m}^{n-1}=\mu\left(u_{m+1}^{n}-2 u_{m}^{n}+u_{m-1}^{n}\right),$$

  with the Courant number now $\mu=k^{2} / h^{2}$. Applying the Fourier technique, find the range of $\mu>0$ for which the method is stable.

  comment

Optimization and Control

• Paper 2, Section II, K

  Optimization and Control | Part II, 2017

  During each of $N$ time periods a venture capitalist, Vicky, is presented with an investment opportunity for which the rate of return for that period is a random variable; the rates of return in successive periods are independent identically distributed random variables with distributions concentrated on $[-1, \infty)$. Thus, if $x_{n}$ is Vicky's capital at period $n$, then $x_{n+1}=\left(1-p_{n}\right) x_{n}+p_{n} x_{n}\left(1+R_{n}\right)$, where $p_{n} \in[0,1]$ is the proportion of her capital she chooses to invest at period $n$, and $R_{n}$ is the rate of return for period $n$. Vicky desires to maximize her expected yield over $N$ periods, where the yield is defined as $\left(\frac{x_{N}}{x_{0}}\right)^{\frac{1}{N}}-1$, and $x_{0}$ and $x_{N}$ are respectively her initial and final capital.

  (a) Express the problem of finding an optimal policy in a dynamic programming framework.

  (b) Show that in each time period, the optimal strategy can be expressed in terms of the quantity $p^{*}$ which solves the optimization problem $\max _{p} \mathbb{E}\left(1+p R_{1}\right)^{1 / N}$. Show that $p^{*}>0$ if $\mathbb{E} R_{1}>0$. [Do not calculate $p^{*}$ explicitly.]

  (c) Compare her optimal policy with the policy which maximizes her expected final capital $x_{N}$.

  comment

• Paper 3, Section II, K

  Optimization and Control | Part II, 2017

  A particle follows a discrete-time trajectory on $\mathbb{R}$ given by

  $$x_{t+1}=\left(A x_{t}+u_{t}\right) \xi_{t}+\epsilon_{t}$$

  for $t=1,2, \ldots, T$. Here $T \geqslant 2$ is a fixed integer, $A$ is a real constant, $x_{t}$ and $u_{t}$ are the position of the particle and control action at time $t$, respectively, and $\left(\xi_{t}, \epsilon_{t}\right)_{t=1}^{T}$ is a sequence of independent random vectors with

  $$\mathbb{E} \xi_{t}=\mathbb{E} \epsilon_{t}=0, \operatorname{var}\left(\xi_{t}\right)=V_{\xi}>0, \operatorname{var}\left(\epsilon_{t}\right)=V_{\epsilon}>0 \text { and } \operatorname{cov}\left(\xi_{t}, \epsilon_{t}\right)=0$$

  Find the optimal control, i.e. the control action $u_{t}$, defined as a function of $\left(x_{1}, \ldots, x_{t} ; u_{1}, \ldots, u_{t-1}\right)$, that minimizes

  $$\sum_{t=1}^{T} x_{t}^{2}+c \sum_{t=1}^{T-1} u_{t}^{2}$$

  where $c>0$ is given.

  On which of $V_{\epsilon}$ and $V_{\xi}$ does the optimal control depend?

  Find the limiting form of the optimal control as $T \rightarrow \infty$, and the minimal average cost per unit time.

  comment

• Paper 4, Section II, $29 \mathrm{~K}$

  Optimization and Control | Part II, 2017

  A file of $X$ gigabytes (GB) is to be transmitted over a communications link. At each time $t$ the sender can choose a transmission rate $u(t)$ within the range $[0,1]$ GB per second. The charge for transmitting at rate $u(t)$ at time $t$ is $u(t) p(t)$. The function $p$ is fully known at time $t=0$. If it takes a total time $T$ to transmit the file then there is a delay cost of $\gamma T^{2}, \gamma>0$. Thus $u$ and $T$ are to be chosen to minimize

  $$\int_{0}^{T} u(t) p(t) d t+\gamma T^{2}$$

  where $u(t) \in[0,1], d x(t) / d t=-u(t), x(0)=X$ and $x(T)=0$. Using Pontryagin's maximum principle, or otherwise, show that a property of the optimal policy is that there exists $p^{*}$ such that $u(t)=1$ if $p(t)<p^{*}$ and $u(t)=0$ if $p(t)>p^{*}$.

  Show that the optimal $p^{*}$ and $T$ are related by $p^{*}=p(T)+2 \gamma T$.

  Suppose $p(t)=t+1 / t$ and $X=1$. Show that it is optimal to transmit at a constant rate $u(t)=1$ between times $T-1 \leqslant t \leqslant T$, where $T$ is the unique positive solution to the equation

  $$\frac{1}{(T-1) T}=2 \gamma T+1$$

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  The position and momentum operators of the harmonic oscillator can be written as

  $$\hat{x}=\left(\frac{\hbar}{2 m \omega}\right)^{1 / 2}\left(a+a^{\dagger}\right), \quad \hat{p}=\left(\frac{\hbar m \omega}{2}\right)^{1 / 2} i\left(a^{\dagger}-a\right)$$

  where $m$ is the mass, $\omega$ is the frequency and the Hamiltonian is

  $$H=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2}$$

  Assuming that

  $$[\hat{x}, \hat{p}]=i \hbar$$

  derive the commutation relations for $a$ and $a^{\dagger}$. Construct the Hamiltonian in terms of $a$ and $a^{\dagger}$. Assuming that there is a unique ground state, explain how all other energy eigenstates can be constructed from it. Determine the energy of each of these eigenstates.

  Consider the modified Hamiltonian

  $$H^{\prime}=H+\lambda \hbar \omega\left(a^{2}+a^{\dagger 2}\right)$$

  where $\lambda$ is a dimensionless parameter. Use perturbation theory to calculate the modified energy levels to second order in $\lambda$, quoting any standard formulae that you require. Show that the modified Hamiltonian can be written as

  $$H^{\prime}=\frac{1}{2 m}(1-2 \lambda) \hat{p}^{2}+\frac{1}{2} m \omega^{2}(1+2 \lambda) \hat{x}^{2} .$$

  Assuming $|\lambda|<\frac{1}{2}$, calculate the modified energies exactly. Show that the results are compatible with those obtained from perturbation theory.

  comment

• Paper 2, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  Let $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ be a set of Hermitian operators obeying

  $$\left[\sigma_{i}, \sigma_{j}\right]=2 i \epsilon_{i j k} \sigma_{k} \quad \text { and } \quad(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=1$$

  where $\mathbf{n}$ is any unit vector. Show that $(*)$ implies that

  $$(\mathbf{a} \cdot \boldsymbol{\sigma})(\mathbf{b} \cdot \boldsymbol{\sigma})=\mathbf{a} \cdot \mathbf{b}+i(\mathbf{a} \times \mathbf{b}) \cdot \boldsymbol{\sigma}$$

  for any vectors a and $\mathbf{b}$. Explain, with reference to the properties $(*)$, how $\boldsymbol{\sigma}$ can be related to the intrinsic angular momentum $\mathbf{S}$ for a particle of spin $\frac{1}{2}$.

  Show that the operators $P_{\pm}=\frac{1}{2}(1 \pm \mathbf{n} \cdot \boldsymbol{\sigma})$ are Hermitian and obey

  $$P_{\pm}^{2}=P_{\pm}, \quad P_{+} P_{-}=P_{-} P_{+}=0$$

  Show how $P_{\pm}$can be used to write any state $|\chi\rangle$ as a linear combination of eigenstates of $\mathbf{n} \cdot \boldsymbol{\sigma}$. Use this to deduce that if the system is in a normalised state $|\chi\rangle$ when $\mathbf{n} \cdot \boldsymbol{\sigma}$ is measured, then the results $\pm 1$ will be obtained with probabilities

  $$\| P_{\pm}|\chi\rangle \|^{2}=\frac{1}{2}(1 \pm\langle\chi|\mathbf{n} \cdot \boldsymbol{\sigma}| \chi\rangle)$$

  If $|\chi\rangle$ is a state corresponding to the system having spin up along a direction defined by a unit vector $\mathbf{m}$, show that a measurement will find the system to have spin up along $\mathbf{n}$ with probability $\frac{1}{2}(1+\mathbf{n} \cdot \mathbf{m})$.

  comment

• Paper 3, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  The angular momentum operators $\mathbf{J}=\left(J_{1}, J_{2}, J_{3}\right)$ obey the commutation relations

  $$\begin{aligned} &{\left[J_{3}, J_{\pm}\right]=\pm J_{\pm}} \\ &{\left[J_{+}, J_{-}\right]=2 J_{3}} \end{aligned}$$

  where $J_{\pm}=J_{1} \pm i J_{2}$.

  A quantum mechanical system involves the operators $a, a^{\dagger}, b$ and $b^{\dagger}$ such that

  $$\begin{gathered} {\left[a, a^{\dagger}\right]=\left[b, b^{\dagger}\right]=1} \\ {[a, b]=\left[a^{\dagger}, b\right]=\left[a, b^{\dagger}\right]=\left[a^{\dagger}, b^{\dagger}\right]=0 .} \end{gathered}$$

  Define $K_{+}=a^{\dagger} b, K_{-}=a b^{\dagger}$ and $K_{3}=\frac{1}{2}\left(a^{\dagger} a-b^{\dagger} b\right)$. Show that $K_{\pm}$and $K_{3}$ obey the same commutation relations as $J_{\pm}$and $J_{3}$.

  Suppose that the system is in the state $|0\rangle$ such that $a|0\rangle=b|0\rangle=0$. Show that $\left(a^{\dagger}\right)^{2}|0\rangle$ is an eigenstate of $K_{3}$. Let $K^{2}=\frac{1}{2}\left(K_{+} K_{-}+K_{-} K_{+}\right)+K_{3}^{2}$. Show that $\left(a^{\dagger}\right)^{2}|0\rangle$ is an eigenstate of $K^{2}$ and find the eigenvalue. How many other states do you expect to find with same value of $K^{2}$ ? Find them.

  comment

• Paper 4, Section II, C

  Principles of Quantum Mechanics | Part II, 2017

  The Hamiltonian for a quantum system in the Schrödinger picture is

  $$H_{0}+\lambda V(t),$$

  where $H_{0}$ is independent of time and the parameter $\lambda$ is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Let $|n\rangle$ and $|m\rangle$ be eigenstates of $H_{0}$ with distinct eigenvalues $E_{n}$ and $E_{m}$ respectively. Show that if the system was in the state $|n\rangle$ in the remote past, then the probability of measuring it to be in a different state $|m\rangle$ at a time $t$ is

  $$\frac{\lambda^{2}}{\hbar^{2}}\left|\int_{-\infty}^{t} d t^{\prime}\left\langle m\left|V\left(t^{\prime}\right)\right| n\right\rangle e^{i\left(E_{m}-E_{n}\right) t^{\prime} / \hbar}\right|^{2}+O\left(\lambda^{3}\right)$$

  Let the system be a simple harmonic oscillator with $H_{0}=\hbar \omega\left(a^{\dagger} a+\frac{1}{2}\right)$, where $\left[a, a^{\dagger}\right]=1$. Let $|0\rangle$ be the ground state which obeys $a|0\rangle=0$. Suppose

  $$V(t)=e^{-p|t|}\left(a+a^{\dagger}\right),$$

  with $p>0$. In the remote past the system was in the ground state. Find the probability, to lowest non-trivial order in $\lambda$, for the system to be in the first excited state in the far future.

  comment

Principles of Statistics

• Paper 1, Section II, $28 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  For a positive integer $n$, we want to estimate the parameter $p$ in the binomial statistical model $\{\operatorname{Bin}(n, p), p \in[0,1]\}$, based on an observation $X \sim \operatorname{Bin}(n, p)$.

  (a) Compute the maximum likelihood estimator for $p$. Show that the posterior distribution for $p$ under a uniform prior on $[0,1]$ is $\operatorname{Beta}(a, b)$, and specify $a$ and $b$. [The p.d.f. of $\operatorname{Beta}(a, b)$ is given by

  $$\left.f_{a, b}(p)=\frac{(a+b-1) !}{(a-1) !(b-1) !} p^{a-1}(1-p)^{b-1} .\right]$$

  (b) (i) For a risk function $L$, define the risk of an estimator $\hat{p}$ of $p$, and the Bayes risk under a prior $\pi$ for $p$.

  (ii) Under the loss function

  $$L(\hat{p}, p)=\frac{(\hat{p}-p)^{2}}{p(1-p)}$$

  find a Bayes optimal estimator for the uniform prior. Give its risk as a function of $p$.

  (iii) Give a minimax optimal estimator for the loss function $L$ given above. Justify your answer.

  comment

• Paper 2, Section II, $26 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  We consider the problem of estimating $\theta$ in the model $\{f(x, \theta): \theta \in(0, \infty)\}$, where

  $$f(x, \theta)=(1-\alpha)(x-\theta)^{-\alpha} 1\{x \in[\theta, \theta+1]\}$$

  Here $1\{A\}$ is the indicator of the set $A$, and $\alpha \in(0,1)$ is known. This estimation is based on a sample of $n$ i.i.d. $X_{1}, \ldots, X_{n}$, and we denote by $X_{(1)}<\ldots<X_{(n)}$ the ordered sample.

  (a) Compute the mean and the variance of $X_{1}$. Construct an unbiased estimator of $\theta$ taking the form $\tilde{\theta}_{n}=\bar{X}_{n}+c(\alpha)$, where $\bar{X}_{n}=n^{-1} \sum_{i=1}^{n} X_{i}$, specifying $c(\alpha)$.

  (b) Show that $\tilde{\theta}_{n}$ is consistent and find the limit in distribution of $\sqrt{n}\left(\tilde{\theta}_{n}-\theta\right)$. Justify your answer, citing theorems that you use.

  (c) Find the maximum likelihood estimator $\hat{\theta}_{n}$ of $\theta$. Compute $\mathbf{P}\left(\hat{\theta}_{n}-\theta>t\right)$ for all real $t$. Is $\hat{\theta}_{n}$ unbiased?

  (d) For $t>0$, show that $\mathbf{P}\left(n^{\beta}\left(\hat{\theta}_{n}-\theta\right)>t\right)$ has a limit in $(0,1)$ for some $\beta>0$. Give explicitly the value of $\beta$ and the limit. Why should one favour using $\hat{\theta}_{n}$ over $\tilde{\theta}_{n}$ ?

  comment

• Paper 3, Section II, $26 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  We consider the problem of estimating an unknown $\theta_{0}$ in a statistical model $\{f(x, \theta), \theta \in \Theta\}$ where $\Theta \subset \mathbb{R}$, based on $n$ i.i.d. observations $X_{1}, \ldots, X_{n}$ whose distribution has p.d.f. $f\left(x, \theta_{0}\right)$.

  In all the parts below you may assume that the model satisfies necessary regularity conditions.

  (a) Define the score function $S_{n}$ of $\theta$. Prove that $S_{n}\left(\theta_{0}\right)$ has mean 0 .

  (b) Define the Fisher Information $I(\theta)$. Show that it can also be expressed as

  $$I(\theta)=-\mathbb{E}_{\theta}\left[\frac{d^{2}}{d \theta^{2}} \log f\left(X_{1}, \theta\right)\right]$$

  (c) Define the maximum likelihood estimator $\hat{\theta}_{n}$ of $\theta$. Give without proof the limits of $\hat{\theta}_{n}$ and of $\sqrt{n}\left(\hat{\theta}_{n}-\theta_{0}\right.$ ) (in a manner which you should specify). [Be as precise as possible when describing a distribution.]

  (d) Let $\psi: \Theta \rightarrow \mathbb{R}$ be a continuously differentiable function, and $\tilde{\theta}_{n}$ another estimator of $\theta_{0}$ such that $\left|\hat{\theta}_{n}-\tilde{\theta}_{n}\right| \leqslant 1 / n$ with probability 1 . Give the limits of $\psi\left(\tilde{\theta}_{n}\right)$ and of $\sqrt{n}\left(\psi\left(\tilde{\theta}_{n}\right)-\psi\left(\theta_{0}\right)\right)$ (in a manner which you should specify).

  comment

• Paper 4, Section II, $27 \mathrm{~K}$

  Principles of Statistics | Part II, 2017

  For the statistical model $\left\{\mathcal{N}_{d}(\theta, \Sigma), \theta \in \mathbb{R}^{d}\right\}$, where $\Sigma$ is a known, positive-definite $d \times d$ matrix, we want to estimate $\theta$ based on $n$ i.i.d. observations $X_{1}, \ldots, X_{n}$ with distribution $\mathcal{N}_{d}(\theta, \Sigma)$.

  (a) Derive the maximum likelihood estimator $\hat{\theta}_{n}$ of $\theta$. What is the distribution of $\hat{\theta}_{n}$ ?

  (b) For $\alpha \in(0,1)$, construct a confidence region $C_{n}^{\alpha}$ such that $\mathbf{P}_{\theta}\left(\theta \in C_{n}^{\alpha}\right)=1-\alpha$.

  (c) For $\Sigma=I_{d}$, compute the maximum likelihood estimator of $\theta$ for the following parameter spaces:

  (i) $\Theta=\left\{\theta:\|\theta\|_{2}=1\right\}$.

  (ii) $\Theta=\left\{\theta: v^{\top} \theta=0\right\}$ for some unit vector $v \in \mathbb{R}^{d}$.

  (d) For $\Sigma=I_{d}$, we want to test the null hypothesis $\Theta_{0}=\{0\}$ (i.e. $\left.\theta=0\right)$ against the composite alternative $\Theta_{1}=\mathbb{R}^{d} \backslash\{0\}$. Compute the likelihood ratio statistic $\Lambda\left(\Theta_{1}, \Theta_{0}\right)$ and give its distribution under the null hypothesis. Compare this result with the statement of Wilks' theorem.

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2017

  (a) Give the definition of the Borel $\sigma$-algebra on $\mathbb{R}$ and a Borel function $f: E \rightarrow \mathbb{R}$ where $(E, \mathcal{E})$ is a measurable space.

  (b) Suppose that $\left(f_{n}\right)$ is a sequence of Borel functions which converges pointwise to a function $f$. Prove that $f$ is a Borel function.

  (c) Let $R_{n}:[0,1) \rightarrow \mathbb{R}$ be the function which gives the $n$th binary digit of a number in $[0,1$ ) (where we do not allow for the possibility of an infinite sequence of 1 s). Prove that $R_{n}$ is a Borel function.

  (d) Let $f:[0,1)^{2} \rightarrow[0, \infty]$ be the function such that $f(x, y)$ for $x, y \in[0,1)^{2}$ is equal to the number of digits in the binary expansions of $x, y$ which disagree. Prove that $f$ is non-negative measurable.

  (e) Compute the Lebesgue measure of $f^{-1}([0, \infty))$, i.e. the set of pairs of numbers in $[0,1)$ whose binary expansions disagree in a finite number of digits.

  comment

• Paper 2, Section II, J

  Probability and Measure | Part II, 2017

  (a) Give the definition of the Fourier transform $\widehat{f}$ of a function $f \in L^{1}\left(\mathbb{R}^{d}\right)$.

  (b) Explain what it means for Fourier inversion to hold.

  (c) Prove that Fourier inversion holds for $g_{t}(x)=(2 \pi t)^{-d / 2} e^{-\|x\|^{2} /(2 t)}$. Show all of the steps in your computation. Deduce that Fourier inversion holds for Gaussian convolutions, i.e. any function of the form $f * g_{t}$ where $t>0$ and $f \in L^{1}\left(\mathbb{R}^{d}\right)$.

  (d) Prove that any function $f$ for which Fourier inversion holds has a bounded, continuous version. In other words, there exists $g$ bounded and continuous such that $f(x)=g(x)$ for a.e. $x \in \mathbb{R}^{d}$.

  (e) Does Fourier inversion hold for $f=\mathbf{1}_{[0,1]}$ ?

  comment

• Paper 3, Section II, J

  Probability and Measure | Part II, 2017

  (a) Suppose that $\mathcal{X}=\left(X_{n}\right)$ is a sequence of random variables on a probability space $(\Omega, \mathcal{F}, \mathbb{P})$. Give the definition of what it means for $\mathcal{X}$ to be uniformly integrable.

  (b) State and prove Hölder's inequality.

  (c) Explain what it means for a family of random variables to be $L^{p}$ bounded. Prove that an $L^{p}$ bounded sequence is uniformly integrable provided $p>1$.

  (d) Prove or disprove: every sequence which is $L^{1}$ bounded is uniformly integrable.

  comment

• Paper 4, Section II, J

  Probability and Measure | Part II, 2017

  (a) Suppose that $(E, \mathcal{E}, \mu)$ is a finite measure space and $\theta: E \rightarrow E$ is a measurable map. Prove that $\mu_{\theta}(A)=\mu\left(\theta^{-1}(A)\right)$ defines a measure on $(E, \mathcal{E})$.

  (b) Suppose that $\mathcal{A}$ is a $\pi$-system which generates $\mathcal{E}$. Using Dynkin's lemma, prove that $\theta$ is measure-preserving if and only if $\mu_{\theta}(A)=\mu(A)$ for all $A \in \mathcal{A}$.

  (c) State Birkhoff's ergodic theorem and the maximal ergodic lemma.

  (d) Consider the case $(E, \mathcal{E}, \mu)=([0,1), \mathcal{B}([0,1)), \mu)$ where $\mu$ is Lebesgue measure on $[0,1)$. Let $\theta:[0,1) \rightarrow[0,1)$ be the following map. If $x=\sum_{n=1}^{\infty} 2^{-n} \omega_{n}$ is the binary expansion of $x$ (where we disallow infinite sequences of $1 \mathrm{~s}$ ), then $\theta(x)=$ $\sum_{n=1}^{\infty} 2^{-n}\left(\omega_{n-1} \mathbf{1}_{n \in E}+\omega_{n+1} \mathbf{1}_{n \in O}\right)$ where $E$ and $O$ are respectively the even and odd elements of $\mathbb{N}$.

  (i) Prove that $\theta$ is measure-preserving. [You may assume that $\theta$ is measurable.]

  (ii) Prove or disprove: $\theta$ is ergodic.

  comment

Representation Theory

• Paper 1, Section II, G

  Representation Theory | Part II, 2017

  (a) Prove that if there exists a faithful irreducible complex representation of a finite group $G$, then the centre $Z(G)$ is cyclic.

  (b) Define the permutations $a, b, c \in S_{6}$ by

  $$a=\left(\begin{array}{lll} 1 & 2 & 3 \end{array}\right), b=\left(\begin{array}{lll} 4 & 5 & 6 \end{array}\right), c=\left(\begin{array}{ll} 2 & 3 \end{array}\right)(45),$$

  and let $E=\langle a, b, c\rangle$.

  (i) Using the relations $a^{3}=b^{3}=c^{2}=1, a b=b a, c^{-1} a c=a^{-1}$ and $c^{-1} b c=b^{-1}$, prove that $E$ has order 18 .

  (ii) Suppose that $\varepsilon$ and $\eta$ are complex cube roots of unity. Prove that there is a (matrix) representation $\rho$ of $E$ over $\mathbb{C}$ such that

  $$a \mapsto\left(\begin{array}{cc} \varepsilon & 0 \\ 0 & \varepsilon^{-1} \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} \eta & 0 \\ 0 & \eta^{-1} \end{array}\right), \quad c \mapsto\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)$$

  (iii) For which values of $\varepsilon, \eta$ is $\rho$ faithful? For which values of $\varepsilon, \eta$ is $\rho$ irreducible?

  (c) Note that $\langle a, b\rangle$ is a normal subgroup of $E$ which is isomorphic to $C_{3} \times C_{3}$. By inducing linear characters of this subgroup, or otherwise, obtain the character table of $E$.

  Deduce that $E$ has the property that $Z(E)$ is cyclic but $E$ has no faithful irreducible representation over $\mathbb{C}$.

  comment

• Paper 2, Section II, G

  Representation Theory | Part II, 2017

  In this question you may assume the following result. Let $\chi$ be a character of a finite group $G$ and let $g \in G$. If $\chi(g)$ is a rational number, then $\chi(g)$ is an integer.

  (a) If $a$ and $b$ are positive integers, we denote their highest common factor by $(a, b)$. Let $g$ be an element of order $n$ in the finite group $G$. Suppose that $g$ is conjugate to $g^{i}$ for all $i$ with $1 \leqslant i \leqslant n$ and $(i, n)=1$. Prove that $\chi(g)$ is an integer for all characters $\chi$ of $G$.

  [You may use the following result without proof. Let $\omega$ be an $n$th root of unity. Then

  is an integer.]

  Deduce that all the character values of symmetric groups are integers.

  (b) Let $G$ be a group of odd order.

  Let $\chi$ be an irreducible character of $G$ with $\chi=\bar{\chi}$. Prove that

  $$\left\langle\chi, 1_{G}\right\rangle=\frac{1}{|G|}(\chi(1)+2 \alpha),$$

  where $\alpha$ is an algebraic integer. Deduce that $\chi=1_{G}$.

  $$\begin{aligned} & \sum_{1 \leqslant i \leqslant n,} \omega^{i} \\ & \begin{aligned}&1 \leqslant i \leqslant n \\&(i, n)=1\end{aligned} \end{aligned}$$

  comment

• Paper 3, Section II, G

  Representation Theory | Part II, 2017

  (a) State Burnside's $p^{a} q^{b}$ theorem.

  (b) Let $P$ be a non-trivial group of prime power order. Show that if $H$ is a non-trivial normal subgroup of $P$, then $H \cap Z(P) \neq\{1\}$.

  Deduce that a non-abelian simple group cannot have an abelian subgroup of prime power index.

  (c) Let $\rho$ be a representation of the finite group $G$ over $\mathbb{C}$. Show that $\delta: g \mapsto \operatorname{det}(\rho(g))$ is a linear character of $G$. Assume that $\delta(g)=-1$ for some $g \in G$. Show that $G$ has a normal subgroup of index 2 .

  Now let $E$ be a group of order $2 k$, where $k$ is an odd integer. By considering the regular representation of $E$, or otherwise, show that $E$ has a normal subgroup of index $2 .$

  Deduce that if $H$ is a non-abelian simple group of order less than 80 , then $H$ has order 60 .

  comment

• Paper 4, Section II, G

  Representation Theory | Part II, 2017

  Let $G=\mathrm{SU}(2)$ and let $V_{n}$ be the vector space of complex homogeneous polynomials of degree $n$ in two variables.

  (a) Prove that $V_{n}$ has the structure of an irreducible representation for $G$.

  (b) State and prove the Clebsch-Gordan theorem.

  (c) Quoting without proof any properties of symmetric and exterior powers which you need, decompose $\mathrm{S}^{2} V_{n}$ and $\Lambda^{2} V_{n}(n \geqslant 1)$ into irreducible $G$-spaces.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2017

  By considering the singularity at $\infty$, show that any injective analytic map $f: \mathbb{C} \rightarrow \mathbb{C}$ has the form $f(z)=a z+b$ for some $a \in \mathbb{C}^{*}$ and $b \in \mathbb{C}$.

  State the Riemann-Hurwitz formula for a non-constant analytic map $f: R \rightarrow S$ of compact Riemann surfaces $R$ and $S$, explaining each term that appears.

  Suppose $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ is analytic of degree 2. Show that there exist Möbius transformations $S$ and $T$ such that

  $$S f T: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$$

  is the map given by $z \mapsto z^{2}$.

  comment

• Paper 2, Section II, F

  Riemann Surfaces | Part II, 2017

  Let $f$ be a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$. Let $P$ be a fundamental parallelogram whose boundary contains no zeros or poles of $f$. Show that the number of zeros of $f$ in $P$ is the same as the number of poles of $f$ in $P$, both counted with multiplicities.

  Suppose additionally that $f$ is even. Show that there exists a rational function $Q(z)$ such that $f=Q(\wp)$, where $\wp$ is the Weierstrass $\wp$-function.

  Suppose $f$ is a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$, and $F$ is a meromorphic antiderivative of $f$, so that $F^{\prime}=f$. Is it necessarily true that $F$ is an elliptic function? Justify your answer.

  [You may use standard properties of the Weierstrass $\wp$-function throughout.]

  comment

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2017

  Let $n \geqslant 2$ be a positive even integer. Consider the subspace $R$ of $\mathbb{C}^{2}$ given by the equation $w^{2}=z^{n}-1$, where $(z, w)$ are coordinates in $\mathbb{C}^{2}$, and let $\pi: R \rightarrow \mathbb{C}$ be the restriction of the projection map to the first factor. Show that $R$ has the structure of a Riemann surface in such a way that $\pi$ becomes an analytic map. If $\tau$ denotes projection onto the second factor, show that $\tau$ is also analytic. [You may assume that $R$ is connected.]

  Find the ramification points and the branch points of both $\pi$ and $\tau$. Compute the ramification indices at the ramification points.

  Assume that, by adding finitely many points, it is possible to compactify $R$ to a Riemann surface $\bar{R}$ such that $\pi$ extends to an analytic map $\bar{\pi}: \bar{R} \rightarrow \mathbb{C}_{\infty}$. Find the genus of $\bar{R}$ (as a function of $n$ ).

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2017

  The dataset ChickWeights records the weight of a group of chickens fed four different diets at a range of time points. We perform the following regressions in $R$.

  

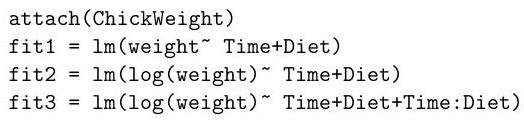
  (i) Which hypothesis test does the following command perform? State the degrees of freedom, and the conclusion of the test.

  

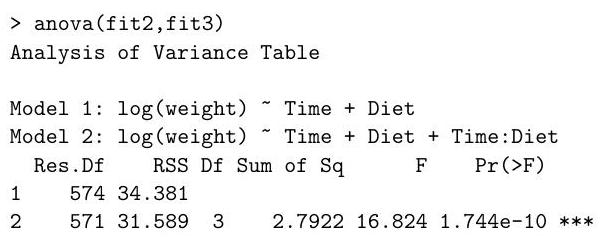
  (ii) Define a diagnostic plot that might suggest the logarithmic transformation of the response in fit2.

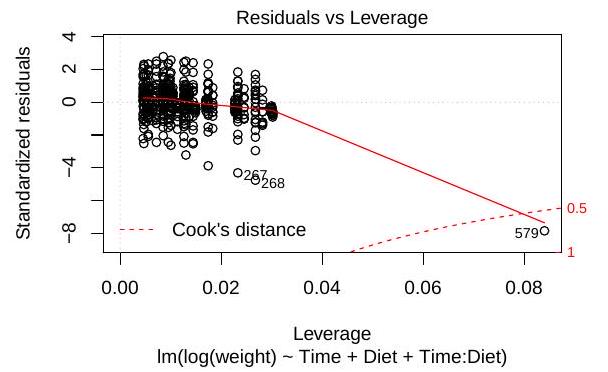
  (iii) Define the dashed line in the following plot, generated with the command plot(fit3). What does it tell us about the data point 579 ?

  

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2017

  The Cambridge Lawn Tennis Club organises a tournament in which every match consists of 11 games, all of which are played. The player who wins 6 or more games is declared the winner.

  For players $a$ and $b$, let $n_{a b}$ be the total number of games they play against each other, and let $y_{a b}$ be the number of these games won by player $a$. Let $\tilde{n}_{a b}$ and $\tilde{y}_{a b}$ be the corresponding number of matches.

  A statistician analysed the tournament data using a Binomial Generalised Linear Model (GLM) with outcome $y_{a b}$. The probability $P_{a b}$ that $a$ wins a game against $b$ is modelled by

  $$\log \left(\frac{P_{a b}}{1-P_{a b}}\right)=\beta_{a}-\beta_{b},$$

  with an appropriate corner point constraint. You are asked to re-analyse the data, but the game-level results have been lost and you only know which player won each match.

  We define a new GLM for the outcomes $\tilde{y}_{a b}$ with $\tilde{P}_{a b}=\mathbb{E} \tilde{y}_{a b} / \tilde{n}_{a b}$ and $g\left(\tilde{P}_{a b}\right)=$ $\beta_{a}-\beta_{b}$, where the $\beta_{a}$ are defined in $(*)$. That is, $\beta_{a}-\beta_{b}$ is the log-odds that $a$ wins a game against $b$, not a match.

  Derive the form of the new link function $g$. [You may express your answer in terms of a cumulative distribution function.]

  comment

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2017

  A statistician is interested in the power of a $t$-test with level $5 \%$ in linear regression; that is, the probability of rejecting the null hypothesis $\beta_{0}=0$ with this test under an alternative with $\beta_{0}>0$.

  (a) State the distribution of the least-squares estimator $\hat{\beta}_{0}$, and hence state the form of the $t$-test statistic used.

  (b) Prove that the power does not depend on the other coefficients $\beta_{j}$ for $j>0$.

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2017

  For Fisher's method of Iteratively Reweighted Least-Squares and Newton-Raphson optimisation of the log-likelihood, the vector of parameters $\beta$ is updated using an iteration

  $$\beta^{(m+1)}=\beta^{(m)}+M\left(\beta^{(m)}\right)^{-1} U\left(\beta^{(m)}\right),$$

  for a specific function $M$. How is $M$ defined in each method?

  Prove that they are identical in a Generalised Linear Model with the canonical link function.

  comment

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2017

  A Cambridge scientist is testing approaches to slow the spread of a species of moth in certain trees. Two groups of 30 trees were treated with different organic pesticides, and a third group of 30 trees was kept under control conditions. At the end of the summer the trees are classified according to the level of leaf damage, obtaining the following contingency table.

  

  Which of the following Generalised Linear Model fitting commands is appropriate for these data? Why? Describe the model being fit.

  

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2017

  The dataset diesel records the number of diesel cars which go through a block of Hills Road in 6 disjoint periods of 30 minutes, between 8AM and 11AM. The measurements are repeated each day for 10 days. Answer the following questions based on the code below, which is shown with partial output.

  (a) Can we reject the model fit. 1 at a $1 \%$ level? Justify your answer.

  (b) What is the difference between the deviance of the models fit. 2 and fit.3?

  (c) Which of fit. 2 and fit. 3 would you use to perform variable selection by backward stepwise selection? Why?

  (d) How does the final plot differ from what you expect under the model in fit.2? Provide a possible explanation and suggest a better model.

  $>$ head (diesel)

  period num.cars day

  $\begin{array}{llll}1 & 1 & 69 & 1\end{array}$

  $\begin{array}{lllll}2 & 2 & 97 & 1\end{array}$

  $\begin{array}{llll}3 & 3 & 103 & 1\end{array}$

  $\begin{array}{llll}4 & 4 & 99 & 1\end{array}$

  $\begin{array}{llll}5 & 5 & 67 & 1\end{array}$

  $6 \quad 6 \quad 911$

  $>$ fit. $1=$ glm(num.cars period, data=diesel, family=poisson)

  summary (fit.1)

  Deviance Residuals:

  Min 1Q Median 3Q Max

  $\begin{array}{lllll}-4.0188 & -1.4837 & -0.2117 & 1.6257 & 4.5965\end{array}$

  Coefficients:

  Estimate Std. Error $z$ value $\operatorname{Pr}(>|z|)$

  (Intercept) $4.628535 \quad 0.029288158 .035<2 \mathrm{e}-16 * * *$

  period $-0.006073 \quad 0.007551-0.804 \quad 0.421$

  Signif. codes: 0 ? $* * *$ ? $0.001 ? * * ? 0.01$ ? $*$ ? $0.05$ ?.? $0.1$ ? ? 1

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $262.36$ on 59 degrees of freedom

  Residual deviance: $261.72$ on 58 degrees of freedom

  AIC: $651.2$

  $>$ diesel$period.factor = factor(diesel$period)

  $>$ fit. $2=$ glm (num.cars period.factor, data=diesel, family=poisson)

  $\operatorname{summary}$ (fit.2)

  Coefficients:

  Estimate Std. Error z value $\operatorname{Pr}(>|z|)$

  Part II, $2017 \quad$ List of Questions

  [TURN OVER

  comment

Statistical Physics

• Paper 1, Section II, D

  Statistical Physics | Part II, 2017

  Explain what is meant by the microcanonical ensemble for a quantum system. Sketch how to derive the probability distribution for the canonical ensemble from the microcanonical ensemble. Under what physical conditions should each type of ensemble be used?

  A paramagnetic solid contains atoms with magnetic moment $\boldsymbol{\mu}=\mu_{B} \mathbf{J}$, where $\mu_{B}$ is a positive constant and $\mathbf{J}$ is the intrinsic angular momentum of the atom. In an applied magnetic field $\mathbf{B}$, the energy of an atom is $-\boldsymbol{\mu} \cdot \mathbf{B}$. Consider $\mathbf{B}=(0,0, B)$. Each atom has total angular momentum $J \in \mathbb{Z}$, so the possible values of $J_{z}=m \in \mathbb{Z}$ are $-J \leqslant m \leqslant J$.

  Show that the partition function for a single atom is

  $$Z_{1}(T, B)=\frac{\sinh \left(x\left(J+\frac{1}{2}\right)\right)}{\sinh (x / 2)}$$

  where $x=\mu_{B} B / k T$.

  Compute the average magnetic moment $\left\langle\mu_{z}\right\rangle$ of the atom. Sketch $\left\langle\mu_{z}\right\rangle / J$ for $J=1$, $J=2$ and $J=3$ on the same graph.

  The total magnetization is $M_{z}=N\left\langle\mu_{z}\right\rangle$, where $N$ is the number of atoms. The magnetic susceptibility is defined by

  $$\chi=\left(\frac{\partial M_{z}}{\partial B}\right)_{T}$$

  Show that the solid obeys Curie's law at high temperatures. Compute the susceptibility at low temperatures and give a physical explanation for the result.

  comment

• Paper 2, Section II, 34D

  Statistical Physics | Part II, 2017

  (a) The entropy of a thermodynamic ensemble is defined by the formula

  $$S=-k \sum_{n} p(n) \log p(n)$$

  where $k$ is the Boltzmann constant. Explain what is meant by $p(n)$ in this formula. Write down an expression for $p(n)$ in the grand canonical ensemble, defining any variables you need. Hence show that the entropy $S$ is related to the grand canonical partition function $\mathcal{Z}(T, \mu, V)$ by

  $$S=k\left[\frac{\partial}{\partial T}(T \log \mathcal{Z})\right]_{\mu, V}$$

  (b) Consider a gas of non-interacting fermions with single-particle energy levels $\epsilon_{i}$.

  (i) Show that the grand canonical partition function $\mathcal{Z}$ is given by

  $$\log \mathcal{Z}=\sum_{i} \log \left(1+e^{-\left(\epsilon_{i}-\mu\right) /(k T)}\right)$$

  (ii) Assume that the energy levels are continuous with density of states $g(\epsilon)=A V \epsilon^{a}$, where $A$ and $a$ are positive constants. Prove that

  $$\log \mathcal{Z}=V T^{b} f(\mu / T)$$

  and give expressions for the constant $b$ and the function $f$.

  (iii) The gas is isolated and undergoes a reversible adiabatic change. By considering the ratio $S / N$, prove that $\mu / T$ remains constant. Deduce that $V T^{c}$ and $p V^{d}$ remain constant in this process, where $c$ and $d$ are constants whose values you should determine.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2017

  (a) Describe the Carnot cycle using plots in the $(p, V)$-plane and the $(T, S)$-plane. In which steps of the cycle is heat absorbed or emitted by the gas? In which steps is work done on, or by, the gas?

  (b) An ideal monatomic gas undergoes a reversible cycle described by a triangle in the $(p, V)$-plane with vertices at the points $A, B, C$ with coordinates $\left(p_{0}, V_{0}\right),\left(2 p_{0}, V_{0}\right)$ and $\left(p_{0}, 2 V_{0}\right)$ respectively. The cycle is traversed in the order $A B C A$.

  (i) Write down the equation of state and an expression for the internal energy of the gas.

  (ii) Derive an expression relating $T d S$ to $d p$ and $d V$. Use your expression to calculate the heat supplied to, or emitted by, the gas along $A B$ and $C A$.

  (iii) Show that heat is supplied to the gas along part of the line $B C$, and is emitted by the gas along the other part of the line.

  (iv) Calculate the efficiency $\eta=W / Q$ where $W$ is the total work done by the cycle and $Q$ is the total heat supplied.

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2017

  The van der Waals equation of state is

  $$p=\frac{k T}{v-b}-\frac{a}{v^{2}}$$

  where $p$ is the pressure, $v=V / N$ is the volume divided by the number of particles, $T$ is the temperature, $k$ is Boltzmann's constant and $a, b$ are positive constants.

  (i) Prove that the Gibbs free energy $G=E+p V-T S$ satisfies $G=\mu N$. Hence obtain an expression for $(\partial \mu / \partial p)_{T, N}$ and use it to explain the Maxwell construction for determining the pressure at which the gas and liquid phases can coexist at a given temperature.

  (ii) Explain what is meant by the critical point and determine the values $p_{c}, v_{c}, T_{c}$ corresponding to this point.

  (iii) By defining $\bar{p}=p / p_{c}, \bar{v}=v / v_{c}$ and $\bar{T}=T / T_{c}$, derive the law of corresponding states:

  $$\bar{p}=\frac{8 \bar{T}}{3 \bar{v}-1}-\frac{3}{\bar{v}^{2}} .$$

  (iv) To investigate the behaviour near the critical point, let $\bar{T}=1+t$ and $\bar{v}=1+\phi$, where $t$ and $\phi$ are small. Expand $\bar{p}$ to cubic order in $\phi$ and hence show that

  $$\left(\frac{\partial \bar{p}}{\partial \phi}\right)_{t}=-\frac{9}{2} \phi^{2}+\mathcal{O}\left(\phi^{3}\right)+t[-6+\mathcal{O}(\phi)] .$$

  At fixed small $t$, let $\phi_{l}(t)$ and $\phi_{g}(t)$ be the values of $\phi$ corresponding to the liquid and gas phases on the co-existence curve. By changing the integration variable from $p$ to $\phi$, use the Maxwell construction to show that $\phi_{l}(t)=-\phi_{g}(t)$. Deduce that, as the critical point is approached along the co-existence curve,

  $$\bar{v}_{\text {gas }}-\bar{v}_{\text {liquid }} \sim\left(T_{c}-T\right)^{1 / 2}$$

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2017

  (a) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $\Delta_{0}, \Delta_{1}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $\mathbb{E}\left[\left|\Delta_{i}\right|\right]<\infty$ and $\mathbb{E}\left[\Delta_{i}\right]=0, i \geqslant 0$. Further, let

  $$X_{0}=\Delta_{0} \quad \text { and } \quad X_{n+1}=X_{n}+\Delta_{n+1} f_{n}\left(X_{0}, \ldots, X_{n}\right), \quad n \geqslant 0$$

  where

  $$f_{n}\left(x_{0}, \ldots, x_{n}\right)=\frac{1}{n+1} \sum_{i=0}^{n} x_{i}$$

  Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the natural filtration $\mathcal{F}_{n}=$ $\sigma\left(X_{0}, \ldots, X_{n}\right)$.

  (c) State and prove the optional stopping theorem for a bounded stopping time $\tau$.

  comment

• Paper 2, Section II, $27 \mathrm{~J}$

  Stochastic Financial Models | Part II, 2017

  (a) What is a Brownian motion?

  (b) Let $\left(B_{t}, t \geqslant 0\right)$ be a Brownian motion. Show that the process $\tilde{B}_{t}:=\frac{1}{c} B_{c^{2} t}$, $c \in \mathbb{R} \backslash\{0\}$, is also a Brownian motion.

  (c) Let $Z:=\sup _{t \geqslant 0} B_{t}$. Show that $c Z \stackrel{(d)}{=} Z$ for all $c>0$ (i.e. $c Z$ and $Z$ have the same laws). Conclude that $Z \in\{0,+\infty\}$ a.s.

  (d) Show that $\mathbb{P}[Z=+\infty]=1$.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models | Part II, 2017

  (a) State the fundamental theorem of asset pricing for a multi-period model.

  Consider a market model in which there is no arbitrage, the prices for all European put and call options are already known and there is a riskless asset $S^{0}=\left(S_{t}^{0}\right)_{t \in\{0, \ldots, T\}}$ with $S_{t}^{0}=(1+r)^{t}$ for some $r \geqslant 0$. The holder of a so-called 'chooser option' $C\left(K, t_{0}, T\right)$ has the right to choose at a preassigned time $t_{0} \in\{0,1, \ldots, T\}$ between a European call and a European put option on the same asset $S^{1}$, both with the same strike price $K$ and the same maturity $T$. [We assume that at time $t_{0}$ the holder will take the option having the higher price at that time.]

  (b) Show that the payoff function of the chooser option is given by

  $$C\left(K, t_{0}, T\right)= \begin{cases}\left(S_{T}^{1}-K\right)^{+} & \text {if } S_{t_{0}}^{1}>K(1+r)^{t_{0}-T} \\ \left(K-S_{T}^{1}\right)^{+} & \text {otherwise }\end{cases}$$

  (c) Show that the price $\pi\left(C\left(K, t_{0}, T\right)\right)$ of the chooser option $C\left(K, t_{0}, T\right)$ is given by

  $$\pi\left(C\left(K, t_{0}, T\right)\right)=\pi(E C(K, T))+\pi\left(E P\left(K(1+r)^{t_{0}-T}, t_{0}\right)\right),$$

  where $\pi(E C(K, T))$ and $\pi(E P(K, T))$ denote the price of a European call and put option, respectively, with strike $K$ and maturity $T$.

  comment

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2017

  (a) Describe the (Cox-Ross-Rubinstein) binomial model. When is the model arbitragefree? How is the equivalent martingale measure characterised in this case?

  (b) What is the price and the hedging strategy for any given contingent claim $C$ in the binomial model?

  (c) For any fixed $0<t<T$ and $K>0$, the payoff function of a forward-start-option is given by

  $$\left(\frac{S_{T}^{1}}{S_{t}^{1}}-K\right)^{+}$$

  Find a formula for the price of the forward-start-option in the binomial model.

  comment

Topics in Analysis

• Paper 1, Section I, 2F

  Topics in Analysis | Part II, 2017

  State Liouville's theorem on the approximation of algebraic numbers by rationals.

  Suppose that we have a sequence $\zeta_{n}$ with $\zeta_{n} \in\{0,1\}$. State and prove a necessary and sufficient condition on the $\zeta_{n}$ for

  $$\sum_{n=0}^{\infty} \zeta_{n} 10^{-n !}$$

  to be transcendental.

  comment

• Paper 2, Section I, F

  Topics in Analysis | Part II, 2017

  Are the following statements true or false? Give reasons, quoting any theorems that you need.

  (i) There is a sequence of polynomials $P_{n}$ with $P_{n}(t) \rightarrow \sin t$ uniformly on $\mathbb{R}$ as $n \rightarrow \infty$.

  (ii) If $f: \mathbb{R} \rightarrow \mathbb{R}$ is continuous, then there is a sequence of polynomials $Q_{n}$ with $Q_{n}(t) \rightarrow f(t)$ for each $t \in \mathbb{R}$ as $n \rightarrow \infty$.

  (iii) If $g:[1, \infty) \rightarrow \mathbb{R}$ is continuous with $g(t) \rightarrow 0$ as $t \rightarrow \infty$, then there is a sequence of polynomials $R_{n}$ with $R_{n}(1 / t) \rightarrow g(t)$ uniformly on $[1, \infty)$ as $n \rightarrow \infty$.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2017

  State and prove Baire's category theorem for complete metric spaces. Give an example to show that it may fail if the metric space is not complete.

  Let $f_{n}:[0,1] \rightarrow \mathbb{R}$ be a sequence of continuous functions such that $f_{n}(x)$ converges for all $x \in[0,1]$. Show that if $\epsilon>0$ is fixed we can find an $N \geqslant 0$ and a non-empty open interval $J \subseteq[0,1]$ such that $\left|f_{n}(x)-f_{m}(x)\right| \leqslant \epsilon$ for all $x \in J$ and all $n, m \geqslant N$.

  Let $g:[0,1] \rightarrow \mathbb{R}$ be defined by

  $$g(x)= \begin{cases}1 & \text { if } x \text { is rational } \\ 0 & \text { if } x \text { is irrational. }\end{cases}$$

  Show that we cannot find continuous functions $g_{n}:[0,1] \rightarrow \mathbb{R}$ with $g_{n}(x) \rightarrow g(x)$ for each $x \in[0,1]$ as $n \rightarrow \infty .$

  Define a sequence of continuous functions $h_{n}:[0,1] \rightarrow \mathbb{R}$ and a discontinuous function $h:[0,1] \rightarrow \mathbb{R}$ with $h_{n}(x) \rightarrow h(x)$ for each $x \in[0,1]$ as $n \rightarrow \infty$.

  comment

• Paper 3, Section I, 2F

  Topics in Analysis | Part II, 2017

  (a) Suppose that $g: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ is a continuous function such that there exists a $K>0$ with $\|g(\mathbf{x})-\mathbf{x}\| \leqslant K$ for all $\mathbf{x} \in \mathbb{R}^{2}$. By constructing a suitable map $f$ from the closed unit disc into itself, show that there exists a $\mathbf{t} \in \mathbb{R}^{2}$ with $g(\mathbf{t})=\mathbf{0}$.

  (b) Show that $g$ is surjective.

  (c) Show that the result of part (b) may be false if we drop the condition that $g$ is continuous.

  comment

• Paper 4, Section I, F

  Topics in Analysis | Part II, 2017

  If $x \in(0,1]$, set

  $$x=\frac{1}{N(x)+T(x)}$$

  where $N(x)$ is an integer and $1>T(x) \geqslant 0$. Let $N(0)=T(0)=0$.

  If $x$ is also irrational, write down the continued fraction expansion in terms of $N T^{j}(x)\left(\right.$ where $\left.N T^{0}(x)=N(x)\right)$.

  Let $X$ be a random variable taking values in $[0,1]$ with probability density function

  $$f(x)=\frac{1}{(\log 2)(1+x)}$$

  Show that $T(X)$ has the same distribution as $X$.

  comment

• Paper 4, Section II, 11F

  Topics in Analysis | Part II, 2017

  (a) Suppose that $\gamma:[0,1] \rightarrow \mathbb{C}$ is continuous with $\gamma(0)=\gamma(1)$ and $\gamma(t) \neq 0$ for all $t \in[0,1]$. Show that if $\gamma(0)=|\gamma(0)| \exp \left(i \theta_{0}\right)$ (with $\theta_{0}$ real) we can define a continuous function $\theta:[0,1] \rightarrow \mathbb{R}$ such that $\theta(0)=\theta_{0}$ and $\gamma(t)=|\gamma(t)| \exp (i \theta(t))$. Hence define the winding number $w(\gamma)=w(0, \gamma)$ of $\gamma$ around 0 .

  (b) Show that $w(\gamma)$ can take any integer value.

  (c) If $\gamma_{1}$ and $\gamma_{2}$ satisfy the requirements of the definition, and $\left(\gamma_{1} \times \gamma_{2}\right)(t)=\gamma_{1}(t) \gamma_{2}(t)$, show that

  $$w\left(\gamma_{1} \times \gamma_{2}\right)=w\left(\gamma_{1}\right)+w\left(\gamma_{2}\right)$$

  (d) If $\gamma_{1}$ and $\gamma_{2}$ satisfy the requirements of the definition and $\left|\gamma_{1}(t)-\gamma_{2}(t)\right|<\left|\gamma_{1}(t)\right|$ for all $t \in[0,1]$, show that

  $$w\left(\gamma_{1}\right)=w\left(\gamma_{2}\right)$$

  (e) State and prove a theorem that says that winding number is unchanged under an appropriate homotopy.

  comment

Waves

• Paper 1, Section II, B

  Waves | Part II, 2017

  Derive the wave equation governing the pressure disturbance $\tilde{p}$, for linearised, constant entropy sound waves in a compressible inviscid fluid of density $\rho_{0}$ and sound speed $c_{0}$, which is otherwise at rest.

  Consider a harmonic acoustic plane wave with wavevector $\mathbf{k}_{I}=k_{I}(\sin \theta, \cos \theta, 0)$ and unit-amplitude pressure disturbance. Determine the resulting velocity field $\mathbf{u}$.

  Consider such an acoustic wave incident from $y<0$ on a thin elastic plate at $y=0$. The regions $y<0$ and $y>0$ are occupied by gases with densities $\rho_{1}$ and $\rho_{2}$, respectively, and sound speeds $c_{1}$ and $c_{2}$, respectively. The kinematic boundary conditions at the plate are those appropriate for an inviscid fluid, and the (linearised) dynamic boundary condition is

  $$m \frac{\partial^{2} \eta}{\partial t^{2}}+B \frac{\partial^{4} \eta}{\partial x^{4}}+[\tilde{p}(x, 0, t)]_{-}^{+}=0$$

  where $m$ and $B$ are the mass and bending moment per unit area of the plate, and $y=\eta(x, t)$ (with $\left|\mathbf{k}_{I} \eta\right| \ll 1$ ) is its perturbed position. Find the amplitudes of the reflected and transmitted pressure perturbations, expressing your answers in terms of the dimensionless parameter

  $$\beta=\frac{k_{I} \cos \theta\left(m c_{1}^{2}-B k_{I}^{2} \sin ^{4} \theta\right)}{\rho_{1} c_{1}^{2}}$$

  (i) If $\rho_{1}=\rho_{2}=\rho_{0}$ and $c_{1}=c_{2}=c_{0}$, under what condition is the incident wave perfectly transmitted?

  (ii) If $\rho_{1} c_{1} \gg \rho_{2} c_{2}$, comment on the reflection coefficient, and show that waves incident at a sufficiently large angle are reflected as if from a pressure-release surface (i.e. an interface where $\tilde{p}=0$ ), no matter how large the plate mass and bending moment may be.

  comment

• Paper 2, Section II, B

  Waves | Part II, 2017

  Show that, for a one-dimensional flow of a perfect gas (with $\gamma>1$ ) at constant entropy, the Riemann invariants $R_{\pm}=u \pm 2\left(c-c_{0}\right) /(\gamma-1)$ are constant along characteristics $d x / d t=u \pm c .$

  Define a simple wave. Show that in a right-propagating simple wave

  $$\frac{\partial u}{\partial t}+\left(c_{0}+\frac{1}{2}(\gamma+1) u\right) \frac{\partial u}{\partial x}=0$$

  In some circumstances, dissipative effects may be modelled by

  $$\frac{\partial u}{\partial t}+\left(c_{0}+\frac{1}{2}(\gamma+1) u\right) \frac{\partial u}{\partial x}=-\alpha u$$

  where $\alpha$ is a positive constant. Suppose also that $u$ is prescribed at $t=0$ for all $x$, say $u(x, 0)=u_{0}(x)$. Demonstrate that, unless a shock develops, a solution of the form

  $$u(x, t)=u_{0}(\xi) e^{-\alpha t}$$

  can be found, where, for each $x$ and $t, \xi$ is determined implicitly as the solution of the equation

  $$x-c_{0} t=\xi+\frac{\gamma+1}{2 \alpha}\left(1-e^{-\alpha t}\right) u_{0}(\xi)$$

  Deduce that, despite the presence of dissipative effects, a shock will still form at some $(x, t)$ unless $\alpha>\alpha_{c}$, where

  $$\alpha_{c}=\frac{1}{2}(\gamma+1) \max _{u_{0}^{\prime}<0}\left|u_{0}^{\prime}(\xi)\right|$$

  comment

• Paper 3, Section II, B

  Waves | Part II, 2017

  Waves propagating in a slowly-varying medium satisfy the local dispersion relation $\omega=\Omega(\mathbf{k} ; \mathbf{x}, t)$ in the standard notation. Derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  governing the evolution of a wave packet specified by $\varphi(\mathbf{x}, t)=A(\mathbf{x}, t ; \varepsilon) e^{i \theta(\mathbf{x}, t) / \varepsilon}$, where $0<\varepsilon \ll 1$. A formal justification is not required, but the meaning of the $d / d t$ notation should be carefully explained.

  The dispersion relation for two-dimensional, small amplitude, internal waves of wavenumber $\mathbf{k}=(k, 0, m)$, relative to Cartesian coordinates $(x, y, z)$ with $z$ vertical, propagating in an inviscid, incompressible, stratified fluid that would otherwise be at rest, is given by

  $$\omega^{2}=\frac{N^{2} k^{2}}{k^{2}+m^{2}},$$

  where $N$ is the Brunt-Väisälä frequency and where you may assume that $k>0$ and $\omega>0$. Derive the modified dispersion relation if the fluid is not at rest, and instead has a slowly-varying mean flow $(U(z), 0,0)$.

  In the case that $U^{\prime}(z)>0, U(0)=0$ and $N$ is constant, show that a disturbance with wavenumber $\mathbf{k}=(k, 0,0)$ generated at $z=0$ will propagate upwards but cannot go higher than a critical level $z=z_{c}$, where $U\left(z_{c}\right)$ is equal to the apparent wave speed in the $x$-direction. Find expressions for the vertical wave number $m$ as $z \rightarrow z_{c}$ from below, and show that it takes an infinite time for the wave to reach the critical level.

  comment

• Paper 4, Section II, 38B

  Waves | Part II, 2017

  Consider the Rossby-wave equation

  $$\frac{\partial}{\partial t}\left(\frac{\partial^{2}}{\partial x^{2}}-\ell^{2}\right) \varphi+\beta \frac{\partial \varphi}{\partial x}=0,$$

  where $\ell>0$ and $\beta>0$ are real constants. Find and sketch the dispersion relation for waves with wavenumber $k$ and frequency $\omega(k)$. Find and sketch the phase velocity $c(k)$ and the group velocity $c_{g}(k)$, and identify in which direction(s) the wave crests travel, and the corresponding direction(s) of the group velocity.

  Write down the solution with initial value

  $$\varphi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  where $A(k)$ is real and $A(-k)=A(k)$. Use the method of stationary phase to obtain leading-order approximations to $\varphi(x, t)$ for large $t$, with $x / t$ having the constant value $V$, for

  (i) $0<V<\beta / 8 \ell^{2}$,

  (ii) $-\beta / \ell^{2}<V \leqslant 0$,

  where the solutions for the stationary points should be left in implicit form. [It is helpful to note that $\omega(-k)=-\omega(k)$.]

  Briefly discuss the nature of the solution for $V>\beta / 8 \ell^{2}$ and $V<-\beta / \ell^{2}$. [Detailed calculations are not required.]

  [Hint: You may assume that

  $$\int_{-\infty}^{\infty} e^{\pm i \gamma u^{2}} d u=\left(\frac{\pi}{\gamma}\right)^{\frac{1}{2}} e^{\pm i \pi / 4}$$

  for $\gamma>0 .]$

  comment