Part II, 2014, Paper 2

Algebraic Geometry

• Paper 2, Section II, H

  Algebraic Geometry | Part II, 2014

  (i) Let $k$ be an algebraically closed field, $n \geqslant 1$, and $S$ a subset of $k^{n}$.

  Let $I(S)=\left\{f \in k\left[x_{1}, \ldots, x_{n}\right] \mid f(p)=0\right.$ when $\left.p \in S\right\}$. Show that $I(S)$ is an ideal, and that $k\left[x_{1}, \ldots, x_{n}\right] / I(S)$ does not have any non-zero nilpotent elements.

  Let $X \subseteq \mathbf{A}^{n}, Y \subseteq \mathbf{A}^{m}$ be affine varieties, and $\Phi: k[Y] \rightarrow k[X]$ be a $k$-algebra homomorphism. Show that $\Phi$ determines a map of sets from $X$ to $Y$.

  (ii) Let $X$ be an irreducible affine variety. Define the dimension of $X, \operatorname{dim} X$ (in terms of the tangent spaces of $X$ ) and the transcendence dimension of $X, \operatorname{tr} \cdot \operatorname{dim} X$.

  State the Noether normalization theorem. Using this, or otherwise, prove that the transcendence dimension of $X$ equals the dimension of $X$.

  comment

Algebraic Topology

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2014

  Let $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ be a matrix with integer entries. Considering $S^{1}$ as the quotient space $\mathbb{R} / \mathbb{Z}$, show that the function

  $$\begin{aligned} \varphi_{A}: S^{1} \times S^{1} & \longrightarrow S^{1} \times S^{1} \\ ([x],[y]) & \longmapsto([a x+b y],[c x+d y]) \end{aligned}$$

  is well-defined and continuous. If in addition $\operatorname{det}(A)=\pm 1$, show that $\varphi_{A}$ is a homeomorphism.

  State the Seifert-van Kampen theorem. Let $X_{A}$ be the space obtained by gluing together two copies of $S^{1} \times D^{2}$ along their boundaries using the homeomorphism $\varphi_{A}$. Show that the fundamental group of $X_{A}$ is cyclic and determine its order.

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  (a) A classical particle of mass $m$ scatters on a central potential $V(r)$ with energy $E$, impact parameter $b$, and scattering angle $\theta$. Define the corresponding differential cross-section.

  For particle trajectories in the Coulomb potential,

  $$V_{C}(r)=\frac{e^{2}}{4 \pi \epsilon_{0} r}$$

  the impact parameter is given by

  $$b=\frac{e^{2}}{8 \pi \epsilon_{0} E} \cot \left(\frac{\theta}{2}\right)$$

  Find the differential cross-section as a function of $E$ and $\theta$.

  (b) A quantum particle of mass $m$ and energy $E=\hbar^{2} k^{2} / 2 m$ scatters in a localised potential $V(\mathbf{r})$. With reference to the asymptotic form of the wavefunction at large $|\mathbf{r}|$, define the scattering amplitude $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$ as a function of the incident and outgoing wavevectors $\mathbf{k}$ and $\mathbf{k}^{\prime}$ (where $|\mathbf{k}|=\left|\mathbf{k}^{\prime}\right|=k$ ). Define the differential cross-section for this process and express it in terms of $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$.

  Now consider a potential of the form $V(\mathbf{r})=\lambda U(\mathbf{r})$, where $\lambda \ll 1$ is a dimensionless coupling and $U$ does not depend on $\lambda$. You may assume that the Schrödinger equation for the wavefunction $\psi(\mathbf{k} ; \mathbf{r})$ of a scattering state with incident wavevector $\mathbf{k}$ may be written as the integral equation

  $$\psi(\mathbf{k} ; \mathbf{r})=\exp (i \mathbf{k} \cdot \mathbf{r})+\frac{2 m \lambda}{\hbar^{2}} \int d^{3} r^{\prime} \mathcal{G}_{0}^{(+)}\left(k ; \mathbf{r}-\mathbf{r}^{\prime}\right) U\left(\mathbf{r}^{\prime}\right) \psi\left(\mathbf{k} ; \mathbf{r}^{\prime}\right)$$

  where

  $$\mathcal{G}_{0}^{(+)}(k ; \mathbf{r})=-\frac{1}{4 \pi} \frac{\exp (i k|\mathbf{r}|)}{|\mathbf{r}|}$$

  Show that the corresponding scattering amplitude is given by

  $$f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)=-\frac{m \lambda}{2 \pi \hbar^{2}} \int d^{3} r^{\prime} \exp \left(-i \mathbf{k}^{\prime} \cdot \mathbf{r}^{\prime}\right) U\left(\mathbf{r}^{\prime}\right) \psi\left(\mathbf{k} ; \mathbf{r}^{\prime}\right)$$

  By expanding the wavefunction in powers of $\lambda$ and keeping only the leading term, calculate the leading-order contribution to the differential cross-section, and evaluate it for the case of the Yukawa potential

  $$V(\mathbf{r})=\lambda \frac{\exp (-\mu r)}{r}$$

  By taking a suitable limit, obtain the differential cross-section for quantum scattering in the Coulomb potential $V_{C}(r)$ defined in Part (a) above, correct to leading order in an expansion in powers of the constant $\tilde{\alpha}=e^{2} / 4 \pi \epsilon_{0}$. Express your answer as a function of the particle energy $E$ and scattering angle $\theta$, and compare it to the corresponding classical cross-section calculated in Part (a).

  Part II, $2014 \quad$ List of Questions

  [TURN OVER

  comment

Applied Probability

• Paper 2, Section II, J

  Applied Probability | Part II, 2014

  (i) Explain what the Moran model and the infinite alleles model are. State Ewens' sampling formula for the distribution of the allelic frequency spectrum $\left(a_{1}, \ldots, a_{n}\right)$ in terms of $\theta$ where $\theta=N u$ with $u$ denoting the mutation rate per individual and $N$ the population size.

  Let $K_{n}$ be the number of allelic types in a sample of size $n$. Give, without justification, an expression for $\mathbb{E}\left(K_{n}\right)$ in terms of $\theta$.

  (ii) Let $K_{n}$ and $\theta$ be as above. Show that for $1 \leqslant k \leqslant n$ we have that

  $$P\left(K_{n}=k\right)=C \frac{\theta^{k}}{\theta(\theta+1) \cdots(\theta+n-1)}$$

  for some constant $C$ that does not depend on $\theta$.

  Show that, given $\left\{K_{n}=k\right\}$, the distribution of the allelic frequency spectrum $\left(a_{1}, \ldots, a_{n}\right)$ does not depend on $\theta$.

  Show that the value of $\theta$ which maximises $\mathbb{P}\left(K_{n}=k\right)$ is the one for which $k=\mathbb{E}\left(K_{n}\right)$.

  comment

Classical Dynamics

• Paper 2, Section I, A

  Classical Dynamics | Part II, 2014

  The components of the angular velocity $\omega$ of a rigid body and of the position vector $\mathbf{r}$ are given in a body frame.

  (a) The kinetic energy of the rigid body is defined as

  $$T=\frac{1}{2} \int d^{3} \mathbf{r} \rho(\mathbf{r}) \dot{\mathbf{r}} \cdot \dot{\mathbf{r}}$$

  Given that the centre of mass is at rest, show that $T$ can be written in the form

  $$T=\frac{1}{2} I_{a b} \omega_{a} \omega_{b},$$

  where the explicit form of the tensor $I_{a b}$ should be determined.

  (b) Explain what is meant by the principal moments of inertia.

  (c) Consider a rigid body with principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$, which are all unequal. Derive Euler's equations of torque-free motion

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} \end{aligned}$$

  (d) The body rotates about the principal axis with moment of inertia $I_{1}$. Derive the condition for stable rotation.

  comment

• Paper 2, Section II, A

  Classical Dynamics | Part II, 2014

  A planar pendulum consists of a mass $m$ at the end of a light rod of length $l$. The pivot of the pendulum is attached to a bead of mass $M$, which slides along a horizontal rod without friction. The bead is connected to the ends of the horizontal rod by two identical springs of force constant $k$. The pivot constrains the pendulum to swing in the vertical plane through the horizontal rod. The horizontal rod is mounted on a bracket, so the system could rotate about the vertical axis which goes through its centre as shown in the figure.

  

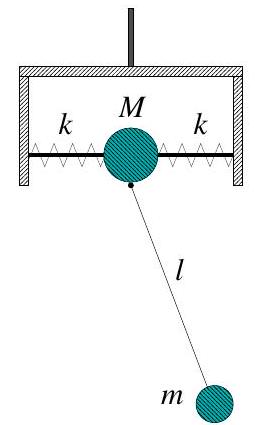
  (a) Initially, the system is not allowed to rotate about the vertical axis.

  (i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

  (ii) Write down expression(s) for any conserved quantities. Justify your answer.

  (iii) Derive the equations of motion.

  (iv) For $M=m / 2$ and $g m / k l=3$, find the frequencies of small oscillations around the stable equilibrium and the corresponding normal modes. Describe the respective motions of the system.

  (b) Assume now that the system is free to rotate about the vertical axis without friction. Write down the Lagrangian of the system. Identify and calculate the additional conserved quantity.

  comment

Coding and Cryptography

• Paper 2, Section $I$, I

  Coding and Cryptography | Part II, 2014

  Let $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ be a decodable binary code defined on a finite alphabet $\mathcal{A}$. Let $l(a)$ be the length of the code word $c(a)$. Prove that

  $$\sum_{a \in \mathcal{A}} 2^{-l(a)} \leqslant 1$$

  Show that, for the decodable code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ described above, there is a prefixfree code $p: \mathcal{A} \rightarrow\{0,1\}^{*}$ with each code word $p(a)$ having length $l(a)$. [You may use, without proof, any standard results from the course.]

  comment

• Paper 2, Section II, I

  Coding and Cryptography | Part II, 2014

  What is the information capacity of a memoryless, time-independent channel? Compute the information capacity of a binary symmetric channel with probability $p$ of error. Show the steps in your computation.

  Binary digits are transmitted through a noisy channel, which is memoryless and time-independent. With probability $\alpha(0<\alpha<1)$ the digit is corrupted and noise is received, otherwise the digit is transmitted unchanged. So, if we denote the input by 0 and 1 and the output as $0, *$ and 1 with $*$ denoting the noise, the transition matrix is

  $$\left(\begin{array}{cc} 1-\alpha & 0 \\ \alpha & \alpha \\ 0 & 1-\alpha \end{array}\right)$$

  Compute the information capacity of this channel.

  Explain how to code a message for transmission through the channel described above, and how to decode it, so that the probability of error for each bit is arbitrarily small.

  comment

Cosmology

• Paper 2, Section I, E

  Cosmology | Part II, 2014

  A self-gravitating fluid with density $\rho$, pressure $P(\rho)$ and velocity $\mathbf{v}$ in a gravitational potential $\Phi$ obeys the equations

  $$\begin{aligned} \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \mathbf{v}) &=0 \\ \frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v} \cdot \nabla) \mathbf{v}+\frac{\nabla P}{\rho}+\nabla \Phi &=\mathbf{0} \\ \nabla^{2} \Phi &=4 \pi G \rho \end{aligned}$$

  Assume that there exists a static constant solution of these equations with $\mathbf{v}=\mathbf{0}, \rho=\rho_{0}$ and $\Phi=\Phi_{0}$, for which $\nabla \Phi_{0}$ can be neglected. This solution is perturbed. Show that, to first order in the perturbed quantities, the density perturbations satisfy

  $$\frac{\partial^{2} \rho_{1}}{\partial t^{2}}=c_{s}^{2} \nabla^{2} \rho_{1}+4 \pi G \rho_{0} \rho_{1}$$

  where $\rho=\rho_{0}+\rho_{1}(\mathbf{x}, t)$ and $c_{s}^{2}=d P / d \rho$. Show that there are solutions to this equation of the form

  $$\rho_{1}(\mathbf{x}, t)=A \exp [-i \mathbf{k} \cdot \mathbf{x}+i \omega t]$$

  where $A, \omega$ and $\mathbf{k}$ are constants and

  $$\omega^{2}=c_{s}^{2} \mathbf{k} \cdot \mathbf{k}-4 \pi G \rho_{0}$$

  Interpret these solutions physically in the limits of small and large $|\mathbf{k}|$, explaining what happens to density perturbations on large and small scales, and determine the critical wavenumber that divides the two distinct behaviours of the perturbation.

  comment

Differential Geometry

• Paper 2, Section II, G

  Differential Geometry | Part II, 2014

  Define the terms Gaussian curvature $K$ and mean curvature $H$ for a smooth embedded oriented surface $S \subset \mathbf{R}^{3}$. [You may assume the fact that the derivative of the Gauss map is self-adjoint.] If $K=H^{2}$ at all points of $S$, show that both $H$ and $K$ are locally constant. [Hint: Use the symmetry of second partial derivatives of the field of unit normal vectors.]

  If $K=H^{2}=0$ at all points of $S$, show that the unit normal vector $\mathbf{N}$ to $S$ is locally constant and that $S$ is locally contained in a plane. If $K=H^{2}$ is a strictly positive constant on $S$ and $\phi: U \rightarrow S$ is a local parametrization (where $U$ is connected) on $S$ with unit normal vector $\mathbf{N}(u, v)$ for $(u, v) \in U$, show that $\phi(u, v)+\mathbf{N}(u, v) / H$ is constant on $U$. Deduce that $S$ is locally contained in a sphere of radius $1 /|H|$.

  If $S$ is connected with $K=H^{2}$ at all points of $S$, deduce that $S$ is contained in either a plane or a sphere.

  comment

Dynamical Systems

• Paper 2, Section I, D

  Dynamical Systems | Part II, 2014

  Consider the system

  $$\begin{aligned} \dot{x} &=-x+y+y^{2} \\ \dot{y} &=\mu-x y \end{aligned}$$

  Show that when $\mu=0$ the fixed point at the origin has a stationary bifurcation.

  Find the centre subspace of the extended system linearised about $(x, y, \mu)=(0,0,0)$.

  Find an approximation to the centre manifold giving $y$ as a function of $x$ and $\mu$, including terms up to quadratic order.

  Hence deduce an expression for $\dot{x}$ on the centre manifold, and identify the type of bifurcation at $\mu=0$.

  comment

Fluid Dynamics II

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2014

  Air is blown over the surface of a large, deep reservoir of water in such a way as to exert a tangential stress in the $x$-direction of magnitude $K x^{2}$ for $x>0$, with $K>0$. The water is otherwise at rest and occupies the region $y>0$. The surface $y=0$ remains flat.

  Find order-of-magnitude estimates for the boundary-layer thickness $\delta(x)$ and tangential surface velocity $U(x)$ in terms of the relevant physical parameters.

  Using the boundary-layer equations, find the ordinary differential equation governing the dimensionless function $f$ defined in the streamfunction

  $$\psi(x, y)=U(x) \delta(x) f(\eta), \quad \text { where } \eta=y / \delta(x)$$

  What are the boundary conditions on $f$ ?

  Does $f \rightarrow 0$ as $\eta \rightarrow \infty$ ? Why, or why not?

  The total horizontal momentum flux $P(X)$ across the vertical line $x=X$ is proportional to $X^{a}$ for $X>0$. Find the exponent $a$. By considering the steadiness of the momentum balance in the region $0<x<X$, explain why the value of $a$ is consistent with the form of the stress exerted on the boundary.

  comment

Further Complex Methods

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2014

  Suppose $z=0$ is a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane. Define the monodromy matrix $M$ around $z=0$.

  Demonstrate that if

  $$M=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)$$

  then the differential equation admits a solution of the form $a(z)+b(z) \log z$, where $a(z)$ and $b(z)$ are single-valued functions.

  comment

• Paper 2, Section II, 14B

  Further Complex Methods | Part II, 2014

  Use the Euler product formula

  $$\Gamma(z)=\lim _{n \rightarrow \infty} \frac{n ! n^{z}}{z(z+1) \ldots(z+n)}$$

  to show that:

  (i) $\Gamma(z+1)=z \Gamma(z)$;

  (ii) $\frac{1}{\Gamma(z)}=z e^{\gamma z} \prod_{k=1}^{\infty}\left(1+\frac{z}{k}\right) e^{-z / k}$, where $\gamma=\lim _{n \rightarrow \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n\right)$.

  Deduce that

  $$\frac{d}{d z} \log (\Gamma(z))=-\gamma-\frac{1}{z}+z \sum_{k=1}^{\infty} \frac{1}{k(z+k)}$$

  comment

Galois Theory

• Paper 2, Section II, H

  Galois Theory | Part II, 2014

  Describe the Galois correspondence for a finite Galois extension $L / K$.

  Let $L$ be the splitting field of $X^{4}-2$ over $\mathbb{Q}$. Compute the Galois group $G$ of $L / \mathbb{Q}$. For each subgroup of $G$, determine the corresponding subfield of $L$.

  Let $L / K$ be a finite Galois extension whose Galois group is isomorphic to $S_{n}$. Show that $L$ is the splitting field of a separable polynomial of degree $n$.

  comment

General Relativity

• Paper 2, Section II, E

  General Relativity | Part II, 2014

  Show how the geodesic equations and hence the Christoffel symbols $\Gamma^{a} b c$ can be obtained from a Lagrangian.

  In units with $c=1$, the FLRW spacetime line element is

  $$d s^{2}=-d t^{2}+a^{2}(t)\left(d x^{2}+d y^{2}+d z^{2}\right)$$

  Show that $\Gamma_{01}^{1}=\dot{a} / a$.

  You are given that, for the above metric, $G_{0}{ }^{0}=-3 \dot{a}^{2} / a^{2}$ and $G_{1}^{1}=-2 \ddot{a} / a-\dot{a}^{2} / a^{2}$, where $G_{a}^{b}$ is the Einstein tensor, which is diagonal. Verify by direct calculation that $\nabla_{b} G_{a}^{b}=0$.

  Solve the vacuum Einstein equations in the presence of a cosmological constant to determine the form of $a(t)$.

  comment

Geometry and Groups

• Paper 2, Section I, F

  Geometry and Groups | Part II, 2014

  Let $g, h$ be non-identity Möbius transformations. Prove that $g$ and $h$ commute if and only if one of the following holds:

  1. $\operatorname{Fix}(g)=\operatorname{Fix}(h)$;

  2. $g, h$ are involutions each of which exchanges the other's fixed points.

  Give an example to show that the second case can occur.

  comment

Graph Theory

• Paper 2, Section II, I

  Graph Theory | Part II, 2014

  Let $k$ and $n$ be integers with $1 \leqslant k<n$. Show that every connected graph of order $n$, in which $d(u)+d(v) \geqslant k$ for every pair $u, v$ of non-adjacent vertices, contains a path of length $k$.

  Let $k$ and $n$ be integers with $1 \leqslant k \leqslant n$. Show that a graph of order $n$ that contains no path of length $k$ has at most $(k-1) n / 2$ edges, and that this value is achieved only if $k$ divides $n$ and $G$ is the union of $n / k$ disjoint copies of $K_{k}$. [Hint: Proceed by induction on $n$ and consider a vertex of minimum degree.]

  comment

Integrable Systems

• Paper 2, Section II, D

  Integrable Systems | Part II, 2014

  Let $u=u(x)$ be a smooth function that decays rapidly as $|x| \rightarrow \infty$ and let $L=-\partial_{x}^{2}+u(x)$ denote the associated Schrödinger operator. Explain very briefly each of the terms appearing in the scattering data

  $$S=\left\{\left\{\chi_{n}, c_{n}\right\}_{n=1}^{N}, R(k)\right\},$$

  associated with the operator $L$. What does it mean to say $u(x)$ is reflectionless?

  Given $S$, define the function

  $$F(x)=\sum_{n=1}^{N} c_{n}^{2} e^{-\chi_{n} x}+\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{\mathrm{i} k x} R(k) \mathrm{d} k$$

  If $K=K(x, y)$ is the unique solution to the GLM equation

  $$K(x, y)+F(x+y)+\int_{x}^{\infty} K(x, z) F(z+y) \mathrm{d} z=0$$

  what is the relationship between $u(x)$ and $K(x, x)$ ?

  Now suppose that $u=u(x, t)$ is time dependent and that it solves the KdV equation $u_{t}+u_{x x x}-6 u u_{x}=0$. Show that $L=-\partial_{x}^{2}+u(x, t)$ obeys the Lax equation

  $$L_{t}=[L, A], \quad \text { where } A=4 \partial_{x}^{3}-3\left(u \partial_{x}+\partial_{x} u\right) .$$

  Show that the discrete eigenvalues of $L$ are time independent.

  In what follows you may assume the time-dependent scattering data take the form

  $$S(t)=\left\{\left\{\chi_{n}, c_{n} e^{4 \chi_{n}^{3} t}\right\}_{n=1}^{N}, R(k, 0) e^{8 \mathrm{i} k^{3} t}\right\} .$$

  Show that if $u(x, 0)$ is reflectionless, then the solution to the KdV equation takes the form

  $$u(x, t)=-2 \frac{\partial^{2}}{\partial x^{2}} \log [\operatorname{det} A(x, t)]$$

  where $A$ is an $N \times N$ matrix which you should determine.

  Assume further that $R(k, 0)=k^{2} f(k)$, where $f$ is smooth and decays rapidly at infinity. Show that, for any fixed $x$,

  $$\int_{-\infty}^{\infty} e^{\mathrm{i} k x} R(k, 0) e^{8 \mathrm{i} k^{3} t} \mathrm{~d} k=O\left(t^{-1}\right) \quad \text { as } t \rightarrow \infty$$

  Comment briefly on the significance of this result.

  [You may assume $\frac{1}{\operatorname{det} A} \frac{\mathrm{d}}{\mathrm{d} x}(\operatorname{det} A)=\operatorname{tr}\left(A^{-1} \frac{\mathrm{d} A}{\mathrm{~d} x}\right)$ for a non-singular matrix $A(x)$.]

  comment

Linear Analysis

• Paper 2, Section II, G

  Linear Analysis | Part II, 2014

  (a) Let $X$ and $Y$ be Banach spaces, and let $T: X \rightarrow Y$ be a surjective linear map. Assume that there is a constant $c>0$ such that $\|T x\| \geqslant c\|x\|$ for all $x \in X$. Show that $T$ is continuous. [You may use any standard result from general Banach space theory provided you clearly state it.] Give an example to show that the assumption that $X$ and $Y$ are complete is necessary.

  (b) Let $C$ be a closed subset of a Banach space $X$ such that

  (i) $x_{1}+x_{2} \in C$ for each $x_{1}, x_{2} \in C$;

  (ii) $\lambda x \in C$ for each $x \in C$ and $\lambda>0$;

  (iii) for each $x \in X$, there exist $x_{1}, x_{2} \in C$ such that $x=x_{1}-x_{2}$.

  Prove that, for some $M>0$, the unit ball of $X$ is contained in the closure of the set

  $$\left\{x_{1}-x_{2}: x_{i} \in C, \quad\left\|x_{i}\right\| \leqslant M(i=1,2)\right\} .$$

  [You may use without proof any version of the Baire Category Theorem.] Deduce that, for some $K>0$, every $x \in X$ can be written as $x=x_{1}-x_{2}$ with $x_{i} \in C$ and $\left\|x_{i}\right\| \leqslant K\|x\|(i=1,2) .$

  comment

Logic and Set Theory

• Paper 2, Section II, I

  Logic and Set Theory | Part II, 2014

  Write down the recursive definitions of ordinal addition, multiplication and exponentiation. Show that, for any nonzero ordinal $\alpha$, there exist unique ordinals $\beta, \gamma$ and $n$ such that $\alpha=\omega^{\beta} . n+\gamma, \gamma<\omega^{\beta}$ and $0<n<\omega$.

  Hence or otherwise show that $\alpha$ (that is, the set of ordinals less than $\alpha$ ) is closed under addition if and only if $\alpha=\omega^{\beta}$ for some $\beta$. Show also that an infinite ordinal $\alpha$ is closed under multiplication if and only if $\alpha=\omega^{\left(\omega^{\gamma}\right)}$ for some $\gamma$.

  [You may assume the standard laws of ordinal arithmetic, and the fact that $\alpha \leqslant \omega^{\alpha}$ for all $\alpha$.]

  comment

Mathematical Biology

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2014

  Consider an experiment where two or three individuals are added to a population with probability $\lambda_{2}$ and $\lambda_{3}$ respectively per unit time. The death rate in the population is a constant $\beta$ per individual per unit time.

  Write down the master equation for the probability $p_{n}(t)$ that there are $n$ individuals in the population at time $t$. From this, derive an equation for $\frac{\partial \phi}{\partial t}$, where $\phi$ is the generating function

  $$\phi(s, t)=\sum_{n=0}^{\infty} s^{n} p_{n}(t)$$

  Find the solution for $\phi$ in steady state, and show that the mean and variance of the population size are given by

  $$\langle n\rangle=3 \frac{\lambda_{3}}{\beta}+2 \frac{\lambda_{2}}{\beta}, \quad \operatorname{var}(n)=6 \frac{\lambda_{3}}{\beta}+3 \frac{\lambda_{2}}{\beta} .$$

  Hence show that, for a free choice of $\lambda_{2}$ and $\lambda_{3}$ subject to a given target mean, the experimenter can minimise the variance by only adding two individuals at a time.

  comment

• Paper 2, Section II, B

  Mathematical Biology | Part II, 2014

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} \frac{\partial u}{\partial t} &=\frac{a u}{v}-u^{2}+d_{1} \frac{\partial^{2} u}{\partial x^{2}} \\ \frac{\partial v}{\partial t} &=v^{2}-\frac{v}{u^{2}}+d_{2} \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  where $a, d_{1}, d_{2}>0$.

  Find the range of $a$ for which the spatially homogeneous system has a stable equilibrium solution with $u>0$ and $v>0$. Determine when the equilibrium is a stable focus, and sketch the phase diagram for this case (restricting attention to $u>0$ and $v>0)$.

  For the case when the homogeneous system is stable, consider spatial perturbations proportional to $\cos (k x)$ of the solution found above. Briefly explain why the system will be stable to spatial perturbations with very small or very large $k$. Find conditions for the system to be unstable to a spatial perturbation (for some range of $k$ which need not be given). Sketch the region satisfying these conditions in the $\left(a, d_{1} / d_{2}\right)$ plane.

  Find $k_{c}$, the critical wavenumber at the onset of instability, in terms of $a$ and $d_{1}$.

  comment

Number Fields

• Paper 2, Section II, F

  Number Fields | Part II, 2014

  (i) Show that each prime ideal in a number field $K$ divides a unique rational prime $p$. Define the ramification index and residue class degree of such an ideal. State and prove a formula relating these numbers, for all prime ideals dividing a given rational prime $p$, to the degree of $K$ over $\mathbb{Q}$.

  (ii) Show that if $\zeta_{n}$ is a primitive $n$th root of unity then $\prod_{j=1}^{n-1}\left(1-\zeta_{n}^{j}\right)=n$. Deduce that if $n=p q$, where $p$ and $q$ are distinct primes, then $1-\zeta_{n}$ is a unit in $\mathbb{Z}\left[\zeta_{n}\right]$.

  (iii) Show that if $K=\mathbb{Q}\left(\zeta_{p}\right)$ where $p$ is prime, then any prime ideal of $K$ dividing $p$ has ramification index at least $p-1$. Deduce that $[K: \mathbb{Q}]=p-1$.

  comment

Number Theory

• Paper 2, Section I, F

  Number Theory | Part II, 2014

  Show that

  $$\sum_{p \leqslant x} \frac{1}{p} \geqslant \log \log x-\frac{1}{2}$$

  Deduce that there are infinitely many primes.

  comment

Numerical Analysis

• Paper 2, Section II, D

  Numerical Analysis | Part II, 2014

  Consider the one-dimensional advection equation

  $$u_{t}=u_{x}, \quad-\infty<x<\infty, \quad t \geqslant 0$$

  subject to an initial condition $u(x, 0)=\varphi(x)$. Consider discretization of this equation with finite differences on an equidistant space-time $\left\{(m h, n k), m \in \mathbb{Z}, n \in \mathbb{Z}^{+}\right\}$with step size $h>0$ in space and step size $k>0$ in time. Define the Courant number $\mu$ and explain briefly how such a discretization can be used to derive numerical schemes in which solutions $u_{m}^{n} \approx u(m h, n k), m \in \mathbb{Z}$ and $n \in \mathbb{Z}^{+}$satisfy equations of the form

  $$\sum_{i=r}^{s} a_{i} u_{m+i}^{n+1}=\sum_{i=r}^{s} b_{i} u_{m+i}^{n}$$

  where the coefficients $a_{i}, b_{i}$ are independent of $m, n$.

  (i) Define the order of a numerical scheme such as (1). Define what a convergent numerical scheme is. Explain the notion of stability and state the Lax equivalence theorem that connects convergence and stability of numerical schemes for linear partial differential equations.

  (ii) Consider the following example of (1):

  $$u_{m}^{n+1}=u_{m}^{n}+\frac{\mu}{2}\left(u_{m+1}^{n}-u_{m-1}^{n}\right)+\frac{\mu^{2}}{2}\left(u_{m+1}^{n}-2 u_{m}^{n}+u_{m-1}^{n}\right) .$$

  Determine conditions on $\mu$ such that the scheme $(2)$ is stable and convergent. What is the order of this scheme?

  comment

Optimization and Control

• Paper 2, Section II, J

  Optimization and Control | Part II, 2014

  Describe the elements of a discrete-time stochastic dynamic programming equation for the problem of maximizing the expected sum of non-negative rewards over an infinite horizon. Give an example to show that there may not exist an optimal policy. Prove that if a policy has a value function that satisfies the dynamic programming equation then the policy is optimal.

  A squirrel collects nuts for the coming winter. There are plenty of nuts lying around, but each time the squirrel leaves its lair it risks being caught by a predator. Assume that the outcomes of the squirrel's journeys are independent, that it is caught with probability $p$, and that it returns safely with a random weight of nuts, exponentially distributed with parameter $\lambda$. By solving the dynamic programming equation for the value function $F(x)$, find a policy maximizing the expected weight of nuts collected for the winter. Here the state variable $x$ takes values in $\mathbb{R}_{+}$(the weight of nuts so far collected) or $-1$ (a no-return state when the squirrel is caught).

  comment

Partial Differential Equations

• Paper 2, Section II, D

  Partial Differential Equations | Part II, 2014

  In this question, functions are all real-valued, and

  $$H_{p e r}^{s}=\left\{u=\sum_{m \in \mathbb{Z}} \hat{u}(m) e^{i m x} \in L^{2}:\|u\|_{H^{s}}^{2}=\sum_{m \in \mathbb{Z}}\left(1+m^{2}\right)^{s}|\hat{u}(m)|^{2}<\infty\right\}$$

  are the Sobolev spaces of functions $2 \pi$-periodic in $x$, for $s=0,1,2, \ldots$

  State Parseval's theorem. For $s=0,1$ prove that the norm $\|u\|_{H^{s}}$ is equivalent to the norm ||$_{s}$ defined by

  $$\|u\|_{s}^{2}=\sum_{r=0}^{s} \int_{-\pi}^{+\pi}\left(\partial_{x}^{r} u\right)^{2} d x$$

  Consider the Cauchy problem

  $$u_{t}-u_{x x}=f, \quad u(x, 0)=u_{0}(x), \quad t \geqslant 0,$$

  where $f=f(x, t)$ is a smooth function which is $2 \pi$-periodic in $x$, and the initial value $u_{0}$ is also smooth and $2 \pi$-periodic. Prove that if $u$ is a smooth solution which is $2 \pi$-periodic in $x$, then it satisfies

  $$\int_{0}^{T}\left(u_{t}^{2}+u_{x x}^{2}\right) d t \leqslant C\left(\left\|u_{0}\right\|_{H^{1}}^{2}+\int_{0}^{T} \int_{-\pi}^{\pi}|f(x, t)|^{2} d x d t\right)$$

  for some number $C>0$ which does not depend on $u$ or $f$.

  State the Lax-Milgram lemma. Prove, using the Lax-Milgram lemma, that if

  $$f(x, t)=e^{\lambda t} g(x)$$

  with $g \in H_{p e r}^{0}$ and $\lambda>0$, then there exists a weak solution to (1) of the form $u(x, t)=e^{\lambda t} \phi(x)$ with $\phi \in H_{\text {per. }}^{1}$. Does the same hold for all $\lambda \in \mathbb{R}$ ? Briefly explain your answer.

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  (i) Let $a$ and $a^{\dagger}$ be the annihilation and creation operators, respectively, for a simple harmonic oscillator whose Hamiltonian is

  $$H_{0}=\omega\left(a^{\dagger} a+\frac{1}{2}\right),$$

  with $\left[a, a^{\dagger}\right]=1$. Explain how the set of eigenstates $\{|n\rangle: n=0,1,2, \ldots\}$ of $H_{0}$ is obtained and deduce the corresponding eigenvalues. Show that

  (ii) Consider a system whose unperturbed Hamiltonian is

  $$H_{0}=\left(a^{\dagger} a+\frac{1}{2}\right)+2\left(b^{\dagger} b+\frac{1}{2}\right)$$

  where $\left[a, a^{\dagger}\right]=1, \quad\left[b, b^{\dagger}\right]=1$ and all other commutators are zero. Find the degeneracies of the eigenvalues of $H_{0}$ with energies $E_{0}=\frac{3}{2}, \frac{5}{2}, \frac{7}{2}, \frac{9}{2}$ and $\frac{11}{2}$.

  The system is perturbed so that it is now described by the Hamiltonian

  $$H=H_{0}+\lambda H^{\prime},$$

  where $H^{\prime}=\left(a^{\dagger}\right)^{2} b+a^{2} b^{\dagger}$. Using degenerate perturbation theory, calculate to $O(\lambda)$ the energies of the eigenstates associated with the level $E_{0}=\frac{9}{2}$.

  Write down the eigenstates, to $O(\lambda)$, associated with these perturbed energies. By explicit evaluation show that they are in fact exact eigenstates of $H$ with these energies as eigenvalues.

  $$\begin{aligned} & a|0\rangle=0 \\ & a|n\rangle=\sqrt{n}|n-1\rangle, \quad n \geqslant 1, \\ & a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle, \quad n \geqslant 0 . \end{aligned}$$

  comment

Principles of Statistics

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2014

  In a general decision problem, define the concepts of a Bayes rule and of admissibility. Show that a unique Bayes rule is admissible.

  Consider i.i.d. observations $X_{1}, \ldots, X_{n}$ from a $\operatorname{Poisson}(\theta), \theta \in \Theta=(0, \infty)$, model. Can the maximum likelihood estimator $\hat{\theta}_{M L E}$ of $\theta$ be a Bayes rule for estimating $\theta$ in quadratic risk for any prior distribution on $\theta$ that has a continuous probability density on $(0, \infty) ?$ Justify your answer.

  Now model the $X_{i}$ as i.i.d. copies of $X \mid \theta \sim \operatorname{Poisson}(\theta)$, where $\theta$ is drawn from a prior that is a Gamma distribution with parameters $\alpha>0$ and $\lambda>0$ (given below). Show that the posterior distribution of $\theta \mid X_{1}, \ldots, X_{n}$ is a Gamma distribution and find its parameters. Find the Bayes rule $\hat{\theta}_{B A Y E S}$ for estimating $\theta$ in quadratic risk for this prior. [The Gamma probability density function with parameters $\alpha>0, \lambda>0$ is given by

  $$f(\theta)=\frac{\lambda^{\alpha} \theta^{\alpha-1} e^{-\lambda \theta}}{\Gamma(\alpha)}, \quad \theta>0$$

  where $\Gamma(\alpha)$ is the usual Gamma function.]

  Finally assume that the $X_{i}$ have actually been generated from a fixed Poisson $\left(\theta_{0}\right)$ distribution, where $\theta_{0}>0$. Show that $\sqrt{n}\left(\hat{\theta}_{B A Y E S}-\hat{\theta}_{M L E}\right)$ converges to zero in probability and deduce the asymptotic distribution of $\sqrt{n}\left(\hat{\theta}_{B A Y E S}-\theta_{0}\right)$ under the joint law $P_{\theta_{0}}^{\mathbb{N}}$ of the random variables $X_{1}, X_{2}, \ldots$. [You may use standard results from lectures without proof provided they are clearly stated.]

  comment

Probability and Measure

• Paper 2, Section II, $26 K$

  Probability and Measure | Part II, 2014

  State and prove the monotone convergence theorem.

  Let $\left(E_{1}, \mathcal{E}_{1}, \mu_{1}\right)$ and $\left(E_{2}, \mathcal{E}_{2}, \mu_{2}\right)$ be finite measure spaces. Define the product $\sigma$-algebra $\mathcal{E}=\mathcal{E}_{1} \otimes \mathcal{E}_{2}$ on $E_{1} \times E_{2}$.

  Define the product measure $\mu=\mu_{1} \otimes \mu_{2}$ on $\mathcal{E}$, and show carefully that $\mu$ is countably additive.

  [You may use without proof any standard facts concerning measurability provided these are clearly stated.]

  comment

Representation Theory

• Paper 2, Section II, H

  Representation Theory | Part II, 2014

  In this question work over $\mathbb{C}$. Let $H$ be a subgroup of $G$. State Mackey's restriction formula, defining all the terms you use. Deduce Mackey's irreducibility criterion.

  Let $G=\left\langle g, r: g^{m}=r^{2}=1, r g r^{-1}=g^{-1}\right\rangle$ (the dihedral group of order $2 m$ ) and let $H=\langle g\rangle$ (the cyclic subgroup of $G$ of order $m$ ). Write down the $m$ inequivalent irreducible characters $\chi_{k}(1 \leqslant k \leqslant m)$ of $H$. Determine the values of $k$ for which the induced character $\operatorname{Ind}_{H}^{G} \chi_{k}$ is irreducible.

  comment

Riemann Surfaces

• Paper 2, Section II, H

  Riemann Surfaces | Part II, 2014

  State and prove the Valency Theorem and define the degree of a non-constant holomorphic map between compact Riemann surfaces.

  Let $X$ be a compact Riemann surface of genus $g$ and $\pi: X \rightarrow \mathbb{C}_{\infty}$ a holomorphic map of degree two. Find the cardinality of the set $R$ of ramification points of $\pi$. Find also the cardinality of the set of branch points of $\pi$. [You may use standard results from lectures provided they are clearly stated.]

  Define $\sigma: X \rightarrow X$ as follows: if $p \in R$, then $\sigma(p)=p$; otherwise, $\sigma(p)=q$ where $q$ is the unique point such that $\pi(q)=\pi(p)$ and $p \neq q$. Show that $\sigma$ is a conformal equivalence with $\pi \sigma=\pi$ and $\sigma \sigma=$ id.

  comment

Statistical Modelling

• Paper 2, Section I, K

  Statistical Modelling | Part II, 2014

  Define the concept of an exponential dispersion family. Show that the family of scaled binomial distributions $\frac{1}{n} \operatorname{Bin}(n, p)$, with $p \in(0,1)$ and $n \in \mathbb{N}$, is of exponential dispersion family form.

  Deduce the mean of the scaled binomial distribution from the exponential dispersion family form.

  What is the canonical link function in this case?

  comment

Statistical Physics

• Paper 2, Section II, E

  Statistical Physics | Part II, 2014

  Briefly describe the microcanonical, canonical and grand canonical ensembles. Why do they agree in the thermodynamic limit?

  A harmonic oscillator in one spatial dimension has Hamiltonian

  $$H=\frac{p^{2}}{2 m}+\frac{m}{2} \omega^{2} x^{2}$$

  Here $p$ and $x$ are the momentum and position of the oscillator, $m$ is its mass and $\omega$ its frequency. The harmonic oscillator is placed in contact with a heat bath at temperature $T$. What is the relevant ensemble?

  Treating the harmonic oscillator classically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  Treating the harmonic oscillator quantum mechanically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  In what limit of temperature do the classical and quantum results agree? Explain why they differ away from this limit. Describe an experiment for which this difference has implications.

  comment

Stochastic Financial Models

• Paper 2, Section II, K

  Stochastic Financial Models | Part II, 2014

  An agent has expected-utility preferences over his possible wealth at time 1 ; that is, the wealth $Z$ is preferred to wealth $Z^{\prime}$ if and only if $E U(Z) \geqslant E U\left(Z^{\prime}\right)$, where the function $U: \mathbb{R} \rightarrow \mathbb{R}$ is strictly concave and twice continuously differentiable. The agent can trade in a market, with the time-1 value of his portfolio lying in an affine space $\mathcal{A}$ of random variables. Assuming cash can be held between time 0 and time 1 , define the agent's time-0 utility indifference price $\pi(Y)$ for a contingent claim with time-1 value $Y$. Assuming any regularity conditions you may require, prove that the map $Y \mapsto \pi(Y)$ is concave.

  

  Consider a market with two claims with time-1 values $X$ and $Y$. Their joint distribution is

  $$\left(\begin{array}{l} X \\ Y \end{array}\right) \sim N\left(\left(\begin{array}{l} \mu_{X} \\ \mu_{Y} \end{array}\right),\left(\begin{array}{ll} V_{X X} & V_{X Y} \\ V_{Y X} & V_{Y Y} \end{array}\right)\right) .$$

  At time 0 , arbitrary quantities of the claim $X$ can be bought at price $p$, but $Y$ is not marketed. Derive an explicit expression for $\pi(Y)$ in the case where

  $$U(x)=-\exp (-\gamma x)$$

  where $\gamma>0$ is a given constant.

  comment

Topics in Analysis

• Paper 2, Section I, G

  Topics in Analysis | Part II, 2014

  State Chebyshev's equal ripple criterion.

  Let

  $$h(t)=\prod_{\ell=1}^{n}\left(t-\cos \frac{(2 \ell-1) \pi}{2 n}\right)$$

  Show that if $q(t)=\sum_{j=0}^{n} a_{j} t^{j}$ where $a_{0}, \ldots, a_{n}$ are real constants with $\left|a_{n}\right| \geqslant 1$, then

  $$\sup _{t \in[-1,1]}|h(t)| \leqslant \sup _{t \in[-1,1]}|q(t)|$$

  comment

• Paper 2, Section II, G

  Topics in Analysis | Part II, 2014

  Let $\gamma:[0,1] \rightarrow \mathbb{C}$ be a continuous map never taking the value 0 and satisfying $\gamma(0)=\gamma(1)$. Define the degree (or winding number) $w(\gamma ; 0)$ of $\gamma$ about 0 . Prove the following:

  (i) $w(1 / \gamma ; 0)=w\left(\gamma^{-} ; 0\right)$, where $\gamma^{-}(t)=\gamma(1-t)$.

  (ii) If $\sigma:[0,1] \rightarrow \mathbb{C}$ is continuous, $\sigma(0)=\sigma(1)$ and $|\sigma(t)|<|\gamma(t)|$ for each $0 \leqslant t \leqslant 1$, then $w(\gamma+\sigma ; 0)=w(\gamma ; 0)$.

  (iii) If $\gamma_{m}:[0,1] \rightarrow \mathbb{C}, m=1,2, \ldots$, are continuous maps with $\gamma_{m}(0)=\gamma_{m}(1)$, which converge to $\gamma$ uniformly on $[0,1]$ as $m \rightarrow \infty$, then $w\left(\gamma_{m} ; 0\right)=w(\gamma ; 0)$ for sufficiently large $m$.

  Let $\alpha:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map such that $\alpha(0)=\alpha(1)$ and $\left|\alpha(t)-e^{2 \pi i t}\right| \leqslant 1$ for each $t \in[0,1]$. Deduce from the results of (ii) and (iii) that $w(\alpha ; 0)=1$.

  [You may not use homotopy invariance of the winding number without proof.]

  comment

Waves

• Paper 2, Section II, 38C

  Waves | Part II, 2014

  The function $\phi(x, t)$ satisfies the equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}-\frac{\partial^{2} \phi}{\partial x^{2}}=\frac{\partial^{4} \phi}{\partial x^{2} \partial t^{2}}$$

  Derive the dispersion relation, and sketch graphs of frequency, phase velocity and group velocity as functions of the wavenumber. In the case of a localised initial disturbance, will it be the shortest or the longest waves that are to be found at the front of a dispersing wave packet? Do the wave crests move faster or slower than the wave packet?

  Give the solution to the initial-value problem for which at $t=0$

  $$\phi=\int_{-\infty}^{\infty} A(k) e^{i k x} d k \quad \text { and } \quad \frac{\partial \phi}{\partial t}=0$$

  and $\phi(x, 0)$ is real. Use the method of stationary phase to obtain an approximation for $\phi(V t, t)$ for fixed $0<V<1$ and large $t$. If, in addition, $\phi(x, 0)=\phi(-x, 0)$, deduce an approximation for the sequence of times at which $\phi(V t, t)=0$.

  You are given that $\phi(t, t)$ decreases like $t^{-1 / 4}$ for large $t$. Give a brief physical explanation why this rate of decay is slower than for $0<V<1$. What can be said about $\phi(V t, t)$ for large $t$ if $V>1$ ? [Detailed calculation is not required in these cases.]

  [You may assume that $\int_{-\infty}^{\infty} e^{-a u^{2}} d u=\sqrt{\frac{\pi}{a}} \quad$ for $\left.\operatorname{Re}(a) \geqslant 0, a \neq 0 .\right]$

  comment