Part II, 2014

Algebraic Geometry

• Paper 1, Section II, H

  Algebraic Geometry | Part II, 2014

  Let $k$ be an algebraically closed field and $n \geqslant 1$. We say that $f \in k\left[x_{1}, \ldots, x_{n}\right]$ is singular at $p \in \mathbf{A}^{n}$ if either $p$ is a singularity of the hypersurface $\{f=0\}$ or $f$ has an irreducible factor $h$ of multiplicity strictly greater than one with $h(p)=0$. Given $d \geqslant 1$, let $X=\left\{f \in k\left[x_{1}, \ldots, x_{n}\right] \mid \operatorname{deg} f \leqslant d\right\}$ and let

  $$Y=\left\{(f, p) \in X \times \mathbf{A}^{n} \mid f \text { is singular at } p\right\}$$

  (i) Show that $X \simeq \mathbf{A}^{N}$ for some $N$ (you need not determine $N$ ) and that $Y$ is a Zariski closed subvariety of $X \times \mathbf{A}^{n}$.

  (ii) Show that the fibres of the projection map $Y \rightarrow \mathbf{A}^{n}$ are linear subspaces of $\operatorname{dim} e n s i o n N-(n+1)$. Conclude that $\operatorname{dim} Y<\operatorname{dim} X$.

  (iii) Hence show that $\{f \in X \mid \operatorname{deg} f=d, Z(f)$ smooth $\}$ is dense in $X$.

  [You may use standard results from lectures if they are accurately quoted.]

  comment

• Paper 2, Section II, H

  Algebraic Geometry | Part II, 2014

  (i) Let $k$ be an algebraically closed field, $n \geqslant 1$, and $S$ a subset of $k^{n}$.

  Let $I(S)=\left\{f \in k\left[x_{1}, \ldots, x_{n}\right] \mid f(p)=0\right.$ when $\left.p \in S\right\}$. Show that $I(S)$ is an ideal, and that $k\left[x_{1}, \ldots, x_{n}\right] / I(S)$ does not have any non-zero nilpotent elements.

  Let $X \subseteq \mathbf{A}^{n}, Y \subseteq \mathbf{A}^{m}$ be affine varieties, and $\Phi: k[Y] \rightarrow k[X]$ be a $k$-algebra homomorphism. Show that $\Phi$ determines a map of sets from $X$ to $Y$.

  (ii) Let $X$ be an irreducible affine variety. Define the dimension of $X, \operatorname{dim} X$ (in terms of the tangent spaces of $X$ ) and the transcendence dimension of $X, \operatorname{tr} \cdot \operatorname{dim} X$.

  State the Noether normalization theorem. Using this, or otherwise, prove that the transcendence dimension of $X$ equals the dimension of $X$.

  comment

• Paper 3, Section II, H

  Algebraic Geometry | Part II, 2014

  Let $f \in k[x]$ be a polynomial with distinct roots, $\operatorname{deg} f=d>2$, char $k=0$, and let $C \subseteq \mathbf{P}^{2}$ be the projective closure of the affine curve

  $$y^{d-1}=f(x)$$

  Show that $C$ is smooth, with a single point at $\infty$.

  Pick an appropriate $\omega \in \Omega_{k(C) / k}^{1}$ and compute the valuation $v_{q}(\omega)$ for all $q \in C$.

  Hence determine $\operatorname{deg} \mathcal{K}_{C}$.

  comment

• Paper 4, Section II, H

  Algebraic Geometry | Part II, 2014

  Let $X$ be a smooth projective curve of genus $g>0$ over an algebraically closed field of characteristic $\neq 2$, and suppose there is a degree 2 morphism $\pi: X \rightarrow \mathbf{P}^{1}$. How many ramification points of $\pi$ are there?

  Suppose $Q$ and $R$ are distinct ramification points of $\pi$. Show that $Q \nsim R$, but $2 Q \sim 2 R$.

  Now suppose $g=2$. Show that every divisor of degree 2 on $X$ is linearly equivalent to $P+P^{\prime}$ for some $P, P^{\prime} \in X$, and deduce that every divisor of degree 0 is linearly equivalent to $P_{1}-P_{2}$ for some $P_{1}, P_{2} \in X$.

  Show that the subgroup $\left\{[D] \in C l^{0}(X) \mid 2[D]=0\right\}$ of the divisor class group of $X$ has order $16 .$

  comment

Algebraic Topology

• Paper 1, Section II, F

  Algebraic Topology | Part II, 2014

  Define what it means for a map $p: \widetilde{X} \rightarrow X$ to be a covering space. State the homotopy lifting lemma.

  Let $p:\left(\tilde{X}, \tilde{x}_{0}\right) \rightarrow\left(X, x_{0}\right)$ be a based covering space and let $f:\left(Y, y_{0}\right) \rightarrow\left(X, x_{0}\right)$ be a based map from a path-connected and locally path-connected space. Show that there is a based lift $\tilde{f}:\left(Y, y_{0}\right) \rightarrow\left(\tilde{X}, \tilde{x}_{0}\right)$ of $f$ if and only if $f_{*}\left(\pi_{1}\left(Y, y_{0}\right)\right) \subseteq p_{*}\left(\pi_{1}\left(\widetilde{X}, \tilde{x}_{0}\right)\right)$.

  comment

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2014

  Let $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ be a matrix with integer entries. Considering $S^{1}$ as the quotient space $\mathbb{R} / \mathbb{Z}$, show that the function

  $$\begin{aligned} \varphi_{A}: S^{1} \times S^{1} & \longrightarrow S^{1} \times S^{1} \\ ([x],[y]) & \longmapsto([a x+b y],[c x+d y]) \end{aligned}$$

  is well-defined and continuous. If in addition $\operatorname{det}(A)=\pm 1$, show that $\varphi_{A}$ is a homeomorphism.

  State the Seifert-van Kampen theorem. Let $X_{A}$ be the space obtained by gluing together two copies of $S^{1} \times D^{2}$ along their boundaries using the homeomorphism $\varphi_{A}$. Show that the fundamental group of $X_{A}$ is cyclic and determine its order.

  comment

• Paper 3, Section II, F

  Algebraic Topology | Part II, 2014

  Let $K$ be a simplicial complex in $\mathbb{R}^{N}$, which we may also consider as lying in $\mathbb{R}^{N+1}$ using the first $N$ coordinates. Write $c=(0,0, \ldots, 0,1) \in \mathbb{R}^{N+1}$. Show that if $\left\langle v_{0}, v_{1}, \ldots, v_{n}\right\rangle$ is a simplex of $K$ then $\left\langle v_{0}, v_{1}, \ldots, v_{n}, c\right\rangle$ is a simplex in $\mathbb{R}^{N+1}$.

  Let $L \leqslant K$ be a subcomplex and let $\bar{K}$ be the collection

  $$K \cup\left\{\left\langle v_{0}, v_{1}, \ldots, v_{n}, c\right\rangle \mid\left\langle v_{0}, v_{1}, \ldots, v_{n}\right\rangle \in L\right\} \cup\{\langle c\rangle\}$$

  of simplices in $\mathbb{R}^{N+1}$. Show that $\bar{K}$ is a simplicial complex.

  If $|K|$ is a Möbius band, and $|L|$ is its boundary, show that

  $$H_{i}(\bar{K}) \cong \begin{cases}\mathbb{Z} & \text { if } i=0 \\ \mathbb{Z} / 2 & \text { if } i=1 \\ 0 & \text { if } i \geqslant 2\end{cases}$$

  comment

• Paper 4, Section II, F

  Algebraic Topology | Part II, 2014

  State the Lefschetz fixed point theorem.

  Let $X$ be an orientable surface of genus $g$ (which you may suppose has a triangulation), and let $f: X \rightarrow X$ be a continuous map such that

  1. $f^{3}=\operatorname{Id}_{X}$,

  2. $f$ has no fixed points.

  By considering the eigenvalues of the linear map $f_{*}: H_{1}(X ; \mathbb{Q}) \rightarrow H_{1}(X ; \mathbb{Q})$, and their multiplicities, show that $g$ must be congruent to 1 modulo 3 .

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  A particle of mass $m$ scatters on a localised potential well $V(x)$ in one dimension. With reference to the asymptotic behaviour of the wavefunction as $x \rightarrow \pm \infty$, define the reflection and transmission amplitudes, $r$ and $t$, for a right-moving incident particle of wave number $k$. Define also the corresponding amplitudes, $r^{\prime}$ and $t^{\prime}$, for a left-moving incident particle of wave number $k$. Derive expressions for $r^{\prime}$ and $t^{\prime}$ in terms of $r$ and $t$.

  (a) Define the $S$-matrix, giving its elements in terms of $r$ and $t$. Using the relation

  $$|r|^{2}+|t|^{2}=1$$

  (which you need not derive), show that the S-matrix is unitary. How does the S-matrix simplify if the potential well satisfies $V(-x)=V(x)$ ?

  (b) Consider the potential well

  $$V(x)=-\frac{3 \hbar^{2}}{m} \frac{1}{\cosh ^{2}(x)}$$

  The corresponding Schrödinger equation has an exact solution

  $$\psi_{k}(x)=\exp (i k x)\left[3 \tanh ^{2}(x)-3 i k \tanh (x)-\left(1+k^{2}\right)\right]$$

  with energy $E=\hbar^{2} k^{2} / 2 m$, for every real value of $k$. [You do not need to verify this.] Find the S-matrix for scattering on this potential. What special feature does the scattering have in this case?

  (c) Explain the connection between singularities of the S-matrix and bound states of the potential well. By analytic continuation of the solution $\psi_{k}(x)$ to appropriate complex values of $k$, find the wavefunctions and energies of the bound states of the well. [You do not need to normalise the wavefunctions.]

  comment

• Paper 2, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  (a) A classical particle of mass $m$ scatters on a central potential $V(r)$ with energy $E$, impact parameter $b$, and scattering angle $\theta$. Define the corresponding differential cross-section.

  For particle trajectories in the Coulomb potential,

  $$V_{C}(r)=\frac{e^{2}}{4 \pi \epsilon_{0} r}$$

  the impact parameter is given by

  $$b=\frac{e^{2}}{8 \pi \epsilon_{0} E} \cot \left(\frac{\theta}{2}\right)$$

  Find the differential cross-section as a function of $E$ and $\theta$.

  (b) A quantum particle of mass $m$ and energy $E=\hbar^{2} k^{2} / 2 m$ scatters in a localised potential $V(\mathbf{r})$. With reference to the asymptotic form of the wavefunction at large $|\mathbf{r}|$, define the scattering amplitude $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$ as a function of the incident and outgoing wavevectors $\mathbf{k}$ and $\mathbf{k}^{\prime}$ (where $|\mathbf{k}|=\left|\mathbf{k}^{\prime}\right|=k$ ). Define the differential cross-section for this process and express it in terms of $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$.

  Now consider a potential of the form $V(\mathbf{r})=\lambda U(\mathbf{r})$, where $\lambda \ll 1$ is a dimensionless coupling and $U$ does not depend on $\lambda$. You may assume that the Schrödinger equation for the wavefunction $\psi(\mathbf{k} ; \mathbf{r})$ of a scattering state with incident wavevector $\mathbf{k}$ may be written as the integral equation

  $$\psi(\mathbf{k} ; \mathbf{r})=\exp (i \mathbf{k} \cdot \mathbf{r})+\frac{2 m \lambda}{\hbar^{2}} \int d^{3} r^{\prime} \mathcal{G}_{0}^{(+)}\left(k ; \mathbf{r}-\mathbf{r}^{\prime}\right) U\left(\mathbf{r}^{\prime}\right) \psi\left(\mathbf{k} ; \mathbf{r}^{\prime}\right)$$

  where

  $$\mathcal{G}_{0}^{(+)}(k ; \mathbf{r})=-\frac{1}{4 \pi} \frac{\exp (i k|\mathbf{r}|)}{|\mathbf{r}|}$$

  Show that the corresponding scattering amplitude is given by

  $$f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)=-\frac{m \lambda}{2 \pi \hbar^{2}} \int d^{3} r^{\prime} \exp \left(-i \mathbf{k}^{\prime} \cdot \mathbf{r}^{\prime}\right) U\left(\mathbf{r}^{\prime}\right) \psi\left(\mathbf{k} ; \mathbf{r}^{\prime}\right)$$

  By expanding the wavefunction in powers of $\lambda$ and keeping only the leading term, calculate the leading-order contribution to the differential cross-section, and evaluate it for the case of the Yukawa potential

  $$V(\mathbf{r})=\lambda \frac{\exp (-\mu r)}{r}$$

  By taking a suitable limit, obtain the differential cross-section for quantum scattering in the Coulomb potential $V_{C}(r)$ defined in Part (a) above, correct to leading order in an expansion in powers of the constant $\tilde{\alpha}=e^{2} / 4 \pi \epsilon_{0}$. Express your answer as a function of the particle energy $E$ and scattering angle $\theta$, and compare it to the corresponding classical cross-section calculated in Part (a).

  Part II, $2014 \quad$ List of Questions

  [TURN OVER

  comment

• Paper 3, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  In the nearly-free electron model a particle of mass $m$ moves in one dimension in a periodic potential of the form $V(x)=\lambda U(x)$, where $\lambda \ll 1$ is a dimensionless coupling and $U(x)$ has a Fourier series

  $$U(x)=\sum_{l=-\infty}^{+\infty} U_{l} \exp \left(\frac{2 \pi i}{a} l x\right)$$

  with coefficients obeying $U_{-l}=U_{l}^{*}$ for all $l$.

  Ignoring any degeneracies in the spectrum, the exact energy $E(k)$ of a Bloch state with wavenumber $k$ can be expanded in powers of $\lambda$ as

  $$E(k)=E_{0}(k)+\lambda\langle k|U| k\rangle+\lambda^{2} \sum_{k^{\prime} \neq k} \frac{\left\langle k|U| k^{\prime}\right\rangle\left\langle k^{\prime}|U| k\right\rangle}{E_{0}(k)-E_{0}\left(k^{\prime}\right)}+O\left(\lambda^{3}\right)$$

  where $|k\rangle$ is a normalised eigenstate of the free Hamiltonian $\hat{H}_{0}=\hat{p}^{2} / 2 m$ with momentum $p=\hbar k$ and energy $E_{0}(k)=\hbar^{2} k^{2} / 2 m$.

  Working on a finite interval of length $L=N a$, where $N$ is a positive integer, we impose periodic boundary conditions on the wavefunction:

  $$\psi(x+N a)=\psi(x)$$

  What are the allowed values of the wavenumbers $k$ and $k^{\prime}$ which appear in (1)? For these values evaluate the matrix element $\left\langle k|U| k^{\prime}\right\rangle$.

  For what values of $k$ and $k^{\prime}$ does (1) cease to be a good approximation? Explain your answer. Quoting any results you need from degenerate perturbation theory, calculate to $O(\lambda)$ the location and width of the gaps between allowed energy bands for the periodic potential $V(x)$, in terms of the Fourier coefficients $U_{l}$.

  Hence work out the allowed energy bands for the following potentials:

  $$\begin{aligned} &\text { (i) } \quad V(x)=2 \lambda \cos \left(\frac{2 \pi x}{a}\right), \\ &\text { (ii) } \quad V(x)=\lambda a \sum_{n=-\infty}^{+\infty} \delta(x-n a) . \end{aligned}$$

  comment

• Paper 4, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  Let $\Lambda$ be a Bravais lattice in three dimensions. Define the reciprocal lattice $\Lambda^{*}$.

  State and prove Bloch's theorem for a particle moving in a potential $V(\mathbf{x})$ obeying

  $$V(\mathbf{x}+\ell)=V(\mathbf{x}) \quad \forall \ell \in \Lambda, \mathbf{x} \in \mathbb{R}^{3}$$

  Explain what is meant by a Brillouin zone for this potential and how it is related to the reciprocal lattice.

  A simple cubic lattice $\Lambda_{1}$ is given by the set of points

  $$\Lambda_{1}=\left\{\ell \in \mathbb{R}^{3}: \ell=n_{1} \hat{\mathbf{i}}+n_{2} \hat{\mathbf{j}}+n_{3} \hat{\mathbf{k}}, n_{1}, n_{2}, n_{3} \in \mathbb{Z}\right\}$$

  where $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are unit vectors parallel to the Cartesian coordinate axes in $\mathbb{R}^{3}$. A bodycentred cubic $\left(\mathrm{BCC}\right.$ ) lattice $\Lambda_{B C C}$ is obtained by adding to $\Lambda_{1}$ the points at the centre of each cube, i.e. all points of the form

  $$\ell+\frac{1}{2}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}), \quad \ell \in \Lambda_{1}$$

  Show that $\Lambda_{B C C}$ is Bravais with primitive vectors

  $$\begin{aligned} \mathbf{a}_{1} &=\frac{1}{2}(\hat{\mathbf{j}}+\hat{\mathbf{k}}-\hat{\mathbf{i}}) \\ \mathbf{a}_{2} &=\frac{1}{2}(\hat{\mathbf{k}}+\hat{\mathbf{i}}-\hat{\mathbf{j}}) \\ \mathbf{a}_{3} &=\frac{1}{2}(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}) \end{aligned}$$

  Find the reciprocal lattice $\Lambda_{B C C}^{*}$. Hence find a consistent choice for the first Brillouin zone of a potential $V(\mathbf{x})$ obeying

  $$\begin{aligned} & V(\mathbf{x}+\ell)=V(\mathbf{x}) \quad \forall \ell \in \Lambda_{B C C}, \mathbf{x} \in \mathbb{R}^{3} \\ & \text { [Hint: The matrix } \left.M=\frac{1}{2}\left(\begin{array}{rrr}-1 & 1 & 1 \\1 & -1 & 1 \\1 & 1 & -1\end{array}\right) \text { has inverse } M^{-1}=\left(\begin{array}{lll}0 & 1 & 1 \\1 & 0 & 1 \\1 & 1 & 0\end{array}\right) .\right] \end{aligned}$$

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2014

  (i) Explain what a $Q$-matrix is. Let $Q$ be a $Q$-matrix. Define the notion of a Markov chain $\left(X_{t}, t \geqslant 0\right)$ in continuous time with $Q$-matrix given by $Q$, and give a construction of $\left(X_{t}, t \geqslant 0\right)$. [You are not required to justify this construction.]

  (ii) A population consists of $N_{t}$ individuals at time $t \geqslant 0$. We assume that each individual gives birth to a new individual at constant rate $\lambda>0$. As the population is competing for resources, we assume that for each $n \geqslant 1$, if $N_{t}=n$, then any individual in the population at time $t$ dies in the time interval $[t, t+h)$ with probability $\delta_{n} h+o(h)$, where $\left(\delta_{n}\right)_{n=1}^{\infty}$ is a given sequence satisfying $\delta_{1}=0, \delta_{n}>0$ for $n \geqslant 2$. Formulate a Markov chain model for $\left(N_{t}, t \geqslant 0\right)$ and write down the $Q$-matrix explicitly. Then find a necessary and sufficient condition on $\left(\delta_{n}\right)_{n=1}^{\infty}$ so that the Markov chain has an invariant distribution. Compute the invariant distribution in the case where $\delta_{n}=\mu(n-1)$ and $\mu>0$.

  comment

• Paper 2, Section II, J

  Applied Probability | Part II, 2014

  (i) Explain what the Moran model and the infinite alleles model are. State Ewens' sampling formula for the distribution of the allelic frequency spectrum $\left(a_{1}, \ldots, a_{n}\right)$ in terms of $\theta$ where $\theta=N u$ with $u$ denoting the mutation rate per individual and $N$ the population size.

  Let $K_{n}$ be the number of allelic types in a sample of size $n$. Give, without justification, an expression for $\mathbb{E}\left(K_{n}\right)$ in terms of $\theta$.

  (ii) Let $K_{n}$ and $\theta$ be as above. Show that for $1 \leqslant k \leqslant n$ we have that

  $$P\left(K_{n}=k\right)=C \frac{\theta^{k}}{\theta(\theta+1) \cdots(\theta+n-1)}$$

  for some constant $C$ that does not depend on $\theta$.

  Show that, given $\left\{K_{n}=k\right\}$, the distribution of the allelic frequency spectrum $\left(a_{1}, \ldots, a_{n}\right)$ does not depend on $\theta$.

  Show that the value of $\theta$ which maximises $\mathbb{P}\left(K_{n}=k\right)$ is the one for which $k=\mathbb{E}\left(K_{n}\right)$.

  comment

• Paper 3, Section II, J

  Applied Probability | Part II, 2014

  (i) Define a Poisson process $\left(N_{t}, t \geqslant 0\right)$ with intensity $\lambda$. Specify without justification the distribution of $N_{t}$. Let $T_{1}, T_{2}, \ldots$ denote the jump times of $\left(N_{t}, t \geqslant 0\right)$. Derive the joint distribution of $\left(T_{1}, \ldots, T_{n}\right)$ given $\left\{N_{t}=n\right\}$.

  (ii) Let $\left(N_{t}, t \geqslant 0\right)$ be a Poisson process with intensity $\lambda>0$ and let $X_{1}, X_{2}, \ldots$ be a sequence of i.i.d. random variables, independent of $\left(N_{t}, t \geqslant 0\right)$, all having the same distribution as a random variable $X$. Show that if $g(s, x)$ is a real-valued function of real variables $s, x$, and $T_{j}$ are the jump times of $\left(N_{t}, t \geqslant 0\right)$ then

  $$\mathbb{E}\left[\exp \left\{\theta \sum_{j=1}^{N_{t}} g\left(T_{j}, X_{j}\right)\right\}\right]=\exp \left\{\lambda \int_{0}^{t}\left(\mathbb{E}\left(e^{\theta g(s, X)}\right)-1\right) d s\right\}$$

  for all $\theta \in \mathbb{R}$. [Hint: Condition on $\left\{N_{t}=n\right\}$ and $T_{1}, \ldots, T_{n}$, using (i).]

  (iii) A university library is open from 9 am to $5 \mathrm{pm}$. Students arrive at times of a Poisson process with intensity $\lambda$. Each student spends a random amount of time in the library, independently of the other students. These times are identically distributed for all students and have the same distribution as a random variable $X$. Show that the number of students in the library at $5 \mathrm{pm}$ is a Poisson random variable with a mean that you should specify.

  comment

• Paper 4, Section II, J

  Applied Probability | Part II, 2014

  (i) Define the $M / M / 1$ queue with arrival rate $\lambda$ and service rate $\mu$. Find conditions on the parameters $\lambda$ and $\mu$ for the queue to be transient, null recurrent, and positive recurrent, briefly justifying your answers. In the last case give with justification the invariant distribution explicitly. Answer the same questions for an $M / M / \infty$ queue.

  (ii) At a taxi station, customers arrive at a rate of 3 per minute, and taxis at a rate of 2 per minute. Suppose that a taxi will wait no matter how many other taxis are present. However, if a person arriving does not find a taxi waiting he or she leaves to find alternative transportation.

  Find the long-run proportion of arriving customers who get taxis, and find the average number of taxis waiting in the long run.

  An agent helps to assign customers to taxis, and so long as there are taxis waiting he is unable to have his coffee. Once a taxi arrives, how long will it take on average before he can have another sip of his coffee?

  comment

Asymptotic Methods

• Paper 1, Section II, C

  Asymptotic Methods | Part II, 2014

  (a) Consider the integral

  $$I(k)=\int_{0}^{\infty} f(t) e^{-k t} d t, \quad k>0$$

  Suppose that $f(t)$ possesses an asymptotic expansion for $t \rightarrow 0^{+}$of the form

  $$f(t) \sim t^{\alpha} \sum_{n=0}^{\infty} a_{n} t^{\beta n}, \quad \alpha>-1, \quad \beta>0$$

  where $a_{n}$ are constants. Derive an asymptotic expansion for $I(k)$ as $k \rightarrow \infty$ in the form

  $$I(k) \sim \sum_{n=0}^{\infty} \frac{A_{n}}{k^{\gamma+\beta n}}$$

  giving expressions for $A_{n}$ and $\gamma$ in terms of $\alpha, \beta, n$ and the gamma function. Hence establish the asymptotic approximation as $k \rightarrow \infty$

  $$I_{1}(k)=\int_{0}^{1} e^{k t} t^{-a}\left(1-t^{2}\right)^{-b} d t \sim 2^{-b} \Gamma(1-b) e^{k} k^{b-1}\left(1+\frac{(a+b / 2)(1-b)}{k}\right)$$

  where $a<1, b<1$.

  (b) Using Laplace's method, or otherwise, find the leading-order asymptotic approximation as $k \rightarrow \infty$ for

  $$I_{2}(k)=\int_{0}^{\infty} e^{-\left(2 k^{2} / t+t^{2} / k\right)} d t$$

  [You may assume that $\Gamma(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t$ for $\operatorname{Re} z>0$,

  $$\text { and that } \left.\int_{-\infty}^{\infty} e^{-q t^{2}} d t=\sqrt{\pi / q} \text { for } q>0 .\right]$$

  comment

• Paper 3, Section II, C

  Asymptotic Methods | Part II, 2014

  (a) Find the Stokes ray for the function $f(z)$ as $z \rightarrow 0$ with $0<\arg z<\pi$, where

  $$f(z)=\sinh \left(z^{-1}\right)$$

  (b) Describe how the leading-order asymptotic behaviour as $x \rightarrow \infty$ of

  $$I(x)=\int_{a}^{b} f(t) e^{i x g(t)} d t$$

  may be found by the method of stationary phase, where $f$ and $g$ are real functions and the integral is taken along the real line. You should consider the cases for which:

  (i) $g^{\prime}(t)$ is non-zero in $[a, b)$ and has a simple zero at $t=b$.

  (ii) $g^{\prime}(t)$ is non-zero apart from having one simple zero at $t=t_{0}$, where $a<t_{0}<b$.

  (iii) $g^{\prime}(t)$ has more than one simple zero in $(a, b)$ with $g^{\prime}(a) \neq 0$ and $g^{\prime}(b) \neq 0$.

  Use the method of stationary phase to find the leading-order asymptotic form as $x \rightarrow \infty$ of

  $$J(x)=\int_{0}^{1} \cos \left(x\left(t^{4}-t^{2}\right)\right) d t$$

  [You may assume that $\left.\int_{-\infty}^{\infty} e^{i u^{2}} d u=\sqrt{\pi} e^{i \pi / 4} .\right]$

  comment

• Paper 4, Section II, C

  Asymptotic Methods | Part II, 2014

  Derive the leading-order Liouville Green (or WKBJ) solution for $\epsilon \ll 1$ to the ordinary differential equation

  $$\epsilon^{2} \frac{d^{2} f}{d y^{2}}+\Phi(y) f=0$$

  where $\Phi(y)>0$.

  The function $f(y ; \epsilon)$ satisfies the ordinary differential equation

  $$\epsilon^{2} \frac{d^{2} f}{d y^{2}}+\left(1+\frac{1}{y}-\frac{2 \epsilon^{2}}{y^{2}}\right) f=0$$

  subject to the boundary condition $f^{\prime \prime}(0)=2$. Show that the Liouville-Green solution of (1) for $\epsilon \ll 1$ takes the asymptotic forms

  where $\alpha_{1}, \alpha_{2}, B$ and $\theta_{2}$ are constants.

  $\left[\right.$ Hint: You may assume that $\left.\int_{0}^{y} \sqrt{1+u^{-1}} d u=\sqrt{y(1+y)}+\sinh ^{-1} \sqrt{y} \cdot\right]$

  Explain, showing the relevant change of variables, why the leading-order asymptotic behaviour for $0 \leqslant y \ll 1$ can be obtained from the reduced equation

  $$\frac{d^{2} f}{d x^{2}}+\left(\frac{1}{x}-\frac{2}{x^{2}}\right) f=0$$

  The unique solution to $(2)$ with $f^{\prime \prime}(0)=2$ is $f=x^{1 / 2} J_{3}\left(2 x^{1 / 2}\right)$, where the Bessel function $J_{3}(z)$ is known to have the asymptotic form

  $$J_{3}(z) \sim\left(\frac{2}{\pi z}\right)^{1 / 2} \cos \left(z-\frac{7 \pi}{4}\right) \text { as } z \rightarrow \infty .$$

  Hence find the values of $\alpha_{1}$ and $\alpha_{2}$.

  $$\begin{aligned} & f \sim \alpha_{1} y^{\frac{1}{4}} \exp (2 i \sqrt{y} / \epsilon)+\alpha_{2} y^{\frac{1}{4}} \exp (-2 i \sqrt{y} / \epsilon) \quad \text { for } \quad \epsilon^{2} \ll y \ll 1 \\ & \text { and } \quad f \sim B \cos \left[\theta_{2}+(y+\log \sqrt{y}) / \epsilon\right] \quad \text { for } \quad y \gg 1, \end{aligned}$$

  comment

Classical Dynamics

• Paper 1, Section I, A

  Classical Dynamics | Part II, 2014

  Consider a one-dimensional dynamical system with generalized coordinate and momentum $(q, p)$.

  (a) Define the Poisson bracket $\{f, g\}$ of two functions $f(q, p, t)$ and $g(q, p, t)$.

  (b) Verify the Leibniz rule

  $$\{f g, h\}=f\{g, h\}+g\{f, h\}$$

  (c) Explain what is meant by a canonical transformation $(q, p) \rightarrow(Q, P)$.

  (d) State the condition for a transformation $(q, p) \rightarrow(Q, P)$ to be canonical in terms of the Poisson bracket $\{Q, P\}$. Use this to determine whether or not the following transformations are canonical:

  (i) $Q=\frac{q^{2}}{2}, P=\frac{p}{q}$,

  (ii) $Q=\tan q, P=p \cos q$,

  (iii) $Q=\sqrt{2 q} e^{t} \cos p, P=\sqrt{2 q} e^{-t} \sin p$.

  comment

• Paper 2, Section I, A

  Classical Dynamics | Part II, 2014

  The components of the angular velocity $\omega$ of a rigid body and of the position vector $\mathbf{r}$ are given in a body frame.

  (a) The kinetic energy of the rigid body is defined as

  $$T=\frac{1}{2} \int d^{3} \mathbf{r} \rho(\mathbf{r}) \dot{\mathbf{r}} \cdot \dot{\mathbf{r}}$$

  Given that the centre of mass is at rest, show that $T$ can be written in the form

  $$T=\frac{1}{2} I_{a b} \omega_{a} \omega_{b},$$

  where the explicit form of the tensor $I_{a b}$ should be determined.

  (b) Explain what is meant by the principal moments of inertia.

  (c) Consider a rigid body with principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$, which are all unequal. Derive Euler's equations of torque-free motion

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} \end{aligned}$$

  (d) The body rotates about the principal axis with moment of inertia $I_{1}$. Derive the condition for stable rotation.

  comment

• Paper 2, Section II, A

  Classical Dynamics | Part II, 2014

  A planar pendulum consists of a mass $m$ at the end of a light rod of length $l$. The pivot of the pendulum is attached to a bead of mass $M$, which slides along a horizontal rod without friction. The bead is connected to the ends of the horizontal rod by two identical springs of force constant $k$. The pivot constrains the pendulum to swing in the vertical plane through the horizontal rod. The horizontal rod is mounted on a bracket, so the system could rotate about the vertical axis which goes through its centre as shown in the figure.

  

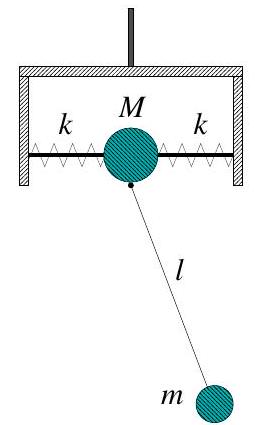
  (a) Initially, the system is not allowed to rotate about the vertical axis.

  (i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

  (ii) Write down expression(s) for any conserved quantities. Justify your answer.

  (iii) Derive the equations of motion.

  (iv) For $M=m / 2$ and $g m / k l=3$, find the frequencies of small oscillations around the stable equilibrium and the corresponding normal modes. Describe the respective motions of the system.

  (b) Assume now that the system is free to rotate about the vertical axis without friction. Write down the Lagrangian of the system. Identify and calculate the additional conserved quantity.

  comment

• Paper 3, Section I, A

  Classical Dynamics | Part II, 2014

  (a) The action for a one-dimensional dynamical system with a generalized coordinate $q$ and Lagrangian $L$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

  State the principle of least action. Write the expression for the Hamiltonian in terms of the generalized velocity $\dot{q}$, the generalized momentum $p$ and the Lagrangian $L$. Use it to derive Hamilton's equations from the principle of least action.

  (b) The motion of a particle of charge $q$ and mass $m$ in an electromagnetic field with scalar potential $\phi(\mathbf{r}, t)$ and vector potential $\mathbf{A}(\mathbf{r}, t)$ is characterized by the Lagrangian

  $$L=\frac{m \dot{\mathbf{r}}^{2}}{2}-q(\phi-\dot{\mathbf{r}} \cdot \mathbf{A})$$

  (i) Write down the Hamiltonian of the particle.

  (ii) Consider a particle which moves in three dimensions in a magnetic field with $\mathbf{A}=(0, B x, 0)$, where $B$ is a constant. There is no electric field. Obtain Hamilton's equations for the particle.

  comment

• Paper 4, Section I, A

  Classical Dynamics | Part II, 2014

  Consider a heavy symmetric top of mass $M$ with principal moments of inertia $I_{1}$, $I_{2}$ and $I_{3}$, where $I_{1}=I_{2} \neq I_{3}$. The top is pinned at point $P$, which is at a distance $l$ from the centre of mass, $C$, as shown in the figure.

  

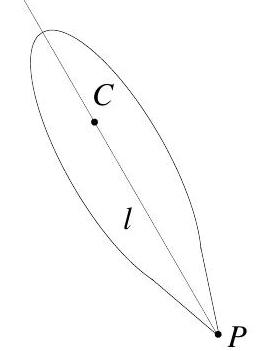
  Its angular velocity in a body frame $\left(\mathbf{e}_{\mathbf{1}}, \mathbf{e}_{\mathbf{2}}, \mathbf{e}_{\mathbf{3}}\right)$ is given by

  $$\boldsymbol{\omega}=[\dot{\phi} \sin \theta \sin \psi+\dot{\theta} \cos \psi] \mathbf{e}_{1}+[\dot{\phi} \sin \theta \cos \psi-\dot{\theta} \sin \psi] \mathbf{e}_{2}+[\dot{\psi}+\dot{\phi} \cos \theta] \mathbf{e}_{3}$$

  where $\phi, \theta$ and $\psi$ are the Euler angles.

  (a) Assuming that $\left\{\mathbf{e}_{a}\right\}, a=1,2,3$, are chosen to be the principal axes, write down the Lagrangian of the top in terms of $\omega_{a}$ and the principal moments of inertia. Hence find the Lagrangian in terms of the Euler angles.

  (b) Find all conserved quantities. Show that $\omega_{3}$, the spin of the top, is constant.

  (c) By eliminating $\dot{\phi}$ and $\dot{\psi}$, derive a second-order differential equation for $\theta$.

  comment

• Paper 4, Section II, A

  Classical Dynamics | Part II, 2014

  (a) Consider a system with one degree of freedom, which undergoes periodic motion in the potential $V(q)$. The system's Hamiltonian is

  $$H(p, q)=\frac{p^{2}}{2 m}+V(q)$$

  (i) Explain what is meant by the angle and action variables, $\theta$ and $I$, of the system and write down the integral expression for the action variable $I$. Is $I$ conserved? Is $\theta$ conserved?

  (ii) Consider $V(q)=\lambda q^{6}$, where $\lambda$ is a positive constant. Find $I$ in terms of $\lambda$, the total energy $E$, the mass $M$, and a dimensionless constant factor (which you need not compute explicitly).

  (iii) Hence describe how $E$ changes with $\lambda$ if $\lambda$ varies slowly with time. Justify your answer.

  (b) Consider now a particle which moves in a plane subject to a central force-field $\mathbf{F}=-k r^{-2} \hat{\mathbf{r}}$.

  (i) Working in plane polar coordinates $(r, \phi)$, write down the Hamiltonian of the system. Hence deduce two conserved quantities. Prove that the system is integrable and state the number of action variables.

  (ii) For a particle which moves on an elliptic orbit find the action variables associated with radial and tangential motions. Can the relationship between the frequencies of the two motions be deduced from this result? Justify your answer.

  (iii) Describe how $E$ changes with $m$ and $k$ if one or both of them vary slowly with time.

  [You may use

  $$\int_{r_{1}}^{r_{2}}\left\{\left(1-\frac{r_{1}}{r}\right)\left(\frac{r_{2}}{r}-1\right)\right\}^{\frac{1}{2}} d r=\frac{\pi}{2}\left(r_{1}+r_{2}\right)-\pi \sqrt{r_{1} r_{2}}$$

  where $0<r_{1}<r_{2}$.]

  comment

Coding and Cryptography

• Paper 1, Section I, $4 \mathrm{I}$

  Coding and Cryptography | Part II, 2014

  State and prove Gibbs' inequality.

  Show that, for a pair of discrete random variables $X$ and $Y$, each taking finitely many values, the joint entropy $H(X, Y)$ satisfies

  $$H(X, Y) \leqslant H(X)+H(Y)$$

  with equality precisely when $X$ and $Y$ are independent.

  comment

• Paper 1, Section II, I

  Coding and Cryptography | Part II, 2014

  Describe, briefly, either the RSA or the Elgamal public key cipher. You should explain, without proof, why it is believed to be difficult to break the cipher you describe.

  How can such a cipher be used to sign messages? You should explain how the intended recipient of the message can (a) know from whom it came; (b) know that the message has not been changed; and (c) demonstrate that the sender must have signed it.

  Let $I_{0}, I_{1}, \ldots, I_{N}$ be friendly individuals each of whom has a public key cipher. $I_{0}$ wishes to send a message to $I_{N}$ by passing it first to $I_{1}$, then $I_{1}$ passes it to $I_{2}, I_{2}$ to $I_{3}$, until finally it is received by $I_{N}$. At each stage the message can be modified to show from whom it was received and to whom it is sent. Devise a way in which these modifications can be made so that $I_{N}$ can be confident both of the content of the original message and that the message has been passed through the intermediaries $I_{1}, I_{2}, \ldots, I_{N-1}$ in that order and has not been modified by an enemy agent. Assume that it takes a negligible time to transmit a message from $I_{k}$ to $I_{k+1}$ for each $k$, but the time needed to modify a message is not negligible.

  comment

• Paper 2, Section $I$, I

  Coding and Cryptography | Part II, 2014

  Let $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ be a decodable binary code defined on a finite alphabet $\mathcal{A}$. Let $l(a)$ be the length of the code word $c(a)$. Prove that

  $$\sum_{a \in \mathcal{A}} 2^{-l(a)} \leqslant 1$$

  Show that, for the decodable code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ described above, there is a prefixfree code $p: \mathcal{A} \rightarrow\{0,1\}^{*}$ with each code word $p(a)$ having length $l(a)$. [You may use, without proof, any standard results from the course.]

  comment

• Paper 2, Section II, I

  Coding and Cryptography | Part II, 2014

  What is the information capacity of a memoryless, time-independent channel? Compute the information capacity of a binary symmetric channel with probability $p$ of error. Show the steps in your computation.

  Binary digits are transmitted through a noisy channel, which is memoryless and time-independent. With probability $\alpha(0<\alpha<1)$ the digit is corrupted and noise is received, otherwise the digit is transmitted unchanged. So, if we denote the input by 0 and 1 and the output as $0, *$ and 1 with $*$ denoting the noise, the transition matrix is

  $$\left(\begin{array}{cc} 1-\alpha & 0 \\ \alpha & \alpha \\ 0 & 1-\alpha \end{array}\right)$$

  Compute the information capacity of this channel.

  Explain how to code a message for transmission through the channel described above, and how to decode it, so that the probability of error for each bit is arbitrarily small.

  comment

• Paper 3, Section I, I

  Coding and Cryptography | Part II, 2014

  Let $A$ be a random variable that takes values in the finite alphabet $\mathcal{A}$. Prove that there is a decodable binary code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ that satisfies

  $$H(A) \leqslant \mathbb{E}(l(A)) \leqslant H(A)+1$$

  where $l(a)$ is the length of the code word $c(a)$ and $H(A)$ is the entropy of $A$.

  Is it always possible to find such a code with $\mathbb{E}(l(A))=H(A) ?$ Justify your answer.

  comment

• Paper 4, Section I, I

  Coding and Cryptography | Part II, 2014

  Explain what is meant by a Bose-Ray Chaudhuri-Hocquenghem (BCH) code with design distance $\delta$. Prove that, for such a code, the minimum distance between code words is at least $\delta$. How many errors will the code detect? How many errors will it correct?

  comment

Cosmology

• Paper 1, Section I, E

  Cosmology | Part II, 2014

  Which particle states are expected to be relativistic and which interacting when the temperature $T$ of the early universe satisfies (i) $10^{10} \mathrm{~K}<T<5 \times 10^{10} \mathrm{~K}$, (ii) $5 \times 10^{9} \mathrm{~K}<T<10^{10} \mathrm{~K}$, (iii) $T<5 \times 10^{9} \mathrm{~K}$ ?

  Calculate the total spin weight factor, $g_{*}$, of the relativistic particles and the total spin weight factor, $g_{I}$, of the interacting particles, in each of the three temperature intervals.

  What happens when the temperature falls below $5 \times 10^{9} \mathrm{~K} ?$ Calculate the ratio of the temperatures of neutrinos and photons. Find the effective value of $g_{*}$ after the universe cools below this temperature. [Note that the equilibrium entropy density is given by $s=\left(\rho c^{2}+P\right) / T$, where $\rho$ is the density and $P$ is the pressure.]

  comment

• Paper 1, Section II, E

  Cosmology | Part II, 2014

  What are the cosmological flatness and horizon problems? Explain what form of time evolution of the cosmological expansion scale factor $a(t)$ must occur during a period of inflationary expansion in a Friedmann universe. How can inflation solve the horizon and flatness problems? [You may assume an equation of state where pressure $P$ is proportional to density $\rho$.]

  The universe has Hubble expansion rate $H=\dot{a} / a$ and contains only a scalar field $\phi$ with self-interaction potential $V(\phi)>0$. The density and pressure are given by

  $$\begin{aligned} \rho &=\frac{1}{2} \dot{\phi}^{2}+V(\phi) \\ P &=\frac{1}{2} \dot{\phi}^{2}-V(\phi) \end{aligned}$$

  in units where $c=\hbar=1$. Show that the conservation equation

  $$\dot{\rho}+3 H(\rho+P)=0$$

  requires

  $$\ddot{\phi}+3 H \dot{\phi}+d V / d \phi=0 .$$

  If the Friedmann equation has the form

  $$3 H^{2}=8 \pi G \rho$$

  and the scalar-field potential has the form

  $$V(\phi)=V_{0} e^{-\lambda \phi}$$

  where $V_{0}$ and $\lambda$ are positive constants, show that there is an exact cosmological solution with

  $$\begin{aligned} &a(t) \propto t^{16 \pi G / \lambda^{2}} \\ &\phi(t)=\phi_{0}+\frac{2}{\lambda} \ln (t), \end{aligned}$$

  where $\phi_{0}$ is a constant. Find the algebraic relation between $\lambda, V_{0}$ and $\phi_{0}$. Show that a solution only exists when $0<\lambda^{2}<48 \pi G$. For what range of values of $\lambda^{2}$ does inflation occur? Comment on what happens when $\lambda \rightarrow 0$.

  comment

• Paper 2, Section I, E

  Cosmology | Part II, 2014

  A self-gravitating fluid with density $\rho$, pressure $P(\rho)$ and velocity $\mathbf{v}$ in a gravitational potential $\Phi$ obeys the equations

  $$\begin{aligned} \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \mathbf{v}) &=0 \\ \frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v} \cdot \nabla) \mathbf{v}+\frac{\nabla P}{\rho}+\nabla \Phi &=\mathbf{0} \\ \nabla^{2} \Phi &=4 \pi G \rho \end{aligned}$$

  Assume that there exists a static constant solution of these equations with $\mathbf{v}=\mathbf{0}, \rho=\rho_{0}$ and $\Phi=\Phi_{0}$, for which $\nabla \Phi_{0}$ can be neglected. This solution is perturbed. Show that, to first order in the perturbed quantities, the density perturbations satisfy

  $$\frac{\partial^{2} \rho_{1}}{\partial t^{2}}=c_{s}^{2} \nabla^{2} \rho_{1}+4 \pi G \rho_{0} \rho_{1}$$

  where $\rho=\rho_{0}+\rho_{1}(\mathbf{x}, t)$ and $c_{s}^{2}=d P / d \rho$. Show that there are solutions to this equation of the form

  $$\rho_{1}(\mathbf{x}, t)=A \exp [-i \mathbf{k} \cdot \mathbf{x}+i \omega t]$$

  where $A, \omega$ and $\mathbf{k}$ are constants and

  $$\omega^{2}=c_{s}^{2} \mathbf{k} \cdot \mathbf{k}-4 \pi G \rho_{0}$$

  Interpret these solutions physically in the limits of small and large $|\mathbf{k}|$, explaining what happens to density perturbations on large and small scales, and determine the critical wavenumber that divides the two distinct behaviours of the perturbation.

  comment

• Paper 3, Section I, E

  Cosmology | Part II, 2014

  Consider a finite sphere of zero-pressure material of uniform density $\rho(t)$ which expands with radius $r(t)=a(t) r_{0}$, where $r_{0}$ is an arbitary constant, due to the evolution of the expansion scale factor $a(t)$. The sphere has constant total mass $M$ and its radius satisfies

  $$\ddot{r}=-\frac{d \Phi}{d r}$$

  where

  $$\Phi(r)=-\frac{G M}{r}-\frac{1}{6} \Lambda r^{2} c^{2},$$

  with $\Lambda$ constant. Show that the scale factor obeys the equation

  $$\frac{\dot{a}^{2}}{a^{2}}=\frac{8 \pi G \rho}{3}-\frac{K c^{2}}{a^{2}}+\frac{1}{3} \Lambda c^{2},$$

  where $K$ is a constant. Explain why the sign, but not the magnitude, of $K$ is important. Find exact solutions of this equation for $a(t)$ when

  (i) $K=\Lambda=0$ and $\rho(t) \neq 0$,

  (ii) $\rho=K=0$ and $\Lambda>0$,

  (iii) $\rho=\Lambda=0$ and $K \neq 0$.

  Which two of the solutions (i)-(iii) are relevant for describing the evolution of the universe after the radiation-dominated era?

  comment

• Paper 3, Section II, E

  Cosmology | Part II, 2014

  The luminosity distance to an astronomical light source is given by $d_{L}=\chi / a(t)$, where $a(t)$ is the expansion scale factor and $\chi$ is the comoving distance in the universe defined by $d t=a(t) d \chi$. A zero-curvature Friedmann universe containing pressure-free matter and a cosmological constant with density parameters $\Omega_{m}$ and $\Omega_{\Lambda} \equiv 1-\Omega_{m}$, respectively, obeys the Friedmann equation

  $$H^{2}=H_{0}^{2}\left(\frac{\Omega_{m 0}}{a^{3}}+\Omega_{\Lambda 0}\right)$$

  where $H=(d a / d t) / a$ is the Hubble expansion rate of the universe and the subscript 0 denotes present-day values, with $a_{0} \equiv 1$.

  If $z$ is the redshift, show that

  $$d_{L}(z)=\frac{1+z}{H_{0}} \int_{0}^{z} \frac{d z^{\prime}}{\left[\left(1-\Omega_{\Lambda 0}\right)\left(1+z^{\prime}\right)^{3}+\Omega_{\Lambda 0}\right]^{1 / 2}}$$

  Find $d_{L}(z)$ when $\Omega_{\Lambda 0}=0$ and when $\Omega_{m 0}=0$. Roughly sketch the form of $d_{L}(z)$ for these two cases. What is the effect of a cosmological constant $\Lambda$ on the luminosity distance at a fixed value of $z$ ? Briefly describe how the relation between luminosity distance and redshift has been used to establish the acceleration of the expansion of the universe.

  comment

• Paper 4, Section I, E

  Cosmology | Part II, 2014

  A homogeneous and isotropic universe, with cosmological constant $\Lambda$, has expansion scale factor $a(t)$ and Hubble expansion rate $H=\dot{a} / a$. The universe contains matter with density $\rho$ and pressure $P$ which satisfy the positive-energy condition $\rho+3 P / c^{2} \geqslant 0$. The acceleration equation is

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)+\frac{1}{3} \Lambda c^{2}$$

  If $\Lambda \leqslant 0$, show that

  $$\frac{d}{d t}\left(H^{-1}\right) \geqslant 1$$

  Deduce that $H \rightarrow \infty$ and $a \rightarrow 0$ at a finite time in the past or the future. What property of $H$ distinguishes the two cases?

  Give a simple counterexample with $\rho=P=0$ to show that this deduction fails to hold when $\Lambda>0$.

  comment

Differential Geometry

• Paper 1, Section II, G

  Differential Geometry | Part II, 2014

  Define the concepts of (smooth) manifold and manifold with boundary for subsets of $\mathbf{R}^{N}$.

  Let $X \subset \mathbf{R}^{6}$ be the subset defined by the equations

  $$x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-x_{4}^{2}=1, \quad x_{4}^{2}-x_{5}^{2}-x_{6}^{2}=-1 .$$

  Prove that $X$ is a manifold of dimension four.

  For $a>0$, let $B(a) \subset \mathbf{R}^{6}$ denote the spherical ball $x_{1}^{2}+\ldots+x_{6}^{2} \leqslant a$. Prove that $X \cap B(a)$ is empty if $a<2$, is a manifold diffeomorphic to $S^{2} \times S^{1}$ if $a=2$, and is a manifold with boundary if $a>2$, with each component of the boundary diffeomorphic to $S^{2} \times S^{1}$.

  [You may quote without proof any general results from lectures that you may need.]

  comment

• Paper 2, Section II, G

  Differential Geometry | Part II, 2014

  Define the terms Gaussian curvature $K$ and mean curvature $H$ for a smooth embedded oriented surface $S \subset \mathbf{R}^{3}$. [You may assume the fact that the derivative of the Gauss map is self-adjoint.] If $K=H^{2}$ at all points of $S$, show that both $H$ and $K$ are locally constant. [Hint: Use the symmetry of second partial derivatives of the field of unit normal vectors.]

  If $K=H^{2}=0$ at all points of $S$, show that the unit normal vector $\mathbf{N}$ to $S$ is locally constant and that $S$ is locally contained in a plane. If $K=H^{2}$ is a strictly positive constant on $S$ and $\phi: U \rightarrow S$ is a local parametrization (where $U$ is connected) on $S$ with unit normal vector $\mathbf{N}(u, v)$ for $(u, v) \in U$, show that $\phi(u, v)+\mathbf{N}(u, v) / H$ is constant on $U$. Deduce that $S$ is locally contained in a sphere of radius $1 /|H|$.

  If $S$ is connected with $K=H^{2}$ at all points of $S$, deduce that $S$ is contained in either a plane or a sphere.

  comment

• Paper 3, Section II, G

  Differential Geometry | Part II, 2014

  Let $\alpha: I \rightarrow S$ be a parametrized curve on a smooth embedded surface $S \subset \mathbf{R}^{3}$. Define what is meant by a vector field $V$ along $\alpha$ and the concept of such a vector field being parallel. If $V$ and $W$ are both parallel vector fields along $\alpha$, show that the inner product $\langle V(t), W(t)\rangle$ is constant.

  Given a local parametrization $\phi: U \rightarrow S$, define the Christoffel symbols $\Gamma_{j k}^{i}$ on $U$. Given a vector $v_{0} \in T_{\alpha(0)} S$, prove that there exists a unique parallel vector field $V(t)$ along $\alpha$ with $V(0)=v_{0}$ (recall that $V(t)$ is called the parallel transport of $v_{0}$ along $\alpha$ ).

  Suppose now that the image of $\alpha$ also lies on another smooth embedded surface $S^{\prime} \subset \mathbf{R}^{3}$ and that $T_{\alpha(t)} S=T_{\alpha(t)} S^{\prime}$ for all $t \in I$. Show that parallel transport of a vector $v_{0}$ is the same whether calculated on $S$ or $S^{\prime}$. Suppose $S$ is the unit sphere in $\mathbf{R}^{3}$ with centre at the origin and let $\alpha:[0,2 \pi] \rightarrow S$ be the curve on $S$ given by

  $$\alpha(t)=(\sin \phi \cos t, \sin \phi \sin t, \cos \phi)$$

  for some fixed angle $\phi$. Suppose $v_{0} \in T_{P} S$ is the unit tangent vector to $\alpha$ at $P=\alpha(0)=$ $\alpha(2 \pi)$ and let $v_{1}$ be its image in $T_{P} S$ under parallel transport along $\alpha$. Show that the angle between $v_{0}$ and $v_{1}$ is $2 \pi \cos \phi$.

  [Hint: You may find it useful to consider the circular cone $S^{\prime}$ which touches the sphere $S$ along the curve $\alpha$.]

  comment

• Paper 4, Section II, G

  Differential Geometry | Part II, 2014

  Let $I=[0, l]$ be a closed interval, $k(s), \tau(s)$ smooth real valued functions on $I$ with $k$ strictly positive at all points, and $\mathbf{t}_{0}, \mathbf{n}_{0}, \mathbf{b}_{0}$ a positively oriented orthonormal triad of vectors in $\mathbf{R}^{3}$. An application of the fundamental theorem on the existence of solutions to ODEs implies that there exists a unique smooth family of triples of vectors $\mathbf{t}(s), \mathbf{n}(s), \mathbf{b}(s)$ for $s \in I$ satisfying the differential equations

  $$\mathbf{t}^{\prime}=k \mathbf{n}, \quad \mathbf{n}^{\prime}=-k \mathbf{t}-\tau \mathbf{b}, \quad \mathbf{b}^{\prime}=\tau \mathbf{n}$$

  with initial conditions $\mathbf{t}(0)=\mathbf{t}_{0}, \mathbf{n}(0)=\mathbf{n}_{0}$ and $\mathbf{b}(0)=\mathbf{b}_{0}$, and that $\{\mathbf{t}(s), \mathbf{n}(s), \mathbf{b}(s)\}$ forms a positively oriented orthonormal triad for all $s \in I$. Assuming this fact, consider $\alpha: I \rightarrow \mathbf{R}^{3}$ defined by $\alpha(s)=\int_{0}^{s} \mathbf{t}(t) d t$; show that $\alpha$ defines a smooth immersed curve parametrized by arc-length, which has curvature and torsion given by $k(s)$ and $\tau(s)$, and that $\alpha$ is uniquely determined by this property up to rigid motions of $\mathbf{R}^{3}$. Prove that $\alpha$ is a plane curve if and only if $\tau$ is identically zero.

  If $a>0$, calculate the curvature and torsion of the smooth curve given by

  $$\alpha(s)=(a \cos (s / c), a \sin (s / c), b s / c), \quad \text { where } c=\sqrt{a^{2}+b^{2}}$$

  Suppose now that $\alpha:[0,2 \pi] \rightarrow \mathbf{R}^{3}$ is a smooth simple closed curve parametrized by arc-length with curvature everywhere positive. If both $k$ and $\tau$ are constant, show that $k=1$ and $\tau=0$. If $k$ is constant and $\tau$ is not identically zero, show that $k>1$. Explain what it means for $\alpha$ to be knotted; if $\alpha$ is knotted and $\tau$ is constant, show that $k(s)>2$ for some $s \in[0,2 \pi]$. [You may use standard results from the course if you state them precisely.]

  comment

Dynamical Systems

• Paper 1, Section I, D

  Dynamical Systems | Part II, 2014

  Consider the system

  $$\begin{aligned} &\dot{x}=y+x y \\ &\dot{y}=x-\frac{3}{2} y+x^{2} \end{aligned}$$

  Show that the origin is a hyperbolic fixed point and find the stable and unstable invariant subspaces of the linearised system.

  Calculate the stable and unstable manifolds correct to quadratic order, expressing $y$ as a function of $x$ for each.

  comment

• Paper 2, Section I, D

  Dynamical Systems | Part II, 2014

  Consider the system

  $$\begin{aligned} \dot{x} &=-x+y+y^{2} \\ \dot{y} &=\mu-x y \end{aligned}$$

  Show that when $\mu=0$ the fixed point at the origin has a stationary bifurcation.

  Find the centre subspace of the extended system linearised about $(x, y, \mu)=(0,0,0)$.

  Find an approximation to the centre manifold giving $y$ as a function of $x$ and $\mu$, including terms up to quadratic order.

  Hence deduce an expression for $\dot{x}$ on the centre manifold, and identify the type of bifurcation at $\mu=0$.

  comment

• Paper 3, Section $I$, D

  Dynamical Systems | Part II, 2014

  Define the Poincaré index of a closed curve $\mathcal{C}$ for a vector field $\mathbf{f}(\mathbf{x}), \mathbf{x} \in \mathbb{R}^{2}$.

  Explain carefully why the index of $\mathcal{C}$ is fully determined by the fixed points of the dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ that lie within $\mathcal{C}$.

  What is the Poincaré index for a closed curve $\mathcal{C}$ if it (a) encloses only a saddle point, (b) encloses only a focus and (c) encloses only a node?

  What is the Poincaré index for a closed curve $\mathcal{C}$ that is a periodic trajectory of the dynamical system?

  A dynamical system in $\mathbb{R}^{2}$ has 2 saddle points, 1 focus and 1 node. What is the maximum number of different periodic orbits? [For the purposes of this question, two orbits are said to be different if they enclose different sets of fixed points.]

  comment

• Paper 3, Section II, D

  Dynamical Systems | Part II, 2014

  Let $f: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. Explain what is meant by saying that $f$ has a horseshoe.

  A map $g$ on the interval $[a, b]$ is a tent map if

  (i) $g(a)=a$ and $g(b)=a$;

  (ii) for some $c$ with $a<c<b, g$ is linear and increasing on the interval $[a, c]$, linear and decreasing on the interval $[c, b]$, and continuous at $c$.

  Consider the tent map defined on the interval $[0,1]$ by

  $$f(x)= \begin{cases}\mu x & 0 \leqslant x \leqslant \frac{1}{2} \\ \mu(1-x) & \frac{1}{2} \leqslant x \leqslant 1\end{cases}$$

  with $1<\mu \leqslant 2$. Find the corresponding expressions for $f^{2}(x)=f(f(x))$.

  Find the non-zero fixed point $x_{0}$ and the points $x_{-1}<\frac{1}{2}<x_{-2}$ that satisfy

  $$f^{2}\left(x_{-2}\right)=f\left(x_{-1}\right)=x_{0}=f\left(x_{0}\right) .$$

  Sketch graphs of $f$ and $f^{2}$ showing the points corresponding to $x_{-2}, x_{-1}$ and $x_{0}$. Indicate the values of $f$ and $f^{2}$ at their maxima and minima and also the gradients of each piece of their graphs.

  Identify a subinterval of $[0,1]$ on which $f^{2}$ is a tent map. Hence demonstrate that $f^{2}$ has a horseshoe if $\mu \geqslant 2^{1 / 2}$.

  Explain briefly why $f^{4}$ has a horseshoe when $\mu \geqslant 2^{1 / 4}$.

  Why are there periodic points of $f$ arbitrarily close to $x_{0}$ for $\mu \geqslant 2^{1 / 2}$, but no such points for $2^{1 / 4} \leqslant \mu<2^{1 / 2}$ ? Explain carefully any results or terms that you use.

  comment

• Paper 4, Section I, D

  Dynamical Systems | Part II, 2014

  Consider the map $x_{n+1}=\lambda x_{n}\left(1-x_{n}^{2}\right)$ for $-1 \leqslant x_{n} \leqslant 1$. What is the maximum value, $\lambda_{\max }$, for which the interval $[-1,1]$ is mapped into itself?

  Analyse the first two bifurcations that occur as $\lambda$ increases from 0 towards $\lambda_{\max }$, including an identification of the values of $\lambda$ at which the bifurcation occurs and the type of bifurcation.

  What type of bifurcation do you expect as the third bifurcation? Briefly give your reasoning.

  comment

• Paper 4, Section II, D

  Dynamical Systems | Part II, 2014

  A dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ has a fixed point at the origin. Define the terms Lyapunov stability, asymptotic stability and Lyapunov function with respect to this fixed point. State and prove Lyapunov's first theorem and state (without proof) La Salle's invariance principle.

  (a) Consider the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-y-x^{3}+x^{5} \end{aligned}$$

  Construct a Lyapunov function of the form $V=f(x)+g(y)$. Deduce that the origin is asymptotically stable, explaining your reasoning carefully. Find the greatest value of $y_{0}$ such that use of this Lyapunov function guarantees that the trajectory through $\left(0, y_{0}\right)$ approaches the origin as $t \rightarrow \infty$.

  (b) Consider the system

  $$\begin{aligned} &\dot{x}=x+4 y+x^{2}+2 y^{2}, \\ &\dot{y}=-3 x-3 y . \end{aligned}$$

  Show that the origin is asymptotically stable and that the basin of attraction of the origin includes the region $x^{2}+x y+y^{2}<\frac{1}{4}$.

  comment

Electrodynamics

• Paper 1, Section II, 36C

  Electrodynamics | Part II, 2014

  (i) Starting from the field-strength tensor $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$, where $A^{\mu}=(\phi / c, \mathbf{A})$ is the 4-vector potential with components such that

  $$\mathbf{E}=-\frac{\partial \mathbf{A}}{\partial t}-\boldsymbol{\nabla} \phi \quad \text { and } \quad \mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$$

  derive the transformation laws for the components of the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ under the standard Lorentz boost $x^{\prime \mu}=\Lambda_{\nu}^{\mu} x^{\nu}$ with

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  (ii) Two point charges, each with electric charge $q$, are at rest and separated by a distance $d$ in some inertial frame $S$. By transforming the fields from the rest frame $S$, calculate the magnitude and direction of the force between the two charges in an inertial frame in which the charges are moving with speed $\beta c$ in a direction perpendicular to their separation.

  (iii) The 4-force for a particle with 4-momentum $p^{\mu}$ is $F^{\mu}=d p^{\mu} / d \tau$, where $\tau$ is proper time. Show that the components of $F^{\mu}$ in an inertial frame in which the particle has 3 -velocity $\mathbf{v}$ are

  $$F^{\mu}=\gamma(\mathbf{F} \cdot \mathbf{v} / c, \mathbf{F})$$

  where $\gamma=\left(1-\mathbf{v} \cdot \mathbf{v} / c^{2}\right)^{-1 / 2}$ and $\mathbf{F}$ is the 3-force acting on the particle. Hence verify that your result in (ii) above is consistent with Lorentz transforming the electromagnetic 3 -force from the rest frame $S$.

  comment

• Paper 3, Section II, C

  Electrodynamics | Part II, 2014

  The 4-vector potential $A^{\mu}(t, \mathbf{x})$ (in the Lorenz gauge $\partial_{\mu} A^{\mu}=0$ ) due to a localised source with conserved 4-vector current $J^{\mu}$ is

  $$A^{\mu}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int \frac{J^{\mu}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} d^{3} \mathbf{x}^{\prime}$$

  where $t_{\text {ret }}=t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right| / c$. For a source that varies slowly in time, show that the spatial components of $A^{\mu}$ at a distance $r=|\mathbf{x}|$ that is large compared to the spatial extent of the source are

  $$\left.\mathbf{A}(t, \mathbf{x}) \approx \frac{\mu_{0}}{4 \pi r} \frac{d \mathbf{P}}{d t}\right|_{t-r / c}$$

  where $\mathbf{P}$ is the electric dipole moment of the source, which you should define. Explain what is meant by the far-field region, and calculate the leading-order part of the magnetic field there.

  A point charge $q$ moves non-relativistically in a circle of radius $a$ in the $(x, y)$ plane with angular frequency $\omega$ (such that $a \omega \ll c$ ). Show that the magnetic field in the far-field at the point $\mathbf{x}$ with spherical polar coordinates $r, \theta$ and $\phi$ has components along the $\theta$ and $\phi$ directions given by

  $$\begin{aligned} &B_{\theta} \approx-\frac{\mu_{0} \omega^{2} q a}{4 \pi r c} \sin [\omega(t-r / c)-\phi] \\ &B_{\phi} \approx \frac{\mu_{0} \omega^{2} q a}{4 \pi r c} \cos [\omega(t-r / c)-\phi] \cos \theta \end{aligned}$$

  Calculate the total power radiated by the charge.

  comment

• Paper 4, Section II, 35C

  Electrodynamics | Part II, 2014

  (i) The action $S$ for a point particle of rest mass $m$ and charge $q$ moving along a trajectory $x^{\mu}(\lambda)$ in the presence of an electromagnetic 4 -vector potential $A^{\mu}$ is

  $$S=-m c \int\left(-\eta_{\mu \nu} \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda}\right)^{1 / 2} d \lambda+q \int A_{\mu} \frac{d x^{\mu}}{d \lambda} d \lambda$$

  where $\lambda$ is an arbitrary parametrization of the path and $\eta_{\mu \nu}$ is the Minkowski metric. By varying the action with respect to $x^{\mu}(\lambda)$, derive the equation of motion $m \ddot{x}^{\mu}=q F^{\mu} \dot{x}^{\nu}$, where $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ and overdots denote differentiation with respect to proper time for the particle.

  (ii) The particle moves in constant electric and magnetic fields with non-zero Cartesian components $E_{z}=E$ and $B_{y}=B$, with $B>E / c>0$ in some inertial frame. Verify that a suitable 4-vector potential has components

  $$A^{\mu}=(0,0,0,-B x-E t)$$

  in that frame.

  Find the equations of motion for $x, y, z$ and $t$ in terms of proper time $\tau$. For the case of a particle that starts at rest at the spacetime origin at $\tau=0$, show that

  $$\ddot{z}+\frac{q^{2}}{m^{2}}\left(B^{2}-\frac{E^{2}}{c^{2}}\right) z=\frac{q E}{m} .$$

  Find the trajectory $x^{\mu}(\tau)$ and sketch its projection onto the $(x, z)$ plane.

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2014

  A particle of arbitrary shape and volume $4 \pi a^{3} / 3$ moves at velocity $\mathbf{U}(t)$ through an unbounded incompressible fluid of density $\rho$ and viscosity $\mu$. The Reynolds number of the flow is very small so that the inertia of the fluid can be neglected. Show that the particle experiences a force $\mathbf{F}(t)$ due to the surface stresses given by

  $$F_{i}(t)=-\mu a A_{i j} U_{j}(t)$$

  where $A_{i j}$ is a dimensionless second-rank tensor determined solely by the shape and orientation of the particle. State the reason why $A_{i j}$ must be positive definite.

  Show further that, if the particle has the same reflectional symmetries as a cube, then

  $$A_{i j}=\lambda \delta_{i j}$$

  Let $b$ be the radius of the smallest sphere that contains the particle (still assuming cubic symmetry). By considering the Stokes flow associated with this sphere, suitably extended, and using the minimum dissipation theorem (which should be stated carefully), show that

  $$\lambda \leqslant 6 \pi b / a .$$

  [You may assume the expression for the Stokes drag on a sphere.]

  comment

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2014

  Air is blown over the surface of a large, deep reservoir of water in such a way as to exert a tangential stress in the $x$-direction of magnitude $K x^{2}$ for $x>0$, with $K>0$. The water is otherwise at rest and occupies the region $y>0$. The surface $y=0$ remains flat.

  Find order-of-magnitude estimates for the boundary-layer thickness $\delta(x)$ and tangential surface velocity $U(x)$ in terms of the relevant physical parameters.

  Using the boundary-layer equations, find the ordinary differential equation governing the dimensionless function $f$ defined in the streamfunction

  $$\psi(x, y)=U(x) \delta(x) f(\eta), \quad \text { where } \eta=y / \delta(x)$$

  What are the boundary conditions on $f$ ?

  Does $f \rightarrow 0$ as $\eta \rightarrow \infty$ ? Why, or why not?

  The total horizontal momentum flux $P(X)$ across the vertical line $x=X$ is proportional to $X^{a}$ for $X>0$. Find the exponent $a$. By considering the steadiness of the momentum balance in the region $0<x<X$, explain why the value of $a$ is consistent with the form of the stress exerted on the boundary.

  comment

• Paper 3, Section II, B

  Fluid Dynamics II | Part II, 2014

  A rigid sphere of radius $a$ falls under gravity through an incompressible fluid of density $\rho$ and viscosity $\mu$ towards a rigid horizontal plane. The minimum gap $h_{0}(t)$ between the sphere and the plane satisfies $h_{0} \ll a$. Find an approximation for the gap thickness $h(r, t)$ between the sphere and the plane in the region $r \ll a$, where $r$ is the distance from the axis of symmetry.

  For a prescribed value of $\dot{h}_{0}=d h_{0} / d t$, use lubrication theory to find the radial velocity and the fluid pressure in the region $r \ll a$. Explain why the approximations of lubrication theory require $h_{0} \ll a$ and $\rho h_{0} \dot{h}_{0} \ll \mu$.

  Calculate the total vertical force due to the motion that is exerted by the fluid on the sphere. Deduce that if the sphere is settling under its own weight (corrected for buoyancy) then $h_{0}(t)$ decreases exponentially. What is the exponential decay rate for a solid sphere of density $\rho_{s}$ in a fluid of density $\rho_{f}$ ?

  comment

• Paper 4, Section II, B

  Fluid Dynamics II | Part II, 2014

  An incompressible fluid of density $\rho$ and kinematic viscosity $\nu$ is confined in a channel with rigid stationary walls at $y=\pm h$. A spatially uniform pressure gradient $-G \cos \omega t$ is applied in the $x$-direction. What is the physical significance of the dimensionless number $S=\omega h^{2} / \nu ?$

  Assuming that the flow is unidirectional and time-harmonic, obtain expressions for the velocity profile and the total flux. [You may leave your answers as the real parts of complex functions.]

  In each of the limits $S \rightarrow 0$ and $S \rightarrow \infty$, find and sketch the flow profiles, find leading-order asymptotic expressions for the total flux, and give a physical interpretation.

  Suppose now that $G=0$ and that the channel walls oscillate in their own plane with velocity $U \cos \omega t$ in the $x$-direction. Without explicit calculation of the solution, sketch the flow profile in each of the limits $S \rightarrow 0$ and $S \rightarrow \infty$.

  comment

Further Complex Methods

• Paper 1, Section $I$, B

  Further Complex Methods | Part II, 2014

  Show that the Cauchy-Riemann equations for $f: \mathbb{C} \rightarrow \mathbb{C}$ are equivalent to

  $$\frac{\partial f}{\partial \bar{z}}=0 \text {, }$$

  where $z=x+i y$, and $\partial / \partial \bar{z}$ should be defined in terms of $\partial / \partial x$ and $\partial / \partial y$. Use Green's theorem, together with the formula $d z d \bar{z}=-2 i d x d y$, to establish the generalised Cauchy formula

  $$\oint_{\gamma} f(z, \bar{z}) d z=-\iint_{D} \frac{\partial f}{\partial \bar{z}} d z d \bar{z}$$

  where $\gamma$ is a contour in the complex plane enclosing the region $D$ and $f$ is sufficiently differentiable.

  comment

• Paper 1, Section II, 14B

  Further Complex Methods | Part II, 2014

  Obtain solutions of the second-order ordinary differential equation

  $$z w^{\prime \prime}-w=0$$

  in the form

  $$w(z)=\int_{\gamma} f(t) e^{-z t} d t$$

  where the function $f$ and the choice of contour $\gamma$ should be determined from the differential equation.

  Show that a non-trivial solution can be obtained by choosing $\gamma$ to be a suitable closed contour, and find the resulting solution in this case, expressing your answer in the form of a power series.

  Describe a contour $\gamma$ that would provide a second linearly independent solution for the case $\operatorname{Re}(z)>0$.

  comment

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2014

  Suppose $z=0$ is a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane. Define the monodromy matrix $M$ around $z=0$.

  Demonstrate that if

  $$M=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)$$

  then the differential equation admits a solution of the form $a(z)+b(z) \log z$, where $a(z)$ and $b(z)$ are single-valued functions.

  comment

• Paper 2, Section II, 14B

  Further Complex Methods | Part II, 2014

  Use the Euler product formula

  $$\Gamma(z)=\lim _{n \rightarrow \infty} \frac{n ! n^{z}}{z(z+1) \ldots(z+n)}$$

  to show that:

  (i) $\Gamma(z+1)=z \Gamma(z)$;

  (ii) $\frac{1}{\Gamma(z)}=z e^{\gamma z} \prod_{k=1}^{\infty}\left(1+\frac{z}{k}\right) e^{-z / k}$, where $\gamma=\lim _{n \rightarrow \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n\right)$.

  Deduce that

  $$\frac{d}{d z} \log (\Gamma(z))=-\gamma-\frac{1}{z}+z \sum_{k=1}^{\infty} \frac{1}{k(z+k)}$$

  comment

• Paper 3, Section I, B

  Further Complex Methods | Part II, 2014

  State the conditions for a point $z=z_{0}$ to be a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane.

  Find all singular points of the Airy equation

  $$w^{\prime \prime}(z)-z w(z)=0$$

  and determine whether they are regular or irregular.

  comment

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2014

  Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a function such that

  $$f\left(z+\omega_{1}\right)=f(z), \quad f\left(z+\omega_{2}\right)=f(z)$$

  where $\omega_{1}, \omega_{2} \in \mathbb{C} \backslash\{0\}$ and $\omega_{1} / \omega_{2}$ is not real. Show that if $f$ is analytic on $\mathbb{C}$ then it is a constant. [Liouville's theorem may be used if stated.] Give an example of a non-constant meromorphic function which satisfies (1).

  comment

Galois Theory

• Paper 1, Section II, 18H

  Galois Theory | Part II, 2014

  What is meant by the statement that $L$ is a splitting field for $f \in K[X] ?$

  Show that if $f \in K[X]$, then there exists a splitting field for $f$ over $K$. Explain the sense in which a splitting field for $f$ over $K$ is unique.

  Determine the degree $[L: K]$ of a splitting field $L$ of the polynomial $f=X^{4}-4 X^{2}+2$ over $K$ in the cases (i) $K=\mathbb{Q}$, (ii) $K=\mathbb{F}_{5}$, and (iii) $K=\mathbb{F}_{7}$.

  comment

• Paper 2, Section II, H

  Galois Theory | Part II, 2014

  Describe the Galois correspondence for a finite Galois extension $L / K$.

  Let $L$ be the splitting field of $X^{4}-2$ over $\mathbb{Q}$. Compute the Galois group $G$ of $L / \mathbb{Q}$. For each subgroup of $G$, determine the corresponding subfield of $L$.

  Let $L / K$ be a finite Galois extension whose Galois group is isomorphic to $S_{n}$. Show that $L$ is the splitting field of a separable polynomial of degree $n$.

  comment

• Paper 3, Section II, H

  Galois Theory | Part II, 2014

  Let $L / K$ be an algebraic extension of fields, and $x \in L$. What does it mean to say that $x$ is separable over $K$ ? What does it mean to say that $L / K$ is separable?

  Let $K=\mathbb{F}_{p}(t)$ be the field of rational functions over $\mathbb{F}_{p}$.

  (i) Show that if $x$ is inseparable over $K$ then $K(x)$ contains a $p$ th root of $t$.

  (ii) Show that if $L / K$ is finite there exists $n \geqslant 0$ and $y \in L$ such that $y^{p^{n}}=t$ and $L / K(y)$ is separable.

  Show that $Y^{2}+t Y+t$ is an irreducible separable polynomial over the field of rational functions $K=\mathbb{F}_{2}(t)$. Find the degree of the splitting field of $X^{4}+t X^{2}+t$ over $K$.

  comment

• Paper 4, Section II, H

  Galois Theory | Part II, 2014

  (i) Let $G$ be a finite subgroup of the multiplicative group of a field. Show that $G$ is cyclic.

  (ii) Let $\Phi_{n}(X)$ be the $n$th cyclotomic polynomial. Let $p$ be a prime not dividing $n$, and let $L$ be a splitting field for $\Phi_{n}$ over $\mathbb{F}_{p}$. Show that $L$ has $p^{m}$ elements, where $m$ is the least positive integer such that $p^{m} \equiv 1(\bmod n)$.

  (iii) Find the degrees of the irreducible factors of $X^{35}-1$ over $\mathbb{F}_{2}$, and the number of factors of each degree.

  comment

General Relativity

• Paper 1, Section II, 37E

  General Relativity | Part II, 2014

  For a timelike geodesic in the equatorial plane $\left(\theta=\frac{1}{2} \pi\right)$ of the Schwarzschild spacetime with line element

  $$d s^{2}=-\left(1-r_{s} / r\right) c^{2} d t^{2}+\left(1-r_{s} / r\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  derive the equation

  $$\frac{1}{2} \dot{r}^{2}+V(r)=\frac{1}{2}(E / c)^{2}$$

  where

  $$\frac{2 V(r)}{c^{2}}=1-\frac{r_{s}}{r}+\frac{h^{2}}{c^{2} r^{2}}-\frac{h^{2} r_{s}}{c^{2} r^{3}}$$

  and $h$ and $E$ are constants. The dot denotes the derivative with respect to an affine parameter $\tau$ satisfying $c^{2} d \tau^{2}=-d s^{2}$.

  Given that there is a stable circular orbit at $r=R$, show that

  $$\frac{h^{2}}{c^{2}}=\frac{R^{2} \epsilon}{2-3 \epsilon}$$

  where $\epsilon=r_{s} / R$.

  Compute $\Omega$, the orbital angular frequency (with respect to $\tau$ ).

  Show that the angular frequency $\omega$ of small radial perturbations is given by

  $$\frac{\omega^{2} R^{2}}{c^{2}}=\frac{\epsilon(1-3 \epsilon)}{2-3 \epsilon}$$

  Deduce that the rate of precession of the perihelion of the Earth's orbit, $\Omega-\omega$, is approximately $3 \Omega^{3} T^{2}$, where $T$ is the time taken for light to travel from the Sun to the Earth. [You should assume that the Earth's orbit is approximately circular, with $r_{s} / R \ll 1$ and $\left.E \simeq c^{2} .\right]$

  comment

• Paper 2, Section II, E

  General Relativity | Part II, 2014

  Show how the geodesic equations and hence the Christoffel symbols $\Gamma^{a} b c$ can be obtained from a Lagrangian.

  In units with $c=1$, the FLRW spacetime line element is

  $$d s^{2}=-d t^{2}+a^{2}(t)\left(d x^{2}+d y^{2}+d z^{2}\right)$$

  Show that $\Gamma_{01}^{1}=\dot{a} / a$.

  You are given that, for the above metric, $G_{0}{ }^{0}=-3 \dot{a}^{2} / a^{2}$ and $G_{1}^{1}=-2 \ddot{a} / a-\dot{a}^{2} / a^{2}$, where $G_{a}^{b}$ is the Einstein tensor, which is diagonal. Verify by direct calculation that $\nabla_{b} G_{a}^{b}=0$.

  Solve the vacuum Einstein equations in the presence of a cosmological constant to determine the form of $a(t)$.

  comment

• Paper 3, Section II, $37 \mathrm{E}$

  General Relativity | Part II, 2014

  The vector field $V^{a}$ is the normalised $\left(V_{a} V^{a}=-c^{2}\right)$ tangent to a congruence of timelike geodesics, and $B_{a b}=\nabla_{b} V_{a}$.

  Show that:

  (i) $V^{a} B_{a b}=V^{b} B_{a b}=0$;

  (ii) $V^{c} \nabla_{c} B_{a b}=-B_{b}^{c} B_{a c}-R_{a c b}^{d} V^{c} V_{d}$.

  [You may use the Ricci identity $\nabla_{c} \nabla_{b} X_{a}=\nabla_{b} \nabla_{c} X_{a}-R_{a c b}^{d} X_{d}$.]

  Now assume that $B_{a b}$ is symmetric and let $\theta=B_{a}{ }^{a}$. By writing $B_{a b}=\widetilde{B}_{a b}+\frac{1}{4} \theta g_{a b}$, or otherwise, show that

  $$\frac{d \theta}{d \tau} \leqslant-\frac{1}{4} \theta^{2}-R_{00}$$

  where $R_{00}=R_{a b} V^{a} V^{b}$ and $\frac{d \theta}{d \tau} \equiv V^{a} \nabla_{a} \theta$. [You may use without proof the result that \left.\widetilde{B}_{a b} \widetilde{B}^{a b} \geqslant 0 .\right]

  Assume, in addition, that the stress-energy tensor $T_{a b}$ takes the perfect-fluid form $\left(\rho+p / c^{2}\right) V_{a} V_{b}+p g_{a b}$ and that $\rho c^{2}+3 p>0$. Show that

  $$\frac{d \theta^{-1}}{d \tau}>\frac{1}{4}$$

  and deduce that, if $\theta(0)<0$, then $|\theta(\tau)|$ will become unbounded for some value of $\tau$ less than $4 /|\theta(0)|$.

  comment

• Paper 4, Section II, E

  General Relativity | Part II, 2014

  A plane-wave spacetime has line element

  $$d s^{2}=H d u^{2}+2 d u d v+d x^{2}+d y^{2}$$

  where $H=x^{2}-y^{2}$. Show that the line element is unchanged by the coordinate transformation

  $$u=\bar{u}, \quad v=\bar{v}+\bar{x} e^{\bar{u}}-\frac{1}{2} e^{2 \bar{u}}, \quad x=\bar{x}-e^{\bar{u}}, \quad y=\bar{y}$$

  Show more generally that the line element is unchanged by coordinate transformations of the form

  $$u=\bar{u}+a, \quad v=\bar{v}+b \bar{x}+c, \quad x=\bar{x}+p, \quad y=\bar{y}$$

  where $a, b, c$ and $p$ are functions of $\bar{u}$, which you should determine and which depend in total on four parameters (arbitrary constants of integration).

  Deduce (without further calculation) that the line element is unchanged by a 6parameter family of coordinate transformations, of which a 5 -parameter family leave invariant the surfaces $u=$ constant.

  For a general coordinate transformation $x^{a}=x^{a}\left(\bar{x}^{b}\right)$, give an expression for the transformed Ricci tensor $\bar{R}_{c d}$ in terms of the Ricci tensor $R_{a b}$ and the transformation matrices $\frac{\partial x^{a}}{\partial \bar{x}^{c}}$. Calculate $\bar{R}_{\bar{x} \bar{x}}$ when the transformation is given by $(*)$ and deduce that $R_{v v}=R_{v x}$

  comment

Geometry and Groups

• Paper 1, Section I, F

  Geometry and Groups | Part II, 2014

  Let $G \leqslant S O(3)$ be a finite group. Suppose $G$ does not preserve any plane in $\mathbb{R}^{3}$. Show that for any point $p$ in the unit sphere $S^{2} \subset \mathbb{R}^{3}$, the stabiliser $\operatorname{Stab}_{G}(p)$ contains at most 5 elements.

  comment

• Paper 1, Section II, F

  Geometry and Groups | Part II, 2014

  Prove that an orientation-preserving isometry of the ball-model of hyperbolic space $\mathbb{H}^{3}$ which fixes the origin is an element of $S O(3)$. Hence, or otherwise, prove that a finite subgroup of the group of orientation-preserving isometries of hyperbolic space $\mathbb{H}^{3}$ has a common fixed point.

  Can an infinite non-cyclic subgroup of the isometry group of $\mathbb{H}^{3}$ have a common fixed point? Can any such group be a Kleinian group? Justify your answers.

  comment

• Paper 2, Section I, F

  Geometry and Groups | Part II, 2014

  Let $g, h$ be non-identity Möbius transformations. Prove that $g$ and $h$ commute if and only if one of the following holds:

  1. $\operatorname{Fix}(g)=\operatorname{Fix}(h)$;

  2. $g, h$ are involutions each of which exchanges the other's fixed points.

  Give an example to show that the second case can occur.

  comment

• Paper 3, Section I, F

  Geometry and Groups | Part II, 2014

  Let $\mathbb{H}^{2}$ denote the hyperbolic plane, and $T \subset \mathbb{H}^{2}$ be a non-degenerate triangle, i.e. the bounded region enclosed by three finite-length geodesic arcs. Prove that the three angle bisectors of $T$ meet at a point.

  Must the three vertices of $T$ lie on a hyperbolic circle? Justify your answer.

  comment

• Paper 4, Section I, F

  Geometry and Groups | Part II, 2014

  Define the limit set $\Lambda(G)$ of a Kleinian group $G$. Assuming that $G$ has no finite orbit in $\mathbb{H}^{3} \cup S_{\infty}^{2}$, and that $\Lambda(G) \neq \emptyset$, prove that if $E \subset \mathbb{C} \cup\{\infty\}$ is any non-empty closed set which is invariant under $G$, then $\Lambda(G) \subset E$.

  comment

• Paper 4, Section II, F

  Geometry and Groups | Part II, 2014

  Define the $s$-dimensional Hausdorff measure $\mathcal{H}^{s}(F)$ of a set $F \subset \mathbb{R}^{N}$. Explain briefly how properties of this measure may be used to define the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of such a set.

  Prove that the limit sets of conjugate Kleinian groups have equal Hausdorff dimension. Hence, or otherwise, prove that there is no subgroup of $\mathbb{P} S L(2, \mathbb{R})$ which is conjugate in $\mathbb{P} S L(2, \mathbb{C})$ to $\mathbb{P} S L(2, \mathbb{Z} \oplus \mathbb{Z} i)$.

  comment

Graph Theory

• Paper 1, Section II, I

  Graph Theory | Part II, 2014

  Show that a graph is bipartite if and only if all of its cycles are of even length.

  Show that a bridgeless plane graph is bipartite if and only if all of its faces are of even length.

  Let $G$ be an Eulerian plane graph. Show that the faces of $G$ can be coloured with two colours so that no two contiguous faces have the same colour. Deduce that it is possible to assign a direction to each edge of $G$ in such a way that the edges around each face form a directed cycle.

  comment

• Paper 2, Section II, I

  Graph Theory | Part II, 2014

  Let $k$ and $n$ be integers with $1 \leqslant k<n$. Show that every connected graph of order $n$, in which $d(u)+d(v) \geqslant k$ for every pair $u, v$ of non-adjacent vertices, contains a path of length $k$.

  Let $k$ and $n$ be integers with $1 \leqslant k \leqslant n$. Show that a graph of order $n$ that contains no path of length $k$ has at most $(k-1) n / 2$ edges, and that this value is achieved only if $k$ divides $n$ and $G$ is the union of $n / k$ disjoint copies of $K_{k}$. [Hint: Proceed by induction on $n$ and consider a vertex of minimum degree.]

  comment

• Paper 3, Section II, I

  Graph Theory | Part II, 2014

  Prove that $\chi(G) \leqslant \Delta(G)+1$ for every graph $G$. Prove further that, if $\kappa(G) \geqslant 3$, then $\chi(G) \leqslant \Delta(G)$ unless $G$ is complete.

  Let $k \geqslant 2$. A graph $G$ is said to be $k$-critical if $\chi(G)=k+1$, but $\chi(G-v)=k$ for every vertex $v$ of $G$. Show that, if $G$ is $k$-critical, then $\kappa(G) \geqslant 2$.

  Let $k \geqslant 2$, and let $H$ be the graph $K_{k+1}$ with an edge removed. Show that $H$ has the following property: it has two vertices which receive the same colour in every $k$-colouring of $H$. By considering two copies of $H$, construct a $k$-colourable graph $G$ of order $2 k+1$ with the following property: it has three vertices which receive the same colour in every $k$-colouring of $G$.

  Construct, for all integers $k \geqslant 2$ and $\ell \geqslant 2$, a $k$-critical graph $G$ of order $\ell k+1$ with $\kappa(G)=2 .$

  comment

• Paper 4, Section II, I

  Graph Theory | Part II, 2014

  Define the Ramsey number $R^{(r)}(s, t)$. What is the value of $R^{(1)}(s, t)$ ? Prove that $R^{(r)}(s, t) \leqslant 1+R^{(r-1)}\left(R^{(r)}(s-1, t), R^{(r)}(s, t-1)\right)$ holds for $r \geqslant 2$ and deduce that $R^{(r)}(s, t)$ exists.

  Show that $R^{(2)}(3,3)=6$ and that $R^{(2)}(3,4)=9$.

  Show that $7 \leqslant R^{(3)}(4,4) \leqslant 19$. [Hint: For the lower bound, choose a suitable subset $U$ and colour e red if $|U \cap e|$ is odd.]

  comment

Integrable Systems

• Paper 1, Section II, D

  Integrable Systems | Part II, 2014

  Consider the coordinate transformation

  $$g^{\epsilon}:(x, u) \mapsto(\tilde{x}, \tilde{u})=(x \cos \epsilon-u \sin \epsilon, x \sin \epsilon+u \cos \epsilon)$$

  Show that $g^{\epsilon}$ defines a one-parameter group of transformations. Define what is meant by the generator $V$ of a one-parameter group of transformations and compute it for the above case.

  Now suppose $u=u(x)$. Explain what is meant by the first prolongation $\mathrm{pr}^{(1)} g^{\epsilon}$ of $g^{\epsilon}$. Compute $\mathrm{pr}^{(1)} g^{\epsilon}$ in this case and deduce that

  $$\mathrm{pr}^{(1)} V=V+\left(1+u_{x}^{2}\right) \frac{\partial}{\partial u_{x}}$$

  Similarly find $\mathrm{pr}^{(2)} V$.

  Define what is meant by a Lie point symmetry of the first-order differential equation $\Delta\left[x, u, u_{x}\right]=0$. Describe this condition in terms of the vector field that generates the Lie point symmetry. Consider the case

  $$\Delta\left[x, u, u_{x}\right] \equiv u_{x}-\frac{u+x f\left(x^{2}+u^{2}\right)}{x-u f\left(x^{2}+u^{2}\right)}$$

  where $f$ is an arbitrary smooth function of one variable. Using $(\star)$, show that $g^{\epsilon}$ generates a Lie point symmetry of the corresponding differential equation.

  comment

• Paper 2, Section II, D

  Integrable Systems | Part II, 2014

  Let $u=u(x)$ be a smooth function that decays rapidly as $|x| \rightarrow \infty$ and let $L=-\partial_{x}^{2}+u(x)$ denote the associated Schrödinger operator. Explain very briefly each of the terms appearing in the scattering data

  $$S=\left\{\left\{\chi_{n}, c_{n}\right\}_{n=1}^{N}, R(k)\right\},$$

  associated with the operator $L$. What does it mean to say $u(x)$ is reflectionless?

  Given $S$, define the function

  $$F(x)=\sum_{n=1}^{N} c_{n}^{2} e^{-\chi_{n} x}+\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{\mathrm{i} k x} R(k) \mathrm{d} k$$

  If $K=K(x, y)$ is the unique solution to the GLM equation

  $$K(x, y)+F(x+y)+\int_{x}^{\infty} K(x, z) F(z+y) \mathrm{d} z=0$$

  what is the relationship between $u(x)$ and $K(x, x)$ ?

  Now suppose that $u=u(x, t)$ is time dependent and that it solves the KdV equation $u_{t}+u_{x x x}-6 u u_{x}=0$. Show that $L=-\partial_{x}^{2}+u(x, t)$ obeys the Lax equation

  $$L_{t}=[L, A], \quad \text { where } A=4 \partial_{x}^{3}-3\left(u \partial_{x}+\partial_{x} u\right) .$$

  Show that the discrete eigenvalues of $L$ are time independent.

  In what follows you may assume the time-dependent scattering data take the form

  $$S(t)=\left\{\left\{\chi_{n}, c_{n} e^{4 \chi_{n}^{3} t}\right\}_{n=1}^{N}, R(k, 0) e^{8 \mathrm{i} k^{3} t}\right\} .$$

  Show that if $u(x, 0)$ is reflectionless, then the solution to the KdV equation takes the form

  $$u(x, t)=-2 \frac{\partial^{2}}{\partial x^{2}} \log [\operatorname{det} A(x, t)]$$

  where $A$ is an $N \times N$ matrix which you should determine.

  Assume further that $R(k, 0)=k^{2} f(k)$, where $f$ is smooth and decays rapidly at infinity. Show that, for any fixed $x$,

  $$\int_{-\infty}^{\infty} e^{\mathrm{i} k x} R(k, 0) e^{8 \mathrm{i} k^{3} t} \mathrm{~d} k=O\left(t^{-1}\right) \quad \text { as } t \rightarrow \infty$$

  Comment briefly on the significance of this result.

  [You may assume $\frac{1}{\operatorname{det} A} \frac{\mathrm{d}}{\mathrm{d} x}(\operatorname{det} A)=\operatorname{tr}\left(A^{-1} \frac{\mathrm{d} A}{\mathrm{~d} x}\right)$ for a non-singular matrix $A(x)$.]

  comment

• Paper 3, Section II, D

  Integrable Systems | Part II, 2014

  What does it mean to say that a finite-dimensional Hamiltonian system is integrable? State the Arnold-Liouville theorem.

  A six-dimensional dynamical system with coordinates $\left(x_{1}, x_{2}, x_{3}, y_{1}, y_{2}, y_{3}\right)$ is governed by the differential equations

  $$\frac{\mathrm{d} x_{i}}{\mathrm{~d} t}=-\frac{1}{2 \pi} \sum_{j \neq i} \frac{\Gamma_{j}\left(y_{i}-y_{j}\right)}{\left(x_{i}-x_{j}\right)^{2}+\left(y_{i}-y_{j}\right)^{2}}, \quad \frac{\mathrm{d} y_{i}}{\mathrm{~d} t}=\frac{1}{2 \pi} \sum_{j \neq i} \frac{\Gamma_{j}\left(x_{i}-x_{j}\right)}{\left(x_{i}-x_{j}\right)^{2}+\left(y_{i}-y_{j}\right)^{2}}$$

  for $i=1,2,3$, where $\left\{\Gamma_{i}\right\}_{i=1}^{3}$ are positive constants. Show that these equations can be written in the form

  $$\Gamma_{i} \frac{\mathrm{d} x_{i}}{\mathrm{~d} t}=\frac{\partial F}{\partial y_{i}}, \quad \Gamma_{i} \frac{\mathrm{d} y_{i}}{\mathrm{~d} t}=-\frac{\partial F}{\partial x_{i}}, \quad i=1,2,3$$

  for an appropriate function $F$. By introducing the coordinates

  $$\mathbf{q}=\left(x_{1}, x_{2}, x_{3}\right), \quad \mathbf{p}=\left(\Gamma_{1} y_{1}, \Gamma_{2} y_{2}, \Gamma_{3} y_{3}\right),$$

  show that the system can be written in Hamiltonian form

  $$\frac{\mathrm{d} \mathbf{q}}{\mathrm{d} t}=\frac{\partial H}{\partial \mathbf{p}}, \quad \frac{\mathrm{d} \mathbf{p}}{\mathrm{d} t}=-\frac{\partial H}{\partial \mathbf{q}}$$

  for some Hamiltonian $H=H(\mathbf{q}, \mathbf{p})$ which you should determine.

  Show that the three functions

  $$A=\sum_{i=1}^{3} \Gamma_{i} x_{i}, \quad B=\sum_{i=1}^{3} \Gamma_{i} y_{i}, \quad C=\sum_{i=1}^{3} \Gamma_{i}\left(x_{i}^{2}+y_{i}^{2}\right)$$

  are first integrals of the Hamiltonian system.

  Making use of the fundamental Poisson brackets $\left\{q_{i}, q_{j}\right\}=\left\{p_{i}, p_{j}\right\}=0$ and $\left\{q_{i}, p_{j}\right\}=\delta_{i j}$, show that

  $$\{A, C\}=2 B, \quad\{B, C\}=-2 A$$

  Hence show that the Hamiltonian system is integrable.

  comment

Linear Analysis

• Paper 1, Section II, G

  Linear Analysis | Part II, 2014

  Let $X$ and $Y$ be normed spaces. What is an isomorphism between $X$ and $Y$ ? Show that a bounded linear map $T: X \rightarrow Y$ is an isomorphism if and only if $T$ is surjective and there is a constant $c>0$ such that $\|T x\| \geqslant c\|x\|$ for all $x \in X$. Show that if there is an isomorphism $T: X \rightarrow Y$ and $X$ is complete, then $Y$ is complete.

  Show that two normed spaces of the same finite dimension are isomorphic. [You may assume without proof that any two norms on a finite-dimensional space are equivalent.] Briefly explain why this implies that every finite-dimensional space is complete, and every closed and bounded subset of a finite-dimensional space is compact.

  Let $Z$ and $F$ be subspaces of a normed space $X$ with $Z \cap F=\{0\}$. Assume that $Z$ is closed in $X$ and $F$ is finite-dimensional. Prove that $Z+F$ is closed in $X$. [Hint: First show that the function $x \mapsto d(x, Z)=\inf \{\|x-z\|: z \in Z\}$ restricted to the unit sphere of F achieves its minimum.]

  comment

• Paper 2, Section II, G

  Linear Analysis | Part II, 2014

  (a) Let $X$ and $Y$ be Banach spaces, and let $T: X \rightarrow Y$ be a surjective linear map. Assume that there is a constant $c>0$ such that $\|T x\| \geqslant c\|x\|$ for all $x \in X$. Show that $T$ is continuous. [You may use any standard result from general Banach space theory provided you clearly state it.] Give an example to show that the assumption that $X$ and $Y$ are complete is necessary.

  (b) Let $C$ be a closed subset of a Banach space $X$ such that

  (i) $x_{1}+x_{2} \in C$ for each $x_{1}, x_{2} \in C$;

  (ii) $\lambda x \in C$ for each $x \in C$ and $\lambda>0$;

  (iii) for each $x \in X$, there exist $x_{1}, x_{2} \in C$ such that $x=x_{1}-x_{2}$.

  Prove that, for some $M>0$, the unit ball of $X$ is contained in the closure of the set

  $$\left\{x_{1}-x_{2}: x_{i} \in C, \quad\left\|x_{i}\right\| \leqslant M(i=1,2)\right\} .$$

  [You may use without proof any version of the Baire Category Theorem.] Deduce that, for some $K>0$, every $x \in X$ can be written as $x=x_{1}-x_{2}$ with $x_{i} \in C$ and $\left\|x_{i}\right\| \leqslant K\|x\|(i=1,2) .$

  comment

• Paper 3, Section II, G

  Linear Analysis | Part II, 2014

  (i) State carefully the theorems of Stone-Weierstrass and Arzelá-Ascoli (work with real scalars only).

  (ii) Let $\mathcal{F}$ denote the family of functions on $[0,1]$ of the form

  $$f(x)=\sum_{n=1}^{\infty} a_{n} \sin (n x)$$

  where the $a_{n}$ are real and $\left|a_{n}\right| \leqslant 1 / n^{3}$ for all $n \in \mathbb{N}$. Prove that any sequence in $\mathcal{F}$ has a subsequence that converges uniformly on $[0,1]$.

  (iii) Let $f:[0,1] \rightarrow \mathbb{R}$ be a continuous function such that $f(0)=0$ and $f^{\prime}(0)$ exists. Show that for each $\varepsilon>0$ there exists a real polynomial $p$ having only odd powers, i.e. of the form

  $$p(x)=a_{1} x+a_{3} x^{3}+\cdots+a_{2 m-1} x^{2 m-1},$$

  such that $\sup _{x \in[0,1]}|f(x)-p(x)|<\varepsilon$. Show that the same holds without the assumption that $f$ is differentiable at 0 .

  comment

• Paper 4, Section II, G

  Linear Analysis | Part II, 2014

  Define the spectrum $\sigma(T)$ and the approximate point spectrum $\sigma_{\mathrm{ap}}(T)$ of a bounded linear operator $T$ on a Banach space. Prove that $\sigma_{\mathrm{ap}}(T) \subset \sigma(T)$ and that $\sigma(T)$ is a closed and bounded subset of $\mathbb{C}$. [You may assume without proof that the set of invertible operators is open.]

  Let $T$ be a hermitian operator on a non-zero Hilbert space. Prove that $\sigma(T)$ is not empty

  Let $K$ be a non-empty, compact subset of $\mathbb{C}$. Show that there is a bounded linear operator $T: \ell_{2} \rightarrow \ell_{2}$ with $\sigma(T)=K .$ [You may assume without proof that a compact metric space is separable.]

  comment

Logic and Set Theory

• Paper 1, Section II, I

  Logic and Set Theory | Part II, 2014

  Explain what is meant by saying that a binary relation $r \subseteq a \times a$ is well-founded. Show that $r$ is well-founded if and only if, for any set $b$ and any function $f: \mathcal{P} b \rightarrow b$, there exists a unique function $g: a \rightarrow b$ satisfying

  $$g(x)=f(\{g(y) \mid\langle y, x\rangle \in r\})$$

  for all $x \in a$. [Hint: For 'if', it suffices to take $b=\{0,1\}$, with $f: \mathcal{P} b \rightarrow b$ defined by $\left.f\left(b^{\prime}\right)=1 \Leftrightarrow 1 \in b^{\prime} .\right]$

  comment

• Paper 2, Section II, I

  Logic and Set Theory | Part II, 2014

  Write down the recursive definitions of ordinal addition, multiplication and exponentiation. Show that, for any nonzero ordinal $\alpha$, there exist unique ordinals $\beta, \gamma$ and $n$ such that $\alpha=\omega^{\beta} . n+\gamma, \gamma<\omega^{\beta}$ and $0<n<\omega$.

  Hence or otherwise show that $\alpha$ (that is, the set of ordinals less than $\alpha$ ) is closed under addition if and only if $\alpha=\omega^{\beta}$ for some $\beta$. Show also that an infinite ordinal $\alpha$ is closed under multiplication if and only if $\alpha=\omega^{\left(\omega^{\gamma}\right)}$ for some $\gamma$.

  [You may assume the standard laws of ordinal arithmetic, and the fact that $\alpha \leqslant \omega^{\alpha}$ for all $\alpha$.]

  comment

• Paper 3, Section II, I

  Logic and Set Theory | Part II, 2014

  Explain what is meant by a structure for a first-order signature $\Sigma$, and describe briefly how first-order terms and formulae in the language over $\Sigma$ are interpreted in a structure. Suppose that $A$ and $B$ are $\Sigma$-structures, and that $\phi$ is a conjunction of atomic formulae over $\Sigma$ : show that an $n$-tuple $\left(\left(a_{1}, b_{1}\right), \ldots,\left(a_{n}, b_{n}\right)\right)$ belongs to the interpretation $\llbracket \phi \rrbracket_{A \times B}$ of $\phi$ in $A \times B$ if and only if $\left(a_{1}, \ldots, a_{n}\right) \in \llbracket \phi \rrbracket_{A}$ and $\left(b_{1}, \ldots, b_{n}\right) \in \llbracket \phi \rrbracket B$.

  A first-order theory $\mathbb{T}$ is called regular if its axioms all have the form

  $$(\forall \vec{x})(\phi \Rightarrow(\exists \vec{y}) \psi),$$

  where $\vec{x}$and $\vec{y}$ are (possibly empty) strings of variables and $\phi$ and $\psi$ are conjunctions of atomic formulae (possibly the empty conjunction $T$ ). Show that if $A$ and $B$ are models of a regular theory $\mathbb{T}$, then so is $A \times B$.

  Now suppose that $\mathbb{T}$ is a regular theory, and that a sentence of the form

  $$(\forall \vec{x})\left(\phi \Rightarrow\left(\psi_{1} \vee \psi_{2} \vee \cdots \vee \psi_{n}\right)\right)$$

  is derivable from the axioms of $\mathbb{T}$, where $\phi$ and the $\psi_{i}$ are conjunctions of atomic formulae. Show that the sentence $(\forall \vec{x})\left(\phi \Rightarrow \psi_{i}\right)$ is derivable for some $i$. [Hint: Suppose not, and use the Completeness Theorem to obtain a suitable family of $\mathbb{T}$-models $A_{1}, \ldots, A_{n}$.]

  comment

• Paper 4, Section II, I

  Logic and Set Theory | Part II, 2014

  Explain what is meant by a chain-complete poset. State the Bourbaki-Witt fixedpoint theorem.

  We call a poset $(P, \leqslant)$ Bourbakian if every order-preserving map $f: P \rightarrow P$ has a least fixed point $\mu(f)$. Suppose $P$ is Bourbakian, and let $f, g: P \rightrightarrows P$ be order-preserving maps with $f(x) \leqslant g(x)$ for all $x \in P$; show that $\mu(f) \leqslant \mu(g)$. [Hint: Consider the function $h: P \rightarrow P$ defined by $h(x)=f(x)$ if $x \leqslant \mu(g), h(x)=\mu(g)$ otherwise.]

  Suppose $P$ is Bourbakian and $f: \alpha \rightarrow P$ is an order-preserving map from an ordinal to $P$. Show that there is an order-preserving map $g: P \rightarrow P$ whose fixed points are exactly the upper bounds of the set $\{f(\beta) \mid \beta<\alpha\}$, and deduce that this set has a least upper bound.

  Let $C$ be a chain with no greatest member. Using the Axiom of Choice and Hartogs' Lemma, show that there is an order-preserving map $f: \alpha \rightarrow C$, for some ordinal $\alpha$, whose image has no upper bound in $C$. Deduce that any Bourbakian poset is chain-complete.

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2014

  A population model for two species is given by

  $$\begin{aligned} &\frac{d N}{d t}=a N-b N P-k N^{2} \\ &\frac{d P}{d t}=-d P+c N P \end{aligned}$$

  where $a, b, c, d$ and $k$ are positive parameters. Show that this may be rescaled to

  $$\begin{aligned} &\frac{d u}{d \tau}=u(1-v-\beta u) \\ &\frac{d v}{d \tau}=-\alpha v(1-u) \end{aligned}$$

  and give $\alpha$ and $\beta$ in terms of the original parameters.

  For $\beta<1$ find all fixed points in $u \geqslant 0, v \geqslant 0$, and analyse their stability. Assuming that both populations are present initially, what does this suggest will be the long-term outcome?

  comment

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2014

  Consider an experiment where two or three individuals are added to a population with probability $\lambda_{2}$ and $\lambda_{3}$ respectively per unit time. The death rate in the population is a constant $\beta$ per individual per unit time.

  Write down the master equation for the probability $p_{n}(t)$ that there are $n$ individuals in the population at time $t$. From this, derive an equation for $\frac{\partial \phi}{\partial t}$, where $\phi$ is the generating function

  $$\phi(s, t)=\sum_{n=0}^{\infty} s^{n} p_{n}(t)$$

  Find the solution for $\phi$ in steady state, and show that the mean and variance of the population size are given by

  $$\langle n\rangle=3 \frac{\lambda_{3}}{\beta}+2 \frac{\lambda_{2}}{\beta}, \quad \operatorname{var}(n)=6 \frac{\lambda_{3}}{\beta}+3 \frac{\lambda_{2}}{\beta} .$$

  Hence show that, for a free choice of $\lambda_{2}$ and $\lambda_{3}$ subject to a given target mean, the experimenter can minimise the variance by only adding two individuals at a time.

  comment

• Paper 2, Section II, B

  Mathematical Biology | Part II, 2014

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} \frac{\partial u}{\partial t} &=\frac{a u}{v}-u^{2}+d_{1} \frac{\partial^{2} u}{\partial x^{2}} \\ \frac{\partial v}{\partial t} &=v^{2}-\frac{v}{u^{2}}+d_{2} \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  where $a, d_{1}, d_{2}>0$.

  Find the range of $a$ for which the spatially homogeneous system has a stable equilibrium solution with $u>0$ and $v>0$. Determine when the equilibrium is a stable focus, and sketch the phase diagram for this case (restricting attention to $u>0$ and $v>0)$.

  For the case when the homogeneous system is stable, consider spatial perturbations proportional to $\cos (k x)$ of the solution found above. Briefly explain why the system will be stable to spatial perturbations with very small or very large $k$. Find conditions for the system to be unstable to a spatial perturbation (for some range of $k$ which need not be given). Sketch the region satisfying these conditions in the $\left(a, d_{1} / d_{2}\right)$ plane.

  Find $k_{c}$, the critical wavenumber at the onset of instability, in terms of $a$ and $d_{1}$.

  comment

• Paper 3, Section $I$, B

  Mathematical Biology | Part II, 2014

  An epidemic model is given by

  $$\begin{aligned} &\frac{d S}{d t}=-r I S \\ &\frac{d I}{d t}=+r I S-a I \end{aligned}$$

  where $S(t)$ are the susceptibles, $I(t)$ are the infecteds, and $a$ and $r$ are positive parameters. The basic reproduction ratio is defined as $R_{0}=r N / a$, where $N$ is the total population size. Find a condition on $R_{0}$ for an epidemic to be possible if, initially, $S \approx N$ and $I$ is small but non-zero.

  Now suppose a proportion $p$ of the population was vaccinated (with a completely effective vaccine) so that initially $S \approx(1-p) N$. On a sketch of the $\left(R_{0}, p\right)$ plane, mark the regions where an epidemic is still possible, where the vaccination will prevent an epidemic, and where no vaccination was necessary.

  For the case when an epidemic is possible, show that $\sigma$, the proportion of the initially susceptible population that has not been infected by the end of an epidemic, satisfies

  $$\sigma-\frac{1}{(1-p) R_{0}} \log \sigma \approx 1$$

  comment

• Paper 3, Section II, B

  Mathematical Biology | Part II, 2014

  A discrete-time model for breathing is given by

  $$\begin{aligned} V_{n+1} &=\alpha C_{n-k}, \\ C_{n+1}-C_{n} &=\gamma-\beta V_{n+1}, \end{aligned}$$

  where $V_{n}$ is the volume of each breath in time step $n$ and $C_{n}$ is the concentration of carbon dioxide in the blood at the end of time step $n$. The parameters $\alpha, \beta$ and $\gamma$ are all positive. Briefly explain the biological meaning of each of the above equations.

  Find the steady state. For $k=0$ and $k=1$ determine the stability of the steady state.

  For general (integer) $k>1$, by seeking parameter values when the modulus of a perturbation to the steady state is constant, find the range of parameters where the solution is stable. What is the periodicity of the constant-modulus solution at the edge of this range? Comment on how the size of the range depends on $k$.

  This can be developed into a more realistic model by changing the term $-\beta V_{n+1}$ to $-\beta C_{n} V_{n+1}$ in (2). Briefly explain the biological meaning of this change. Show that for both $k=0$ and $k=1$ the new steady state is stable if $0<a<1$, where $a=\sqrt{\alpha \beta \gamma}$.

  comment

• Paper 4, Section I, B

  Mathematical Biology | Part II, 2014

  The concentration $c(x, t)$ of a chemical in one dimension obeys the equations

  $$\frac{\partial c}{\partial t}=\frac{\partial}{\partial x}\left(c^{2} \frac{\partial c}{\partial x}\right), \quad \int_{-\infty}^{\infty} c(x, t) d x=1$$

  State the physical interpretation of each equation.

  Seek a similarity solution of the form $c=t^{\alpha} f(\xi)$, where $\xi=t^{\beta} x$. Find equations involving $\alpha$ and $\beta$ from the differential equation and the integral. Show that these are satisfied by $\alpha=\beta=-1 / 4$.

  Find the solution for $f(\xi)$. Find and sketch the solution for $c(x, t)$.

  comment

Number Fields

• Paper 1, Section II, F

  Number Fields | Part II, 2014

  State a result involving the discriminant of a number field that implies that the class group is finite.

  Use Dedekind's theorem to factor $2,3,5$ and 7 into prime ideals in $K=\mathbb{Q}(\sqrt{-34})$. By factoring $1+\sqrt{-34}$ and $4+\sqrt{-34}$, or otherwise, prove that the class group of $K$ is cyclic, and determine its order.

  comment

• Paper 2, Section II, F

  Number Fields | Part II, 2014

  (i) Show that each prime ideal in a number field $K$ divides a unique rational prime $p$. Define the ramification index and residue class degree of such an ideal. State and prove a formula relating these numbers, for all prime ideals dividing a given rational prime $p$, to the degree of $K$ over $\mathbb{Q}$.

  (ii) Show that if $\zeta_{n}$ is a primitive $n$th root of unity then $\prod_{j=1}^{n-1}\left(1-\zeta_{n}^{j}\right)=n$. Deduce that if $n=p q$, where $p$ and $q$ are distinct primes, then $1-\zeta_{n}$ is a unit in $\mathbb{Z}\left[\zeta_{n}\right]$.

  (iii) Show that if $K=\mathbb{Q}\left(\zeta_{p}\right)$ where $p$ is prime, then any prime ideal of $K$ dividing $p$ has ramification index at least $p-1$. Deduce that $[K: \mathbb{Q}]=p-1$.

  comment

• Paper 4, Section II, F

  Number Fields | Part II, 2014

  Explain what is meant by an integral basis for a number field. Splitting into the cases $d \equiv 1(\bmod 4)$ and $d \equiv 2,3(\bmod 4)$, find an integral basis for $K=\mathbb{Q}(\sqrt{d})$ where $d \neq 0,1$ is a square-free integer. Justify your answer.

  Find the fundamental unit in $\mathbb{Q}(\sqrt{13})$. Determine all integer solutions to the equation $x^{2}+x y-3 y^{2}=17$.

  comment

Number Theory

• Paper 1, Section I, $1 F$

  Number Theory | Part II, 2014

  Define what it means for a number $N$ to be a pseudoprime to the base $b$.

  Show that if there is a base $b$ to which $N$ is not a pseudoprime, then $N$ is a pseudoprime to at most half of all possible bases.

  Let $n$ be an integer greater than 1 such that $F_{n}=2^{2^{n}}+1$ is composite. Show that $F_{n}$ is a pseudoprime to the base 2 .

  comment

• Paper 2, Section I, F

  Number Theory | Part II, 2014

  Show that

  $$\sum_{p \leqslant x} \frac{1}{p} \geqslant \log \log x-\frac{1}{2}$$

  Deduce that there are infinitely many primes.

  comment

• Paper 3, Section I, $1 F$

  Number Theory | Part II, 2014

  Show that the continued fraction for $\sqrt{51}$ is $[7 ; \overline{7,14}]$.

  Hence, or otherwise, find positive integers $x$ and $y$ that satisfy the equation $x^{2}-51 y^{2}=1 .$

  Are there integers $x$ and $y$ such that $x^{2}-51 y^{2}=-1$ ?

  comment

• Paper 3, Section II, F

  Number Theory | Part II, 2014

  State and prove Lagrange's theorem about polynomial congruences modulo a prime.

  Define the Euler totient function $\phi$.

  Let $p$ be a prime and let $d$ be a positive divisor of $p-1$. Show that there are exactly $\phi(d)$ elements of $(\mathbb{Z} / p \mathbb{Z})^{\times}$with order $d .$

  Deduce that $(\mathbb{Z} / p \mathbb{Z})^{\times}$is cyclic.

  Let $g$ be a primitive root modulo $p^{2}$. Show that $g$ must be a primitive root modulo $p$.

  Let $g$ be a primitive root modulo $p$. Must it be a primitive root modulo $p^{2}$ ? Give a proof or a counterexample.

  comment

• Paper 4, Section I, F

  Number Theory | Part II, 2014

  State the Chinese Remainder Theorem.

  Find all solutions to the simultaneous congruences

  $$\begin{aligned} &x \equiv 2 \quad(\bmod 3) \\ &x \equiv 3(\bmod 5) \\ &x \equiv 5(\bmod 7) \end{aligned}$$

  A positive integer is said to be square-free if it is the product of distinct primes. Show that there are 100 consecutive numbers that are not square-free.

  comment

• Paper 4, Section II, F

  Number Theory | Part II, 2014

  Define the Legendre and Jacobi symbols.

  State the law of quadratic reciprocity for the Legendre symbol.

  State the law of quadratic reciprocity for the Jacobi symbol, and deduce it from the corresponding result for the Legendre symbol.

  Let $p$ be a prime with $p \equiv 1(\bmod 4)$. Prove that the sum of the quadratic residues in the set $\{1,2, \ldots, p-1\}$ is equal to the sum of the quadratic non-residues in this set.

  For which primes $p$ is 7 a quadratic residue?

  comment

Numerical Analysis

• Paper 1, Section II, 40D

  Numerical Analysis | Part II, 2014

  (i) Consider the numerical approximation of the boundary-value problem

  $$\begin{gathered} u^{\prime \prime}=f, \quad u:[0,1] \rightarrow \mathbb{R}, \\ u(0)=\varphi_{0}, \quad u(1)=\varphi_{1}, \end{gathered}$$

  where $\varphi_{0}, \varphi_{1}$ are given constants and $f$ is a given smooth function on $[0,1]$. A grid $\left\{x_{1}, x_{2}, \ldots, x_{N}\right\}, N \geqslant 3$, on $[0,1]$ is given by

  $$x_{1}=\alpha_{1} h, \quad x_{i}=x_{i-1}+h \text { for } i=2, \ldots, N-1, \quad x_{N}=1-\alpha_{2} h$$

  where $0<\alpha_{1}, \alpha_{2}<1, \alpha_{1}+\alpha_{2}=1$ and $h=1 / N$. Derive finite-difference approximations for $u^{\prime \prime}\left(x_{i}\right)$, for $i=1, \ldots, N$, using at most one neighbouring grid point of $x_{i}$ on each side. Hence write down a numerical scheme to solve the problem, displaying explicitly the entries of the system matrix $A$ in the resulting system of linear equations $A u=b$, $A \in \mathbb{R}^{N \times N}, u, b \in \mathbb{R}^{N}$. What is the overall order of this numerical scheme? Explain briefly one strategy by which the order could be improved with the same grid.

  (ii) Consider the numerical approximation of the boundary-value problem

  $$\begin{aligned} &\nabla^{2} u=f, \quad u: \Omega \rightarrow \mathbb{R}, \\ &u(x)=0 \text { for all } x \in \partial \Omega \end{aligned}$$

  where $\Omega \subset \mathbb{R}^{2}$ is an arbitrary, simply connected bounded domain with smooth boundary $\partial \Omega$, and $f$ is a given smooth function. Define the 9-point formula used to approximate the Laplacian. Using this formula and an equidistant grid inside $\Omega$, define a numerical scheme for which the system matrix is symmetric and negative definite. Prove that the system matrix of your scheme has these properties for all choices of ordering of the grid points.

  Part II, $2014 \quad$ List of Questions

  [TURN OVER

  comment

• Paper 2, Section II, D

  Numerical Analysis | Part II, 2014

  Consider the one-dimensional advection equation

  $$u_{t}=u_{x}, \quad-\infty<x<\infty, \quad t \geqslant 0$$

  subject to an initial condition $u(x, 0)=\varphi(x)$. Consider discretization of this equation with finite differences on an equidistant space-time $\left\{(m h, n k), m \in \mathbb{Z}, n \in \mathbb{Z}^{+}\right\}$with step size $h>0$ in space and step size $k>0$ in time. Define the Courant number $\mu$ and explain briefly how such a discretization can be used to derive numerical schemes in which solutions $u_{m}^{n} \approx u(m h, n k), m \in \mathbb{Z}$ and $n \in \mathbb{Z}^{+}$satisfy equations of the form

  $$\sum_{i=r}^{s} a_{i} u_{m+i}^{n+1}=\sum_{i=r}^{s} b_{i} u_{m+i}^{n}$$

  where the coefficients $a_{i}, b_{i}$ are independent of $m, n$.

  (i) Define the order of a numerical scheme such as (1). Define what a convergent numerical scheme is. Explain the notion of stability and state the Lax equivalence theorem that connects convergence and stability of numerical schemes for linear partial differential equations.

  (ii) Consider the following example of (1):

  $$u_{m}^{n+1}=u_{m}^{n}+\frac{\mu}{2}\left(u_{m+1}^{n}-u_{m-1}^{n}\right)+\frac{\mu^{2}}{2}\left(u_{m+1}^{n}-2 u_{m}^{n}+u_{m-1}^{n}\right) .$$

  Determine conditions on $\mu$ such that the scheme $(2)$ is stable and convergent. What is the order of this scheme?

  comment

• Paper 3, Section II, D

  Numerical Analysis | Part II, 2014

  Consider the linear system

  $$A x=b$$

  where $A \in \mathbb{R}^{n \times n}$ and $b, x \in \mathbb{R}^{n}$.

  (i) Define the Jacobi iteration method with relaxation parameter $\omega$ for solving (1).

  (ii) Assume that $A$ is a symmetric positive-definite matrix whose diagonal part $D$ is such that the matrix $2 D-A$ is also positive definite. Prove that the relaxed Jacobi iteration method always converges if the relaxation parameter $\omega$ is equal to $1 .$

  (iii) Let $A$ be the tridiagonal matrix with diagonal elements $a_{i i}=\alpha$ and off-diagonal elements $a_{i+1, i}=a_{i, i+1}=\beta$, where $0<\beta<\frac{1}{2} \alpha$. For which values of $\omega$ (expressed in terms of $\alpha$ and $\beta$ ) does the relaxed Jacobi iteration method converge? What choice of $\omega$ gives the optimal convergence speed?

  [You may quote without proof any relevant results about the convergence of iterative methods and about the eigenvalues of matrices.]

  comment

• Paper 4, Section II, D

  Numerical Analysis | Part II, 2014

  Let $A$ be a real symmetric $n \times n$ matrix with $n$ distinct real eigenvalues $\lambda_{1}<\lambda_{2}<$ $\cdots<\lambda_{n}$ and a corresponding orthogonal basis of normalized real eigenvectors $\left\{\mathbf{w}_{i}\right\}_{i=1}^{n}$.

  (i) Let $s \in \mathbb{R}$ satisfy $s<\lambda_{1}$. Given a unit vector $\mathbf{x}^{(0)} \in \mathbb{R}^{n}$, the iteration scheme

  $$\begin{gathered} (A-s I) \mathbf{y}=\mathbf{x}^{(k)} \\ \mathbf{x}^{(k+1)}=\mathbf{y} /\|\mathbf{y}\| \end{gathered}$$

  generates a sequence of vectors $\mathbf{x}^{(k+1)}$ for $k=0,1,2, \ldots$. Assuming that $\mathbf{x}^{(0)}=\sum c_{i} \mathbf{w}_{i}$ with $c_{1} \neq 0$, prove that $\mathbf{x}^{(k)}$ tends to $\pm \mathbf{w}_{1}$ as $k \rightarrow \infty$. What happens to $\mathbf{x}^{(k)}$ if $s>\lambda_{1}$ ? [Consider all cases.]

  (ii) Describe how to implement an inverse-iteration algorithm to compute the eigenvalues and eigenvectors of $A$, given some initial estimates for the eigenvalues.

  (iii) Let $n=2$. For iterates $\mathbf{x}^{(k)}$ of an inverse-iteration algorithm with a fixed value of $s \neq \lambda_{1}, \lambda_{2}$, show that if

  $$\mathbf{x}^{(k)}=\left(\mathbf{w}_{1}+\epsilon_{k} \mathbf{w}_{2}\right) /\left(1+\epsilon_{k}^{2}\right)^{1 / 2}$$

  where $\left|\epsilon_{k}\right|$ is small, then $\left|\epsilon_{k+1}\right|$ is of the same order of magnitude as $\left|\epsilon_{k}\right|$.

  (iv) Let $n=2$ still. Consider the iteration scheme

  $$s_{k}=\left(\mathbf{x}^{(k)}, A \mathbf{x}^{(k)}\right), \quad\left(A-s_{k} I\right) \mathbf{y}=\mathbf{x}^{(k)}, \quad \mathbf{x}^{(k+1)}=\mathbf{y} /\|\mathbf{y}\|$$

  for $k=0,1,2, \ldots$, where $(,$, denotes the inner product. Show that with this scheme $\left|\epsilon_{k+1}\right|=\left|\epsilon_{k}\right|^{3} .$

  comment

Optimization and Control

• Paper 2, Section II, J

  Optimization and Control | Part II, 2014

  Describe the elements of a discrete-time stochastic dynamic programming equation for the problem of maximizing the expected sum of non-negative rewards over an infinite horizon. Give an example to show that there may not exist an optimal policy. Prove that if a policy has a value function that satisfies the dynamic programming equation then the policy is optimal.

  A squirrel collects nuts for the coming winter. There are plenty of nuts lying around, but each time the squirrel leaves its lair it risks being caught by a predator. Assume that the outcomes of the squirrel's journeys are independent, that it is caught with probability $p$, and that it returns safely with a random weight of nuts, exponentially distributed with parameter $\lambda$. By solving the dynamic programming equation for the value function $F(x)$, find a policy maximizing the expected weight of nuts collected for the winter. Here the state variable $x$ takes values in $\mathbb{R}_{+}$(the weight of nuts so far collected) or $-1$ (a no-return state when the squirrel is caught).

  comment

• Paper 3, Section II, J

  Optimization and Control | Part II, 2014

  A particle follows a discrete-time trajectory on $\mathbb{R}$ given by

  $$x_{t+1}=A x_{t}+\xi_{t} u_{t}+\epsilon_{t}$$

  for $t=1,2, \ldots, T$, where $T \geqslant 2$ is a fixed integer, $A$ is a real constant, $x_{t}$ is the position of the particle and $u_{t}$ is the control action at time $t$, and $\left(\xi_{t}, \epsilon_{t}\right)_{t=1}^{T}$ is a sequence of independent random vectors with $\mathbb{E} \xi_{t}=\mathbb{E} \epsilon_{t}=0, \operatorname{var}\left(\xi_{t}\right)=V_{\xi}>0, \operatorname{var}\left(\epsilon_{t}\right)=V_{\epsilon}>0$ and $\operatorname{cov}\left(\xi_{t}, \epsilon_{t}\right)=0$.

  Find the closed-loop control, i.e. the control action $u_{t}$ defined as a function of $\left(x_{1}, \ldots, x_{t} ; u_{1}, \ldots, u_{t-1}\right)$, that minimizes

  $$\sum_{t=1}^{T} x_{t}^{2}+c \sum_{t=1}^{T-1} u_{t}$$

  where $c>0$ is given. [Note that this function is quadratic in $x$, but linear in $u$.]

  Does the closed-loop control depend on $V_{\epsilon}$ or on $V_{\xi}$ ? Deduce the form of the optimal open-loop control.

  comment

• Paper 4, Section II, J

  Optimization and Control | Part II, 2014

  A girl begins swimming from a point $(0,0)$ on the bank of a straight river. She swims at a constant speed $v$ relative to the water. The speed of the downstream current at a distance $y$ from the shore is $c(y)$. Hence her trajectory is described by

  $$\dot{x}=v \cos \theta+c(y), \quad \dot{y}=v \sin \theta$$

  where $\theta$ is the angle at which she swims relative to the direction of the current.

  She desires to reach a downstream point $(1,0)$ on the same bank as she starts, as quickly as possible. Construct the Hamiltonian for this problem, and describe how Pontryagin's maximum principle can be used to give necessary conditions that must hold on an optimal trajectory. Given that $c(y)$ is positive, increasing and differentiable in $y$, show that on an optimal trajectory

  $$\frac{d}{d t} \tan (\theta(t))=-c^{\prime}(y(t))$$

  comment

Partial Differential Equations

• Paper 1, Section II, D

  Partial Differential Equations | Part II, 2014

  State the Cauchy-Kovalevskaya theorem, including a definition of the term noncharacteristic.

  For which values of the real number $a$, and for which functions $f$, does the CauchyKovalevskaya theorem ensure that the Cauchy problem

  $$u_{t t}=u_{x x}+a u_{x x x x}, \quad u(x, 0)=0, u_{t}(x, 0)=f(x)$$

  has a local solution?

  Now consider the Cauchy problem (1) in the case that $f(x)=\sum_{m \in \mathbb{Z}} \hat{f}(m) e^{i m x}$ is a smooth $2 \pi$-periodic function.

  (i) Show that if $a \leqslant 0$ there exists a unique smooth solution $u$ for all times, and show that for all $T \geqslant 0$ there exists a number $C=C(T)>0$, independent of $f$, such that

  $$\int_{-\pi}^{+\pi}|u(x, t)|^{2} d x \leqslant C \int_{-\pi}^{+\pi}|f(x)|^{2} d x$$

  for all $t:|t| \leqslant T$.

  (ii) If $a=1$ does there exist a choice of $C=C(T)$ for which (2) holds? Give a full justification for your answer.

  comment

• Paper 2, Section II, D

  Partial Differential Equations | Part II, 2014

  In this question, functions are all real-valued, and

  $$H_{p e r}^{s}=\left\{u=\sum_{m \in \mathbb{Z}} \hat{u}(m) e^{i m x} \in L^{2}:\|u\|_{H^{s}}^{2}=\sum_{m \in \mathbb{Z}}\left(1+m^{2}\right)^{s}|\hat{u}(m)|^{2}<\infty\right\}$$

  are the Sobolev spaces of functions $2 \pi$-periodic in $x$, for $s=0,1,2, \ldots$

  State Parseval's theorem. For $s=0,1$ prove that the norm $\|u\|_{H^{s}}$ is equivalent to the norm ||$_{s}$ defined by

  $$\|u\|_{s}^{2}=\sum_{r=0}^{s} \int_{-\pi}^{+\pi}\left(\partial_{x}^{r} u\right)^{2} d x$$

  Consider the Cauchy problem

  $$u_{t}-u_{x x}=f, \quad u(x, 0)=u_{0}(x), \quad t \geqslant 0,$$

  where $f=f(x, t)$ is a smooth function which is $2 \pi$-periodic in $x$, and the initial value $u_{0}$ is also smooth and $2 \pi$-periodic. Prove that if $u$ is a smooth solution which is $2 \pi$-periodic in $x$, then it satisfies

  $$\int_{0}^{T}\left(u_{t}^{2}+u_{x x}^{2}\right) d t \leqslant C\left(\left\|u_{0}\right\|_{H^{1}}^{2}+\int_{0}^{T} \int_{-\pi}^{\pi}|f(x, t)|^{2} d x d t\right)$$

  for some number $C>0$ which does not depend on $u$ or $f$.

  State the Lax-Milgram lemma. Prove, using the Lax-Milgram lemma, that if

  $$f(x, t)=e^{\lambda t} g(x)$$

  with $g \in H_{p e r}^{0}$ and $\lambda>0$, then there exists a weak solution to (1) of the form $u(x, t)=e^{\lambda t} \phi(x)$ with $\phi \in H_{\text {per. }}^{1}$. Does the same hold for all $\lambda \in \mathbb{R}$ ? Briefly explain your answer.

  comment

• Paper 3, Section II, D

  Partial Differential Equations | Part II, 2014

  (a) Consider variable-coefficient operators of the form

  $$P u=-\sum_{j, k=1}^{n} a_{j k} \partial_{j} \partial_{k} u+\sum_{j=1}^{n} b_{j} \partial_{j} u+c u$$

  whose coefficients are defined on a bounded open set $\Omega \subset \mathbb{R}^{n}$ with smooth boundary $\partial \Omega$. Let $a_{j k}$ satisfy the condition of uniform ellipticity, namely

  $$m\|\xi\|^{2} \leqslant \sum_{j, k=1}^{n} a_{j k}(x) \xi_{j} \xi_{k} \leqslant M\|\xi\|^{2} \quad \text { for all } x \in \Omega \text { and } \xi \in \mathbb{R}^{n}$$

  for suitably chosen positive numbers $m, M$.

  State and prove the weak maximum principle for solutions of $P u=0$. [Any results from linear algebra and calculus needed in your proof should be stated clearly, but need not be proved.]

  (b) Consider the nonlinear elliptic equation

  $$-\Delta u+e^{u}=f$$

  for $u: \mathbb{R}^{n} \rightarrow \mathbb{R}$ satisfying the additional condition

  $$\lim _{|x| \rightarrow \infty} u(x)=0 .$$

  Assume that $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$. Prove that any two $C^{2}$ solutions of (1) which also satisfy (2) are equal.

  Now let $u \in C^{2}\left(\mathbb{R}^{n}\right)$ be a solution of $(1)$ and (2). Prove that if $f(x)<1$ for all $x$ then $u(x)<0$ for all $x$. Prove that if $\max _{x} f(x)=L \geqslant 1$ then $u(x) \leqslant \ln L$ for all $x$.

  comment

• Paper 4, Section II, D

  Partial Differential Equations | Part II, 2014

  (a) Derive the solution of the one-dimensional wave equation

  $$u_{t t}-u_{x x}=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x),$$

  with Cauchy data given by $C^{2}$ functions $u_{j}=u_{j}(x), j=0,1$, and where $x \in \mathbb{R}$ and $u_{t t}=\partial_{t}^{2} u$ etc. Explain what is meant by the property of finite propagation speed for the wave equation. Verify that the solution to (1) satisfies this property.

  (b) Consider the Cauchy problem

  $$u_{t t}-u_{x x}+x^{2} u=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x)$$

  By considering the quantities

  $$e=\frac{1}{2}\left(u_{t}^{2}+u_{x}^{2}+x^{2} u^{2}\right) \quad \text { and } \quad p=-u_{t} u_{x}$$

  prove that solutions of (2) also satisfy the property of finite propagation speed.

  (c) Define what is meant by a strongly continuous one-parameter group of unitary operators on a Hilbert space. Consider the Cauchy problem for the Schrödinger equation for $\psi(x, t) \in \mathbb{C}$ :

  $$i \psi_{t}=-\psi_{x x}+x^{2} \psi, \quad \psi(x, 0)=\psi_{0}(x), \quad-\infty<x<\infty$$

  [In the following you may use without proof the fact that there is an orthonormal set of (real-valued) Schwartz functions $\left\{f_{j}(x)\right\}_{j=1}^{\infty}$ which are eigenfunctions of the differential operator $P=-\partial_{x}^{2}+x^{2}$ with eigenvalues $2 j+1$, i.e.

  $$P f_{j}=(2 j+1) f_{j}, \quad f_{j} \in \mathcal{S}(\mathbb{R}), \quad\left(f_{j}, f_{k}\right)_{L^{2}}=\int_{\mathbb{R}} f_{j}(x) f_{k}(x) d x=\delta_{j k},$$

  and which have the property that any function $u \in L^{2}$ can be written uniquely as a sum $u(x)=\sum_{j}\left(f_{j}, u\right)_{L^{2}} f_{j}(x)$ which converges in the metric defined by the $L^{2}$ norm.]

  Write down the solution to (3) in the case that $\psi_{0}$ is given by a finite sum $\psi_{0}=\sum_{j=1}^{N}\left(f_{j}, \psi_{0}\right)_{L^{2}} f_{j}$ and show that your formula extends to define a strongly continuous one-parameter group of unitary operators on the Hilbert space $L^{2}$ of square-integrable (complex-valued) functions, with inner product $(f, g)_{L^{2}}=\int_{\mathbb{R}} \overline{f(x)} g(x) d x$.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  Let $\hat{x}, \hat{p}$ and $H(\hat{x}, \hat{p})=\hat{p}^{2} / 2 m+V(\hat{x})$ be the position operator, momentum operator and Hamiltonian for a particle moving in one dimension. Let $|\psi\rangle$ be the state vector for the particle. The position and momentum eigenstates have inner products

  $$\langle x \mid p\rangle=\frac{1}{\sqrt{2 \pi \hbar}} \exp (i p x / \hbar), \quad\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right) \quad \text { and } \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right) .$$

  Show that

  $$\langle x|\hat{p}| \psi\rangle=-i \hbar \frac{\partial}{\partial x} \psi(x) \quad \text { and } \quad\langle p|\hat{x}| \psi\rangle=i \hbar \frac{\partial}{\partial p} \tilde{\psi}(p)$$

  where $\psi(x)$ and $\tilde{\psi}(p)$ are the wavefunctions in the position representation and momentum representation, respectively. Show how $\psi(x)$ and $\tilde{\psi}(p)$ may be expressed in terms of each other.

  For general $V(\hat{x})$, express $\langle p|V(\hat{x})| \psi\rangle$ in terms of $\tilde{\psi}(p)$, and hence write down the time-independent Schrödinger equation in the momentum representation satisfied by $\tilde{\psi}(p)$.

  Consider now the case $V(x)=-\left(\hbar^{2} \lambda / m\right) \delta(x), \lambda>0$. Show that there is a bound state with energy $E=-\varepsilon, \varepsilon>0$, with wavefunction $\tilde{\psi}(p)$ satisfying

  $$\tilde{\psi}(p)=\frac{\hbar \lambda}{\pi} \frac{1}{2 m \varepsilon+p^{2}} \int_{-\infty}^{\infty} \tilde{\psi}\left(p^{\prime}\right) d p^{\prime}$$

  Hence show that there is a unique value for $\varepsilon$ and determine this value.

  comment

• Paper 2, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  (i) Let $a$ and $a^{\dagger}$ be the annihilation and creation operators, respectively, for a simple harmonic oscillator whose Hamiltonian is

  $$H_{0}=\omega\left(a^{\dagger} a+\frac{1}{2}\right),$$

  with $\left[a, a^{\dagger}\right]=1$. Explain how the set of eigenstates $\{|n\rangle: n=0,1,2, \ldots\}$ of $H_{0}$ is obtained and deduce the corresponding eigenvalues. Show that

  (ii) Consider a system whose unperturbed Hamiltonian is

  $$H_{0}=\left(a^{\dagger} a+\frac{1}{2}\right)+2\left(b^{\dagger} b+\frac{1}{2}\right)$$

  where $\left[a, a^{\dagger}\right]=1, \quad\left[b, b^{\dagger}\right]=1$ and all other commutators are zero. Find the degeneracies of the eigenvalues of $H_{0}$ with energies $E_{0}=\frac{3}{2}, \frac{5}{2}, \frac{7}{2}, \frac{9}{2}$ and $\frac{11}{2}$.

  The system is perturbed so that it is now described by the Hamiltonian

  $$H=H_{0}+\lambda H^{\prime},$$

  where $H^{\prime}=\left(a^{\dagger}\right)^{2} b+a^{2} b^{\dagger}$. Using degenerate perturbation theory, calculate to $O(\lambda)$ the energies of the eigenstates associated with the level $E_{0}=\frac{9}{2}$.

  Write down the eigenstates, to $O(\lambda)$, associated with these perturbed energies. By explicit evaluation show that they are in fact exact eigenstates of $H$ with these energies as eigenvalues.

  $$\begin{aligned} & a|0\rangle=0 \\ & a|n\rangle=\sqrt{n}|n-1\rangle, \quad n \geqslant 1, \\ & a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle, \quad n \geqslant 0 . \end{aligned}$$

  comment

• Paper 3, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  Let $\mathbf{J}=\left(J_{1}, J_{2}, J_{3}\right)$ and $|j m\rangle$ denote the standard angular-momentum operators and states so that, in units where $\hbar=1$,

  $$\mathbf{J}^{2}|j m\rangle=j(j+1)|j m\rangle, \quad J_{3}|j m\rangle=m|j m\rangle$$

  Show that $U(\theta)=\exp \left(-i \theta J_{2}\right)$ is unitary. Define

  $$J_{i}(\theta)=U(\theta) J_{i} U^{-1}(\theta) \quad \text { for } i=1,2,3$$

  and

  $$|j m\rangle_{\theta}=U(\theta)|j m\rangle \text {. }$$

  Find expressions for $J_{1}(\theta), J_{2}(\theta)$ and $J_{3}(\theta)$ as linear combinations of $J_{1}, J_{2}$ and $J_{3}$. Briefly explain why $U(\theta)$ represents a rotation of $\mathbf{J}$ through angle $\theta$ about the 2-axis.

  Show that

  $$J_{3}(\theta)|j m\rangle_{\theta}=m|j m\rangle_{\theta}$$

  Express $|10\rangle_{\theta}$ as a linear combination of the states $|1 m\rangle, m=-1,0,1$. By expressing $J_{1}$ in terms of $J_{\pm}$, use $(*)$ to determine the coefficients in this expansion.

  A particle of spin 1 is in the state $|10\rangle$ at time $t=0$. It is subject to the Hamiltonian

  $$H=-\mu \mathbf{B} \cdot \mathbf{J}$$

  where $\mathbf{B}=(0, \mathbf{B}, 0)$. At time $t$ the value of $J_{3}$ is measured and found to be $J_{3}=0$. At time $2 t$ the value of $J_{3}$ is measured again and found to be $J_{3}=1$. Show that the joint probability for these two values to be measured is

  $$\frac{1}{8} \sin ^{2}(2 \mu B t) .$$

  [The following result may be quoted: $\left.J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .\right]$

  comment

• Paper 4, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  Define the interaction picture for a quantum mechanical system with Schrödinger picture Hamiltonian $H_{0}+V(t)$ and explain why the interaction and Schrödinger pictures give the same physical predictions for transition rates between eigenstates of $H_{0}$. Derive the equation of motion for the interaction picture states $|\overline{\psi(t)}\rangle$.

  A system consists of just two states $|1\rangle$ and $|2\rangle$, with respect to which

  $$H_{0}=\left(\begin{array}{cc} E_{1} & 0 \\ 0 & E_{2} \end{array}\right), \quad V(t)=\hbar \lambda\left(\begin{array}{cc} 0 & e^{i \omega t} \\ e^{-i \omega t} & 0 \end{array}\right)$$

  Writing the interaction picture state as $\overline{\langle(t)}\rangle=a_{1}(t)|1\rangle+a_{2}(t)|2\rangle$, show that the interaction picture equation of motion can be written as

  $$i \dot{a}_{1}(t)=\lambda e^{i \mu t} a_{2}(t), \quad i \dot{a}_{2}(t)=\lambda e^{-i \mu t} a_{1}(t)$$

  where $\mu=\omega-\omega_{21}$ and $\omega_{21}=\left(E_{2}-E_{1}\right) / \hbar$. Hence show that $a_{2}(t)$ satisfies

  $$\ddot{a}_{2}+i \mu \dot{a}_{2}+\lambda^{2} a_{2}=0 .$$

  Given that $a_{2}(0)=0$, show that the solution takes the form

  $$a_{2}(t)=\alpha e^{-i \mu t / 2} \sin \Omega t,$$

  where $\Omega$ is a frequency to be determined and $\alpha$ is a complex constant of integration.

  Substitute this solution for $a_{2}(t)$ into $(*)$ to determine $a_{1}(t)$ and, by imposing the normalization condition $\||\overline{\psi(t)}\rangle \|^{2}=1$ at $t=0$, show that $|\alpha|^{2}=\lambda^{2} / \Omega^{2}$.

  At time $t=0$ the system is in the state $|1\rangle$. Write down the probability of finding the system in the state $|2\rangle$ at time $t$.

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2014

  State without proof the inequality known as the Cramér-Rao lower bound in a parametric model $\{f(\cdot, \theta): \theta \in \Theta\}, \Theta \subseteq \mathbb{R}$. Give an example of a maximum likelihood estimator that attains this lower bound, and justify your answer.

  Give an example of a parametric model where the maximum likelihood estimator based on observations $X_{1}, \ldots, X_{n}$ is biased. State without proof an analogue of the Cramér-Rao inequality for biased estimators.

  Define the concept of a minimax decision rule, and show that the maximum likelihood estimator $\hat{\theta}_{M L E}$ based on $X_{1}, \ldots, X_{n}$ in a $N(\theta, 1)$ model is minimax for estimating $\theta \in \Theta=\mathbb{R}$ in quadratic risk.

  comment

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2014

  In a general decision problem, define the concepts of a Bayes rule and of admissibility. Show that a unique Bayes rule is admissible.

  Consider i.i.d. observations $X_{1}, \ldots, X_{n}$ from a $\operatorname{Poisson}(\theta), \theta \in \Theta=(0, \infty)$, model. Can the maximum likelihood estimator $\hat{\theta}_{M L E}$ of $\theta$ be a Bayes rule for estimating $\theta$ in quadratic risk for any prior distribution on $\theta$ that has a continuous probability density on $(0, \infty) ?$ Justify your answer.

  Now model the $X_{i}$ as i.i.d. copies of $X \mid \theta \sim \operatorname{Poisson}(\theta)$, where $\theta$ is drawn from a prior that is a Gamma distribution with parameters $\alpha>0$ and $\lambda>0$ (given below). Show that the posterior distribution of $\theta \mid X_{1}, \ldots, X_{n}$ is a Gamma distribution and find its parameters. Find the Bayes rule $\hat{\theta}_{B A Y E S}$ for estimating $\theta$ in quadratic risk for this prior. [The Gamma probability density function with parameters $\alpha>0, \lambda>0$ is given by

  $$f(\theta)=\frac{\lambda^{\alpha} \theta^{\alpha-1} e^{-\lambda \theta}}{\Gamma(\alpha)}, \quad \theta>0$$

  where $\Gamma(\alpha)$ is the usual Gamma function.]

  Finally assume that the $X_{i}$ have actually been generated from a fixed Poisson $\left(\theta_{0}\right)$ distribution, where $\theta_{0}>0$. Show that $\sqrt{n}\left(\hat{\theta}_{B A Y E S}-\hat{\theta}_{M L E}\right)$ converges to zero in probability and deduce the asymptotic distribution of $\sqrt{n}\left(\hat{\theta}_{B A Y E S}-\theta_{0}\right)$ under the joint law $P_{\theta_{0}}^{\mathbb{N}}$ of the random variables $X_{1}, X_{2}, \ldots$. [You may use standard results from lectures without proof provided they are clearly stated.]

  comment

• Paper 3, Section II, J

  Principles of Statistics | Part II, 2014

  State and prove Wilks' theorem about testing the simple hypothesis $H_{0}: \theta=\theta_{0}$, against the alternative $H_{1}: \theta \in \Theta \backslash\left\{\theta_{0}\right\}$, in a one-dimensional regular parametric model $\{f(\cdot, \theta): \theta \in \Theta\}, \Theta \subseteq \mathbb{R}$. [You may use without proof the results from lectures on the consistency and asymptotic distribution of maximum likelihood estimators, as well as on uniform laws of large numbers. Necessary regularity conditions can be assumed without statement.]

  Find the maximum likelihood estimator $\hat{\theta}_{n}$ based on i.i.d. observations $X_{1}, \ldots, X_{n}$ in a $N(0, \theta)$-model, $\theta \in \Theta=(0, \infty)$. Deduce the limit distribution as $n \rightarrow \infty$ of the sequence of statistics

  $$-n\left(\log \left(\overline{X^{2}}\right)-\left(\overline{X^{2}}-1\right)\right)$$

  where $\overline{X^{2}}=(1 / n) \sum_{i=1}^{n} X_{i}^{2}$ and $X_{1}, \ldots, X_{n}$ are i.i.d. $N(0,1)$.

  comment

• Paper 4, Section II, J

  Principles of Statistics | Part II, 2014

  Suppose you have at hand a pseudo-random number generator that can simulate an i.i.d. sequence of uniform $U[0,1]$ distributed random variables $U_{1}^{*}, \ldots, U_{N}^{*}$ for any $N \in \mathbb{N}$. Construct an algorithm to simulate an i.i.d. sequence $X_{1}^{*}, \ldots, X_{N}^{*}$ of standard normal $N(0,1)$ random variables. [Should your algorithm depend on the inverse of any cumulative probability distribution function, you are required to provide an explicit expression for this inverse function.]

  Suppose as a matter of urgency you need to approximately evaluate the integral

  $$I=\frac{1}{\sqrt{2 \pi}} \int_{\mathbb{R}} \frac{1}{(\pi+|x|)^{1 / 4}} e^{-x^{2} / 2} d x$$

  Find an approximation $I_{N}$ of this integral that requires $N$ simulation steps from your pseudo-random number generator, and which has stochastic accuracy

  $$\operatorname{Pr}\left(\left|I_{N}-I\right|>N^{-1 / 4}\right) \leqslant N^{-1 / 2}$$

  where Pr denotes the joint law of the simulated random variables. Justify your answer.

  comment

Probability and Measure

• Paper 1, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2014

  What is meant by the Borel $\sigma$-algebra on the real line $\mathbb{R}$ ?

  Define the Lebesgue measure of a Borel subset of $\mathbb{R}$ using the concept of outer measure.

  Let $\mu$ be the Lebesgue measure on $\mathbb{R}$. Show that, for any Borel set $B$ which is contained in the interval $[0,1]$, and for any $\varepsilon>0$, there exist $n \in \mathbb{N}$ and disjoint intervals $I_{1}, \ldots, I_{n}$ contained in $[0,1]$ such that, for $A=I_{1} \cup \cdots \cup I_{n}$, we have

  $$\mu(A \triangle B) \leqslant \varepsilon$$

  where $A \triangle B$ denotes the symmetric difference $(A \backslash B) \cup(B \backslash A)$.

  Show that there does not exist a Borel set $B$ contained in $[0,1]$ such that, for all intervals $I$ contained in $[0,1]$,

  $$\mu(B \cap I)=\mu(I) / 2$$

  comment

• Paper 2, Section II, $26 K$

  Probability and Measure | Part II, 2014

  State and prove the monotone convergence theorem.

  Let $\left(E_{1}, \mathcal{E}_{1}, \mu_{1}\right)$ and $\left(E_{2}, \mathcal{E}_{2}, \mu_{2}\right)$ be finite measure spaces. Define the product $\sigma$-algebra $\mathcal{E}=\mathcal{E}_{1} \otimes \mathcal{E}_{2}$ on $E_{1} \times E_{2}$.

  Define the product measure $\mu=\mu_{1} \otimes \mu_{2}$ on $\mathcal{E}$, and show carefully that $\mu$ is countably additive.

  [You may use without proof any standard facts concerning measurability provided these are clearly stated.]

  comment

• Paper 3, Section II, K

  Probability and Measure | Part II, 2014

  (i) Let $(E, \mathcal{E}, \mu)$ be a measure space. What does it mean to say that a function $\theta: E \rightarrow E$ is a measure-preserving transformation?

  What does it mean to say that $\theta$ is ergodic?

  State Birkhoff's almost everywhere ergodic theorem.

  (ii) Consider the set $E=(0,1]^{2}$ equipped with its Borel $\sigma$-algebra and Lebesgue measure. Fix an irrational number $a \in(0,1]$ and define $\theta: E \rightarrow E$ by

  $$\theta\left(x_{1}, x_{2}\right)=\left(x_{1}+a, x_{2}+a\right)$$

  where addition in each coordinate is understood to be modulo 1 . Show that $\theta$ is a measurepreserving transformation. Is $\theta$ ergodic? Justify your answer.

  Let $f$ be an integrable function on $E$ and let $\bar{f}$ be the invariant function associated with $f$ by Birkhoff's theorem. Write down a formula for $\bar{f}$ in terms of $f$. [You are not expected to justify this answer.]

  comment

• Paper 4, Section II, K

  Probability and Measure | Part II, 2014

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent identically distributed random variables. Set $S_{n}=X_{1}+\cdots+X_{n}$.

  (i) State the strong law of large numbers in terms of the random variables $X_{n}$.

  (ii) Assume now that the $X_{n}$ are non-negative and that their expectation is infinite. Let $R \in(0, \infty)$. What does the strong law of large numbers say about the limiting behaviour of $S_{n}^{R} / n$, where $S_{n}^{R}=\left(X_{1} \wedge R\right)+\cdots+\left(X_{n} \wedge R\right)$ ?

  Deduce that $S_{n} / n \rightarrow \infty$ almost surely.

  Show that

  $$\sum_{n=0}^{\infty} \mathbb{P}\left(X_{n} \geqslant n\right)=\infty$$

  Show that $X_{n} \geqslant R n$ infinitely often almost surely.

  (iii) Now drop the assumption that the $X_{n}$ are non-negative but continue to assume that $\mathbb{E}\left(\left|X_{1}\right|\right)=\infty$. Show that, almost surely,

  $$\limsup _{n \rightarrow \infty}\left|S_{n}\right| / n=\infty$$

  comment

Representation Theory

• Paper 1, Section II, H

  Representation Theory | Part II, 2014

  (i) Let $K$ be any field and let $\lambda \in K$. Let $J_{\lambda, n}$ be the $n \times n$ Jordan block

  $$J_{\lambda, n}=\left(\begin{array}{ccccc} \lambda & 1 & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & & \vdots \\ \vdots & & \ddots & \ddots & 0 \\ \vdots & & & \ddots & 1 \\ 0 & \cdots & \cdots & 0 & \lambda \end{array}\right)$$

  Compute $J_{\lambda, n}^{r}$ for each $r \geqslant 0$.

  (ii) Let $G$ be a cyclic group of order $N$, and let $K$ be an algebraically closed field of characteristic $p \geqslant 0$. Determine all the representations of $G$ on vector spaces over $K$, up to equivalence. Which are irreducible? Which do not split as a direct sum $W \oplus W^{\prime}$, with $W \neq 0$ and $W^{\prime} \neq 0 ?$

  comment

• Paper 2, Section II, H

  Representation Theory | Part II, 2014

  In this question work over $\mathbb{C}$. Let $H$ be a subgroup of $G$. State Mackey's restriction formula, defining all the terms you use. Deduce Mackey's irreducibility criterion.

  Let $G=\left\langle g, r: g^{m}=r^{2}=1, r g r^{-1}=g^{-1}\right\rangle$ (the dihedral group of order $2 m$ ) and let $H=\langle g\rangle$ (the cyclic subgroup of $G$ of order $m$ ). Write down the $m$ inequivalent irreducible characters $\chi_{k}(1 \leqslant k \leqslant m)$ of $H$. Determine the values of $k$ for which the induced character $\operatorname{Ind}_{H}^{G} \chi_{k}$ is irreducible.

  comment

• Paper 3, Section II, H

  Representation Theory | Part II, 2014

  (i) State Frobenius' theorem for transitive permutation groups acting on a finite set. Define Frobenius group and show that any finite Frobenius group (with an appropriate action) satisfies the hypotheses of Frobenius' theorem.

  (ii) Consider the group

  $$F_{p, q}:=\left\langle a, b: a^{p}=b^{q}=1, b^{-1} a b=a^{u}\right\rangle$$

  where $p$ is prime, $q$ divides $p-1$ ( $q$ not necessarily prime), and $u$ has multiplicative order $q$ modulo $p$ (such elements $u$ exist since $q$ divides $p-1)$. Let $S$ be the subgroup of $\mathbb{Z}_{p}^{\times}$ consisting of the powers of $u$, so that $|S|=q$. Write $r=(p-1) / q$, and let $v_{1}, \ldots, v_{r}$ be coset representatives for $S$ in $\mathbb{Z}_{p}^{\times}$.

  (a) Show that $F_{p, q}$ has $q+r$ conjugacy classes and that a complete list of the classes comprises $\{1\},\left\{a^{v_{j} s}: s \in S\right\}(1 \leqslant j \leqslant r)$ and $\left\{a^{m} b^{n}: 0 \leqslant m \leqslant p-1\right\}(1 \leqslant n \leqslant q-1)$.

  (b) By observing that the derived subgroup $F_{p, q}^{\prime}=\langle a\rangle$, find $q$ 1-dimensional characters of $F_{p, q}$. [Appropriate results may be quoted without proof.]

  (c) Let $\varepsilon=e^{2 \pi i / p}$. For $v \in \mathbb{Z}_{p}^{\times}$denote by $\psi_{v}$ the character of $\langle a\rangle$ defined by $\psi_{v}\left(a^{x}\right)=\varepsilon^{v x}(0 \leqslant x \leqslant p-1)$. By inducing these characters to $F_{p, q}$, or otherwise, find $r$ distinct irreducible characters of degree $q$.

  comment

• Paper 4, Section II, H

  Representation Theory | Part II, 2014

  Let $G=\mathrm{SU}(2)$.

  (i) Sketch a proof that there is an isomorphism of topological groups $G /\{\pm I\} \cong$ $\mathrm{SO}(3)$

  (ii) Let $V_{2}$ be the irreducible complex representation of $G$ of dimension 3. Compute the character of the (symmetric power) representation $S^{n}\left(V_{2}\right)$ of $G$ for any $n \geqslant 0$. Show that the dimension of the space of invariants $\left(S^{n}\left(V_{2}\right)\right)^{G}$, meaning the subspace of $S^{n}\left(V_{2}\right)$ where $G$ acts trivially, is 1 for $n$ even and 0 for $n$ odd. [Hint: You may find it helpful to restrict to the unit circle subgroup $S^{1} \leqslant G$. The irreducible characters of $G$ may be quoted without proof.]

  Using the fact that $V_{2}$ yields the standard 3-dimensional representation of $\mathrm{SO}(3)$, show that $\bigoplus_{n \geqslant 0} S^{n} V_{2} \cong \mathbb{C}[x, y, z]$. Deduce that the ring of complex polynomials in three variables $x, y, z$ which are invariant under the action of $\mathrm{SO}(3)$ is a polynomial ring in one generator. Find a generator for this polynomial ring.

  comment

Riemann Surfaces

• Paper 1, Section II, H

  Riemann Surfaces | Part II, 2014

  If $X$ is a Riemann surface and $p: Y \rightarrow X$ is a covering map of topological spaces, show that there is a conformal structure on $Y$ such that $p: Y \rightarrow X$ is analytic.

  Let $f(z)$ be the complex polynomial $z^{5}-1$. Consider the subspace $R$ of $\mathbb{C}^{2}=\mathbb{C} \times \mathbb{C}$ given by the equation $w^{2}=f(z)$, where $(z, w)$ denotes coordinates in $\mathbb{C}^{2}$, and let $\pi: R \rightarrow \mathbb{C}$ be the restriction of the projection map onto the first factor. Show that $R$ has the structure of a Riemann surface which makes $\pi$ an analytic map. If $\tau$ denotes projection onto the second factor, show that $\tau$ is also analytic. [You may assume that $R$ is connected.]

  Find the ramification points and the branch points of both $\pi$ and $\tau$. Compute also the ramification indices at the ramification points.

  Assuming that it is possible to add a point $P$ to $R$ so that $X=R \cup\{P\}$ is a compact Riemann surface and $\tau$ extends to a holomorphic map $\tau: X \rightarrow \mathbb{C}_{\infty}$ such that $\tau^{-1}(\infty)=\{P\}$, compute the genus of $X .$

  comment

• Paper 2, Section II, H

  Riemann Surfaces | Part II, 2014

  State and prove the Valency Theorem and define the degree of a non-constant holomorphic map between compact Riemann surfaces.

  Let $X$ be a compact Riemann surface of genus $g$ and $\pi: X \rightarrow \mathbb{C}_{\infty}$ a holomorphic map of degree two. Find the cardinality of the set $R$ of ramification points of $\pi$. Find also the cardinality of the set of branch points of $\pi$. [You may use standard results from lectures provided they are clearly stated.]

  Define $\sigma: X \rightarrow X$ as follows: if $p \in R$, then $\sigma(p)=p$; otherwise, $\sigma(p)=q$ where $q$ is the unique point such that $\pi(q)=\pi(p)$ and $p \neq q$. Show that $\sigma$ is a conformal equivalence with $\pi \sigma=\pi$ and $\sigma \sigma=$ id.

  comment

• Paper 3, Section II, H

  Riemann Surfaces | Part II, 2014

  State the Uniformization Theorem.

  Show that any domain of $\mathbb{C}$ whose complement has more than one point is uniformized by the unit disc $\Delta .$ [You may use the fact that for $\mathbb{C}_{\infty}$ the group of automorphisms consists of Möbius transformations, and for $\mathbb{C}$ it consists of maps of the form $z \mapsto a z+b$ with $a \in \mathbb{C}^{*}$ and $b \in \mathbb{C}$.

  Let $X$ be the torus $\mathbb{C} / \Lambda$, where $\Lambda$ is a lattice. Given $p \in X$, show that $X \backslash\{p\}$ is uniformized by the unit $\operatorname{disc} \Delta$.

  Is it true that a holomorphic map from $\mathbb{C}$ to a compact Riemann surface of genus two must be constant? Justify your answer.

  comment

Statistical Modelling

• Paper 1, Section $I$, K

  Statistical Modelling | Part II, 2014

  Write down the model being fitted by the following $\mathrm{R}$ command, where $y \in\{0,1,2, \ldots\}^{n}$ and $X$ is an $n \times p$ matrix with real-valued entries.

  fit $<-\operatorname{glm}(\mathrm{y} \sim \mathrm{X}, \mathrm{family}=$ poisson)

  Write down the log-likelihood for the model. Explain why the command

  $\operatorname{sum}(y)-\operatorname{sum}($ predict (fit, type $=$ "response" $))$

  gives the answer 0, by arguing based on the log-likelihood you have written down. [Hint: Recall that if $Z \sim \operatorname{Pois}(\mu)$ then

  $$\mathbb{P}(Z=k)=\frac{\mu^{k} e^{-\mu}}{k !}$$

  for $k \in\{0,1,2, \ldots\}$.]

  comment

• Paper 1, Section II, $13 K$

  Statistical Modelling | Part II, 2014

  Consider the normal linear model where the $n$-vector of responses $Y$ satisfies $Y=X \beta+\varepsilon$ with $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Here $X$ is an $n \times p$ matrix of predictors with full column rank where $n \geqslant p+3$, and $\beta \in \mathbb{R}^{p}$ is an unknown vector of regression coefficients. Let $X_{0}$ be the matrix formed from the first $p_{0}<p$ columns of $X$, and partition $\beta$ as $\beta=\left(\beta_{0}^{T}, \beta_{1}^{T}\right)^{T}$ where $\beta_{0} \in \mathbb{R}^{p_{0}}$ and $\beta_{1} \in \mathbb{R}^{p-p_{0}}$. Denote the orthogonal projections onto the column spaces of $X$ and $X_{0}$ by $P$ and $P_{0}$ respectively.

  It is desired to test the null hypothesis $H_{0}: \beta_{1}=0$ against the alternative hypothesis $H_{1}: \beta_{1} \neq 0$. Recall that the $F$-test for testing $H_{0}$ against $H_{1}$ rejects $H_{0}$ for large values of

  $$F=\frac{\left\|\left(P-P_{0}\right) Y\right\|^{2} /\left(p-p_{0}\right)}{\|(I-P) Y\|^{2} /(n-p)} .$$

  Show that $(I-P)\left(P-P_{0}\right)=0$, and hence prove that the numerator and denominator of $F$ are independent under either hypothesis.

  Show that

  $$\mathbb{E}_{\beta, \sigma^{2}}(F)=\frac{(n-p)\left(\tau^{2}+1\right)}{n-p-2}$$

  where $\tau^{2}=\frac{\left\|\left(P-P_{0}\right) X \beta\right\|^{2}}{\left(p-p_{0}\right) \sigma^{2}}$.

  [In this question you may use the following facts without proof: $P-P_{0}$ is an orthogonal projection with rank $p-p_{0}$; any $n \times n$ orthogonal projection matrix $\Pi$ satisfies $\|\Pi \varepsilon\|^{2} \sim \sigma^{2} \chi_{\nu}^{2}$, where $\nu=\operatorname{rank}(\Pi) ;$ and if $Z \sim \chi_{\nu}^{2}$ then $\mathbb{E}\left(Z^{-1}\right)=(\nu-2)^{-1}$ when $\left.\nu>2 .\right]$

  comment

• Paper 2, Section I, K

  Statistical Modelling | Part II, 2014

  Define the concept of an exponential dispersion family. Show that the family of scaled binomial distributions $\frac{1}{n} \operatorname{Bin}(n, p)$, with $p \in(0,1)$ and $n \in \mathbb{N}$, is of exponential dispersion family form.

  Deduce the mean of the scaled binomial distribution from the exponential dispersion family form.

  What is the canonical link function in this case?

  comment

• Paper 3, Section I, $5 K$

  Statistical Modelling | Part II, 2014

  In an experiment to study factors affecting the production of the plastic polyvinyl chloride $(\mathrm{PVC})$, three experimenters each used eight devices to produce the PVC and measured the sizes of the particles produced. For each of the 24 combinations of device and experimenter, two size measurements were obtained.

  The experimenters and devices used for each of the 48 measurements are stored in $\mathrm{R}$ as factors in the objects experimenter and device respectively, with the measurements themselves stored in the vector psize. The following analysis was performed in $\mathrm{R}$.

  

  Let $X$ and $X_{0}$ denote the design matrices obtained by model.matrix(fit) and model.matrix (fit0) respectively, and let $Y$ denote the response psize. Let $P$ and $P_{0}$ denote orthogonal projections onto the column spaces of $X$ and $X_{0}$ respectively.

  For each of the following quantities, write down their numerical values if they appear in the analysis of variance table above; otherwise write 'unknown'.

  1. $\|(I-P) Y\|^{2}$

  2. $\left\|X\left(X^{T} X\right)^{-1} X^{T} Y\right\|^{2}$

  3. $\left\|\left(I-P_{0}\right) Y\right\|^{2}-\|(I-P) Y\|^{2}$

  4. $\frac{\left\|\left(P-P_{0}\right) Y\right\|^{2} / 14}{\|(I-P) Y\|^{2} / 24}$

  5. $\sum_{i=1}^{48} Y_{i} / 48$

  Out of the two models that have been fitted, which appears to be the more appropriate for the data according to the analysis performed, and why?

  comment

• Paper 4, Section I, $5 K$

  Statistical Modelling | Part II, 2014

  Consider the normal linear model where the $n$-vector of responses $Y$ satisfies $Y=X \beta+\varepsilon$ with $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ and $X$ is an $n \times p$ design matrix with full column rank. Write down a $(1-\alpha)$-level confidence set for $\beta$.

  Define the Cook's distance for the observation $\left(Y_{i}, x_{i}\right)$ where $x_{i}^{T}$ is the $i$ th row of $X$, and give its interpretation in terms of confidence sets for $\beta$.

  In the model above with $n=100$ and $p=4$, you observe that one observation has Cook's distance 3.1. Would you be concerned about the influence of this observation? Justify your answer.

  [Hint: You may find some of the following facts useful:

  1. If $Z \sim \chi_{4}^{2}$, then $\mathbb{P}(Z \leqslant 1.06)=0.1, \mathbb{P}(Z \leqslant 7.78)=0.9$.

  2. If $Z \sim F_{4,96}$, then $\mathbb{P}(Z \leqslant 0.26)=0.1, \mathbb{P}(Z \leqslant 2.00)=0.9$.

  3. If $Z \sim F_{96,4}$, then $\left.\mathbb{P}(Z \leqslant 0.50)=0.1, \mathbb{P}(Z \leqslant 3.78)=0.9 .\right]$

  comment

• Paper 4, Section II, K

  Statistical Modelling | Part II, 2014

  In a study on infant respiratory disease, data are collected on a sample of 2074 infants. The information collected includes whether or not each infant developed a respiratory disease in the first year of their life; the gender of each infant; and details on how they were fed as one of three categories (breast-fed, bottle-fed and supplement). The data are tabulated in $\mathrm{R}$ as follows:

  $\begin{array}{rrrrr} & \text { disease } & \text { nondisease } & \text { gender } & \text { food } \\ 1 & 77 & 381 & \text { Boy } & \text { Bottle-fed } \\ 2 & 19 & 128 & \text { Boy } & \text { Supplement } \\ 3 & 47 & 447 & \text { Boy } & \text { Breast-fed } \\ 4 & 48 & 336 & \text { Girl } & \text { Bottle-fed } \\ 5 & 16 & 111 & \text { Girl } & \text { Supplement } \\ 6 & 31 & 433 & \text { Girl } & \text { Breast-fed }\end{array}$

  Write down the model being fit by the $R$ commands on the following page:

  

  The following (slightly abbreviated) output from $R$ is obtained.

  

  Briefly explain the justification for the standard errors presented in the output above.

  Explain the relevance of the output of the following $R$ code to the data being studied, justifying your answer:

  $>\exp (c(-0.6693-1.96 * 0.153,-0.6693+1.96 * 0.153))$

  [1] $0.3793940 \quad 0.6911351$

  [Hint: It may help to recall that if $Z \sim N(0,1)$ then $\mathbb{P}(Z \geqslant 1.96)=0.025 .]$

  Let $D_{1}$ be the deviance of the model fitted by the following $\mathrm{R}$ command.

  $>$ fit $1<-$ glm (disease/total gender + food + gender:food,

  $+$ family = binomial, weights = total $)$

  What is the numerical value of $D_{1}$ ? Which of the two models that have been fitted should you prefer, and why?

  comment

Statistical Physics

• Paper 1, Section II, E

  Statistical Physics | Part II, 2014

  Write down the equation of state and the internal energy of a monatomic ideal gas.

  Describe the meaning of an adiabatic process. Derive the equation for an adiabatic process in the pressure-volume $(P, V)$ plane for a monatomic ideal gas.

  Briefly describe the Carnot cycle. Sketch the Carnot cycle in the $(P, V)$ plane and in the temperature entropy $(T, S)$ plane.

  The Diesel cycle is an idealised version of the process realised in the Diesel engine. It consists of the following four reversible steps:

  

  Sketch the Diesel cycle for a monatomic gas in the $(P, V)$ plane and the $(T, S)$ plane. Determine the equations for the curves $B \rightarrow C$ and $D \rightarrow A$ in the $(T, S)$ plane.

  The efficiency $\eta$ of the cycle is defined as

  $$\eta=1-\frac{Q_{\text {out }}}{Q_{\text {in }}}$$

  where $Q_{\text {in }}$ is the heat entering the gas in step $B \rightarrow C$ and $Q_{\text {out }}$ is the heat leaving the gas in step $D \rightarrow A$. Calculate $\eta$ as a function of the temperatures at points $A, B, C$ and $D$.

  comment

• Paper 2, Section II, E

  Statistical Physics | Part II, 2014

  Briefly describe the microcanonical, canonical and grand canonical ensembles. Why do they agree in the thermodynamic limit?

  A harmonic oscillator in one spatial dimension has Hamiltonian

  $$H=\frac{p^{2}}{2 m}+\frac{m}{2} \omega^{2} x^{2}$$

  Here $p$ and $x$ are the momentum and position of the oscillator, $m$ is its mass and $\omega$ its frequency. The harmonic oscillator is placed in contact with a heat bath at temperature $T$. What is the relevant ensemble?

  Treating the harmonic oscillator classically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  Treating the harmonic oscillator quantum mechanically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  In what limit of temperature do the classical and quantum results agree? Explain why they differ away from this limit. Describe an experiment for which this difference has implications.

  comment

• Paper 3, Section II, E

  Statistical Physics | Part II, 2014

  In the grand canonical ensemble, at temperature $T$ and chemical potential $\mu$, what is the probability of finding a system in a state with energy $E$ and particle number $N$ ?

  A particle with spin degeneracy $g_{s}$ and mass $m$ moves in $d \geqslant 2$ spatial dimensions with dispersion relation $E=\hbar^{2} k^{2} / 2 m$. Compute the density of states $g(E)$. [You may denote the area of a unit $(d-1)$-dimensional sphere as $S_{d-1}$.]

  Treating the particles as non-interacting fermions, determine the energy $E$ of a gas in terms of the pressure $P$ and volume $V$.

  Derive an expression for the Fermi energy in terms of the number density of particles. Compute the degeneracy pressure at zero temperature in terms of the number of particles and the Fermi energy.

  Show that at high temperatures the gas obeys the ideal gas law (up to small corrections which you need not compute).

  comment

• Paper 4, Section II, E

  Statistical Physics | Part II, 2014

  The Dieterici equation of state of a gas is

  $$P=\frac{k_{B} T}{v-b} \exp \left(-\frac{a}{k_{B} T v}\right)$$

  where $P$ is the pressure, $v=V / N$ is the volume divided by the number of particles, $T$ is the temperature, and $k_{B}$ is the Boltzmann constant. Provide a physical interpretation for the constants $a$ and $b$.

  Briefly explain how the Dieterici equation captures the liquid-gas phase transition. What is the maximum temperature at which such a phase transition can occur?

  The Gibbs free energy is given by

  $$G=E+P V-T S$$

  where $E$ is the energy and $S$ is the entropy. Explain why the Gibbs free energy is proportional to the number of particles in the system.

  On either side of a first-order phase transition the Gibbs free energies are equal. Use this fact to derive the Clausius-Clapeyron equation for a line along which there is a first-order liquid-gas phase transition,

  $$\frac{d P}{d T}=\frac{L}{T\left(V_{\text {gas }}-V_{\text {liquid }}\right)}$$

  where $L$ is the latent heat which you should define.

  Assume that the volume of liquid is negligible compared to the volume of gas and that the latent heat is constant. Further assume that the gas can be well approximated by the ideal gas law. Solve $(*)$ to obtain an equation for the phase-transition line in the $(P, T)$ plane.

  comment

Stochastic Financial Models

• Paper 1, Section II, K

  Stochastic Financial Models | Part II, 2014

  Suppose that $\bar{S}_{t} \equiv\left(S_{t}^{0}, \ldots, S_{t}^{d}\right)^{T}$ denotes the vector of prices of $d+1$ assets at times $t=0,1, \ldots$, and that $\bar{\theta}_{t} \equiv\left(\theta_{t}^{0}, \ldots, \theta_{t}^{d}\right)^{T}$ denotes the vector of the numbers of the $d+1$ different assets held by an investor from time $t-1$ to time $t$. Assuming that asset 0 is a bank account paying zero interest, that is, $S_{t}^{0}=1$ for all $t \geqslant 0$, explain what is meant by the statement that the portfolio process $\left(\bar{\theta}_{t}\right)_{t \geqslant 0}$ is self-financing. If the portfolio process is self-financing, prove that for any $t>0$

  $$\bar{\theta}_{t} \cdot \bar{S}_{t}-\bar{\theta}_{0} \cdot \bar{S}_{0}=\sum_{j=1}^{t} \theta_{j} \cdot \Delta S_{j}$$

  where $S_{j} \equiv\left(S_{j}^{1}, \ldots, S_{j}^{d}\right)^{T}, \Delta S_{j}=S_{j}-S_{j-1}$, and $\theta_{j} \equiv\left(\theta_{j}^{1}, \ldots, \theta_{j}^{d}\right)^{T}$.

  Suppose now that the $\Delta S_{t}$ are independent with common $N(0, V)$ distribution. Let

  $$F(z)=\inf E\left[\sum_{t \geqslant 1}(1-\beta) \beta^{t}\left\{\left(\bar{\theta}_{t} \cdot \bar{S}_{t}-\bar{\theta}_{0} \cdot \bar{S}_{0}\right)^{2}+\sum_{j=1}^{t}\left|\Delta \theta_{j}\right|^{2}\right\} \mid \theta_{0}=z\right]$$

  where $\beta \in(0,1)$ and the infimum is taken over all self-financing portfolio processes $\left(\bar{\theta}_{t}\right)_{t \geqslant 0}$ with $\theta_{0}^{0}=0$. Explain why $F$ should satisfy the equation

  $$F(z)=\beta \inf _{y}\left[y \cdot V y+|y-z|^{2}+F(y)\right]$$

  If $Q$ is a positive-definite symmetric matrix satisfying the equation

  $$Q=\beta(V+I+Q)^{-1}(V+Q)$$

  show that $(*)$ has a solution of the form $F(z)=z \cdot Q z$.

  comment

• Paper 2, Section II, K

  Stochastic Financial Models | Part II, 2014

  An agent has expected-utility preferences over his possible wealth at time 1 ; that is, the wealth $Z$ is preferred to wealth $Z^{\prime}$ if and only if $E U(Z) \geqslant E U\left(Z^{\prime}\right)$, where the function $U: \mathbb{R} \rightarrow \mathbb{R}$ is strictly concave and twice continuously differentiable. The agent can trade in a market, with the time-1 value of his portfolio lying in an affine space $\mathcal{A}$ of random variables. Assuming cash can be held between time 0 and time 1 , define the agent's time-0 utility indifference price $\pi(Y)$ for a contingent claim with time-1 value $Y$. Assuming any regularity conditions you may require, prove that the map $Y \mapsto \pi(Y)$ is concave.

  

  Consider a market with two claims with time-1 values $X$ and $Y$. Their joint distribution is

  $$\left(\begin{array}{l} X \\ Y \end{array}\right) \sim N\left(\left(\begin{array}{l} \mu_{X} \\ \mu_{Y} \end{array}\right),\left(\begin{array}{ll} V_{X X} & V_{X Y} \\ V_{Y X} & V_{Y Y} \end{array}\right)\right) .$$

  At time 0 , arbitrary quantities of the claim $X$ can be bought at price $p$, but $Y$ is not marketed. Derive an explicit expression for $\pi(Y)$ in the case where

  $$U(x)=-\exp (-\gamma x)$$

  where $\gamma>0$ is a given constant.

  comment

• Paper 3, Section II, $29 K$

  Stochastic Financial Models | Part II, 2014

  Derive the Black-Scholes formula $C\left(S_{0}, K, r, T, \sigma\right)$ for the time- 0 price of a European call option with expiry $T$ and strike $K$ written on an asset with volatility $\sigma$ and time-0 price $S_{0}$, and where $r$ is the riskless rate of interest. Explain what is meant by the delta hedge for this option, and determine it explicitly.

  In terms of the Black-Scholes call option price formula $C$, find the time- 0 price of a forward-starting option, which pays $\left(S_{T}-\lambda S_{t}\right)^{+}$at time $T$, where $0<t<T$ and $\lambda>0$ are given. Find the price of an option which pays $\max \left\{S_{T}, \lambda S_{t}\right\}$ at time $T$. How would this option be hedged?

  comment

• Paper 4, Section II, K

  Stochastic Financial Models | Part II, 2014

  Write down the Black-Scholes partial differential equation (PDE), and explain briefly its relevance to option pricing.

  Show how a change of variables reduces the Black-Scholes PDE to the heat equation:

  $$\begin{aligned} &\frac{\partial f}{\partial t}+\frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}}=0 \text { for all }(t, x) \in[0, T) \times \mathbb{R}, \\ &f(T, x)=\varphi(x) \text { for all } x \in \mathbb{R} \end{aligned}$$

  where $\varphi$ is a given boundary function.

  Consider the following numerical scheme for solving the heat equation on the equally spaced grid $\left(t_{n}, x_{k}\right) \in[0, T] \times \mathbb{R}$ where $t_{n}=n \Delta t$ and $x_{k}=k \Delta x, n=0,1, \ldots, N$ and $k \in \mathbb{Z}$, and $\Delta t=T / N$. We approximate $f\left(t_{n}, x_{k}\right)$ by $f_{k}^{n}$ where

  $$0=\frac{f^{n+1}-f^{n}}{\Delta t}+\theta L f^{n+1}+(1-\theta) L f^{n}, \quad f_{k}^{N}=\varphi\left(x_{k}\right)$$

  and $\theta \in[0,1]$ is a constant and the operator $L$ is the matrix with non-zero entries $L_{k k}=-\frac{1}{(\Delta x)^{2}}$ and $L_{k, k+1}=L_{k, k-1}=\frac{1}{2(\Delta x)^{2}}$. By considering what happens when $\varphi(x)=\exp (i \omega x)$, show that the finite-difference scheme $(*)$ is stable if and only if

  $$1 \geqslant \lambda(2 \theta-1),$$

  where $\lambda \equiv \Delta t /(\Delta x)^{2}$. For what values of $\theta$ is the scheme $(*)$ unconditionally stable?

  comment

Topics in Analysis

• Paper 1, Section I, $2 \mathrm{G}$

  Topics in Analysis | Part II, 2014

  (i) State Brouwer's fixed point theorem in the plane and an equivalent theorem concerning mapping a triangle $T$ to its boundary $\partial T$.

  (ii) Let $A$ be a $3 \times 3$ matrix with positive real entries. Use the theorems you stated in (i) to prove that $A$ has an eigenvector with positive entries.

  comment

• Paper 2, Section I, G

  Topics in Analysis | Part II, 2014

  State Chebyshev's equal ripple criterion.

  Let

  $$h(t)=\prod_{\ell=1}^{n}\left(t-\cos \frac{(2 \ell-1) \pi}{2 n}\right)$$

  Show that if $q(t)=\sum_{j=0}^{n} a_{j} t^{j}$ where $a_{0}, \ldots, a_{n}$ are real constants with $\left|a_{n}\right| \geqslant 1$, then

  $$\sup _{t \in[-1,1]}|h(t)| \leqslant \sup _{t \in[-1,1]}|q(t)|$$

  comment

• Paper 2, Section II, G

  Topics in Analysis | Part II, 2014

  Let $\gamma:[0,1] \rightarrow \mathbb{C}$ be a continuous map never taking the value 0 and satisfying $\gamma(0)=\gamma(1)$. Define the degree (or winding number) $w(\gamma ; 0)$ of $\gamma$ about 0 . Prove the following:

  (i) $w(1 / \gamma ; 0)=w\left(\gamma^{-} ; 0\right)$, where $\gamma^{-}(t)=\gamma(1-t)$.

  (ii) If $\sigma:[0,1] \rightarrow \mathbb{C}$ is continuous, $\sigma(0)=\sigma(1)$ and $|\sigma(t)|<|\gamma(t)|$ for each $0 \leqslant t \leqslant 1$, then $w(\gamma+\sigma ; 0)=w(\gamma ; 0)$.

  (iii) If $\gamma_{m}:[0,1] \rightarrow \mathbb{C}, m=1,2, \ldots$, are continuous maps with $\gamma_{m}(0)=\gamma_{m}(1)$, which converge to $\gamma$ uniformly on $[0,1]$ as $m \rightarrow \infty$, then $w\left(\gamma_{m} ; 0\right)=w(\gamma ; 0)$ for sufficiently large $m$.

  Let $\alpha:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map such that $\alpha(0)=\alpha(1)$ and $\left|\alpha(t)-e^{2 \pi i t}\right| \leqslant 1$ for each $t \in[0,1]$. Deduce from the results of (ii) and (iii) that $w(\alpha ; 0)=1$.

  [You may not use homotopy invariance of the winding number without proof.]

  comment

• Paper 3, Section I, G

  Topics in Analysis | Part II, 2014

  State Runge's theorem about uniform approximation of holomorphic functions by polynomials.

  Let $\mathbb{R}_{+} \subset \mathbb{C}$ be the subset of non-negative real numbers and let

  $$\Delta=\{z \in \mathbb{C}:|z|<1\} .$$

  Prove that there is a sequence of complex polynomials which converges to the function $1 / z$ uniformly on each compact subset of $\Delta \backslash \mathbb{R}_{+}$.

  comment

• Paper 3, Section II, G

  Topics in Analysis | Part II, 2014

  Define what is meant by a nowhere dense set in a metric space. State a version of the Baire Category Theorem. Show that any complete non-empty metric space without isolated points is uncountable.

  Let $A$ be the set of real numbers whose decimal expansion does not use the digit 6 . (A terminating decimal representation is used when it exists.) Show that there exists a real number which cannot be written as $a+q$ with $a \in A$ and $q \in \mathbb{Q}$.

  comment

• Paper 4, Section I, $2 G$

  Topics in Analysis | Part II, 2014

  State Liouville's theorem on approximation of algebraic numbers by rationals.

  Prove that the number $\sum_{n=0}^{\infty} \frac{1}{2^{n^{n}}}$ is transcendental.

  comment

Waves

• Paper 1, Section II, C

  Waves | Part II, 2014

  State the equations that relate strain to displacement and stress to strain in a uniform, linear, isotropic elastic solid with Lamé moduli $\lambda$ and $\mu$. In the absence of body forces, the Cauchy momentum equation for the infinitesimal displacements $\mathbf{u}(\mathbf{x}, t)$ is

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=\boldsymbol{\nabla} \cdot \boldsymbol{\sigma}$$

  where $\rho$ is the density and $\boldsymbol{\sigma}$ the stress tensor. Show that both the dilatation $\boldsymbol{\nabla} \cdot \mathbf{u}$ and the rotation $\nabla \wedge \mathbf{u}$ satisfy wave equations, and find the wave-speeds $c_{P}$ and $c_{S}$.

  A plane harmonic $\mathrm{P}$-wave with wavevector $\mathbf{k}$ lying in the $(x, z)$ plane is incident from $z<0$ at an oblique angle on the planar interface $z=0$ between two elastic solids with different densities and elastic moduli. Show in a diagram the directions of all the reflected and transmitted waves, labelled with their polarisations, assuming that none of these waves are evanescent. State the boundary conditions on components of $\mathbf{u}$ and $\boldsymbol{\sigma}$ that would, in principle, determine the amplitudes.

  Now consider a plane harmonic P-wave of unit amplitude incident with $\mathbf{k}=$ $k(\sin \theta, 0, \cos \theta)$ on the interface $z=0$ between two elastic (and inviscid) liquids with wave-speed $c_{P}$ and modulus $\lambda$ in $z<0$ and wave-speed $c_{P}^{\prime}$ and modulus $\lambda^{\prime}$ in $z>0$. Obtain solutions for the reflected and transmitted waves. Show that the amplitude of the reflected wave is zero if

  $$\sin ^{2} \theta=\frac{Z^{\prime 2}-Z^{2}}{Z^{\prime 2}-\left(c_{P}^{\prime} Z / c_{P}\right)^{2}}$$

  where $Z=\lambda / c_{P}$ and $Z^{\prime}=\lambda^{\prime} / c_{P}^{\prime}$

  comment

• Paper 2, Section II, 38C

  Waves | Part II, 2014

  The function $\phi(x, t)$ satisfies the equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}-\frac{\partial^{2} \phi}{\partial x^{2}}=\frac{\partial^{4} \phi}{\partial x^{2} \partial t^{2}}$$

  Derive the dispersion relation, and sketch graphs of frequency, phase velocity and group velocity as functions of the wavenumber. In the case of a localised initial disturbance, will it be the shortest or the longest waves that are to be found at the front of a dispersing wave packet? Do the wave crests move faster or slower than the wave packet?

  Give the solution to the initial-value problem for which at $t=0$

  $$\phi=\int_{-\infty}^{\infty} A(k) e^{i k x} d k \quad \text { and } \quad \frac{\partial \phi}{\partial t}=0$$

  and $\phi(x, 0)$ is real. Use the method of stationary phase to obtain an approximation for $\phi(V t, t)$ for fixed $0<V<1$ and large $t$. If, in addition, $\phi(x, 0)=\phi(-x, 0)$, deduce an approximation for the sequence of times at which $\phi(V t, t)=0$.

  You are given that $\phi(t, t)$ decreases like $t^{-1 / 4}$ for large $t$. Give a brief physical explanation why this rate of decay is slower than for $0<V<1$. What can be said about $\phi(V t, t)$ for large $t$ if $V>1$ ? [Detailed calculation is not required in these cases.]

  [You may assume that $\int_{-\infty}^{\infty} e^{-a u^{2}} d u=\sqrt{\frac{\pi}{a}} \quad$ for $\left.\operatorname{Re}(a) \geqslant 0, a \neq 0 .\right]$

  comment

• Paper 3, Section II, 39C

  Waves | Part II, 2014

  The equations describing small-amplitude motions in a stably stratified, incompressible, inviscid fluid are

  $$\frac{\partial \tilde{\rho}}{\partial t}+w \frac{\mathrm{d} \rho_{0}}{\mathrm{~d} z}=0, \quad \rho_{0} \frac{\partial \mathbf{u}}{\partial t}=\tilde{\rho} \mathbf{g}-\nabla \tilde{p}, \quad \boldsymbol{\nabla} \cdot \mathbf{u}=0$$

  where $\rho_{0}(z)$ is the background stratification, $\tilde{\rho}(\mathbf{x}, t)$ and $\tilde{p}(\mathbf{x}, t)$ are the perturbations about an undisturbed hydrostatic state, $\mathbf{u}(\mathbf{x}, t)=(u, v, w)$ is the velocity, and $\mathbf{g}=(0,0,-g)$.

  Show that

  $$\left[\frac{\partial^{2}}{\partial t^{2}} \nabla^{2}+N^{2}\left(\nabla^{2}-\frac{\partial^{2}}{\partial z^{2}}\right)\right] w=0$$

  stating any approximation made, and define the Brunt-Väisälä frequency $N$.

  Deduce the dispersion relation for plane harmonic waves with wavevector $\mathbf{k}=$ $(k, 0, m)$. Calculate the group velocity and verify that it is perpendicular to $\mathbf{k}$.

  Such a stably stratified fluid with a uniform value of $N$ occupies the region $z>h(x, t)$ above a moving lower boundary $z=h(x, t)$. Find the velocity field $w(x, z, t)$ generated by the boundary motion for the case $h=\epsilon \sin [k(x-U t)]$, where $0<\epsilon k \ll 1$ and $U>0$ is a constant.

  For the case $k^{2}<N^{2} / U^{2}$, sketch the orientation of the wave crests, the direction of propagation of the crests, and the direction of the group velocity.

  comment

• Paper 4, Section II, C

  Waves | Part II, 2014

  A one-dimensional shock wave propagates at a constant speed along a tube aligned with the $x$-axis and containing a perfect gas. In the reference frame where the shock is at rest at $x=0$, the gas has speed $U_{0}$, density $\rho_{0}$ and pressure $p_{0}$ in the region $x<0$ and speed $U_{1}$, density $\rho_{1}$ and pressure $p_{1}$ in the region $x>0$.

  Write down equations of conservation of mass, momentum and energy across the shock. Show that

  $$\frac{\gamma}{\gamma-1}\left(\frac{p_{1}}{\rho_{1}}-\frac{p_{0}}{\rho_{0}}\right)=\frac{p_{1}-p_{0}}{2}\left(\frac{1}{\rho_{1}}+\frac{1}{\rho_{0}}\right)$$

  where $\gamma$ is the ratio of specific heats.

  From now on, assume $\gamma=2$ and let $P=p_{1} / p_{0}$. Show that $\frac{1}{3}<\rho_{1} / \rho_{0}<3$.

  The increase in entropy from $x<0$ to $x>0$ is given by $\Delta S=C_{V} \log \left(p_{1} \rho_{0}^{2} / p_{0} \rho_{1}^{2}\right)$, where $C_{V}$ is a positive constant. Show that $\Delta S$ is a monotonic function of $P$.

  If $\Delta S>0$, deduce that $P>1, \rho_{1} / \rho_{0}>1,\left(U_{0} / c_{0}\right)^{2}>1$ and $\left(U_{1} / c_{1}\right)^{2}<1$, where $c_{0}$ and $c_{1}$ are the sound speeds in $x<0$ and $x>0$, respectively. Given that $\Delta S$ must have the same sign as $U_{0}$ and $U_{1}$, interpret these inequalities physically in terms of the properties of the flow upstream and downstream of the shock.

  comment