Part II, 2010, Paper 3

Algebraic Geometry

• Paper 3, Section II, G

  Algebraic Geometry | Part II, 2010

  (i) Let $X$ be a curve, and $p \in X$ be a smooth point on $X$. Define what a local parameter at $p$ is.

  Now let $f: X \rightarrow Y$ be a rational map to a quasi-projective variety $Y$. Show that if $Y$ is projective, $f$ extends to a morphism defined at $p$.

  Give an example where this fails if $Y$ is not projective, and an example of a morphism $f: \mathbb{C}^{2} \backslash\{0\} \rightarrow \mathbf{P}^{1}$ which does not extend to $0 .$

  (ii) Let $V=Z\left(X_{0}^{8}+X_{1}^{8}+X_{2}^{8}\right)$ and $W=Z\left(X_{0}^{4}+X_{1}^{4}+X_{2}^{4}\right)$ be curves in $\mathbf{P}^{2}$ over a field of characteristic not equal to 2 . Let $\phi: V \rightarrow W$ be the map $\left[X_{0}: X_{1}: X_{2}\right] \mapsto\left[X_{0}^{2}: X_{1}^{2}: X_{2}^{2}\right]$. Determine the degree of $\phi$, and the ramification $e_{p}$ for all $p \in V$.

  comment

Algebraic Topology

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2010

  Suppose $X$ is a finite simplicial complex and that $H_{*}(X)$ is a free abelian group for each value of $*$. Using the Mayer-Vietoris sequence or otherwise, compute $H_{*}\left(S^{1} \times X\right)$ in terms of $H_{*}(X)$. Use your result to compute $H_{*}\left(T^{n}\right)$.

  [Note that $T^{n}=S^{1} \times \ldots \times S^{1}$, where there are $n$ factors in the product.]

  comment

Applications of Quantum Mechanics

• Paper 3, Section II, B

  Applications of Quantum Mechanics | Part II, 2010

  State Bloch's theorem for a one dimensional lattice which is invariant under translations by $a$.

  A simple model of a crystal consists of a one-dimensional linear array of identical sites with separation $a$. At the $n$th site the Hamiltonian, neglecting all other sites, is $H_{n}$ and an electron may occupy either of two states, $\phi_{n}(x)$ and $\chi_{n}(x)$, where

  $$H_{n} \phi_{n}(x)=E_{0} \phi_{n}(x), \quad H_{n} \chi_{n}(x)=E_{1} \chi_{n}(x),$$

  and $\phi_{n}$ and $\chi_{n}$ are orthonormal. How are $\phi_{n}(x)$ and $\chi_{n}(x)$ related to $\phi_{0}(x)$ and $\chi_{0}(x)$ ?

  The full Hamiltonian is $H$ and is invariant under translations by $a$. Write trial wavefunctions $\psi(x)$ for the eigenstates of this model appropriate to a tight binding approximation if the electron has probability amplitudes $b_{n}$ and $c_{n}$ to be in the states $\phi_{n}$ and $\chi_{n}$ respectively.

  Assume that the only non-zero matrix elements in this model are, for all $n$,

  $$\begin{aligned} &\left(\phi_{n}, H_{n} \phi_{n}\right)=E_{0}, \quad\left(\chi_{n}, H_{n} \chi_{n}\right)=E_{1} \\ &\left(\phi_{n}, V \phi_{n \pm 1}\right)=\left(\chi_{n}, V \chi_{n \pm 1}\right)=\left(\phi_{n}, V \chi_{n \pm 1}\right)=\left(\chi_{n}, V \phi_{n \pm 1}\right)=-A, \end{aligned}$$

  where $H=H_{n}+V$ and $A>0$. Show that the time-dependent Schrödinger equation governing the amplitudes becomes

  $$\begin{aligned} i \hbar \dot{b}_{n} &=E_{0} b_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right) \\ i \hbar \dot{c}_{n} &=E_{1} c_{n}-A\left(c_{n+1}+c_{n-1}+b_{n+1}+b_{n-1}\right) \end{aligned}$$

  By examining solutions of the form

  $$\left(\begin{array}{l} b_{n} \\ c_{n} \end{array}\right)=\left(\begin{array}{l} B \\ C \end{array}\right) e^{i(k n a-E t / \hbar)}$$

  show that the allowed energies of the electron are two bands given by

  $$E=\frac{1}{2}\left(E_{0}+E_{1}-4 A \cos k a\right) \pm \frac{1}{2} \sqrt{\left(E_{0}-E_{1}\right)^{2}+16 A^{2} \cos ^{2} k a}$$

  Define the Brillouin zone for this system and find the energies at the top and bottom of both bands. Hence, show that the energy gap between the bands is

  $$\Delta E=-4 A+\sqrt{\left(E_{1}-E_{0}\right)^{2}+16 A^{2}}$$

  Show that the wavefunctions $\psi(x)$ satisfy Bloch's theorem.

  Describe briefly what are the crucial differences between insulators, conductors and semiconductors.

  comment

Applied Probability

• Paper 3, Section II, I

  Applied Probability | Part II, 2010

  Cars looking for a parking space are directed to one of three unlimited parking lots A, B and C. First, immediately after the entrance, the road forks: one direction is to lot A, the other to B and C. Shortly afterwards, the latter forks again, between B and C. See the diagram below.

  

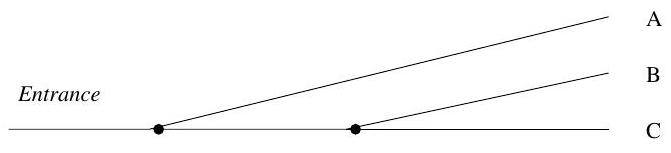
  The policeman at the first road fork directs an entering car with probability $1 / 3$ to A and with probability $2 / 3$ to the second fork. The policeman at the second fork sends the passing cars to $\mathrm{B}$ or $\mathrm{C}$ alternately: cars $1,3,5, \ldots$ approaching the second fork go to $\mathrm{B}$ and cars $2,4,6, \ldots$ to $\mathrm{C}$.

  Assuming that the total arrival process $(N(t))$ of cars is Poisson of rate $\lambda$, consider the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right), t \geqslant 0$, where $X^{i}(t)$ is the number of cars directed to lot $i$ by time $t$, for $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$. The times for a car to travel from the first to the second fork, or from a fork to the parking lot, are all negligible.

  (a) Characterise each of the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right)$, by specifying if it is (i) Poisson, (ii) renewal or (iii) delayed renewal. Correspondingly, specify the rate, the holding-time distribution and the distribution of the delay.

  (b) In the case of a renewal process, determine the equilibrium delay distribution.

  (c) Given $s, t>0$, write down explicit expressions for the probability $\mathbb{P}\left(X^{i}(s)=X^{i}(s+t)\right)$ that the interval $(s, t+s)$ is free of points in the corresponding process, $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$.

  comment

Asymptotic Methods

• Paper 3, Section II, C

  Asymptotic Methods | Part II, 2010

  Consider the ordinary differential equation

  $$y^{\prime \prime}=(|x|-E) y$$

  subject to the boundary conditions $y(\pm \infty)=0$. Write down the general form of the Liouville-Green solutions for this problem for $E>0$ and show that asymptotically the eigenvalues $E_{n}, n \in \mathbb{N}$ and $E_{n}<E_{n+1}$, behave as $E_{n}=\mathrm{O}\left(n^{2 / 3}\right)$ for large $n$.

  comment

Classical Dynamics

• Paper 3, Section I, D

  Classical Dynamics | Part II, 2010

  Euler's equations for the angular velocity $\boldsymbol{\omega}=\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ of a rigid body, viewed in the body frame, are

  $$I_{1} \frac{d \omega_{1}}{d t}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}$$

  and cyclic permutations, where the principal moments of inertia are assumed to obey $I_{1}<I_{2}<I_{3}$.

  Write down two quadratic first integrals of the motion.

  There is a family of solutions $\boldsymbol{\omega}(t)$, unique up to time-translations $t \rightarrow\left(t-t_{0}\right)$, which obey the boundary conditions $\boldsymbol{\omega} \rightarrow(0, \Omega, 0)$ as $t \rightarrow-\infty$ and $\boldsymbol{\omega} \rightarrow(0,-\Omega, 0)$ as $t \rightarrow \infty$, for a given positive constant $\Omega$. Show that, for such a solution, one has

  $$\mathbf{L}^{2}=2 E I_{2},$$

  where $\mathbf{L}$ is the angular momentum and $E$ is the kinetic energy.

  By eliminating $\omega_{1}$ and $\omega_{3}$ in favour of $\omega_{2}$, or otherwise, show that, in this case, the second Euler equation reduces to

  $$\frac{d s}{d \tau}=1-s^{2}$$

  where $s=\omega_{2} / \Omega$ and $\tau=\Omega t\left[\left(I_{1}-I_{2}\right)\left(I_{2}-I_{3}\right) / I_{1} I_{3}\right]^{1 / 2}$. Find the general solution $s(\tau)$.

  [You are not expected to calculate $\omega_{1}(t)$ or $\left.\omega_{3}(t) .\right]$

  comment

Coding and Cryptography

• Paper 3, Section I, $4 \mathrm{H}$

  Coding and Cryptography | Part II, 2010

  What is a linear code? What is a parity check matrix for a linear code? What is the minimum distance $d(C)$ for a linear code $C ?$

  If $C_{1}$ and $C_{2}$ are linear codes having a certain relation (which you should specify), define the bar product $C_{1} \mid C_{2}$. Show that

  $$d\left(C_{1} \mid C_{2}\right)=\min \left\{2 d\left(C_{1}\right), d\left(C_{2}\right)\right\}$$

  If $C_{1}$ has parity check matrix $P_{1}$ and $C_{2}$ has parity check matrix $P_{2}$, find a parity check matrix for $C_{1} \mid C_{2}$.

  comment

Cosmology

• Paper 3, Section I, D

  Cosmology | Part II, 2010

  Consider a homogenous and isotropic universe with mass density $\rho(t)$, pressure $P(t)$ and scale factor $a(t)$. As the universe expands its energy changes according to the relation $d E=-P d V$. Use this to derive the fluid equation

  $$\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+\frac{P}{c^{2}}\right)$$

  Use conservation of energy applied to a test particle at the boundary of a spherical fluid element to derive the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi}{3} G \rho-\frac{k}{a^{2}} c^{2}$$

  where $k$ is a constant. State any assumption you have made. Briefly state the significance of $k$.

  comment

• Paper 3, Section II, D

  Cosmology | Part II, 2010

  The number density for particles in thermal equilibrium, neglecting quantum effects, is

  $$n=g_{s} \frac{4 \pi}{h^{3}} \int p^{2} d p \exp (-(E(p)-\mu) / k T)$$

  where $g_{s}$ is the number of degrees of freedom for the particle with energy $E(p)$ and $\mu$ is its chemical potential. Evaluate $n$ for a non-relativistic particle.

  Thermal equilibrium between two species of non-relativistic particles is maintained by the reaction

  $$a+\alpha \leftrightarrow b+\beta$$

  where $\alpha$ and $\beta$ are massless particles. Evaluate the ratio of number densities $n_{a} / n_{b}$ given that their respective masses are $m_{a}$ and $m_{b}$ and chemical potentials are $\mu_{a}$ and $\mu_{b}$.

  Explain how a reaction like the one above is relevant to the determination of the neutron to proton ratio in the early universe. Why does this ratio not fall rapidly to zero as the universe cools?

  Explain briefly the process of primordial nucleosynthesis by which neutrons are converted into stable helium nuclei. Letting

  $$Y_{H e}=\rho_{H e} / \rho$$

  be the fraction of the universe's helium, compute $Y_{H e}$ as a function of the ratio $r=n_{n} / n_{p}$ at the time of nucleosynthesis.

  comment

Differential Geometry

• Paper 3, Section II, H

  Differential Geometry | Part II, 2010

  (i) State and prove the Theorema Egregium.

  (ii) Define the notions principal curvatures, principal directions and umbilical point.

  (iii) Let $S \subset \mathbb{R}^{3}$ be a connected compact regular surface (without boundary), and let $D \subset S$ be a dense subset of $S$ with the following property. For all $p \in D$, there exists an open neighbourhood $\mathcal{U}_{p}$ of $p$ in $S$ such that for all $\theta \in[0,2 \pi), \psi_{p, \theta}\left(\mathcal{U}_{p}\right)=\mathcal{U}_{p}$, where $\psi_{p, \theta}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ denotes rotation by $\theta$ around the line through $p$ perpendicular to $T_{p} S$. Show that $S$ is in fact a sphere.

  comment

Dynamical Systems

• Paper 3, Section I, D

  Dynamical Systems | Part II, 2010

  Let $I=[0,1)$. The sawtooth (Bernoulli shift) map $F: I \rightarrow I$ is defined by

  $$F(x)=2 x[\bmod 1]$$

  Describe the effect of $F$ using binary notation. Show that $F$ is continuous on $I$ except at $x=\frac{1}{2}$. Show also that $F$ has $N$-periodic points for all $N \geqslant 2$. Are they stable?

  Explain why $F$ is chaotic, using Glendinning's definition.

  comment

• Paper 3, Section II, D

  Dynamical Systems | Part II, 2010

  Describe informally the concepts of extended stable manifold theory. Illustrate your discussion by considering the 2-dimensional flow

  $$\dot{x}=\mu x+x y-x^{3}, \quad \dot{y}=-y+y^{2}-x^{2},$$

  where $\mu$ is a parameter with $|\mu| \ll 1$, in a neighbourhood of the origin. Determine the nature of the bifurcation.

  comment

Electrodynamics

• Paper 3, Section II, B

  Electrodynamics | Part II, 2010

  A particle of rest-mass $m$, electric charge $q$, is moving relativistically along the path $x^{\mu}(s)$ where $s$ parametrises the path.

  Write down an action for which the extremum determines the particle's equation of motion in an electromagnetic field given by the potential $A^{\mu}(x)$.

  Use your action to derive the particle's equation of motion in a form where $s$ is the proper time.

  Suppose that the electric and magnetic fields are given by

  $$\begin{aligned} \mathbf{E} &=(0,0, E) \\ \mathbf{B} &=(0, B, 0) \end{aligned}$$

  where $E$ and $B$ are constants and $B>E>0$.

  Find $x^{\mu}(s)$ given that the particle starts at rest at the origin when $s=0$.

  Describe qualitatively the motion of the particle.

  comment

Fluid Dynamics II

• Paper 3, Section II, A

  Fluid Dynamics II | Part II, 2010

  The equation for the vorticity $\omega(x, y)$ in two-dimensional incompressible flow takes the form

  $$\frac{\partial \omega}{\partial t}+u \frac{\partial \omega}{\partial x}+v \frac{\partial \omega}{\partial y}=\nu\left(\frac{\partial^{2} \omega}{\partial x^{2}}+\frac{\partial^{2} \omega}{\partial y^{2}}\right)$$

  where

  $$u=\frac{\partial \psi}{\partial y}, \quad v=-\frac{\partial \psi}{\partial x} \quad \text { and } \quad \omega=-\left(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}\right)$$

  and $\psi(x, y)$ is the stream function.

  Show that this equation has a time-dependent similarity solution of the form

  $$\psi=C x H(t)^{-1} \phi(\eta), \quad \omega=-C x H(t)^{-3} \phi_{\eta \eta}(\eta) \quad \text { for } \quad \eta=y H(t)^{-1}$$

  if $H(t)=\sqrt{2 C t}$ and $\phi$ satisfies the equation

  $$3 \phi_{\eta \eta}+\eta \phi_{\eta \eta \eta}-\phi_{\eta} \phi_{\eta \eta}+\phi \phi_{\eta \eta \eta}+\frac{1}{R} \phi_{\eta \eta \eta \eta}=0$$

  and $R=C / \nu$ is the effective Reynolds number.

  Show that this solution is appropriate for the problem of two-dimensional flow between the rigid planes $y=\pm H(t)$, and determine the boundary conditions on $\phi$ in that case.

  Verify that $(*)$ has exact solutions, satisfying the boundary conditions, of the form

  $$\phi=\frac{(-1)^{k}}{k \pi} \sin (k \pi \eta)-\eta, \quad k=1,2, \ldots$$

  when $R=k^{2} \pi^{2} / 4$. Sketch this solution when $k$ is large, and discuss whether such solutions are likely to be realised in practice.

  comment

Further Complex Methods

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2010

  Let $\Gamma(z)$ and $\zeta(z)$ denote the gamma and the zeta functions respectively, namely

  $$\begin{aligned} &\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0 \\ &\zeta(z)=\sum_{m=1}^{\infty} \frac{1}{m^{z}}, \quad \operatorname{Re} z>1 \end{aligned}$$

  By employing a series expansion of $\left(1-e^{-x}\right)^{-2}$, prove the following identity

  $$\int_{0}^{\infty} \frac{x^{z}}{\left(e^{x}-1\right)^{2}} d x=\Gamma(z+1)[\zeta(z)-\zeta(z+1)], \quad \operatorname{Re} z>1$$

  comment

Galois Theory

• Paper 3, Section II, H

  Galois Theory | Part II, 2010

  Let $K$ be a field of characteristic 0 . It is known that soluble extensions of $K$ are contained in a succession of cyclotomic and Kummer extensions. We will refine this statement.

  Let $n$ be a positive integer. The $n$-th cyclotomic field over a field $K$ is denoted by $K\left(\boldsymbol{\mu}_{n}\right)$. Let $\zeta_{n}$ be a primitive $n$-th root of unity in $K\left(\boldsymbol{\mu}_{n}\right)$.

  (i) Write $\zeta_{3} \in \mathbb{Q}\left(\boldsymbol{\mu}_{3}\right), \zeta_{5} \in \mathbb{Q}\left(\boldsymbol{\mu}_{5}\right)$ in terms of radicals. Write $\mathbb{Q}\left(\boldsymbol{\mu}_{3}\right) / \mathbb{Q}$ and $\mathbb{Q}\left(\boldsymbol{\mu}_{5}\right) / \mathbb{Q}$ as a succession of Kummer extensions.

  (ii) Let $n>1$, and $F:=K\left(\zeta_{1}, \zeta_{2}, \ldots, \zeta_{n-1}\right)$. Show that $F\left(\boldsymbol{\mu}_{n}\right) / F$ can be written as a succession of Kummer extensions, using the structure theorem of finite abelian groups (in other words, roots of unity can be written in terms of radicals). Show that every soluble extension of $K$ is contained in a succession of Kummer extensions.

  comment

Geometry of Group Actions

• Paper 3, Section I, F

  Geometry of Group Actions | Part II, 2010

  Let $U$ be a "triangular" region in the unit disc $\mathbb{D}$ bounded by three hyperbolic geodesics $\gamma_{1}, \gamma_{2}, \gamma_{3}$ that do not meet in $\mathbb{D}$ nor on its boundary. Let $J_{k}$ be inversion in $\gamma_{k}$ and set

  $$A=J_{2} \circ J_{1} ; \quad B=J_{3} \circ J_{2} .$$

  Let $G$ be the group generated by the Möbius transformations $A$ and $B$. Describe briefly a fundamental set for the group $G$ acting on $\mathbb{D}$.

  Prove that $G$ is a free group on the two generators $A$ and $B$. Describe the quotient surface $\mathbb{D} / G$.

  comment

Graph Theory

• Paper 3, Section II, F

  Graph Theory | Part II, 2010

  Let $G$ be a graph of order $n$. Show that $G$ must contain an independent set of $\left\lceil\sum_{v \in G} \frac{1}{d(v)+1}\right]$ vertices (where $\lceil x\rceil$ denotes the least integer $\left.\geqslant x\right)$.

  [Hint: take a random ordering of the vertices of $G$, and consider the set of those vertices which are adjacent to no earlier vertex in the ordering.]

  Fix an integer $m<n$ with $m$ dividing $n$, and suppose that $e(G)=m\left(\begin{array}{c}n / m \\ 2\end{array}\right)$.

  (i) Deduce that $G$ must contain an independent set of $m$ vertices.

  (ii) Must $G$ contain an independent set of $m+1$ vertices?

  comment

Integrable Systems

• Paper 3, Section II, E

  Integrable Systems | Part II, 2010

  Consider a vector field

  $$V=\alpha x \frac{\partial}{\partial x}+\beta t \frac{\partial}{\partial t}+\gamma v \frac{\partial}{\partial v}$$

  on $\mathbb{R}^{3}$, where $\alpha, \beta$ and $\gamma$ are constants. Find the one-parameter group of transformations generated by this vector field.

  Find the values of the constants $(\alpha, \beta, \gamma)$ such that $V$ generates a Lie point symmetry of the modified $\mathrm{KdV}$ equation ( $\mathrm{KKdV}$ )

  $$v_{t}-6 v^{2} v_{x}+v_{x x x}=0, \quad \text { where } \quad v=v(x, t)$$

  Show that the function $u=u(x, t)$ given by $u=v^{2}+v_{x}$ satisfies the KdV equation and find a Lie point symmetry of $\mathrm{KdV}$ corresponding to the Lie point symmetry of $\mathrm{mKdV}$ which you have determined from $V$.

  comment

Linear Analysis

• Paper 3, Section II, H

  Linear Analysis | Part II, 2010

  State and prove the Stone-Weierstrass theorem for real-valued functions.

  [You may use without proof the fact that the function $s \rightarrow|s|$ can be uniformly approximated by polynomials on $[-1,1] .]$

  comment

Logic and Set Theory

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2010

  Define the sets $V_{\alpha}, \alpha \in O N$. What is meant by the rank of a set?

  Explain briefly why, for every $\alpha$, there exists a set of rank $\alpha$.

  Let $x$ be a transitive set of rank $\alpha$. Show that $x$ has an element of rank $\beta$ for every $\beta<\alpha$.

  For which $\alpha$ does there exist a finite set of rank $\alpha$ ? For which $\alpha$ does there exist a finite transitive set of rank $\alpha$ ? Justify your answers.

  [Standard properties of rank may be assumed.]

  comment

Mathematical Biology

• Paper 3, Section I, A

  Mathematical Biology | Part II, 2010

  A population of aerobic bacteria swims in a laterally-infinite layer of fluid occupying $-\infty<x<\infty,-\infty<y<\infty$, and $-d / 2<z<d / 2$, with the top and bottom surfaces in contact with air. Assuming that there is no fluid motion and that all physical quantities depend only on $z$, the oxygen concentration $c$ and bacterial concentration $n$ obey the coupled equations

  $$\begin{aligned} \frac{\partial c}{\partial t} &=D_{c} \frac{\partial^{2} c}{\partial z^{2}}-k n \\ \frac{\partial n}{\partial t} &=D_{n} \frac{\partial^{2} n}{\partial z^{2}}-\frac{\partial}{\partial z}\left(\mu n \frac{\partial c}{\partial z}\right) \end{aligned}$$

  Consider first the case in which there is no chemotaxis, so $n$ has the spatially-uniform value $\bar{n}$. Find the steady-state oxygen concentration consistent with the boundary conditions $c(\pm d / 2)=c_{0}$. Calculate the Fick's law flux of oxygen into the layer and justify your answer on physical grounds.

  Now allowing chemotaxis and cellular diffusion, show that the equilibrium oxygen concentration satisfies

  $$\frac{d^{2} c}{d z^{2}}-\frac{k n_{0}}{D_{c}} \exp \left(\mu c / D_{n}\right)=0$$

  where $n_{0}$ is a suitable normalisation constant that need not be found.

  comment

• Paper 3, Section II, A

  Mathematical Biology | Part II, 2010

  Consider an epidemic model in which $S(x, t)$ is the local population density of susceptibles and $I(x, t)$ is the density of infectives

  $$\begin{aligned} &\frac{\partial S}{\partial t}=-r I S \\ &\frac{\partial I}{\partial t}=D \frac{\partial^{2} I}{\partial x^{2}}+r I S-a I \end{aligned}$$

  where $r, a$, and $D$ are positive. If $S_{0}$ is a characteristic population value, show that the rescalings $I / S_{0} \rightarrow I, S / S_{0} \rightarrow S,\left(r S_{0} / D\right)^{1 / 2} x \rightarrow x, r S_{0} t \rightarrow t$ reduce this system to

  $$\begin{aligned} &\frac{\partial S}{\partial t}=-I S \\ &\frac{\partial I}{\partial t}=\frac{\partial^{2} I}{\partial x^{2}}+I S-\lambda I \end{aligned}$$

  where $\lambda$ should be found.

  Travelling wavefront solutions are of the form $S(x, t)=S(z), I(x, t)=I(z)$, where $z=x-c t$ and $c$ is the wave speed, and we seek solutions with boundary conditions $S(\infty)=1, S^{\prime}(\infty)=0, I(\infty)=I(-\infty)=0$. Under the travelling-wave assumption reduce the rescaled PDEs to ODEs, and show by linearisation around the leading edge of the advancing front that the requirement that $I$ be non-negative leads to the condition $\lambda<1$ and hence the wave speed relation

  $$c \geqslant 2(1-\lambda)^{1 / 2}, \quad \lambda<1$$

  Using the two ODEs you have obtained, show that the surviving susceptible population fraction $\sigma=S(-\infty)$ after the passage of the front satisfies

  $$\sigma-\lambda \ln \sigma=1,$$

  and sketch $\sigma$ as a function of $\lambda$.

  comment

Number Theory

• Paper 3, Section I, G

  Number Theory | Part II, 2010

  (i) Let $M$ and $N$ be positive integers, such that $N$ is not a perfect square. If $M<\sqrt{N}$, show that every solution of the equation

  $$x^{2}-N y^{2}=M$$

  in positive integers $x, y$ comes from some convergent of the continued fraction of $\sqrt{N}$.

  (ii) Find a solution in positive integers $x, y$ of

  $$x^{2}-29 y^{2}=5$$

  comment

• Paper 3, Section II, G

  Number Theory | Part II, 2010

  State precisely the Miller-Rabin primality test.

  (i) Let $p$ be a prime $\geqslant 5$, and define

  $$N=\frac{4^{p}-1}{3}$$

  Prove that $N$ is a composite odd integer, and that $N$ is a pseudo-prime to the base 2 .

  (ii) Let $M$ be an odd integer greater than 1 such that $M$ is a pseudo-prime to the base 2 . Prove that $2^{M}-1$ is always a strong pseudo-prime to the base 2 .

  comment

Numerical Analysis

• Paper 3, Section II, A

  Numerical Analysis | Part II, 2010

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1], u=0$ on $\partial \Omega$, is discretized with the five-point formula

  $$u_{i, j-1}+u_{i, j+1}+u_{i+1, j}+u_{i-1, j}-4 u_{i, j}=h^{2} f_{i, j}$$

  where $1 \leqslant i, j \leqslant M, u_{i, j} \approx u(i h, j h)$ and $(i h, j h)$ are grid points.

  Let $u(x, y)$ be the exact solution, and let $e_{i, j}=u_{i, j}-u(i h, j h)$ be the error of the five-point formula at the $(i, j)$ th grid point. Justifying each step, prove that

  $$\|\mathbf{e}\|=\left[\sum_{i, j=1}^{M}\left|e_{i, j}\right|^{2}\right]^{1 / 2} \leqslant c h \quad \text { for sufficiently small } h>0,$$

  where $c$ is some constant independent of $h$.

  comment

Optimization and Control

• Paper 3, Section II, J

  Optimization and Control | Part II, 2010

  Consider an infinite-horizon controlled Markov process having per-period costs $c(x, u) \geqslant 0$, where $x \in \mathcal{X}$ is the state of the system, and $u \in \mathcal{U}$ is the control. Costs are discounted at rate $\beta \in(0,1]$, so that the objective to be minimized is

  $$\mathbb{E}\left[\sum_{t \geqslant 0} \beta^{t} c\left(X_{t}, u_{t}\right) \mid X_{0}=x\right]$$

  What is meant by a policy $\pi$ for this problem?

  Let $\mathcal{L}$ denote the dynamic programming operator

  $$\mathcal{L} f(x) \equiv \inf _{u \in \mathcal{U}}\left\{c(x, u)+\beta \mathbb{E}\left[f\left(X_{1}\right) \mid X_{0}=x, u_{0}=u\right]\right\}$$

  Further, let $F$ denote the value of the optimal control problem:

  $$F(x)=\inf _{\pi} \mathbb{E}^{\pi}\left[\sum_{t \geqslant 0} \beta^{t} c\left(X_{t}, u_{t}\right) \mid X_{0}=x\right]$$

  where the infimum is taken over all policies $\pi$, and $\mathbb{E}^{\pi}$ denotes expectation under policy $\pi$. Show that the functions $F_{t}$ defined by

  $$F_{t+1}=\mathcal{L} F_{t} \quad(t \geqslant 0), \quad F_{0} \equiv 0$$

  increase to a limit $F_{\infty} \in[0, \infty] .$ Prove that $F_{\infty} \leqslant F$. Prove that $F=\mathcal{L} F$

  Suppose that $\Phi=\mathcal{L} \Phi \geqslant 0$. Prove that $\Phi \geqslant F$.

  [You may assume that there is a function $u_{*}: \mathcal{X} \rightarrow \mathcal{U}$ such that

  $$\mathcal{L} \Phi(x)=c\left(x, u_{*}(x)\right)+\beta \mathbb{E}\left[\Phi\left(X_{1}\right) \mid X_{0}=x, u_{0}=u_{*}(x)\right]$$

  though the result remains true without this simplifying assumption.]

  comment

Partial Differential Equations

• Paper 3, Section II, 30E

  Partial Differential Equations | Part II, 2010

  Consider the Schrödinger equation

  $$i \partial_{t} \Psi=-\frac{1}{2} \Delta \Psi, \quad x \in \mathbb{R}^{n}, t>0$$

  for complex-valued solutions $\Psi(x, t)$ and where $\Delta$ is the Laplacian.

  (a) Derive, by using a Fourier transform and its inversion, the fundamental solution of the Schrödinger equation. Obtain the solution of the initial value problem

  $$\begin{aligned} i \partial_{t} \Psi=-\frac{1}{2} \Delta \Psi, & x \in \mathbb{R}^{n}, \quad t>0 \\ \Psi(x, 0)=f(x), & x \in \mathbb{R}^{n} \end{aligned}$$

  as a convolution.

  (b) Consider the Wigner-transform of the solution of the Schrödinger equation

  $$w(x, \xi, t)=\frac{1}{(2 \pi)^{n}} \int_{\mathbb{R}^{n}} \Psi\left(x+\frac{1}{2} y, t\right) \bar{\Psi}\left(x-\frac{1}{2} y, t\right) e^{-i y \cdot \xi} \mathrm{d}^{n} y$$

  defined for $x \in \mathbb{R}^{n}, \xi \in \mathbb{R}^{n}, t>0$. Derive an evolution equation for $w$ by using the Schrödinger equation. Write down the solution of this evolution equation for given initial data $w(x, \xi, 0)=g(x, \xi)$.

  comment

Principles of Quantum Mechanics

• Paper 3, Section II, C

  Principles of Quantum Mechanics | Part II, 2010

  What are the commutation relations between the position operator $\hat{x}$ and momentum operator $\hat{p}$ ? Show that this is consistent with $\hat{x}, \hat{p}$ being hermitian.

  The annihilation operator for a harmonic oscillator is

  $$a=\sqrt{\frac{1}{2 \hbar}}(\hat{x}+i \hat{p})$$

  in units where the mass and frequency of the oscillator are 1 . Derive the relation $\left[a, a^{\dagger}\right]=1$. Write down an expression for the Hamiltonian

  $$H=\frac{1}{2} \hat{p}^{2}+\frac{1}{2} \hat{x}^{2}$$

  in terms of the operator $N=a^{\dagger} a$.

  Assume there exists a unique ground state $|0\rangle$ of $H$ such that $a|0\rangle=0$. Explain how the space of eigenstates $|n\rangle$, is formed, and deduce the energy eigenvalues for these states. Show that

  $$a|n\rangle=A|n-1\rangle, \quad a^{\dagger}|n\rangle=B|n+1\rangle$$

  finding $A$ and $B$ in terms of $n$.

  Calculate the energy eigenvalues of the Hamiltonian for two harmonic oscillators

  $$H=H_{1}+H_{2}, \quad H_{i}=\frac{1}{2} \hat{p}_{i}^{2}+\frac{1}{2} \hat{x}_{i}^{2}, \quad i=1,2 .$$

  What is the degeneracy of the $n^{\text {th }}$energy level? Suppose that the two oscillators are then coupled by adding the extra term

  $$\Delta H=\lambda \hat{x}_{1} \hat{x}_{2}$$

  to $H$, where $\lambda \ll 1$. Calculate the energies for the states of the unperturbed system with the three lowest energy eigenvalues to first order in $\lambda$ using perturbation theory.

  [You may assume standard perturbation theory results.]

  comment

Principles of Statistics

• Paper 3, Section II, $\mathbf{2 7 J}$

  Principles of Statistics | Part II, 2010

  Define the normal and extensive form solutions of a Bayesian statistical decision problem involving parameter $\Theta$, random variable $X$, and loss function $L(\theta, a)$. How are they related? Let $R_{0}=R_{0}(\Pi)$ be the Bayes loss of the optimal act when $\Theta \sim \Pi$ and no data can be observed. Express the Bayes risk $R_{1}$ of the optimal statistical decision rule in terms of $R_{0}$ and the joint distribution of $(\Theta, X)$.

  The real parameter $\Theta$ has distribution $\Pi$, having probability density function $\pi(\cdot)$. Consider the problem of specifying a set $S \subseteq \mathbb{R}$ such that the loss when $\Theta=\theta$ is $L(\theta, S)=c|S|-\mathbf{1}_{S}(\theta)$, where $\mathbf{1}_{S}$ is the indicator function of $S$, where $c>0$, and where $|S|=\int_{S} d x$. Show that the "highest density" region $S^{*}:=\{\theta: \pi(\theta) \geqslant c\}$ supplies a Bayes act for this decision problem, and explain why $R_{0}(\Pi) \leqslant 0$.

  For the case $\Theta \sim \mathcal{N}\left(\mu, \sigma^{2}\right)$, find an expression for $R_{0}$ in terms of the standard normal distribution function $\Phi$.

  Suppose now that $c=0.5$, that $\Theta \sim \mathcal{N}(0,1)$ and that $X \mid \Theta \sim \mathcal{N}(\Theta, 1 / 9)$. Show that $R_{1}<R_{0}$.

  comment

Probability and Measure

• Paper 3, Section II, I

  Probability and Measure | Part II, 2010

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables with common density function

  $$f(x)=\frac{1}{\pi\left(1+x^{2}\right)}$$

  Fix $\alpha \in[0,1]$ and set

  $$Y_{n}=\operatorname{sgn}\left(X_{n}\right)\left|X_{n}\right|^{\alpha}, \quad S_{n}=Y_{1}+\ldots+Y_{n}$$

  Show that for all $\alpha \in[0,1]$ the sequence of random variables $S_{n} / n$ converges in distribution and determine the limit.

  [Hint: In the case $\alpha=1$ it may be useful to prove that $\mathbb{E}\left(e^{i u X_{1}}\right)=e^{-|u|}$, for all $\left.u \in \mathbb{R} .\right]$

  Show further that for all $\alpha \in[0,1 / 2)$ the sequence of random variables $S_{n} / \sqrt{n}$ converges in distribution and determine the limit.

  [You should state clearly any result about random variables from the course to which you appeal. You are not expected to evaluate explicitly the integral

  $$m(\alpha)=\int_{0}^{\infty} \frac{x^{\alpha}}{\pi\left(1+x^{2}\right)} d x$$

  comment

Representation Theory

• Paper 3, Section II, F

  Representation Theory | Part II, 2010

  Show that the degree of a complex irreducible character of a finite group is a factor of the order of the group.

  State and prove Burnside's $p^{a} q^{b}$ theorem. You should quote clearly any results you use.

  Prove that for any group of odd order $n$ having precisely $k$ conjugacy classes, the integer $n-k$ is divisible by 16 .

  comment

Riemann Surfaces

• Paper 3, Section II, G

  Riemann Surfaces | Part II, 2010

  Show that the analytic isomorphisms (i.e. conformal equivalences) of the Riemann sphere $\mathbb{C}_{\infty}$ to itself are given by the non-constant Möbius transformations.

  State the Riemann-Hurwitz formula for a non-constant analytic map between compact Riemann surfaces, carefully explaining the terms which occur.

  Suppose now that $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ is an analytic map of degree 2 ; show that there exist Möbius transformations $S$ and $T$ such that

  $$S f T: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$$

  is the map given by $z \mapsto z^{2}$.

  comment

Statistical Modelling

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2010

  Consider the linear model $Y=X \beta+\varepsilon$, where $Y$ is a $n \times 1$ random vector, $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$, and where the $n \times p$ nonrandom matrix $X$ is known and has full column rank $p$. Derive the maximum likelihood estimator $\hat{\sigma}^{2}$ of $\sigma^{2}$. Without using Cochran's theorem, show carefully that $\hat{\sigma}^{2}$ is biased. Suggest another estimator $\tilde{\sigma}^{2}$ for $\sigma^{2}$ that is unbiased.

  comment

Statistical Physics

• Paper 3, Section II, C

  Statistical Physics | Part II, 2010

  (i) Given the following density of states for a particle in 3 dimensions

  $$g(\varepsilon)=K V \varepsilon^{1 / 2}$$

  write down the partition function for a gas of $N$ such non-interacting particles, assuming they can be treated classically. From this expression, calculate the energy $E$ of the system and the heat capacities $C_{V}$ and $C_{P}$. You may take it as given that $P V=\frac{2}{3} E$.

  [Hint: The formula $\int_{0}^{\infty} d y y^{2} e^{-y^{2}}=\sqrt{\pi} / 4$ may be useful.]

  (ii) Using thermodynamic relations obtain the relation between heat capacities and compressibilities

  $$\frac{C_{P}}{C_{V}}=\frac{\kappa_{T}}{\kappa_{S}}$$

  where the isothermal and adiabatic compressibilities are given by

  $$\kappa=-\frac{1}{V} \frac{\partial V}{\partial P},$$

  derivatives taken at constant temperature and entropy, respectively.

  (iii) Find $\kappa_{T}$ and $\kappa_{S}$ for the ideal gas considered above.

  comment

Stochastic Financial Models

• Paper 3, Section II, I

  Stochastic Financial Models | Part II, 2010

  Consider a market with two assets, a riskless bond and a risky stock, both of whose initial (time-0) prices are $B_{0}=1=S_{0}$. At time 1 , the price of the bond is a constant $B_{1}=R>0$ and the price of the stock $S_{1}$ is uniformly distributed on the interval $[0, C]$ where $C>R$ is a constant.

  Describe the set of state price densities.

  Consider a contingent claim whose payout at time 1 is given by $S_{1}^{2}$. Use the fundamental theorem of asset pricing to show that, if there is no arbitrage, the initial price of the claim is larger than $R$ and smaller than $C$.

  Now consider an investor with initial wealth $X_{0}=1$, and assume $C=3 R$. The investor's goal is to maximize his expected utility of time-1 wealth $\mathbb{E} U\left[R+\pi\left(S_{1}-R\right)\right]$, where $U(x)=\sqrt{x}$. Show that the optimal number of shares of stock to hold is $\pi^{*}=1$.

  What would be the investor's marginal utility price of the contingent claim described above?

  comment

Topics in Analysis

• Paper 3, Section I, F

  Topics in Analysis | Part II, 2010

  Let $A=\{z \in \mathbb{C}: 1 / 2 \leqslant|z| \leqslant 2\}$ and suppose that $f$ is complex analytic on an open subset containing $A$.

  (i) Give an example, with justification, to show that there need not exist a sequence of complex polynomials converging to $f$ uniformly on $A$.

  (ii) Let $R \subset \mathbb{C}$ be the positive real axis and $B=A \backslash R$. Prove that there exists a sequence of complex polynomials $p_{1}, p_{2}, p_{3}, \ldots$ such that $p_{j} \rightarrow f$ uniformly on each compact subset of $B$.

  (iii) Let $p_{1}, p_{2}, p_{3}, \ldots$ be the sequence of polynomials in (ii). If this sequence converges uniformly on $A$, show that $\int_{C} f(z) d z=0$, where $C=\{z \in \mathbb{C}:|z|=1\}$.

  comment

• Paper 3, Section II, F

  Topics in Analysis | Part II, 2010

  (i) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map with $\gamma(0)=\gamma(1)$. Define the winding number $w(\gamma ; 0)$ of $\gamma$ about the origin.

  (ii) For $j=0,1$, let $\gamma_{j}:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be continuous with $\gamma_{j}(0)=\gamma_{j}(1)$. Make the following statement precise, and prove it: if $\gamma_{0}$ can be continuously deformed into $\gamma_{1}$ through a family of continuous curves missing the origin, then $w\left(\gamma_{0} ; 0\right)=w\left(\gamma_{1} ; 0\right)$.

  [You may use without proof the following fact: if $\gamma, \delta:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ are continuous with $\gamma(0)=\gamma(1), \delta(0)=\delta(1)$ and if $|\gamma(t)|<|\delta(t)|$ for each $t \in[0,1]$, then $w(\gamma+\delta ; 0)=w(\delta ; 0)$.]

  (iii) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be continuous with $\gamma(0)=\gamma(1)$. If $\gamma(t)$ is not equal to a negative real number for each $t \in[0,1]$, prove that $w(\gamma ; 0)=0$.

  (iv) Let $D=\{z \in \mathbb{C}:|z| \leqslant 1\}$ and $C=\{z \in \mathbb{C}:|z|=1\}$. If $g: D \rightarrow C$ is continuous, prove that for each non-zero integer $n$, there is at least one point $z \in C$ such that $z^{n}+g(z)=0$.

  comment

Waves

• Paper 3, Section II, 38A

  Waves | Part II, 2010

  Consider the equation

  $$\frac{\partial^{2} \phi}{\partial t \partial x}=-\alpha \phi$$

  where $\alpha$ is a positive constant. Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$. Sketch graphs of the phase velocity $c(k)$ and the group velocity $c_{g}(k)$.

  A disturbance localized near $x=0$ at $t=0$ evolves into a dispersing wave packet. Will the wavelength and frequency of the waves passing a stationary observer located at a large positive value of $x$ increase or decrease for $t>0$ ? In which direction do the crests pass the observer?

  Write down the solution $\phi(x, t)$ with initial value

  $$\phi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  What can be said about $A(-k)$ if $\phi$ is real?

  Use the method of stationary phase to obtain an approximation for $\phi(V t, t)$ for fixed $V>0$ and large $t$. What can be said about the solution at $x=-V t$ for large $t$ ?

  [You may assume that $\int_{-\infty}^{\infty} e^{-a u^{2}} d u=\sqrt{\frac{\pi}{a}}$ for $\operatorname{Re}(a) \geqslant 0, a \neq 0$.]

  comment