Part II, 2007, Paper 1

Algebraic Topology

• 1.II.21H

  Algebraic Topology | Part II, 2007

  (i) Compute the fundamental group of the Klein bottle. Show that this group is not abelian, for example by defining a suitable homomorphism to the symmetric group $S_{3}$.

  (ii) Let $X$ be the closed orientable surface of genus 2 . How many (connected) double coverings does $X$ have? Show that the fundamental group of $X$ admits a homomorphism onto the free group on 2 generators.

  comment

Applications of Quantum Mechanics

• 1.II.33A

  Applications of Quantum Mechanics | Part II, 2007

  In a certain spherically symmetric potential, the radial wavefunction for particle scattering in the $l=0$ sector ( $S$-wave), for wavenumber $k$ and $r \gg 0$, is

  $$R(r, k)=\frac{A}{k r}\left(g(-k) e^{-i k r}-g(k) e^{i k r}\right)$$

  where

  $$g(k)=\frac{k+i \kappa}{k-i \alpha}$$

  with $\kappa$ and $\alpha$ real, positive constants. Scattering in sectors with $l \neq 0$ can be neglected. Deduce the formula for the $S$-matrix in this case and show that it satisfies the expected symmetry and reality properties. Show that the phase shift is

  $$\delta(k)=\tan ^{-1} \frac{k(\kappa+\alpha)}{k^{2}-\kappa \alpha}$$

  What is the scattering length for this potential?

  From the form of the radial wavefunction, deduce the energies of the bound states, if any, in this system. If you were given only the $S$-matrix as a function of $k$, and no other information, would you reach the same conclusion? Are there any resonances here?

  [Hint: Recall that $S(k)=e^{2 i \delta(k)}$ for real $k$, where $\delta(k)$ is the phase shift.]

  comment

Applied Probability

• 1.II.26J

  Applied Probability | Part II, 2007

  An open air rock concert is taking place in beautiful Pine Valley, and enthusiastic fans from the entire state of Alifornia are heading there long before the much anticipated event. The arriving cars have to be directed to one of three large (practically unlimited) parking lots, $a, b$ and $c$ situated near the valley entrance. The traffic cop at the entrance to the valley decides to direct every third car (in the order of their arrival) to a particular lot. Thus, cars $1,4,7,10$ and so on are directed to lot $a$, cars $2,5,8,11$ to lot $b$ and cars $3,6,9,12$ to lot $c$.

  Suppose that the total arrival process $N(t), t \geqslant 0$, at the valley entrance is Poisson, of rate $\lambda>0$ (the initial time $t=0$ is taken to be considerably ahead of the actual event). Consider the processes $X^{a}(t), X^{b}(t)$ and $X^{c}(t)$ where $X^{i}(t)$ is the number of cars arrived in lot $i$ by time $t, i=a, b, c$. Assume for simplicity that the time to reach a parking lot from the entrance is negligible so that the car enters its specified lot at the time it crosses the valley entrance.

  (a) Give the probability density function of the time of the first arrival in each of the processes $X^{a}(t), X^{b}(t), X^{c}(t)$.

  (b) Describe the distribution of the time between two subsequent arrivals in each of these processes. Are these times independent? Justify your answer.

  (c) Which of these processes are delayed renewal processes (where the distribution of the first arrival time differs from that of the inter-arrival time)?

  (d) What are the corresponding equilibrium renewal processes?

  (e) Describe how the direction rule should be changed for $X^{a}(t), X^{b}(t)$ and $X^{c}(t)$ to become Poisson processes, of rate $\lambda / 3$. Will these Poisson processes be independent? Justify your answer.

  comment

Asymptotic Methods

• 1.II.30B

  Asymptotic Methods | Part II, 2007

  State Watson's lemma, describing the asymptotic behaviour of the integral

  $$I(\lambda)=\int_{0}^{A} e^{-\lambda t} f(t) d t, \quad A>0$$

  as $\lambda \rightarrow \infty$, given that $f(t)$ has the asymptotic expansion

  $$f(t) \sim t^{\alpha} \sum_{n=0}^{\infty} a_{n} t^{n \beta}$$

  as $t \rightarrow 0_{+}$, where $\beta>0$ and $\alpha>-1$.

  Give an account of Laplace's method for finding asymptotic expansions of integrals of the form

  $$J(z)=\int_{-\infty}^{\infty} e^{-z p(t)} q(t) d t$$

  for large real $z$, where $p(t)$ is real for real $t$.

  Deduce the following asymptotic expansion of the contour integral

  $$\int_{-\infty-i \pi}^{\infty+i \pi} \exp (z \cosh t) d t=2^{1 / 2} i e^{z} \Gamma\left(\frac{1}{2}\right)\left[z^{-1 / 2}+\frac{1}{8} z^{-3 / 2}+O\left(z^{-5 / 2}\right)\right]$$

  as $z \rightarrow \infty$.

  comment

Classical Dynamics

• 1.I.9C

  Classical Dynamics | Part II, 2007

  The action for a system with generalized coordinates, $q_{i}(t)$, for a time interval $\left[t_{1}, t_{2}\right]$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L\left(q_{i}, \dot{q}_{i}\right) d t$$

  where $L$ is the Lagrangian, and where the end point values $q_{i}\left(t_{1}\right)$ and $q_{i}\left(t_{2}\right)$ are fixed at specified values. Derive Lagrange's equations from the principle of least action by considering the variation of $S$ for all possible paths.

  What is meant by the statement that a particular coordinate $q_{j}$ is ignorable? Show that there is an associated constant of the motion, to be specified in terms of $L$.

  A particle of mass $m$ is constrained to move on the surface of a sphere of radius $a$ under a potential, $V(\theta)$, for which the Lagrangian is given by

  $$L=\frac{m}{2} a^{2}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)-V(\theta)$$

  Identify an ignorable coordinate and find the associated constant of the motion, expressing it as a function of the generalized coordinates. Evaluate the quantity

  $$H=\dot{q}_{i} \frac{\partial L}{\partial \dot{q}_{i}}-L$$

  in terms of the same generalized coordinates, for this case. Is $H$ also a constant of the motion? If so, why?

  comment

Coding and Cryptography

• 1.I.4G

  Coding and Cryptography | Part II, 2007

  Let $\Sigma_{1}$ and $\Sigma_{2}$ be alphabets of sizes $m$ and $a$. What does it mean to say that $f: \Sigma_{1} \rightarrow \Sigma_{2}^{*}$ is a decipherable code? State the inequalities of Kraft and Gibbs, and deduce that if letters are drawn from $\Sigma_{1}$ with probabilities $p_{1}, \ldots, p_{m}$ then the expected word length is at least $H\left(p_{1}, \ldots, p_{m}\right) / \log a$.

  comment

• 1.II.11G

  Coding and Cryptography | Part II, 2007

  Define the bar product $C_{1} \mid C_{2}$ of linear codes $C_{1}$ and $C_{2}$, where $C_{2}$ is a subcode of $C_{1}$. Relate the rank and minimum distance of $C_{1} \mid C_{2}$ to those of $C_{1}$ and $C_{2}$. Show that if $C^{\perp}$ denotes the dual code of $C$, then

  $$\left(C_{1} \mid C_{2}\right)^{\perp}=C_{2}^{\perp} \mid C_{1}^{\perp}$$

  Using the bar product construction, or otherwise, define the Reed-Muller code $R M(d, r)$ for $0 \leqslant r \leqslant d$. Show that if $0 \leqslant r \leqslant d-1$, then the dual of $R M(d, r)$ is again a Reed-Muller code.

  comment

Cosmology

• 1.I.10A

  Cosmology | Part II, 2007

  Describe the motion of light rays in an expanding universe with scale factor $a(t)$, and derive the redshift formula

  $$1+z=\frac{a\left(t_{0}\right)}{a\left(t_{\mathrm{e}}\right)},$$

  where the light is emitted at time $t_{\mathrm{e}}$ and observed at time $t_{0}$.

  A galaxy at comoving position $\mathbf{x}$ is observed to have a redshift $z$. Given that the galaxy emits an amount of energy $L$ per unit time, show that the total energy per unit time crossing a sphere centred on the galaxy and intercepting the earth is $L /(1+z)^{2}$. Hence, show that the energy per unit time per unit area passing the earth is

  $$\frac{L}{(1+z)^{2}} \frac{1}{4 \pi|\mathbf{x}|^{2} a^{2}\left(t_{0}\right)}$$

  comment

• 1.II.15A

  Cosmology | Part II, 2007

  In a homogeneous and isotropic universe, the scale factor $a(t)$ obeys the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho,$$

  where $\rho$ is the matter density, which, together with the pressure $P$, satisfies

  $$\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+P / c^{2}\right)$$

  Here, $k$ is a constant curvature parameter. Use these equations to show that the rate of change of the Hubble parameter $H=\dot{a} / a$ satisfies

  $$\dot{H}+H^{2}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  Suppose that an expanding Friedmann universe is filled with radiation (density $\rho_{R}$ and pressure $\left.P_{R}=\rho_{R} c^{2} / 3\right)$ as well as a "dark energy" component (density $\rho_{\Lambda}$ and pressure $\left.P_{\Lambda}=-\rho_{\Lambda} c^{2}\right)$. Given that the energy densities of these two components are measured today $\left(t=t_{0}\right)$ to be

  $$\rho_{R 0}=\beta \frac{3 H_{0}^{2}}{8 \pi G} \quad \text { and } \quad \rho_{\Lambda 0}=\frac{3 H_{0}^{2}}{8 \pi G} \quad \text { with constant } \beta>0 \quad \text { and } \quad a\left(t_{0}\right)=1,$$

  show that the curvature parameter must satisfy $k c^{2}=\beta H_{0}^{2}$. Hence derive the following relations for the Hubble parameter and its time derivative:

  $$\begin{aligned} H^{2} &=\frac{H_{0}^{2}}{a^{4}}\left(\beta-\beta a^{2}+a^{4}\right) \\ \dot{H} &=-\beta \frac{H_{0}^{2}}{a^{4}}\left(2-a^{2}\right) \end{aligned}$$

  Show qualitatively that universes with $\beta>4$ will recollapse to a Big Crunch in the future. [Hint: Sketch $a^{4} H^{2}$ and $a^{4} \dot{H}$ versus $a^{2}$ for representative values of $\beta$.]

  For $\beta=4$, find an explicit solution for the scale factor $a(t)$ satisfying $a(0)=0$. Find the limiting behaviours of this solution for large and small $t$. Comment briefly on their significance.

  comment

Differential Geometry

• 1.II.24H

  Differential Geometry | Part II, 2007

  Let $f: X \rightarrow Y$ be a smooth map between manifolds without boundary. Recall that $f$ is a submersion if $d f_{x}: T_{x} X \rightarrow T_{f(x)} Y$ is surjective for all $x \in X$. The canonical submersion is the standard projection of $\mathbb{R}^{k}$ onto $\mathbb{R}^{l}$ for $k \geqslant l$, given by

  $$\left(x_{1}, \ldots, x_{k}\right) \mapsto\left(x_{1}, \ldots, x_{l}\right)$$

  (i) Let $f$ be a submersion, $x \in X$ and $y=f(x)$. Show that there exist local coordinates around $x$ and $y$ such that $f$, in these coordinates, is the canonical submersion. [You may assume the inverse function theorem.]

  (ii) Show that submersions map open sets to open sets.

  (iii) If $X$ is compact and $Y$ connected, show that every submersion is surjective. Are there submersions of compact manifolds into Euclidean spaces $\mathbb{R}^{k}$ with $k \geqslant 1$ ?

  comment

Dynamical Systems

• 1.I.7E

  Dynamical Systems | Part II, 2007

  Given a non-autonomous $k$ th-order differential equation

  $$\frac{d^{k} y}{d t^{k}}=g\left(t, y, \frac{d y}{d t}, \frac{d^{2} y}{d t^{2}}, \ldots, \frac{d^{k-1} y}{d t^{k-1}}\right)$$

  with $y \in \mathbb{R}$, explain how it may be written in the autonomous first-order form $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ for suitably chosen vectors $\mathbf{x}$ and $\mathbf{f}$.

  Given an autonomous system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{n}$, define the corresponding flow $\boldsymbol{\phi}_{t}(\mathbf{x})$. What is $\phi_{s}\left(\phi_{t}(\mathbf{x})\right)$ equal to? Define the orbit $\mathcal{O}(\mathbf{x})$ through $\mathbf{x}$ and the limit set $\omega(\mathbf{x})$ of $\mathbf{x}$. Define a homoclinic orbit.

  comment

Electrodynamics

• 1.II.34E

  Electrodynamics | Part II, 2007

  Frame $\mathcal{S}^{\prime}$ is moving with uniform speed $v$ in the $z$-direction relative to a laboratory frame $\mathcal{S}$. Using Cartesian coordinates and units such that $c=1$, the relevant Lorentz transformation is

  $$t^{\prime}=\gamma(t-v z), \quad x^{\prime}=x, \quad y^{\prime}=y, \quad z^{\prime}=\gamma(z-v t)$$

  where $\gamma=1 / \sqrt{1-v^{2}}$. A straight thin wire of infinite extent lies along the $z$-axis and carries charge and current line densities $\sigma$ and $J$ per unit length, as measured in $\mathcal{S}$. Stating carefully your assumptions show that the corresponding quantities in $\mathcal{S}^{\prime}$ are given by

  $$\sigma^{\prime}=\gamma(\sigma-v J), \quad J^{\prime}=\gamma(J-v \sigma)$$

  Using cylindrical polar coordinates, and the integral forms of the Maxwell equations $\nabla \cdot \mathbf{E}=\mu_{0} \rho$ and $\nabla \times \mathbf{B}=\mu_{0} \mathbf{j}$, derive the electric and magnetic fields outside the wire in both frames.

  In a standard notation the Lorentz transformation for the electric and magnetic fields is

  $$\mathbf{E}_{\|}^{\prime}=\mathbf{E}_{\|}, \quad \mathbf{B}_{\|}^{\prime}=\mathbf{B}_{\|}, \quad \quad \mathbf{E}_{\perp}^{\prime}=\gamma\left(\mathbf{E}_{\perp}+\mathbf{v} \times \mathbf{B}_{\perp}\right), \quad \mathbf{B}_{\perp}^{\prime}=\gamma\left(\mathbf{B}_{\perp}-\mathbf{v} \times \mathbf{E}_{\perp}\right)$$

  Is your result consistent with this?

  comment

Fluid Dynamics II

• 1.II.36B

  Fluid Dynamics II | Part II, 2007

  Discuss how the methods of lubrication theory may be used to find viscous fluid flows in thin layers or narrow gaps, explaining carefully what inequalities need to hold in order that the theory may apply.

  Viscous fluid of kinematic viscosity $\nu$ flows under the influence of gravity $g$, down an inclined plane making an angle $\alpha \ll 1$ with the horizontal. The fluid layer lies between $y=0$ and $y=h(x, t)$, where $x, y$ are distances measured down the plane and perpendicular to it, and $|\partial h / \partial x|$ is of the same order as $\alpha$. Give conditions involving $h, \alpha, \nu$ and $g$ that ensure that lubrication theory can be used, and solve the lubrication equations, together with the equation of mass conservation, to obtain an equation for $h$ in the form

  $$\frac{\partial h}{\partial t}=\frac{\partial}{\partial x}\left(-A h^{3}+B h^{3} \frac{\partial h}{\partial x}\right)$$

  where $A, B$ are constants to be determined. Show that there is a steady solution with $\partial h / \partial x=k=$ constant, and interpret this physically. Show also that a solution of this equation exists in the form of a front, with $h(x, t)=F(\xi)$, where $\xi=x-c t, F(0)=0$, and $F(\xi) \rightarrow h_{0}$ as $\xi \rightarrow-\infty$. Determine $c$ in terms of $h_{0}$, find the shape of the front implicitly in the form $\xi=G(h)$, and show that $h \propto(-\xi)^{1 / 3}$ as $\xi \rightarrow 0$ from below.

  comment

Further Complex Methods

• 1.I.8B

  Further Complex Methods | Part II, 2007

  The coefficients $p(z)$ and $q(z)$ of the differential equation

  $$w^{\prime \prime}(z)+p(z) w^{\prime}(z)+q(z) w(z)=0$$

  are analytic in the punctured disc $0<|z|<R$, and $w_{1}(z)$ and $w_{2}(z)$ are linearly independent solutions in the neighbourhood of the point $z_{0}$ in the disc. By considering the effect of analytically continuing $w_{1}$ and $w_{2}$, show that the equation $(*)$ has a non-trivial solution of the form

  $$w(z)=z^{\sigma} \sum_{n=-\infty}^{\infty} c_{n} z^{n}$$

  comment

• 1.II.14B

  Further Complex Methods | Part II, 2007

  The function $J(z)$ is defined by

  $$J(z)=\int_{\mathcal{P}} t^{z-1}(1-t)^{b-1} d t$$

  where $b$ is a constant (which is not an integer). The path of integration, $\mathcal{P}$, is the Pochhammer contour, defined as follows. It starts at a point $A$ on the axis between 0 and 1 , then it circles the points 1 and 0 in the negative sense, then it circles the points 1 and 0 in the positive sense, returning to $A$. At the start of the path, $\arg (t)=\arg (1-t)=0$ and the integrand is defined at other points on $\mathcal{P}$ by analytic continuation along $\mathcal{P}$.

  (i) For what values of $z$ is $J(z)$ analytic? Give brief reasons for your answer.

  (ii) Show that, in the case $\operatorname{Re} z>0$ and $\operatorname{Re} b>0$,

  $$J(z)=-4 e^{-\pi i(z+b)} \sin (\pi z) \sin (\pi b) \mathrm{B}(z, b)$$

  where $\mathrm{B}(z, b)$ is the Beta function.

  (iii) Deduce that the only singularities of $\mathrm{B}(z, b)$ are simple poles. Explain carefully what happens if $z$ is a positive integer.

  comment

Galois Theory

• 1.II.18F

  Galois Theory | Part II, 2007

  Let $L / K / M$ be field extensions. Define the degree $[K: M]$ of the field extension $K / M$, and state and prove the tower law.

  Now let $K$ be a finite field. Show $\# K=p^{n}$, for some prime $p$ and positive integer $n$. Show also that $K$ contains a subfield of order $p^{m}$ if and only if $m \mid n$.

  If $f \in K[x]$ is an irreducible polynomial of degree $d$ over the finite field $K$, determine its Galois group.

  comment

General Relativity

• 1.II.35A

  General Relativity | Part II, 2007

  Starting from the Riemann tensor for a metric $g_{a b}$, define the Ricci tensor $R_{a b}$ and the scalar curvature $R$.

  The Riemann tensor obeys

  $$\nabla_{e} R_{a b c d}+\nabla_{c} R_{a b d e}+\nabla_{d} R_{a b e c}=0$$

  Deduce that

  $$\nabla^{a} R_{a b}=\frac{1}{2} \nabla_{b} R$$

  Write down Einstein's field equations in the presence of a matter source, with energymomentum tensor $T_{a b}$. How is the relation $(*)$ important for the consistency of Einstein's equations?

  Show that, for a scalar function $\phi$, one has

  $$\nabla^{2} \nabla_{a} \phi=\nabla_{a} \nabla^{2} \phi+R_{a b} \nabla^{b} \phi .$$

  Assume that

  $$R_{a b}=\nabla_{a} \nabla_{b} \phi$$

  for a scalar field $\phi$. Show that the quantity

  $$R+\nabla^{a} \phi \nabla_{a} \phi$$

  is then a constant.

  comment

Geometry of Group Actions

• 1.II.12G

  Geometry of Group Actions | Part II, 2007

  Define the Hausdorff $d$-dimensional measure $\mathcal{H}^{d}(C)$ and the Hausdorff dimension of a subset $C$ of $\mathbb{R}$.

  Set $s=\log 2 / \log 3$. Define the Cantor set $C$ and show that its Hausdorff $s$-dimensional measure is at most $1 .$

  Let $\left(X_{n}\right)$ be independent Bernoulli random variables that take the values 0 and 2 , each with probability $\frac{1}{2}$. Define

  $$\xi=\sum_{n=1}^{\infty} \frac{X_{n}}{3^{n}}$$

  Show that $\xi$ is a random variable that takes values in the Cantor set $C$.

  Let $U$ be a subset of $\mathbb{R}$ with $3^{-(k+1)} \leqslant \operatorname{diam}(U)<3^{-k}$. Show that $\mathbb{P}(\xi \in U) \leqslant 2^{-k}$ and deduce that, for any set $U \subset \mathbb{R}$, we have

  $$\mathbb{P}(\xi \in U) \leqslant 2(\operatorname{diam}(U))^{s}$$

  Hence, or otherwise, prove that $\mathcal{H}^{s}(C) \geqslant \frac{1}{2}$ and that the Cantor set has Hausdorff dimension $s$.

  comment

Graph Theory

• 1.II.17H

  Graph Theory | Part II, 2007

  Let $G$ be a connected cubic graph drawn in the plane with each edge in the boundary of two distinct faces. Show that the associated map is 4 -colourable if and only if $G$ is 3 -edge colourable.

  Is the above statement true if the plane is replaced by the torus and all faces are required to be simply connected? Give a proof or a counterexample.

  comment

Integrable Systems

• 1.II.31E

  Integrable Systems | Part II, 2007

  (i) Using the Cole-Hopf transformation

  $$u=-\frac{2 \nu}{\phi} \frac{\partial \phi}{\partial x}$$

  map the Burgers equation

  $$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^{2} u}{\partial x^{2}}$$

  to the heat equation

  $$\frac{\partial \phi}{\partial t}=\nu \frac{\partial^{2} \phi}{\partial x^{2}}$$

  (ii) Given that the solution of the heat equation on the infinite line $\mathbb{R}$ with initial condition $\phi(x, 0)=\Phi(x)$ is given by

  $$\phi(x, t)=\frac{1}{\sqrt{4 \pi \nu t}} \int_{-\infty}^{\infty} \Phi(\xi) e^{-\frac{(x-\xi)^{2}}{4 \nu t}} d \xi$$

  show that the solution of the analogous problem for the Burgers equation with initial condition $u(x, 0)=U(x)$ is given by

  $$u=\frac{\int_{-\infty}^{\infty} \frac{x-\xi}{t} e^{-\frac{1}{2 \nu} G(x, \xi, t)} d \xi}{\int_{-\infty}^{\infty} e^{-\frac{1}{2 \nu} G(x, \xi, t)} d \xi}$$

  where the function $G$ is to be determined in terms of $U$.

  (iii) Determine the ODE characterising the scaling reduction of the spherical modified Korteweg-de Vries equation

  $$\frac{\partial u}{\partial t}+6 u^{2} \frac{\partial u}{\partial x}+\frac{\partial^{3} u}{\partial x^{3}}+\frac{u}{t}=0$$

  comment

Linear Analysis

• 1.II.22G

  Linear Analysis | Part II, 2007

  Let $X$ be a normed vector space over $\mathbb{R}$. Define the dual space $X^{*}$ and show directly that $X^{*}$ is a Banach space. Show that the map $\phi: X \rightarrow X^{* *}$ defined by $\phi(x) v=v(x)$, for all $x \in X, v \in X^{*}$, is a linear map. Using the Hahn-Banach theorem, show that $\phi$ is injective and $|\phi(x)|=|x|$.

  Give an example of a Banach space $X$ for which $\phi$ is not surjective. Justify your answer.

  comment

Mathematical Biology

• 1.I.6B

  Mathematical Biology | Part II, 2007

  A chemostat is a well-mixed tank of given volume $V_{0}$ that contains water in which lives a population $N(t)$ of bacteria that consume nutrient whose concentration is $C(t)$ per unit volume. An inflow pipe supplies a solution of nutrient at concentration $C_{0}$ and at a constant flow rate of $Q$ units of volume per unit time. The mixture flows out at the same rate through an outflow pipe. The bacteria consume the nutrient at a rate $N K(C)$, where

  $$K(C)=\frac{K_{\max } C}{K_{0}+C}$$

  and the bacterial population grows at a rate $\gamma N K(C)$, where $0<\gamma<1$.

  Write down the differential equations for $N(t), C(t)$ and show that they can be rescaled into the following form:

  $$\begin{aligned} &\frac{d n}{d \tau}=\alpha \frac{c n}{1+c}-n \\ &\frac{d c}{d \tau}=-\frac{c n}{1+c}-c+\beta \end{aligned}$$

  where $\alpha, \beta$ are positive constants, to be found.

  Show that this system of equations has a non-trivial steady state if $\alpha>1$ and $\beta>\frac{1}{\alpha-1}$, and that it is stable.

  comment

Number Fields

• 1.II.20H

  Number Fields | Part II, 2007

  Let $K=\mathbb{Q}(\sqrt{-26})$.

  (a) Show that $\mathcal{O}_{K}=\mathbb{Z}[\sqrt{-26}]$ and that the discriminant $d_{K}$ is equal to $-104$.

  (b) Show that 2 ramifies in $\mathcal{O}_{K}$ by showing that $[2]=\mathfrak{p}_{2}^{2}$, and that $\mathfrak{p}_{2}$ is not a principal ideal. Show further that $[3]=\mathfrak{p}_{3} \overline{\mathfrak{p}}_{3}$ with $\mathfrak{p}_{3}=[3,1-\sqrt{-26}]$. Deduce that neither $\mathfrak{p}_{3}$ nor $\mathfrak{p}_{3}^{2}$ is a principal ideal, but $\mathfrak{p}_{3}^{3}=[1-\sqrt{-26}]$.

  (c) Show that 5 splits in $\mathcal{O}_{K}$ by showing that $[5]=\mathfrak{p}_{5} \overline{\mathfrak{p}}_{5}$, and that

  $$N_{K / \mathbb{Q}}(2+\sqrt{-26})=30$$

  Deduce that $\mathfrak{p}_{2} \mathfrak{p}_{3} \mathfrak{p}_{5}$ has trivial class in the ideal class group of $K$. Conclude that the ideal class group of $K$ is cyclic of order six.

  [You may use the fact that $\left.\frac{2}{\pi} \sqrt{104} \approx 6.492 .\right]$

  comment

Number Theory

• 1.I.1F

  Number Theory | Part II, 2007

  State the prime number theorem, and Bertrand's postulate.

  Let $S$ be a finite set of prime numbers, and write $f_{s}(x)$ for the number of positive integers no larger than $x$, all of whose prime factors belong to $S$. Prove that

  $$f_{s}(x) \leqslant 2^{\#(S)} \sqrt{x}$$

  where $\#(S)$ denotes the number of elements in $S$. Deduce that, if $x$ is a strictly positive integer, we have

  $$\pi(x) \geqslant \frac{\log x}{2 \log 2} .$$

  comment

Numerical Analysis

• 1.II.38C

  Numerical Analysis | Part II, 2007

  (a) For a numerical method to solve $y^{\prime}=f(t, y)$, define the linear stability domain and state when such a method is A-stable.

  (b) Determine all values of the real parameter $a$ for which the Runge-Kutta method

  $$\begin{aligned} k_{1} &=f\left(t_{n}+\left(\frac{1}{2}-a\right) h, y_{n}+h\left[\frac{1}{4} k_{1}+\left(\frac{1}{4}-a\right) k_{2}\right]\right) \\ k_{2} &=f\left(t_{n}+\left(\frac{1}{2}+a\right) h, y_{n}+h\left[\left(\frac{1}{4}+a\right) k_{1}+\frac{1}{4} k_{2}\right]\right) \\ y_{n+1} &=y_{n}+\frac{1}{2} h\left(k_{1}+k_{2}\right) \end{aligned}$$

  is A-stable.

  comment

Partial Differential Equations

• 1.II.29A

  Partial Differential Equations | Part II, 2007

  (i) Consider the problem of solving the equation

  $$\sum_{j=1}^{n} a_{j}(\mathbf{x}) \frac{\partial u}{\partial x_{j}}=b(\mathbf{x}, u)$$

  for a $C^{1}$ function $u=u(\mathbf{x})=u\left(x_{1}, \ldots, x_{n}\right)$, with data specified on a $C^{1}$ hypersurface $\mathcal{S} \subset \mathbb{R}^{n}$

  $$u(\mathbf{x})=\phi(\mathbf{x}), \quad \forall \mathbf{x} \in \mathcal{S}$$

  Assume that $a_{1}, \ldots, a_{n}, \phi, b$ are $C^{1}$ functions. Define the characteristic curves and explain what it means for the non-characteristic condition to hold at a point on $\mathcal{S}$. State a local existence and uniqueness theorem for the problem.

  (ii) Consider the case $n=2$ and the equation

  $$\frac{\partial u}{\partial x_{1}}-\frac{\partial u}{\partial x_{2}}=x_{2} u$$

  with data $u\left(x_{1}, 0\right)=\phi\left(x_{1}, 0\right)=f\left(x_{1}\right)$ specified on the axis $\left\{\mathbf{x} \in \mathbb{R}^{2}: x_{2}=0\right\}$. Obtain a formula for the solution.

  (iii) Consider next the case $n=2$ and the equation

  $$\frac{\partial u}{\partial x_{1}}-\frac{\partial u}{\partial x_{2}}=0$$

  with data $u(\mathbf{g}(s))=\phi(\mathbf{g}(s))=f(s)$ specified on the hypersurface $\mathcal{S}$, which is given parametrically as $\mathcal{S} \equiv\left\{\mathbf{x} \in \mathbb{R}^{2}: \mathbf{x}=\mathbf{g}(s)\right\}$ where $\mathbf{g}: \mathbb{R} \rightarrow \mathbb{R}^{2}$ is defined by

  $$\begin{aligned} &\mathbf{g}(s)=(s, 0), \quad s<0 \\ &\mathbf{g}(s)=\left(s, s^{2}\right), \quad s \geqslant 0 \end{aligned}$$

  Find the solution $u$ and show that it is a global solution. (Here "global" means $u$ is $C^{1}$ on all of $\mathbb{R}^{2}$.)

  (iv) Consider next the equation

  $$\frac{\partial u}{\partial x_{1}}+\frac{\partial u}{\partial x_{2}}=0$$

  to be solved with the same data given on the same hypersurface as in (iii). Explain, with reference to the characteristic curves, why there is generally no global $C^{1}$ solution. Discuss the existence of local solutions defined in some neighbourhood of a given point $\mathbf{y} \in \mathcal{S}$ for various $\mathbf{y}$. [You need not give formulae for the solutions.]

  comment

Principles of Quantum Mechanics

• 1.II.32D

  Principles of Quantum Mechanics | Part II, 2007

  A particle in one dimension has position and momentum operators $\hat{x}$ and $\hat{p}$ whose eigenstates obey

  $$\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right), \quad\langle x \mid p\rangle=(2 \pi \hbar)^{-1 / 2} e^{i x p / \hbar}$$

  Given a state $|\psi\rangle$, define the corresponding position-space and momentum-space wavefunctions $\psi(x)$ and $\tilde{\psi}(p)$ and show how each of these can be expressed in terms of the other. Derive the form taken in momentum space by the time-independent Schrödinger equation

  $$\left(\frac{\hat{p}^{2}}{2 m}+V(\hat{x})\right)|\psi\rangle=E|\psi\rangle$$

  for a general potential $V$.

  Now let $V(x)=-\left(\hbar^{2} \lambda / m\right) \delta(x)$ with $\lambda$ a positive constant. Show that the Schrödinger equation can be written

  $$\left(\frac{p^{2}}{2 m}-E\right) \tilde{\psi}(p)=\frac{\hbar \lambda}{2 \pi m} \int_{-\infty}^{\infty} d p^{\prime} \tilde{\psi}\left(p^{\prime}\right)$$

  and verify that it has a solution $\tilde{\psi}(p)=N /\left(p^{2}+\alpha^{2}\right)$ for unique choices of $\alpha$ and $E$, to be determined (you need not find the normalisation constant, $N$ ). Check that this momentum space wavefunction can also be obtained from the position space solution $\psi(x)=\sqrt{\lambda} e^{-\lambda|x|}$.

  comment

Principles of Statistics

• 1.II.27I

  Principles of Statistics | Part II, 2007

  Suppose that $X$ has density $f(\cdot \mid \theta)$ where $\theta \in \Theta$. What does it mean to say that statistic $T \equiv T(X)$ is sufficient for $\theta$ ?

  Suppose that $\theta=(\psi, \lambda)$, where $\psi$ is the parameter of interest, and $\lambda$ is a nuisance parameter, and that the sufficient statistic $T$ has the form $T=(C, S)$. What does it mean to say that the statistic $S$ is ancillary? If it is, how (according to the conditionality principle) do we test hypotheses on $\psi ?$ Assuming that the set of possible values for $X$ is discrete, show that $S$ is ancillary if and only if the density (probability mass function) $f(x \mid \psi, \lambda)$ factorises as

  $$f(x \mid \psi, \lambda)=\varphi_{0}(x) \varphi_{C}(C(x), S(x), \psi) \varphi_{S}(S(x), \lambda)$$

  for some functions $\varphi_{0}, \varphi_{C}$, and $\varphi_{S}$ with the properties

  $$\sum_{x \in C^{-1}(c) \cap S^{-1}(s)} \varphi_{0}(x)=1=\sum_{s} \varphi_{S}(s, \lambda)=\sum_{s} \sum_{c} \varphi_{C}(c, s, \psi)$$

  for all $c, s, \psi$, and $\lambda$.

  Suppose now that $X_{1}, \ldots, X_{n}$ are independent observations from a $\Gamma(a, b)$ distribution, with density

  $$f(x \mid a, b)=(b x)^{a-1} e^{-b x} b I_{\{x>0\}} / \Gamma(a) .$$

  Assuming that the criterion (*) holds also for observations which are not discrete, show that it is not possible to find $(C(X), S(X))$ sufficient for $(a, b)$ such that $S$ is ancillary when $b$ is regarded as a nuisance parameter, and $a$ is the parameter of interest.

  comment

Probability and Measure

• 1.II.25J

  Probability and Measure | Part II, 2007

  Let $E$ be a set and $\mathcal{E} \subseteq \mathcal{P}(E)$ be a set system.

  (a) Explain what is meant by a $\pi$-system, a $d$-system and a $\sigma$-algebra.

  (b) Show that $\mathcal{E}$ is a $\sigma$-algebra if and only if $\mathcal{E}$ is a $\pi$-system and a $d$-system.

  (c) Which of the following set systems $\mathcal{E}_{1}, \mathcal{E}_{2}, \mathcal{E}_{3}$ are $\pi$-systems, $d$-systems or $\sigma$-algebras? Justify your answers. ( $\#(A)$ denotes the number of elements in $A$.)

  $E_{1}=\{1,2, \ldots, 10\}$ and $\mathcal{E}_{1}=\left\{A \subseteq E_{1}: \#(A)\right.$ is even $\}$,

  $E_{2}=\mathbb{N}=\{1,2, \ldots\}$ and $\mathcal{E}_{2}=\left\{A \subseteq E_{2}: \#(A)\right.$ is even or $\left.\#(A)=\infty\right\}$,

  $E_{3}=\mathbb{R}$ and $\mathcal{E}_{3}=\{(a, b): a, b \in \mathbb{R}, a<b\} \cup\{\emptyset\} .$

  (d) State and prove the theorem on the uniqueness of extension of a measure.

  [You may use standard results from the lectures without proof, provided they are clearly stated.]

  comment

Representation Theory

• 1.II.19H

  Representation Theory | Part II, 2007

  A finite group $G$ has seven conjugacy classes $C_{1}=\{e\}, C_{2}, \ldots, C_{7}$ and the values of five of its irreducible characters are given in the following table.

  $\begin{array}{rrrrrrr}C_{1} & C_{2} & C_{3} & C_{4} & C_{5} & C_{6} & C_{7} \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 \\ 4 & 0 & 1 & -1 & 2 & -1 & 0 \\ 4 & 0 & 1 & -1 & -2 & 1 & 0 \\ 5 & 1 & -1 & 0 & 1 & 1 & -1\end{array}$

  Calculate the number of elements in the various conjugacy classes and complete the character table.

  [You may not identify $G$ with any known group, unless you justify doing so.]

  comment

Riemann Surfaces

• 1.II.23F

  Riemann Surfaces | Part II, 2007

  Define a complex structure on the unit sphere $S^{2} \subset \mathbb{R}^{3}$ using stereographic projection charts $\varphi, \psi$. Let $U \subset \mathbb{C}$ be an open set. Show that a continuous non-constant map $F: U \rightarrow S^{2}$ is holomorphic if and only if $\varphi \circ F$ is a meromorphic function. Deduce that a non-constant rational function determines a holomorphic map $S^{2} \rightarrow S^{2}$. Define what is meant by a rational function taking the value $a \in \mathbb{C} \cup\{\infty\}$ with multiplicity $m$ at infinity.

  Define the degree of a rational function. Show that any rational function $f$ satisfies $(\operatorname{deg} f)-1 \leqslant \operatorname{deg} f^{\prime} \leqslant 2 \operatorname{deg} f$ and give examples to show that the bounds are attained. Is it true that the product $f . g$ satisfies $\operatorname{deg}(f . g)=\operatorname{deg} f+\operatorname{deg} g$, for any non-constant rational functions $f$ and $g$ ? Justify your answer.

  comment

Set Theory and Logic

• 1.II.16G

  Set Theory and Logic | Part II, 2007

  By a directed set in a poset $(P, \leqslant)$, we mean a nonempty subset $D$ such that any pair $\{x, y\}$ of elements of $D$ has an upper bound in $D$. We say $(P, \leqslant)$ is directed-complete if each directed subset $D \subseteq P$ has a least upper bound in $P$. Show that a poset is complete if and only if it is directed-complete and has joins for all its finite subsets. Show also that, for any two sets $A$ and $B$, the set $[A>B]$ of partial functions from $A$ to $B$, ordered by extension, is directed-complete.

  Let $(P, \leqslant)$ be a directed-complete poset, and $f: P \rightarrow P$ an order-preserving map which is inflationary, i.e. satisfies $x \leqslant f(x)$ for all $x \in P$. We define a subset $C \subseteq P$ to be closed if it satisfies $(x \in C) \rightarrow(f(x) \in C)$, and is also closed under joins of directed sets (i.e., $D \subseteq C$ and $D$ directed imply $\bigvee D \in C$ ). We write $x \ll y$ to mean that every closed set containing $x$ also contains $y$. Show that $\ll$ is a partial order on $P$, and that $x \ll y$ implies $x \leqslant y$. Now consider the set $H$ of all functions $h: P \rightarrow P$ which are order-preserving and satisfy $x \ll h(x)$ for all $x$. Show that $H$ is closed under composition of functions, and deduce that, for each $x \in P$, the set $H_{x}=\{h(x) \mid h \in H\}$ is directed. Defining $h_{0}(x)=V H_{x}$ for each $x$, show that the function $h_{0}$ belongs to $H$, and deduce that $h_{0}(x)$ is the least fixed point of $f$ lying above $x$, for each $x \in P$.

  comment

Statistical Modelling

• 1.I.5I

  Statistical Modelling | Part II, 2007

  According to the Independent newspaper (London, 8 March 1994) the Metropolitan Police in London reported 30475 people as missing in the year ending March 1993. For those aged 18 or less, 96 of 10527 missing males and 146 of 11363 missing females were still missing a year later. For those aged 19 and above, the values were 157 of 5065 males and 159 of 3520 females. This data is summarised in the table below.

  \begin{array}{rrrrr} & \multicolumn{3}{r}{\text { age }} \\ 1 & \text { Kender } & \text { M } & 96 & 10527 \\ 2 & \text { Kid } & \text { F } & 146 & 11363 \\ 3 & \text { Adult } & \text { M } & 157 & 5065 \\ 4 & \text { Adult } & \text { F } & 159 & 3520 \end{array}

  Explain and interpret the $\mathrm{R}$ commands and (slightly abbreviated) output below. You should describe the model being fitted, explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary. In particular, what is the worst of the four categories for the probability of remaining missing a year later?

  

  For a person who was missing in the year ending in March 1993, find a formula, as a function of age and gender, for the estimated expected probability that they are still missing a year later.

  comment

• 1.II.13I

  Statistical Modelling | Part II, 2007

  This problem deals with data collected as the number of each of two different strains of Ceriodaphnia organisms are counted in a controlled environment in which reproduction is occurring among the organisms. The experimenter places into the containers a varying concentration of a particular component of jet fuel that impairs reproduction. Hence it is anticipated that as the concentration of jet fuel grows, the mean number of organisms should decrease.

  The table below gives a subset of the data. The full dataset has $n=70$ rows. The first column provides the number of organisms, the second the concentration of jet fuel (in grams per litre) and the third specifies the strain of the organism.

  $$\begin{array}{lll} \text { number fuel } & \text { strain } \\ 82 & 0 & 1 \\ 58 & 0 & 0 \\ 45 & 0.5 & 1 \\ 27 & 0.5 & 0 \\ 29 & 0.75 & 1 \\ 15 & 1.25 & 1 \\ 6 & 1.25 & 1 \\ 8 & 1.5 & 0 \\ 4 & 1.75 & 0 \\ . & . & . \end{array}$$

  Explain and interpret the $R$ commands and (slightly abbreviated) output below. In particular, you should describe the model being fitted, explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary.

  

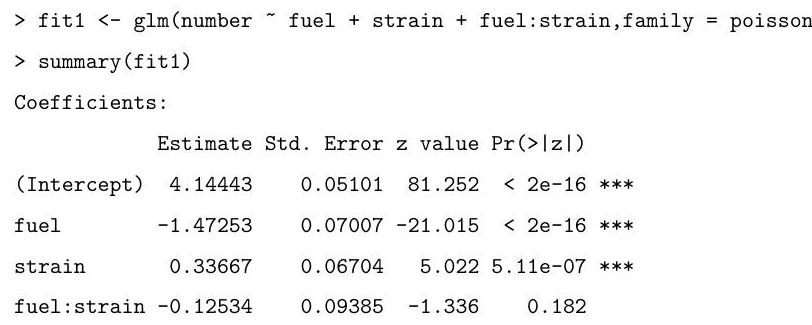
  The following $\mathrm{R}$ code fits two very similar models. Briefly explain the difference between these models and the one above. Motivate the fitting of these models in light of

  Part II 2007 the summary from the fit of the one above.

  

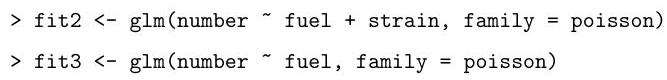
  Denote by $H_{1}, H_{2}, H_{3}$ the three hypotheses being fitted in sequence above.

  Explain the hypothesis tests, including an approximate test of the fit of $H_{1}$, that can be performed using the output from the following $\mathrm{R}$ code. Use these numbers to comment on the most appropriate model for the data.

  $>c(f i t 1 \$ d e v$, fit2$dev, fit3$dev)

  [1] $84.59557 \quad 86.37646118 .99503$

  $>\operatorname{qchisq}(0.95, \mathrm{df}=1)$

  [1] $3.841459$

  comment

Stochastic Financial Models

• 1.II.28J

  Stochastic Financial Models | Part II, 2007

  (i) What does it mean to say that a process $\left(M_{t}\right)_{t \geqslant 0}$ is a martingale? What does the martingale convergence theorem tell us when applied to positive martingales?

  (ii) What does it mean to say that a process $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion? Show that $\sup _{t \geqslant 0} B_{t}=\infty$ with probability one.

  (iii) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion. Find $\mu$ such that

  $$S_{t}=\exp \left(x_{0}+\sigma B_{t}+\mu t\right)$$

  is a martingale. Discuss the limiting behaviour of $S_{t}$ and $\mathbb{E}\left(S_{t}\right)$ for this $\mu$ as $t \rightarrow \infty$.

  comment

Topics in Analysis

• 1.I.2F

  Topics in Analysis | Part II, 2007

  Let $n$ be an integer with $n \geqslant 1$. Are the following statements true or false? Give proofs.

  (i) There exists a real polynomial $T_{n}$ of degree $n$ such that

  $$T_{n}(\cos t)=\cos n t$$

  for all real $t$.

  (ii) There exists a real polynomial $R_{n}$ of degree $n$ such that

  $$R_{n}(\cosh t)=\cosh n t$$

  for all real $t$.

  (iii) There exists a real polynomial $S_{n}$ of degree $n$ such that

  $$S_{n}(\cos t)=\sin n t$$

  for all real $t$.

  comment

Waves

• 1.II.37C

  Waves | Part II, 2007

  A uniform elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ occupies the region between rigid plane boundaries $y=0$ and $y=h$. Show that SH waves can propagate in the $x$ direction within this layer, and find the dispersion relation for such waves.

  Deduce for each mode (a) the cutoff frequency, (b) the phase velocity, and (c) the group velocity.

  Show also that for each mode the kinetic energy and elastic energy are equal in an average sense to be made precise.

  [You may assume that the elastic energy per unit volume $W=\frac{1}{2}\left(\lambda e_{k k}^{2}+2 \mu e_{i j} e_{i j}\right)$.]

  comment