Part II, 2006, Paper 1

Algebraic Topology

• 1.II.21H

  Algebraic Topology | Part II, 2006

  Compute the homology groups of the "pinched torus" obtained by identifying a meridian circle $S^{1} \times\{p\}$ on the torus $S^{1} \times S^{1}$ to a point, for some point $p \in S^{1}$.

  comment

Applications of Quantum Mechanics

• 1.II.33A

  Applications of Quantum Mechanics | Part II, 2006

  Consider a particle of mass $m$ and momentum $\hbar k$ moving under the influence of a spherically symmetric potential $V(r)$ such that $V(r)=0$ for $r \geqslant a$. Define the scattering amplitude $f(\theta)$ and the phase shift $\delta_{\ell}(k)$. Here $\theta$ is the scattering angle. How is $f(\theta)$ related to the differential cross section?

  Obtain the partial-wave expansion

  $$f(\theta)=\frac{1}{k} \sum_{\ell=0}^{\infty}(2 \ell+1) e^{i \delta_{\ell}} \sin \delta_{\ell} P_{\ell}(\cos \theta) .$$

  Let $R_{\ell}(r)$ be a solution of the radial Schrödinger equation, regular at $r=0$, for energy $\hbar^{2} k^{2} / 2 m$ and angular momentum $\ell$. Let

  $$Q_{\ell}(k)=a \frac{R_{\ell}^{\prime}(a)}{R_{\ell}(a)}-k a \frac{j_{\ell}^{\prime}(k a)}{j_{\ell}(k a)}$$

  Obtain the relation

  $$\tan \delta_{\ell}=\frac{Q_{\ell}(k) j_{\ell}^{2}(k a) k a}{Q_{\ell}(k) n_{\ell}(k a) j_{\ell}(k a) k a-1} .$$

  Suppose that

  $$\tan \delta_{\ell} \approx \frac{\gamma}{k_{0}-k},$$

  for some $\ell$, with all other $\delta_{\ell}$ small for $k \approx k_{0}$. What does this imply for the differential cross section when $k \approx k_{0}$ ?

  [For $V=0$, the two independent solutions of the radial Schrödinger equation are $j_{\ell}(k r)$ and $n_{\ell}(k r)$ with

  $$\begin{aligned} j_{\ell}(\rho) & \sim \frac{1}{\rho} \sin \left(\rho-\frac{1}{2} \ell \pi\right), \quad n_{\ell}(\rho) \sim-\frac{1}{\rho} \cos \left(\rho-\frac{1}{2} \ell \pi\right) \quad \text { as } \quad \rho \rightarrow \infty \\ e^{i \rho \cos \theta} &=\sum_{\ell=0}^{\infty}(2 \ell+1) i^{\ell} j_{\ell}(\rho) P_{\ell}(\cos \theta) \end{aligned}$$

  Note that the Wronskian $\rho^{2}\left(j_{\ell}(\rho) n_{\ell}^{\prime}(\rho)-j_{\ell}^{\prime}(\rho) n_{\ell}(\rho)\right)$ is independent of $\left.\rho .\right]$

  comment

Applied Probability

• 1.II.26J

  Applied Probability | Part II, 2006

  (a) What is a $Q$-matrix? What is the relationship between the transition matrix $P(t)$ of a continuous time Markov process and its generator $Q$ ?

  (b) A pond has three lily pads, labelled 1, 2, and 3. The pond is also the home of a frog that hops from pad to pad in a random fashion. The position of the frog is a continuous time Markov process on $\{1,2,3\}$ with generator

  $$Q=\left(\begin{array}{ccc} -1 & 1 & 0 \\ 1 & -2 & 1 \\ 1 & 0 & -1 \end{array}\right)$$

  Sketch an arrow diagram corresponding to $Q$ and determine the communicating classes. Find the probability that the frog is on pad 2 in equilibrium. Find the probability that the frog is on pad 2 at time $t$ given that the frog is on pad 1 at time 0 .

  comment

Asymptotic Methods

• 1.II $. 30 \mathrm{~B}$

  Asymptotic Methods | Part II, 2006

  Two real functions $p(t), q(t)$ of a real variable $t$ are given on an interval $[0, b]$, where $b>0$. Suppose that $q(t)$ attains its minimum precisely at $t=0$, with $q^{\prime}(0)=0$, and that $q^{\prime \prime}(0)>0$. For a real argument $x$, define

  $$I(x)=\int_{0}^{b} p(t) e^{-x q(t)} d t$$

  Explain how to obtain the leading asymptotic behaviour of $I(x)$ as $x \rightarrow+\infty$ (Laplace's method).

  The modified Bessel function $I_{\nu}(x)$ is defined for $x>0$ by:

  $$I_{\nu}(x)=\frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} \cos (\nu \theta) d \theta-\frac{\sin (\nu \pi)}{\pi} \int_{0}^{\infty} e^{-x(\cosh t)-\nu t} d t .$$

  Show that

  $$I_{\nu}(x) \sim \frac{e^{x}}{\sqrt{2 \pi x}}$$

  as $x \rightarrow \infty$ with $\nu$ fixed.

  comment

Classical Dynamics

• 1.I.9C

  Classical Dynamics | Part II, 2006

  Hamilton's equations for a system with $n$ degrees of freedom can be written in vector form as

  $$\dot{\mathbf{x}}=J \frac{\partial H}{\partial \mathbf{x}}$$

  where $\mathbf{x}=\left(q_{1}, \ldots, q_{n}, p_{1}, \ldots, p_{n}\right)^{T}$ is a $2 n$-vector and the $2 n \times 2 n$ matrix $J$ takes the form

  $$J=\left(\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right)$$

  where 1 is the $n \times n$ identity matrix. Derive the condition for a transformation of the form $x_{i} \rightarrow y_{i}(\mathbf{x})$ to be canonical. For a system with a single degree of freedom, show that the following transformation is canonical for all nonzero values of $\alpha$ :

  $$Q=\tan ^{-1}\left(\frac{\alpha q}{p}\right), \quad P=\frac{1}{2}\left(\alpha q^{2}+\frac{p^{2}}{\alpha}\right)$$

  comment

• 1.II.15C

  Classical Dynamics | Part II, 2006

  (a) In the Hamiltonian framework, the action is defined as

  $$S=\int\left(p_{a} \dot{q}_{a}-H\left(q_{a}, p_{a}, t\right)\right) d t$$

  Derive Hamilton's equations from the principle of least action. Briefly explain how the functional variations in this derivation differ from those in the derivation of Lagrange's equations from the principle of least action. Show that $H$ is a constant of the motion whenever $\partial H / \partial t=0$.

  (b) What is the invariant quantity arising in Liouville's theorem? Does the theorem depend on assuming $\partial H / \partial t=0$ ? State and prove Liouville's theorem for a system with a single degree of freedom.

  (c) A particle of mass $m$ bounces elastically along a perpendicular between two parallel walls a distance $b$ apart. Sketch the path of a single cycle in phase space, assuming that the velocity changes discontinuously at the wall. Compute the action $I=\oint p d q$ as a function of the energy $E$ and the constants $m, b$. Verify that the period of oscillation $T$ is given by $T=d I / d E$. Suppose now that the distance $b$ changes slowly. What is the relevant adiabatic invariant? How does $E$ change as a function of $b$ ?

  comment

Coding and Cryptography

• 1.I.4G

  Coding and Cryptography | Part II, 2006

  Define a linear feedback shift register. Explain the Berlekamp-Massey method for "breaking" a key stream produced by a linear feedback shift register of unknown length. Use it to find the feedback polynomial of a linear feedback shift register with output sequence

  $$010111100010 \ldots$$

  comment

Cosmology

• 1.I.10D

  Cosmology | Part II, 2006

  (a) Introduce the concept of comoving co-ordinates in a homogeneous and isotropic universe and explain how the velocity of a galaxy is determined by the scale factor $a$. Express the Hubble parameter $H_{0}$ today in terms of the scale factor.

  (b) The Raychaudhuri equation states that the acceleration of the universe is determined by the mass density $\rho$ and the pressure $P$ as

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  Now assume that the matter constituents of the universe satisfy $\rho+3 P / c^{2} \geqslant 0$. In this case explain clearly why the Hubble time $H_{0}^{-1}$ sets an upper limit on the age of the universe; equivalently, that the scale factor must vanish $\left(a\left(t_{i}\right)=0\right)$ at some time $t_{i}<t_{0}$ with $t_{0}-t_{i} \leqslant H_{0}^{-1}$.

  The observed Hubble time is $H_{0}^{-1}=1 \times 10^{10}$ years. Discuss two reasons why the above upper limit does not seem to apply to our universe.

  comment

Differential Geometry

• 1.II.24H

  Differential Geometry | Part II, 2006

  (a) State and prove the inverse function theorem for a smooth map $f: X \rightarrow Y$ between manifolds without boundary.

  [You may assume the inverse function theorem for functions in Euclidean space.]

  (b) Let $p$ be a real polynomial in $k$ variables such that for some integer $m \geqslant 1$,

  $$p\left(t x_{1}, \ldots, t x_{k}\right)=t^{m} p\left(x_{1}, \ldots, x_{k}\right)$$

  for all real $t>0$ and all $y=\left(x_{1}, \ldots, x_{k}\right) \in \mathbb{R}^{k}$. Prove that the set $X_{a}$ of points $y$ where $p(y)=a$ is a $(k-1)$-dimensional submanifold of $\mathbb{R}^{k}$, provided it is not empty and $a \neq 0$.

  [You may use the pre-image theorem provided that it is clearly stated.]

  (c) Show that the manifolds $X_{a}$ with $a>0$ are all diffeomorphic. Is $X_{a}$ with $a>0$ necessarily diffeomorphic to $X_{b}$ with $b<0$ ?

  comment

Dynamical Systems

• 1.I.7E

  Dynamical Systems | Part II, 2006

  Find the fixed points of the system

  $$\begin{aligned} &\dot{x}=x(x+2 y-3) \\ &\dot{y}=y(3-2 x-y) \end{aligned}$$

  Local linearization shows that all the fixed points with $x y=0$ are saddle points. Why can you be certain that this remains true when nonlinear terms are taken into account? Classify the fixed point with $x y \neq 0$ by its local linearization. Show that the equation has Hamiltonian form, and thus that your classification is correct even when the nonlinear effects are included.

  Sketch the phase plane.

  comment

• 1.II.14E

  Dynamical Systems | Part II, 2006

  (a) An autonomous dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$ has a periodic orbit $\mathbf{x}=\mathbf{X}(t)$ with period $T$. The linearized evolution of a small perturbation $\mathbf{x}=\mathbf{X}(t)+\boldsymbol{\eta}(t)$ is given by $\eta_{i}(t)=\Phi_{i j}(t) \eta_{j}(0)$. Obtain the differential equation and initial condition satisfied by the matrix $\boldsymbol{\Phi}(t)$.

  Define the Floquet multipliers of the orbit. Explain why one of the multipliers is always unity and show that the other is given by

  $$\exp \left(\int_{0}^{T} \nabla \cdot \mathbf{f}(\mathbf{X}(t)) d t\right)$$

  (b) Use the 'energy-balance' method for nearly Hamiltonian systems to find a leadingorder approximation to the amplitude of the limit cycle of the equation

  $$\ddot{x}+\epsilon\left(\alpha x^{2}+\beta \dot{x}^{2}-\gamma\right) \dot{x}+x=0,$$

  where $0<\epsilon \ll 1$ and $(\alpha+3 \beta) \gamma>0$.

  Compute a leading-order approximation to the nontrivial Floquet multiplier of the limit cycle and hence determine its stability.

  [You may assume that $\int_{0}^{2 \pi} \sin ^{2} \theta \cos ^{2} \theta d \theta=\pi / 4$ and $\int_{0}^{2 \pi} \cos ^{4} \theta d \theta=3 \pi / 4$.]

  comment

Electrodynamics

• 1.II $. 34 \mathrm{E} \quad$

  Electrodynamics | Part II, 2006

  $\mathcal{S}$ and $\mathcal{S}^{\prime}$ are two reference frames with $\mathcal{S}^{\prime}$ moving with constant speed $v$ in the $x$-direction relative to $\mathcal{S}$. The co-ordinates $x^{a}$ and ${x^{\prime}}^{a}$ are related by $d x^{\prime a}=L^{a}{ }_{b} d x^{b}$ where

  $$L_{b}^{a}=\left(\begin{array}{cccc} \gamma & -\gamma v & 0 & 0 \\ -\gamma v & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  and $\gamma=\left(1-v^{2}\right)^{-1 / 2}$. What is the transformation rule for the scalar potential $\varphi$ and vector potential A between the two frames?

  As seen in $\mathcal{S}^{\prime}$ there is an infinite uniform stationary distribution of charge along the $x$-axis with uniform line density $\sigma$. Determine the electric and magnetic fields $\mathbf{E}$ and B both in $\mathcal{S}^{\prime}$ and $\mathcal{S}$. Check your answer by verifying explicitly the invariance of the two quadratic Lorentz invariants.

  Comment briefly on the limit $|v| \ll 1$.

  comment

Fluid Dynamics II

• 1.II.36B

  Fluid Dynamics II | Part II, 2006

  Write down the boundary conditions that are satisfied at the interface between two viscous fluids in motion. Briefly discuss the physical meaning of these boundary conditions.

  A layer of incompressible fluid of density $\rho$ and viscosity $\mu$ flows steadily down a plane inclined at an angle $\theta$ to the horizontal. The layer is of uniform thickness $h$ measured perpendicular to the plane and the viscosity of the overlying air can be neglected. Using co-ordinates parallel and perpendicular to the plane, write down the equations of motion, and the boundary conditions on the plane and on the free top surface. Determine the pressure and velocity fields. Show that the volume flux down the plane is $\frac{1}{3} \rho g h^{3} \sin \theta / \mu$ per unit cross-slope width.

  Consider now the case where a second layer of fluid, of uniform thickness $\alpha h$, viscosity $\beta \mu$, and density $\rho$ flows steadily on top of the first layer. Determine the pressure and velocity fields in each layer. Why does the velocity profile in the bottom layer depend on $\alpha$ but not on $\beta$ ?

  comment

Further Complex Methods

• 1.I.8E

  Further Complex Methods | Part II, 2006

  The function $f(t)$ satisfies $f(t)=0$ for $t<1$ and

  $$f(t+1)-\frac{1}{2} f(t)=H(t),$$

  where $H(t)$ is the Heaviside step function. By taking Laplace transforms, show that, for $t \geqslant 1$,

  $$f(t)=2+2^{1-t} \sum_{n=-\infty}^{\infty} \frac{e^{2 \pi n i t}}{2 \pi n i-\log 2}$$

  and verify directly from the inversion integral that your solution satisfies $f(t)=0$ for $t<1$.

  comment

Galois Theory

• 1.II.18H

  Galois Theory | Part II, 2006

  Let $K$ be a field and $f$ a separable polynomial over $K$ of degree $n$. Explain what is meant by the Galois group $G$ of $f$ over $K$. Show that $G$ is a transitive subgroup of $S_{n}$ if and only if $f$ is irreducible. Deduce that if $n$ is prime, then $f$ is irreducible if and only if $G$ contains an $n$-cycle.

  Let $f$ be a polynomial with integer coefficients, and $p$ a prime such that $\bar{f}$, the reduction of $f$ modulo $p$, is separable. State a theorem relating the Galois group of $f$ over $\mathbb{Q}$ to that of $\bar{f}$ over $\mathbb{F}_{p}$.

  Determine the Galois group of the polynomial $x^{5}-15 x-3$ over $\mathbb{Q}$.

  comment

General Relativity

• 1.II.35A

  General Relativity | Part II, 2006

  Let $\phi(x)$ be a scalar field and $\nabla_{a}$ denote the Levi-Civita covariant derivative operator of a metric tensor $g_{a b}$. Show that

  $$\nabla_{a} \nabla_{b} \phi=\nabla_{b} \nabla_{a} \phi$$

  If the Ricci tensor, $R_{a b}$, of the metric $g_{a b}$ satisfies

  $$R_{a b}=\partial_{a} \phi \partial_{b} \phi,$$

  find the energy momentum tensor $T_{a b}$ and use the contracted Bianchi identity to show that, if $\partial_{a} \phi \neq 0$, then

  $$\nabla_{a} \nabla^{a} \phi=0$$

  Show further that $(*)$ implies

  $$\partial_{a}\left(\sqrt{-g} g^{a b} \partial_{b} \phi\right)=0$$

  comment

Geometry and Groups

• 1.I $. 3 \mathrm{~F} \quad$

  Geometry and Groups | Part II, 2006

  Suppose $S_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is a similarity with contraction factor $c_{i} \in(0,1)$ for $1 \leqslant i \leqslant k$. Let $X$ be the unique non-empty compact invariant set for the $S_{i}$ 's. State a formula for the Hausdorff dimension of $X$, under an assumption on the $S_{i}$ 's you should state. Hence compute the Hausdorff dimension of the subset $X$ of the square $[0,1]^{2}$ defined by dividing the square into a $5 \times 5$ array of squares, removing the open middle square $(2 / 5,3 / 5)^{2}$, then removing the middle $1 / 25$ th of each of the remaining 24 squares, and so on.

  comment

• 1.II.12F

  Geometry and Groups | Part II, 2006

  Compute the area of the ball of radius $r$ around a point in the hyperbolic plane. Deduce that, for any tessellation of the hyperbolic plane by congruent, compact tiles, the number of tiles which are at most $n$ "steps" away from a given tile grows exponentially in $n$. Give an explicit example of a tessellation of the hyperbolic plane.

  comment

Graph Theory

• 1.II .17F

  Graph Theory | Part II, 2006

  State and prove Euler's formula relating the number of vertices, edges and faces of a connected plane graph

  Deduce that a planar graph of order $n \geqslant 3$ has size at most $3 n-6$. What bound can be given if the planar graph contains no triangles?

  Without invoking the four colour theorem, prove that a planar graph that contains no triangles is 4-colourable.

  comment

Integrable Systems

• 1.II.31E

  Integrable Systems | Part II, 2006

  (a) Let $q(x, t)$ satisfy the heat equation

  $$\frac{\partial q}{\partial t}=\frac{\partial^{2} q}{\partial x^{2}}$$

  Find the function $X$, which depends linearly on $\partial q / \partial x, q, k$, such that the heat equation can be written in the form

  $$\frac{\partial}{\partial t}\left(e^{-i k x+k^{2} t} q\right)+\frac{\partial}{\partial x}\left(e^{-i k x+k^{2} t} X\right)=0, \quad k \in \mathbb{C} .$$

  Use this equation to construct a Lax pair for the heat equation.

  (b) Use the above result, as well as the Cole-Hopf transformation, to construct a Lax pair for the Burgers equation

  $$\frac{\partial Q}{\partial t}-2 Q \frac{\partial Q}{\partial x}=\frac{\partial^{2} Q}{\partial x^{2}}$$

  (c) Find the second-order ordinary differential equation satisfied by the similarity solution of the so-called cylindrical $\mathrm{KdV}$ equation:

  $$\frac{\partial q}{\partial t}+\frac{\partial^{3} q}{\partial x^{3}}+q \frac{\partial q}{\partial x}+\frac{q}{3 t}=0, \quad t \neq 0$$

  comment

Linear Analysis

• 1.II.22G

  Linear Analysis | Part II, 2006

  Let $U$ be a vector space. Define what it means for two norms $\|\cdot\|_{1}$ and $\left\|_{\cdot} \cdot\right\|_{2}$ on $U$ to be Lipschitz equivalent. Give an example of a vector space and two norms which are not Lipschitz equivalent.

  Show that, if $U$ is finite dimensional, all norms on $U$ are Lipschitz equivalent. Deduce that a finite dimensional subspace of a normed vector space is closed.

  Show that a normed vector space $W$ is finite dimensional if and only if $W$ contains a non-empty open set with compact closure.

  comment

Logic and Set Theory

• 1.II.16H

  Logic and Set Theory | Part II, 2006

  Explain what it means for a poset to be chain-complete. State Zorn's Lemma, and use it to prove that, for any two elements $a$ and $b$ of a distributive lattice $L$ with $b \not{\leftarrow} a$, there exists a lattice homomorphism $f: L \rightarrow\{0,1\}$ with $f(a)=0$ and $f(b)=1$. Explain briefly how this result implies the completeness theorem for propositional logic.

  comment

Mathematical Biology

• 1.I.6B

  Mathematical Biology | Part II, 2006

  A large population of some species has probability $P(n, t)$ of taking the value $n$ at time $t$. Explain the use of the generating function $\phi(s, t)=\sum_{n=0}^{\infty} s^{n} P(n, t)$, and give expressions for $P(n, t)$ and $\langle n\rangle$ in terms of $\phi$.

  A particular population is subject to a birth-death process, so that the probability of an increase from $n$ to $n+1$ in unit time is $\alpha+\beta n$, while the probability of a decrease from $n$ to $n-1$ is $\gamma n$, with $\gamma>\beta$. Show that the master equation for $P(n, t)$ is

  $$\frac{\partial P(n, t)}{\partial t}=(\alpha+\beta(n-1)) P(n-1, t)+\gamma(n+1) P(n+1, t)-(\alpha+(\beta+\gamma) n) P(n, t)$$

  Derive the equation satisfied by $\phi$, and show that in the statistically steady state, when $\phi$ and $P$ are independent of time, $\phi$ takes the form

  $$\phi(s)=\left(\frac{\gamma-\beta}{\gamma-\beta s}\right)^{\alpha / \beta}$$

  Using the equation for $\phi$, or otherwise, find $\langle n\rangle$.

  comment

Number Fields

• 1.II.20G

  Number Fields | Part II, 2006

  Let $\alpha, \beta, \gamma$ denote the zeros of the polynomial $x^{3}-n x-1$, where $n$ is an integer. The discriminant of the polynomial is defined as

  $$\Delta=\Delta\left(1, \alpha, \alpha^{2}\right)=(\alpha-\beta)^{2}(\beta-\gamma)^{2}(\gamma-\alpha)^{2}$$

  Prove that, if $\Delta$ is square-free, then $1, \alpha, \alpha^{2}$ is an integral basis for $k=\mathbb{Q}(\alpha)$.

  By verifying that

  $$\alpha(\alpha-\beta)(\alpha-\gamma)=2 n \alpha+3$$

  and further that the field norm of the expression on the left is $-\Delta$, or otherwise, show that $\Delta=4 n^{3}-27$. Hence prove that, when $n=1$ and $n=2$, an integral basis for $k$ is $1, \alpha, \alpha^{2}$.

  comment

Number Theory

• 1.I.1H

  Number Theory | Part II, 2006

  State the theorem of the primitive root for an odd prime power modulus.

  Prove that 3 is a primitive root modulo $7^{n}$ for all integers $n \geqslant 1$. Is 2 a primitive root modulo $7^{n}$ for all integers $n \geqslant 1$ ?

  Prove that there is no primitive root modulo 8 .

  comment

Numerical Analysis

• 1.II.38C

  Numerical Analysis | Part II, 2006

  (a) Define the Jacobi method with relaxation for solving the linear system $A x=b$.

  (b) Let $A$ be a symmetric positive definite matrix with diagonal part $D$ such that the matrix $2 D-A$ is also positive definite. Prove that the iteration always converges if the relaxation parameter $\omega$ is equal to 1 .

  (c) Let $A$ be the tridiagonal matrix with diagonal elements $a_{i i}=1$ and off-diagonal elements $a_{i+1, i}=a_{i, i+1}=1 / 4$. Prove that convergence occurs if $\omega$ satisfies $0<\omega \leqslant 4 / 3$. Explain briefly why the choice $\omega=1$ is optimal.

  [You may quote without proof any relevant result about the convergence of iterative methods and about the eigenvalues of matrices.]

  comment

Partial Differential Equations

• 1.II.29A

  Partial Differential Equations | Part II, 2006

  (a) State a local existence theorem for solving first order quasi-linear partial differential equations with data specified on a smooth hypersurface.

  (b) Solve the equation

  $$\frac{\partial u}{\partial x}+x \frac{\partial u}{\partial y}=0$$

  with boundary condition $u(x, 0)=f(x)$ where $f \in C^{1}(\mathbb{R})$, making clear the domain on which your solution is $C^{1}$. Comment on this domain with reference to the noncharacteristic condition for an initial hypersurface (including a definition of this concept).

  (c) Solve the equation

  $$u^{2} \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0$$

  with boundary condition $u(x, 0)=x$ and show that your solution is $C^{1}$ on some open set containing the initial hypersurface $y=0$. Comment on the significance of this, again with reference to the non-characteristic condition.

  comment

Principles of Quantum Mechanics

• 1.II.32D

  Principles of Quantum Mechanics | Part II, 2006

  A particle in one dimension has position and momentum operators $\hat{x}$ and $\hat{p}$. Explain how to introduce the position-space wavefunction $\psi(x)$ for a quantum state $|\psi\rangle$ and use this to derive a formula for $\||\psi\rangle \|^{2}$. Find the wavefunctions for $\hat{x}|\psi\rangle$ and $\hat{p}|\psi\rangle$ in terms of $\psi(x)$, stating clearly any standard properties of position and momentum eigenstates which you require.

  Define annihilation and creation operators $a$ and $a^{\dagger}$ for a harmonic oscillator of unit mass and frequency and write the Hamiltonian

  $$H=\frac{1}{2} \hat{p}^{2}+\frac{1}{2} \hat{x}^{2}$$

  in terms of them. Let $\left|\psi_{\alpha}\right\rangle$ be a normalized eigenstate of $a$ with eigenvalue $\alpha$, a complex number. Show that $\left|\psi_{\alpha}\right\rangle$ cannot be an eigenstate of $H$ unless $\alpha=0$, and that $\left|\psi_{0}\right\rangle$ is an eigenstate of $H$ with the lowest possible energy. Find a normalized wavefunction for $\left|\psi_{\alpha}\right\rangle$ for any $\alpha$. Do there exist normalizable eigenstates of $a^{\dagger}$ ? Justify your answer.

  comment

Principles of Statistics

• 1.II $. 27 \mathrm{~J} \quad$

  Principles of Statistics | Part II, 2006

  (a) What is a loss function? What is a decision rule? What is the risk function of a decision rule? What is the Bayes risk of a decision rule with respect to a prior $\pi$ ?

  (b) Let $\theta \mapsto R(\theta, d)$ denote the risk function of decision rule $d$, and let $r(\pi, d)$ denote the Bayes risk of decision rule $d$ with respect to prior $\pi$. Suppose that $d^{*}$ is a decision rule and $\pi_{0}$ is a prior over the parameter space $\Theta$ with the two properties

  (i) $r\left(\pi_{0}, d^{*}\right)=\min _{d} r\left(\pi_{0}, d\right)$

  (ii) $\sup _{\theta} R\left(\theta, d^{*}\right)=r\left(\pi_{0}, d^{*}\right)$.

  Prove that $d^{*}$ is minimax.

  (c) Suppose now that $\Theta=\mathcal{A}=\mathbb{R}$, where $\mathcal{A}$ is the space of possible actions, and that the loss function is

  $$L(\theta, a)=\exp (-\lambda a \theta),$$

  where $\lambda$ is a positive constant. If the law of the observation $X$ given parameter $\theta$ is $N\left(\theta, \sigma^{2}\right)$, where $\sigma>0$ is known, show (using (b) or otherwise) that the rule

  $$d^{*}(x)=x / \sigma^{2} \lambda$$

  is minimax.

  comment

Probability and Measure

• 1.II $. 25 \mathrm{~J} \quad$

  Probability and Measure | Part II, 2006

  Let $\left(X_{n}\right)_{n \in \mathbb{N}}$ be a sequence of (real-valued, Borel-measurable) random variables on the probability space $(\Omega, \mathcal{A}, \mathbb{P})$.

  (a) Let $\left(A_{n}\right)_{n \in \mathbb{N}}$ be a sequence of events in $\mathcal{A}$.

  What does it mean for the events $\left(A_{n}\right)_{n \in \mathbb{N}}$ to be independent?

  What does it mean for the random variables $\left(X_{n}\right)_{n \in \mathbb{N}}$ to be independent?

  (b) Define the tail $\sigma$-algebra $\mathcal{T}$ for a sequence $\left(X_{n}\right)_{n \in \mathbb{N}}$ and state Kolmogorov's $0-1$ law.

  (c) Consider the following events in $\mathcal{A}$,

  $$\begin{gathered} \left\{X_{n} \leqslant 0 \text { eventually }\right\} \\ \left\{\lim _{n \rightarrow \infty} X_{1}+\ldots+X_{n} \text { exists }\right\} \\ \left\{X_{1}+\ldots+X_{n} \leqslant 0 \text { infinitely often }\right\} \end{gathered}$$

  Which of them are tail events for $\left(X_{n}\right)_{n \in \mathbb{N}}$ ? Justify your answers.

  (d) Let $\left(X_{n}\right)_{n \in \mathbb{N}}$ be independent random variables with

  $$\mathbb{P}\left(X_{n}=0\right)=\mathbb{P}\left(X_{n}=1\right)=\frac{1}{2} \quad \text { for all } n \in \mathbb{N},$$

  and define $U_{n}=X_{1} X_{2}+X_{2} X_{3}+\ldots+X_{2 n} X_{2 n+1}$.

  Show that $U_{n} / n \rightarrow c$ a.s. for some $c \in \mathbb{R}$, and determine $c$.

  [Standard results may be used without proof, but should be clearly stated.]

  comment

Representation Theory

• 1.II.19F

  Representation Theory | Part II, 2006

  (a) Let $G$ be a finite group and $X$ a finite set on which $G$ acts. Define the permutation representation $\mathbb{C}[X]$ and compute its character.

  (b) Let $G$ and $U$ be the following subgroups of $\mathrm{GL}_{2}\left(\mathbb{F}_{p}\right)$, where $p$ is a prime,

  $$G=\left\{\left(\begin{array}{cc} a & b \\ 0 & 1 \end{array}\right) \mid a \in \mathbb{F}_{p}^{\times}, b \in \mathbb{F}_{p}\right\}, \quad U=\left\{\left(\begin{array}{ll} 1 & b \\ 0 & 1 \end{array}\right) \mid b \in \mathbb{F}_{p}\right\}$$

  (i) Decompose $\mathbb{C}[G / U]$ into irreducible representations.

  (ii) Let $\psi: U \rightarrow \mathbb{C}^{\times}$be a non-trivial, one-dimensional representation. Determine the character of the induced representation $\operatorname{Ind}_{U}^{G} \psi$, and decompose $\operatorname{Ind}_{U}^{G} \psi$ into irreducible representations.

  (iii) List all of the irreducible representations of $G$ and show that your list is complete.

  comment

Riemann Surfaces

• 1.II.23F

  Riemann Surfaces | Part II, 2006

  Let $\Lambda=\mathbb{Z}+\mathbb{Z} \tau$ be a lattice in $\mathbb{C}$, where $\tau$ is a fixed complex number with positive imaginary part. The Weierstrass $\wp$-function is the unique meromorphic $\Lambda$-periodic function on $\mathbb{C}$ such that $\wp$ is holomorphic on $\mathbb{C} \backslash \Lambda$, and $\wp(z)-1 / z^{2} \rightarrow 0$ as $z \rightarrow 0$.

  Show that $\wp(-z)=\wp(z)$ and find all the zeros of $\wp^{\prime}$ in $\mathbb{C}$.

  Show that $\wp$ satisfies a differential equation

  $$\wp^{\prime}(z)^{2}=Q(\wp(z))$$

  for some cubic polynomial $Q(w)$. Further show that

  $$Q(w)=4\left(w-\wp\left(\frac{1}{2}\right)\right)\left(w-\wp\left(\frac{1}{2} \tau\right)\right)\left(w-\wp\left(\frac{1}{2}(1+\tau)\right)\right)$$

  and that the three roots of $Q$ are distinct.

  [Standard properties of meromorphic doubly-periodic functions may be used without proof provided these are accurately stated, but any properties of the $\wp$-function that you use must be deduced from first principles.]

  comment

Statistical Modelling

• 1.I.5I

  Statistical Modelling | Part II, 2006

  Assume that observations $Y=\left(Y_{1}, \ldots, Y_{n}\right)^{T}$ satisfy the linear model

  $$Y=X \beta+\epsilon$$

  where $X$ is an $n \times p$ matrix of known constants of full $\operatorname{rank} p<n$, where $\beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{T}$ is unknown and $\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Write down a $(1-\alpha)$-level confidence set for $\beta$.

  Define Cook's distance for the observation $\left(x_{i}, Y_{i}\right)$, where $x_{i}^{T}$ is the $i$ th row of $X$. Give its interpretation in terms of confidence sets for $\beta$.

  In the above model with $n=50$ and $p=2$, you observe that one observation has Cook's distance 1.3. Would you be concerned about the influence of this observation?

  [You may find some of the following facts useful:

  (i) If $Z \sim \chi_{2}^{2}$, then $\mathbb{P}(Z \leqslant 0.21)=0.1, \mathbb{P}(Z \leqslant 1.39)=0.5$ and $\mathbb{P}(Z \leqslant 4.61)=0.9$.

  (ii) If $Z \sim F_{2,48}$, then $\mathbb{P}(Z \leqslant 0.11)=0.1, \mathbb{P}(Z \leqslant 0.70)=0.5$ and $\mathbb{P}(Z \leqslant 2.42)=0.9$.

  (iii) If $Z \sim F_{48,2}$, then $\mathbb{P}(Z \leqslant 0.41)=0.1, \mathbb{P}(Z \leqslant 1.42)=0.5$ and $\mathbb{P}(Z \leqslant 9.47)=0.9$. ]

  comment

• 1.II.13I

  Statistical Modelling | Part II, 2006

  The table below gives a year-by-year summary of the career batting record of the baseball player Babe Ruth. The first column gives his age at the start of each season and the second gives the number of 'At Bats' (AB) he had during the season. For each At Bat, it is recorded whether or not he scored a 'Hit'. The third column gives the total number of Hits he scored in the season, and the final column gives his 'Average' for the season, defined as the number of Hits divided by the number of At Bats.

  $\begin{array}{rrrr}\text { Age } & \text { AB } & \text { Hits } & \text { Average } \\ 19 & 10 & 2 & 0.200 \\ 20 & 92 & 29 & 0.315 \\ 21 & 136 & 37 & 0.272 \\ 22 & 123 & 40 & 0.325 \\ 23 & 317 & 95 & 0.300 \\ 24 & 432 & 139 & 0.322 \\ 25 & 457 & 172 & 0.376 \\ 26 & 540 & 204 & 0.378 \\ 27 & 406 & 128 & 0.315 \\ 28 & 522 & 205 & 0.393 \\ 29 & 529 & 200 & 0.378 \\ 30 & 359 & 134 & 0.373 \\ 31 & 495 & 184 & 0.372 \\ 32 & 540 & 192 & 0.356 \\ 33 & 536 & 173 & 0.323 \\ 34 & 499 & 172 & 0.345 \\ 35 & 518 & 186 & 0.359 \\ 36 & 534 & 199 & 0.373 \\ 39 & 365 & 156 & 0.341 \\ 30 & 72 & 13 & 0.181 \\ 359 & 138 & 0.301 \\ 32 & 105 & 0.288 \\ 3 & & & \\ 3 & 123\end{array}$

  Explain and interpret the $\mathrm{R}$ commands below. In particular, you should explain the model that is being fitted, the approximation leading to the given standard errors and the test that is being performed in the last line of output.

  

  Assuming that any required packages are loaded, draw a careful sketch of the graph that you would expect to see on entering the following lines of code:

  

  comment

Stochastic Financial Models

• 1.II.28I

  Stochastic Financial Models | Part II, 2006

  Over two periods a stock price $\left\{S_{t}: t=0,1,2\right\}$ moves on a binomial tree.

  

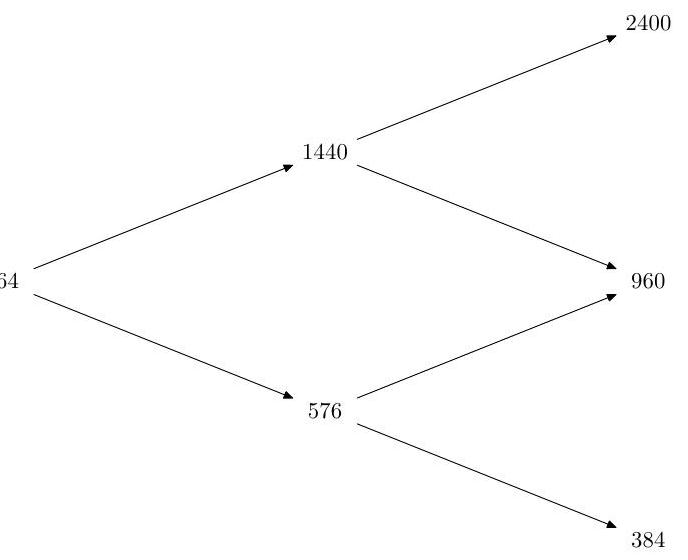
  Assuming that the riskless rate is constant at $r=1 / 3$, verify that all risk-neutral up-probabilities are given by one value $p \in(0,1)$. Find the time- 0 value of the following three put options all struck at $K=S_{0}=864=2^{5} \times 3^{3}$, with expiry 2 :

  (a) a European put;

  (b) an American put;

  (c) a European put modified by raising the strike to $K=992$ at time 1 if the stock went down in the first period.

  comment

Topics in Analysis

• 1.I.2G

  Topics in Analysis | Part II, 2006

  State Brouwer's fixed-point theorem, and also an equivalent version of the theorem that concerns retractions of the disc. Prove that these two versions are equivalent.

  comment

• 1.II.11G

  Topics in Analysis | Part II, 2006

  Let $\mathbb{T}=\{z:|z|=1\}$ be the unit circle in $\mathbb{C}$, and let $\phi: \mathbb{T} \rightarrow \mathbb{C}$ be a continuous function that never takes the value 0 . Define the degree (or winding number) of $\phi$ about 0 . [You need not prove that the degree is well-defined.]

  Denote the degree of $\phi$ about 0 by $w(\phi)$. Prove the following facts.

  (i) If $\phi_{1}$ and $\phi_{2}$ are two functions with the properties of $\phi$ above, then $w\left(\phi_{1} \cdot \phi_{2}\right)=$ $w\left(\phi_{1}\right)+w\left(\phi_{2}\right)$

  (ii) If $\psi$ is any continuous function such that $|\psi(z)|<|\phi(z)|$ for every $z \in \mathbb{T}$, then $w(\phi+\psi)=w(\phi)$.

  Using these facts, calculate the degree $w(\phi)$ when $\phi$ is given by the formula $\phi(z)=$ $(3 z-2)(z-3)(2 z+1)+1 .$

  comment

Waves

• 1.II $37 \mathrm{C}$

  Waves | Part II, 2006

  An elastic solid occupies the region $y<0$. The wave speeds in the solid are $c_{\mathrm{p}}$ and $c_{\mathrm{s}}$. A P-wave with dilatational potential

  $$\phi=\exp \left\{i k\left(x \sin \theta+y \cos \theta-c_{\mathrm{p}} t\right)\right\}$$

  is incident from $y<0$ on a rigid barrier at $y=0$. Obtain the reflected waves.

  Are there circumstances where the reflected S-wave is evanescent? Give reasons for your answer.

  comment