Part II, 2004, Paper 3

Algebraic Curves

• B3.10

  Algebraic Curves | Part II, 2004

  (i) Let $f: X \rightarrow Y$ be a morphism of smooth projective curves. Define the divisor $f^{*}(D)$ if $D$ is a divisor on $Y$, and state the "finiteness theorem".

  (ii) Suppose $f: X \rightarrow \mathbb{P}^{1}$ is a morphism of degree 2 , that $X$ is smooth projective, and that $X \neq \mathbb{P}^{1}$. Let $P, Q \in X$ be distinct ramification points for $f$. Show that, as elements of $c l(X)$, we have $[P] \neq[Q]$, but $2[P]=2[Q]$.

  comment

Algebraic Topology

• B3.7

  Algebraic Topology | Part II, 2004

  A finite simplicial complex $K$ is the union of subcomplexes $L$ and $M$. Describe the Mayer-Vietoris exact sequence that relates the homology groups of $K$ to those of $L$, $M$ and $L \cap M$. Define all the homomorphisms in the sequence, proving that they are well-defined (a proof of exactness is not required).

  A surface $X$ is constructed by identifying together (by means of a homeomorphism) the boundaries of two Möbius strips $Y$ and $Z$. Assuming relevant triangulations exist, determine the homology groups of $X$.

  comment

Algorithms and Networks

• A3.10

  Algorithms and Networks | Part II, 2004

  (i) Consider the problem

  $$\begin{aligned} \text { minimise } & f(x) \\ \text { subject to } & g(x)=b, x \in X, \end{aligned}$$

  where $f: \mathbb{R}^{n} \longrightarrow \mathbb{R}, g: \mathbb{R}^{n} \longrightarrow \mathbb{R}^{m}, X \subseteq \mathbb{R}^{n}, x \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. State the Lagrange Sufficiency Theorem for problem $(*)$. What is meant by saying that this problem is strong Lagrangian? How is this related to the Lagrange Sufficiency Theorem? Define a supporting hyperplane and state a condition guaranteeing that problem $(*)$ is strong Lagrangian.

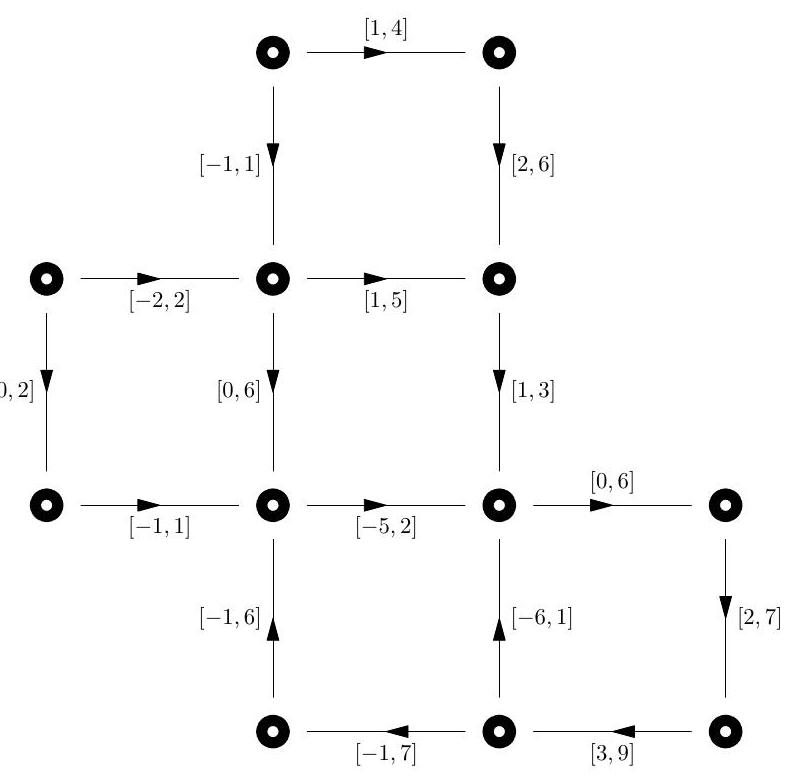
  (ii) Define the terms flow, divergence, circulation, potential and differential for a network with nodes $N$ and $\operatorname{arcs} A$.

  State the feasible differential problem for a network with span intervals $D(j)=$ $\left[d^{-}(j), d^{+}(j)\right], j \in A .$

  State, without proof, the Feasible Differential Theorem.

  [You must carefully define all quantities used in your statements.]

  Show that the network below does not support a feasible differential.

  

  Part II 2004

  comment

Applications of Quantum Mechanics

• B3.23

  Applications of Quantum Mechanics | Part II, 2004

  For a periodic potential $V(\mathbf{r})=V(\mathbf{r}+\ell)$, where $\ell$ is a lattice vector, show that we may write

  $$V(\mathbf{r})=\sum_{\mathbf{g}} a_{\mathbf{g}} e^{i \mathbf{g} \cdot \mathbf{r}}, \quad a_{\mathbf{g}}^{*}=a_{-\mathbf{g}}$$

  where the set of $g$ should be defined.

  Show how to construct general wave functions satisfying $\psi(\mathbf{r}+\boldsymbol{\ell})=e^{i \mathbf{k} \cdot \boldsymbol{\ell}} \psi(\mathbf{r})$ in terms of free plane-wave wave-functions.

  Show that the nearly free electron model gives an energy gap $2\left|a_{\mathbf{g}}\right|$ when $\mathbf{k}=\frac{1}{2} \mathbf{g}$.

  Explain why, for a periodic potential, the allowed energies form bands $E_{n}(\mathbf{k})$ where $\mathbf{k}$ may be restricted to a single Brillouin zone. Show that $E_{n}(\mathbf{k})=E_{n}(\mathbf{k}+\mathbf{g})$ if $\mathbf{k}$ and $\mathbf{k}+\mathbf{g}$ belong to the Brillouin zone.

  How are bands related to whether a material is a conductor or an insulator?

  comment

Applied Probability

• B3.13

  Applied Probability | Part II, 2004

  Let $\left(X_{t}, t \geq 0\right)$ be a renewal process with holding times $\left(S_{n}, n=1,2, \ldots\right)$ and $\left(Y_{t}, t \geq 0\right)$ be a renewal-reward process over $\left(X_{t}\right)$ with a sequence of rewards $\left(W_{n}, n=1,2, \ldots\right)$. Under assumptions on $\left(S_{n}\right)$ and $\left(W_{n}\right)$ which you should state clearly, prove that the ratios

  $$X_{t} / t \text { and } Y_{t} / t$$

  converge as $t \rightarrow \infty$. You should specify the form of convergence guaranteed by your assumptions. The law of large numbers, in the appropriate form, for sums $S_{1}+\ldots+S_{n}$ and $W_{1}+\ldots+W_{n}$ can be used without proof.

  In a mountain resort, when you rent skiing equipment you are given two options. (1) You buy an insurance waiver that costs $C / 4$ where $C$ is the daily equipment rent. Under this option, the shop will immediately replace, at no cost to you, any piece of equipment you break during the day, no matter how many breaks you had. (2) If you don't buy the waiver, you'll pay $3 C$ in the case of any break.

  To find out which option is better for me, I decided to set up two models of renewalreward process $\left(Y_{t}\right)$. In the first model, (Option 1), all of the holding times $S_{n}$ are equal to 6 . In the second model, given that there is no break on day $n$ (an event of probability $4 / 5)$, we have $S_{n}=6, W_{n}=C$, but given that there is a break on day $n$, we have that $S_{n}$ is uniformly distributed on $(0,6)$, and $W_{n}=4 C$. (In the second model, I would not continue skiing after a break, whereas in the first I would.)

  Calculate in each of these models the limit

  $$\lim _{t \rightarrow \infty} Y_{t} / t$$

  representing the long-term average cost of a unit of my skiing time.

  comment

Dynamics of Differential Equations

• B3.4

  Dynamics of Differential Equations | Part II, 2004

  (i) Describe the use of the stroboscopic method for obtaining approximate solutions to the second order equation

  $$\ddot{x}+x=\epsilon f(x, \dot{x}, t)$$

  when $|\epsilon| \ll 1$. In particular, by writing $x=R \cos (t+\phi), \dot{x}=-R \sin (t+\phi)$, obtain expressions in terms of $f$ for the rate of change of $R$ and $\phi$. Evaluate these expressions when $f=x^{2} \cos t$.

  (ii) In planetary orbit theory a crude model of an orbit subject to perturbation from a distant body is given by the equation

  $$\frac{d^{2} u}{d \theta^{2}}+u=\lambda-\delta^{2} u^{-2}-2 \delta^{3} u^{-3} \cos \theta$$

  where $0<\delta \ll 1,\left(u^{-1}, \theta\right)$ are polar coordinates in the plane, and $\lambda$ is a positive constant.

  (a) Show that when $\delta=0$ all bounded orbits are closed.

  (b) Now suppose $\delta \neq 0$, and look for almost circular orbits with $u=\lambda+\delta w(\theta)+a \delta^{2}$, where $a$ is a constant. By writing $w=R(\theta) \cos (\theta+\phi(\theta))$, and by making a suitable choice of the constant $a$, use the stroboscopic method to find equations for $d w / d \theta$ and $d \phi / d \theta$. By writing $z=R \exp (i \phi)$ and considering $d z / d \theta$, or otherwise, determine $R(\theta)$ and $\phi(\theta)$ in the case $R(0)=R_{0}, \phi(0)=0$. Hence describe the orbits of the system.

  comment

Electromagnetism

• A3.5 B3.3

  Electromagnetism | Part II, 2004

  (i) State Maxwell's equations and show that the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ can be expressed in terms of a scalar potential $\phi$ and a vector potential $\mathbf{A}$. Hence derive the inhomogeneous wave equations that are satisfied by $\phi$ and $\mathbf{A}$ respectively.

  (ii) The plane $x=0$ separates a vacuum in the half-space $x<0$ from a perfectly conducting medium occupying the half-space $x>0$. Derive the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at $x=0$.

  A plane electromagnetic wave with a magnetic field $\mathbf{B}=B(t, x, z) \hat{\mathbf{y}}$, travelling in the $x z$-plane at an angle $\theta$ to the $x$-direction, is incident on the interface at $x=0$. If the wave has frequency $\omega$ show that the total magnetic field is given by

  $$\mathbf{B}=B_{0} \cos \left(\frac{\omega x}{c} \cos \theta\right) \exp \left[i\left(\frac{\omega z}{c} \sin \theta-\omega t\right)\right] \hat{\mathbf{y}}$$

  where $B_{0}$ is a constant. Hence find the corresponding electric field $\mathbf{E}$, and obtain the surface charge density and the surface current at the interface.

  comment

Fluid Dynamics II

• B3.24

  Fluid Dynamics II | Part II, 2004

  Using the Milne-Thompson circle theorem, or otherwise, write down the complex potential $w$ describing inviscid incompressible two-dimensional flow past a circular cylinder of radius $a$ centred on the origin, with circulation $\kappa$ and uniform velocity $(U, V)$ in the far field.

  Hence, or otherwise, find an expression for the velocity field if the cylinder is replaced by a flat plate of length $4 a$, centred on the origin and aligned with the $x$-axis. Evaluate the velocity field on the two sides of the plate and confirm that the normal velocity is zero.

  Explain the significance of the Kutta condition, and determine the value of the circulation that satisfies the Kutta condition when $U>0$.

  With this value of the circulation, calculate the difference in pressure between the upper and lower sides of the plate at position $x(-2 a \leq x \leq 2 a)$. Comment briefly on the value of the pressure at the leading edge and the force that this would produce if the plate had a small non-zero thickness.

  Determine the force on the plate, explaining carefully the direction in which it acts.

  [The Blasius formula $F_{x}-i F_{y}=\frac{i \rho}{2} \oint_{C}\left(\frac{d w}{d z}\right)^{2} d z$, where $C$ is a closed contour lying just outside the body, may be used without proof.]

  comment

Foundations of Quantum Mechanics

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2004

  (i) A quantum mechanical system consists of two identical non-interacting particles with associated single-particle wave functions $\psi_{i}(x)$ and energies $E_{i}, i=1,2, \ldots$, where $E_{1}<E_{2}<\ldots$ Show how the states for the two lowest energy levels of the system are constructed and discuss their degeneracy when the particles have (a) spin 0 , (b) spin $1 / 2$.

  (ii) The Pauli matrices are defined to be

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  State how the spin operators $s_{1}, s_{2}, s_{3}$ may be expressed in terms of the Pauli matrices, and show that they describe states with total angular momentum $\frac{1}{2} \hbar$.

  An electron is at rest in the presence of a magnetic field $\mathbf{B}=(B, 0,0)$, and experiences an interaction potential $-\mu \boldsymbol{\sigma} \cdot \mathbf{B}$. At $t=0$ the state of the electron is the eigenstate of $s_{3}$ with eigenvalue $\frac{1}{2} \hbar$. Calculate the probability that at later time $t$ the electron will be measured to be in the eigenstate of $s_{3}$ with eigenvalue $\frac{1}{2} \hbar$.

  Part II 2004

  comment

Functional Analysis

• A3.3 B3.2

  Functional Analysis | Part II, 2004

  (i) Let $H$ be an infinite-dimensional Hilbert space. Show that $H$ has a (countable) orthonormal basis if and only if $H$ has a countable dense subset. [You may assume familiarity with the Gram-Schmidt process.]

  State and prove Bessel's inequality.

  (ii) State Parseval's equation. Using this, prove that if $H$ has a countable dense subset then there is a surjective isometry from $H$ to $l^{2}$.

  Explain carefully why the functions $e^{i n \theta}, n \in \mathbb{Z}$, form an orthonormal basis for $L^{2}(\mathbb{T})$

  comment

Galois Theory

• B3.6

  Galois Theory | Part II, 2004

  Let $K$ be a field, and $G$ a finite subgroup of $K^{*}$. Show that $G$ is cyclic.

  Define the cyclotomic polynomials $\Phi_{m}$, and show from your definition that

  $$X^{m}-1=\prod_{d \mid m} \Phi_{d}(X)$$

  Deduce that $\Phi_{m}$ is a polynomial with integer coefficients.

  Let $p$ be a prime with $(m, p)=1$. Let $\Phi_{m} \equiv f_{1} \ldots f_{r} \quad(\bmod p)$, where $f_{i} \in \mathbb{F}_{p}[X]$ are irreducible. Show that for each $i$ the degree of $f_{i}$ is equal to the order of $p$ in the group $(\mathbb{Z} / m \mathbb{Z})^{*}$.

  Use this to write down an irreducible polynomial of degree 10 over $\mathbb{F}_{2}$.

  comment

Geometry of Surfaces

• A3.7

  Geometry of Surfaces | Part II, 2004

  (i) The catenoid is the surface $C$ in Euclidean $\mathbb{R}^{3}$, with co-ordinates $x, y, z$ and Riemannian metric $d s^{2}=d x^{2}+d y^{2}+d z^{2}$ obtained by rotating the curve $y=\cosh x$ about the $x$-axis, while the helicoid is the surface $H$ swept out by a line which lies along the $x$-axis at time $t=0$, and at time $t=t_{0}$ is perpendicular to the $z$-axis, passes through the point $\left(0,0, t_{0}\right)$ and makes an angle $t_{0}$ with the $x$-axis.

  Find co-ordinates on each of $C$ and $H$ and write $x, y, z$ in terms of these co-ordinates.

  (ii) Compute the induced Riemannian metrics on $C$ and $H$ in terms of suitable coordinates. Show that $H$ and $C$ are locally isometric. By considering the $x$-axis in $H$, show that this local isometry cannot be extended to a rigid motion of any open subset of Euclidean $\mathbb{R}^{3}$.

  comment

Groups, Rings and Fields

• A3.4

  Groups, Rings and Fields | Part II, 2004

  (i) Let $K \leqslant \mathbb{C}$ be a field and $L \leqslant \mathbb{C}$ a finite normal extension of $K$. If $H$ is a finite subgroup of order $m$ in the Galois group $G(L \mid K)$, show that $L$ is a normal extension of the $H$-invariant subfield $I(H)$ of degree $m$ and that $G(L \mid I(H))=H$. [You may assume the theorem of the primitive element.]

  (ii) Show that the splitting field over $\mathbb{Q}$ of the polynomial $x^{4}+2$ is $\mathbb{Q}[\sqrt[4]{2}, i]$ and deduce that its Galois group has order 8. Exhibit a subgroup of order 4 of the Galois group, and determine the corresponding invariant subfield.

  comment

Hilbert Spaces

• B3.8

  Hilbert Spaces | Part II, 2004

  Let $H$ be a Hilbert space. An operator $T$ in $L(H)$ is normal if $T T^{*}=T^{*} T$. Suppose that $T$ is normal and that $\sigma(T) \subseteq \mathbb{R}$. Let $U=(T+i I)(T-i I)^{-1}$.

  (a) Suppose that $A$ is invertible and $A T=T A$. Show that $A^{-1} T=T A^{-1}$.

  (b) Show that $U$ is normal, and that $\sigma(U) \subseteq\{\lambda:|\lambda|=1\}$.

  (c) Show that $U^{-1}$ is normal.

  (d) Show that $U$ is unitary.

  (e) Show that $T$ is Hermitian.

  [You may use the fact that, if $S$ is normal, the spectral radius of $S$ is equal to $\|S\| .$ ]

  comment

Logic, Computation and Set Theory

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2004

  (i) State and prove the Compactness Theorem for first-order predicate logic.

  State and prove the Upward Löwenheim-Skolem Theorem.

  [You may use the Completeness Theorem for first-order predicate logic.]

  (ii) For each of the following theories, either give axioms (in the language of posets) for the theory or prove carefully that the theory is not axiomatisable.

  (a) The theory of posets having no maximal element.

  (b) The theory of posets having a unique maximal element.

  (c) The theory of posets having infinitely many maximal elements.

  (d) The theory of posets having finitely many maximal elements.

  (e) The theory of countable posets having a unique maximal element.

  comment

Markov Chains

• A3.1 B3.1

  Markov Chains | Part II, 2004

  (i) Give the definition of the time-reversal of a discrete-time Markov chain $\left(X_{n}\right)$. Define a reversible Markov chain and check that every probability distribution satisfying the detailed balance equations is invariant.

  (ii) Customers arrive in a hairdresser's shop according to a Poisson process of rate $\lambda>0$. The shop has $s$ hairstylists and $N$ waiting places; each stylist is working (on a single customer) provided that there is a customer to serve, and any customer arriving when the shop is full (i.e. the numbers of customers present is $N+s$ ) is not admitted and never returns. Every admitted customer waits in the queue and then is served, in the first-come-first-served order (say), the service taking an exponential time of rate $\mu>0$; the service times of admitted customers are independent. After completing his/her service, the customer leaves the shop and never returns.

  Set up a Markov chain model for the number $X_{t}$ of customers in the shop at time $t \geq 0$. Assuming $\lambda<s \mu$, calculate the equilibrium distribution $\pi$ of this chain and explain why it is unique. Show that $\left(X_{t}\right)$ in equilibrium is time-reversible, i.e. $\forall T>0,\left(X_{t}, 0 \leq t \leq T\right)$ has the same distribution as $\left(Y_{t}, 0 \leq t \leq T\right)$ where $Y_{t}=X_{T-t}$, and $X_{0} \sim \pi$.

  comment

Mathematical Methods

• A3.17

  Mathematical Methods | Part II, 2004

  (i) Give a brief description of the method of matched asymptotic expansions, as applied to a differential equation of the type

  $$\epsilon y^{\prime \prime}+K y^{\prime}+f(y)=0, \quad 0<x<1,$$

  where $0<\epsilon \ll 1, K$ is a non-zero constant, $f$ is a suitable smooth function and the boundary values $y(0), y(1)$ are specified. An outline of Van Dyke's asymptotic matching principle should be included.

  (ii) Consider the boundary-value problem

  $$\epsilon y^{\prime \prime}+y^{\prime}-(2 x+1) y=0, \quad y(0)=0, \quad y(1)=e^{2}$$

  with $0<\epsilon \ll 1$. Find the integrating factor for the leading-order outer problem. Hence obtain the first two terms in the outer expansion.

  Rewrite the problem using an appropriate stretched inner variable. Hence obtain the first two terms of the inner exansion.

  Use van Dyke's matching principle to determine all the constants. Hence show that $y^{\prime}(0)=\epsilon^{-1}+\frac{25}{3}+O(\epsilon) .$

  comment

Methods of Mathematical Physics

• B3.19

  Methods of Mathematical Physics | Part II, 2004

  The function $w(z)$ satisfies the third-order differential equation

  $$\frac{d^{3} w}{d z^{3}}-z w=0$$

  subject to the conditions $w(z) \rightarrow 0$ as $z \rightarrow \pm i \infty$ and $w(0)=1$. Obtain an integral representation for $w(z)$ of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  and determine the function $f(t)$ and the contour $\gamma$.

  Using the change of variable $t=z^{1 / 3} \tau$, or otherwise, compute the leading term in the asymptotic expansion of $w(z)$ as $z \rightarrow+\infty$.

  comment

Nonlinear Dynamical Systems

• A3.6 B3.17

  Nonlinear Dynamical Systems | Part II, 2004

  (i) Consider a system in $\mathbb{R}^{2}$ that is almost Hamiltonian:

  $$\dot{x}=\frac{\partial H}{\partial y}+\epsilon g_{1}(x, y), \quad \dot{y}=-\frac{\partial H}{\partial x}+\epsilon g_{2}(x, y)$$

  where $H=H(x, y)$ and $|\epsilon| \ll 1$. Show that if the system has a periodic orbit $\mathcal{C}$ then $\oint_{\mathcal{C}} g_{2} d x-g_{1} d y=0$, and explain how to evaluate this orbit approximately for small $\epsilon$. Illustrate your method by means of the system

  $$\dot{x}=y+\epsilon x\left(1-x^{2}\right), \quad \dot{y}=-x .$$

  (ii) Consider the system

  $$\dot{x}=y, \quad \dot{y}=x-x^{3}+\epsilon y\left(1-\alpha x^{2}\right)$$

  (a) Show that when $\epsilon=0$ the system is Hamiltonian, and find the Hamiltonian. Sketch the trajectories in the case $\epsilon=0$. Identify the value $H_{c}$ of $H$ for which there is a homoclinic orbit.

  (b) Suppose $\epsilon>0$. Show that the small change $\Delta H$ in $H$ around an orbit of the Hamiltonian system can be expressed to leading order as an integral of the form

  $$\int_{x_{1}}^{x_{2}} \mathcal{F}(x, H) d x$$

  where $x_{1}, x_{2}$ are the extrema of the $x$-coordinates of the orbits of the Hamiltonian system, distinguishing between the cases $H<H_{c}, H>H_{c}$.

  (c) Find the value of $\alpha$, correct to leading order in $\epsilon$, at which the system has a homoclinic orbit.

  (d) By examining the eigenvalues of the Jacobian at the origin, determine the stability of the homoclinic orbit, being careful to state clearly any standard results that you use.

  comment

Nonlinear Waves

• A3.18

  Nonlinear Waves | Part II, 2004

  (i) Let $\Phi^{+}(t)$ and $\Phi^{-}(t)$ denote the boundary values of functions which are analytic inside and outside the unit disc centred on the origin, respectively. Let $C$ denote the boundary of this disc. Suppose that $\Phi^{+}(t)$ and $\Phi^{-}(t)$ satisfy the jump condition

  $$\Phi^{+}(t)=t^{-2} \Phi^{-}(t)+t^{-1}+\alpha\left(t^{-1}+t-t^{-3}\right), \quad t \in C,$$

  where $\alpha$ is a constant.

  Find the canonical solution of the associated homogeneous Riemann-Hilbert problem. Write down the orthogonality conditions.

  (ii) Consider the linear singular integral equation

  $$\left(t+t^{-1}\right) \psi(t)+\frac{t-t^{-1}}{\pi i} \oint_{C} \frac{\psi(\tau)}{\tau-t} d \tau=2+2 \alpha\left(1+t^{2}-t^{-2}\right)$$

  where $\oint$ denotes the principal value integral.

  Show that the associated Riemann-Hilbert problem has the jump condition defined in Part (i) above. Using this fact, find the value of the constant $\alpha$ that allows equation $(*)$ to have a solution. For this particular value of $\alpha$ find the unique solution $\psi(t)$.

  comment

Number Theory

• A3.9

  Number Theory | Part II, 2004

  (i) Find a solution in integers of the Pell equation $x^{2}-17 y^{2}=1$.

  (ii) Define the continued fraction expansion of a real number $\theta>1$ and show that it converges to $\theta$.

  Show that if $N>0$ is a nonsquare integer and $x$ and $y$ are integer solutions of $x^{2}-N y^{2}=1$, then $x / y$ is a convergent of $\sqrt{N}$.

  comment

Numerical Analysis

• A3.19 B3.20

  Numerical Analysis | Part II, 2004

  (i) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant x \leqslant 1, \quad t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x), 0 \leqslant x \leqslant 1$, and with zero boundary conditions at $x=0$ and $x=1$, can be solved by the method

  $$u_{m}^{n+1}=u_{m}^{n}+\mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right), \quad m=1,2, \ldots, M, \quad n \geqslant 0,$$

  where $\Delta x=1 /(M+1), \mu=\Delta t /(\Delta x)^{2}$, and $u_{m}^{n} \approx u(m \Delta x, n \Delta t)$. Prove that $\mu \leqslant \frac{1}{2}$ implies convergence.

  (ii) By discretizing the same equation and employing the same notation as in Part (i), determine conditions on $\mu>0$ such that the method

  $$\begin{aligned} &\left(\frac{1}{12}-\frac{1}{2} \mu\right) u_{m-1}^{n+1}+\left(\frac{5}{6}+\mu\right) u_{m}^{n+1}+\left(\frac{1}{12}-\frac{1}{2} \mu\right) u_{m+1}^{n+1}= \\ &\left(\frac{1}{12}+\frac{1}{2} \mu\right) u_{m-1}^{n}+\left(\frac{5}{6}-\mu\right) u_{m}^{n}+\left(\frac{1}{12}+\frac{1}{2} \mu\right) u_{m+1}^{n} \end{aligned}$$

  is stable.

  comment

Optimization and Control

• B3.14

  Optimization and Control | Part II, 2004

  The strength of the economy evolves according to the equation

  $$\ddot{x}_{t}=-\alpha^{2} x_{t}+u_{t},$$

  where $x_{0}=\dot{x}_{0}=0$ and $u_{t}$ is the effort that the government puts into reform at time $t, t \geq 0$. The government wishes to maximize its chance of re-election at a given future time $T$, where this chance is some monotone increasing function of

  $$x_{T}-\frac{1}{2} \int_{0}^{T} u_{t}^{2} d t$$

  Use Pontryagin's maximum principle to determine the government's optimal reform policy, and show that the optimal trajectory of $x_{t}$ is

  $$x_{t}=\frac{t}{2} \alpha^{-2} \cos (\alpha(T-t))-\frac{1}{2} \alpha^{-3} \cos (\alpha T) \sin (\alpha t) .$$

  comment

Partial Differential Equations

• B3.18

  Partial Differential Equations | Part II, 2004

  (i) Find $w:[0, \infty) \times \mathbb{R} \longrightarrow \mathbb{R}$ such that $w(t, \cdot)$ is a Schwartz function of $\xi$ for each $t$ and solves

  $$\begin{gathered} w_{t}(t, \xi)+\left(1+\xi^{2}\right) w(t, \xi)=g(\xi), \\ w(0, \xi)=w_{0}(\xi), \end{gathered}$$

  where $g$ and $w_{0}$ are given Schwartz functions and $w_{t}$ denotes $\partial_{t} w$. If $\mathcal{F}$ represents the Fourier transform operator in the $\xi$ variables only and $\mathcal{F}^{-1}$ represents its inverse, show that the solution $w$ satisfies

  $$\partial_{t}\left(\mathcal{F}^{-1}\right) w(t, x)=\mathcal{F}^{-1}\left(\partial_{t} w\right)(t, x)$$

  and calculate $\lim _{t \rightarrow \infty} w(t, \cdot)$ in Schwartz space.

  (ii) Using the results of Part (i), or otherwise, show that there exists a solution of the initial value problem

  $$\begin{gathered} u_{t}(t, x)-u_{x x}(t, x)+u(t, x)=f(x) \\ u(0, x)=u_{0} \end{gathered}$$

  with $f$ and $u_{0}$ given Schwartz functions, such that

  $$\|u(t, \cdot)-\phi\|_{L^{\infty}(\mathbb{R})} \longrightarrow 0$$

  as $t \rightarrow \infty$ in Schwartz space, where $\phi$ is the solution of

  $$-\phi^{\prime \prime}+\phi=f .$$

  comment

Principles of Dynamics

• A3.2

  Principles of Dynamics | Part II, 2004

  (i) Explain the concept of a canonical transformation from coordinates $\left(q^{a}, p^{a}\right)$ to $\left(Q^{a}, P^{a}\right)$. Derive the transformations corresponding to generating functions $F_{1}\left(t, q^{a}, Q^{a}\right)$ and $F_{2}\left(t, q^{a}, P^{a}\right)$.

  (ii) A particle moving in an electromagnetic field is described by the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-e\left(\phi-\frac{\dot{\mathbf{x}} \cdot \mathbf{A}}{c}\right)$$

  where $c$ is constant

  (a) Derive the equations of motion in terms of the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$.

  (b) Show that $\mathbf{E}$ and $\mathbf{B}$ are invariant under the gauge transformation

  $$\mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda, \quad \phi \rightarrow \phi-\frac{1}{c} \frac{\partial \Lambda}{\partial t}$$

  for $\operatorname{arbitrary} \Lambda(t, \mathbf{x})$.

  (c) Construct the Hamiltonian. Find the generating function $F_{2}$ for the canonical transformation which implements the gauge transformation (1).

  comment

Principles of Statistics

• A3.12 B3.15

  Principles of Statistics | Part II, 2004

  (i) What is a sufficient statistic? What is a minimal sufficient statistic? Explain the terms nuisance parameter and ancillary statistic.

  (ii) Let $U_{1}, \ldots, U_{n}$ be independent random variables with common uniform( $([0,1])$ distribution, and suppose you observe $X_{i} \equiv a U_{i}^{-\beta}, i=1, \ldots, n$, where the positive parameters $a, \beta$ are unknown. Write down the joint density of $X_{1}, \ldots, X_{n}$ and prove that the statistic

  $$(m, p) \equiv\left(\min _{1 \leqslant j \leqslant n}\left\{X_{j}\right\}, \prod_{j=1}^{n} X_{j}\right)$$

  is minimal sufficient for $(a, \beta)$. Find the maximum-likelihood estimator $(\hat{a}, \hat{\beta})$ of $(a, \beta)$.

  Regarding $\beta$ as the parameter of interest and $a$ as the nuisance parameter, is $m$ ancillary? Find the mean and variance of $\hat{\beta}$. Hence find an unbiased estimator of $\beta$.

  comment

Probability and Measure

• B3.12

  Probability and Measure | Part II, 2004

  (a) Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\theta: \Omega \rightarrow \Omega$ be measurable. What is meant by saying that $\theta$ is measure-preserving? Define an invariant event and an invariant random variable, and explain what is meant by saying that $\theta$ is ergodic.

  (b) Let $m$ be a probability measure on $(\mathbb{R}, \mathcal{B})$. Let

  $$\Omega=\mathbb{R}^{\mathbb{N}}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{i} \in \mathbb{R} \text { for } i \geqslant 1\right\}$$

  let $\mathcal{F}$ be the smallest $\sigma$-field of $\Omega$ with respect to which the coordinate maps $X_{n}(x)=x_{n}$, for $x \in \Omega, n \geqslant 1$, are measurable, and let $\mathbb{P}$ be the unique probability measure on $(\Omega, \mathcal{F})$ satisfying

  $$\mathbb{P}\left(X_{i} \in A_{i} \text { for } 1 \leqslant i \leqslant n\right)=\prod_{i=1}^{n} m\left(A_{i}\right)$$

  for all $A_{i} \in \mathcal{B}, n \geqslant 1$. Define $\theta: \Omega \rightarrow \Omega$ by $\theta(x)=\left(x_{2}, x_{3}, \ldots\right)$ for $x=\left(x_{1}, x_{2}, \ldots\right)$.

  (i) Show that $\theta$ is measurable and measure-preserving.

  (ii) Define the tail $\sigma$-field $\mathcal{T}$ of the coordinate maps $X_{1}, X_{2}, \ldots$, and show that the invariant $\sigma$-field $\mathcal{I}$ of $\theta$ satisfies $\mathcal{I} \subseteq \mathcal{T}$. Deduce that $\theta$ is ergodic. [Any general result used must be stated clearly but the proof may be omitted.]

  (c) State Birkhoff's ergodic theorem and explain how to deduce that, given independent identically-distributed integrable random variables $Y_{1}, Y_{2}, \ldots$, there exists $\nu \in \mathbb{R}$ such that

  $$\frac{1}{n}\left(Y_{1}+Y_{2}+\cdots+Y_{n}\right) \rightarrow \nu \quad \text { a.e. as } \quad n \rightarrow \infty .$$

  comment

Representation Theory

• B3.5

  Representation Theory | Part II, 2004

  Compute the character table for the group $A_{5}$ of even permutations of five elements. You may wish to follow the steps below.

  (a) List the conjugacy classes in $A_{5}$ and their orders.

  (b) $A_{5}$ acts on $\mathbb{C}^{5}$ by permuting the standard basis vectors. Show that $\mathbb{C}^{5}$ splits as $\mathbb{C} \oplus V$, where $\mathbb{C}$ is the trivial 1-dimensional representation and $V$ is irreducible.

  (c) By using the formula for the character of the symmetric square $S^{2} V$,

  $$\chi_{S^{2} V}(g)=\frac{1}{2}\left[\chi_{V}(g)^{2}+\chi_{V}\left(g^{2}\right)\right]$$

  decompose $S^{2} V$ to produce a 5-dimensional, irreducible representation, and find its character.

  (d) Show that the exterior square $\Lambda^{2} V$ decomposes into two distinct irreducibles and compute their characters, to complete the character table of $A_{5}$.

  [Hint: You can save yourself some computational effort if you can explain why the automorphism of $A_{5}$, defined by conjugation by a transposition in $S_{5}$, must swap the two summands of $\Lambda^{2} V$.]

  comment

Riemann Surfaces

• B3.9

  Riemann Surfaces | Part II, 2004

  (a) Let $f: R \rightarrow S$ be a non-constant holomorphic map between compact connected Riemann surfaces $R$ and $S$.

  Define the branching order $v_{f}(p)$ at a point $p \in R$ and show that it is well-defined. Show further that if $h$ is a holomorphic map on $S$ then $v_{h \circ f}(p)=v_{h}(f(p)) v_{f}(p)$.

  Define the degree of $f$ and state the Riemann-Hurwitz formula. Show that if $R$ has Euler characteristic 0 then either $S$ is the 2 -sphere or $v_{p}(f)=1$ for all $p \in R$.

  (b) Let $P$ and $Q$ be complex polynomials of degree $m \geq 2$ with no common roots. Explain briefly how the rational function $P(z) / Q(z)$ induces a holomorphic map $F$ from the 2-sphere $S^{2} \cong \mathbb{C} \cup\{\infty\}$ to itself. What is the degree of $F$ ? Show that there is at least one and at most $2 m-2$ points $w \in S^{2}$ such that the number of distinct solutions $z \in S^{2}$ of the equation $F(z)=w$ is strictly less than $\operatorname{deg} F$.

  comment

Statistical Physics

• B3.22

  Statistical Physics | Part II, 2004

  Describe briefly why a low density gas can be investigated using classical statistical mechanics.

  Explain why, for a gas of $N$ structureless atoms, the measure on phase space is

  $$\frac{1}{N !} \frac{d^{3 N} q d^{3 N} p}{(2 \pi \hbar)^{3 N}}$$

  and the probability density in phase space is proportional to

  $$e^{-E(q, p) / T}$$

  where $T$ is the temperature in energy units.

  Derive the Maxwell probability distribution for atomic speeds $v$,

  $$\rho(v)=\left(\frac{m}{2 \pi T}\right)^{3 / 2} 4 \pi v^{2} e^{-m v^{2} / 2 T}$$

  Why is this valid even if the atoms interact?

  Find the mean value $\bar{v}$ of the speed of the atoms.

  Is $\frac{1}{2} m(\bar{v})^{2}$ the mean kinetic energy of the atoms?

  comment

Statistical Physics and Cosmology

• A3.14

  Statistical Physics and Cosmology | Part II, 2004

  (i) In equilibrium, the number density of a non-relativistic particle species is given by

  $$n=g_{\mathrm{s}}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} e^{\left(\mu-m c^{2}\right) / k T}$$

  where $m$ is the mass, $\mu$ is the chemical potential and $g_{\mathrm{s}}$ is the spin degeneracy. At around $t=100$ seconds, deuterium $D$ forms through the nuclear fusion of nonrelativistic protons $p$ and neutrons $n$ via the interaction:

  $$p+n \leftrightarrow D$$

  What is the relationship between the chemical potentials of the three species when they are in chemical equilibrium? Show that the ratio of their number densities can be expressed as

  $$\frac{n_{D}}{n_{n} n_{p}} \approx\left(\frac{h^{2}}{\pi m_{p} k T}\right)^{3 / 2} e^{B_{D} / k T},$$

  where the deuterium binding energy is $B_{D}=\left(m_{n}+m_{p}-m_{D}\right) c^{2}$ and you may take $g_{D}=4$. Now consider the fractional densities $X_{a}=n_{a} / n_{B}$, where $n_{B}$ is the baryon number of the universe, to re-express the ratio above in the form

  $$\frac{X_{D}}{X_{n} X_{p}}$$

  which incorporates the baryon-to-photon ratio $\eta$ of the universe. [You may assume that the photon density is $n_{\gamma}=\frac{16 \pi \zeta(3)}{(h c)^{3}}(k T)^{3}$.] From this expression, explain why deuterium does not form until well below the temperature $k T \approx B_{D}$.

  (ii) The number density $n=N / V$ for a photon gas in equilibrium is given by the formula

  $$n=\frac{8 \pi}{c^{3}} \int_{0}^{\infty} \frac{\nu^{2} d \nu}{e^{h \nu / k T}-1},$$

  where $\nu$ is the photon frequency. By considering the substitution $x=h \nu / k T$, show that the photon number density can be expressed in the form

  $$n=\alpha T^{3}$$

  where the constant $\alpha$ need not be evaluated explicitly.

  State the equation of state for a photon gas and explain why the chemical potential of the photon vanishes. Assuming that the photon energy density $\epsilon=E / V=(4 \sigma / c) T^{4}$, use the first law $d E=T d S-P d V+\mu d N$ to show that the entropy density is given by

  $$s=S / V=\frac{16 \sigma}{3 c} T^{3}$$

  Hence explain why, when photons are in equilibrium at early times in our universe, their temperature varies inversely with the scale factor: $T \propto a^{-1}$.

  comment

Stochastic Financial Models

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2004

  (i) Consider a single-period binomial model of a riskless asset (asset 0 ), worth 1 at time 0 and $1+r$ at time 1 , and a risky asset (asset 1 ), worth 1 at time 0 and worth $u$ at time 1 if the period was good, otherwise worth $d$. Assuming that

  $$d<1+r<u$$

  show how any contingent claim $Y$ to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition $(*)$, and indicate how the analysis of the single-period model extends to many periods.

  (ii) Now suppose that $u=5 / 3, d=2 / 3, r=1 / 3$, and that the risky asset is worth $S_{0}=864=2^{5} \times 3^{3}$ at time zero. Show that the time- 0 value of an American put option with strike $K=S_{0}$ and expiry at time $t=3$ is equal to 79 , and find the optimal exercise policy.

  comment

Symmetries and Groups in Physics

• A3.15

  Symmetries and Groups in Physics | Part II, 2004

  (i) Show that the character of an $S U(2)$ transformation in the $2 l+1$ dimensional irreducible representation $d_{l}$ is given by

  $$\chi_{l}(\theta)=\frac{\sin [(l+1 / 2) \theta]}{\sin [\theta / 2]}$$

  What are the characters of irreducible $S O(3)$ representations?

  (ii) The isospin representation of two-particle states of pions and nucleons is spanned by the basis $T=\left\{\left|\pi^{+} p\right\rangle,\left|\pi^{+} n\right\rangle,\left|\pi^{0} p\right\rangle,\left|\pi^{0} n\right\rangle,\left|\pi^{-} p\right\rangle,\left|\pi^{-} n\right\rangle\right\}$.

  Pions form an isospin triplet with $\pi^{+}=|1,1\rangle, \pi^{0}=|1,0\rangle, \pi^{-}=|1,-1\rangle$; and nucleons form an isospin doublet with $p=|1 / 2,1 / 2\rangle, n=|1 / 2,-1 / 2\rangle$. Find the values of the isospin for the irreducible representations into which $T$ will decompose.

  Using $I_{-}|j, m\rangle=\sqrt{(j-m+1)(j+m)}|j, m-1\rangle$, write the states of the basis $T$ in terms of isospin states.

  Consider the transitions

  $$\begin{array}{ll} \pi^{+} p & \rightarrow \pi^{+} p \\ \pi^{-} p & \rightarrow \pi^{-} p \\ \pi^{-} p & \rightarrow \pi^{0} n \end{array}$$

  and show that their amplitudes satisfy a linear relation.

  comment

Transport Processes

• A3.16

  Transport Processes | Part II, 2004

  (i) Viscous, incompressible fluid of viscosity $\mu$ flows steadily in the $x$-direction in a uniform channel $0<y<h$. The plane $y=0$ is fixed and the plane $y=h$ has constant $x$-velocity $U$. Neglecting gravity, derive from first principles the equations of motion of the fluid and show that the $x$-component of the fluid velocity is $u(y)$ and satisfies

  $$0=-P_{x}+\mu u_{y y},$$

  where $P(x)$ is the pressure in the fluid. Write down the boundary conditions on $u$. Hence show that the volume flow rate $Q=\int_{0}^{h} u d y$ is given by

  $$Q=\frac{U h}{2}-\frac{P_{x} h^{3}}{12 \mu}$$

  (ii) A heavy rectangular body of width $L$ and infinite length (in the $z$-direction) is pivoted about one edge at $(x, y)=(0,0)$ above a fixed rigid horizontal plane $y=0$. The body has weight $W$ per unit length in the $z$-direction, its centre of mass is distance $L / 2$ from the pivot, and it is falling under gravity towards the fixed plane through a viscous, incompressible fluid. Let $\alpha(t) \ll 1$ be the angle between the body and the plane. Explain the approximations of lubrication theory which permit equations (1) and (2) of Part (i) to apply to the flow in the gap between the two surfaces.

  Deduce that, in the gap,

  $$P_{x}=\frac{6 \mu \dot{\alpha}}{x \alpha^{3}},$$

  where $\dot{\alpha}=d \alpha / d t$. By taking moments about $(x, y)=(0,0)$, deduce that $\alpha(t)$ is given by

  $$\frac{1}{\alpha^{2}}-\frac{1}{\alpha_{0}^{2}}=\frac{2 W t}{3 \mu L}$$

  where $\alpha(0)=\alpha_{0}$.

  comment

Waves in Fluid and Solid Media

• B3.25

  Waves in Fluid and Solid Media | Part II, 2004

  The dispersion relation for sound waves of frequency $\omega$ in a stationary, homogeneous gas is $\omega=c|\mathbf{k}|$, where $c$ is the speed of sound and $\mathbf{k}$ is the wavevector. Derive the dispersion relation for sound waves of frequency $\omega$ in a uniform flow with velocity U.

  For a slowly-varying medium with a local dispersion relation $\omega=\Omega(\mathbf{k} ; \mathbf{x}, t)$, derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  The meaning of the notation $d / d t$ should be carefully explained.

  Suppose that two-dimensional sound waves with initial wavevector $\left(k_{0}, l_{0}\right)$ are generated at the origin in a gas occupying the half-space $y>0$. The gas has a mean velocity $(\gamma y, 0)$, where $0<\gamma \ll\left(k_{0}^{2}+l_{0}^{2}\right)^{\frac{1}{2}}$. Show that

  (a) if $k_{0}>0$ and $l_{0}>0$ then an initially upward propagating wavepacket returns to the level $y=0$ within a finite time, after having reached a maximum height that should be identified;

  (b) if $k_{0}<0$ and $l_{0}>0$ then an initially upward propagating wavepacket continues to propagate upwards for all time.

  For the case of a fixed frequency disturbance comment briefly on whether or not there is a quiet zone.

  comment