Part II, 2004, Paper 2

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2004

  For each of the following curves $C$

  (i) $C=\left\{(x, y) \in \mathbb{A}^{2} \mid x^{3}-x=y^{2}\right\} \quad$ (ii) $C=\left\{(x, y) \in \mathbb{A}^{2} \mid x^{2} y+x y^{2}=x^{4}+y^{4}\right\}$

  compute the points at infinity of $\bar{C} \subset \mathbb{P}^{2}$ (i.e. describe $\bar{C} \backslash C$ ), and find the singular points of the projective curve $\bar{C}$.

  At which points of $\bar{C}$ is the rational map $\bar{C} \rightarrow \mathbb{P}^{1}$, given by $(X: Y: Z) \mapsto(X: Y)$, not defined? Justify your answer.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2004

  Let $K$ and $L$ be finite simplicial complexes. Define the $n$-th chain group $C_{n}(K)$ and the boundary homomorphism $d_{n}: C_{n}(K) \rightarrow C_{n-1}(K)$. Prove that $d_{n-1} d_{n}=0$ and define the homology groups of $K$. Explain briefly how a simplicial map $f: K \rightarrow L$ induces a homomorphism $f_{\star}$ of homology groups.

  Suppose now that $K$ consists of the proper faces of a 3-dimensional simplex. Calculate from first principles the homology groups of $K$. If a simplicial map $f: K \rightarrow K$ gives a homeomorphism of the underlying polyhedron $|K|$, is the induced homology map $f_{\star}$ necessarily the identity?

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2004

  (i) Define the minimum path and the maximum tension problems for a network with span intervals specified for each arc. State without proof the connection between the two problems, and describe the Max Tension Min Path algorithm of solving them.

  (ii) Find the minimum path between nodes $\mathbf{S}$ and $\mathbf{S}^{\prime}$ in the network below. The span intervals are displayed alongside the arcs.

  

  Part II 2004

  comment

Applications of Quantum Mechanics

• B2.23

  Applications of Quantum Mechanics | Part II, 2004

  The wave function for a single particle with a potential $V(r)$ has the asymptotic form for large $r$

  $$\psi(r, \theta) \sim e^{i k r \cos \theta}+f(\theta) \frac{e^{i k r}}{r} .$$

  How is $f(\theta)$ related to observable quantities? Show how $f(\theta)$ can be expressed in terms of phase shifts $\delta_{\ell}(k)$ for $\ell=0,1,2, \ldots$..

  Assume that $V(r)=0$ for $r \geq a$, and let $R_{\ell}(r)$ denote the solution of the radial Schrödinger equation, regular at $r=0$, with energy $\hbar^{2} k^{2} / 2 m$ and angular momentum $\ell$. Let $N_{\ell}(k)=a R_{\ell}^{\prime}(a) / R_{\ell}(a)$. Show that

  $$\tan \delta_{\ell}(k)=\frac{N_{\ell}(k) j_{\ell}(k a)-k a j_{\ell}^{\prime}(k a)}{N_{\ell}(k) n_{\ell}(k a)-k a n_{\ell}^{\prime}(k a)} .$$

  Assuming that $N_{\ell}(k)$ is a smooth function for $k \approx 0$, determine the expected behaviour of $\delta_{\ell}(k)$ as $k \rightarrow 0$. Show that for $k \rightarrow 0$ then $f(\theta) \rightarrow c$, with $c$ a constant, and determine $c$ in terms of $N_{0}(0)$.

  [For $V=0$ the two independent solutions of the radial Schrödinger equation are $j_{\ell}(k r)$ and $n_{\ell}(k r)$ with

  $$\begin{aligned} j_{\ell}(\rho) & \sim \frac{1}{\rho} \sin \left(\rho-\frac{1}{2} \ell \pi\right), n_{\ell}(\rho) \sim-\frac{1}{\rho} \cos \left(\rho-\frac{1}{2} \ell \pi\right) \text { as } \rho \rightarrow \\ j_{\ell}(\rho) & \propto \rho^{\ell}, n_{\ell}(\rho) \propto \rho^{-\ell-1} \text { as } \rho \rightarrow 0 \\ e^{i \rho \cos \theta} &=\sum_{\ell=0}^{\infty}(2 \ell+1) i^{\ell} j_{\ell}(\rho) P_{\ell}(\cos \theta), \\ j_{0}(\rho) &=\frac{\sin \rho}{\rho}, \quad n_{0}(\rho)=-\frac{\cos \rho}{\rho} \end{aligned}$$

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2004

  Let $M$ be a Poisson random measure of intensity $\lambda$ on the plane $\mathbb{R}^{2}$. Denote by $C(r)$ the circle $\left\{x \in \mathbb{R}^{2}:\|x\|<r\right\}$ of radius $r$ in $\mathbb{R}^{2}$ centred at the origin and let $R_{k}$ be the largest radius such that $C\left(R_{k}\right)$ contains precisely $k$ points of $M$. [Thus $C\left(R_{0}\right)$ is the largest circle about the origin containing no points of $M, C\left(R_{1}\right)$ is the largest circle about the origin containing a single point of $M$, and so on.] Calculate $\mathbb{E} R_{0}, \mathbb{E} R_{1}$ and $\mathbb{E} R_{2}$.

  Now let $N$ be a Poisson random measure of intensity $\lambda$ on the line $\mathbb{R}^{1}$. Let $L_{k}$ be the length of the largest open interval that covers the origin and contains precisely $k$ points of $N$. [Thus $L_{0}$ gives the length of the largest interval containing the origin but no points of $N, L_{1}$ gives the length of the largest interval containing the origin and a single point of $N$, and so on.] Calculate $\mathbb{E} L_{0}, \mathbb{E} L_{1}$ and $\mathbb{E} L_{2}$.

  comment

Coding and Cryptography

• A2.9

  Coding and Cryptography | Part II, 2004

  (i) Describe how a stream cypher operates. What is a one-time pad?

  A one-time pad is used to send the message $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} y_{7}$ which is encoded as 0101011. By mistake, it is reused to send the message $y_{0} x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ which is encoded as 0100010. Show that $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ is one of two possible messages, and find the two possibilities.

  (ii) Describe the RSA system associated with a public key $e$, a private key $d$ and the product $N$ of two large primes.

  Give a simple example of how the system is vulnerable to a homomorphism attack. Explain how a signature system prevents such an attack. [You are not asked to give an explicit signature system.]

  Explain how to factorise $N$ when $e, d$ and $N$ are known.

  comment

Combinatorics

• B2.5

  Combinatorics | Part II, 2004

  State and prove Sperner's lemma on antichains.

  The family $\mathcal{A} \subset \mathcal{P}[n]$ is said to split $[n]$ if, for all distinct $i, j \in[n]$, there exists $A \in \mathcal{A}$ with $i \in A$ but $j \notin A$. Prove that if $\mathcal{A}$ splits $[n]$ then $n \leq\left(\begin{array}{c}a \\ \lfloor a / 2\rfloor\end{array}\right)$, where $a=|\mathcal{A}|$.

  Show moreover that, if $\mathcal{A}$ splits $[n]$ and no element of $[n]$ is in more than $k<\lfloor a / 2\rfloor$ members of $\mathcal{A}$, then $n \leq\left(\begin{array}{l}a \\ k\end{array}\right)$.

  comment

Computational Statistics and Statistical Modelling

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2004

  (i) Suppose we have independent observations $Y_{1}, \ldots, Y_{n}$, and we assume that for $i=1, \ldots, n, Y_{i}$ is Poisson with mean $\mu_{i}$, and $\log \left(\mu_{i}\right)=\beta^{T} x_{i}$, where $x_{1}, \ldots, x_{n}$ are given covariate vectors each of dimension $p$, where $\beta$ is an unknown vector of dimension $p$, and $p<n$. Assuming that $\left\{x_{1}, \ldots, x_{n}\right\}$ span $\mathbb{R}^{p}$, find the equation for $\hat{\beta}$, the maximum likelihood estimator of $\beta$, and write down the large-sample distribution of $\hat{\beta}$.

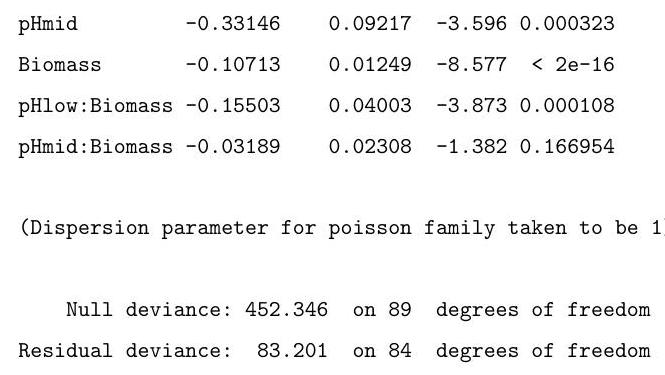
  (ii) A long-term agricultural experiment had 90 grassland plots, each $25 \mathrm{~m} \times 25 \mathrm{~m}$, differing in biomass, soil pH, and species richness (the count of species in the whole plot). While it was well-known that species richness declines with increasing biomass, it was not known how this relationship depends on soil pH, which for the given study has possible values "low", "medium" or "high", each taken 30 times. Explain the commands input, and interpret the resulting output in the (slightly edited) $R$ output below, in which "species" represents the species count.

  (The first and last 2 lines of the data are reproduced here as an aid. You may assume that the factor pH has been correctly set up.)

  

  

  comment

Dynamics of Differential Equations

• B2.4

  Dynamics of Differential Equations | Part II, 2004

  (i) Define carefully what is meant by a Hopf bifurcation in a two-dimensional dynamical system. Write down the normal form for this bifurcation, correct to cubic order, and distinguish between bifurcations of supercritical and subcritical type. Describe, without detailed calculations, how a general two-dimensional system with a Hopf bifurcation at the origin can be reduced to normal form by a near-identity transformation.

  (ii) A Takens-Bogdanov bifurcation of a fixed point of a two-dimensional system is characterised by a Jacobian with the canonical form

  $$A=\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right)$$

  at the bifurcation point. Consider the system

  $$\begin{aligned} &\dot{x}=y+\alpha_{1} x^{2}+\beta_{1} x y+\gamma_{1} y^{2} \\ &\dot{y}=\alpha_{2} x^{2}+\beta_{2} x y+\gamma_{2} y^{2} \end{aligned}$$

  Show that a near-identity transformation of the form

  $$\begin{aligned} &\xi=x+a_{1} x^{2}+b_{1} x y+c_{1} y^{2} \\ &\eta=y+a_{2} x^{2}+b_{2} x y+c_{2} y^{2} \end{aligned}$$

  exists that reduces the system to the normal (canonical) form, correct up to quadratic terms,

  $$\dot{\xi}=\eta, \quad \dot{\eta}=\alpha_{2} \xi^{2}+\left(\beta_{2}+2 \alpha_{1}\right) \xi \eta .$$

  It is known that the general form of the equations near the bifurcation point can be written (setting $p=\alpha_{2}, q=\beta_{2}+2 \alpha_{1}$ )

  $$\dot{\xi}=\eta, \quad \dot{\eta}=\lambda \xi+\mu \eta+p \xi^{2}+q \xi \eta .$$

  Find all the fixed points of this system, and the values of $\lambda, \mu$ for which these fixed points have (a) steady state bifurcations and (b) Hopf bifurcations.

  comment

Electrodynamics

• B2.21

  Electrodynamics | Part II, 2004

  A particle of rest mass $m$ and charge $q$ moves along a path $x^{a}(s)$, where $s$ is the particle's proper time. The equation of motion is

  $$m \ddot{x}^{a}=q F^{a b} \eta_{b c} \dot{x}^{c}$$

  where $\dot{x}^{a}=d x^{a} / d s$ etc., $F^{a b}$ is the Maxwell field tensor $\left(F^{01}=-E_{x}, F^{23}=-B_{x}\right.$, where $E_{x}$ and $B_{x}$ are the $x$-components of the electric and magnetic fields) and $\eta_{b c}$ is the Minkowski metric tensor. Show that $\dot{x}_{a} \ddot{x}^{a}=0$ and interpret both the equation of motion and this equation in the classical limit.

  The electromagnetic field is given in cartesian coordinates by $\mathbf{E}=(0, E, 0)$ and $\mathbf{B}=(0,0, E)$, where $E$ is constant and uniform. The particle starts from rest at the origin. Show that the orbit is given by

  $$9 x^{2}=2 \alpha y^{3}, \quad z=0$$

  where $\alpha=q E / m$.

  comment

Electromagnetism

• A2.5

  Electromagnetism | Part II, 2004

  (i) Write down the general solution of Poisson's equation. Derive from Maxwell's equations the Biot-Savart law for the magnetic field of a steady localised current distribution.

  (ii) A plane rectangular loop with sides of length $a$ and $b$ lies in the plane $z=0$ and is centred on the origin. Show that when $r=|\mathbf{r}| \gg a, b$, the vector potential $\mathbf{A}(\mathbf{r})$ is given approximately by

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \frac{\mathbf{m} \wedge \mathbf{r}}{r^{3}}$$

  where $\mathbf{m}=I a b \hat{\mathbf{z}}$ is the magnetic moment of the loop.

  Hence show that the magnetic field $\mathbf{B}(\mathbf{r})$ at a great distance from an arbitrary small plane loop of area $A$, situated in the $x y$-plane near the origin and carrying a current $I$, is given by

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0} I A}{4 \pi r^{5}}\left(3 x z, 3 y z, 2 r^{2}-3 x^{2}-3 y^{2}\right)$$

  comment

Fluid Dynamics II

• B2.25

  Fluid Dynamics II | Part II, 2004

  An incompressible fluid with density $\rho$ and viscosity $\mu$ is forced by a pressure difference $\Delta p$ through the narrow gap between two parallel circular cylinders of radius $a$ with axes $2 a+b$ apart. Explaining any approximations made, show that, provided $b \ll a$ and $\rho b^{3} \Delta p \ll \mu^{2} a$, the volume flux (per unit length of cylinder) is

  $$\frac{2 b^{5 / 2} \Delta p}{9 \pi a^{1 / 2} \mu}$$

  when the cylinders are stationary.

  Show also that when the two cylinders rotate with angular velocities $\Omega$ and $-\Omega$ respectively, the change in the volume flux is

  $$\frac{4}{3} b a \Omega .$$

  For the case $\Delta p=0$, find and sketch the function $f(x)=u_{0}(x) /(a \Omega)$, where $u_{0}$ is the centreline velocity at position $x$ along the gap in the direction of flow. Comment on the values taken by $f$.

  comment

Foundations of Quantum Mechanics

• A2.13 B2.22

  Foundations of Quantum Mechanics | Part II, 2004

  (i) The creation and annihilation operators for a harmonic oscillator of angular frequency $\omega$ satisfy the commutation relation $\left[a, a^{\dagger}\right]=1$. Write down an expression for the Hamiltonian $H$ in terms of $a$ and $a^{\dagger}$.

  There exists a unique ground state $|0\rangle$ of $H$ such that $a|0\rangle=0$. Explain how the space of eigenstates $|n\rangle, n=0,1,2, \ldots$ of $H$ is formed, and deduce the eigenenergies for these states. Show that

  $$a|n\rangle=\sqrt{n}|n-1\rangle, \quad a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle$$

  (ii) Write down the number operator $N$ of the harmonic oscillator in terms of $a$ and $a^{\dagger}$. Show that

  $$N|n\rangle=n|n\rangle$$

  The operator $K_{r}$ is defined to be

  $$K_{r}=\frac{a^{\dagger r} a^{r}}{r !}, \quad r=0,1,2, \ldots$$

  Show that $K_{r}$ commutes with $N$. Show also that

  $$K_{r}|n\rangle= \begin{cases}\frac{n !}{(n-r) ! r !}|n\rangle & r \leq n \\ 0 & r>n\end{cases}$$

  By considering the action of $K_{r}$ on the state $|n\rangle$ show that

  $$\sum_{r=0}^{\infty}(-1)^{r} K_{r}=|0\rangle\langle 0|$$

  comment

Functional Analysis

• A2.3 B2.2

  Functional Analysis | Part II, 2004

  (i) Prove Riesz's Lemma, that if $V$ is a normed space and $A$ is a vector subspace of $V$ such that for some $0 \leqslant k<1$ we have $d(x, A) \leqslant k$ for all $x \in V$ with $\|x\|=1$, then $A$ is dense in $V$. [Here $d(x, A)$ denotes the distance from $x$ to $A$.]

  Deduce that any normed space whose unit ball is compact is finite-dimensional. [You may assume that every finite-dimensional normed space is complete.]

  Give an example of a sequence $f_{1}, f_{2}, \ldots$ in an infinite-dimensional normed space such that $\left\|f_{n}\right\| \leqslant 1$ for all $n$, but $f_{1}, f_{2}, \ldots$ has no convergent subsequence.

  (ii) Let $V$ be a vector space, and let $\|\cdot\|_{1}$ and $\|.\|_{2}$ be two norms on $V$. What does it mean to say that $\|\cdot\|_{1}$ and $\|.\|_{2}$ are equivalent?

  Show that on a finite-dimensional vector space all norms are equivalent. Deduce that every finite-dimensional normed space is complete.

  Exhibit two norms on the vector space $l^{1}$ that are not equivalent.

  In addition, exhibit two norms on the vector space $l^{\infty}$ that are not equivalent.

  comment

General Relativity

• A2.15 B2.24

  General Relativity | Part II, 2004

  (i) State and prove Birkhoff's theorem.

  (ii) Derive the Schwarzschild metric and discuss its relevance to the problem of gravitational collapse and the formation of black holes.

  [Hint: You may assume that the metric takes the form

  $$d s^{2}=-e^{\nu(r, t)} d t^{2}+e^{\lambda(r, t)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  and that the non-vanishing components of the Einstein tensor are given by

  $$\begin{aligned} & G_{t t}=\frac{e^{2 \nu+\lambda}}{r^{2}}\left(-1+e^{\lambda}+r \lambda^{\prime}\right), \quad G_{r t}=e^{(\nu+\lambda) / 2} \frac{\dot{\lambda}}{r}, \quad G_{r r}=\frac{e^{\lambda}}{r^{2}}\left(1-e^{-\lambda}+r \nu^{\prime}\right), \\ & G_{\theta \theta}=\frac{1}{4} r^{2} e^{-\lambda}\left[2 \nu^{\prime \prime}+\left(\nu^{\prime}\right)^{2}+\frac{2}{r}\left(\nu^{\prime}-\lambda^{\prime}\right)-\nu^{\prime} \lambda^{\prime}\right]-\frac{1}{4} r^{2} e^{-\nu}\left[2 \ddot{\lambda}+(\dot{\lambda})^{2}-\dot{\lambda} \dot{\nu}\right] \\ =&\left.G_{r t} \text { and } G_{\phi \phi}=\sin ^{2} \theta G_{\theta \theta} .\right] \end{aligned}$$

  comment

Geometry of Surfaces

• A2.7

  Geometry of Surfaces | Part II, 2004

  (i) What is a geodesic on a surface $M$ with Riemannian metric, and what are geodesic polar co-ordinates centred at a point $P$ on $M$ ? State, without proof, formulae for the Riemannian metric and the Gaussian curvature in terms of geodesic polar co-ordinates.

  (ii) Show that a surface with constant Gaussian curvature 0 is locally isometric to the Euclidean plane.

  comment

Graph Theory

• A2.8

  Graph Theory | Part II, 2004

  (i) State a result of Euler, relating the number of vertices, edges and faces of a plane graph. Show that if $G$ is a plane graph then $\chi(G) \leq 5$.

  (ii) Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that

  $$p_{G}(t)=t^{n}-a_{1} t^{n-1}+a_{2} t^{n-2}+\ldots+(-1)^{n} a_{n}$$

  where $a_{1}, \ldots, a_{n}$ are non-negative integers. Explain, with proof, how the chromatic polynomial is related to the number of vertices, edges and triangles in $G$. Show that if $C_{n}$ is a cycle of length $n \geq 3$, then

  $$p_{C_{n}}(t)=(t-1)^{n}+(-1)^{n}(t-1) .$$

  comment

Groups, Rings and Fields

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2004

  (i) State Gauss' Lemma on polynomial irreducibility. State and prove Eisenstein's criterion.

  (ii) Which of the following polynomials are irreducible over $\mathbb{Q}$ ? Justify your answers.

  (a) $x^{7}-3 x^{3}+18 x+12$

  (b) $x^{4}-4 x^{3}+11 x^{2}-3 x-5$

  (c) $1+x+x^{2}+\ldots+x^{p-1}$ with $p$ prime

  [Hint: consider substituting $y=x-1$.]

  (d) $x^{n}+p x+p^{2}$ with $p$ prime.

  [Hint: show any factor has degree at least two, and consider powers of $p$ dividing coefficients.]

  comment

Information Theory

• B2.14

  Information Theory | Part II, 2004

  For integer-valued random variables $X$ and $Y$, define the relative entropy $h_{Y}(X)$ of $X$ relative to $Y$.

  Prove that $h_{Y}(X) \geqslant 0$, with equality if and only if $\mathbb{P}(X=x)=\mathbb{P}(Y=x)$ for all $x$.

  By considering $Y$, a geometric random variable with parameter chosen appropriately, show that if the mean $\mathbb{E} X=\mu<\infty$, then

  $$h(X) \leqslant(\mu+1) \log (\mu+1)-\mu \log \mu,$$

  with equality if $X$ is geometric.

  comment

Logic, Computation and Set Theory

• B2.11

  Logic, Computation and Set Theory | Part II, 2004

  Define the sets $V_{\alpha}, \alpha \in O N$. Show that each $V_{\alpha}$ is transitive, and explain why $V_{\alpha} \subseteq V_{\beta}$ whenever $\alpha \leqslant \beta$. Prove that every set $x$ is a member of some $V_{\alpha}$.

  Which of the following are true and which are false? Give proofs or counterexamples as appropriate. You may assume standard properties of rank.

  (a) If the rank of a set $x$ is a (non-zero) limit then $x$ is infinite.

  (b) If the rank of a set $x$ is a successor then $x$ is finite.

  (c) If the rank of a set $x$ is countable then $x$ is countable.

  comment

Markov Chains

• A2.1

  Markov Chains | Part II, 2004

  (i) Let $J$ be a proper subset of the finite state space $I$ of an irreducible Markov chain $\left(X_{n}\right)$, whose transition matrix $P$ is partitioned as

  $$P=J^{J}\left(\begin{array}{ll} A & J^{c} \\ C & D \end{array}\right)$$

  If only visits to states in $J$ are recorded, we see a $J$-valued Markov chain $\left(\tilde{X}_{n}\right)$; show that its transition matrix is

  $$\tilde{P}=A+B \sum_{n \geqslant 0} D^{n} C=A+B(I-D)^{-1} C$$

  (ii) Local MP Phil Anderer spends his time in London in the Commons $(C)$, in his flat $(F)$, in the bar $(B)$ or with his girlfriend $(G)$. Each hour, he moves from one to another according to the transition matrix $P$, though his wife (who knows nothing of his girlfriend) believes that his movements are governed by transition matrix $P^{W}$ :

  

  The public only sees Phil when he is in $J=\{C, F, B\}$; calculate the transition matrix $\tilde{P}$ which they believe controls his movements.

  Each time the public Phil moves to a new location, he phones his wife; write down the transition matrix which governs the sequence of locations from which the public Phil phones, and calculate its invariant distribution.

  Phil's wife notes down the location of each of his calls, and is getting suspicious - he is not at his flat often enough. Confronted, Phil swears his fidelity and resolves to dump his troublesome transition matrix, choosing instead

  

  Will this deal with his wife's suspicions? Explain your answer.

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2004

  (i) Consider the integral equation

  $$\phi(x)=-\lambda \int_{a}^{b} K(x, t) \phi(t) d t+g(x)$$

  for $\phi$ in the interval $a \leq x \leq b$, where $\lambda$ is a real parameter and $g(x)$ is given. Describe the method of successive approximations for solving ( $\dagger$ ).

  Suppose that

  $$|K(x, t)| \leq M, \quad \forall x, t \in[a, b]$$

  By using the Cauchy-Schwarz inequality, or otherwise, show that the successive-approximation series for $\phi(x)$ converges absolutely provided

  $$|\lambda|<\frac{1}{M(b-a)} .$$

  (ii) The real function $\psi(x)$ satisfies the differential equation

  $$-\psi^{\prime \prime}(x)+\lambda \psi(x)=h(x), \quad 0<x<1$$

  where $h(x)$ is a given smooth function on $[0,1]$, subject to the boundary conditions

  $$\psi^{\prime}(0)=\psi(0), \quad \psi(1)=0 .$$

  By integrating $(\star)$, or otherwise, show that $\psi(x)$ obeys

  $$\psi(0)=\frac{1}{2} \int_{0}^{1}(1-t) h(t) d t-\frac{1}{2} \lambda \int_{0}^{1}(1-t) \psi(t) d t$$

  Hence, or otherwise, deduce that $\psi(x)$ obeys an equation of the form ( $\dagger$ ), with

  $$\begin{gathered} K(x, t)= \begin{cases}\frac{1}{2}(1-x)(1+t), & 0 \leq t \leq x \leq 1 \\ \frac{1}{2}(1+x)(1-t), & 0 \leq x \leq t \leq 1\end{cases} \\ \text { and } g(x)=\int_{0}^{1} K(x, t) h(t) d t \end{gathered}$$

  Deduce that the series solution for $\psi(x)$ converges provided $|\lambda|<2$.

  comment

Methods of Mathematical Physics

• B2.19

  Methods of Mathematical Physics | Part II, 2004

  (a) The Beta function is defined by

  $$\mathrm{B}(p, q)=\int_{0}^{1} x^{p-1}(1-x)^{q-1} d x$$

  Show that

  $$\mathrm{B}(p, q)=\int_{1}^{\infty} x^{-p-q}(x-1)^{q-1} d x$$

  (b) The function $J(p, q)$ is defined by

  $$J(p, q)=\int_{\gamma} t^{p-1}(1-t)^{q-1} d t$$

  where the integrand has a branch cut along the positive real axis. Just above the cut, $\arg t=0$. For $t>1$ just above the cut, arg $(1-t)=-\pi$. The contour $\gamma$ runs from $t=\infty e^{2 \pi i}$, round the origin in the negative sense, to $t=\infty$ (i.e. the contour is a reflection of the usual Hankel contour). What restriction must be placed on $p$ and $q$ for the integral to converge?

  By evaluating $J(p, q)$ in two ways, show that

  $$\left(1-e^{2 \pi i p}\right) \mathrm{B}(p, q)+\left(e^{-\pi i(q-1)}-e^{\pi i(2 p+q-1)}\right) \mathrm{B}(1-p-q, q)=0,$$

  where $p$ and $q$ are any non-integer complex numbers.

  Using the identity

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  deduce that

  $$\Gamma(p) \Gamma(1-p) \sin (\pi p)=\Gamma(p+q) \Gamma(1-p-q) \sin [\pi(1-p-q)]$$

  and hence that

  $$\pi=\Gamma(q) \Gamma(1-q) \sin [\pi(1-q)]$$

  comment

Nonlinear Dynamical Systems

• A2.6 B2.17

  Nonlinear Dynamical Systems | Part II, 2004

  (i) A linear system in $\mathbb{R}^{2}$ takes the form $\dot{\mathbf{x}}=\mathrm{Ax}$. Explain (without detailed calculation but by giving examples) how to classify the dynamics of the system in terms of the determinant and the trace of A. Show your classification graphically, and describe the dynamics that occurs on the boundaries of the different regions on your diagram.

  (ii) A nonlinear system in $\mathbb{R}^{2}$ has the form $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}), \mathbf{f}(0)=0$. The Jacobian (linearization) $A$ of $\mathbf{f}$ at the origin is non-hyperbolic, with one eigenvalue of $A$ in the left-hand half-plane. Define the centre manifold for this system, and explain (stating carefully any results you use) how the dynamics near the origin may be reduced to a one-dimensional system on the centre manifold.

  A dynamical system of this type has the form

  $$\begin{aligned} &\dot{x}=a x^{3}+b x y+c x^{5}+d x^{3} y+e x y^{2}+f x^{7}+g x^{5} y \\ &\dot{y}=-y+x^{2}-x^{4} \end{aligned}$$

  Find the coefficients for the expansion of the centre manifold correct up to and including terms of order $x^{6}$, and write down in terms of these coefficients the equation for the dynamics on the centre manifold up to order $x^{7}$. Using this reduced equation, give a complete set of conditions on the coefficients $a, b, c, \ldots$ that guarantee that the origin is stable.

  comment

Nonlinear Waves

• A2.18

  Nonlinear Waves | Part II, 2004

  (i) Let $u(x, t)$ satisfy the Burgers equation

  $$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^{2} u}{\partial x^{2}}$$

  where $\nu$ is a positive constant. Consider solutions of the form $u=u(X)$, where $X=x-U t$ and $U$ is a constant, such that

  $$u \rightarrow u_{2}, \quad \frac{\partial u}{\partial X} \rightarrow 0 \quad \text { as } \quad X \rightarrow-\infty ; \quad u \rightarrow u_{1}, \quad \frac{\partial u}{\partial X} \rightarrow 0 \quad \text { as } \quad X \rightarrow \infty$$

  with $u_{2}>u_{1}$.

  Show that $U$ satisfies the so-called shock condition

  $$U=\frac{1}{2}\left(u_{2}+u_{1}\right)$$

  By using the factorisation

  $$\frac{1}{2} u^{2}-U u+A=\frac{1}{2}\left(u-u_{1}\right)\left(u-u_{2}\right)$$

  where $A$ is the constant of integration, express $u$ in terms of $X, u_{1}, u_{2}$ and $\nu$.

  (ii) According to shallow-water theory, river waves are characterised by the PDEs

  $$\begin{gathered} \frac{\partial v}{\partial t}+v \frac{\partial v}{\partial x}+g \cos \alpha \frac{\partial h}{\partial x}=g \sin \alpha-C_{f} \frac{v^{2}}{h} \\ \frac{\partial h}{\partial t}+v \frac{\partial h}{\partial x}+h \frac{\partial v}{\partial x}=0 \end{gathered}$$

  where $h(x, t)$ denotes the depth of the river, $v(x, t)$ denotes the mean velocity, $\alpha$ is the constant angle of inclination, and $C_{f}$ is the constant friction coefficient.

  Find the characteristic velocities and the characteristic form of the equations. Find the Riemann variables and show that if $C_{f}=0$ then the Riemann variables vary linearly with $t$ on the characteristics.

  comment

Number Fields

• B2.9

  Number Fields | Part II, 2004

  Let $m$ be an integer greater than 1 and let $\zeta_{m}$ denote a primitive $m$-th root of unity in $\mathbb{C}$. Let $\mathcal{O}$ be the ring of integers of $\mathbb{Q}\left(\zeta_{m}\right)$. If $p$ is a prime number with $(p, m)=1$, outline the proof that

  $$p \mathcal{O}=\wp_{1} \cdots \wp_{r},$$

  where the $\wp_{i}$ are distinct prime ideals of $\mathcal{O}$, and $r=\varphi(m) / f$ with $f$ the least integer $\geqslant 1$ such that $p^{f} \equiv 1 \bmod m$. [Here $\varphi(m)$ is the Euler $\varphi$-function of $\left.m\right]$.

  Determine the factorisations of $2,3,5$ and 11 in $\mathbb{Q}\left(\zeta_{5}\right)$. For each integer $n \geqslant 1$, prove that, in the ring of integers of $\mathbb{Q}\left(\zeta_{5^{n}}\right)$, there is a unique prime ideal dividing 2 , and a unique prime ideal dividing 3 .

  comment

Numerical Analysis

• A2.19 B2.20

  Numerical Analysis | Part II, 2004

  (i) The five-point equations, which are obtained when the Poisson equation $\nabla^{2} u=f$ (with Dirichlet boundary conditions) is discretized in a square, are

  $$-u_{m-1, n}-u_{m, n-1}-u_{m+1, n}-u_{m, n+1}+4 u_{m, n}=f_{m, n}, \quad m, n=1,2, \ldots, M,$$

  where $u_{0, n}, u_{M+1, n}, u_{m, 0}, u_{m, M+1}=0$ for all $m, n=1,2, \ldots, M$.

  Formulate the Gauss-Seidel method for the above linear system and prove its convergence. In the proof you should carefully state any theorems you use. [You may use Part (ii) of this question.]

  (ii) By arranging the two-dimensional arrays $\left\{u_{m, n}\right\}_{m, n=1, \ldots, M}$ and $\left\{b_{m, n}\right\}_{m, n=1, \ldots, M}$ into the column vectors $\mathbf{u} \in \mathbb{R}^{M^{2}}$ and $\mathbf{b} \in \mathbb{R}^{M^{2}}$ respectively, the linear system described in Part (i) takes the matrix form $A \mathbf{u}=\mathbf{b}$. Prove that, regardless of the ordering of the points on the grid, the matrix $A$ is symmetric and positive definite.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2004

  A gambler is presented with a sequence of $n \geqslant 6$ random numbers, $N_{1}, N_{2}, \ldots, N_{n}$, one at a time. The distribution of $N_{k}$ is

  $$P\left(N_{k}=k\right)=1-P\left(N_{k}=-k\right)=p,$$

  where $1 /(n-2)<p \leq 1 / 3$. The gambler must choose exactly one of the numbers, just after it has been presented and before any further numbers are presented, but must wait until all the numbers are presented before his payback can be decided. It costs $£ 1$ to play the game. The gambler receives payback as follows: nothing if he chooses the smallest of all the numbers, $£ 2$ if he chooses the largest of all the numbers, and $£ 1$ otherwise.

  Show that there is an optimal strategy of the form "Choose the first number $k$ such that either (i) $N_{k}>0$ and $k \geq n-r_{0}$, or (ii) $k=n-1$ ", where you should determine the constant $r_{0}$ as explicitly as you can.

  comment

Partial Differential Equations

• B2.18

  Partial Differential Equations | Part II, 2004

  (a) State and prove the Duhamel principle for the wave equation.

  (b) Let $u \in C^{2}\left([0, T] \times \mathbb{R}^{n}\right)$ be a solution of

  $$u_{t t}+u_{t}-\Delta u+u=0$$

  where $\Delta$ is taken in the variables $x \in \mathbb{R}^{n}$ and $u_{t}=\partial_{t} u$ etc.

  Using an 'energy method', or otherwise, show that, if $u=u_{t}=0$ on the set $\left\{t=0,\left|x-x_{0}\right| \leqslant t_{0}\right\}$ for some $\left(t_{0}, x_{0}\right) \in[0, T] \times \mathbb{R}^{n}$, then $u$ vanishes on the region $K(t, x)=\left\{(t, x): 0 \leqslant t \leqslant t_{0},\left|x-x_{0}\right| \leqslant t_{0}-t\right\}$. Hence deduce uniqueness for the Cauchy problem for the above PDE with Schwartz initial data.

  comment

Principles of Dynamics

• A2.2 B2.1

  Principles of Dynamics | Part II, 2004

  (i) Consider a light rigid circular wire of radius $a$ and centre $O$. The wire lies in a vertical plane, which rotates about the vertical axis through $O$. At time $t$ the plane containing the wire makes an angle $\phi(t)$ with a fixed vertical plane. A bead of mass $m$ is threaded onto the wire. The bead slides without friction along the wire, and its location is denoted by $A$. The angle between the line $O A$ and the downward vertical is $\theta(t)$.

  Show that the Lagrangian of the system is

  $$\frac{m a^{2}}{2} \dot{\theta}^{2}+\frac{m a^{2}}{2} \dot{\phi}^{2} \sin ^{2} \theta+m g a \cos \theta .$$

  Calculate two independent constants of the motion, and explain their physical significance.

  (ii) A dynamical system has Hamiltonian $H(q, p, \lambda)$, where $\lambda$ is a parameter. Consider an ensemble of identical systems chosen so that the number density of systems, $f(q, p, t)$, in the phase space element $d q d p$ is either zero or one. Prove Liouville's Theorem, namely that the total area of phase space occupied by the ensemble is time-independent.

  Now consider a single system undergoing periodic motion $q(t), p(t)$. Give a heuristic argument based on Liouville's Theorem to show that the area enclosed by the orbit,

  $$I=\oint p d q$$

  is approximately conserved as the parameter $\lambda$ is slowly varied (i.e. that $I$ is an adiabatic invariant).

  Consider $H(q, p, \lambda)=\frac{1}{2} p^{2}+\lambda q^{2 n}$, with $n$ a positive integer. Show that as $\lambda$ is slowly varied the energy of the system, $E$, varies as

  $$E \propto \lambda^{1 /(n+1)} .$$

  comment

Principles of Statistics

• A2.11 B2.16

  Principles of Statistics | Part II, 2004

  (i) In the context of a decision-theoretic approach to statistics, what is a loss function? a decision rule? the risk function of a decision rule? the Bayes risk of a decision rule? the Bayes rule with respect to a given prior distribution?

  Show how the Bayes rule with respect to a given prior distribution is computed.

  (ii) A sample of $n$ people is to be tested for the presence of a certain condition. A single real-valued observation is made on each one; this observation comes from density $f_{0}$ if the condition is absent, and from density $f_{1}$ if the condition is present. Suppose $\theta_{i}=0$ if the $i^{\text {th }}$person does not have the condition, $\theta_{i}=1$ otherwise, and suppose that the prior distribution for the $\theta_{i}$ is that they are independent with common distribution $P\left(\theta_{i}=1\right)=p \in(0,1)$, where $p$ is known. If $X_{i}$ denotes the observation made on the $i^{\text {th }}$person, what is the posterior distribution of the $\theta_{i}$ ?

  Now suppose that the loss function is defined by

  $$L_{0}(\theta, a) \equiv \sum_{j=1}^{n}\left(\alpha a_{j}\left(1-\theta_{j}\right)+\beta\left(1-a_{j}\right) \theta_{j}\right)$$

  for action $a \in[0,1]^{n}$, where $\alpha, \beta$ are positive constants. If $\pi_{j}$ denotes the posterior probability that $\theta_{j}=1$ given the data, prove that the Bayes rule for this prior and this loss function is to take $a_{j}=1$ if $\pi_{j}$ exceeds the threshold value $\alpha /(\alpha+\beta)$, and otherwise to take $a_{j}=0$.

  In an attempt to control the proportion of false positives, it is proposed to use a different loss function, namely,

  $$L_{1}(\theta, a) \equiv L_{0}(\theta, a)+\gamma I_{\left\{\sum a_{j}>0\right\}}\left(1-\frac{\sum \theta_{j} a_{j}}{\sum a_{j}}\right)$$

  where $\gamma>0$. Prove that the Bayes rule is once again a threshold rule, that is, we take action $a_{j}=1$ if and only if $\pi_{j}>\lambda$, and determine $\lambda$ as fully as you can.

  comment

Probability and Measure

• B2.12

  Probability and Measure | Part II, 2004

  Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and let $1 \leqslant p \leqslant \infty$.

  (a) Define the $L^{p}$-norm $\|f\|_{p}$ of a measurable function $f: \Omega \rightarrow \mathbb{R}$, and define the space $L^{p}(\Omega, \mathcal{F}, \mu) .$

  (b) Prove Minkowski's inequality:

  $$\|f+g\|_{p} \leqslant\|f\|_{p}+\|g\|_{p} \text { for } f, g \in L^{p}(\Omega, \mathcal{F}, \mu), 1 \leqslant p \leqslant \infty$$

  [You may use Hölder's inequality without proof provided it is clearly stated.]

  (c) Explain what is meant by saying that $L^{p}(\Omega, \mathcal{F}, \mu)$ is complete. Show that $L^{\infty}(\Omega, \mathcal{F}, \mu)$ is complete.

  (d) Suppose that $\left\{f_{n}: n \geqslant 1\right\}$ is a sequence of measurable functions satisfying $\left\|f_{n}\right\|_{p} \rightarrow 0$ as $n \rightarrow \infty$.

  (i) Show that if $p=\infty$, then $f_{n} \rightarrow 0$ almost everywhere.

  (ii) When $1 \leqslant p<\infty$, give an example of a measure space $(\Omega, \mathcal{F}, \mu)$ and such a sequence $\left\{f_{n}\right\}$ such that, for all $\omega \in \Omega, f_{n}(\omega) \nrightarrow 0$ as $n \rightarrow \infty$.

  comment

Quantum Physics

• A2.14

  Quantum Physics | Part II, 2004

  (i) A simple model of a crystal consists of an infinite linear array of sites equally spaced with separation $b$. The probability amplitude for an electron to be at the $n$-th site is $c_{n}, n=0, \pm 1, \pm 2, \ldots$. The Schrödinger equation for the $\left\{c_{n}\right\}$ is

  $$E c_{n}=E_{0} c_{n}-A\left(c_{n-1}+c_{n+1}\right)$$

  where $A$ is real and positive. Show that the allowed energies $E$ of the electron must lie in a band $\left|E-E_{0}\right| \leq 2 A$, and that the dispersion relation for $E$ written in terms of a certain parameter $k$ is given by

  $$E=E_{0}-2 A \cos k b$$

  What is the physical interpretation of $E_{0}, A$ and $k$ ?

  (ii) Explain briefly the idea of group velocity and show that it is given by

  $$v=\frac{1}{\hbar} \frac{d E(k)}{d k},$$

  for an electron of momentum $\hbar k$ and energy $E(k)$.

  An electron of charge $q$ confined to one dimension moves in a periodic potential under the influence of an electric field $\mathcal{E}$. Show that the equation of motion for the electron is

  $$\dot{v}=\frac{q \mathcal{E}}{\hbar^{2}} \frac{d^{2} E}{d k^{2}},$$

  where $v(t)$ is the group velocity of the electron at time $t$. Explain why

  $$m^{*}=\hbar^{2}\left(\frac{d^{2} E}{d k^{2}}\right)^{-1}$$

  can be interpreted as an effective mass.

  Show briefly how the absence from a band of an electron of charge $q$ and effective mass $m^{*}<0$ can be interpreted as the presence of a 'hole' carrier of charge $-q$ and effective mass $-m^{*}$.

  In the model of Part (i) show that

  (a) for $k^{2} \ll 12 / b^{2}$ an electron behaves like a free particle of mass $\hbar^{2} /\left(2 A b^{2}\right)$;

  (b) for $(\pi / b-k)^{2} \ll 12 / b^{2}$ a hole behaves like a free particle of mass $\hbar^{2} /\left(2 A b^{2}\right)$.

  comment

Representation Theory

• B2.6

  Representation Theory | Part II, 2004

  Let $H$ be a group with three generators $c, g, h$ and relations $c^{p}=g^{p}=h^{p}=1$, $c g=g c, c h=h c$ and $g h=c h g$ where $p$ is a prime number.

  (a) Show that $|H|=p^{3}$. Show that the conjugacy classes of $H$ are the singletons $\{1\},\{c\}, \ldots,\left\{c^{p-1}\right\}$ and the sets $\left\{g^{m} h^{n}, c g^{m} h^{n}, \ldots, c^{p-1} g^{m} h^{n}\right\}$, as $m, n$ range from 0 to $p-1$, but $(m, n) \neq(0,0)$.

  (b) Find $p^{2}$ 1-dimensional representations of $H$.

  (c) Let $\omega \neq 1$ be a $p$ th root of unity. Show that the following defines an irreducible representation of $H$ on $\mathbb{C}^{p}$ :

  $$\begin{gathered} \rho(c)=\omega \mathrm{Id}, \\ \rho(g) \mathbf{e}_{k}=\omega^{k} \mathbf{e}_{k}, \\ \rho(h) \mathbf{e}_{p}=\mathbf{e}_{1} \text { and } \rho(h) \mathbf{e}_{k}=\mathbf{e}_{k+1} \text { if } k<p \end{gathered}$$

  where the $\mathbf{e}_{k}$ are the standard basis vectors of $\mathbb{C}^{p}$.

  (d) Show that (b) and (c) cover all irreducible isomorphism classes.

  comment

Theoretical Geophysics

• A2.16

  Theoretical Geophysics | Part II, 2004

  (i) Sketch the rays in a small region near the relevant boundary produced by reflection and refraction of a $P$-wave incident (a) from the mantle on the core-mantle boundary, (b) from the outer core on the inner-core boundary, and (c) from the mantle on the Earth's surface. [In each case, the region should be sufficiently small that the boundary appears to be planar.]

  Describe the ray paths denoted by $S S, P c P, S K S$ and $P K I K P$.

  Sketch the travel-time $(T-\Delta)$ curves for $P$ and $P c P$ paths from a surface source.

  (ii) From the surface of a flat Earth, an explosive source emits $P$-waves downwards into a stratified sequence of homogeneous horizontal elastic layers of thicknesses $h_{1}, h_{2}, h_{3}, \ldots$ and $P$-wave speeds $\alpha_{1}<\alpha_{2}<\alpha_{3}<\ldots$. A line of seismometers on the surface records the travel times of the various arrivals as a function of the distance $x$ from the source. Calculate the travel times, $T_{d}(x)$ and $T_{r}(x)$, of the direct wave and the wave that reflects exactly once at the bottom of layer 1 .

  Show that the travel time for the head wave that refracts in layer $n$ is given by

  $$T_{n}=\frac{x}{\alpha_{n}}+\sum_{i=1}^{n-1} \frac{2 h_{i}}{\alpha_{i}}\left(1-\frac{\alpha_{i}^{2}}{\alpha_{n}^{2}}\right)^{1 / 2}$$

  Sketch the travel-time curves for $T_{r}, T_{d}$ and $T_{2}$ on a single diagram and show that $T_{2}$ is tangent to $T_{r}$.

  Explain how the $\alpha_{i}$ and $h_{i}$ can be constructed from the travel times of first arrivals provided that each head wave is the first arrival for some range of $x$.

  comment

Waves in Fluid and Solid Media

• B2.26

  Waves in Fluid and Solid Media | Part II, 2004

  The linearised equation of motion governing small disturbances in a homogeneous elastic medium of density $\rho$ is

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+\mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})+\mu \nabla^{2} \mathbf{u}$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement, and $\lambda$ and $\mu$ are the Lamé constants. Derive solutions for plane longitudinal waves $P$ with wavespeed $c_{P}$, and plane shear waves $S$ with wavespeed $c_{S}$.

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with an elastic solid with shear modulus $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a vacuum in $y>h$. A harmonic plane $S H$ wave of frequency $\omega$ and unit amplitude propagates from $y<0$ towards the interface $y=0$. The wavevector is in the $x y$-plane, and makes an angle $\theta$ with the $y$-axis. Derive the complex amplitude, $R$, of the reflected $S H$ wave in $y<0$. Evaluate $|R|$ for all possible values of $\bar{c}_{S} / c_{S}$, and explain your answer.

  comment