Part II, 2003, Paper 4
Part II, 2003, Paper 4
Jump to course
B4.9
Let be a smooth curve of genus 0 over an algebraically closed field . Show that
Now let be a plane projective curve defined by an irreducible homogeneous cubic polynomial.
(a) Show that if is smooth then is not isomorphic to . Standard results on the canonical class may be assumed without proof, provided these are clearly stated.
(b) Show that if has a singularity then there exists a non-constant morphism from to .
B4.5
State the Mayer-Vietoris theorem. You should give the definition of all the homomorphisms involved.
Compute the homology groups of the union of the 2 -sphere with the line segment from the North pole to the South pole.
A4.11
Define the optimal distribution problem. State what it means for a circuit to be flow-augmenting, and what it means for to be unbalanced. State the optimality theorem for flows. Describe the simplex-on-a-graph algorithm, giving a brief justification of its stopping rules.
Consider the problem of finding, in the network shown below, a minimum-cost flow from to of value 2 . Here the circled numbers are the upper arc capacities, the lower arc capacities all being zero, and the uncircled numbers are costs. Apply the simplex-on-agraph algorithm to solve this problem, taking as initial flow the superposition of a unit flow along the path and a unit flow along the path .
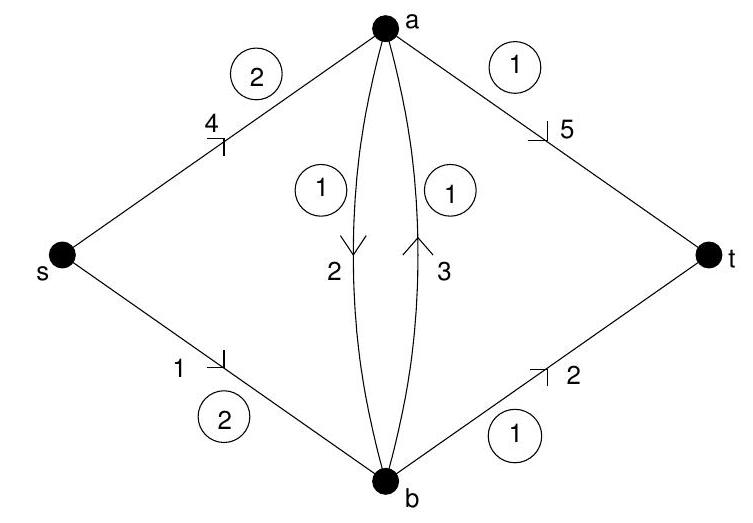
Part II 2003
B4.24
Atoms of mass in an infinite one-dimensional periodic array, with interatomic spacing , have perturbed positions , for integer . The potential between neighbouring atoms is
for positive constant . Write down the Lagrangian for the variables . Find the frequency of a normal mode of wavenumber . Define the Brillouin zone and explain why may be restricted to lie within it.
Assume now that the array is periodically-identified, so that there are effectively only atoms in the array and the atomic displacements satisfy the periodic boundary conditions . Determine the allowed values of within the Brillouin zone. Show, for allowed wavenumbers and , that
By writing as
where the sum is over allowed values of , find the Lagrangian for the variables , and hence the Hamiltonian as a function of and the conjugate momenta . Show that the Hamiltonian operator of the quantum theory can be written in the form
where is a constant and are harmonic oscillator annihilation and creation operators. What is the physical interpretation of and ? How does this show that phonons have quantized energies?
B4.12
Explain what is meant by a renewal process and by a renewal-reward process.
State and prove the law of large numbers for renewal-reward processes.
A component used in a manufacturing process has a maximum lifetime of 2 years and is equally likely to fail at any time during that period. If the component fails whilst in use, it is replaced immediately by a similar component, at a cost of . The factory owner may alternatively replace the component before failure, at a time of his choosing, at a cost of . What should the factory owner do?
B4.1
Write an essay on the Kruskal-Katona theorem. As well as stating the theorem and giving a detailed sketch of a proof, you should describe some further results that may be derived from it.
A4.14
The nave height , and the nave length for 16 Gothic-style cathedrals and 9 Romanesque-style cathedrals, all in England, have been recorded, and the corresponding output (slightly edited) is given below.

You may assume that are in suitable units, and that "style" has been set up as a factor with levels 1,2 corresponding to Gothic, Romanesque respectively.
(a) Explain carefully, with suitable graph(s) if necessary, the results of this analysis.
(b) Using the general model (in the conventional notation) explain carefully the theory needed for (a).
[Standard theorems need not be proved.]
B4.4
Define the 'pull-back' homomorphism of differential forms determined by the smooth map and state its main properties.
If is a diffeomorphism between open subsets of with coordinates on and on and the -form is equal to on , state and prove the expression for as a multiple of .
Define the integral of an -form over an oriented -manifold and prove that it is well-defined.
Show that the inclusion map , of an oriented -submanifold (without boundary) into , determines an element of . If and , for and fixed in , what is the relation between and , where is the fundamental cohomology class of and is the projection onto the first factor?
B4.17
Let be an orientation-preserving invertible map of the circle onto itself, with a lift . Define the rotation numbers and .
Suppose that , where and are coprime integers. Prove that the map has periodic points of least period , and no periodic points with any least period not equal to .
Now suppose that is irrational. Explain the distinction between wandering and non-wandering points under . Let be the set of limit points of the sequence . Prove
(a) that the set is independent of and is the smallest closed, non-empty, -invariant subset of ;
(b) that is the set of non-wandering points of ;
(c) that is either the whole of or a Cantor set in .
A4.6
Explain what is meant by a steady-state bifurcation of a fixed point of an ODE , in , where is a real parameter. Give examples for of equations exhibiting saddle-node, transcritical and pitchfork bifurcations.
Consider the system in , with ,
Show that the fixed point has a bifurcation when , while the fixed points have a bifurcation when . By finding the first approximation to the extended centre manifold, construct the normal form at the bifurcation point in each case, and determine the respective bifurcation types. Deduce that for just greater than , and for just less than 1 , there is a stable pair of "mixed-mode" solutions with .
B4.21
Describe the physical meaning of the various components of the stress-energy tensor of the electromagnetic field.
Suppose that one is given an electric field and a magnetic field . Show that the angular momentum about the origin of these fields is
where the integral is taken over all space.
A point electric charge is at the origin, and has electric field
A point magnetic monopole of strength is at and has magnetic field
Find the component, along the axis between the electric charge and the magnetic monopole, of the angular momentum of the electromagnetic field about the origin.
[Hint: You may find it helpful to express both and as gradients of scalar potentials.]
A4.5
Let be the electric field due to a continuous static charge distribution for which as . Starting from consideration of a finite system of point charges, deduce that the electrostatic energy of the charge distribution is
where the volume integral is taken over all space.
A sheet of perfectly conducting material in the form of a surface , with unit normal , carries a surface charge density . Let denote the normal components of the electric field on either side of . Show that
Three concentric spherical shells of perfectly conducting material have radii with . The innermost and outermost shells are held at zero electric potential. The other shell is held at potential . Find the potentials in and in . Compute the surface charge density on the shell of radius . Use the formula to compute the electrostatic energy of the system.
B4.26
Show that the complex potential in the complex plane,
describes irrotational, inviscid flow past the rigid cylinder , placed in a uniform flow with circulation .
Show that the transformation
maps the circle in the plane onto the flat plate airfoil in the plane . Hence, write down an expression for the complex potential, , of uniform flow past the flat plate, with circulation . Indicate very briefly how the value of might be chosen to yield a physical solution.
Calculate the turning moment, , exerted on the flat plate by the flow.
(You are given that
where is the fluid density and the integral is to be completed around a contour enclosing the circle ).
A4.15 B4.22
Discuss the quantum mechanics of the one-dimensional harmonic oscillator using creation and annihilation operators, showing how the energy levels are calculated.
A quantum mechanical system consists of two interacting harmonic oscillators and has the Hamiltonian
For , what are the degeneracies of the three lowest energy levels? For compute, to lowest non-trivial order in perturbation theory, the energies of the ground state and first excited state.
[Standard results for perturbation theory may be stated without proof.]
A4.3
(i) State the Monotone Convergence Theorem and explain briefly how to prove it.
(ii) For which real values of is ?
Let . Using the Monotone Convergence Theorem and the identity
prove carefully that
B4.3
Write an essay on finite fields and their Galois theory.
A4.17 B4.25
What are "inertial coordinates" and what is their physical significance? [A proof of the existence of inertial coordinates is not required.] Let be the origin of inertial coordinates and let be the curvature tensor at (with all indices lowered). Show that can be expressed entirely in terms of second partial derivatives of the metric , evaluated at . Use this expression to deduce that (a) (b) (c) .
Starting from the expression for in terms of the Christoffel symbols, show (again by using inertial coordinates) that
Obtain the contracted Bianchi identities and explain why the Einstein equations take the form
where is the energy-momentum tensor of the matter and is an arbitrary constant.
A4.7
Write an essay on the Theorema Egregium for surfaces in .
A4.9
Write an essay on the vertex-colouring of graphs drawn on compact surfaces other than the sphere. You should include a proof of Heawood's bound, and an example of a surface for which this bound is not attained.
A4.4
Write an essay on the theory of invariants. Your essay should discuss the theorem on the finite generation of the ring of invariants, the theorem on elementary symmetric functions, and some examples of calculation of rings of invariants.
B4.7
Let be a Hilbert space and let .
(a) Show that if then is invertible.
(b) Prove that if is invertible and if satisfies , then is invertible.
(c) Define what it means for to be compact. Prove that the set of compact operators on is a closed subset of .
(d) Prove that is compact if and only if there is a sequence in , where each operator has finite rank, such that as .
(e) Suppose that , where is invertible and is compact. Prove that then, also, , where is invertible and has finite rank.
B4.13
State and prove the Fano and generalized Fano inequalities.
A4.8 B4.10
Write an essay on propositional logic. You should include all relevant definitions, and should cover the Completeness Theorem, as well as the Compactness Theorem and the Decidability Theorem.
[You may assume that the set of primitive propositions is countable. You do not need to give proofs of simple examples of syntactic implication, such as the fact that is a theorem or that and syntactically imply .]
A4.1
Consider a pack of cards labelled . We repeatedly take the top card and insert it uniformly at random in one of the 52 possible places, that is, either on the top or on the bottom or in one of the 50 places inside the pack. How long on average will it take for the bottom card to reach the top?
Let denote the probability that after iterations the cards are found in increasing order. Show that, irrespective of the initial ordering, converges as , and determine the limit . You should give precise statements of any general results to which you appeal.
Show that, at least until the bottom card reaches the top, the ordering of cards inserted beneath it is uniformly random. Hence or otherwise show that, for all ,
A4.21
Let denote the solution for of
subject to the conditions that and as , where ; it may be assumed that for . Write in the form
and consider an asymptotic expansion of the form
valid in the limit with . Find and .
It is known that the solution is of the form
where
and the constant factor depends on . By letting , show that the expression
satisfies the relevant differential equation with an error of as . Comment on the relationship between your answers for and .
B4.19
By setting , where and are to be suitably chosen, explain how to find integral representations of the solutions of the equation
where is a non-zero real constant and is complex. Discuss in the particular case that is restricted to be real and positive and distinguish the different cases that arise according to the of .
Show that in this particular case, by choosing as a closed contour around the origin, it is possible to express a solution in the form
where is a constant.
Show also that for there are solutions that satisfy
where is a constant.
A4.22
Let denote the boundary values of functions which are analytic inside and outside a disc of radius centred at the origin. Let denote the boundary of this disc.
Suppose that satisfy the jump condition
(a) Show that the associated index is 1 .
(b) Find the canonical solution of the homogeneous problem, i.e. the solution satisfying
(c) Find the general solution of the Riemann-Hilbert problem satisfying the above jump condition as well as
(d) Use the above result to solve the linear singular integral problem
B4.6
Write an essay on the Dirichlet unit theorem with particular reference to quadratic fields.
A4.10
Write an essay describing the factor base method for factorising a large odd positive integer . Your essay should include a detailed explanation of how the continued fraction of can be used to find a suitable factor base.
A4.23 B4.20
Write an essay on the conjugate gradient method. Your essay should include:
(a) a statement of the method and a sketch of its derivation;
(b) discussion, without detailed proofs, but with precise statements of relevant theorems, of the conjugacy of the search directions;
(c) a description of the standard form of the algorithm;
(d) discussion of the connection of the method with Krylov subspaces.
B4.14
The scalars , are related by the equations
where is a sequence of uncorrelated random variables with means of 0 and variances of 1. Given that is an unbiased estimate of of variance 1 , the control variable is to be chosen at time on the basis of the information , where and . Let be the Kalman filter estimates of computed from
by appropriate choices of . Show that the variance of is .
Define and
Show that , where and
How would the expression for differ if had a variance different from
B4.18
Discuss the basic properties of the Fourier transform and how it is used in the study of partial differential equations.
The essay should include: definition and basic properties, inversion theorem, applications to establishing well-posedness of evolution partial differential equations with constant coefficients.
A4.2
The action of a Hamiltonian system may be regarded as a function of the final coordinates , and the final time by setting
where the initial coordinates and time are held fixed, and are the solutions to Hamilton's equations with Hamiltonian , satisfying .
(a) Show that under an infinitesimal change of the final coordinates and time , the change in is
(b) Hence derive the Hamilton-Jacobi equation
(c) If we can find a solution to ,
where are integration constants, then we can use as a generating function of type , where
Show that the Hamiltonian in the new coordinates vanishes.
(d) Write down and solve the Hamilton-Jacobi equation for the one-dimensional simple harmonic oscillator, where . Show the solution takes the form . Using this as a generating function show that the new coordinates are constants of the motion and give their physical interpretation.
A4.13 B4.15
Write an account, with appropriate examples, of inference in multiparameter exponential families. Your account should include a discussion of natural statistics and their properties and of various conditional tests on natural parameters.
B4.11
Let be integrable with respect to Lebesgue measure on . Prove that, if
for every sub-interval of , then almost everywhere on .
Now define
Prove that is continuous on . Show that, if is zero on , then is zero almost everywhere on .
Suppose now that is bounded and Lebesgue integrable on . By applying the Dominated Convergence Theorem to
or otherwise, show that, if is differentiable on , then almost everywhere on .
The functions have the properties:
(a) converges pointwise to a differentiable function on ,
(b) each has a continuous derivative with on ,
(c) converges pointwise to some function on .
Deduce that
almost everywhere on .
A4.16
Describe the energy band structure available to electrons moving in crystalline materials. How can it be used to explain the properties of crystalline materials that are conductors, insulators and semiconductors?
Where does the Fermi energy lie in an intrinsic semiconductor? Describe the process of doping of semiconductors and explain the difference between -type and -type doping. What is the effect of the doping on the position of the Fermi energy in the two cases?
Why is there a potential difference across a junction of -type and -type semiconductors?
Derive the relation
between the current, , and the voltage, , across an junction, where is the total minority current in the semiconductor and is the charge on the electron, is the temperature and is Boltzmann's constant. Your derivation should include an explanation of the terms majority current and minority current.
Why can the junction act as a rectifier?
B4.2
Assume that the group of matrices of determinant 1 with entries from the field has presentation
Show that the subgroup generated by is central and that the quotient group can be identified with the alternating group . Assuming further that has seven conjugacy classes find the character table.
Is it true that every irreducible character is induced up from the character of a 1-dimensional representation of some subgroup?
[Hint: You may find it useful to note that may be regarded as a subgroup of , providing a faithful 2-dimensional representation; the subgroup generated by and is the quaternion group of order 8 , acting irreducibly.]
B4.8
(a) Define the degree of a meromorphic function on the Riemann sphere . State the Riemann-Hurwitz theorem.
Let and be two rational functions on the sphere . Show that
Deduce that
(b) Describe the topological type of the Riemann surface defined by the equation in . [You should analyse carefully the behaviour as and approach .]
B4.23
A gas of non-interacting identical bosons in volume , with one-particle energy levels , is in equilibrium at temperature and chemical potential . Let be the number of particles in the th one-particle state. Write down an expression for the grand partition function . Write down an expression for the probability of finding a given set of occupation numbers of the one-particle states. Hence determine the mean occupation numbers (the Bose-Einstein distribution). Write down expressions, in terms of the mean occupation numbers, for the total energy and total number of particles .
Write down an expression for the grand potential in terms of . Given that
show that can be written in the form
for some function , which you should determine. Hence show that for any change of the gas that leaves the mean occupation numbers unchanged. Consider a (quasi-static) change of with this property. Using the formula
and given that for each , show that
What is the value of for photons?
Let , so that is a function only of and . Why does the energy density depend only on Using the Maxwell relation
and the first law of thermodynamics for reversible changes, show that
and hence that
for some power that you should determine. Show further that
Hence verify, given , that is left unchanged by a change of at constant .
A4.18
Let be the density of states of a particle in volume as a function of the magnitude of the particle's momentum. Explain why , where is Planck's constant. Write down the Bose-Einstein and Fermi-Dirac distributions for the (average) number of particles of an ideal gas with momentum . Hence write down integrals for the (average) total number of particles and the (average) total energy as functions of temperature and chemical potential . Why do and also depend on the volume
Electromagnetic radiation in thermal equilibrium can be regarded as a gas of photons. Why are photons "ultra-relativistic" and how is photon momentum related to the frequency of the radiation? Why does a photon gas have zero chemical potential? Use your formula for to express the energy density of electromagnetic radiation in the form
where is a function of that you should determine up to a dimensionless multiplicative constant. Show that is independent of when , where is Boltzmann's constant. Let be the value of at the maximum of the function ; how does depend on ?
Let be the photon number density at temperature . Show that for some power , which you should determine. Why is unchanged as the volume is increased quasi-statically? How does depend on under these circumstances? Applying your result to the Cosmic Microwave Background Radiation (CMBR), deduce how the temperature of the CMBR depends on the scale factor of the Universe. At a time when , the Universe underwent a transition from an earlier time at which it was opaque to a later time at which it was transparent. Explain briefly the reason for this transition and its relevance to the CMBR.
An ideal gas of fermions of mass is in equilibrium at temperature and chemical potential with a gas of its own anti-particles and photons . Assuming that chemical equilibrium is maintained by the reaction
determine the chemical potential of the antiparticles. Let and be the number densities of and , respectively. What will their values be for if ? Given that , but , show that
where is the fermion number density at zero chemical potential and is a positive function of the dimensionless ratio . What is when ?
Given that , obtain an expression for the ratio in terms of and the function . Supposing that is either a proton or neutron, why should you expect the ratio to remain constant as the Universe expands?
A4.12 B4.16
A single-period market contains risky assets, , initially worth , and at time 1 worth random amounts whose first two moments are given by
An agent with given initial wealth is considering how to invest in the available assets, and has asked for your advice. Develop the theory of the mean-variance efficient frontier far enough to exhibit explicitly the minimum-variance portfolio achieving a required mean return, assuming that is non-singular. How does your analysis change if a riskless asset is added to the market? Under what (sufficient) conditions would an agent maximising expected utility actually choose a portfolio on the mean-variance efficient frontier?
A4.20
Define the Rossby number. Under what conditions will a fluid flow be at (a) high and (b) low values of the Rossby number? Briefly describe both an oceanographic and a meteorological example of each type of flow.
Explain the concept of quasi-geostrophy for a thin layer of homogeneous fluid in a rapidly rotating system. Write down the quasi-geostrophic approximation for the vorticity in terms of the pressure, the fluid density and the rate of rotation. Define the potential vorticity and state the associated conservation law.
A broad current flows directly eastwards ( direction) with uniform velocity across a flat ocean basin of depth . The current encounters a low, two-dimensional ridge of width and height , whose axis is aligned in the north-south direction. Neglecting any effects of stratification and assuming a constant vertical rate of rotation , such that the Rossby number is small, determine the effect of the ridge on the current. Show that the direction of the current after it leaves the ridge is dependent on the cross-sectional area of the ridge, but not on the explicit form of .
A4.19
A shallow layer of fluid of viscosity , density and depth lies on a rigid horizontal plane and is bounded by impermeable barriers at and . Gravity acts vertically and a wind above the layer causes a shear stress to be exerted on the upper surface in the direction. Surface tension is negligible compared to gravity.
(a) Assuming that the steady flow in the layer can be analysed using lubrication theory, show that the horizontal pressure gradient is given by and hence that
Show also that the fluid velocity at the surface is equal to , and sketch the velocity profile for .
(b) In the case in which is a constant, , and assuming that the difference between and its average value remains small compared with , show that
provided that
(c) Surfactant at surface concentration is added to the surface, so that now
where is a positive constant. The surfactant is advected by the surface fluid velocity and also experiences a surface diffusion with diffusivity . Write down the equation for conservation of surfactant, and hence show that
From equations (1), (2) and (3) deduce that
where is a constant. Assuming once more that , and that at , show further that
provided that
B4.27
Show that the equations governing isotropic linear elasticity have plane-wave solutions, identifying them as or waves.
A semi-infinite elastic medium in (where is the vertical coordinate) with density and Lamé moduli and is overlaid by a layer of thickness (in ) of a second elastic medium with density and Lamé moduli and . The top surface at is free, i.e. the surface tractions vanish there. The speed of S-waves is lower in the layer, i.e. . For a time-harmonic SH-wave with horizontal wavenumber and frequency , which oscillates in the slow top layer and decays exponentially into the fast semi-infinite medium, derive the dispersion relation for the apparent wave speed ,
Show graphically that there is always one root, and at least one higher mode if .