Part II, 2003, Paper 2

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2003

  (a) For which polynomials $f(x)$ of degree $d>0$ does the equation $y^{2}=f(x)$ define a smooth affine curve?

  (b) Now let $C$ be the completion of the curve defined in (a) to a projective curve. For which polynomials $f(x)$ of degree $d>0$ is $C$ a smooth projective curve?

  (c) Suppose that $C$, defined in (b), is a smooth projective curve. Consider a map $p: C \rightarrow \mathbb{P}^{1}$, given by $p(x, y)=x$. Find the degree and the ramification points of $p$.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2003

  Define the fundamental group of a topological space and explain briefly why a continuous map gives rise to a homomorphism between fundamental groups.

  Let $X$ be a subspace of the Euclidean space $\mathbb{R}^{3}$ which contains all of the points $(x, y, 0)$ with $(x, y) \neq(0,0)$, and which does not contain any of the points $(0,0, z)$. Show that $X$ has an infinite fundamental group.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2003

  (i) Consider a network with node set $N$ and set of directed arcs $A$ equipped with functions $d^{+}: A \rightarrow \mathbb{Z}$ and $d^{-}: A \rightarrow \mathbb{Z}$ with $d^{-} \leqslant d^{+}$. Given $u: N \rightarrow \mathbb{R}$ we define the differential $\Delta u: A \rightarrow \mathbb{R}$ by $\Delta u(j)=u\left(i^{\prime}\right)-u(i)$ for $j=\left(i, i^{\prime}\right) \in A$. We say that $\Delta u$ is a feasible differential if

  $$d^{-}(j) \leqslant \Delta u(j) \leqslant d^{+}(j) \text { for all } j \in A$$

  Write down a necessary and sufficient condition on $d^{+}, d^{-}$for the existence of a feasible differential and prove its necessity.

  Assuming Minty's Lemma, describe an algorithm to construct a feasible differential and outline how this algorithm establishes the sufficiency of the condition you have given.

  (ii) Let $E \subseteq S \times T$, where $S, T$ are finite sets. A matching in $E$ is a subset $M \subseteq E$ such that, for all $s, s^{\prime} \in S$ and $t, t^{\prime} \in T$,

  $$\begin{array}{lll} (s, t),\left(s^{\prime}, t\right) \in M & \text { implies } & s=s^{\prime} \\ (s, t),\left(s, t^{\prime}\right) \in M & \text { implies } & t=t^{\prime} \end{array}$$

  A matching $M$ is maximal if for any other matching $M^{\prime}$ with $M \subseteq M^{\prime}$ we must have $M=M^{\prime}$. Formulate the problem of finding a maximal matching in $E$ in terms of an optimal distribution problem on a suitably defined network, and hence in terms of a standard linear optimization problem.

  [You may assume that the optimal distribution subject to integer constraints is integervalued.]

  comment

Applications of Quantum Mechanics

• B2.22

  Applications of Quantum Mechanics | Part II, 2003

  The Hamiltonian $H_{0}$ for a single electron atom has energy eigenstates $\left|\psi_{n}\right\rangle$ with energy eigenvalues $E_{n}$. There is an interaction with an electromagnetic wave of the form

  $$H_{1}=-e \mathbf{r} \cdot \boldsymbol{\epsilon} \cos (\mathbf{k} \cdot \mathbf{r}-\omega t), \quad \omega=|\mathbf{k}| c,$$

  where $\boldsymbol{\epsilon}$ is the polarisation vector. At $t=0$ the atom is in the state $\left|\psi_{0}\right\rangle$. Find a formula for the probability amplitude, to first order in $e$, to find the atom in the state $\left|\psi_{1}\right\rangle$ at time $t$. If the atom has a size $a$ and $|\mathbf{k}| a \ll 1$ what are the selection rules which are relevant? For $t$ large, under what circumstances will the transition rate be approximately constant?

  [You may use the result

  $$\left.\int_{-\infty}^{\infty} \frac{\sin ^{2} \lambda t}{\lambda^{2}} d \lambda=\pi|t| . \quad\right]$$

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2003

  Let $S_{k}$ be the sum of $k$ independent exponential random variables of rate $k \mu$. Compute the moment generating function of $S_{k}$.

  Consider, for each fixed $k$ and for $0<\lambda<\mu$, an $M / G / 1$ queue with arrival rate $\lambda$ and with service times distributed as $S_{k}$. Assume that the queue is empty at time 0 and write $T_{k}$ for the earliest time at which a customer departs leaving the queue empty. Show that, as $k \rightarrow \infty, T_{k}$ converges in distribution to a random variable $T$ whose moment generating function $M_{T}(\theta)$ satisfies

  $$\log \left(1-\frac{\theta}{\lambda}\right)+\log M_{T}(\theta)=\left(\frac{\theta-\lambda}{\mu}\right)\left(1-M_{T}(\theta)\right)$$

  Hence obtain the mean value of $T$.

  For what service-time distribution would the empty-to-empty time correspond exactly to $T$ ?

  comment

Coding and Cryptography

• A2.9

  Coding and Cryptography | Part II, 2003

  (i) Answer the following questions briefly but clearly.

  (a) How does coding theory apply when the error rate $p>1 / 2$ ?

  (b) Give an example of a code which is not a linear code.

  (c) Give an example of a linear code which is not a cyclic code.

  (d) Give an example of a general feedback register with output $k_{j}$, and initial fill $\left(k_{0}, k_{1}, \ldots, k_{N}\right)$, such that

  $$\left(k_{n}, k_{n+1}, \ldots, k_{n+N}\right) \neq\left(k_{0}, k_{1}, \ldots, k_{N}\right)$$

  for all $n \geqslant 1$.

  (e) Explain why the original Hamming code can not always correct two errors.

  (ii) Describe the Rabin-Williams scheme for coding a message $x$ as $x^{2}$ modulo a certain $N$. Show that, if $N$ is chosen appropriately, breaking this code is equivalent to factorising the product of two primes.

  comment

Combinatorics

• B2.5

  Combinatorics | Part II, 2003

  Prove Ramsey's theorem in its usual infinite form, namely, that if $\mathbb{N}^{(r)}$ is finitely coloured then there is an infinite subset $M \subset \mathbb{N}$ such that $M^{(r)}$ is monochromatic.

  Now let the graph $\mathbb{N}^{(2)}$ be coloured with an infinite number of colours in such a way that there is no infinite $M \subset \mathbb{N}$ with $M^{(2)}$ monochromatic. By considering a suitable 2-colouring of the set $\mathbb{N}^{(4)}$ of 4 -sets, show that there is an infinite $M \subset \mathbb{N}$ with the property that any two edges of $M^{(2)}$ of the form $a d, b c$ with $a<b<c<d$ have different colours.

  By considering two further 2-colourings of $\mathbb{N}^{(4)}$, show that there is an infinite $M \subset \mathbb{N}$ such that any two non-incident edges of $M^{(2)}$ have different colours.

  comment

Computational Statistics and Statistical Modelling

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2003

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \quad \log \mu_{i}=\alpha+\beta t_{i}, \quad \text { for } \quad i=1, \ldots, n,$$

  where $\alpha, \beta$ are two unknown parameters, and $t_{1}, \ldots, t_{n}$ are given covariates, each of dimension 1. Find equations for $\hat{\alpha}, \hat{\beta}$, the maximum likelihood estimators of $\alpha, \beta$, and show how an estimate of $\operatorname{var}(\hat{\beta})$ may be derived, quoting any standard theorems you may need.

  (ii) By 31 December 2001, the number of new vCJD patients, classified by reported calendar year of onset, were

  $$8,10,11,14,17,29,23$$

  for the years

  $$1994, \ldots, 2000 \text { respectively }$$

  Discuss carefully the (slightly edited) $R$ output for these data given below, quoting any standard theorems you may need.

  year

  year

  [1] 1994199519961997199819992000

  $>$ tot

  [1] $\begin{array}{lllllll}8 & 10 & 11 & 14 & 17 & 29 & 23\end{array}$

  first.glm - glm(tot year, family = poisson)

  $>\operatorname{summary}$ (first.glm)

  Call:

  glm(formula $=$ tot year, family $=$ poisson $)$

  Coefficients

  Estimate Std. Error z value $\operatorname{Pr}(>|z|)$

  (Intercept) $-407.8128599 .35366-4.1054 .05 \mathrm{e}-05$

  year $\quad 0.20556 \quad 0.04973 \quad 4.1333 .57 e-05$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $20.7753$ on 6 degrees of freedom

  Residual deviance: $2.7931$ on 5 degrees of freedom

  Number of Fisher Scoring iterations: 3

  Part II 2003

  comment

Differentiable Manifolds

• B2.7

  Differentiable Manifolds | Part II, 2003

  Let $M$ and $N$ be smooth manifolds. If $\pi: M \times N \rightarrow M$ is the projection onto the first factor and $\pi^{*}$ is the map in cohomology induced by the pull-back map on differential forms, show that $\pi^{*}\left(H^{k}(M)\right)$ is a direct summand of $H^{k}(M \times N)$ for each $k \geqslant 0$.

  Taking $H^{k}(M)$ to be zero for $k<0$ and $k>\operatorname{dim} M$, show that for $n \geqslant 1$ and all $k$

  $$H^{k}\left(M \times S^{n}\right) \cong H^{k}(M) \oplus H^{k-n}(M)$$

  [You might like to use induction in n.]

  comment

Dynamics of Differential Equations

• A2.6 B2.4

  Dynamics of Differential Equations | Part II, 2003

  (i) What is a Liapunov function?

  Consider the second order ODE

  $$\dot{x}=y, \quad \dot{y}=-y-\sin ^{3} x$$

  By finding a suitable Liapunov function of the form $V(x, y)=f(x)+g(y)$, where $f$ and $g$ are to be determined, show that the origin is asymptotically stable. Using your form of $V$, find the greatest value of $y_{0}$ such that a trajectory through $\left(0, y_{0}\right)$ is guaranteed to tend to the origin as $t \rightarrow \infty$.

  [Any theorems you use need not be proved but should be clearly stated.]

  (ii) Explain the use of the stroboscopic method for investigating the dynamics of equations of the form $\ddot{x}+x=\epsilon f(x, \dot{x}, t)$, when $|\epsilon| \ll 1$. In particular, for $x=R \cos (t+\theta)$, $\dot{x}=-R \sin (t+\theta)$ derive the equations, correct to order $\epsilon$,

  $$\dot{R}=-\epsilon\langle f \sin (t+\theta)\rangle, \quad R \dot{\theta}=-\epsilon\langle f \cos (t+\theta)\rangle$$

  where the brackets denote an average over the period of the unperturbed oscillator.

  Find the form of the right hand sides of these equations explicitly when $f=$ $\Gamma x^{2} \cos t-3 q x$, where $\Gamma>0, q \neq 0$. Show that apart from the origin there is another fixed point of $(*)$, and determine its stability. Sketch the trajectories in $(R, \theta)$ space in the case $q>0$. What do you deduce about the dynamics of the full equation?

  [You may assume that $\left\langle\cos ^{2} t\right\rangle=\frac{1}{2},\left\langle\cos ^{4} t\right\rangle=\frac{3}{8},\left\langle\cos ^{2} t \sin ^{2} t\right\rangle=\frac{1}{8}$.]

  comment

Electrodynamics

• B2.20

  Electrodynamics | Part II, 2003

  A plane electromagnetic wave of frequency $\omega$ and wavevector $\mathbf{k}$ has an electromagnetic potential given by

  $$A^{a}=A \epsilon^{a} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}$$

  where $A$ is the amplitude of the wave and $\epsilon^{a}$ is the polarization vector. Explain carefully why there are two independent polarization states for such a wave, and why $|\mathbf{k}|^{2}=\omega^{2}$.

  A wave travels in the positive $z$-direction with polarization vector $\epsilon^{a}=(0,1, i, 0)$. It is incident at $z=0$ on a plane surface which conducts perfectly in the $x$-direction, but not at all in the $y$-direction. Find an expression for the electromagnetic potential of the radiation that is reflected from this surface.

  comment

Foundations of Quantum Mechanics

• A2.13 B2.21

  Foundations of Quantum Mechanics | Part II, 2003

  (i) Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture. Explain how the two pictures provide equivalent descriptions of observable results.

  Derive the equation of motion for an operator in the Heisenberg picture.

  (ii) For a particle moving in one dimension, the Hamiltonian is

  $$\hat{H}=\frac{\hat{p}^{2}}{2 m}+V(\hat{x}),$$

  where $\hat{x}$ and $\hat{p}$ are the position and momentum operators, and the state vector is $|\Psi\rangle$.

  Eigenstates of $\hat{x}$ and $\hat{p}$ satisfy

  $$\langle x \mid p\rangle=\left(\frac{1}{2 \pi \hbar}\right)^{1 / 2} e^{i p x / \hbar}, \quad\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right) .$$

  Use standard methods in the Dirac formalism to show that

  $$\begin{aligned} &\left\langle x|\hat{p}| x^{\prime}\right\rangle=-i \hbar \frac{\partial}{\partial x} \delta\left(x-x^{\prime}\right) \\ &\left\langle p|\hat{x}| p^{\prime}\right\rangle=i \hbar \frac{\partial}{\partial p} \delta\left(p-p^{\prime}\right) \end{aligned}$$

  Calculate $\left\langle x|\hat{H}| x^{\prime}\right\rangle$ and express $\langle x|\hat{p}| \Psi\rangle,\langle x|\hat{H}| \Psi\rangle$ in terms of the position space wave function $\Psi(x)$.

  Compute the momentum space Hamiltonian for the harmonic oscillator with potential $V(\hat{x})=\frac{1}{2} m \omega^{2} \hat{x}^{2}$.

  comment

Functional Analysis

• A2.3 B2.2

  Functional Analysis | Part II, 2003

  (i) Define the dual of a normed vector space $(E,\|\cdot\|)$. Show that the dual is always a complete normed space.

  Prove that the vector space $\ell_{1}$, consisting of those real sequences $\left(x_{n}\right)_{n=1}^{\infty}$ for which the norm

  $$\left\|\left(x_{n}\right)\right\|_{1}=\sum_{n=1}^{\infty}\left|x_{n}\right|$$

  is finite, has the vector space $\ell_{\infty}$ of all bounded sequences as its dual.

  (ii) State the Stone-Weierstrass approximation theorem.

  Let $K$ be a compact subset of $\mathbb{R}^{n}$. Show that every $f \in C_{\mathbb{R}}(K)$ can be uniformly approximated by a sequence of polynomials in $n$ variables.

  Let $f$ be a continuous function on $[0,1] \times[0,1]$. Deduce that

  $$\int_{0}^{1}\left(\int_{0}^{1} f(x, y) d x\right) d y=\int_{0}^{1}\left(\int_{0}^{1} f(x, y) d y\right) d x$$

  comment

General Relativity

• A2.15 B2.23

  General Relativity | Part II, 2003

  (i) What is a "stationary" metric? What distinguishes a stationary metric from a "static" metric?

  A Killing vector field $K^{a}$ of a metric $g_{a b}$ satisfies

  $$K_{a ; b}+K_{b ; a}=0$$

  Show that this is equivalent to

  $$g_{a b, c} K^{c}+g_{a c} K_{, b}^{c}+g_{c b} K_{, a}^{c}=0$$

  Hence show that a constant vector field $K^{a}$ with one non-zero component, $K^{4}$ say, is a Killing vector field if $g_{a b}$ is independent of $x^{4}$.

  (ii) Given that $K^{a}$ is a Killing vector field, show that $K_{a} u^{a}$ is constant along the geodesic worldline of a massive particle with 4-velocity $u^{a}$. Hence find the energy $\varepsilon$ of a particle of unit mass moving in a static spacetime with metric

  $$d s^{2}=h_{i j} d x^{i} d x^{j}-e^{2 U} d t^{2}$$

  where $h_{i j}$ and $U$ are functions only of the space coordinates $x^{i}$. By considering a particle with speed small compared with that of light, and given that $U \ll 1$, show that $h_{i j}=\delta_{i j}$ to lowest order in the Newtonian approximation, and that $U$ is the Newtonian potential.

  A metric admits an antisymmetric tensor $Y_{a b}$ satisfying

  $$Y_{a b ; c}+Y_{a c ; b}=0$$

  Given a geodesic $x^{a}(\lambda)$, let $s_{a}=Y_{a b} \dot{x}^{b}$. Show that $s_{a}$ is parallelly propagated along the geodesic, and that it is orthogonal to the tangent vector of the geodesic. Hence show that the scalar

  $$\phi=s^{a} s_{a}$$

  is constant along the geodesic.

  comment

Geometry of Surfaces

• A2.7

  Geometry of Surfaces | Part II, 2003

  (i) What are geodesic polar coordinates at a point $P$ on a surface $M$ with a Riemannian metric $d s^{2}$ ?

  Assume that

  $$d s^{2}=d r^{2}+H(r, \theta)^{2} d \theta^{2}$$

  for geodesic polar coordinates $r, \theta$ and some function $H$. What can you say about $H$ and $d H / d r$ at $r=0$ ?

  (ii) Given that the Gaussian curvature $K$ may be computed by the formula $K=-H^{-1} \partial^{2} H / \partial r^{2}$, show that for small $R$ the area of the geodesic disc of radius $R$ centred at $P$ is

  $$\pi R^{2}-(\pi / 12) K R^{4}+a(R),$$

  where $a(R)$ is a function satisfying $\lim _{R \rightarrow 0} a(R) / R^{4}=0$.

  comment

Groups, Rings and Fields

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2003

  (i) In each of the following two cases, determine a highest common factor in $\mathbb{Z}[i]$ :

  (a) $3+4 i, 4-3 i$;

  (b) $3+4 i, 1+2 i$.

  (ii) State and prove the Eisenstein criterion for irreducibility of polynomials with integer coefficients. Show that, if $p$ is prime, the polynomial

  $$1+x+\cdots+x^{p-1}$$

  is irreducible over $\mathbb{Z}$.

  comment

Information Theory

• B2.14

  Information Theory | Part II, 2003

  Let $\mathcal{X}$ be a binary linear code of length $n$, rank $k$ and distance $d$. Let $x=$ $\left(x_{1}, \ldots, x_{n}\right) \in \mathcal{X}$ be a codeword with exactly $d$ non-zero digits.

  (a) Prove that $n \geqslant d+k-1$ (the Singleton bound).

  (b) Prove that truncating $\mathcal{X}$ on the non-zero digits of $x$ produces a code $\mathcal{X}^{\prime}$ of length $n-d$, rank $k-1$ and distance $d^{\prime}$ for some $d^{\prime} \geqslant\left\lceil\frac{d}{2}\right\rceil$. Here $\lceil a\rceil$ is the integer satisfying $a \leqslant\lceil a\rceil<a+1, a \in \mathbb{R}$.

  [Hint: Assume the opposite. Then, given $y \in \mathcal{X}$ and its truncation $y^{\prime} \in \mathcal{X}^{\prime}$, consider the coordinates where $x$ and $y$ have 1 in common (i.e. $x_{j}=y_{j}=1$ ) and where they differ $\left(\right.$ e.g. $x_{j}=1$ and $\left.y_{j}=0\right)$.]

  (c) Deduce that $n \geqslant d+\sum_{1 \leqslant \ell \leqslant k-1}\left\lceil\frac{d}{2^{\ell}}\right\rceil$ (an improved Singleton bound).

  comment

Logic, Computation and Set Theory

• B2.11

  Logic, Computation and Set Theory | Part II, 2003

  State the Axiom of Replacement.

  Show that for any set $x$ there is a transitive set $y$ that contains $x$, indicating where in your argument you have used the Axiom of Replacement. No form of recursion theorem may be assumed without proof.

  Which of the following are true and which are false? Give proofs or counterexamples as appropriate. You may assume standard properties of ordinals.

  (a) If $x$ is a transitive set then $x$ is an ordinal.

  (b) If each member of a set $x$ is an ordinal then $x$ is an ordinal.

  (c) If $x$ is a transitive set and each member of $x$ is an ordinal then $x$ is an ordinal.

  comment

Markov Chains

• A2.1

  Markov Chains | Part II, 2003

  (i) What is meant by a Poisson process of rate $\lambda$ ? Show that if $\left(X_{t}\right)_{t \geqslant 0}$ and $\left(Y_{t}\right)_{t \geqslant 0}$ are independent Poisson processes of rates $\lambda$ and $\mu$ respectively, then $\left(X_{t}+Y_{t}\right)_{t \geqslant 0}$ is also a Poisson process, and determine its rate.

  (ii) A Poisson process of rate $\lambda$ is observed by someone who believes that the first holding time is longer than all subsequent holding times. How long on average will it take before the observer is proved wrong?

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2003

  (i) Explain how to solve the Fredholm integral equation of the second kind,

  $$f(x)=\mu \int_{a}^{b} K(x, t) f(t) d t+g(x)$$

  in the case where $K(x, t)$ is of the separable (degenerate) form

  $$K(x, t)=a_{1}(x) b_{1}(t)+a_{2}(x) b_{2}(t)$$

  (ii) For what values of the real constants $\lambda$ and $A$ does the equation

  $$u(x)=\lambda \sin x+A \int_{0}^{\pi}(\cos x \cos t+\cos 2 x \cos 2 t) u(t) d t$$

  have (a) a unique solution, (b) no solution?

  comment

Methods of Mathematical Physics

• B2.18

  Methods of Mathematical Physics | Part II, 2003

  Let $\widehat{y}(p)$ be the Laplace transform of $y(t)$, where $y(t)$ satisfies

  $$y^{\prime}(t)=y(\pi-t)$$

  and

  $$y(0)=1 ; \quad y(\pi)=k ; \quad y(t)=0 \text { for } t<0 \text { and for } t>\pi$$

  Show that

  $$p \widehat{y}(p)+k e^{-\pi p}-1=e^{-\pi p} \widehat{y}(-p)$$

  and hence deduce that

  $$\widehat{y}(p)=\frac{(k+p)-(1+p k) e^{-\pi p}}{1+p^{2}}$$

  Use the inversion formula for Laplace transforms to find $y(t)$ for $t>\pi$ and deduce that a solution of the above boundary value problem exists only if $k=-1$. Hence find $y(t)$ for $0 \leqslant t \leqslant \pi$.

  comment

Nonlinear Waves and Integrable Systems

• A2.18

  Nonlinear Waves and Integrable Systems | Part II, 2003

  (i) Write down the shock condition associated with the equation

  $$\rho_{t}+q_{x}=0$$

  where $q=q(\rho)$. Discuss briefly two possible heuristic approaches to justifying this shock condition.

  (ii) According to shallow water theory, waves on a uniformly sloping beach are described by the equations

  $$\begin{aligned} &\frac{\partial h}{\partial t}+\frac{\partial}{\partial x}(h u)=0, \\ &\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+g \frac{\partial \eta}{\partial x}=0, \quad h=\alpha x+\eta, \end{aligned}$$

  where $\alpha$ is the constant slope of the beach, $g$ is the gravitational acceleration, $u(x, t)$ is the fluid velocity, and $\eta(x, t)$ is the elevation of the fluid surface above the undisturbed level.

  Find the characteristic velocities and the characteristic form of the equations.

  What are the Riemann variables and how do they vary with $t$ on the characteristics?

  comment

Number Fields

• B2.9

  Number Fields | Part II, 2003

  By Dedekind's theorem, or otherwise, factorise $2,3,5$ and 7 into prime ideals in the field $K=\mathbb{Q}(\sqrt{-34})$. Show that the ideal equations

  $$[\omega]=[5, \omega][7, \omega], \quad[\omega+3]=[2, \omega+3][5, \omega+3]^{2}$$

  hold in $K$, where $\omega=1+\sqrt{-34}$. Hence, prove that the ideal class group of $K$ is cyclic of order $4 .$

  [It may be assumed that the Minkowski constant for $K$ is $2 / \pi$.]

  comment

Numerical Analysis

• A2.19 B2.19

  Numerical Analysis | Part II, 2003

  (i) Explain briefly what is meant by the convergence of a numerical method for ordinary differential equations.

  (ii) Suppose the sufficiently-smooth function $f: \mathbb{R} \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$ obeys the Lipschitz condition: there exists $\lambda>0$ such that

  $$\|\mathbf{f}(t, \mathbf{x})-\mathbf{f}(t, \mathbf{y})\| \leqslant \lambda\|\mathbf{x}-\mathbf{y}\|, \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^{d}, t \geqslant 0$$

  Prove from first principles, without using the Dahlquist equivalence theorem, that the trapezoidal rule

  $$\mathbf{y}_{n+1}=\mathbf{y}_{n}+\frac{1}{2} h\left[\mathbf{f}\left(t_{n}, \mathbf{y}_{n}\right)+\mathbf{f}\left(t_{n+1}, \mathbf{y}_{n+1}\right)\right]$$

  for the solution of the ordinary differential equation

  $$\mathbf{y}^{\prime}=\mathbf{f}(t, \mathbf{y}), \quad t \geqslant 0, \quad \mathbf{y}(0)=\mathbf{y}_{0},$$

  converges.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2003

  The owner of a put option may exercise it on any one of the days $1, \ldots, h$, or not at all. If he exercises it on day $t$, when the share price is $x_{t}$, his profit will be $p-x_{t}$. Suppose the share price obeys $x_{t+1}=x_{t}+\epsilon_{t}$, where $\epsilon_{1}, \epsilon_{2}, \ldots$ are i.i.d. random variables for which $E\left|\epsilon_{t}\right|<\infty$. Let $F_{s}(x)$ be the maximal expected profit the owner can obtain when there are $s$ further days to go and the share price is $x$. Show that

  (a) $F_{s}(x)$ is non-decreasing in $s$,

  (b) $F_{s}(x)+x$ is non-decreasing in $x$, and

  (c) $F_{s}(x)$ is continuous in $x$.

  Deduce that there exists a non-decreasing sequence, $a_{1}, \ldots, a_{h}$, such that expected profit is maximized by exercising the option the first day that $x_{t} \leqslant a_{t}$.

  Now suppose that the option never expires, so effectively $h=\infty$. Show by examples that there may or may not exist an optimal policy of the form 'exercise the option the first day that $x_{t} \leqslant a$.

  comment

Partial Differential Equations

• B2.17

  Partial Differential Equations | Part II, 2003

  (a) If $f$ is a radial function on $\mathbb{R}^{n}$ (i.e. $f(x)=\phi(r)$ with $r=|x|$ for $x \in \mathbb{R}^{n}$ ), and $n>2$, then show that $f$ is harmonic on $\mathbb{R}^{n}-\{0\}$ if and only if

  $$\phi(r)=a+b r^{2-n}$$

  for $a, b \in \mathbb{R}$.

  (b) State the mean value theorem for harmonic functions and prove it for $n>2$.

  (c) Generalise the statement and the proof of the mean value theorem to the case of a subharmonic function, i.e. a $C^{2}$ function such that $\Delta u \leqslant 0$.

  comment

Principles of Dynamics

• A2.2 B2.1

  Principles of Dynamics | Part II, 2003

  (i) The trajectory $\mathbf{x}(t)$ of a non-relativistic particle of mass $m$ and charge $q$ moving in an electromagnetic field obeys the Lorentz equation

  $$m \ddot{\mathbf{x}}=q\left(\mathbf{E}+\frac{\dot{\mathbf{x}}}{c} \wedge \mathbf{B}\right) .$$

  Show that this equation follows from the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-q\left(\phi-\frac{\dot{\mathbf{x}} \cdot \mathbf{A}}{c}\right)$$

  where $\phi(\mathbf{x}, t)$ is the electromagnetic scalar potential and $\mathbf{A}(\mathbf{x}, t)$ the vector potential, so that

  $$\mathbf{E}=-\frac{1}{c} \dot{\mathbf{A}}-\nabla \phi \text { and } \mathbf{B}=\nabla \wedge \mathbf{A}$$

  (ii) Let $\mathbf{E}=0$. Consider a particle moving in a constant magnetic field which points in the $z$ direction. Show that the particle moves in a helix about an axis pointing in the $z$ direction. Evaluate the radius of the helix.

  comment

Principles of Statistics

• A2.11 B2.16

  Principles of Statistics | Part II, 2003

  (i) Outline briefly the Bayesian approach to hypothesis testing based on Bayes factors.

  (ii) Let $Y_{1}, Y_{2}$ be independent random variables, both uniformly distributed on $\left(\theta-\frac{1}{2}, \theta+\frac{1}{2}\right)$. Find a minimal sufficient statistic for $\theta$. Let $Y_{(1)}=\min \left\{Y_{1}, Y_{2}\right\}$, $Y_{(2)}=\max \left\{Y_{1}, Y_{2}\right\}$. Show that $R=Y_{(2)}-Y_{(1)}$ is ancilliary and explain why the Conditionality Principle would lead to inference about $\theta$ being drawn from the conditional distribution of $\frac{1}{2}\left\{Y_{(1)}+Y_{(2)}\right\}$ given $R$. Find the form of this conditional distribution.

  comment

Probability and Measure

• B2.12

  Probability and Measure | Part II, 2003

  Let $H$ be a Hilbert space and let $V$ be a closed subspace of $H$. Let $x \in H$. Show that there is a unique decomposition $x=u+v$ such that $v \in V$ and $u \in V^{\perp}$.

  Now suppose $(\Omega, \mathcal{F}, \mathbb{P})$ is a probability space and let $X \in L^{2}(\Omega, \mathcal{F}, \mathbb{P})$. Suppose $\mathcal{G}$ is a sub- $\sigma$-algebra of $\mathcal{F}$. Define $\mathbb{E}(X \mid \mathcal{G})$ using a decomposition of the above type. Show that $\mathbb{E}\left(\mathbb{E}(X \mid \mathcal{G}) .1_{A}\right)=\mathbb{E}\left(X .1_{A}\right)$ for each set $A \in \mathcal{G}$.

  Let $\mathcal{G}_{1} \subseteq \mathcal{G}_{2}$ be two sub- $\sigma$-algebras of $\mathcal{F}$. Show that (a) $\mathbb{E}\left(\mathbb{E}\left(X \mid \mathcal{G}_{1}\right) \mid \mathcal{G}_{2}\right)=\mathbb{E}\left(X \mid \mathcal{G}_{1}\right)$; (b) $\mathbb{E}\left(\mathbb{E}\left(X \mid \mathcal{G}_{2}\right) \mid \mathcal{G}_{1}\right)=\mathbb{E}\left(X \mid \mathcal{G}_{1}\right)$.

  No general theorems about projections on Hilbert spaces may be quoted without proof.

  comment

Quantum Physics

• A2.14

  Quantum Physics | Part II, 2003

  (i) A system of $N$ distinguishable non-interacting particles has energy levels $E_{i}$ with degeneracy $g_{i}, 1 \leqslant i<\infty$, for each particle. Show that in thermal equilibrium the number of particles $N_{i}$ with energy $E_{i}$ is given by

  $$N_{i}=g_{i} e^{-\beta\left(E_{i}-\mu\right)}$$

  where $\beta$ and $\mu$ are parameters whose physical significance should be briefly explained.

  A gas comprises a set of atoms with non-degenerate energy levels $E_{i}, 1 \leqslant i<\infty$. Assume that the gas is dilute and the motion of the atoms can be neglected. For such a gas the atoms can be treated as distinguishable. Show that when the system is at temperature $T$, the number of atoms $N_{i}$ at level $i$ and the number $N_{j}$ at level $j$ satisfy

  $$\frac{N_{i}}{N_{j}}=e^{-\left(E_{i}-E_{j}\right) / k T}$$

  where $k$ is Boltzmann's constant.

  (ii) A system of bosons has a set of energy levels $W_{a}$ with degeneracy $f_{a}, 1 \leqslant a<\infty$, for each particle. In thermal equilibrium at temperature $T$ the number $n_{a}$ of particles in level $a$ is

  $$n_{a}=\frac{f_{a}}{e^{\left(W_{a}-\mu\right) / k T}-1} \text {. }$$

  What is the value of $\mu$ when the particles are photons?

  Given that the density of states $\rho(\omega)$ for photons of frequency $\omega$ in a cubical box of side $L$ is

  $$\rho(\omega)=L^{3} \frac{\omega^{2}}{\pi^{2} c^{3}}$$

  where $c$ is the speed of light, show that at temperature $T$ the density of photons in the frequency range $\omega \rightarrow \omega+d \omega$ is $n(\omega) d \omega$ where

  $$n(\omega)=\frac{\omega^{2}}{\pi^{2} c^{3}} \frac{1}{e^{\hbar \omega / k T}-1}$$

  Deduce the energy density, $\epsilon(\omega)$, for photons of frequency $\omega$.

  The cubical box is occupied by the gas of atoms described in Part (i) in the presence of photons at temperature $T$. Consider the two atomic levels $i$ and $j$ where $E_{i}>E_{j}$ and $E_{i}-E_{j}=\hbar \omega$. The rate of spontaneous photon emission for the transition $i \rightarrow j$ is $A_{i j}$. The rate of absorption is $B_{j i} \epsilon(\omega)$ and the rate of stimulated emission is $B_{i j} \epsilon(\omega)$. Show that the requirement that these processes maintain the atoms and photons in thermal equilibrium yields the relations

  $$B_{i j}=B_{j i}$$

  and

  $$A_{i j}=\left(\frac{\hbar \omega^{3}}{\pi^{2} c^{3}}\right) B_{i j}$$

  comment

Representation Theory

• B2.6

  Representation Theory | Part II, 2003

  Let $V_{n}$ be the space of homogeneous polynomials of degree $n$ in two variables $z_{1}$ and $z_{2}$. Define a left action of $G=S U_{2}$ on the space of polynomials by setting

  $$(g P) z=P(z g),$$

  where $P \in \mathbb{C}\left[z_{1}, z_{2}\right], \quad g=\left(\begin{array}{cc}a & b \\ c & d\end{array}\right), \quad z=\left(z_{1}, z_{2}\right) \quad$ and $\quad z g=\left(a z_{1}+c z_{2}, b z_{1}+d z_{2}\right)$.

  Show that

  (a) the representations $V_{n}$ are irreducible,

  (b) the representations $V_{n}$ exhaust the irreducible representations of $S U_{2}$, and

  

  comment

Theoretical Geophysics

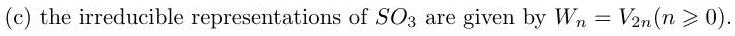
• A2.16

  Theoretical Geophysics | Part II, 2003

  (i) Explain briefly what is meant by the concepts of hydrostatic equilibrium and the buoyancy frequency. Evaluate an expression for the buoyancy frequency in an incompressible inviscid fluid with stable density profile $\rho(z)$.

  (ii) Explain briefly what is meant by the Boussinesq approximation.

  Write down the equations describing motions of small amplitude in an incompressible, stratified, Boussinesq fluid of constant buoyancy frequency.

  Derive the resulting dispersion relationship for plane wave motion. Show that there is a maximum frequency for the waves and explain briefly why this is the case.

  What would be the response to a solid body oscillating at a frequency in excess of the maximum?

  comment

Waves in Fluid and Solid Media

• B2.25

  Waves in Fluid and Solid Media | Part II, 2003

  Starting from the equations for the one-dimensional unsteady flow of a perfect gas of uniform entropy, derive the Riemann invariants

  $$u \pm \frac{2}{\gamma-1} c=\text { constant }$$

  on characteristics

  $$C_{\pm}: \frac{d x}{d t}=u \pm c$$

  A piston moves smoothly down a long tube, with position $x=X(t)$. Gas occupies the tube ahead of the piston, $x>X(t)$. Initially the gas and the piston are at rest, and the speed of sound in the gas is $c_{0}$. For $t>0$, show that the $C_{+}$characteristics are straight lines, provided that a shock-wave has not formed. Hence find a parametric representation of the solution for the velocity $u(x, t)$ of the gas.

  comment