Part II, 2001, Paper 2

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2001

  Let $f: \mathbb{P}^{2} \rightarrow \mathbb{P}^{2}$ be the rational map given by $f\left(X_{0}: X_{1}: X_{2}\right)=\left(X_{1} X_{2}: X_{0} X_{2}\right.$ : $\left.X_{0} X_{1}\right)$. Determine whether $f$ is defined at the following points: $(1: 1: 1),(0: 1: 1),(0:$ $0: 1)$.

  Let $C \subset \mathbb{P}^{2}$ be the curve defined by $X_{1}^{2} X_{2}-X_{0}^{3}=0$. Define a bijective morphism $\alpha: \mathbb{P}^{1} \rightarrow C$. Prove that $\alpha$ is not an isomorphism.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2001

  Show that the fundamental group of the 2-torus $S^{1} \times S^{1}$ is isomorphic to $\mathbf{Z} \times \mathbf{Z}$.

  Show that an injective continuous map from the circle $S^{1}$ to itself induces multiplication by $\pm 1$ on the fundamental group.

  Show that there is no retraction from the solid torus $S^{1} \times D^{2}$ to its boundary.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2001

  (i) Let $G$ be a directed network with nodes $N$ and $\operatorname{arcs} A$. Let $S \subset N$ be a subset of the nodes, $x$ be a flow on $G$, and $y$ be the divergence of $x$. Describe carefully what is meant by a cut $Q=[S, N \backslash S]$. Define the arc-cut incidence $e_{Q}$, and the flux of $x$ across $Q$. Define also the divergence $y(S)$ of $S$. Show that $y(S)=x \cdot e_{Q}$.

  Now suppose that capacity constraints are specified on each of the arcs. Define the upper cut capacity $c^{+}(Q)$ of $Q$. State the feasible distribution problem for a specified divergence $b$, and show that the problem only has a solution if $b(N)=0$ and $b(S) \leqslant c^{+}(Q)$ for all cuts $Q=[S, N \backslash S]$.

  (ii) Describe an algorithm to find a feasible distribution given a specified divergence $b$ and capacity constraints on each arc. Explain what happens when no feasible distribution exists.

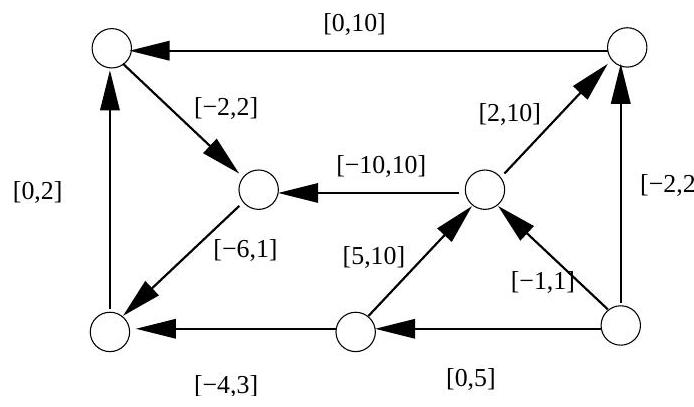
  Illustrate the algorithm by either finding a feasible circulation, or demonstrating that one does not exist, in the network given below. Arcs are labelled with capacity constraint intervals.

  

  Part II

  comment

Applications of Quantum Mechanics

• B2.22

  Applications of Quantum Mechanics | Part II, 2001

  A particle of charge $e$ moves freely within a cubical box of side $a$. Its initial wavefunction is

  $$(2 / a)^{-\frac{3}{2}} \sin (\pi x / a) \sin (\pi y / a) \sin (\pi z / a) .$$

  A uniform electric field $\mathcal{E}$ in the $x$ direction is switched on for a time $T$. Derive from first principles the probability, correct to order $\mathcal{E}^{2}$, that after the field has been switched off the wave function will be found to be

  $$(2 / a)^{-\frac{3}{2}} \sin (2 \pi x / a) \sin (\pi y / a) \sin (\pi z / a) .$$

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2001

  Let $M$ be a Poisson random measure on $E=\mathbb{R} \times[0, \pi)$ with constant intensity $\lambda$. For $(x, \theta) \in E$, denote by $l(x, \theta)$ the line in $\mathbb{R}^{2}$ obtained by rotating the line $\{(x, y): y \in \mathbb{R}\}$ through an angle $\theta$ about the origin.

  Consider the line process $L=M \circ l^{-1}$.

  (i) What is the distribution of the number of lines intersecting the disc $\left\{z \in \mathbb{R}^{2}:|z| \leqslant a\right\}$ ?

  (ii) What is the distribution of the distance from the origin to the nearest line?

  (iii) What is the distribution of the distance from the origin to the $k$ th nearest line?

  comment

Coding and Cryptography

• A2.9

  Coding and Cryptography | Part II, 2001

  (i) Give brief answers to the following questions.

  (a) What is a stream cypher?

  (b) Explain briefly why a one-time pad is safe if used only once but becomes unsafe if used many times.

  (c) What is a feedback register of length $d$ ? What is a linear feedback register of length $d ?$

  (d) A cypher stream is given by a linear feedback register of known length $d$. Show that, given plain text and cyphered text of length $2 d$, we can find the complete cypher stream.

  (e) State and prove a similar result for a general feedback register.

  (ii) Describe the construction of a Reed-Muller code. Establish its information rate and its weight

  comment

Combinatorics

• B2.5

  Combinatorics | Part II, 2001

  As usual, $R_{k}^{(r)}(m)$ denotes the smallest integer $n$ such that every $k$-colouring of $[n]^{(r)}$ yields a monochromatic $m$-subset $M \in[n]^{(m)}$. Prove that $R_{2}^{(2)}(m)>2^{m / 2}$ for $m \geqslant 3$.

  Let $\mathcal{P}([n])$ have the colex order, and for $a, b \in \mathcal{P}([n])$ let $\delta(a, b)=\max a \triangle b$; thus $a<b$ means $\delta(a, b) \in b$. Show that if $a<b<c$ then $\delta(a, b) \neq \delta(b, c)$, and that $\delta(a, c)=\max \{\delta(a, b), \delta(b, c)\} .$

  Given a red-blue colouring of $[n]^{(2)}$, the 4 -colouring

  $$\chi: \mathcal{P}([n])^{(3)} \rightarrow\{\text { red, blue }\} \times\{0,1\}$$

  is defined as follows:

  $$\chi(\{a, b, c\})= \begin{cases}(\text { red, } 0) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is red and } \delta(a, b)<\delta(b, c) \\ (\text { red }, 1) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is red and } \delta(a, b)>\delta(b, c) \\ (\text { blue, } 0) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is blue and } \delta(a, b)<\delta(b, c) \\ \text { (blue, } 1) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is blue and } \delta(a, b)>\delta(b, c)\end{cases}$$

  where $a<b<c$. Show that if $M=\left\{a_{0}, a_{1}, \ldots, a_{m}\right\} \in \mathcal{P}([n])^{(m+1)}$ is monochromatic then $\left\{\delta_{1}, \ldots, \delta_{m}\right\} \in[n]^{(m)}$ is monochromatic, where $\delta_{i}=\delta\left(a_{i-1}, a_{i}\right)$ and $a_{0}<a_{1}<\cdots<a_{m}$.

  Deduce that $R_{4}^{(3)}(m+1)>2^{2^{m / 2}}$ for $m \geqslant 3$.

  comment

Computational Statistics and Statistical Modelling

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2001

  (i) Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\left(y_{i} \theta_{i}-b\left(\theta_{i}\right)\right) / \phi+c\left(y_{i}, \phi\right)\right]$$

  Assume that $E\left(Y_{i}\right)=\mu_{i}$, and that $g\left(\mu_{i}\right)=\beta^{T} x_{i}$, where $g(\cdot)$ is a known 'link' function, $x_{1}, \ldots, x_{n}$ are known covariates, and $\beta$ is an unknown vector. Show that

  $$\mathbb{E}\left(Y_{i}\right)=b^{\prime}\left(\theta_{i}\right), \operatorname{var}\left(Y_{i}\right)=\phi b^{\prime \prime}\left(\theta_{i}\right)=V_{i} \text {, say, }$$

  and hence

  $$\frac{\partial l}{\partial \beta}=\sum_{i=1}^{n} \frac{\left(y_{i}-\mu_{i}\right) x_{i}}{g^{\prime}\left(\mu_{i}\right) V_{i}}, \text { where } l=l(\beta, \phi) \text { is the log-likelihood. }$$

  (ii) The table below shows the number of train miles (in millions) and the number of collisions involving British Rail passenger trains between 1970 and 1984 . Give a detailed interpretation of the $R$ output that is shown under this table:

  $\begin{array}{llll} & \text { year } & \text { collisions } & \text { miles } \\ 1 & 1970 & 3 & 281 \\ 2 & 1971 & 6 & 276 \\ 3 & 1972 & 4 & 268 \\ 4 & 1973 & 7 & 269 \\ 5 & 1974 & 6 & 281 \\ 6 & 1975 & 2 & 271 \\ 7 & 1976 & 2 & 265 \\ 8 & 1977 & 4 & 264 \\ 9 & 1978 & 1 & 267 \\ 10 & 1979 & 7 & 265 \\ 11 & 1980 & 3 & 267 \\ 12 & 1981 & 5 & 260 \\ 13 & 1982 & 6 & 231 \\ 14 & 1983 & 1 & 249\end{array}$

  Call:

  glm(formula $=$ collisions $\sim$ year $+\log ($ miles $)$, family $=$ poisson)

  Coefficients:

  $\begin{array}{lrrrr} & \text { Estimate } & \text { Std. Error } & \text { z value } & \operatorname{Pr}(>|z|) \\ \text { (Intercept) } & 127.14453 & 121.37796 & 1.048 & 0.295 \\ \text { year } & -0.05398 & 0.05175 & -1.043 & 0.297 \\ \log \text { (miles) } & -3.41654 & 4.18616 & -0.816 & 0.414\end{array}$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $15.937$ on 13 degrees of freedom

  Residual deviance: $14.843$ on 11 degrees of freedom

  Number of Fisher Scoring iterations: 4

  Part II

  comment

Differentiable Manifolds

• B2.7

  Differentiable Manifolds | Part II, 2001

  State Stokes' Theorem.

  Prove that, if $M^{m}$ is a compact connected manifold and $\Phi: U \rightarrow \mathbb{R}^{m}$ is a surjective chart on $M$, then for any $\omega \in \Omega^{m}(M)$ there is $\eta \in \Omega^{m-1}(M)$ such that $\operatorname{supp}(\omega+d \eta) \subseteq \Phi^{-1}\left(\mathbf{B}^{m}\right)$, where $\mathbf{B}^{m}$ is the unit ball in $\mathbb{R}^{m}$.

  [You may assume that, if $\omega \in \Omega^{m}\left(\mathbb{R}^{m}\right)$ with $\operatorname{supp}(\omega) \subseteq \mathbf{B}^{m}$ and $\int_{\mathbb{R}^{m}} \omega=0$, then $\exists \eta \in \Omega^{m-1}\left(\mathbb{R}^{m}\right)$ with $\operatorname{supp}(\eta) \subseteq \mathbf{B}^{m}$ such that $\left.d \eta=\omega .\right]$

  By considering the $m$-form

  $$\omega=x_{1} d x_{2} \wedge \ldots \wedge d x_{m+1}+\cdots+x_{m+1} d x_{1} \wedge \ldots \wedge d x_{m}$$

  on $\mathbb{R}^{m+1}$, or otherwise, deduce that $H^{m}\left(S^{m}\right) \cong \mathbb{R}$.

  comment

Dynamics of Differential Equations

• A2.6 B2.4

  Dynamics of Differential Equations | Part II, 2001

  (i) Define a Liapounov function for a flow $\phi$ on $\mathbb{R}^{n}$. Explain what it means for a fixed point of the flow to be Liapounov stable. State and prove Liapounov's first stability theorem.

  (ii) Consider the damped pendulum

  $$\ddot{\theta}+k \dot{\theta}+\sin \theta=0,$$

  where $k>0$. Show that there are just two fixed points (considering the phase space as an infinite cylinder), and that one of these is the origin and is Liapounov stable. Show further that the origin is asymptotically stable, and that the the $\omega$-limit set of each point in the phase space is one or other of the two fixed points, justifying your answer carefully.

  [You should state carefully any theorems you use in your answer, but you need not prove them.]

  comment

Electrodynamics

• B2.20

  Electrodynamics | Part II, 2001

  In a superconductor, there are superconducting charge carriers with number density $n$, mass $m$ and charge $q$. Starting from the quantum mechanical wavefunction $\Psi=R e^{i \Phi}$ (with real $R$ and $\Phi$ ), construct a formula for the electric current and explain carefully why your result is gauge invariant.

  Now show that inside a superconductor a static magnetic field obeys the equation

  $$\nabla^{2} \mathbf{B}=\frac{\mu_{0} n q^{2}}{m} \mathbf{B}$$

  A superconductor occupies the region $z>0$, while for $z<0$ there is a vacuum with a constant magnetic field in the $x$ direction. Show that the magnetic field cannot penetrate deep into the superconductor.

  comment

Electromagnetism

• A2.5

  Electromagnetism | Part II, 2001

  (i) Write down the expression for the electrostatic potential $\phi(\mathbf{r})$ due to a distribution of charge $\rho(\mathbf{r})$ contained in a volume $V$. Perform the multipole expansion of $\phi(\mathbf{r})$ taken only as far as the dipole term.

  (ii) If the volume $V$ is the sphere $|\mathbf{r}| \leqslant a$ and the charge distribution is given by

  $$\rho(\mathbf{r})= \begin{cases}r^{2} \cos \theta & r \leqslant a \\ 0 & r>a\end{cases}$$

  where $r, \theta$ are spherical polar coordinates, calculate the charge and dipole moment. Hence deduce $\phi$ as far as the dipole term.

  Obtain an exact solution for $r>a$ by solving the boundary value problem using trial solutions of the forms

  $$\phi=\frac{A \cos \theta}{r^{2}} \text { for } r>a,$$

  and

  $$\phi=B r \cos \theta+C r^{4} \cos \theta \text { for } r<a .$$

  Show that the solution obtained from the multipole expansion is in fact exact for $r>a$.

  [You may use without proof the result

  $$\left.\nabla^{2}\left(r^{k} \cos \theta\right)=(k+2)(k-1) r^{k-2} \cos \theta, \quad k \in \mathbb{N} .\right]$$

  comment

Fluid Dynamics II

• B2.24

  Fluid Dynamics II | Part II, 2001

  Explain what is meant by a Stokes flow and show that, in such a flow, in the absence of body forces, $\partial \sigma_{i j} / \partial x_{j}=0$, where $\sigma_{i j}$ is the stress tensor.

  State and prove the reciprocal theorem for Stokes flow.

  When a rigid sphere of radius $a$ translates with velocity $\mathbf{U}$ through unbounded fluid at rest at infinity, it may be shown that the traction per unit area, $\boldsymbol{\sigma} \cdot \mathbf{n}$, exerted by the sphere on the fluid, has the uniform value $3 \mu \mathbf{U} / 2 a$ over the sphere surface. Find the drag on the sphere.

  Suppose that the same sphere is free of external forces and is placed with its centre at the origin in an unbounded Stokes flow given in the absence of the sphere as $\mathbf{u}_{s}(\mathbf{x})$. By applying the reciprocal theorem to the perturbation to the flow generated by the presence of the sphere, and assuming this to tend to zero sufficiently rapidly at infinity, show that the instantaneous velocity of the centre of the sphere is

  $$\mathbf{V}=\frac{1}{4 \pi a^{2}} \int_{r=a} \mathbf{u}_{s}(\mathbf{x}) d S$$

  Part II

  comment

Foundations of Quantum Mechanics

• A2.13 B2.21

  Foundations of Quantum Mechanics | Part II, 2001

  (i) Hermitian operators $\hat{x}, \hat{p}$, satisfy $[\hat{x}, \hat{p}]=i \hbar$. The eigenvectors $|p\rangle$, satisfy $\hat{p}|p\rangle=p|p\rangle$ and $\left\langle p^{\prime} \mid p\right\rangle=\delta\left(p^{\prime}-p\right)$. By differentiating with respect to $b$ verify that

  $$e^{-i b \hat{x} / \hbar} \hat{p} e^{i b \hat{x} / \hbar}=\hat{p}+b$$

  and hence show that

  $$e^{i b \hat{x} / \hbar}|p\rangle=|p+b\rangle$$

  Show that

  $$\langle p|\hat{x}| \psi\rangle=i \hbar \frac{\partial}{\partial p}\langle p \mid \psi\rangle$$

  and

  $$\langle p|\hat{p}| \psi\rangle=p\langle p \mid \psi\rangle .$$

  (ii) A quantum system has Hamiltonian $H=H_{0}+H_{1}$, where $H_{1}$ is a small perturbation. The eigenvalues of $H_{0}$ are $\epsilon_{n}$. Give (without derivation) the formulae for the first order and second order perturbations in the energy level of a non-degenerate state. Suppose that the $r$ th energy level of $H_{0}$ has $j$ degenerate states. Explain how to determine the eigenvalues of $H$ corresponding to these states to first order in $H_{1}$.

  In a particular quantum system an orthonormal basis of states is given by $\left|n_{1}, n_{2}\right\rangle$, where $n_{i}$ are integers. The Hamiltonian is given by

  $$H=\sum_{n_{1}, n_{2}}\left(n_{1}^{2}+n_{2}^{2}\right)\left|n_{1}, n_{2}\right\rangle\left\langle n_{1}, n_{2}\left|+\sum_{n_{1}, n_{2}, n_{1}^{\prime}, n_{2}^{\prime}} \lambda_{\left|n_{1}-n_{1}^{\prime}\right|,\left|n_{2}-n_{2}^{\prime}\right|}\right| n_{1}, n_{2}\right\rangle\left\langle n_{1}^{\prime}, n_{2}^{\prime}\right|,$$

  where $\lambda_{r, s}=\lambda_{s, r}, \lambda_{0,0}=0$ and $\lambda_{r, s}=0$ unless $r$ and $s$ are both even.

  Obtain an expression for the ground state energy to second order in the perturbation, $\lambda_{r, s}$. Find the energy eigenvalues of the first excited state to first order in the perturbation. Determine a matrix (which depends on two independent parameters) whose eigenvalues give the first order energy shift of the second excited state.

  comment

Functional Analysis

• A2.3 B2.2

  Functional Analysis | Part II, 2001

  (i) State the Stone-Weierstrass theorem for complex-valued functions. Use it to show that the trigonometric polynomials are dense in the space $C(\mathbb{T})$ of continuous, complexvalued functions on the unit circle $\mathbb{T}$ with the uniform norm.

  Show further that, for $f \in C(\mathbb{T})$, the $n$th Fourier coefficient

  $$\widehat{f}(n)=\frac{1}{2 \pi} \int_{0}^{2 \pi} f\left(e^{i \theta}\right) e^{-i n \theta} d \theta$$

  tends to 0 as $|n|$ tends to infinity.

  (ii) (a) Let $X$ be a normed space with the property that the series $\sum_{n=1}^{\infty} x_{n}$ converges whenever $\left(x_{n}\right)$ is a sequence in $X$ with $\sum_{n=1}^{\infty}\left\|x_{n}\right\|$ convergent. Show that $X$ is a Banach space.

  (b) Let $K$ be a compact metric space and $L$ a closed subset of $K$. Let $R: C(K) \rightarrow$ $C(L)$ be the map sending $f \in C(K)$ to its restriction $R(f)=f \mid L$ to $L$. Show that $R$ is a bounded, linear map and that its image is a subalgebra of $C(L)$ separating the points of

  Show further that, for each function $g$ in the image of $R$, there is a function $f \in C(K)$ with $R(f)=g$ and $\|f\|_{\infty}=\|g\|_{\infty}$. Deduce that every continuous, complexvalued function on $L$ can be extended to a continuous function on all of $K$.

  comment

General Relativity

• A2.15 B2.23

  General Relativity | Part II, 2001

  (i) Show that the geodesic equation follows from a variational principle with Lagrangian

  $$L=g_{a b} \dot{x}^{a} \dot{x}^{b}$$

  where the path of the particle is $x^{a}(\lambda)$, and $\lambda$ is an affine parameter along that path.

  (ii) The Schwarzschild metric is given by

  $$d s^{2}=d r^{2}\left(1-\frac{2 M}{r}\right)^{-1}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-\left(1-\frac{2 M}{r}\right) d t^{2}$$

  Consider a photon which moves within the equatorial plane $\theta=\frac{\pi}{2}$. Using the above Lagrangian, or otherwise, show that

  $$\left(1-\frac{2 M}{r}\right)\left(\frac{d t}{d \lambda}\right)=E, \text { and } r^{2}\left(\frac{d \phi}{d \lambda}\right)=h$$

  for constants $E$ and $h$. Deduce that

  $$\left(\frac{d r}{d \lambda}\right)^{2}=E^{2}-\frac{h^{2}}{r^{2}}\left(1-\frac{2 M}{r}\right)$$

  Assume further that the photon approaches from infinity. Show that the impact parameter $b$ is given by

  $$b=\frac{h}{E}$$

  By considering the equation $(*)$, or otherwise

  (a) show that, if $b^{2}>27 M^{2}$, the photon is deflected but not captured by the black hole;

  (b) show that, if $b^{2}<27 M^{2}$, the photon is captured;

  (c) describe, with justification, the qualitative form of the photon's orbit in the case $b^{2}=27 M^{2}$.

  comment

Geometry of Surfaces

• A2.7

  Geometry of Surfaces | Part II, 2001

  (i) Give the definition of the curvature $\kappa(t)$ of a plane curve $\gamma:[a, b] \longrightarrow \mathbf{R}^{2}$. Show that, if $\gamma:[a, b] \longrightarrow \mathbf{R}^{2}$ is a simple closed curve, then

  $$\int_{a}^{b} \kappa(t)\|\dot{\gamma}(t)\| d t=2 \pi$$

  (ii) Give the definition of a geodesic on a parametrized surface in $\mathbf{R}^{3}$. Derive the differential equations characterizing geodesics. Show that a great circle on the unit sphere is a geodesic.

  comment

Graph Theory

• A2.8

  Graph Theory | Part II, 2001

  (i) Prove that any graph $G$ drawn on a compact surface $S$ with negative Euler characteristic $E(S)$ has a vertex colouring that uses at most

  $$h=\left\lfloor\frac{1}{2}(7+\sqrt{49-24 E(S)})\right\rfloor$$

  colours.

  Briefly discuss whether the result is still true when $E(S) \geqslant 0$.

  (ii) Prove that a graph $G$ is $k$ edge-connected if and only if the removal of no set of less than $k$ edges from $G$ disconnects $G$.

  [If you use any form of Menger's theorem, you must prove it.]

  Let $G$ be a minimal example of a graph that requires $k+1$ colours for a vertex colouring. Show that $G$ must be $k$ edge-connected.

  comment

Groups, Rings and Fields

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2001

  (i) Show that the ring $k=\mathbf{F}_{2}[X] /\left(X^{2}+X+1\right)$ is a field. How many elements does it have?

  (ii) Let $k$ be as in (i). By considering what happens to a chosen basis of the vector space $k^{2}$, or otherwise, find the order of the groups $G L_{2}(k)$ and $S L_{2}(k)$.

  By considering the set of lines in $k^{2}$, or otherwise, show that $S L_{2}(k)$ is a subgroup of the symmetric group $S_{5}$, and identify this subgroup.

  comment

Information Theory

• B2.14

  Information Theory | Part II, 2001

  A subset $\mathcal{C}$ of the Hamming space $\{0,1\}^{n}$ of cardinality $|\mathcal{C}|=r$ and with the minimal (Hamming) distance $\min \left[d\left(x, x^{\prime}\right): x, x^{\prime} \in \mathcal{C}, x \neq x^{\prime}\right]=\delta$ is called an $[n, r, \delta]$-code (not necessarily linear). An $[n, r, \delta]$-code is called maximal if it is not contained in any $[n, r+1, \delta]$-code. Prove that an $[n, r, \delta]$-code is maximal if and only if for any $y \in\{0,1\}^{n}$ there exists $x \in \mathcal{C}$ such that $d(x, y)<\delta$. Conclude that if there are $\delta$ or more changes made in a codeword then the new word is closer to some other codeword than to the original one.

  Suppose that a maximal $[n, r, \delta]$-code is used for transmitting information via a binary memoryless channel with the error probability $p$, and the receiver uses the maximum likelihood decoder. Prove that the probability of erroneous decoding, $\pi_{\mathrm{err}}^{\mathrm{ml}}$, obeys the bounds

  $$1-b(n, \delta-1) \leqslant \pi_{\mathrm{err}}^{\mathrm{ml}} \leqslant 1-b(n,[(\delta-1) / 2])$$

  where

  $$b(n, m)=\sum_{0 \leqslant k \leqslant m}\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k}$$

  is a partial binomial sum and $[\cdot]$ is the integer part.

  comment

Logic, Computation and Set Theory

• B2.11

  Logic, Computation and Set Theory | Part II, 2001

  Let $U$ be an arbitrary set, and $\mathcal{P}(U)$ the power set of $U$. For $X$ a subset of $\mathcal{P}(U)$, the dual $X^{\vee}$ of $X$ is the set $\{y \subseteq U:(\forall x \in X)(y \cap x \neq \emptyset)\}$.

  (i) Show that $X \subseteq Y \rightarrow Y^{\vee} \subseteq X^{\vee}$.

  Show that for $\left\{X_{i}: i \in I\right\}$ a family of subsets of $\mathcal{P}(U)$

  $$\left(\bigcup\left\{X_{i}: i \in I\right\}\right)^{\vee}=\bigcap\left\{X_{i}^{\vee}: i \in I\right\}$$

  (ii) Consider $S=\left\{X \subseteq \mathcal{P}(U): X \subseteq X^{\vee}\right\}$. Show that $S$, $\subseteq$ is a chain-complete poset.

  State Zorn's lemma and use it to deduce that there exists $X$ with $X=X^{\vee}$.

  Show that if $X=X^{\vee}$ then the following hold:

  $X$ is closed under superset; for all $U^{\prime} \subseteq U, X$ contains either $U^{\prime}$ or $U \backslash U^{\prime}$.

  comment

Markov Chains

• A2.1

  Markov Chains | Part II, 2001

  (i) The fire alarm in Mill Lane is set off at random times. The probability of an alarm during the time-interval $(u, u+h)$ is $\lambda(u) h+o(h)$ where the 'intensity function' $\lambda(u)$ may vary with the time $u$. Let $N(t)$ be the number of alarms by time $t$, and set $N(0)=0$. Show, subject to reasonable extra assumptions to be stated clearly, that $p_{i}(t)=P(N(t)=i)$ satisfies

  $$p_{0}^{\prime}(t)=-\lambda(t) p_{0}(t), \quad p_{i}^{\prime}(t)=\lambda(t)\left\{p_{i-1}(t)-p_{i}(t)\right\}, \quad i \geqslant 1 .$$

  Deduce that $N(t)$ has the Poisson distribution with parameter $\Lambda(t)=\int_{0}^{t} \lambda(u) d u$.

  (ii) The fire alarm in Clarkson Road is different. The number $M(t)$ of alarms by time $t$ is such that

  $$P(M(t+h)=m+1 \mid M(t)=m)=\lambda_{m} h+o(h),$$

  where $\lambda_{m}=\alpha m+\beta, m \geqslant 0$, and $\alpha, \beta>0$. Show, subject to suitable extra conditions, that $p_{m}(t)=P(M(t)=m)$ satisfies a set of differential-difference equations to be specified. Deduce without solving these equations in their entirety that $M(t)$ has mean $\beta\left(e^{\alpha t}-1\right) / \alpha$, and find the variance of $M(t)$.

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2001

  (i) A certain physical quantity $q(x)$ can be represented by the series $\sum_{n=0}^{\infty} c_{n} x^{n}$ in $0 \leqslant x<x_{0}$, but the series diverges for $x>x_{0}$. Describe the Euler transformation to a new series which may enable $q(x)$ to be computed for $x>x_{0}$. Give the first four terms of the new series.

  Describe briefly the disadvantages of the method.

  (ii) The series $\sum_{1}^{\infty} c_{r}$ has partial sums $S_{n}=\sum_{1}^{n} c_{r}$. Describe Shanks' method to approximate $S_{n}$ by

  $$S_{n}=A+B C^{n}$$

  giving expressions for $A, B$ and $C$.

  Denote by $B_{N}$ and $C_{N}$ the values of $B$ and $C$ respectively derived from these expressions using $S_{N-1}, S_{N}$ and $S_{N+1}$ for some fixed $N$. Now let $A^{(n)}$ be the value of $A$ obtained from $(*)$ with $B=B_{N}, C=C_{N}$. Show that, if $\left|C_{N}\right|<1$,

  $$\sum_{1}^{\infty} c_{r}=\lim _{n \rightarrow \infty} A^{(n)}$$

  If, in fact, the partial sums satisfy

  $$S_{n}=a+\alpha c^{n}+\beta d^{n}$$

  with $1>|c|>|d|$, show that

  $$A^{(n)}=A+\gamma d^{n}+o\left(d^{n}\right)$$

  where $\gamma$ is to be found.

  comment

Methods of Mathematical Physics

• B2.18

  Methods of Mathematical Physics | Part II, 2001

  The Bessel function $J_{\nu}(z)$ is defined, for $|\arg z|<\pi / 2$, by

  $$J_{\nu}(z)=\frac{1}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \mathrm{e}^{\left(t-t^{-1}\right) z / 2} t^{-\nu-1} d t,$$

  where the path of integration is the Hankel contour and $t^{-\nu-1}$ is the principal branch.

  Use the method of steepest descent to show that, as $z \rightarrow+\infty$,

  $$J_{\nu}(z) \sim(2 / \pi z)^{\frac{1}{2}} \cos (z-\pi \nu / 2-\pi / 4) .$$

  You should give a rough sketch of the steepest descent paths.

  comment

Nonlinear Waves

• A2.18

  Nonlinear Waves | Part II, 2001

  (i) Establish two conservation laws for the $\mathrm{MKdV}$ equation

  $$\frac{\partial u}{\partial t}+u^{2} \frac{\partial u}{\partial x}+\frac{\partial^{3} u}{\partial x^{3}}=0$$

  State sufficient boundary conditions that $u$ should satisfy for the conservation laws to be valid.

  (ii) The equation

  $$\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x}(\rho V)=0$$

  models traffic flow on a single-lane road, where $\rho(x, t)$ represents the density of cars, and $V$ is a given function of $\rho$. By considering the rate of change of the integral

  $$\int_{a}^{b} \rho d x,$$

  show that $V$ represents the velocity of the cars.

  Suppose now that $V=1-\rho$ (in suitable units), and that $0 \leqslant \rho \leqslant 1$ everywhere. Assume that a queue is building up at a traffic light at $x=1$, so that, when the light turns green at $t=0$,

  $$\rho(x, 0)=\left\{\begin{array}{l} 0 \text { for } x<0 \text { and } x>1 \\ x \text { for } 0 \leqslant x<1 . \end{array}\right.$$

  For this problem, find and sketch the characteristics in the $(x, t)$ plane, for $t>0$, paying particular attention to those emerging from the point $(1,0)$. Show that a shock forms at $t=\frac{1}{2}$. Find the density of cars $\rho(x, t)$ for $0<t<\frac{1}{2}$, and all $x$.

  comment

Number Fields

• B2.9

  Number Fields | Part II, 2001

  Determine the ideal class group of $\mathbf{Q}(\sqrt{-11})$.

  Find all solutions of the diophantine equation

  $$y^{2}+11=x^{3} \quad(x, y \in \mathbf{Z})$$

  [Minkowski's bound is $n ! n^{-n}(4 / \pi)^{r_{2}}\left|D_{k}\right|^{1 / 2}$.]

  comment

Numerical Analysis

• A2.19 B2.19

  Numerical Analysis | Part II, 2001

  (i) Define $m$-step BDF (backward differential formula) methods for the numerical solution of ordinary differential equations and derive explicitly their coefficients.

  (ii) Prove that the linear stability domain of the two-step BDF method includes the interval $(-\infty, 0)$.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2001

  A street trader wishes to dispose of $k$ counterfeit Swiss watches. If he offers one for sale at price $u$ he will sell it with probability $a e^{-u}$. Here $a$ is known and less than 1 . Subsequent to each attempted sale (successful or not) there is a probability $1-\beta$ that he will be arrested and can make no more sales. His aim is to choose the prices at which he offers the watches so as to maximize the expected values of his sales up until the time he is arrested or has sold all $k$ watches.

  Let $V(k)$ be the maximum expected amount he can obtain when he has $k$ watches remaining and has not yet been arrested. Explain why $V(k)$ is the solution to

  $$V(k)=\max _{u>0}\left\{a e^{-u}[u+\beta V(k-1)]+\left(1-a e^{-u}\right) \beta V(k)\right\}$$

  Denote the optimal price by $u_{k}$ and show that

  $$u_{k}=1+\beta V(k)-\beta V(k-1)$$

  and that

  $$V(k)=a e^{-u_{k}} /(1-\beta)$$

  Show inductively that $V(k)$ is a nondecreasing and concave function of $k$.

  comment

Partial Differential Equations

• B2.17

  Partial Differential Equations | Part II, 2001

  Define the Schwartz space $\mathcal{S}(\mathbb{R})$ and the corresponding space of tempered distributions $\mathcal{S}^{\prime}(\mathbb{R})$.

  Use the Fourier transform to give an integral formula for the solution of the equation

  $$-\frac{d^{2} u}{d x^{2}}+\frac{d u}{d x}+u=f$$

  for $f \in \mathcal{S}(\mathbb{R})$. Prove that your solution lies in $\mathcal{S}(\mathbb{R})$. Is your formula the unique solution to $(*)$ in the Schwartz space?

  Deduce from this formula an integral expression for the fundamental solution of the operator $P=-\frac{d^{2}}{d x^{2}}+\frac{d}{d x}+1$.

  Let $K$ be the function:

  $$K(x)= \begin{cases}\frac{1}{\sqrt{5}} e^{-(\sqrt{5}-1) x / 2} & \text { for } x \geqslant 0 \\ \frac{1}{\sqrt{5}} e^{(\sqrt{5}+1) x / 2} & \text { for } x \leqslant 0\end{cases}$$

  Using the definition of distributional derivatives verify that this function is a fundamental solution for $P$.

  comment

Principles of Dynamics

• A2.2 B2.1

  Principles of Dynamics | Part II, 2001

  (i) An axially symmetric top rotates freely about a fixed point $O$ on its axis. The principal moments of inertia are $A, A, C$ and the centre of gravity $G$ is a distance $h$ from $O .$

  Define the three Euler angles $\theta, \phi$ and $\psi$, specifying the orientation of the top. Use Lagrange's equations to show that there are three conserved quantities in the motion. Interpret them physically.

  (ii) Initially the top is spinning with angular speed $n$ about $O G$, with $O G$ vertical, before it is slightly disturbed.

  Show that, in the subsequent motion, $\theta$ stays close to zero if $C^{2} n^{2}>4 m g h A$, but if this condition fails then $\theta$ attains a maximum value given approximately by

  $$\cos \theta \approx \frac{C^{2} n^{2}}{2 m g h A}-1$$

  Why is this only an approximation?

  comment

Principles of Statistics

• A2.11 B2.16

  Principles of Statistics | Part II, 2001

  (i) Let $X_{1}, \ldots, X_{n}$ be independent, identically-distributed $N\left(\mu, \mu^{2}\right)$ random variables, $\mu>0$.

  Find a minimal sufficient statistic for $\mu$.

  Let $T_{1}=n^{-1} \sum_{i=1}^{n} X_{i}$ and $T_{2}=\sqrt{n^{-1} \sum_{i=1}^{n} X_{i}^{2}}$. Write down the distribution of $X_{i} / \mu$, and hence show that $Z=T_{1} / T_{2}$ is ancillary. Explain briefly why the Conditionality Principle would lead to inference about $\mu$ being drawn from the conditional distribution of $T_{2}$ given $Z$.

  What is the maximum likelihood estimator of $\mu$ ?

  (ii) Describe briefly the Bayesian approach to predictive inference,

  Let $Z_{1}, \ldots, Z_{n}$ be independent, identically-distributed $N\left(\mu, \sigma^{2}\right)$ random variables, with $\mu, \sigma^{2}$ both unknown. Derive the maximum likelihood estimators $\widehat{\mu}, \widehat{\sigma}^{2}$ of $\mu, \sigma^{2}$ based on $Z_{1}, \ldots, Z_{n}$, and state, without proof, their joint distribution.

  Suppose that it is required to construct a prediction interval

  $I_{1-\alpha} \equiv I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n}\right)$ for a future, independent, random variable $Z_{0}$ with the same $N\left(\mu, \sigma^{2}\right)$ distribution, such that

  $$P\left(Z_{0} \in I_{1-\alpha}\right)=1-\alpha$$

  with the probability over the joint distribution of $Z_{0}, Z_{1}, \ldots, Z_{n}$. Let

  $$I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \sigma^{2}\right)=\left[\bar{Z}_{n}-z_{\alpha / 2} \sigma \sqrt{1+1 / n}, \bar{Z}_{n}+z_{\alpha / 2} \sigma \sqrt{1+1 / n}\right]$$

  where $\bar{Z}_{n}=n^{-1} \sum_{i=1}^{n} Z_{i}$, and $\Phi\left(z_{\beta}\right)=1-\beta$, with $\Phi$ the distribution function of $N(0,1)$.

  Show that $P\left(Z_{0} \in I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \sigma^{2}\right)\right)=1-\alpha$.

  By considering the distribution of $\left(Z_{0}-\bar{Z}_{n}\right) /\left(\widehat{\sigma} \sqrt{\frac{n+1}{n-1}}\right)$, or otherwise, show that

  $$P\left(Z_{0} \in I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)\right)<1-\alpha,$$

  and show how to construct an interval $I_{1-\gamma}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)$ with

  $$P\left(Z_{0} \in I_{1-\gamma}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)\right)=1-\alpha .$$

  [Hint: if $Y$ has the $t$-distribution with $m$ degrees of freedom and $t_{\beta}^{(m)}$ is defined by $P\left(Y<t_{\beta}^{(m)}\right)=1-\beta$ then $t_{\beta}>z_{\beta}$ for $\beta<\frac{1}{2}$.]

  comment

Probability and Measure

• B2.12

  Probability and Measure | Part II, 2001

  (a) Let $\Omega=(0,1), \mathcal{F}=\mathcal{B}((0,1))$ be the Borel $\sigma$-field and let $\mathbb{P}$ be Lebesgue measure on $(\Omega, \mathcal{F})$. What is the distribution of the random variable $Z$, where $Z(\omega)=2 \omega-1$ ?

  Let $\omega=\sum_{n=1}^{\infty} 2^{-n} R_{n}(\omega)$ be the binary expansion of the point $\omega \in \Omega$ and set $U(\omega)=\sum_{n \text { odd }} 2^{-n} Q_{n}(\omega)$, where $Q_{n}(\omega)=2 R_{n}(\omega)-1$. Find a random variable $V$ independent of $U$ such that $U$ and $V$ are identically distributed and $U+\frac{1}{2} V$ is uniformly distributed on $(-1,1)$.

  (b) Now suppose that on some probability triple $X$ and $Y$ are independent, identicallydistributed random variables such that $X+\frac{1}{2} Y$ is uniformly distributed on $(-1,1)$.

  Let $\phi$ be the characteristic function of $X$. Calculate $\phi(t) / \phi(t / 4)$. Show that the distribution of $X$ must be the same as the distribution of the random variable $U$ in (a).

  comment

Quantum Physics

• A2.14

  Quantum Physics | Part II, 2001

  (i) Each particle in a system of $N$ identical fermions has a set of energy levels, $E_{i}$, with degeneracy $g_{i}$, where $1 \leq i<\infty$. Explain why, in thermal equilibrium, the average number of particles with energy $E_{i}$ is

  $$N_{i}=\frac{g_{i}}{e^{\beta\left(E_{i}-\mu\right)}+1} .$$

  The physical significance of the parameters $\beta$ and $\mu$ should be made clear.

  (ii) A simple model of a crystal consists of a linear array of sites with separation $a$. At the $n$th site an electron may occupy either of two states with probability amplitudes $b_{n}$ and $c_{n}$, respectively. The time-dependent Schrödinger equation governing the amplitudes gives

  $$\begin{aligned} &i \hbar \dot{b}_{n}=E_{0} b_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right), \\ &i \hbar \dot{c}_{n}=E_{1} c_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right) \end{aligned}$$

  where $A>0$.

  By examining solutions of the form

  $$\left(\begin{array}{l} b_{n} \\ c_{n} \end{array}\right)=\left(\begin{array}{l} B \\ C \end{array}\right) e^{i(k n a-E t / \hbar)},$$

  show that the energies of the electron fall into two bands given by

  $$E=\frac{1}{2}\left(E_{0}+E_{1}-4 A \cos k a\right) \pm \frac{1}{2} \sqrt{\left(E_{0}-E_{1}\right)^{2}+16 A^{2} \cos ^{2} k a}$$

  Describe briefly how the energy band structure for electrons in real crystalline materials can be used to explain why they are insulators, conductors or semiconductors.

  comment

Representation Theory

• B2.6

  Representation Theory | Part II, 2001

  (i) Let $G$ be a group, and $X$ and $Y$ finite $G$-sets. Define the permutation representation $\mathbf{C}[X]$ and compute its character. Show that

  $$\operatorname{dim}_{\operatorname{Hom}_{G}}(\mathbf{C}[X], \mathbf{C}[Y])$$

  is equal to the number of $G$-orbits in $X \times Y$.

  (ii) Let $G=S_{n}(n \geqslant 4), X=\{1, \ldots, n\}$, and

  $$Z=\{\{i, j\} \subseteq X \mid i \neq j\}$$

  be the set of 2 -element subsets of $X$. Decompose $\mathbf{C}[Z]$ into irreducibles, and determine the dimension of each irreducible constituent.

  comment

Theoretical Geophysics

• A2.16

  Theoretical Geophysics | Part II, 2001

  (i) In a reference frame rotating with constant angular velocity $\boldsymbol{\Omega}$ the equations of motion for an inviscid, incompressible fluid of density $\rho$ in a gravitational field $g=-\nabla \Phi$ are

  $$\rho \frac{D \mathbf{u}}{D t}+2 \rho \boldsymbol{\Omega} \wedge \mathbf{u}=-\nabla p+\rho \mathbf{g}, \quad \nabla \cdot \mathbf{u}=0$$

  Define the Rossby number and explain what is meant by geostrophic flow.

  Derive the vorticity equation

  $$\frac{D \boldsymbol{\omega}}{D t}=(\boldsymbol{\omega}+2 \boldsymbol{\Omega}) \cdot \nabla \mathbf{u}+\frac{\nabla \rho \wedge \nabla p}{\rho^{2}}$$

  $\left[\right.$ Recall that $\mathbf{u} \cdot \nabla \mathbf{u}=\nabla\left(\frac{1}{2} \mathbf{u}^{2}\right)-\mathbf{u} \wedge(\nabla \wedge \mathbf{u})$.]

  Give a physical interpretation for the term $(\boldsymbol{\omega}+2 \boldsymbol{\Omega}) \cdot \nabla \mathbf{u}$.

  (ii) Consider the rotating fluid of part (i), but now let $\rho$ be constant and absorb the effects of gravity into a modified pressure $P=p-\rho \mathbf{g} \cdot \mathbf{x}$. State the linearized equations of motion and the linearized vorticity equation for small-amplitude motions (inertial waves).

  Use the linearized equations of motion to show that

  $$\nabla^{2} P=2 \rho \boldsymbol{\Omega} \cdot \boldsymbol{\omega} .$$

  Calculate the time derivative of the curl of the linearized vorticity equation. Hence show that

  $$\frac{\partial^{2}}{\partial t^{2}}\left(\nabla^{2} \mathbf{u}\right)=-(2 \mathbf{\Omega} \cdot \nabla)^{2} \mathbf{u}$$

  Deduce the dispersion relation for waves proportional to $\exp [i(\mathbf{k} \cdot \mathbf{x}-n t)]$. Show that $|n| \leq 2 \Omega$. Show further that if $n=2 \Omega$ then $P=0$.

  comment

Waves in Fluid and Solid Media

• B2.25

  Waves in Fluid and Solid Media | Part II, 2001

  A semi-infinite elastic medium with shear modulus $\mu_{1}$ and shear-wave speed $c_{1}$ lies in $y<0$. Above it there is a layer $0 \leq y \leqslant h$ of a second elastic medium with shear modulus $\mu_{2}$ and shear-wave speed $c_{2}\left(<c_{1}\right)$. The top boundary $y=h$ is stress-free. Consider a monochromatic shear wave propagating at speed $c$ with wavenumber $k$ in the $x$-direction and with displacements only in the $z$-direction.

  Obtain the dispersion relation

  $$\tan k h \theta=\frac{\mu_{1} c_{2}}{\mu_{2} c_{1}} \frac{1}{\theta}\left(\frac{c_{1}^{2}}{c_{2}^{2}}-1-\theta^{2}\right)^{1 / 2}, \quad \text { where } \quad \theta=\sqrt{\frac{c^{2}}{c_{2}^{2}}-1} .$$

  Deduce that the modes have a cut-off frequency $\pi n c_{1} c_{2} / h \sqrt{c_{1}^{2}-c_{2}^{2}}$ where they propagate at speed $c=c_{1}$.

  comment