Part IB, 2021, Paper 1

Analysis and Topology

• Paper 1, Section II, F

  Analysis and Topology | Part IB, 2021

  Let $f: X \rightarrow Y$ be a map between metric spaces. Prove that the following two statements are equivalent:

  (i) $f^{-1}(A) \subset X$ is open whenever $A \subset Y$ is open.

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for any sequence $x_{n} \rightarrow a$.

  For $f: X \rightarrow Y$ as above, determine which of the following statements are always true and which may be false, giving a proof or a counterexample as appropriate.

  (a) If $X$ is compact and $f$ is continuous, then $f$ is uniformly continuous.

  (b) If $X$ is compact and $f$ is continuous, then $Y$ is compact.

  (c) If $X$ is connected, $f$ is continuous and $f(X)$ is dense in $Y$, then $Y$ is connected.

  (d) If the set $\{(x, y) \in X \times Y: y=f(x)\}$ is closed in $X \times Y$ and $Y$ is compact, then $f$ is continuous.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, B

  Complex Analysis or Complex Methods | Part IB, 2021

  Let $x>0, x \neq 2$, and let $C_{x}$ denote the positively oriented circle of radius $x$ centred at the origin. Define

  $$g(x)=\oint_{C_{x}} \frac{z^{2}+e^{z}}{z^{2}(z-2)} d z$$

  Evaluate $g(x)$ for $x \in(0, \infty) \backslash\{2\}$.

  comment

• Paper 1, Section II, G

  Complex Analysis or Complex Methods | Part IB, 2021

  (a) State a theorem establishing Laurent series of analytic functions on suitable domains. Give a formula for the $n^{\text {th }}$Laurent coefficient.

  Define the notion of isolated singularity. State the classification of an isolated singularity in terms of Laurent coefficients.

  Compute the Laurent series of

  $$f(z)=\frac{1}{z(z-1)}$$

  on the annuli $A_{1}=\{z: 0<|z|<1\}$ and $A_{2}=\{z: 1<|z|\}$. Using this example, comment on the statement that Laurent coefficients are unique. Classify the singularity of $f$ at 0 .

  (b) Let $U$ be an open subset of the complex plane, let $a \in U$ and let $U^{\prime}=U \backslash\{a\}$. Assume that $f$ is an analytic function on $U^{\prime}$ with $|f(z)| \rightarrow \infty$ as $z \rightarrow a$. By considering the Laurent series of $g(z)=\frac{1}{f(z)}$ at $a$, classify the singularity of $f$ at $a$ in terms of the Laurent coefficients. [You may assume that a continuous function on $U$ that is analytic on $U^{\prime}$ is analytic on $U$.]

  Now let $f: \mathbb{C} \rightarrow \mathbb{C}$ be an entire function with $|f(z)| \rightarrow \infty$ as $z \rightarrow \infty$. By considering Laurent series at 0 of $f(z)$ and of $h(z)=f\left(\frac{1}{z}\right)$, show that $f$ is a polynomial.

  (c) Classify, giving reasons, the singularity at the origin of each of the following functions and in each case compute the residue:

  $$g(z)=\frac{\exp (z)-1}{z \log (z+1)} \quad \text { and } \quad h(z)=\sin (z) \sin (1 / z)$$

  comment

Electromagnetism

• Paper 1, Section II, 15D

  Electromagnetism | Part IB, 2021

  (a) Show that the magnetic flux passing through a simple, closed curve $C$ can be written as

  $$\Phi=\oint_{C} \mathbf{A} \cdot \mathbf{d} \mathbf{x},$$

  where $\mathbf{A}$ is the magnetic vector potential. Explain why this integral is independent of the choice of gauge.

  (b) Show that the magnetic vector potential due to a static electric current density $\mathbf{J}$, in the Coulomb gauge, satisfies Poisson's equation

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J}$$

  Hence obtain an expression for the magnetic vector potential due to a static, thin wire, in the form of a simple, closed curve $C$, that carries an electric current $I$. [You may assume that the electric current density of the wire can be written as

  $$\mathbf{J}(\mathbf{x})=I \int_{C} \delta^{(3)}\left(\mathbf{x}-\mathbf{x}^{\prime}\right) \mathbf{d} \mathbf{x}^{\prime}$$

  where $\delta^{(3)}$ is the three-dimensional Dirac delta function.]

  (c) Consider two thin wires, in the form of simple, closed curves $C_{1}$ and $C_{2}$, that carry electric currents $I_{1}$ and $I_{2}$, respectively. Let $\Phi_{i j}$ (where $i, j \in\{1,2\}$ ) be the magnetic flux passing through the curve $C_{i}$ due to the current $I_{j}$ flowing around $C_{j}$. The inductances are defined by $L_{i j}=\Phi_{i j} / I_{j}$. By combining the results of parts (a) and (b), or otherwise, derive Neumann's formula for the mutual inductance,

  $$L_{12}=L_{21}=\frac{\mu_{0}}{4 \pi} \oint_{C_{1}} \oint_{C_{2}} \frac{\mathbf{d} \mathbf{x}_{1} \cdot \mathbf{d} \mathbf{x}_{2}}{\left|\mathbf{x}_{1}-\mathbf{x}_{2}\right|} .$$

  Suppose that $C_{1}$ is a circular loop of radius $a$, centred at $(0,0,0)$ and lying in the plane $z=0$, and that $C_{2}$ is a different circular loop of radius $b$, centred at $(0,0, c)$ and lying in the plane $z=c$. Show that the mutual inductance of the two loops is

  $$\frac{\mu_{0}}{4} \sqrt{a^{2}+b^{2}+c^{2}} f(q)$$

  where

  $$q=\frac{2 a b}{a^{2}+b^{2}+c^{2}}$$

  and the function $f(q)$ is defined, for $0<q<1$, by the integral

  $$f(q)=\int_{0}^{2 \pi} \frac{q \cos \theta d \theta}{\sqrt{1-q \cos \theta}}$$

  comment

Fluid Dynamics

• Paper 1, Section II, A

  Fluid Dynamics | Part IB, 2021

  A two-dimensional flow is given by a velocity potential

  $$\phi(x, y, t)=\epsilon y \sin (x-t)$$

  where $\epsilon$ is a constant.

  (a) Find the corresponding velocity field $\mathbf{u}(x, y, t)$. Determine $\boldsymbol{\nabla} \cdot \mathbf{u}$.

  (b) The time-average $\langle\psi\rangle(x, y)$ of a quantity $\psi(x, y, t)$ is defined as

  $$\langle\psi\rangle(x, y)=\frac{1}{2 \pi} \int_{0}^{2 \pi} \psi(x, y, t) d t .$$

  Show that the time-average of this velocity field is zero everywhere. Write down an expression for the acceleration of fluid particles, and find the time-average of this expression at a fixed point $(x, y)$.

  (c) Now assume that $|\epsilon| \ll 1$. The material particle at $(0,0)$ at $t=0$ is marked with dye. Write down equations for its subsequent motion. Verify that its position $(x, y)$ for $t>0$ is given (correct to terms of order $\epsilon^{2}$ ) by

  $$\begin{aligned} x &=\epsilon^{2}\left(\frac{1}{4} \sin 2 t+\frac{t}{2}-\sin t\right) \\ y &=\epsilon(\cos t-1) \end{aligned}$$

  Deduce the time-average velocity of the dyed particle correct to this order.

  comment

Geometry

• Paper 1, Section I, F

  Geometry | Part IB, 2021

  Let $f: \mathbb{R}^{3} \rightarrow \mathbb{R}$ be a smooth function and let $\Sigma=f^{-1}(0)$ (assumed not empty). Show that if the differential $D f_{p} \neq 0$ for all $p \in \Sigma$, then $\Sigma$ is a smooth surface in $\mathbb{R}^{3}$.

  Is $\left\{(x, y, z) \in \mathbb{R}^{3}: x^{2}+y^{2}=\cosh \left(z^{2}\right)\right\}$ a smooth surface? Is every surface $\Sigma \subset \mathbb{R}^{3}$ of the form $f^{-1}(0)$ for some smooth $f: \mathbb{R}^{3} \rightarrow \mathbb{R}$ ? Justify your answers.

  comment

• Paper 1, Section II, F

  Geometry | Part IB, 2021

  Let $S \subset \mathbb{R}^{3}$ be an oriented surface. Define the Gauss map $N$ and show that the differential $D N_{p}$ of the Gauss map at any point $p \in S$ is a self-adjoint linear map. Define the Gauss curvature $\kappa$ and compute $\kappa$ in a given parametrisation.

  A point $p \in S$ is called umbilic if $D N_{p}$ has a repeated eigenvalue. Let $S \subset \mathbb{R}^{3}$ be a surface such that every point is umbilic and there is a parametrisation $\phi: \mathbb{R}^{2} \rightarrow S$ such that $S=\phi\left(\mathbb{R}^{2}\right)$. Prove that $S$ is part of a plane or part of a sphere. $[$ Hint: consider the symmetry of the mixed partial derivatives $n_{u v}=n_{v u}$, where $n(u, v)=N(\phi(u, v))$ for $\left.(u, v) \in \mathbb{R}^{2} .\right]$

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2021

  Show that a ring $R$ is Noetherian if and only if every ideal of $R$ is finitely generated. Show that if $\phi: R \rightarrow S$ is a surjective ring homomorphism and $R$ is Noetherian, then $S$ is Noetherian.

  State and prove Hilbert's Basis Theorem.

  Let $\alpha \in \mathbb{C}$. Is $\mathbb{Z}[\alpha]$ Noetherian? Justify your answer.

  Give, with proof, an example of a Unique Factorization Domain that is not Noetherian.

  Let $R$ be the ring of continuous functions $\mathbb{R} \rightarrow \mathbb{R}$. Is $R$ Noetherian? Justify your answer.

  comment

Linear Algebra

• Paper 1, Section I, $1 \mathrm{E}$

  Linear Algebra | Part IB, 2021

  Let $V$ be a vector space over $\mathbb{R}, \operatorname{dim} V=n$, and let $\langle,$,$rangle be a non-degenerate anti-$ symmetric bilinear form on $V$.

  Let $v \in V, v \neq 0$. Show that $v^{\perp}$ is of dimension $n-1$ and $v \in v^{\perp}$. Show that if $W \subseteq v^{\perp}$ is a subspace with $W \oplus \mathbb{R} v=v^{\perp}$, then the restriction of $\langle,$,$rangle to W$ is nondegenerate.

  Conclude that the dimension of $V$ is even.

  comment

• Paper 1, Section II, E

  Linear Algebra | Part IB, 2021

  Let $d \geqslant 1$, and let $J_{d}=\left(\begin{array}{ccccc}0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ & & \cdots & \cdots & \\ 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & \ldots & 0 & 0\end{array}\right) \in \operatorname{Mat}_{d}(\mathbb{C})$.

  (a) (i) Compute $J_{d}^{n}$, for all $n \geqslant 0$.

  (ii) Hence, or otherwise, compute $\left(\lambda I+J_{d}\right)^{n}$, for all $n \geqslant 0$.

  (b) Let $V$ be a finite-dimensional vector space over $\mathbb{C}$, and let $\varphi \in \operatorname{End}(V)$. Suppose $\varphi^{n}=0$ for some $n>1$.

  (i) Determine the possible eigenvalues of $\varphi$.

  (ii) What are the possible Jordan blocks of $\varphi$ ?

  (iii) Show that if $\varphi^{2}=0$, there exists a decomposition

  $$V=U \oplus W_{1} \oplus W_{2}$$

  where $\varphi(U)=\varphi\left(W_{1}\right)=0, \varphi\left(W_{2}\right)=W_{1}$, and $\operatorname{dim} W_{2}=\operatorname{dim} W_{1}$.

  comment

Markov Chains

• Paper 1, Section II, 19H

  Markov Chains | Part IB, 2021

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P$. What is a stopping time of $\left(X_{n}\right)_{n \geqslant 0}$ ? What is the strong Markov property?

  The exciting game of 'Unopoly' is played by a single player on a board of 4 squares. The player starts with $£ m$ (where $m \in \mathbb{N}$ ). During each turn, the player tosses a fair coin and moves one or two places in a clockwise direction $(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1)$ according to whether the coin lands heads or tails respectively. The player collects $£ 2$ each time they pass (or land on) square 1. If the player lands on square 3 however, they immediately lose $£ 1$ and go back to square 2. The game continues indefinitely unless the player is on square 2 with $£ 0$, in which case the player loses the game and the game ends.

  

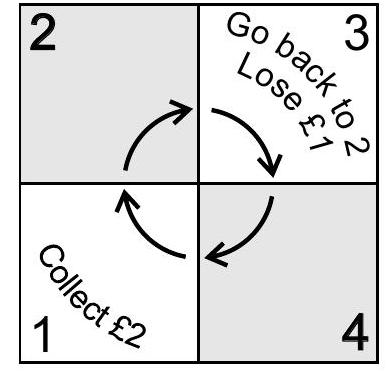
  (a) By setting up an appropriate Markov chain, show that if the player is at square 2 with $£ m$, where $m \geqslant 1$, the probability that they are ever at square 2 with $£(m-1)$ is $2 / 3 .$

  (b) Find the probability of losing the game when the player starts on square 1 with $£ m$, where $m \geqslant 1$.

  [Hint: Take the state space of your Markov chain to be $\{1,2,4\} \times\{0,1, \ldots\}$.]

  comment

Methods

• Paper 1, Section II, C

  Methods | Part IB, 2021

  (a) By introducing the variables $\xi=x+c t$ and $\eta=x-c t$ (where $c$ is a constant), derive d'Alembert's solution of the initial value problem for the wave equation:

  $$u_{t t}-c^{2} u_{x x}=0, \quad u(x, 0)=\phi(x), \quad u_{t}(x, 0)=\psi(x)$$

  where $-\infty<x<\infty, t \geqslant 0$ and $\phi$ and $\psi$ are given functions (and subscripts denote partial derivatives).

  (b) Consider the forced wave equation with homogeneous initial conditions:

  $$u_{t t}-c^{2} u_{x x}=f(x, t), \quad u(x, 0)=0, \quad u_{t}(x, 0)=0$$

  where $-\infty<x<\infty, t \geqslant 0$ and $f$ is a given function. You may assume that the solution is given by

  $$u(x, t)=\frac{1}{2 c} \int_{0}^{t} \int_{x-c(t-s)}^{x+c(t-s)} f(y, s) d y d s$$

  For the forced wave equation $u_{t t}-c^{2} u_{x x}=f(x, t)$, now in the half space $x \geqslant 0$ (and with $t \geqslant 0$ as before), find (in terms of $f$ ) the solution for $u(x, t)$ that satisfies the (inhomogeneous) initial conditions

  $$u(x, 0)=\sin x, \quad u_{t}(x, 0)=0, \quad \text { for } x \geqslant 0$$

  and the boundary condition $u(0, t)=0$ for $t \geqslant 0$.

  comment

Numerical Analysis

• Paper 1, Section I, B

  Numerical Analysis | Part IB, 2021

  Prove, from first principles, that there is an algorithm that can determine whether any real symmetric matrix $A \in \mathbb{R}^{n \times n}$ is positive definite or not, with the computational cost (number of arithmetic operations) bounded by $\mathcal{O}\left(n^{3}\right)$.

  [Hint: Consider the LDL decomposition.]

  comment

• Paper 1, Section II, B

  Numerical Analysis | Part IB, 2021

  For the ordinary differential equation

  $$\boldsymbol{y}^{\prime}=\boldsymbol{f}(t, \boldsymbol{y}), \quad \boldsymbol{y}(0)=\tilde{\boldsymbol{y}}_{0}, \quad t \geqslant 0$$

  where $\boldsymbol{y}(t) \in \mathbb{R}^{N}$ and the function $\boldsymbol{f}: \mathbb{R} \times \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$ is analytic, consider an explicit one-step method described as the mapping

  $$\boldsymbol{y}_{n+1}=\boldsymbol{y}_{n}+h \varphi\left(t_{n}, \boldsymbol{y}_{n}, h\right)$$

  Here $\varphi: \mathbb{R}_{+} \times \mathbb{R}^{N} \times \mathbb{R}_{+} \rightarrow \mathbb{R}^{N}, n=0,1, \ldots$ and $t_{n}=n h$ with time step $h>0$, producing numerical approximations $\boldsymbol{y}_{n}$ to the exact solution $\boldsymbol{y}\left(t_{n}\right)$ of equation $(*)$, with $\boldsymbol{y}_{0}$ being the initial value of the numerical solution.

  (i) Define the local error of a one-step method.

  (ii) Let $\|\cdot\|$ be a norm on $\mathbb{R}^{N}$ and suppose that

  $$\|\boldsymbol{\varphi}(t, \boldsymbol{u}, h)-\boldsymbol{\varphi}(t, \boldsymbol{v}, h)\| \leqslant L\|\boldsymbol{u}-\boldsymbol{v}\|,$$

  for all $h>0, t \in \mathbb{R}, \boldsymbol{u}, \boldsymbol{v} \in \mathbb{R}^{N}$, where $L$ is some positive constant. Let $t^{*}>0$ be given and $\boldsymbol{e}_{0}=\boldsymbol{y}_{0}-\boldsymbol{y}(0)$ denote the initial error (potentially non-zero). Show that if the local error of the one-step method ( $\uparrow$ ) is $\mathcal{O}\left(h^{p+1}\right)$, then

  $$\max _{n=0, \ldots,\left\lfloor t^{*} / h\right\rfloor}\left\|\boldsymbol{y}_{n}-\boldsymbol{y}(n h)\right\| \leqslant e^{t^{*} L}\left\|\boldsymbol{e}_{0}\right\|+\mathcal{O}\left(h^{p}\right), \quad h \rightarrow 0$$

  (iii) Let $N=1$ and consider equation $(*)$ where $f$ is time-independent satisfying $|f(u)-f(v)| \leqslant K|u-v|$ for all $u, v \in \mathbb{R}$, where $K$ is a positive constant. Consider the one-step method given by

  $$y_{n+1}=y_{n}+\frac{1}{4} h\left(k_{1}+3 k_{2}\right), \quad k_{1}=f\left(y_{n}\right), \quad k_{2}=f\left(y_{n}+\frac{2}{3} h k_{1}\right) .$$

  Use part (ii) to show that for this method we have that equation (††) holds (with a potentially different constant $L$ ) for $p=2$.

  comment

Optimization

• Paper 1, Section I, $\mathbf{7 H}$

  Optimization | Part IB, 2021

  (a) Let $f_{i}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be a convex function for each $i=1, \ldots, m$. Show that

  $$x \mapsto \max _{i=1, \ldots, m} f_{i}(x) \quad \text { and } \quad x \mapsto \sum_{i=1}^{m} f_{i}(x)$$

  are both convex functions.

  (b) Fix $c \in \mathbb{R}^{d}$. Show that if $f: \mathbb{R} \rightarrow \mathbb{R}$ is convex, then $g: \mathbb{R}^{d} \rightarrow \mathbb{R}$ given by $g(x)=f\left(c^{T} x\right)$ is convex.

  (c) Fix vectors $a_{1}, \ldots, a_{n} \in \mathbb{R}^{d}$. Let $Q: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be given by

  $$Q(\beta)=\sum_{i=1}^{n} \log \left(1+e^{a_{i}^{T} \beta}\right)+\sum_{j=1}^{d}\left|\beta_{j}\right|$$

  Show that $Q$ is convex. [You may use any result from the course provided you state it.]

  comment

Quantum Mechanics

• Paper 1, Section II, C

  Quantum Mechanics | Part IB, 2021

  Consider a quantum mechanical particle of mass $m$ in a one-dimensional stepped potential well $U(x)$ given by:

  $$U(x)= \begin{cases}\infty & \text { for } x<0 \text { and } x>a \\ 0 & \text { for } 0 \leqslant x \leqslant a / 2 \\ U_{0} & \text { for } a / 2<x \leqslant a\end{cases}$$

  where $a>0$ and $U_{0} \geqslant 0$ are constants.

  (i) Show that all energy levels $E$ of the particle are non-negative. Show that any level $E$ with $0<E<U_{0}$ satisfies

  $$\frac{1}{k} \tan \frac{k a}{2}=-\frac{1}{l} \tanh \frac{l a}{2}$$

  where

  $$k=\sqrt{\frac{2 m E}{\hbar^{2}}}>0 \quad \text { and } \quad l=\sqrt{\frac{2 m\left(U_{0}-E\right)}{\hbar^{2}}}>0$$

  (ii) Suppose that initially $U_{0}=0$ and the particle is in the ground state of the potential well. $U_{0}$ is then changed to a value $U_{0}>0$ (while the particle's wavefunction stays the same) and the energy of the particle is measured. For $0<E<U_{0}$, give an expression in terms of $E$ for prob $(E)$, the probability that the energy measurement will find the particle having energy $E$. The expression may be left in terms of integrals that you need not evaluate.

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2021

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. Bernoulli $(p)$ random variables, where $n \geqslant 3$ and $p \in(0,1)$ is unknown.

  (a) What does it mean for a statistic $T$ to be sufficient for $p$ ? Find such a sufficient statistic $T$.

  (b) State and prove the Rao-Blackwell theorem.

  (c) By considering the estimator $X_{1} X_{2}$ of $p^{2}$, find an unbiased estimator of $p^{2}$ that is a function of the statistic $T$ found in part (a), and has variance strictly smaller than that of $X_{1} X_{2}$.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2021

  (a) Show that if $W_{1}, \ldots, W_{n}$ are independent random variables with common $\operatorname{Exp}(1)$ distribution, then $\sum_{i=1}^{n} W_{i} \sim \Gamma(n, 1)$. [Hint: If $W \sim \Gamma(\alpha, \lambda)$ then $\mathbb{E} e^{t W}=\{\lambda /(\lambda-t)\}^{\alpha}$ if $t<\lambda$ and $\infty$ otherwise.]

  (b) Show that if $X \sim U(0,1)$ then $-\log X \sim \operatorname{Exp}(1)$.

  (c) State the Neyman-Pearson lemma.

  (d) Let $X_{1}, \ldots, X_{n}$ be independent random variables with common density proportional to $x^{\theta} \mathbf{1}_{(0,1)}(x)$ for $\theta \geqslant 0$. Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta=1$, giving the critical region in terms of a quantile of an appropriate gamma distribution. Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta>0$.

  comment

Variational Principles

• Paper 1, Section I, D

  Variational Principles | Part IB, 2021

  Let $D$ be a bounded region of $\mathbb{R}^{2}$, with boundary $\partial D$. Let $u(x, y)$ be a smooth function defined on $D$, subject to the boundary condition that $u=0$ on $\partial D$ and the normalization condition that

  $$\int_{D} u^{2} d x d y=1$$

  Let $I[u]$ be the functional

  $$I[u]=\int_{D}|\nabla u|^{2} d x d y$$

  Show that $I[u]$ has a stationary value, subject to the stated boundary and normalization conditions, when $u$ satisfies a partial differential equation of the form

  $$\nabla^{2} u+\lambda u=0$$

  in $D$, where $\lambda$ is a constant.

  Determine how $\lambda$ is related to the stationary value of the functional $I[u]$. $[$ Hint: Consider $\boldsymbol{\nabla} \cdot(u \boldsymbol{\nabla} u)$.]

  comment