Part IB, 2018, Paper 1

Analysis II

• Paper 1, Section II, F

  Analysis II | Part IB, 2018

  Let $U \subset \mathbb{R}^{n}$ be a non-empty open set and let $f: U \rightarrow \mathbb{R}^{n}$.

  (a) What does it mean to say that $f$ is differentiable? What does it mean to say that $f$ is a $C^{1}$ function?

  If $f$ is differentiable, show that $f$ is continuous.

  State the inverse function theorem.

  (b) Suppose that $U$ is convex, $f$ is $C^{1}$ and that its derivative $D f(a)$ at a satisfies $\|D f(a)-I\|<1$ for all $a \in U$, where $I: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is the identity map and $\|\cdot\|$ denotes the operator norm. Show that $f$ is injective.

  Explain why $f(U)$ is an open subset of $\mathbb{R}^{n}$.

  Must it be true that $f(U)=\mathbb{R}^{n}$ ? What if $U=\mathbb{R}^{n}$ ? Give proofs or counter-examples as appropriate.

  (c) Find the largest set $U \subset \mathbb{R}^{2}$ such that the map $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by $f(x, y)=\left(x^{2}-y^{2}, 2 x y\right)$ satisfies $\|D f(a)-I\|<1$ for every $a \in U$.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, A

  Complex Analysis or Complex Methods | Part IB, 2018

  (a) Show that

  $$w=\log (z)$$

  is a conformal mapping from the right half $z$-plane, $\operatorname{Re}(z)>0$, to the strip

  $$S=\left\{w:-\frac{\pi}{2}<\operatorname{Im}(w)<\frac{\pi}{2}\right\}$$

  for a suitably chosen branch of $\log (z)$ that you should specify.

  (b) Show that

  $$w=\frac{z-1}{z+1}$$

  is a conformal mapping from the right half $z$-plane, $\operatorname{Re}(z)>0$, to the unit disc

  $$D=\{w:|w|<1\}$$

  (c) Deduce a conformal mapping from the strip $S$ to the disc $D$.

  comment

• Paper 1, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2018

  (a) Let $C$ be a rectangular contour with vertices at $\pm R+\pi i$ and $\pm R-\pi i$ for some $R>0$ taken in the anticlockwise direction. By considering

  $$\lim _{R \rightarrow \infty} \oint_{C} \frac{e^{i z^{2} / 4 \pi}}{e^{z / 2}-e^{-z / 2}} d z$$

  show that

  $$\lim _{R \rightarrow \infty} \int_{-R}^{R} e^{i x^{2} / 4 \pi} d x=2 \pi e^{\pi i / 4}$$

  (b) By using a semi-circular contour in the upper half plane, calculate

  $$\int_{0}^{\infty} \frac{x \sin (\pi x)}{x^{2}+a^{2}} d x$$

  for $a>0$.

  [You may use Jordan's Lemma without proof.]

  comment

Electromagnetism

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2018

  Starting from the Lorentz force law acting on a current distribution $\mathbf{J}$ obeying $\boldsymbol{\nabla} \cdot \mathbf{J}=0$, show that the energy of a magnetic dipole $\mathbf{m}$ in the presence of a time independent magnetic field $\mathbf{B}$ is

  $$U=-\mathbf{m} \cdot \mathbf{B}$$

  State clearly any approximations you make.

  [You may use without proof the fact that

  $$\int(\mathbf{a} \cdot \mathbf{r}) \mathbf{J}(\mathbf{r}) \mathrm{d} V=-\frac{1}{2} \mathbf{a} \times \int(\mathbf{r} \times \mathbf{J}(\mathbf{r})) \mathrm{d} V$$

  for any constant vector $\mathbf{a}$, and the identity

  $$(\mathbf{b} \times \boldsymbol{\nabla}) \times \mathbf{c}=\boldsymbol{\nabla}(\mathbf{b} \cdot \mathbf{c})-\mathbf{b}(\boldsymbol{\nabla} \cdot \mathbf{c})$$

  which holds when $\mathbf{b}$ is constant.]

  A beam of slowly moving, randomly oriented magnetic dipoles enters a region where the magnetic field is

  $$\mathbf{B}=\hat{\mathbf{z}} B_{0}+(y \hat{\mathbf{x}}+x \hat{\mathbf{y}}) B_{1},$$

  with $B_{0}$ and $B_{1}$ constants. By considering their energy, briefly describe what happens to those dipoles that are parallel to, and those that are anti-parallel to the direction of $\mathbf{B}$.

  comment

Fluid Dynamics

• Paper 1, Section I, D

  Fluid Dynamics | Part IB, 2018

  Show that the flow with velocity potential

  $$\phi=\frac{q}{2 \pi} \ln r$$

  in two-dimensional, plane-polar coordinates $(r, \theta)$ is incompressible in $r>0$. Determine the flux of fluid across a closed contour $C$ that encloses the origin. What does this flow represent?

  Show that the flow with velocity potential

  $$\phi=\frac{q}{4 \pi} \ln \left(x^{2}+(y-a)^{2}\right)+\frac{q}{4 \pi} \ln \left(x^{2}+(y+a)^{2}\right)$$

  has no normal flow across the line $y=0$. What fluid flow does this represent in the unbounded plane? What flow does it represent for fluid occupying the domain $y>0$ ?

  comment

• Paper 1, Section II, D

  Fluid Dynamics | Part IB, 2018

  A layer of fluid of dynamic viscosity $\mu$, density $\rho$ and uniform thickness $h$ flows down a rigid vertical plane. The adjacent air has uniform pressure $p_{0}$ and exerts a tangential stress on the fluid that is proportional to the surface velocity and opposes the flow, with constant of proportionality $k$. The acceleration due to gravity is $g$.

  (a) Draw a diagram of this situation, including indications of the applied stresses and body forces, a suitable coordinate system and a representation of the expected velocity profile.

  (b) Write down the equations and boundary conditions governing the flow, with a brief description of each, paying careful attention to signs. Solve these equations to determine the pressure and velocity fields in terms of the parameters given above.

  (c) Show that the surface velocity of the fluid layer is $\frac{\rho g h^{2}}{2 \mu}\left(1+\frac{k h}{\mu}\right)^{-1}$.

  (d) Determine the volume flux per unit width of the plane for general values of $k$ and its limiting values when $k \rightarrow 0$ and $k \rightarrow \infty$.

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2018

  (a) State the Gauss-Bonnet theorem for spherical triangles.

  (b) Prove that any geodesic triangulation of the sphere has Euler number equal to $2 .$

  (c) Prove that there is no geodesic triangulation of the sphere in which every vertex is adjacent to exactly 6 triangles.

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2018

  (a) State Sylow's theorems.

  (b) Prove Sylow's first theorem.

  (c) Let $G$ be a group of order 12. Prove that either $G$ has a unique Sylow 3-subgroup or $G \cong A_{4}$.

  comment

Linear Algebra

• Paper 1, Section I, E

  Linear Algebra | Part IB, 2018

  State the Rank-Nullity Theorem.

  If $\alpha: V \rightarrow W$ and $\beta: W \rightarrow X$ are linear maps and $W$ is finite dimensional, show that

  $$\operatorname{dim} \operatorname{Im}(\alpha)=\operatorname{dim} \operatorname{Im}(\beta \alpha)+\operatorname{dim}(\operatorname{Im}(\alpha) \cap \operatorname{Ker}(\beta))$$

  If $\gamma: U \rightarrow V$ is another linear map, show that

  $$\operatorname{dim} \operatorname{Im}(\beta \alpha)+\operatorname{dim} \operatorname{Im}(\alpha \gamma) \leqslant \operatorname{dim} \operatorname{Im}(\alpha)+\operatorname{dim} \operatorname{Im}(\beta \alpha \gamma)$$

  comment

• Paper 1, Section II, E

  Linear Algebra | Part IB, 2018

  Define a Jordan block $J_{m}(\lambda)$. What does it mean for a complex $n \times n$ matrix to be in Jordan normal form?

  If $A$ is a matrix in Jordan normal form for an endomorphism $\alpha: V \rightarrow V$, prove that

  $$\operatorname{dim} \operatorname{Ker}\left((\alpha-\lambda I)^{r}\right)-\operatorname{dim} \operatorname{Ker}\left((\alpha-\lambda I)^{r-1}\right)$$

  is the number of Jordan blocks $J_{m}(\lambda)$ of $A$ with $m \geqslant r$.

  Find a matrix in Jordan normal form for $J_{m}(\lambda)^{2}$. [Consider all possible values of $\lambda$.]

  Find a matrix in Jordan normal form for the complex matrix

  $$\left[\begin{array}{cccc} 0 & 0 & 0 & a_{1} \\ 0 & 0 & a_{2} & 0 \\ 0 & a_{3} & 0 & 0 \\ a_{4} & 0 & 0 & 0 \end{array}\right]$$

  assuming it is invertible.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2018

  A coin-tossing game is played by two players, $A_{1}$ and $A_{2}$. Each player has a coin and the probability that the coin tossed by player $A_{i}$ comes up heads is $p_{i}$, where $0<p_{i}<1, i=1,2$. The players toss their coins according to the following scheme: $A_{1}$ tosses first and then after each head, $A_{2}$ pays $A_{1}$ one pound and $A_{1}$ has the next toss, while after each tail, $A_{1}$ pays $A_{2}$ one pound and $A_{2}$ has the next toss.

  Define a Markov chain to describe the state of the game. Find the probability that the game ever returns to a state where neither player has lost money.

  comment

Methods

• Paper 1, Section II, 14C

  Methods | Part IB, 2018

  Define the convolution $f * g$ of two functions $f$ and $g$. Defining the Fourier transform $\tilde{f}$ of $f$ by

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} \mathrm{e}^{-\mathrm{i} k x} f(x) \mathrm{d} x$$

  show that

  $$\widehat{f * g}(k)=\tilde{f}(k) \tilde{g}(k) .$$

  Given that the Fourier transform of $f(x)=1 / x$ is

  $$\tilde{f}(k)=-\mathrm{i} \pi \operatorname{sgn}(k),$$

  find the Fourier transform of $\sin (x) / x^{2}$.

  comment

Metric and Topological Spaces

• Paper 1, Section II, E

  Metric and Topological Spaces | Part IB, 2018

  What does it mean to say that a topological space is compact? Prove directly from the definition that $[0,1]$ is compact. Hence show that the unit circle $S^{1} \subset \mathbb{R}^{2}$ is compact, proving any results that you use. [You may use without proof the continuity of standard functions.]

  The set $\mathbb{R}^{2}$ has a topology $\mathcal{T}$ for which the closed sets are the empty set and the finite unions of vector subspaces. Let $X$ denote the set $\mathbb{R}^{2} \backslash\{0\}$ with the subspace topology induced by $\mathcal{T}$. By considering the subspace topology on $S^{1} \subset \mathbb{R}^{2}$, or otherwise, show that $X$ is compact.

  comment

Numerical Analysis

• Paper 1, Section I, D

  Numerical Analysis | Part IB, 2018

  The Trapezoidal Rule for solving the differential equation

  $$y^{\prime}(t)=f(t, y), \quad t \in[0, T], \quad y(0)=y_{0}$$

  is defined by

  $$y_{n+1}=y_{n}+\frac{1}{2} h\left[f\left(t_{n}, y_{n}\right)+f\left(t_{n+1}, y_{n+1}\right)\right]$$

  where $h=t_{n+1}-t_{n}$.

  Determine the minimum order of convergence $k$ of this rule for general functions $f$ that are sufficiently differentiable. Show with an explicit example that there is a function $f$ for which the local truncation error is $A h^{k+1}$ for some constant $A$.

  comment

• Paper 1, Section II, D

  Numerical Analysis | Part IB, 2018

  Show that if $\mathbf{u} \in \mathbb{R}^{m} \backslash\{\mathbf{0}\}$ then the $m \times m$ matrix transformation

  $$H_{\mathbf{u}}=I-2 \frac{\mathbf{u} \mathbf{u}^{\top}}{\|\mathbf{u}\|^{2}}$$

  is orthogonal. Show further that, for any two vectors $\mathbf{a}, \mathbf{b} \in \mathbb{R}^{m}$ of equal length,

  $$H_{\mathbf{a}-\mathbf{b}} \mathbf{a}=\mathbf{b} .$$

  Explain how to use such transformations to convert an $m \times n$ matrix $A$ with $m \geqslant n$ into the form $A=Q R$, where $Q$ is an orthogonal matrix and $R$ is an upper-triangular matrix, and illustrate the method using the matrix

  $$A=\left[\begin{array}{rrr} 1 & -1 & 4 \\ 1 & 4 & -2 \\ 1 & 4 & 2 \\ 1 & -1 & 0 \end{array}\right]$$

  comment

Optimization

• Paper 1, Section I, 8H

  Optimization | Part IB, 2018

  What is meant by a transportation problem? Illustrate the transportation algorithm by solving the problem with three sources and three destinations described by the table

  

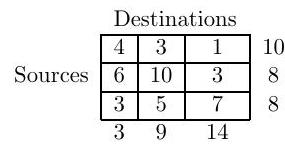
  where the figures in the boxes denote transportation costs, the right-hand column denotes supplies, and the bottom row denotes requirements.

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2018

  The relative motion of a neutron and proton is described by the Schrödinger equation for a single particle of mass $m$ under the influence of the central potential

  $$V(r)=\left\{\begin{array}{rr} -U & r<a \\ 0 & r>a \end{array}\right.$$

  where $U$ and $a$ are positive constants. Solve this equation for a spherically symmetric state of the deuteron, which is a bound state of a proton and a neutron, giving the condition on $U$ for this state to exist.

  [If $\psi$ is spherically symmetric then $\nabla^{2} \psi=\frac{1}{r} \frac{d^{2}}{d r^{2}}(r \psi)$.]

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2018

  $X_{1}, X_{2}, \ldots, X_{n}$ form a random sample from a distribution whose probability density function is

  $$f(x ; \theta)=\left\{\begin{array}{cc} \frac{2 x}{\theta^{2}} & 0 \leqslant x \leqslant \theta \\ 0 & \text { otherwise } \end{array}\right.$$

  where the value of the positive parameter $\theta$ is unknown. Determine the maximum likelihood estimator of the median of this distribution.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2018

  (a) Consider the general linear model $Y=X \theta+\varepsilon$ where $X$ is a known $n \times p$ matrix, $\theta$ is an unknown $p \times 1$ vector of parameters, and $\varepsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with unknown variances $\sigma^{2}$. Show that, provided the matrix $X$ is of rank $p$, the least squares estimate of $\theta$ is

  $$\hat{\theta}=\left(X^{\mathrm{T}} X\right)^{-1} X^{\mathrm{T}} Y$$

  Let

  $$\hat{\varepsilon}=Y-X \hat{\theta}$$

  What is the distribution of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$ ? Write down, in terms of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$, an unbiased estimator of $\sigma^{2}$.

  (b) Four points on the ground form the vertices of a plane quadrilateral with interior angles $\theta_{1}, \theta_{2}, \theta_{3}, \theta_{4}$, so that $\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}=2 \pi$. Aerial observations $Z_{1}, Z_{2}, Z_{3}, Z_{4}$ are made of these angles, where the observations are subject to independent errors distributed as $N\left(0, \sigma^{2}\right)$ random variables.

  (i) Represent the preceding model as a general linear model with observations $\left(Z_{1}, Z_{2}, Z_{3}, Z_{4}-2 \pi\right)$ and unknown parameters $\left(\theta_{1}, \theta_{2}, \theta_{3}\right)$.

  (ii) Find the least squares estimates $\hat{\theta}_{1}, \hat{\theta}_{2}, \hat{\theta}_{3}$.

  (iii) Determine an unbiased estimator of $\sigma^{2}$. What is its distribution?

  comment

Variational Principles

• Paper 1, Section I, B

  Variational Principles | Part IB, 2018

  Find, using a Lagrange multiplier, the four stationary points in $\mathbb{R}^{3}$ of the function $x^{2}+y^{2}+z^{2}$ subject to the constraint $x^{2}+2 y^{2}-z^{2}=1$. By sketching sections of the constraint surface in each of the coordinate planes, or otherwise, identify the nature of the constrained stationary points.

  How would the location of the stationary points differ if, instead, the function $x^{2}+2 y^{2}-z^{2}$ were subject to the constraint $x^{2}+y^{2}+z^{2}=1 ?$

  comment