Part IB, 2017, Paper 4

Analysis II

• Paper 4, Section I, G

  Analysis II | Part IB, 2017

  State the chain rule for the composition of two differentiable functions $f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ and $g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{p}$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be differentiable. For $c \in \mathbb{R}$, let $g(x)=f(x, c-x)$. Compute the derivative of $g$. Show that if $\partial f / \partial x=\partial f / \partial y$ throughout $\mathbb{R}^{2}$, then $f(x, y)=h(x+y)$ for some function $h: \mathbb{R} \rightarrow \mathbb{R}$.

  comment

• Paper 4, Section II, G

  Analysis II | Part IB, 2017

  Let $U \subset \mathbb{R}^{m}$ be a nonempty open set. What does it mean to say that a function $f: U \rightarrow \mathbb{R}^{n}$ is differentiable?

  Let $f: U \rightarrow \mathbb{R}$ be a function, where $U \subset \mathbb{R}^{2}$ is open. Show that if the first partial derivatives of $f$ exist and are continuous on $U$, then $f$ is differentiable on $U$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the function

  $$f(x, y)= \begin{cases}0 & (x, y)=(0,0) \\ \frac{x^{3}+2 y^{4}}{x^{2}+y^{2}} & (x, y) \neq(0,0)\end{cases}$$

  Determine, with proof, where $f$ is differentiable.

  comment

Complex Analysis

• Paper 4, Section I, 4F

  Complex Analysis | Part IB, 2017

  Let $D$ be a star-domain, and let $f$ be a continuous complex-valued function on $D$. Suppose that for every triangle $T$ contained in $D$ we have

  $$\int_{\partial T} f(z) d z=0$$

  Show that $f$ has an antiderivative on $D$.

  If we assume instead that $D$ is a domain (not necessarily a star-domain), does this conclusion still hold? Briefly justify your answer.

  comment

Complex Methods

• Paper 4, Section II, A

  Complex Methods | Part IB, 2017

  By using Fourier transforms and a conformal mapping

  $$w=\sin \left(\frac{\pi z}{a}\right)$$

  with $z=x+i y$ and $w=\xi+i \eta$, and a suitable real constant $a$, show that the solution to

  $$\begin{array}{rlrl} \nabla^{2} \phi & =0 & -2 \pi \leqslant x \leqslant 2 \pi, y \geqslant 0 \\ \phi(x, 0) & =f(x) & -2 \pi \leqslant x \leqslant 2 \pi \\ \phi(\pm 2 \pi, y) & =0 & y>0, \\ \phi(x, y) & \rightarrow 0 & y \rightarrow \infty,-2 \pi \leqslant x \leqslant 2 \pi \end{array}$$

  is given by

  $$\phi(\xi, \eta)=\frac{\eta}{\pi} \int_{-1}^{1} \frac{F\left(\xi^{\prime}\right)}{\eta^{2}+\left(\xi-\xi^{\prime}\right)^{2}} d \xi^{\prime}$$

  where $F\left(\xi^{\prime}\right)$ is to be determined.

  In the case of $f(x)=\sin \left(\frac{x}{4}\right)$, give $F\left(\xi^{\prime}\right)$ explicitly as a function of $\xi^{\prime}$. [You need not evaluate the integral.]

  comment

Electromagnetism

• Paper 4 , Section I, $7 \mathrm{C}$

  Electromagnetism | Part IB, 2017

  A thin wire, in the form of a closed curve $C$, carries a constant current $I$. Using either the Biot-Savart law or the magnetic vector potential, show that the magnetic field far from the loop is of the approximate form

  $$\mathbf{B}(\mathbf{r}) \approx \frac{\mu_{0}}{4 \pi}\left[\frac{3(\mathbf{m} \cdot \mathbf{r}) \mathbf{r}-\mathbf{m}|\mathbf{r}|^{2}}{|\mathbf{r}|^{5}}\right]$$

  where $\mathbf{m}$ is the magnetic dipole moment of the loop. Derive an expression for $\mathbf{m}$ in terms of $I$ and the vector area spanned by the curve $C$.

  comment

Fluid Dynamics

• Paper 4, Section II, D

  Fluid Dynamics | Part IB, 2017

  The linearised equations governing the horizontal components of flow $\mathbf{u}(x, y, t)$ in a rapidly rotating shallow layer of depth $h=h_{0}+\eta(x, y, t)$, where $\eta \ll h_{0}$, are

  $$\begin{gathered} \frac{\partial \mathbf{u}}{\partial t}+\mathbf{f} \times \mathbf{u}=-g \nabla \eta \\ \frac{\partial \eta}{\partial t}+h_{0} \nabla \cdot \mathbf{u}=0 \end{gathered}$$

  where $\mathbf{f}=f \mathbf{e}_{z}$ is the constant Coriolis parameter, and $\mathbf{e}_{z}$ is the unit vector in the vertical direction.

  Use these equations, either in vector form or using Cartesian components, to show that the potential vorticity

  $$\mathbf{Q}=\zeta-\frac{\eta}{h_{0}} \mathbf{f}$$

  is independent of time, where $\zeta=\nabla \times \mathbf{u}$ is the relative vorticity.

  Derive the equation

  $$\frac{\partial^{2} \eta}{\partial t^{2}}-g h_{0} \nabla^{2} \eta+f^{2} \eta=-h_{0} \mathbf{f} \cdot \mathbf{Q}$$

  In the case that $\mathbf{Q} \equiv 0$, determine and sketch the dispersion relation $\omega(k)$ for plane waves with $\eta=A e^{i(k x+\omega t)}$, where $A$ is constant. Discuss the nature of the waves qualitatively: do long waves propagate faster or slower than short waves; how does the phase speed depend on wavelength; does rotation have more effect on long waves or short waves; how dispersive are the waves?

  comment

Geometry

• Paper 4, Section II, G

  Geometry | Part IB, 2017

  What is a hyperbolic line in (a) the disc model (b) the upper half-plane model of the hyperbolic plane? What is the hyperbolic distance $d(P, Q)$ between two points $P, Q$ in the hyperbolic plane? Show that if $\gamma$ is any continuously differentiable curve with endpoints $P$ and $Q$ then its length is at least $d(P, Q)$, with equality if and only if $\gamma$ is a monotonic reparametrisation of the hyperbolic line segment joining $P$ and $Q$.

  What does it mean to say that two hyperbolic lines $L, L^{\prime}$ are (a) parallel (b) ultraparallel? Show that $L$ and $L^{\prime}$ are ultraparallel if and only if they have a common perpendicular, and if so, then it is unique.

  A horocycle is a curve in the hyperbolic plane which in the disc model is a Euclidean circle with exactly one point on the boundary of the disc. Describe the horocycles in the upper half-plane model. Show that for any pair of horocycles there exists a hyperbolic line which meets both orthogonally. For which pairs of horocycles is this line unique?

  comment

Groups, Rings and Modules

• Paper 4, Section I, $2 E$

  Groups, Rings and Modules | Part IB, 2017

  Let $G$ be a non-trivial finite $p$-group and let $Z(G)$ be its centre. Show that $|Z(G)|>1$. Show that if $|G|=p^{3}$ and if $G$ is not abelian, then $|Z(G)|=p$.

  comment

• Paper 4, Section II, E

  Groups, Rings and Modules | Part IB, 2017

  (a) State (without proof) the classification theorem for finitely generated modules over a Euclidean domain. Give the statement and the proof of the rational canonical form theorem.

  (b) Let $R$ be a principal ideal domain and let $M$ be an $R$-submodule of $R^{n}$. Show that $M$ is a free $R$-module.

  comment

Linear Algebra

• Paper 4, Section I, F

  Linear Algebra | Part IB, 2017

  Briefly explain the Gram-Schmidt orthogonalisation process in a real finite-dimensional inner product space $V$.

  For a subspace $U$ of $V$, define $U^{\perp}$, and show that $V=U \oplus U^{\perp}$.

  For which positive integers $n$ does

  $$(f, g)=f(1) g(1)+f(2) g(2)+f(3) g(3)$$

  define an inner product on the space of all real polynomials of degree at most $n$ ?

  comment

• Paper 4, Section II, F

  Linear Algebra | Part IB, 2017

  What is the dual $X^{*}$ of a finite-dimensional real vector space $X$ ? If $X$ has a basis $e_{1}, \ldots, e_{n}$, define the dual basis, and prove that it is indeed a basis of $X^{*}$.

  [No results on the dimension of duals may be assumed without proof.]

  Write down (without making a choice of basis) an isomorphism from $X$ to $X^{* *}$. Prove that your map is indeed an isomorphism.

  Does every basis of $X^{*}$ arise as the dual basis of some basis of $X ?$ Justify your answer.

  A subspace $W$ of $X^{*}$ is called separating if for every non-zero $x \in X$ there is a $T \in W$ with $T(x) \neq 0$. Show that the only separating subspace of $X^{*}$ is $X^{*}$ itself.

  Now let $X$ be the (infinite-dimensional) space of all real polynomials. Explain briefly how we may identify $X^{*}$ with the space of all real sequences. Give an example of a proper subspace of $X^{*}$ that is separating.

  comment

Markov Chains

• Paper 4, Section I, $\mathbf{9 H}$

  Markov Chains | Part IB, 2017

  Prove that the simple symmetric random walk on $\mathbb{Z}^{3}$ is transient.

  [Any combinatorial inequality can be used without proof.]

  comment

Methods

• Paper 4, Section I, A

  Methods | Part IB, 2017

  The Legendre polynomials, $P_{n}(x)$ for integers $n \geqslant 0$, satisfy the Sturm-Liouville equation

  $$\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} P_{n}(x)\right]+n(n+1) P_{n}(x)=0$$

  and the recursion formula

  $$(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1}(x), \quad P_{0}(x)=1, \quad P_{1}(x)=x$$

  (i) For all $n \geqslant 0$, show that $P_{n}(x)$ is a polynomial of degree $n$ with $P_{n}(1)=1$.

  (ii) For all $m, n \geqslant 0$, show that $P_{n}(x)$ and $P_{m}(x)$ are orthogonal over the range $x \in[-1,1]$ when $m \neq n$.

  (iii) For each $n \geqslant 0$ let

  $$R_{n}(x)=\frac{d^{n}}{d x^{n}}\left[\left(x^{2}-1\right)^{n}\right]$$

  Assume that for each $n$ there is a constant $\alpha_{n}$ such that $P_{n}(x)=\alpha_{n} R_{n}(x)$ for all $x$. Determine $\alpha_{n}$ for each $n$.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2017

  (a)

  (i) For the diffusion equation

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  with diffusion constant $K$, state the properties (in terms of the Dirac delta function) that define the fundamental solution $F(x, t)$ and the Green's function $G(x, t ; y, \tau)$.

  You are not required to give expressions for these functions.

  (ii) Consider the initial value problem for the homogeneous equation:

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0, \quad \phi\left(x, t_{0}\right)=\alpha(x) \quad \text { on }-\infty<x<\infty \text { and } t \geqslant t_{0}$$

  and the forced equation with homogeneous initial condition (and given forcing term $h(x, t))$ :

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=h(x, t), \quad \phi(x, 0)=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  Given that $F$ and $G$ in part (i) are related by

  $$G(x, t ; y, \tau)=\Theta(t-\tau) F(x-y, t-\tau)$$

  (where $\Theta(t)$ is the Heaviside step function having value 0 for $t<0$ and 1 for $t>0$, show how the solution of (B) can be expressed in terms of solutions of (A) with suitable initial conditions. Briefly interpret your expression.

  (b) A semi-infinite conducting plate lies in the $\left(x_{1}, x_{2}\right)$ plane in the region $x_{1} \geqslant 0$. The boundary along the $x_{2}$ axis is perfectly insulated. Let $(r, \theta)$ denote standard polar coordinates on the plane. At time $t=0$ the entire plate is at temperature zero except for the region defined by $-\pi / 4<\theta<\pi / 4$ and $1<r<2$ which has constant initial temperature $T_{0}>0$. Subsequently the temperature of the plate obeys the two-dimensional heat equation with diffusion constant $K$. Given that the fundamental solution of the twodimensional heat equation on $\mathbb{R}^{2}$ is

  $$F\left(x_{1}, x_{2}, t\right)=\frac{1}{4 \pi K t} e^{-\left(x_{1}^{2}+x_{2}^{2}\right) /(4 K t)}$$

  show that the origin $(0,0)$ on the plate reaches its maximum temperature at time $t=3 /(8 K \log 2)$.

  comment

Metric and Topological Spaces

• Paper 4, Section II, E

  Metric and Topological Spaces | Part IB, 2017

  Let $f: X \rightarrow Y$ be a continuous map between topological spaces.

  (a) Assume $X$ is compact and that $Z \subseteq X$ is a closed subset. Prove that $Z$ and $f(Z)$ are both compact.

  (b) Suppose that

  (i) $f^{-1}(\{y\})$ is compact for each $y \in Y$, and

  (ii) if $A$ is any closed subset of $X$, then $f(A)$ is a closed subset of $Y$.

  Show that if $K \subseteq Y$ is compact, then $f^{-1}(K)$ is compact.

  $\left[\right.$ Hint: Given an open cover $f^{-1}(K) \subseteq \bigcup_{i \in I} U_{i}$, find a finite subcover, say $f^{-1}(\{y\}) \subseteq$ $\bigcup_{i \in I_{y}} U_{i}$, for each $y \in K$; use closedness of $X \backslash \bigcup_{i \in I_{y}} U_{i}$ and property (ii) to produce an open cover of $K$.]

  comment

Numerical Analysis

• Paper 4, Section I, C

  Numerical Analysis | Part IB, 2017

  For the matrix

  $$A=\left[\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 5 & 5 & 5 \\ 1 & 5 & 14 & 14 \\ 1 & 5 & 14 & \lambda \end{array}\right]$$

  find a factorization of the form

  $$A=L D L^{\top} \text {, }$$

  where $D$ is diagonal and $L$ is lower triangular with ones on its diagonal.

  For what values of $\lambda$ is $A$ positive definite?

  In the case $\lambda=30$ find the Cholesky factorization of $A$.

  comment

Optimization

• Paper 4, Section II, H

  Optimization | Part IB, 2017

  (a) Let $G$ be a flow network with capacities $c_{i j}$ on the edges. Explain the maximum flow problem on this network defining all the notation you need.

  (b) Describe the Ford-Fulkerson algorithm for finding a maximum flow and state the max-flow min-cut theorem.

  (c) Apply the Ford-Fulkerson algorithm to find a maximum flow and a minimum cut of the following network:

  

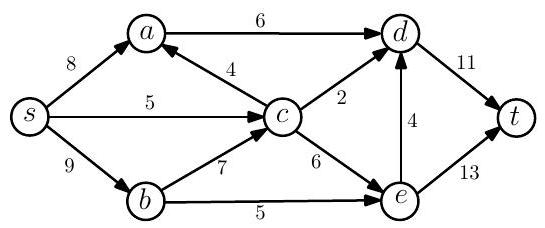
  (d) Suppose that we add $\varepsilon>0$ to each capacity of a flow network. Is it true that the maximum flow will always increase by $\varepsilon$ ? Justify your answer.

  comment

Quantum Mechanics

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2017

  (a) Give a physical interpretation of the wavefunction $\phi(x, t)=A e^{i k x} e^{-i E t / \hbar}$ (where $A, k$ and $E$ are real constants).

  (b) A particle of mass $m$ and energy $E>0$ is incident from the left on the potential step

  $$V(x)=\left\{\begin{array}{cl} 0 & \text { for }-\infty<x<a \\ V_{0} & \text { for } a<x<\infty \end{array}\right.$$

  with $V_{0}>0$.

  State the conditions satisfied by a stationary state at the point $x=a$.

  Compute the probability that the particle is reflected as a function of $E$, and compare your result with the classical case.

  comment

Statistics

• Paper 4, Section II, H

  Statistics | Part IB, 2017

  (a) State and prove the Neyman-Pearson lemma.

  (b) Let $X$ be a real random variable with density $f(x)=(2 \theta x+1-\theta) 1_{[0,1]}(x)$ with $-1 \leqslant \theta \leqslant 1 .$

  Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta=1$.

  Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta>0$.

  comment

Variational Principles

• Paper 4, Section II, $16 \mathrm{D}$

  Variational Principles | Part IB, 2017

  Consider the functional

  $$F[y]=\int_{\alpha}^{\beta} f\left(y, y^{\prime}, x\right) d x$$

  of a function $y(x)$ defined for $x \in[\alpha, \beta]$, with $y$ having fixed values at $x=\alpha$ and $x=\beta$.

  By considering $F[y+\epsilon \xi]$, where $\xi(x)$ is an arbitrary function with $\xi(\alpha)=\xi(\beta)=0$ and $\epsilon \ll 1$, determine that the second variation of $F$ is

  $$\delta^{2} F[y, \xi]=\int_{\alpha}^{\beta}\left\{\xi^{2}\left[\frac{\partial^{2} f}{\partial y^{2}}-\frac{d}{d x}\left(\frac{\partial^{2} f}{\partial y \partial y^{\prime}}\right)\right]+\xi^{\prime 2} \frac{\partial^{2} f}{\partial y^{\prime 2}}\right\} d x$$

  The surface area of an axisymmetric soap film joining two parallel, co-axial, circular rings of radius a distance $2 L$ apart can be expressed by the functional

  $$F[y]=\int_{-L}^{L} 2 \pi y \sqrt{1+y^{\prime 2}} d x$$

  where $x$ is distance in the axial direction and $y$ is radial distance from the axis. Show that the surface area is stationary when

  $$y=E \cosh \frac{x}{E},$$

  where $E$ is a constant that need not be determined, and that the stationary area is a local minimum if

  $$\int_{-L / E}^{L / E}\left(\xi^{\prime 2}-\xi^{2}\right) \operatorname{sech}^{2} z d z>0$$

  for all functions $\xi(z)$ that vanish at $z=\pm L / E$, where $z=x / E$.

  comment