Part IB, 2016, Paper 3

Analysis II

• Paper 3, Section I, G

  Analysis II | Part IB, 2016

  (a) Let $X$ be a subset of $\mathbb{R}$. What does it mean to say that a sequence of functions $f_{n}: X \rightarrow \mathbb{R}(n \in \mathbb{N})$ is uniformly convergent?

  (b) Which of the following sequences of functions are uniformly convergent? Justify your answers.

  (i) $f_{n}:(0,1) \rightarrow \mathbb{R}, \quad f_{n}(x)=\frac{1-x^{n}}{1-x}$

  (ii) $f_{n}:(0,1) \rightarrow \mathbb{R}, \quad f_{n}(x)=\sum_{k=1}^{n} \frac{1}{k^{2}} x^{k}$.

  (iii) $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$, $\quad f_{n}(x)=x / n$.

  (iv) $f_{n}:[0, \infty) \rightarrow \mathbb{R}, \quad f_{n}(x)=x e^{-n x}$.

  comment

• Paper 3, Section II, G

  Analysis II | Part IB, 2016

  Let $X$ be a metric space.

  (a) What does it mean to say that a function $f: X \rightarrow \mathbb{R}$ is uniformly continuous? What does it mean to say that $f$ is Lipschitz? Show that if $f$ is Lipschitz then it is uniformly continuous. Show also that if $\left(x_{n}\right)_{n}$ is a Cauchy sequence in $X$, and $f$ is uniformly continuous, then the sequence $\left(f\left(x_{n}\right)\right)_{n}$ is convergent.

  (b) Let $f: X \rightarrow \mathbb{R}$ be continuous, and $X$ be sequentially compact. Show that $f$ is uniformly continuous. Is $f$ necessarily Lipschitz? Justify your answer.

  (c) Let $Y$ be a dense subset of $X$, and let $g: Y \rightarrow \mathbb{R}$ be a continuous function. Show that there exists at most one continuous function $f: X \rightarrow \mathbb{R}$ such that for all $y \in Y$, $f(y)=g(y)$. Prove that if $g$ is uniformly continuous, then such a function $f$ exists, and is uniformly continuous.

  [A subset $Y \subset X$ is dense if for any nonempty open subset $U \subset X$, the intersection $U \cap Y$ is nonempty.]

  comment

Complex Analysis

• Paper 3, Section II, G

  Complex Analysis | Part IB, 2016

  (a) Prove Cauchy's theorem for a triangle.

  (b) Write down an expression for the winding number $I(\gamma, a)$ of a closed, piecewise continuously differentiable curve $\gamma$ about a point $a \in \mathbb{C}$ which does not lie on $\gamma$.

  (c) Let $U \subset \mathbb{C}$ be a domain, and $f: U \rightarrow \mathbb{C}$ a holomorphic function with no zeroes in $U$. Suppose that for infinitely many positive integers $k$ the function $f$ has a holomorphic $k$-th root. Show that there exists a holomorphic function $F: U \rightarrow \mathbb{C}$ such that $f=\exp F$.

  comment

Complex Methods

• Paper 3, Section I, A

  Complex Methods | Part IB, 2016

  The function $f(x)$ has Fourier transform

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} f(x) e^{-i k x} d x=\frac{-2 k i}{p^{2}+k^{2}},$$

  where $p>0$ is a real constant. Using contour integration, calculate $f(x)$ for $x<0$. [Jordan's lemma and the residue theorem may be used without proof.]

  comment

Electromagnetism

• Paper 3, Section II, D

  Electromagnetism | Part IB, 2016

  (a) State Faraday's law of induction for a moving circuit in a time-dependent magnetic field and define all the terms that appear.

  (b) Consider a rectangular circuit DEFG in the $z=0$ plane as shown in the diagram below. There are two rails parallel to the $x$-axis for $x>0$ starting at $\mathrm{D}$ at $(x, y)=(0,0)$ and $G$ at $(0, L)$. A battery provides an electromotive force $\mathcal{E}_{0}$ between $D$ and $G$ driving current in a positive sense around DEFG. The circuit is completed with a bar resistor of resistance $R$, length $L$ and mass $m$ that slides without friction on the rails; it connects $E$ at $(s(t), 0)$ and $F$ at $(s(t), L)$. The rest of the circuit has no resistance. The circuit is in a constant uniform magnetic field $B_{0}$ parallel to the $z$-axis.

  [In parts (i)-(iv) you can neglect any magnetic field due to current flow.]

  

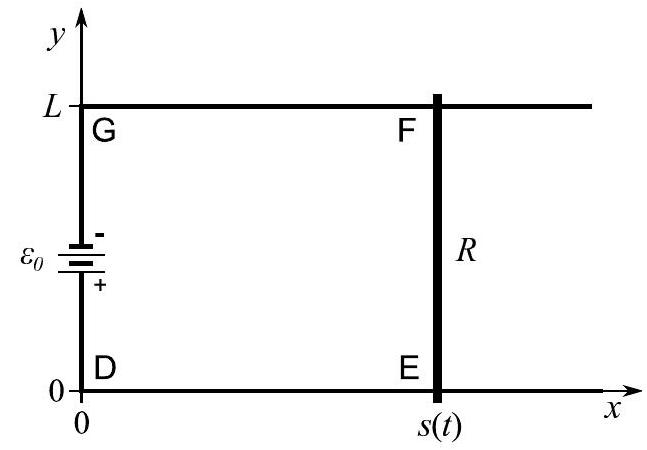
  (i) Calculate the current in the bar and indicate its direction on a diagram of the circuit.

  (ii) Find the force acting on the bar.

  (iii) If the initial velocity and position of the bar are respectively $\dot{s}(0)=v_{0}>0$ and $s(0)=s_{0}>0$, calculate $\dot{s}(t)$ and $s(t)$ for $t>0$.

  (iv) If $\mathcal{E}_{0}=0$, find the total energy dissipated in the circuit after $t=0$ and verify that total energy is conserved.

  (v) Describe qualitatively the effect of the magnetic field caused by the induced current flowing in the circuit when $\mathcal{E}_{0}=0$.

  comment

Fluid Dynamics

• Paper 3, Section II, C

  Fluid Dynamics | Part IB, 2016

  A layer of thickness $h_{1}$ of a fluid of density $\rho_{1}$ is located above a layer of thickness $h_{2}$ of a fluid of density $\rho_{2}>\rho_{1}$. The two-fluid system is bounded by two impenetrable surfaces at $y=h_{1}$ and $y=-h_{2}$ and is assumed to be two-dimensional (i.e. independent of $z$ ). The fluid is subsequently perturbed, and the interface between the two fluids is denoted $y=\eta(x, t)$.

  (a) Assuming irrotational motion in each fluid, state the equations and boundary conditions satisfied by the flow potentials, $\varphi_{1}$ and $\varphi_{2}$.

  (b) The interface is perturbed by small-amplitude waves of the form $\eta=\eta_{0} e^{i(k x-\omega t)}$, with $\eta_{0} k \ll 1$. State the equations and boundary conditions satisfied by the linearised system.

  (c) Calculate the dispersion relation of the waves relating the frequency $\omega$ to the wavenumber $k$.

  comment

Geometry

• Paper 3, Section I, $5 F$

  Geometry | Part IB, 2016

  (a) State Euler's formula for a triangulation of a sphere.

  (b) A sphere is decomposed into hexagons and pentagons with precisely three edges at each vertex. Determine the number of pentagons.

  comment

• Paper 3, Section II, F

  Geometry | Part IB, 2016

  (a) Define the cross-ratio $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ of four distinct points $z_{1}, z_{2}, z_{3}, z_{4} \in \mathbb{C} \cup\{\infty\}$. Show that the cross-ratio is invariant under Möbius transformations. Express $\left[z_{2}, z_{1}, z_{3}, z_{4}\right]$ in terms of $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$.

  (b) Show that $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ is real if and only if $z_{1}, z_{2}, z_{3}, z_{4}$ lie on a line or circle in $\mathbb{C} \cup\{\infty\}$.

  (c) Let $z_{1}, z_{2}, z_{3}, z_{4}$ lie on a circle in $\mathbb{C}$, given in anti-clockwise order as depicted.

  

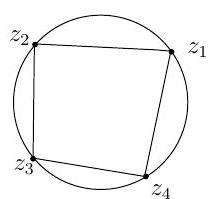
  Show that $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ is a negative real number, and that $\left[z_{2}, z_{1}, z_{3}, z_{4}\right]$ is a positive real number greater than 1 . Show that $\left|\left[z_{1}, z_{2}, z_{3}, z_{4}\right]\right|+1=\left|\left[z_{2}, z_{1}, z_{3}, z_{4}\right]\right|$. Use this to deduce Ptolemy's relation on lengths of edges and diagonals of the inscribed 4-gon:

  $$\left|z_{1}-z_{3}\right|\left|z_{2}-z_{4}\right|=\left|z_{1}-z_{2}\right|\left|z_{3}-z_{4}\right|+\left|z_{2}-z_{3}\right|\left|z_{4}-z_{1}\right|$$

  comment

Groups, Rings and Modules

• Paper 3, Section I, E

  Groups, Rings and Modules | Part IB, 2016

  Let $G$ be a group of order $n$. Define what is meant by a permutation representation of $G$. Using such representations, show $G$ is isomorphic to a subgroup of the symmetric group $S_{n}$. Assuming $G$ is non-abelian simple, show $G$ is isomorphic to a subgroup of $A_{n}$. Give an example of a permutation representation of $S_{3}$ whose kernel is $A_{3}$.

  comment

• Paper 3, Section II, E

  Groups, Rings and Modules | Part IB, 2016

  (a) Define what is meant by an algebraic integer $\alpha$. Show that the ideal

  $$I=\{h \in \mathbb{Z}[x] \mid h(\alpha)=0\}$$

  in $\mathbb{Z}[x]$ is generated by a monic irreducible polynomial $f$. Show that $\mathbb{Z}[\alpha]$, considered as a $\mathbb{Z}$-module, is freely generated by $n$ elements where $n=\operatorname{deg} f$.

  (b) Assume $\alpha \in \mathbb{C}$ satisfies $\alpha^{5}+2 \alpha+2=0$. Is it true that the ideal (5) in $\mathbb{Z}[\alpha]$ is a prime ideal? Is there a ring homomorphism $\mathbb{Z}[\alpha] \rightarrow \mathbb{Z}[\sqrt{-1}]$ ? Justify your answers.

  (c) Show that the only unit elements of $\mathbb{Z}[\sqrt{-5}]$ are 1 and $-1$. Show that $\mathbb{Z}[\sqrt{-5}]$ is not a UFD.

  comment

Linear Algebra

• Paper 3, Section II, F

  Linear Algebra | Part IB, 2016

  Let $\alpha: V \rightarrow V$ be a linear transformation defined on a finite dimensional inner product space $V$ over $\mathbb{C}$. Recall that $\alpha$ is normal if $\alpha$ and its adjoint $\alpha^{*}$ commute. Show that $\alpha$ being normal is equivalent to each of the following statements:

  (i) $\alpha=\alpha_{1}+i \alpha_{2}$ where $\alpha_{1}, \alpha_{2}$ are self-adjoint operators and $\alpha_{1} \alpha_{2}=\alpha_{2} \alpha_{1}$;

  (ii) there is an orthonormal basis for $V$ consisting of eigenvectors of $\alpha$;

  (iii) there is a polynomial $g$ with complex coefficients such that $\alpha^{*}=g(\alpha)$.

  comment

Markov Chains

• Paper 3, Section I, H

  Markov Chains | Part IB, 2016

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain such that $X_{0}=i$. Prove that

  $$\sum_{n=0}^{\infty} \mathbb{P}_{i}\left(X_{n}=i\right)=\frac{1}{\mathbb{P}_{i}\left(X_{n} \neq i \text { for all } n \geqslant 1\right)}$$

  where $1 / 0=+\infty$. [You may use the strong Markov property without proof.]

  comment

Methods

• Paper 3, Section $\mathbf{I}$, A

  Methods | Part IB, 2016

  Calculate the Green's function $G(x ; \xi)$ given by the solution to

  $$\frac{d^{2} G}{d x^{2}}=\delta(x-\xi) ; \quad G(0 ; \xi)=\frac{d G}{d x}(1 ; \xi)=0$$

  where $\xi \in(0,1), x \in(0,1)$ and $\delta(x)$ is the Dirac $\delta$-function. Use this Green's function to calculate an explicit solution $y(x)$ to the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}=x e^{-x}$$

  where $x \in(0,1)$, and $y(0)=y^{\prime}(1)=0$.

  comment

• Paper 3, Section II, B

  Methods | Part IB, 2016

  (a) Show that the Fourier transform of $f(x)=e^{-a^{2} x^{2}}$, for $a>0$, is

  $$\tilde{f}(k)=\frac{\sqrt{\pi}}{a} e^{-\frac{k^{2}}{4 a^{2}}},$$

  stating clearly any properties of the Fourier transform that you use.

  [Hint: You may assume that $\int_{0}^{\infty} e^{-t^{2}} d t=\sqrt{\pi} / 2$.]

  (b) Consider now the Cauchy problem for the diffusion equation in one space dimension, i.e. solving for $\theta(x, t)$ satisfying:

  $$\frac{\partial \theta}{\partial t}=D \frac{\partial^{2} \theta}{\partial x^{2}} \quad \text { with } \theta(x, 0)=g(x)$$

  where $D$ is a positive constant and $g(x)$ is specified. Consider the following property of a solution:

  Property P: If the initial data $g(x)$ is positive and it is non-zero only within a bounded region (i.e. there is a constant $\alpha$ such that $\theta(x, 0)=0$ for all $|x|>\alpha)$, then for any $\epsilon>0$ (however small) and $\beta$ (however large) the solution $\theta(\beta, \epsilon)$ can be non-zero, i.e. the solution can become non-zero arbitrarily far away after an arbitrarily short time.

  Does Property P hold for solutions of the diffusion equation? Justify your answer (deriving any expression for the solution $\theta(x, t)$ that you use).

  (c) Consider now the wave equation in one space dimension:

  $$\frac{\partial^{2} u}{\partial t^{2}}=c^{2} \frac{\partial^{2} u}{\partial x^{2}}$$

  with given initial data $u(x, 0)=\phi(x)$ and $\frac{\partial u}{\partial t}(x, 0)=0$ (and $c$ is a constant).

  Does Property $\mathrm{P}$ (with $g(x)$ and $\theta(\beta, \epsilon)$ now replaced by $\phi(x)$ and $u(\beta, \epsilon)$ respectively) hold for solutions of the wave equation? Justify your answer again as above.

  comment

Metric and Topological Spaces

• Paper 3, Section I, $3 E$

  Metric and Topological Spaces | Part IB, 2016

  Let $X$ be a topological space and $A \subseteq X$ be a subset. A limit point of $A$ is a point $x \in X$ such that any open neighbourhood $U$ of $x$ intersects $A$. Show that $A$ is closed if and only if it contains all its limit points. Explain what is meant by the interior Int $(A)$ and the closure $\bar{A}$ of $A$. Show that if $A$ is connected, then $\bar{A}$ is connected.

  comment

Numerical Analysis

• Paper 3, Section II, D

  Numerical Analysis | Part IB, 2016

  (a) Determine real quadratic functions $a(x), b(x), c(x)$ such that the interpolation formula,

  $$f(x) \approx a(x) f(0)+b(x) f(2)+c(x) f(3),$$

  is exact when $f(x)$ is any real polynomial of degree 2 .

  (b) Use this formula to construct approximations for $f(5)$ and $f^{\prime}(1)$ which are exact when $f(x)$ is any real polynomial of degree 2 . Calculate these approximations for $f(x)=x^{3}$ and comment on your answers.

  (c) State the Peano kernel theorem and define the Peano kernel $K(\theta)$. Use this theorem to find the minimum values of the constants $\alpha$ and $\beta$ such that

  $$\left|f(1)-\frac{1}{3}[f(0)+3 f(2)-f(3)]\right| \leqslant \alpha \max _{\xi \in[0,3]}\left|f^{(2)}(\xi)\right|$$

  and

  $$\left|f(1)-\frac{1}{3}[f(0)+3 f(2)-f(3)]\right| \leqslant \beta\left\|f^{(2)}\right\|_{1}$$

  where $f \in C^{2}[0,3]$. Check that these inequalities hold for $f(x)=x^{3}$.

  comment

Optimization

• Paper 3, Section II, H

  Optimization | Part IB, 2016

  (a) State and prove the Lagrangian sufficiency theorem.

  (b) Let $n \geqslant 1$ be a given constant, and consider the problem:

  $$\operatorname{minimise} \sum_{i=1}^{n}\left(2 y_{i}^{2}+x_{i}^{2}\right) \text { subject to } x_{i}=1+\sum_{k=1}^{i} y_{k} \text { for all } i=1, \ldots, n$$

  Find, with proof, constants $a, b, A, B$ such that the optimal solution is given by

  $$x_{i}=a 2^{i}+b 2^{-i} \text { and } y_{i}=A 2^{i}+B 2^{-i} \text {, for all } i=1, \ldots, n .$$

  comment

Quantum Mechanics

• Paper 3, Section I, B

  Quantum Mechanics | Part IB, 2016

  (a) Consider a quantum particle moving in one space dimension, in a timeindependent real potential $V(x)$. For a wavefunction $\psi(x, t)$, define the probability density $\rho(x, t)$ and probability current $j(x, t)$ and show that

  $$\frac{\partial \rho}{\partial t}+\frac{\partial j}{\partial x}=0$$

  (b) Suppose now that $V(x)=0$ and $\psi(x, t)=\left(e^{i k x}+R e^{-i k x}\right) e^{-i E t / \hbar}$, where $E=\hbar^{2} k^{2} /(2 m), k$ and $m$ are real positive constants, and $R$ is a complex constant. Compute the probability current for this wavefunction. Interpret the terms in $\psi$ and comment on how this relates to the computed expression for the probability current.

  comment

• Paper 3, Section II, B

  Quantum Mechanics | Part IB, 2016

  The spherically symmetric bound state wavefunctions $\psi(r)$ for the Coulomb potential $V=-e^{2} /\left(4 \pi \epsilon_{0} r\right)$ are normalisable solutions of the equation

  $$\frac{d^{2} \psi}{d r^{2}}+\frac{2}{r} \frac{d \psi}{d r}+\frac{2 \lambda}{r} \psi=-\frac{2 m E}{\hbar^{2}} \psi$$

  Here $\lambda=\left(m e^{2}\right) /\left(4 \pi \epsilon_{0} \hbar^{2}\right)$ and $E<0$ is the energy of the state.

  (a) By writing the wavefunction as $\psi(r)=f(r) \exp (-K r)$, for a suitable constant $K$ that you should determine, show that there are normalisable wavefunctions $\psi(r)$ only for energies of the form

  $$E=\frac{-m e^{4}}{32 \pi^{2} \epsilon_{0}^{2} \hbar^{2} N^{2}}$$

  with $N$ being a positive integer.

  (b) The energies in (a) reproduce the predictions of the Bohr model of the hydrogen atom. How do the wavefunctions above compare to the assumptions in the Bohr model?

  comment

Statistics

• Paper 3, Section II, H

  Statistics | Part IB, 2016

  Let $X_{1}, \ldots, X_{n}$ be independent samples from the Poisson distribution with mean $\theta$.

  (a) Compute the maximum likelihood estimator of $\theta$. Is this estimator biased?

  (b) Under the assumption that $n$ is very large, use the central limit theorem to find an approximate $95 \%$ confidence interval for $\theta$. [You may use the notation $z_{\alpha}$ for the number such that $\mathbb{P}\left(Z \geqslant z_{\alpha}\right)=\alpha$ for a standard normal $\left.Z \sim N(0,1) .\right]$

  (c) Now suppose the parameter $\theta$ has the $\Gamma(k, \lambda)$ prior distribution. What is the posterior distribution? What is the Bayes point estimator for $\theta$ for the quadratic loss function $L(\theta, a)=(\theta-a)^{2} ?$ Let $X_{n+1}$ be another independent sample from the same distribution. Given $X_{1}, \ldots, X_{n}$, what is the posterior probability that $X_{n+1}=0$ ?

  [Hint: The density of the $\Gamma(k, \lambda)$ distribution is $f(x ; k, \lambda)=\lambda^{k} x^{k-1} e^{-\lambda x} / \Gamma(k)$, for $x>0$.]

  comment

Variational Principles

• Paper 3, Section I, C

  Variational Principles | Part IB, 2016

  Two points $A$ and $B$ are located on the curved surface of the circular cylinder of radius $R$ with axis along the $z$-axis. We denote their locations by $\left(R, \phi_{A}, z_{A}\right)$ and $\left(R, \phi_{B}, z_{B}\right)$ using cylindrical polar coordinates and assume $\phi_{A} \neq \phi_{B}, z_{A} \neq z_{B}$. A path $\phi(z)$ is drawn on the cylinder to join $A$ and $B$. Show that the path of minimum distance between the points $A$ and $B$ is a helix, and determine its pitch. [For a helix with axis parallel to the $z$ axis, the pitch is the change in $z$ after one complete helical turn.]

  comment