Part IB, 2015, Paper 2

Analysis II

• Paper 2, Section I, G

  Analysis II | Part IB, 2015

  Show that the map $f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ given by

  $$f(x, y, z)=\left(x-y-z, x^{2}+y^{2}+z^{2}, x y z\right)$$

  is differentiable everywhere and find its derivative.

  Stating accurately any theorem that you require, show that $f$ has a differentiable local inverse at a point $(x, y, z)$ if and only if

  $$(x+y)(x+z)(y-z) \neq 0 .$$

  $$\begin{aligned} & p(f)=\sup |f|, \quad q(f)=\sup \left(|f|+\left|f^{\prime}\right|\right), \\ & r(f)=\sup \left|f^{\prime}\right|, \quad s(f)=\left|\int_{-1}^{1} f(x) d x\right| \end{aligned}$$

  comment

• Paper 2, Section II, G

  Analysis II | Part IB, 2015

  Let $E, F$ be normed spaces with norms $\|\cdot\|_{E},\|\cdot\|_{F}$. Show that for a map $f: E \rightarrow F$ and $a \in E$, the following two statements are equivalent:

  (i) For every given $\varepsilon>0$ there exists $\delta>0$ such that $\|f(x)-f(a)\|_{F}<\varepsilon$ whenever $\|x-a\|_{E}<\delta$

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for each sequence $x_{n} \rightarrow a$.

  We say that $f$ is continuous at $a$ if (i), or equivalently (ii), holds.

  Let now $\left(E,\|\cdot\|_{E}\right)$ be a normed space. Let $A \subset E$ be a non-empty closed subset and define $d(x, A)=\inf \left\{\|x-a\|_{E}: a \in A\right\}$. Show that

  $$|d(x, A)-d(y, A)| \leqslant\|x-y\|_{E} \text { for all } x, y \in E .$$

  In the case when $E=\mathbb{R}^{n}$ with the standard Euclidean norm, show that there exists $a \in A$ such that $d(x, A)=\|x-a\|$.

  Let $A, B$ be two disjoint closed sets in $\mathbb{R}^{n}$. Must there exist disjoint open sets $U, V$ such that $A \subset U$ and $B \subset V$ ? Must there exist $a \in A$ and $b \in B$ such that $d(a, b) \leqslant d(x, y)$ for all $x \in A$ and $y \in B$ ? For each answer, give a proof or counterexample as appropriate.

  comment

Complex Analysis or Complex Methods

• Paper 2, Section II, B

  Complex Analysis or Complex Methods | Part IB, 2015

  (i) A function $f(z)$ has a pole of order $m$ at $z=z_{0}$. Derive a general expression for the residue of $f(z)$ at $z=z_{0}$ involving $f$ and its derivatives.

  (ii) Using contour integration along a contour in the upper half-plane, determine the value of the integral

  $$I=\int_{0}^{\infty} \frac{(\ln x)^{2}}{\left(1+x^{2}\right)^{2}} \mathrm{~d} x$$

  comment

Electromagnetism

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2015

  In a constant electric field $\mathbf{E}=(E, 0,0)$ a particle of rest mass $m$ and charge $q>0$ has position $\mathbf{x}$ and velocity $\dot{\mathbf{x}}$. At time $t=0$, the particle is at rest at the origin. Including relativistic effects, calculate $\dot{\mathbf{x}}(t)$.

  Sketch a graph of $|\dot{\mathbf{x}}(t)|$ versus $t$, commenting on the $t \rightarrow \infty$ limit.

  Calculate $|\mathbf{x}(t)|$ as an explicit function of $t$ and find the non-relativistic limit at small times $t$.

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2015

  Consider the magnetic field

  $$\mathbf{B}=b[\mathbf{r}+(k \hat{\mathbf{z}}+l \hat{\mathbf{y}}) \hat{\mathbf{z}} \cdot \mathbf{r}+p \hat{\mathbf{x}}(\hat{\mathbf{y}} \cdot \mathbf{r})+n \hat{\mathbf{z}}(\hat{\mathbf{x}} \cdot \mathbf{r})],$$

  where $b \neq 0, \mathbf{r}=(x, y, z)$ and $\hat{\mathbf{x}}, \hat{\mathbf{y}}, \hat{\mathbf{z}}$ are unit vectors in the $x, y$ and $z$ directions, respectively. Imposing that this satisfies the expected equations for a static magnetic field in a vacuum, find $k, l, n$ and $p$.

  A circular wire loop of radius $a$, mass $m$ and resistance $R$ lies in the $(x, y)$ plane with its centre on the $z$-axis at $z$ and a magnetic field as given above. Calculate the magnetic flux through the loop arising from this magnetic field and also the force acting on the loop when a current $I$ is flowing around the loop in a clockwise direction about the $z$-axis.

  At $t=0$, the centre of the loop is at the origin, travelling with velocity $(0,0, v(t=0))$, where $v(0)>0$. Ignoring gravity and relativistic effects, and assuming that $I$ is only the induced current, find the time taken for the speed to halve in terms of $a, b, R$ and $m$. By what factor does the rate of heat generation change in this time?

  Where is the loop as $t \rightarrow \infty$ as a function of $a, b, R, v(0) ?$

  comment

Fluid Dynamics

• Paper 2, Section I, B

  Fluid Dynamics | Part IB, 2015

  Consider the two-dimensional velocity field $\mathbf{u}=(u, v)$ with

  $$u(x, y)=x^{2}-y^{2}, \quad v(x, y)=-2 x y$$

  (i) Show that the flow is incompressible and irrotational.

  (ii) Derive the velocity potential, $\phi$, and the streamfunction, $\psi$.

  (iii) Plot all streamlines passing through the origin.

  (iv) Show that the complex function $w=\phi+i \psi$ (where $i^{2}=-1$ ) can be written solely as a function of the complex coordinate $z=x+i y$ and determine that function.

  comment

Geometry

• Paper 2, Section II, F

  Geometry | Part IB, 2015

  (a) For each of the following subsets of $\mathbb{R}^{3}$, explain briefly why it is a smooth embedded surface or why it is not.

  $$\begin{aligned} S_{1} &=\{(x, y, z) \mid x=y, z=3\} \cup\{(2,3,0)\} \\ S_{2} &=\left\{(x, y, z) \mid x^{2}+y^{2}-z^{2}=1\right\} \\ S_{3} &=\left\{(x, y, z) \mid x^{2}+y^{2}-z^{2}=0\right\} \end{aligned}$$

  (b) Let $f: U=\{(u, v) \mid v>0\} \rightarrow \mathbb{R}^{3}$ be given by

  $$f(u, v)=\left(u^{2}, u v, v\right),$$

  and let $S=f(U) \subseteq \mathbb{R}^{3}$. You may assume that $S$ is a smooth embedded surface.

  Find the first fundamental form of this surface.

  Find the second fundamental form of this surface.

  Compute the Gaussian curvature of this surface.

  comment

Groups, Rings and Modules

• Paper 2, Section $I$, $2 F$

  Groups, Rings and Modules | Part IB, 2015

  Give four non-isomorphic groups of order 12 , and explain why they are not isomorphic.

  comment

• Paper 2, Section II, F

  Groups, Rings and Modules | Part IB, 2015

  (a) Consider the homomorphism $f: \mathbb{Z}^{3} \rightarrow \mathbb{Z}^{4}$ given by

  $$f(a, b, c)=(a+2 b+8 c, 2 a-2 b+4 c,-2 b+12 c, 2 a-4 b+4 c)$$

  Describe the image of this homomorphism as an abstract abelian group. Describe the quotient of $\mathbb{Z}^{4}$ by the image of this homomorphism as an abstract abelian group.

  (b) Give the definition of a Euclidean domain.

  Fix a prime $p$ and consider the subring $R$ of the rational numbers $\mathbb{Q}$ defined by

  $$R=\{q / r \mid \operatorname{gcd}(p, r)=1\}$$

  where 'gcd' stands for the greatest common divisor. Show that $R$ is a Euclidean domain.

  comment

Linear Algebra

• Paper 2, Section I, $1 \mathrm{E}$

  Linear Algebra | Part IB, 2015

  Let $q$ denote a quadratic form on a real vector space $V$. Define the rank and signature of $q$.

  Find the rank and signature of the following quadratic forms. (a) $q(x, y, z)=x^{2}+y^{2}+z^{2}-2 x z-2 y z$. (b) $q(x, y, z)=x y-x z$.

  (c) $q(x, y, z)=x y-2 z^{2}$.

  comment

• Paper 2, Section II, E

  Linear Algebra | Part IB, 2015

  (i) Suppose $A$ is a matrix that does not have $-1$ as an eigenvalue. Show that $A+I$ is non-singular. Further, show that $A$ commutes with $(A+I)^{-1}$.

  (ii) A matrix $A$ is called skew-symmetric if $A^{T}=-A$. Show that a real skewsymmetric matrix does not have $-1$ as an eigenvalue.

  (iii) Suppose $A$ is a real skew-symmetric matrix. Show that $U=(I-A)(I+A)^{-1}$ is orthogonal with determinant 1 .

  (iv) Verify that every orthogonal matrix $U$ with determinant 1 which does not have $-1$ as an eigenvalue can be expressed as $(I-A)(I+A)^{-1}$ where $A$ is a real skew-symmetric matrix.

  comment

Markov Chains

• Paper 2, Section II, H

  Markov Chains | Part IB, 2015

  (a) What does it mean for a transition matrix $P$ and a distribution $\lambda$ to be in detailed balance? Show that if $P$ and $\lambda$ are in detailed balance then $\lambda=\lambda P$.

  (b) A mathematician owns $r$ bicycles, which she sometimes uses for her journey from the station to College in the morning and for the return journey in the evening. If it is fine weather when she starts a journey, and if there is a bicycle available at the current location, then she cycles; otherwise she takes the bus. Assume that with probability $p$, $0<p<1$, it is fine when she starts a journey, independently of all other journeys. Let $X_{n}$ denote the number of bicycles at the current location, just before the mathematician starts the $n$th journey.

  (i) Show that $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain and write down its transition matrix.

  (ii) Find the invariant distribution of the Markov chain.

  (iii) Show that the Markov chain satisfies the necessary conditions for the convergence theorem for Markov chains and find the limiting probability that the mathematician's $n$th journey is by bicycle.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

Methods

• Paper 2, Section I, C

  Methods | Part IB, 2015

  (i) Write down the trigonometric form for the Fourier series and its coefficients for a function $f:[-L, L) \rightarrow \mathbb{R}$ extended to a $2 L$-periodic function on $\mathbb{R}$.

  (ii) Calculate the Fourier series on $[-\pi, \pi)$ of the function $f(x)=\sin (\lambda x)$ where $\lambda$ is a real constant. Take the limit $\lambda \rightarrow k$ with $k \in \mathbb{Z}$ in the coefficients of this series and briefly interpret the resulting expression.

  comment

• Paper 2, Section II, C

  Methods | Part IB, 2015

  (i) The Laplace operator in spherical coordinates is

  $$\vec{\nabla}^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \phi^{2}}$$

  Show that general, regular axisymmetric solutions $\psi(r, \theta)$ to the equation $\vec{\nabla}^{2} \psi=0$ are given by

  $$\psi(r, \theta)=\sum_{n=0}^{\infty}\left(A_{n} r^{n}+B_{n} r^{-(n+1)}\right) P_{n}(\cos \theta)$$

  where $A_{n}, B_{n}$ are constants and $P_{n}$ are the Legendre polynomials. [You may use without proof that regular solutions to Legendre's equation $-\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} y(x)\right]=\lambda y(x)$ are given by $P_{n}(x)$ with $\lambda=n(n+1)$ and non-negative integer $n$.]

  (ii) Consider a uniformly charged wire in the form of a ring of infinitesimal width with radius $r_{0}=1$ and a constant charge per unit length $\sigma$. By Coulomb's law, the electric potential due to a point charge $q$ at a point a distance $d$ from the charge is

  $$U=\frac{q}{4 \pi \epsilon_{0} d}$$

  where $\epsilon_{0}$ is a constant. Let the $z$-axis be perpendicular to the circle and pass through the circle's centre (see figure). Show that the potential due to the charged ring at a point on the $z$-axis at location $z$ is given by

  

  $$V=\frac{\sigma}{2 \epsilon_{0} \sqrt{1+z^{2}}} .$$

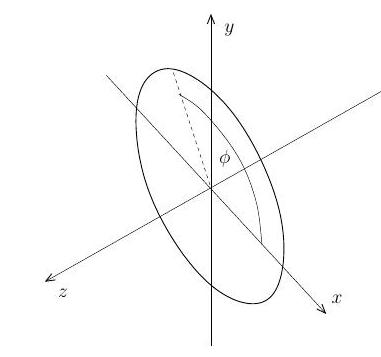
  (iii) The potential $V$ generated by the charged ring of (ii) at arbitrary points (excluding points directly on the ring which can be ignored for this question) is determined by Laplace's equation $\vec{\nabla}^{2} V=0$. Calculate this potential with the boundary condition $\lim _{r \rightarrow \infty} V=0$, where $r=\sqrt{x^{2}+y^{2}+z^{2}}$. [You may use without proof that

  $$\frac{1}{\sqrt{1+x^{2}}}=\sum_{m=0}^{\infty} x^{2 m}(-1)^{m} \frac{(2 m) !}{2^{2 m}(m !)^{2}}$$

  for $|x|<1$. Furthermore, the Legendre polynomials are normalized such that $\left.P_{n}(1)=1 .\right]$

  comment

Metric and Topological Spaces

• Paper 2, Section I, $4 \mathbf{E}$

  Metric and Topological Spaces | Part IB, 2015

  Let $X$ and $Y$ be topological spaces and $f: X \rightarrow Y$ a continuous map. Suppose $H$ is a subset of $X$ such that $f(\bar{H})$ is closed (where $\bar{H}$ denotes the closure of $H$ ). Prove that $f(\bar{H})=\overline{f(H)} .$

  Give an example where $f, X, Y$ and $H$ are as above but $f(\bar{H})$ is not closed.

  comment

Numerical Analysis

• Paper 2, Section II, D

  Numerical Analysis | Part IB, 2015

  Define the linear stability domain for a numerical method to solve $y^{\prime}=f(t, y)$. What is meant by an $A$-stable method? Briefly explain the relevance of these concepts in the numerical solution of ordinary differential equations.

  Consider

  $$y_{n+1}=y_{n}+h\left[\theta f\left(t_{n}, y_{n}\right)+(1-\theta) f\left(t_{n+1}, y_{n+1}\right)\right]$$

  where $\theta \in[0,1]$. What is the order of this method?

  Find the linear stability domain of this method. For what values of $\theta$ is the method A-stable?

  comment

Optimization

• Paper 2, Section I, H

  Optimization | Part IB, 2015

  Define what it means to say that a set $S \subseteq \mathbb{R}^{n}$ is convex. What is meant by an extreme point of a convex set $S$ ?

  Consider the set $S \subseteq \mathbb{R}^{2}$ given by

  $$S=\left\{\left(x_{1}, x_{2}\right): x_{1}+4 x_{2} \leqslant 30,3 x_{1}+7 x_{2} \leqslant 60, x_{1} \geqslant 0, x_{2} \geqslant 0\right\}$$

  Show that $S$ is convex, and give the coordinates of all extreme points of $S$.

  For all possible choices of $c_{1}>0$ and $c_{2}>0$, find the maximum value of $c_{1} x_{1}+c_{2} x_{2}$ subject to $\left(x_{1}, x_{2}\right) \in S$.

  comment

Quantum Mechanics

• Paper 2, Section II, D

  Quantum Mechanics | Part IB, 2015

  A quantum-mechanical harmonic oscillator has Hamiltonian

  $$\hat{H}=\frac{\hat{p}^{2}}{2}+\frac{1}{2} k^{2} \hat{x}^{2}$$

  where $k$ is a positive real constant. Show that $\hat{x}=x$ and $\hat{p}=-i \hbar \frac{\partial}{\partial x}$ are Hermitian operators.

  The eigenfunctions of $(*)$ can be written as

  $$\psi_{n}(x)=h_{n}(x \sqrt{k / \hbar}) \exp \left(-\frac{k x^{2}}{2 \hbar}\right),$$

  where $h_{n}$ is a polynomial of degree $n$ with even (odd) parity for even (odd) $n$ and $n=0,1,2, \ldots$. Show that $\langle\hat{x}\rangle=\langle\hat{p}\rangle=0$ for all of the states $\psi_{n}$.

  State the Heisenberg uncertainty principle and verify it for the state $\psi_{0}$ by computing $(\Delta x)$ and $(\Delta p)$. [Hint: You should properly normalise the state.]

  The oscillator is in its ground state $\psi_{0}$ when the potential is suddenly changed so that $k \rightarrow 4 k$. If the wavefunction is expanded in terms of the energy eigenfunctions of the new Hamiltonian, $\phi_{n}$, what can be said about the coefficient of $\phi_{n}$ for odd $n$ ? What is the probability that the particle is in the new ground state just after the change?

  [Hint: You may assume that if $I_{n}=\int_{-\infty}^{\infty} e^{-a x^{2}} x^{n} d x$ then $I_{0}=\sqrt{\frac{\pi}{a}}$ and $I_{2}=\frac{1}{2 a} \sqrt{\frac{\pi}{a}}$.]

  comment

Statistics

• Paper 2, Section I, H

  Statistics | Part IB, 2015

  Suppose that, given $\theta$, the random variable $X$ has $\mathbb{P}(X=k)=e^{-\theta} \theta^{k} / k !$, $k=0,1,2, \ldots .$ Suppose that the prior density of $\theta$ is $\pi(\theta)=\lambda e^{-\lambda \theta}, \theta>0$, for some known $\lambda(>0)$. Derive the posterior density $\pi(\theta \mid x)$ of $\theta$ based on the observation $X=x$.

  For a given loss function $L(\theta, a)$, a statistician wants to calculate the value of $a$ that minimises the expected posterior loss

  $$\int L(\theta, a) \pi(\theta \mid x) d \theta$$

  Suppose that $x=0$. Find $a$ in terms of $\lambda$ in the following cases:

  (a) $L(\theta, a)=(\theta-a)^{2}$;

  (b) $L(\theta, a)=|\theta-a|$.

  comment

Variational Principles

• Paper 2, Section II, A

  Variational Principles | Part IB, 2015

  A right circular cylinder of radius $a$ and length $l$ has volume $V$ and total surface area $A$. Use Lagrange multipliers to do the following:

  (a) Show that, for a given total surface area, the maximum volume is

  $$V=\frac{1}{3} \sqrt{\frac{A^{3}}{C \pi}}$$

  determining the integer $C$ in the process.

  (b) For a cylinder inscribed in the unit sphere, show that the value of $l / a$ which maximises the area of the cylinder is

  $$D+\sqrt{E}$$

  determining the integers $D$ and $E$ as you do so.

  (c) Consider the rectangular parallelepiped of largest volume which fits inside a hemisphere of fixed radius. Find the ratio of the parallelepiped's volume to the volume of the hemisphere.

  [You need not show that suitable extrema you find are actually maxima.]

  comment