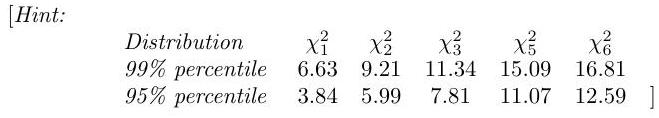Part IB, 2003, Paper 2

Analysis II

• 2.I.1F

  Analysis II | Part IB, 2003

  Explain what it means for a function $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{1}$ to be differentiable at a point $(a, b)$. Show that if the partial derivatives $\partial f / \partial x$ and $\partial f / \partial y$ exist in a neighbourhood of $(a, b)$ and are continuous at $(a, b)$ then $f$ is differentiable at $(a, b)$.

  Let

  $$f(x, y)=\frac{x y}{x^{2}+y^{2}} \quad((x, y) \neq(0,0))$$

  and $f(0,0)=0$. Do the partial derivatives of $f$ exist at $(0,0) ?$ Is $f$ differentiable at $(0,0) ?$ Justify your answers.

  comment

• 2.II.10F

  Analysis II | Part IB, 2003

  Let $V$ be the space of $n \times n$ real matrices. Show that the function

  $$N(A)=\sup \left\{\|A \mathbf{x}\|: \mathbf{x} \in \mathbb{R}^{n},\|\mathbf{x}\|=1\right\}$$

  (where $\|-\|$ denotes the usual Euclidean norm on $\mathbb{R}^{n}$ ) defines a norm on $V$. Show also that this norm satisfies $N(A B) \leqslant N(A) N(B)$ for all $A$ and $B$, and that if $N(A)<\epsilon$ then all entries of $A$ have absolute value less than $\epsilon$. Deduce that any function $f: V \rightarrow \mathbb{R}$ such that $f(A)$ is a polynomial in the entries of $A$ is continuously differentiable.

  Now let $d: V \rightarrow \mathbb{R}$ be the mapping sending a matrix to its determinant. By considering $d(I+H)$ as a polynomial in the entries of $H$, show that the derivative $d^{\prime}(I)$ is the function $H \mapsto \operatorname{tr} H$. Deduce that, for any $A, d^{\prime}(A)$ is the mapping $H \mapsto \operatorname{tr}((\operatorname{adj} A) H)$, where $\operatorname{adj} A$ is the adjugate of $A$, i.e. the matrix of its cofactors.

  [Hint: consider first the case when $A$ is invertible. You may assume the results that the set $U$ of invertible matrices is open in $V$ and that its closure is the whole of $V$, and the identity $(\operatorname{adj} A) A=\operatorname{det} A . I$.]

  comment

Complex Methods

• 2.I.7B

  Complex Methods | Part IB, 2003

  (a) Using the residue theorem, evaluate

  $$\int_{|z|=1}\left(z-\frac{1}{z}\right)^{2 n} \frac{d z}{z}$$

  (b) Deduce that

  $$\int_{0}^{2 \pi} \sin ^{2 n} t d t=\frac{\pi}{2^{2 n-1}} \frac{(2 n) !}{(n !)^{2}}$$

  comment

• 2.II.16B

  Complex Methods | Part IB, 2003

  (a) Show that if $f$ satisfies the equation

  $$f^{\prime \prime}(x)-x^{2} f(x)=\mu f(x), \quad x \in \mathbb{R},$$

  where $\mu$ is a constant, then its Fourier transform $\widehat{f}$ satisfies the same equation, i.e.

  $$\widehat{f}^{\prime \prime}(\lambda)-\lambda^{2} \widehat{f}(\lambda)=\mu \widehat{f}(\lambda) .$$

  (b) Prove that, for each $n \geq 0$, there is a polynomial $p_{n}(x)$ of degree $n$, unique up to multiplication by a constant, such that

  $$f_{n}(x)=p_{n}(x) e^{-x^{2} / 2}$$

  is a solution of $(*)$ for some $\mu=\mu_{n}$.

  (c) Using the fact that $g(x)=e^{-x^{2} / 2}$ satisfies $\widehat{g}=c g$ for some constant $c$, show that the Fourier transform of $f_{n}$ has the form

  $$\widehat{f_{n}}(\lambda)=q_{n}(\lambda) e^{-\lambda^{2} / 2}$$

  where $q_{n}$ is also a polynomial of degree $n$.

  (d) Deduce that the $f_{n}$ are eigenfunctions of the Fourier transform operator, i.e. $\widehat{f_{n}}(x)=c_{n} f_{n}(x)$ for some constants $c_{n} .$

  comment

Further Analysis

• 2.II.13E

  Further Analysis | Part IB, 2003

  (a) Let $f:[1, \infty) \rightarrow \mathbb{C}$ be defined by $f(t)=t^{-1} e^{2 \pi i t}$ and let $X$ be the image of $f$. Prove that $X \cup\{0\}$ is compact and path-connected. [Hint: you may find it helpful to set $\left.s=t^{-1} .\right]$

  (b) Let $g:[1, \infty) \rightarrow \mathbb{C}$ be defined by $g(t)=\left(1+t^{-1}\right) e^{2 \pi i t}$, let $Y$ be the image of $g$ and let $\bar{D}$ be the closed unit $\operatorname{disc}\{z \in \mathbb{C}:|z| \leq 1\}$. Prove that $Y \cup \bar{D}$ is connected. Explain briefly why it is not path-connected.

  comment

Linear Mathematics

• 2.I.6E

  Linear Mathematics | Part IB, 2003

  Let $a_{1}, a_{2}, \ldots, a_{n}$ be distinct real numbers. For each $i$ let $\mathbf{v}_{i}$ be the vector $\left(1, a_{i}, a_{i}^{2}, \ldots, a_{i}^{n-1}\right)$. Let $A$ be the $n \times n$ matrix with rows $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n}$ and let $\mathbf{c}$ be a column vector of size $n$. Prove that $A \mathbf{c}=\mathbf{0}$ if and only if $\mathbf{c}=\mathbf{0}$. Deduce that the vectors $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n} \operatorname{span} \mathbb{R}^{n}$.

  [You may use general facts about matrices if you state them clearly.]

  comment

• 2.II.15E

  Linear Mathematics | Part IB, 2003

  (a) Let $A=\left(a_{i j}\right)$ be an $m \times n$ matrix and for each $k \leqslant n$ let $A_{k}$ be the $m \times k$ matrix formed by the first $k$ columns of $A$. Suppose that $n>m$. Explain why the nullity of $A$ is non-zero. Prove that if $k$ is minimal such that $A_{k}$ has non-zero nullity, then the nullity of $A_{k}$ is 1 .

  (b) Suppose that no column of $A$ consists entirely of zeros. Deduce from (a) that there exist scalars $b_{1}, \ldots, b_{k}$ (where $k$ is defined as in (a)) such that $\sum_{j=1}^{k} a_{i j} b_{j}=0$ for every $i \leqslant m$, but whenever $\lambda_{1}, \ldots, \lambda_{k}$ are distinct real numbers there is some $i \leqslant m$ such that $\sum_{j=1}^{k} a_{i j} \lambda_{j} b_{j} \neq 0$.

  (c) Now let $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{m}$ and $\mathbf{w}_{1}, \mathbf{w}_{2}, \ldots, \mathbf{w}_{m}$ be bases for the same real $m$ dimensional vector space. Let $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}$ be distinct real numbers such that for every $j$ the vectors $\mathbf{v}_{1}+\lambda_{j} \mathbf{w}_{1}, \ldots, \mathbf{v}_{m}+\lambda_{j} \mathbf{w}_{m}$ are linearly dependent. For each $j$, let $a_{1 j}, \ldots, a_{m j}$ be scalars, not all zero, such that $\sum_{i=1}^{m} a_{i j}\left(\mathbf{v}_{i}+\lambda_{j} \mathbf{w}_{i}\right)=\mathbf{0}$. By applying the result of (b) to the matrix $\left(a_{i j}\right)$, deduce that $n \leqslant m$.

  (d) It follows that the vectors $\mathbf{v}_{1}+\lambda \mathbf{w}_{1}, \ldots, \mathbf{v}_{m}+\lambda \mathbf{w}_{m}$ are linearly dependent for at most $m$ values of $\lambda$. Explain briefly how this result can also be proved using determinants.

  comment

Methods

• 2.I.2C

  Methods | Part IB, 2003

  Explain briefly why the second-rank tensor

  $$\int_{S} x_{i} x_{j} d S(\mathbf{x})$$

  is isotropic, where $S$ is the surface of the unit sphere centred on the origin.

  A second-rank tensor is defined by

  $$T_{i j}(\mathbf{y})=\int_{S}\left(y_{i}-x_{i}\right)\left(y_{j}-x_{j}\right) d S(\mathbf{x})$$

  where $S$ is the surface of the unit sphere centred on the origin. Calculate $T(\mathbf{y})$ in the form

  $$T_{i j}=\lambda \delta_{i j}+\mu y_{i} y_{j}$$

  where $\lambda$ and $\mu$ are to be determined.

  By considering the action of $T$ on $\mathbf{y}$ and on vectors perpendicular to $\mathbf{y}$, determine the eigenvalues and associated eigenvectors of $T$.

  comment

• 2.II.11C

  Methods | Part IB, 2003

  State the transformation law for an $n$ th-rank tensor $T_{i j \cdots k}$.

  Show that the fourth-rank tensor

  $$c_{i j k l}=\alpha \delta_{i j} \delta_{k l}+\beta \delta_{i k} \delta_{j l}+\gamma \delta_{i l} \delta_{j k}$$

  is isotropic for arbitrary scalars $\alpha, \beta$ and $\gamma$.

  The stress $\sigma_{i j}$ and strain $e_{i j}$ in a linear elastic medium are related by

  $$\sigma_{i j}=c_{i j k l} e_{k l} .$$

  Given that $e_{i j}$ is symmetric and that the medium is isotropic, show that the stress-strain relationship can be written in the form

  $$\sigma_{i j}=\lambda e_{k k} \delta_{i j}+2 \mu e_{i j}$$

  Show that $e_{i j}$ can be written in the form $e_{i j}=p \delta_{i j}+d_{i j}$, where $d_{i j}$ is a traceless tensor and $p$ is a scalar to be determined. Show also that necessary and sufficient conditions for the stored elastic energy density $E=\frac{1}{2} \sigma_{i j} e_{i j}$ to be non-negative for any deformation of the solid are that

  $$\mu \geq 0 \quad \text { and } \quad \lambda \geq-\frac{2}{3} \mu .$$

  comment

Numerical Analysis

• 2.I.5B

  Numerical Analysis | Part IB, 2003

  Let

  $$A=\left(\begin{array}{cccc} 1 & a & a^{2} & a^{3} \\ a^{3} & 1 & a & a^{2} \\ a^{2} & a^{3} & 1 & a \\ a & a^{2} & a^{3} & 1 \end{array}\right), \quad b=\left(\begin{array}{c} \gamma \\ 0 \\ 0 \\ \gamma a \end{array}\right), \quad \gamma=1-a^{4} \neq 0$$

  Find the LU factorization of the matrix $A$ and use it to solve the system $A x=b$.

  comment

• 2.II.14B

  Numerical Analysis | Part IB, 2003

  Let

  $$f^{\prime \prime}(0) \approx a_{0} f(-1)+a_{1} f(0)+a_{2} f(1)=\mu(f)$$

  be an approximation of the second derivative which is exact for $f \in \mathcal{P}_{2}$, the set of polynomials of degree $\leq 2$, and let

  $$e(f)=f^{\prime \prime}(0)-\mu(f)$$

  be its error.

  (a) Determine the coefficients $a_{0}, a_{1}, a_{2}$.

  (b) Using the Peano kernel theorem prove that, for $f \in C^{3}[-1,1]$, the set of threetimes continuously differentiable functions, the error satisfies the inequality

  $$|e(f)| \leq \frac{1}{3} \max _{x \in[-1,1]}\left|f^{\prime \prime \prime}(x)\right| .$$

  comment

Quadratic Mathematics

• 2.I.8G

  Quadratic Mathematics | Part IB, 2003

  Let $U$ be a finite-dimensional real vector space and $b$ a positive definite symmetric bilinear form on $U \times U$. Let $\psi: U \rightarrow U$ be a linear map such that $b(\psi(x), y)+b(x, \psi(y))=0$ for all $x$ and $y$ in $U$. Prove that if $\psi$ is invertible, then the dimension of $U$ must be even. By considering the restriction of $\psi$ to its image or otherwise, prove that the rank of $\psi$ is always even.

  comment

• 2.II.17G

  Quadratic Mathematics | Part IB, 2003

  Let $S$ be the set of all $2 \times 2$ complex matrices $A$ which are hermitian, that is, $A^{*}=A$, where $A^{*}=\bar{A}^{t}$.

  (a) Show that $S$ is a real 4-dimensional vector space. Consider the real symmetric bilinear form $b$ on this space defined by

  $$b(A, B)=\frac{1}{2}(\operatorname{tr}(A B)-\operatorname{tr}(A) \operatorname{tr}(B)) .$$

  Prove that $b(A, A)=-\operatorname{det} A$ and $b(A, I)=-\frac{1}{2} \operatorname{tr}(A)$, where $I$ denotes the identity matrix.

  (b) Consider the three matrices

  $$A_{1}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), \quad A_{2}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \quad \text { and } \quad A_{3}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)$$

  Prove that the basis $I, A_{1}, A_{2}, A_{3}$ of $S$ diagonalizes $b$. Hence or otherwise find the rank and signature of $b$.

  (c) Let $Q$ be the set of all $2 \times 2$ complex matrices $C$ which satisfy $C+C^{*}=\operatorname{tr}(C) I$. Show that $Q$ is a real 4-dimensional vector space. Given $C \in Q$, put

  $$\Phi(C)=\frac{1-i}{2} \operatorname{tr}(C) I+i C .$$

  Show that $\Phi$ takes values in $S$ and is a linear isomorphism between $Q$ and $S$.

  (d) Define a real symmetric bilinear form on $Q$ by setting $c(C, D)=-\frac{1}{2} \operatorname{tr}(C D)$, $C, D \in Q$. Show that $b(\Phi(C), \Phi(D))=c(C, D)$ for all $C, D \in Q$. Find the rank and signature of the symmetric bilinear form $c$ defined on $Q$.

  comment

Quantum Mechanics

• 2.I.9A

  Quantum Mechanics | Part IB, 2003

  What is meant by the statement than an operator is hermitian?

  A particle of mass $m$ moves in the real potential $V(x)$ in one dimension. Show that the Hamiltonian of the system is hermitian.

  Show that

  $$\begin{aligned} \frac{d}{d t}\langle x\rangle &=\frac{1}{m}\langle p\rangle \\ \frac{d}{d t}\langle p\rangle &=\left\langle-V^{\prime}(x)\right\rangle \end{aligned}$$

  where $p$ is the momentum operator and $\langle A\rangle$ denotes the expectation value of the operator $A$.

  comment

• 2.II.18A

  Quantum Mechanics | Part IB, 2003

  A particle of mass $m$ and energy $E$ moving in one dimension is incident from the left on a potential barrier $V(x)$ given by

  $$V(x)= \begin{cases}V_{0} & 0 \leqslant x \leqslant a \\ 0 & \text { otherwise }\end{cases}$$

  with $V_{0}>0$.

  In the limit $V_{0} \rightarrow \infty, a \rightarrow 0$ with $V_{0} a=U$ held fixed, show that the transmission probability is

  $$T=\left(1+\frac{m U^{2}}{2 E \hbar^{2}}\right)^{-1}$$

  comment

Statistics

• 2.I.3H

  Statistics | Part IB, 2003

  Let $X_{1}, \ldots, X_{n}$ be a random sample from the $N\left(\theta, \sigma^{2}\right)$ distribution, and suppose that the prior distribution for $\theta$ is $N\left(\mu, \tau^{2}\right)$, where $\sigma^{2}, \mu, \tau^{2}$ are known. Determine the posterior distribution for $\theta$, given $X_{1}, \ldots, X_{n}$, and the best point estimate of $\theta$ under both quadratic and absolute error loss.

  comment

• 2.II.12H

  Statistics | Part IB, 2003

  An examination was given to 500 high-school students in each of two large cities, and their grades were recorded as low, medium, or high. The results are given in the table below.

  \begin{tabular}{l|ccc} & Low & Medium & High \ \hline City A & 103 & 145 & 252 \ City B & 140 & 136 & 224 \end{tabular}

  Derive carefully the test of homogeneity and test the hypothesis that the distributions of scores among students in the two cities are the same.

  

  comment