Part IA, 2009

Analysis I

• Paper 1, Section I, $3 \mathbf{F}$

  Analysis I | Part IA, 2009

  Determine the limits as $n \rightarrow \infty$ of the following sequences:

  (a) $a_{n}=n-\sqrt{n^{2}-n}$;

  (b) $b_{n}=\cos ^{2}\left(\pi \sqrt{n^{2}+n}\right)$.

  comment

• Paper 1, Section I, E

  Analysis I | Part IA, 2009

  Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of complex numbers. Prove that there exists $R \in[0, \infty]$ such that the power series $\sum_{n=0}^{\infty} a_{n} z^{n}$ converges whenever $|z|<R$ and diverges whenever $|z|>R$.

  Give an example of a power series $\sum_{n=0}^{\infty} a_{n} z^{n}$ that diverges if $z=\pm 1$ and converges if $z=\pm \mathrm{i}$.

  comment

• Paper 1, Section II, D

  Analysis I | Part IA, 2009

  State and prove Rolle's theorem.

  Let $f$ and $g$ be two continuous, real-valued functions on a closed, bounded interval $[a, b]$ that are differentiable on the open interval $(a, b)$. By considering the determinant

  $$\phi(x)=\left|\begin{array}{ccc} 1 & 1 & 0 \\ f(a) & f(b) & f(x) \\ g(a) & g(b) & g(x) \end{array}\right|=g(x)(f(b)-f(a))-f(x)(g(b)-g(a))$$

  or otherwise, show that there is a point $c \in(a, b)$ with

  $$f^{\prime}(c)(g(b)-g(a))=g^{\prime}(c)(f(b)-f(a))$$

  Suppose that $f, g:(0, \infty) \rightarrow \mathbb{R}$ are differentiable functions with $f(x) \rightarrow 0$ and $g(x) \rightarrow 0$ as $x \rightarrow 0$. Prove carefully that if the $\operatorname{limit}_{x \rightarrow 0} \frac{f^{\prime}(x)}{g^{\prime}(x)}=\ell$ exists and is finite, then the limit $\lim _{x \rightarrow 0} \frac{f(x)}{g(x)}$ also exists and equals $\ell$.

  comment

• Paper 1, Section II, D

  Analysis I | Part IA, 2009

  State and prove the intermediate value theorem.

  Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a continuous function and let $P=(a, b)$ be a point of the plane $\mathbb{R}^{2}$. Show that the set of distances from points $(x, f(x))$ on the graph of $f$ to the point $P$ is an interval $[A, \infty)$ for some value $A \geqslant 0$.

  comment

• Paper 1, Section II, E

  Analysis I | Part IA, 2009

  (a) What does it mean for a function $f:[a, b] \rightarrow \mathbb{R}$ to be Riemann integrable?

  (b) Let $f:[0,1] \rightarrow \mathbb{R}$ be a bounded function. Suppose that for every $\delta>0$ there is a sequence

  $$0 \leqslant a_{1}<b_{1} \leqslant a_{2}<b_{2} \leqslant \ldots \leqslant a_{n}<b_{n} \leqslant 1$$

  such that for each $i$ the function $f$ is Riemann integrable on the closed interval $\left[a_{i}, b_{i}\right]$, and such that $\sum_{i=1}^{n}\left(b_{i}-a_{i}\right) \geqslant 1-\delta$. Prove that $f$ is Riemann integrable on $[0,1]$.

  (c) Let $f:[0,1] \rightarrow \mathbb{R}$ be defined as follows. We set $f(x)=1$ if $x$ has an infinite decimal expansion that consists of 2 s and $7 \mathrm{~s}$ only, and otherwise we set $f(x)=0$. Prove that $f$ is Riemann integrable and determine $\int_{0}^{1} f(x) \mathrm{d} x$.

  comment

• Paper 1, Section II, F

  Analysis I | Part IA, 2009

  For each of the following series, determine for which real numbers $x$ it diverges, for which it converges, and for which it converges absolutely. Justify your answers briefly.

  (a) $\sum_{n \geqslant 1} \frac{3+(\sin x)^{n}}{n}(\sin x)^{n}$,

  (b) $\quad \sum_{n \geqslant 1}|\sin x|^{n} \frac{(-1)^{n}}{\sqrt{n}}$,

  (c)

  $$\sum_{n \geqslant 1} \underbrace{\sin (0.99 \sin (0.99 \ldots \sin (0.99 x) \ldots))}_{n \text { times }} .$$

  comment

Differential Equations

• Paper 2, Section I, C

  Differential Equations | Part IA, 2009

  Solve the differential equation

  $$\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}-5 \frac{\mathrm{d} y}{\mathrm{~d} x}+6 y=\mathrm{e}^{3 x}$$

  subject to the conditions $y=\mathrm{d} y / \mathrm{d} x=0$ when $x=0$.

  comment

• Paper 2, Section I, C

  Differential Equations | Part IA, 2009

  The size of the population of ducks living on the pond of a certain Cambridge college is governed by the equation

  $$\frac{\mathrm{d} N}{\mathrm{~d} t}=\alpha N-N^{2}$$

  where $N=N(t)$ is the number of ducks at time $t$ and $\alpha$ is a positive constant. Given that $N(0)=2 \alpha$, find $N(t)$. What happens as $t \rightarrow \infty$ ?

  comment

• Paper 2, Section II, $7 \mathrm{C}$

  Differential Equations | Part IA, 2009

  Consider the differential equation

  $$x \frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}+(c-x) \frac{\mathrm{d} y}{\mathrm{~d} x}-y=0,$$

  where $c$ is a constant with $0<c<1$. Determine two linearly independent series solutions about $x=0$, giving an explicit expression for the coefficient of the general term in each series.

  Determine the solution of

  $$x \frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}+(c-x) \frac{\mathrm{d} y}{\mathrm{~d} x}-y=x$$

  for which $y(0)=0$ and $\mathrm{d} y / \mathrm{d} x$ is finite at $x=0$.

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  Consider the second-order ordinary differential equation

  $$\ddot{x}+2 k \dot{x}+\omega^{2} x=0,$$

  where $x=x(t)$ and $k$ and $\omega$ are constants with $k>0$. Calculate the general solution in the cases (i) $k<\omega$, (ii) $k=\omega$, (iii) $k>\omega$.

  Now consider the system

  $$\ddot{x}+2 k \dot{x}+\omega^{2} x= \begin{cases}a & \text { when } \dot{x}>0 \\ 0 & \text { when } \dot{x} \leqslant 0\end{cases}$$

  with $x(0)=x_{1}, \dot{x}(0)=0$, where $a$ and $x_{1}$ are positive constants. In the case $k<\omega$ find $x(t)$ in the ranges $0 \leqslant t \leqslant \pi / p$ and $\pi / p \leqslant t \leqslant 2 \pi / p$, where $p=\sqrt{\omega^{2}-k^{2}}$. Hence, determine the value of $x_{1}$ for which $x(t)$ is periodic. For $k>\omega$ can $x(t)$ ever be periodic? Justify your answer.

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  Consider the first-order ordinary differential equation

  $$\frac{\mathrm{d} y}{\mathrm{~d} x}=f_{1}(x) y+f_{2}(x) y^{p}$$

  where $y \geqslant 0$ and $p$ is a positive constant with $p \neq 1$. Let $u=y^{1-p}$. Show that $u$ satisfies

  $$\frac{\mathrm{d} u}{\mathrm{~d} x}=(1-p)\left[f_{1}(x) u+f_{2}(x)\right]$$

  Hence, find the general solution of equation $(*)$ when $f_{1}(x)=1, f_{2}(x)=x$.

  Now consider the case $f_{1}(x)=1, f_{2}(x)=-\alpha^{2}$, where $\alpha$ is a non-zero constant. For $p>1$ find the two equilibrium points of equation $(*)$, and determine their stability. What happens when $0<p<1$ ?

  comment

• Paper 2, Section II, C

  Differential Equations | Part IA, 2009

  (a) The function $y(x, t)$ satisfies the forced wave equation

  $$\frac{\partial^{2} y}{\partial x^{2}}-\frac{\partial^{2} y}{\partial t^{2}}=4$$

  with initial conditions $y(x, 0)=\sin x$ and $\partial y / \partial t(x, 0)=0$. By making the change of variables $u=x+t$ and $v=x-t$, show that

  $$\frac{\partial^{2} y}{\partial u \partial v}=1$$

  Hence, find $y(x, t)$.

  (b) The thickness of an axisymmetric drop of liquid spreading on a flat surface satisfies

  $$\frac{\partial h}{\partial t}=\frac{1}{r} \frac{\partial}{\partial r}\left(r h^{3} \frac{\partial h}{\partial r}\right),$$

  where $h=h(r, t)$ is the thickness of the drop, $r$ is the radial coordinate on the surface and $t$ is time. The drop has radius $R(t)$. The boundary conditions are that $\partial h / \partial r=0$ at $r=0$ and $h(r, t) \propto(R(t)-r)^{1 / 3}$ as $r \rightarrow R(t)$.

  Show that

  $$M=\int_{0}^{R(t)} r h \mathrm{~d} r$$

  is independent of time. Given that $h(r, t)=f\left(r / t^{\alpha}\right) t^{-1 / 4}$ for some function $f$ (which need not be determined) and that $R(t)$ is proportional to $t^{\alpha}$, find $\alpha$.

  comment

Dynamics and Relativity

• Paper 4, Section I, A

  Dynamics and Relativity | Part IA, 2009

  (a) Explain what is meant by a central force acting on a particle moving in three dimensions.

  (b) Show that the orbit of a particle experiencing a central force lies in a plane.

  (c) Show that, in the approximation in which the Sun is regarded as fixed and only its gravitational field is considered, a straight line joining the Sun and an orbiting planet sweeps out equal areas in equal times (Kepler's second law).

  [With respect to the basis vectors $\left(\mathbf{e}_{r}, \mathbf{e}_{\theta}\right)$ of plane polar coordinates, the velocity $\dot{\mathbf{x}}$ and acceleration $\ddot{\mathbf{x}}$ of a particle are given by $\dot{\mathbf{x}}=(\dot{r}, r \dot{\theta})$ and $\ddot{\mathbf{x}}=\left(\ddot{r}-r \dot{\theta}^{2}, r \ddot{\theta}+2 \dot{r} \dot{\theta}\right)$.]

  comment

• Paper 4, Section I, A

  Dynamics and Relativity | Part IA, 2009

  A rocket moves vertically upwards in a uniform gravitational field and emits exhaust gas downwards with time-dependent speed $U(t)$ relative to the rocket. Derive the rocket equation

  $$m(t) \frac{\mathrm{d} v}{\mathrm{~d} t}+U(t) \frac{\mathrm{d} m}{\mathrm{~d} t}=-m(t) g$$

  where $m(t)$ and $v(t)$ are respectively the rocket's mass and upward vertical speed at time $t$. Suppose now that $m(t)=m_{0}-\alpha t, U(t)=U_{0} m_{0} / m(t)$ and $v(0)=0$. What is the condition for the rocket to lift off at $t=0$ ? Assuming that this condition is satisfied, find $v(t)$.

  State the dimensions of all the quantities involved in your expression for $v(t)$, and verify that the expression is dimensionally consistent.

  [ You may assume that all speeds are small compared with the speed of light and neglect any relativistic effects.]

  comment

• Paper 4, Section II, A

  Dynamics and Relativity | Part IA, 2009

  (a) A particle of charge $q$ moves with velocity $v$ in a constant magnetic field B. Give an expression for the Lorentz force $\mathbf{F}$ experienced by the particle. If no other forces act on the particle, show that its kinetic energy is independent of time.

  (b) Four point particles, each of positive charge $Q$, are fixed at the four corners of a square with sides of length $2 a$. Another point particle, of positive charge $q$, is constrained to move in the plane of the square but is otherwise free.

  By considering the form of the electrostatic potential near the centre of the square, show that the state in which the particle of charge $q$ is stationary at the centre of the square is a stable equilibrium. Obtain the frequency of small oscillations about this equilibrium.

  [The Coulomb potential for two point particles of charges $Q$ and $q$ separated by distance $r$ is $\left.Q q / 4 \pi \epsilon_{0} r .\right]$

  comment

• Paper 4, Section II, A

  Dynamics and Relativity | Part IA, 2009

  Obtain the moment of inertia of a uniform disc of radius $a$ and mass $M$ about its axis of rotational symmetry. A uniform rigid body of mass $3 M / 4$ takes the form of a disc of radius $a$ with a concentric circular hole of radius $a / 2$ cut out. Calculate the body's moment of inertia about its axis of rotational symmetry.

  The body rolls without slipping, with its axis of symmetry horizontal, down a plane inclined at angle $\alpha$ to the horizontal. Determine its acceleration and the frictional and normal-reaction forces resulting from contact with the plane.

  comment

• Paper 4, Section II, A

  Dynamics and Relativity | Part IA, 2009

  (a) Write down expressions for the relativistic 3 -momentum $\mathbf{p}$ and energy $E$ of a particle of rest mass $m$ and velocity $\mathbf{v}$. Show that these expressions are consistent with

  $$E^{2}=\mathbf{p} \cdot \mathbf{p} c^{2}+m^{2} c^{4}$$

  Define the 4-momentum $\mathbf{P}$ for such a particle and obtain $(*)$ by considering the invariance properties of $\mathbf{P}$.

  (b) Two particles, each with rest mass $m$ and energy $E$, moving in opposite directions, collide head on. Show that it is consistent with the conservation of 4 -momentum for the collision to result in a set of $n$ particles of rest masses $\mu_{i}$ (for $\left.1 \leqslant i \leqslant n\right)$ only if

  $$E \geqslant \frac{1}{2}\left(\sum_{i=1}^{n} \mu_{i}\right) c^{2} .$$

  (c) A particle of rest mass $m_{1}$ and energy $E_{1}$ is fired at a stationary particle of rest mass $m_{2}$. Show that it is consistent with the conservation of 4 -momentum for the collision to result in a set of $n$ particles of rest masses $\mu_{i}$ (for $1 \leqslant i \leqslant n$ ) only if

  $$E_{1} \geqslant \frac{\left(\sum_{i=1}^{n} \mu_{i}\right)^{2}-m_{1}^{2}-m_{2}^{2}}{2 m_{2}} c^{2}$$

  Deduce the minimum frequency required for a photon fired at a stationary particle of rest mass $m_{2}$ to result in the same set of $n$ particles, assuming that the conservation of 4 -momentum is the only relevant constraint.

  comment

• Paper 4, Section II, A

  Dynamics and Relativity | Part IA, 2009

  Davros departs on a rocket voyage from the planet Skaro, travelling at speed $u$ (where $0<u<c$ ) in the positive $x$ direction in Skaro's rest frame. After travelling a distance $L$ in Skaro's rest frame, he jumps onto another rocket travelling at speed $v^{\prime}$ (where $0<v^{\prime}<c$ ) in the positive $x$ direction in the first rocket's rest frame. After travelling a further distance $L$ in Skaro's rest frame, he jumps onto a third rocket, travelling at speed $w^{\prime \prime}\left(\right.$ where $0<w^{\prime \prime}<c$ ) in the negative $x$ direction in the second rocket's rest frame.

  Let $v$ and $w$ be Davros' speed on the second and third rockets, respectively, in Skaro's rest frame. Show that

  $$v=\left(u+v^{\prime}\right)\left(1+\frac{u v^{\prime}}{c^{2}}\right)^{-1}$$

  Express $w$ in terms of $u, v^{\prime}, w^{\prime \prime}$ and $c$.

  How large must $w^{\prime \prime}$ be, expressed in terms of $u, v^{\prime}$ and $c$, to ensure that Davros eventually returns to Skaro?

  Supposing that $w^{\prime \prime}$ satisfies this condition, draw a spacetime diagram illustrating Davros' journey. Label clearly each point where he boards a rocket and the point of his return to Skaro, and give the coordinates of each point in Skaro's rest frame, expressed in terms of $u, v, w, c$ and $L$.

  Hence, or otherwise, calculate how much older Davros will be on his return, and how much time will have elapsed on Skaro during his voyage, giving your answers in terms of $u, v, w, c$ and $L$.

  [You may neglect any effects due to gravity and any corrections arising from Davros' brief accelerations when getting onto or leaving rockets.

  comment

Groups

• Paper 3 , Section II, D

  Groups | Part IA, 2009

  Let $S(X)$ denote the group of permutations of a finite set $X$. Show that every permutation $\sigma \in S(X)$ can be written as a product of disjoint cycles. Explain briefly why two permutations in $S(X)$ are conjugate if and only if, when they are written as the product of disjoint cycles, they have the same number of cycles of length $n$ for each possible value of $n$.

  Let $\ell(\sigma)$ denote the number of disjoint cycles, including 1-cycles, required when $\sigma$ is written as a product of disjoint cycles. Let $\tau$ be a transposition in $S(X)$ and $\sigma$ any permutation in $S(X)$. Prove that $\ell(\tau \sigma)=\ell(\sigma) \pm 1$.

  comment

• Paper 3, Section I, D

  Groups | Part IA, 2009

  State and prove Lagrange's theorem. Give an example to show that an integer $k$ may divide the order of a group $G$ without there being a subgroup of order $k$.

  comment

• Paper 3, Section I, D

  Groups | Part IA, 2009

  Show that every orthogonal $2 \times 2$ matrix $R$ is the product of at most two reflections in lines through the origin.

  Every isometry of the Euclidean plane $\mathbb{R}^{2}$ can be written as the composition of an orthogonal matrix and a translation. Deduce from this that every isometry of the Euclidean plane $\mathbb{R}^{2}$ is a product of reflections.

  Give an example of an isometry of $\mathbb{R}^{2}$ that is not the product of fewer than three reflections. Justify your answer.

  comment

• Paper 3, Section II, D

  Groups | Part IA, 2009

  What does it mean to say that a subgroup $K$ of a group $G$ is normal?

  Let $\phi: G \rightarrow H$ be a group homomorphism. Is the kernel of $\phi$ always a subgroup of $G$ ? Is it always a normal subgroup? Is the image of $\phi$ always a subgroup of $H$ ? Is it always a normal subgroup? Justify your answers.

  Let $\mathrm{SL}(2, \mathbb{Z})$ denote the set of $2 \times 2$ matrices $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ with $a, b, c, d \in \mathbb{Z}$ and $a d-b c=1$. Show that $\mathrm{SL}(2, \mathbb{Z})$ is a group under matrix multiplication. Similarly, when $\mathbb{Z}_{2}$ denotes the integers modulo 2 , let $\mathrm{SL}\left(2, \mathbb{Z}_{2}\right)$ denote the set of $2 \times 2$ matrices $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ with $a, b, c, d \in \mathbb{Z}_{2}$ and $a d-b c=1$. Show that $\mathrm{SL}\left(2, \mathbb{Z}_{2}\right)$ is also a group under matrix multiplication.

  Let $f: \mathbb{Z} \rightarrow \mathbb{Z}_{2}$ send each integer to its residue modulo 2 . Show that

  $$\phi: \mathrm{SL}(2, \mathbb{Z}) \rightarrow \mathrm{SL}\left(2, \mathbb{Z}_{2}\right) ; \quad\left(\begin{array}{cc} a & b \\ c & d \end{array}\right) \mapsto\left(\begin{array}{ll} f(a) & f(b) \\ f(c) & f(d) \end{array}\right)$$

  is a group homomorphism. Show that the image of $\phi$ is isomorphic to a permutation group.

  comment

• Paper 3, Section II, D

  Groups | Part IA, 2009

  Define the cross-ratio $\left[a_{0}, a_{1}, a_{2}, z\right]$ of four points $a_{0}, a_{1}, a_{2}, z$ in $\mathbb{C} \cup\{\infty\}$, with $a_{0}, a_{1}, a_{2}$ distinct.

  Let $a_{0}, a_{1}, a_{2}$ be three distinct points. Show that, for every value $w \in \mathbb{C} \cup\{\infty\}$, there is a unique point $z \in \mathbb{C} \cup\{\infty\}$ with $\left[a_{0}, a_{1}, a_{2}, z\right]=w$. Let $S$ be the set of points $z$ for which the cross-ratio $\left[a_{0}, a_{1}, a_{2}, z\right]$ is in $\mathbb{R} \cup\{\infty\}$. Show that $S$ is either a circle or else a straight line together with $\infty$.

  A map $J: \mathbb{C} \cup\{\infty\} \rightarrow \mathbb{C} \cup\{\infty\}$ satisfies

  $$\left[a_{0}, a_{1}, a_{2}, J(z)\right]=\overline{\left[a_{0}, a_{1}, a_{2}, z\right]}$$

  for each value of $z$. Show that this gives a well-defined map $J$ with $J^{2}$ equal to the identity.

  When the three points $a_{0}, a_{1}, a_{2}$ all lie on the real line, show that $J$ must be the conjugation map $J: z \mapsto \bar{z}$. Deduce from this that, for any three distinct points $a_{0}, a_{1}, a_{2}$, the map $J$ depends only on the circle (or straight line) through $a_{0}, a_{1}, a_{2}$ and not on their particular values.

  comment

• Paper 3, Section II, D

  Groups | Part IA, 2009

  State and prove the orbit-stabilizer theorem.

  Let $G$ be the group of all symmetries of a regular octahedron, including both orientation-preserving and orientation-reversing symmetries. How many symmetries are there in the group $G$ ? Let $D$ be the set of straight lines that join a vertex of the octahedron to the opposite vertex. How many lines are there in the set $D$ ? Identify the stabilizer in $G$ of one of the lines in $D$.

  comment

Numbers and Sets

• Paper 4, Section I, $2 E$

  Numbers and Sets | Part IA, 2009

  (a) Find integers $x$ and $y$ such that

  $$9 x+12 y \equiv 4 \quad(\bmod 47) \quad \text { and } \quad 6 x+7 y \equiv 14 \quad(\bmod 47)$$

  (b) Calculate $43^{135}(\bmod 137)$.

  comment

• Paper 4, Section I, E

  Numbers and Sets | Part IA, 2009

  Let $R_{1}$ and $R_{2}$ be relations on a set $A$. Let us say that $R_{2}$ extends $R_{1}$ if $x R_{1} y$ implies that $x R_{2} y$. If $R_{2}$ extends $R_{1}$, then let us call $R_{2}$ an extension of $R_{1}$.

  Let $Q$ be a relation on a set $A$. Let $R$ be the extension of $Q$ defined by taking $x R y$ if and only if $x Q y$ or $x=y$. Let $S$ be the extension of $R$ defined by taking $x S y$ if and only if $x R y$ or $y R x$. Finally, let $T$ be the extension of $S$ defined by taking $x T y$ if and only if there is a positive integer $n$ and a sequence $\left(x_{0}, x_{1}, \ldots, x_{n}\right)$ such that $x_{0}=x, x_{n}=y$, and $x_{i-1} S x_{i}$ for each $i$ from 1 to $n$.

  Prove that $R$ is reflexive, $S$ is reflexive and symmetric, and $T$ is an equivalence relation.

  Let $E$ be any equivalence relation that extends $Q$. Prove that $E$ extends $T$.

  comment

• Paper 4, Section II, E

  Numbers and Sets | Part IA, 2009

  Prove that the set of all infinite sequences $\left(\epsilon_{1}, \epsilon_{2}, \ldots\right)$ with every $\epsilon_{i}$ equal to 0 or 1 is uncountable. Deduce that the closed interval $[0,1]$ is uncountable.

  For an ordered set $X$ let $\Sigma(X)$ denote the set of increasing (but not necessarily strictly increasing) sequences in $X$ that are bounded above. For each of $\Sigma(\mathbb{Z}), \Sigma(\mathbb{Q})$ and $\Sigma(\mathbb{R})$, determine (with proof) whether it is uncountable.

  comment

• Paper 4, Section II, E

  Numbers and Sets | Part IA, 2009

  Let $p$ be a prime number and let $\mathbb{Z}_{p}$ denote the set of integers modulo $p$. Let $k$ be an integer with $0 \leqslant k \leqslant p$ and let $A$ be a subset of $\mathbb{Z}_{p}$ of size $k$.

  Let $t$ be a non-zero element of $\mathbb{Z}_{p}$. Show that if $a+t \in A$ whenever $a \in A$ then $k=0$ or $k=p$. Deduce that if $1 \leqslant k \leqslant p-1$, then the sets $A, A+1, \ldots, A+p-1$ are all distinct, where $A+t$ denotes the set $\{a+t: a \in A\}$. Deduce from this that $\left(\begin{array}{l}p \\ k\end{array}\right)$ is a multiple of $p$ whenever $1 \leqslant k \leqslant p-1$.

  Now prove that $(a+1)^{p}=a^{p}+1$ for any $a \in \mathbb{Z}_{p}$, and use this to prove Fermat's little theorem. Prove further that if $Q(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0}$ is a polynomial in $x$ with coefficients in $\mathbb{Z}_{p}$, then the polynomial $(Q(x))^{p}$ is equal to $a_{n} x^{p n}+a_{n-1} x^{p(n-1)}+\ldots+a_{1} x^{p}+a_{0} .$

  comment

• Paper 4, Section II, E

  Numbers and Sets | Part IA, 2009

  (a) State and prove the inclusion-exclusion formula.

  (b) Let $k$ and $m$ be positive integers, let $n=k m$, let $A_{1}, \ldots, A_{k}$ be disjoint sets of size $m$, and let $A=A_{1} \cup \ldots \cup A_{k}$. Let $\mathcal{B}$ be the collection of all subsets $B \subset A$ with the following two properties:

  (i) $|B|=k$;

  (ii) there is at least one $i$ such that $\left|B \cap A_{i}\right|=3$.

  Prove that the number of sets in $\mathcal{B}$ is given by the formula

  $$\sum_{r=1}^{\lfloor k / 3\rfloor}(-1)^{r-1}\left(\begin{array}{c} k \\ r \end{array}\right)\left(\begin{array}{c} m \\ 3 \end{array}\right)^{r}\left(\begin{array}{c} n-r m \\ k-3 r \end{array}\right)$$

  comment

• Paper 4, Section II, E

  Numbers and Sets | Part IA, 2009

  (a) Let $A$ and $B$ be non-empty sets and let $f: A \rightarrow B$.

  Prove that $f$ is an injection if and only if $f$ has a left inverse.

  Prove that $f$ is a surjection if and only if $f$ has a right inverse.

  (b) Let $A, B$ and $C$ be sets and let $f: B \rightarrow A$ and $g: B \rightarrow C$ be functions. Suppose that $f$ is a surjection. Prove that there is a function $h: A \rightarrow C$ such that for every $a \in A$ there exists $b \in B$ with $f(b)=a$ and $g(b)=h(a)$.

  Prove that $h$ is unique if and only if $g(b)=g\left(b^{\prime}\right)$ whenever $f(b)=f\left(b^{\prime}\right)$.

  comment

Probability

• Paper 2, Section $I$, F

  Probability | Part IA, 2009

  Prove the law of total probability: if $A_{1}, \ldots, A_{n}$ are pairwise disjoint events with $\mathbb{P}\left(A_{i}\right)>0$, and $B \subseteq A_{1} \cup \ldots \cup A_{n}$ then $\mathbb{P}(B)=\sum_{i=1}^{n} \mathbb{P}\left(A_{i}\right) \mathbb{P}\left(B \mid A_{i}\right)$.

  There are $n$ people in a lecture room. Their birthdays are independent random variables, and each person's birthday is equally likely to be any of the 365 days of the year. By using the bound $1-x \leqslant e^{-x}$ for $0 \leqslant x \leqslant 1$, prove that if $n \geqslant 29$ then the probability that at least two people have the same birthday is at least $2 / 3$.

  [In calculations, you may take $\sqrt{1+8 \times 365 \ln 3}=56.6$.]

  comment

• Paper 2, Section I, F

  Probability | Part IA, 2009

  Consider a pair of jointly normal random variables $X_{1}, X_{2}$, with mean values $\mu_{1}$, $\mu_{2}$, variances $\sigma_{1}^{2}, \sigma_{2}^{2}$ and correlation coefficient $\rho$ with $|\rho|<1$.

  (a) Write down the joint probability density function for $\left(X_{1}, X_{2}\right)$.

  (b) Prove that $X_{1}, X_{2}$ are independent if and only if $\rho=0$.

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  Let $A_{1}, A_{2}$ and $A_{3}$ be three pairwise disjoint events such that the union $A_{1} \cup A_{2} \cup A_{3}$ is the full event and $\mathbb{P}\left(A_{1}\right), \mathbb{P}\left(A_{2}\right), \mathbb{P}\left(A_{3}\right)>0$. Let $E$ be any event with $\mathbb{P}(E)>0$. Prove the formula

  $$\mathbb{P}\left(A_{i} \mid E\right)=\frac{\mathbb{P}\left(A_{i}\right) \mathbb{P}\left(E \mid A_{i}\right)}{\sum_{j=1,2,3} \mathbb{P}\left(A_{j}\right) \mathbb{P}\left(E \mid A_{j}\right)}$$

  A Royal Navy speedboat has intercepted an abandoned cargo of packets of the deadly narcotic spitamin. This sophisticated chemical can be manufactured in only three places in the world: a plant in Authoristan (A), a factory in Bolimbia (B) and the ultramodern laboratory on board of a pirate submarine Crash (C) cruising ocean waters. The investigators wish to determine where this particular cargo comes from, but in the absence of prior knowledge they have to assume that each of the possibilities A, B and C is equally likely.

  It is known that a packet from A contains pure spitamin in $95 \%$ of cases and is contaminated in $5 \%$ of cases. For B the corresponding figures are $97 \%$ and $3 \%$, and for $\mathrm{C}$ they are $99 \%$ and $1 \%$.

  Analysis of the captured cargo showed that out of 10000 packets checked, 9800 contained the pure drug and the remaining 200 were contaminated. On the basis of this analysis, the Royal Navy captain estimated that $98 \%$ of the packets contain pure spitamin and reported his opinion that with probability roughly $0.5$ the cargo was produced in B and with probability roughly $0.5$ it was produced in C.

  Assume that the number of contaminated packets follows the binomial distribution $\operatorname{Bin}(10000, \delta / 100)$ where $\delta$ equals 5 for $A, 3$ for $B$ and 1 for C. Prove that the captain's opinion is wrong: there is an overwhelming chance that the cargo comes from B.

  [Hint: Let $E$ be the event that 200 out of 10000 packets are contaminated. Compare the ratios of the conditional probabilities $\mathbb{P}(E \mid A), \mathbb{P}(E \mid B)$ and $\mathbb{P}(E \mid C)$. You may find it helpful that $\ln 3 \approx 1.09861$ and $\ln 5 \approx 1.60944$. You may also take $\ln (1-\delta / 100) \approx-\delta / 100$.]

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  Let $X$ and $Y$ be two independent uniformly distributed random variables on $[0,1]$. Prove that $\mathbb{E} X^{k}=\frac{1}{k+1}$ and $\mathbb{E}(X Y)^{k}=\frac{1}{(k+1)^{2}}$, and find $\mathbb{E}(1-X Y)^{k}$, where $k$ is a non-negative integer.

  Let $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)$ be $n$ independent random points of the unit square $\mathcal{S}=\{(x, y): 0 \leqslant x, y \leqslant 1\}$. We say that $\left(X_{i}, Y_{i}\right)$ is a maximal external point if, for each $j=1, \ldots, n$, either $X_{j} \leqslant X_{i}$ or $Y_{j} \leqslant Y_{i}$. (For example, in the figure below there are three maximal external points.) Determine the expected number of maximal external points.

  

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  No-one in their right mind would wish to be a guest at the Virtual Reality Hotel. See the diagram below showing a part of the floor plan of the hotel where rooms are represented by black or white circles. The hotel is built in a shape of a tree: there is one room (reception) situated at level 0, three rooms at level 1 , nine at level 2 , and so on. The rooms are joined by corridors to their neighbours: each room has four neighbours, apart from the reception, which has three neighbours. Each corridor is blocked with probability $1 / 3$ and open for passage in both directions with probability $2 / 3$, independently for different corridors. Every room at level $N$, where $N$ is a given very large number, has an open window through which a guest can (and should) escape into the street. An arriving guest is placed in the reception and then wanders freely, insofar as the blocked corridors allow.

  

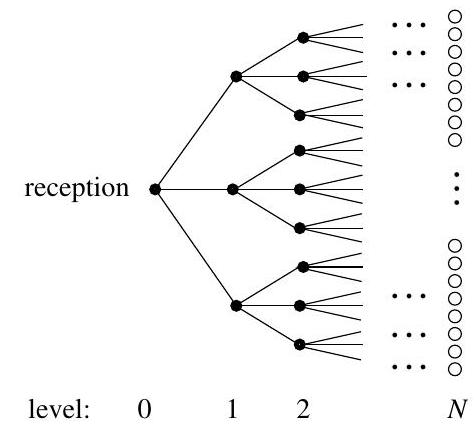
  (a) Prove that the probability that the guest will not escape is close to a solution of the equation $\phi(t)=t$, where $\phi(t)$ is a probability-generating function that you should specify.

  (b) Hence show that the guest's chance of escape is approximately $(9-3 \sqrt{3}) / 4$.

  comment

• Paper 2, Section II, F

  Probability | Part IA, 2009

  I throw two dice and record the scores $S_{1}$ and $S_{2}$. Let $X$ be the sum $S_{1}+S_{2}$ and $Y$ the difference $S_{1}-S_{2}$.

  (a) Suppose that the dice are fair, so the values $1, \ldots, 6$ are equally likely. Calculate the mean and variance of both $X$ and $Y$. Find all the values of $x$ and $y$ at which the probabilities $\mathbb{P}(X=x), \mathbb{P}(Y=y)$ are each either greatest or least. Determine whether the random variables $X$ and $Y$ are independent.

  (b) Now suppose that the dice are unfair, and that they give the values $1, \ldots, 6$ with probabilities $p_{1}, \ldots, p_{6}$ and $q_{1}, \ldots, q_{6}$, respectively. Write down the values of $\mathbb{P}(X=$ 2), $\mathbb{P}(X=7)$ and $\mathbb{P}(X=12)$. By comparing $\mathbb{P}(X=7)$ with $\sqrt{\mathbb{P}(X=2) \mathbb{P}(X=12)}$ and applying the arithmetic-mean-geometric-mean inequality, or otherwise, show that the probabilities $\mathbb{P}(X=2), \mathbb{P}(X=3), \ldots, \mathbb{P}(X=12)$ cannot all be equal.

  comment

Vector Calculus

• Paper 3, Section $I$, B

  Vector Calculus | Part IA, 2009

  State the value of $\partial x_{i} / \partial x_{j}$ and find $\partial r / \partial x_{j}$, where $r=|\mathbf{x}|$.

  A vector field $\mathbf{u}$ is given by

  $$\mathbf{u}=\frac{\mathbf{k}}{r}+\frac{(\mathbf{k} \cdot \mathbf{x}) \mathbf{x}}{r^{3}}$$

  where $\mathbf{k}$ is a constant vector. Calculate the second-rank tensor $d_{i j}=\partial u_{i} / \partial x_{j}$ using suffix notation, and show that $d_{i j}$ splits naturally into symmetric and antisymmetric parts. Deduce that $\boldsymbol{\nabla} \cdot \mathbf{u}=0$ and that

  $$\boldsymbol{\nabla} \times \mathbf{u}=\frac{2 \mathbf{k} \times \mathbf{x}}{r^{3}}$$

  comment

• Paper 3, Section I, B

  Vector Calculus | Part IA, 2009

  What does it mean for a vector field $\mathbf{F}$ to be irrotational ?

  The field $\mathbf{F}$ is irrotational and $\mathbf{x}_{0}$ is a given point. Write down a scalar potential $V(\mathbf{x})$ with $\mathbf{F}=-\nabla V$ and $V\left(\mathbf{x}_{0}\right)=0$. Show that this potential is well defined.

  For what value of $m$ is the field $\frac{\cos \theta \cos \phi}{r} \mathbf{e}_{\theta}+\frac{m \sin \phi}{r} \mathbf{e}_{\phi}$ irrotational, where $(r, \theta, \phi)$ are spherical polar coordinates? What is the corresponding potential $V(\mathbf{x})$ when $\mathbf{x}_{0}$ is the point $r=1, \theta=0$ ?

  $$\left[\text { In spherical polar coordinates } \nabla \times \mathbf{F}=\frac{1}{r^{2} \sin \theta} \mid \begin{array}{ccc} \mathbf{e}_{r} & r \mathbf{e}_{\theta} & r \sin \theta \mathbf{e}_{\phi} \\ \partial / \partial r & \partial / \partial \theta & \partial / \partial \phi \\ F_{r} & r F_{\theta} & r \sin \theta F_{\phi} \end{array}\right] .$$

  comment

• Paper 3, Section II, B

  Vector Calculus | Part IA, 2009

  State the divergence theorem for a vector field $\mathbf{u}(\mathbf{x})$ in a region $V$ of $\mathbb{R}^{3}$ bounded by a smooth surface $S$.

  Let $f(x, y, z)$ be a homogeneous function of degree $n$, that is, $f(k x, k y, k z)=$ $k^{n} f(x, y, z)$ for any real number $k$. By differentiating with respect to $k$, show that

  $$\mathbf{x} \cdot \nabla f=n f$$

  Deduce that

  $$\tag{†} \int_{V} f \mathrm{~d} V=\frac{1}{n+3} \int_{S} f \mathbf{x} \cdot \mathbf{d} \mathbf{A}$$

  Let $V$ be the cone $0 \leqslant z \leqslant \alpha, \alpha \sqrt{x^{2}+y^{2}} \leqslant z$, where $\alpha$ is a positive constant. Verify that $(†)$ holds for the case $f=z^{4}+\alpha^{4}\left(x^{2}+y^{2}\right)^{2}$.

  comment

• Paper 3, Section II, B

  Vector Calculus | Part IA, 2009

  A second-rank tensor $T(\mathbf{y})$ is defined by

  $$T_{i j}(\mathbf{y})=\int_{S}\left(y_{i}-x_{i}\right)\left(y_{j}-x_{j}\right)|\mathbf{y}-\mathbf{x}|^{2 n-2} \mathrm{~d} A(\mathbf{x})$$

  where $\mathbf{y}$ is a fixed vector with $|\mathbf{y}|=a, n>-1$, and the integration is over all points $\mathbf{x}$ lying on the surface $S$ of the sphere of radius $a$, centred on the origin. Explain briefly why $T$ might be expected to have the form

  $$T_{i j}=\alpha \delta_{i j}+\beta y_{i} y_{j}$$

  where $\alpha$ and $\beta$ are scalar constants.

  Show that $\mathbf{y} \cdot(\mathbf{y}-\mathbf{x})=a^{2}(1-\cos \theta)$, where $\theta$ is the angle between $\mathbf{y}$ and $\mathbf{x}$, and find a similar expression for $|\mathbf{y}-\mathbf{x}|^{2}$. Using suitably chosen spherical polar coordinates, show that

  $$y_{i} T_{i j} y_{j}=\frac{\pi a^{2}(2 a)^{2 n+2}}{n+2}$$

  Hence, by evaluating another scalar integral, determine $\alpha$ and $\beta$, and find the value of $n$ for which $T$ is isotropic.

  comment

• Paper 3, Section II, B

  Vector Calculus | Part IA, 2009

  Give a necessary condition for a given vector field $\mathbf{J}$ to be the curl of another vector field $\mathbf{B}$. Is the vector field $\mathbf{B}$ unique? If not, explain why not.

  State Stokes' theorem and use it to evaluate the area integral

  $$\int_{S}\left(y^{2}, z^{2}, x^{2}\right) \cdot \mathbf{d} \mathbf{A}$$

  where $S$ is the half of the ellipsoid

  $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1$$

  that lies in $z \geqslant 0$, and the area element dA points out of the ellipsoid.

  comment

• Paper 3, Section II, B

  Vector Calculus | Part IA, 2009

  Let $S$ be a bounded region of $\mathbb{R}^{2}$ and $\partial S$ be its boundary. Let $u$ be the unique solution to Laplace's equation in $S$, subject to the boundary condition $u=f$ on $\partial S$, where $f$ is a specified function. Let $w$ be any smooth function with $w=f$ on $\partial S$. By writing $w=u+\delta$, or otherwise, show that

  $$\int_{S}|\nabla w|^{2} \mathrm{~d} A \geqslant \int_{S}|\nabla u|^{2} \mathrm{~d} A$$

  Let $S$ be the unit disc in $\mathbb{R}^{2}$. By considering functions of the form $g(r) \cos \theta$ on both sides of $(*)$, where $r$ and $\theta$ are polar coordinates, deduce that

  $$\int_{0}^{1}\left(r\left(\frac{\mathrm{d} g}{\mathrm{~d} r}\right)^{2}+\frac{g^{2}}{r}\right) \mathrm{d} r \geqslant 1$$

  for any differentiable function $g(r)$ satisfying $g(1)=1$ and for which the integral converges at $r=0$.

  $$\left[\nabla f(r, \theta)=\left(\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial \theta}\right), \quad \nabla^{2} f(r, \theta)=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial f}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} f}{\partial \theta^{2}} \cdot\right]$$

  comment

Vectors and Matrices

• Paper 1, Section I, $2 \mathrm{~B}$

  Vectors and Matrices | Part IA, 2009

  Define the Hermitian conjugate $A^{\dagger}$ of an $n \times n$ complex matrix $A$. State the conditions (i) for $A$ to be Hermitian (ii) for $A$ to be unitary.

  In the following, $A, B, C$ and $D$ are $n \times n$ complex matrices and $\mathbf{x}$ is a complex $n$-vector. A matrix $N$ is defined to be normal if $N^{\dagger} N=N N^{\dagger}$.

  (a) Let $A$ be nonsingular. Show that $B=A^{-1} A^{\dagger}$ is unitary if and only if $A$ is normal.

  (b) Let $C$ be normal. Show that $|C \mathbf{x}|=0$ if and only if $\left|C^{\dagger} \mathbf{x}\right|=0$.

  (c) Let $D$ be normal. Deduce from (b) that if $e$ is an eigenvector of $D$ with eigenvalue $\lambda$ then $e$ is also an eigenvector of $D^{\dagger}$ and find the corresponding eigenvalue.

  comment

• Paper 1, Section I, C

  Vectors and Matrices | Part IA, 2009

  Describe geometrically the three sets of points defined by the following equations in the complex $z$ plane:

  (a) $z \bar{\alpha}+\bar{z} \alpha=0$, where $\alpha$ is non-zero;

  (b) $2|z-a|=z+\bar{z}+2 a$, where $a$ is real and non-zero;

  (c) $\log z=\mathrm{i} \log \bar{z}$.

  comment

• Paper 1, Section II, $5 \mathrm{C}$

  Vectors and Matrices | Part IA, 2009

  Let $\mathbf{a}, \mathbf{b}, \mathbf{c}$ be unit vectors. By using suffix notation, prove that

  $$(\mathbf{a} \times \mathbf{b}) \cdot(\mathbf{a} \times \mathbf{c})=\mathbf{b} \cdot \mathbf{c}-(\mathbf{a} \cdot \mathbf{b})(\mathbf{a} \cdot \mathbf{c})$$

  and

  $$(\mathbf{a} \times \mathbf{b}) \times(\mathbf{a} \times \mathbf{c})=[\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})] \mathbf{a}$$

  The three distinct points $A, B, C$ with position vectors $\mathbf{a}, \mathbf{b}, \mathbf{c}$ lie on the surface of the unit sphere centred on the origin $O$. The spherical distance between the points $A$ and $B$, denoted $\delta(A, B)$, is the length of the (shorter) arc of the circle with centre $O$ passing through $A$ and $B$. Show that

  $$\cos \delta(A, B)=\mathbf{a} \cdot \mathbf{b}$$

  A spherical triangle with vertices $A, B, C$ is a region on the sphere bounded by the three circular arcs $A B, B C, C A$. The interior angles of a spherical triangle at the vertices $A, B, C$ are denoted $\alpha, \beta, \gamma$, respectively.

  By considering the normals to the planes $O A B$ and $O A C$, or otherwise, show that

  $$\cos \alpha=\frac{(\mathbf{a} \times \mathbf{b}) \cdot(\mathbf{a} \times \mathbf{c})}{|\mathbf{a} \times \mathbf{b} \| \mathbf{a} \times \mathbf{c}|}$$

  Using identities (1) and (2), prove that

  $$\cos \delta(B, C)=\cos \delta(A, B) \cos \delta(A, C)+\sin \delta(A, B) \sin \delta(A, C) \cos \alpha$$

  and

  $$\frac{\sin \alpha}{\sin \delta(B, C)}=\frac{\sin \beta}{\sin \delta(A, C)}=\frac{\sin \gamma}{\sin \delta(A, B)}$$

  For an equilateral spherical triangle show that $\alpha>\pi / 3$.

  comment

• Paper 1, Section II, $7 \mathrm{~A}$

  Vectors and Matrices | Part IA, 2009

  Let $A$ be an $n \times n$ Hermitian matrix. Show that all the eigenvalues of $A$ are real.

  Suppose now that $A$ has $n$ distinct eigenvalues.

  (a) Show that the eigenvectors of $A$ are orthogonal.

  (b) Define the characteristic polynomial $P_{A}(t)$ of $A$. Let

  $$P_{A}(t)=\sum_{r=0}^{n} a_{r} t^{r}$$

  Prove the matrix identity

  $$\sum_{r=0}^{n} a_{r} A^{r}=0$$

  (c) What is the range of possible values of

  $$\frac{\mathbf{x}^{\dagger} A \mathbf{x}}{\mathbf{x}^{\dagger} \mathbf{x}}$$

  for non-zero vectors $\mathbf{x} \in \mathbb{C}^{n} ?$ Justify your answer.

  (d) For any (not necessarily symmetric) real $2 \times 2$ matrix $B$ with real eigenvalues, let $\lambda_{\max }(B)$ denote its maximum eigenvalue. Is it possible to find a constant $C$ such that

  $$\frac{\mathbf{x}^{\dagger} B \mathbf{x}}{\mathbf{x}^{\dagger} \mathbf{x}} \leqslant C \lambda_{\max }(B)$$

  for all non-zero vectors $\mathbf{x} \in \mathbb{R}^{2}$ and all such matrices $B$ ? Justify your answer.

  comment

• Paper 1, Section II, A

  Vectors and Matrices | Part IA, 2009

  (a) Explain what is meant by saying that a $2 \times 2$ real transformation matrix

  $$\begin{aligned} &A=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \text { preserves the scalar product with respect to the Euclidean metric } \\ &I=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right) \text { on } \mathbb{R}^{2} . \end{aligned}$$

  Derive a description of all such matrices that uses a single real parameter together with choices of $\operatorname{sign}(\pm 1)$. Show that these matrices form a group.

  (b) Explain what is meant by saying that a $2 \times 2$ real transformation matrix $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ preserves the scalar product with respect to the Minkowski metric $J=\left(\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right)$ on $\mathbb{R}^{2}$

  Consider now the set of such matrices with $a>0$. Derive a description of all matrices in this set that uses a single real parameter together with choices of sign $(\pm 1)$. Show that these matrices form a group.

  (c) What is the intersection of these two groups?

  comment

• Paper 1, Section II, B

  Vectors and Matrices | Part IA, 2009

  Explain why the number of solutions $\mathbf{x} \in \mathbb{R}^{3}$ of the matrix equation $A \mathbf{x}=\mathbf{c}$ is 0,1 or infinity, where $A$ is a real $3 \times 3$ matrix and $\mathbf{c} \in \mathbb{R}^{3}$. State conditions on $A$ and $\mathbf{c}$ that distinguish between these possibilities, and state the relationship that holds between any two solutions when there are infinitely many.

  Consider the case

  $$A=\left(\begin{array}{lll} a & a & b \\ b & a & a \\ a & b & a \end{array}\right) \quad \text { and } \mathbf{c}=\left(\begin{array}{l} 1 \\ c \\ 1 \end{array}\right)$$

  Use row and column operations to find and factorize the determinant of $A$.

  Find the kernel and image of the linear map represented by $A$ for all values of $a$ and $b$. Find the general solution to $A \mathbf{x}=\mathbf{c}$ for all values of $a, b$ and $c$ for which a solution exists.

  comment