Paper 2, Section II, F
No-one in their right mind would wish to be a guest at the Virtual Reality Hotel. See the diagram below showing a part of the floor plan of the hotel where rooms are represented by black or white circles. The hotel is built in a shape of a tree: there is one room (reception) situated at level 0, three rooms at level 1 , nine at level 2 , and so on. The rooms are joined by corridors to their neighbours: each room has four neighbours, apart from the reception, which has three neighbours. Each corridor is blocked with probability and open for passage in both directions with probability , independently for different corridors. Every room at level , where is a given very large number, has an open window through which a guest can (and should) escape into the street. An arriving guest is placed in the reception and then wanders freely, insofar as the blocked corridors allow.
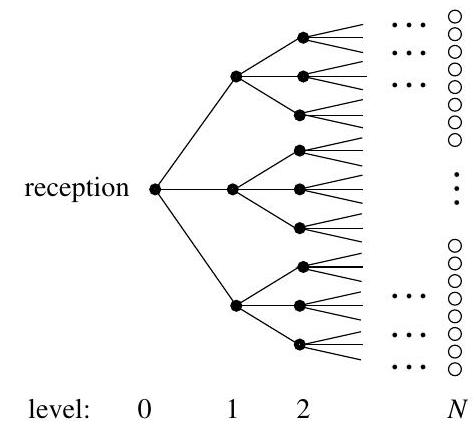
(a) Prove that the probability that the guest will not escape is close to a solution of the equation , where is a probability-generating function that you should specify.
(b) Hence show that the guest's chance of escape is approximately .