Dynamics
Dynamics
Jump to year
4.I.3B
Two particles of masses and have position vectors and at time . The particle of mass experiences a force and the particle of mass experiences a force . Show that the centre of mass moves at a constant velocity, and derive an equation of motion for the relative separation .
Now suppose that , where is a positive constant. The particles are initially at rest a distance apart. Calculate how long it takes before they collide.
4.I.4B
A damped pendulum is described by the equation
where and are real positive constants. Determine the location of all the equilibrium points of the system. Classify the equilibrium points in the two cases and .
4.II.10B
A body of mass moves in the gravitational field of a much larger spherical object of mass located at the origin. Starting from the equations of motion
show that:
(i) the body moves in an orbit of the form
where is the constant angular momentum per unit mass, and and are constants;
(ii) the total energy of the body is
A meteorite is moving very far from the Earth with speed , and in the absence of the effect of the Earth's gravitational field would miss the Earth by a shortest distance (measured from the Earth's centre). Show that in the subsequent motion
and
Use equation to find the distance of closest approach, and show that the meteorite will collide with the Earth if
where is the radius of the Earth.
4.II.11B
An inertial reference frame and another reference frame have a common origin , and rotates with angular velocity with respect to . Show the following:
(i) the rates of change of an arbitrary vector a in frames and are related by
(ii) the accelerations in and are related by
where is the position vector relative to .
A train of mass at latitude in the Northern hemisphere travels North with constant speed along a track which runs North-South. Find the magnitude and direction of the sideways force exerted on the train by the track.
4.II.12B
A uniform solid sphere has mass and radius . Calculate the moment of inertia of the sphere about an axis through its centre.
A long hollow circular cylinder of radius (where ) is held fixed with its axis horizontal. The sphere is held initially at rest in contact with the inner surface of the cylinder at , where and is the angle between the line joining the centre of the sphere to the cylinder axis and the downward vertical, as shown in the figure.
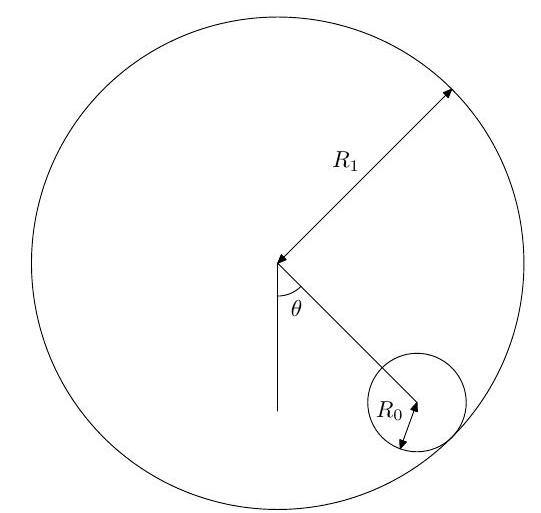
The sphere is then released, and rolls without slipping. Show that the angular velocity of the sphere is
Show further that the time, , it takes the sphere to reach is
If, instead, the cylinder and sphere surfaces are highly polished, so that the sphere now slides without rolling, find the time, , it takes to reach .
Without further calculation, explain qualitatively how your answers for and would be affected if the solid sphere were replaced by a hollow spherical shell of the same radius and mass.
4.II.9B
An octopus of mass swims horizontally in a straight line by jet propulsion. At time the octopus is at rest, and its internal cavity contains a mass of water (so that the mass of the octopus plus water is ). It then starts to move by ejecting the water backwards at a constant rate units of mass per unit time and at a constant speed relative to itself. The speed of the octopus at time is , and the mass of the octopus plus remaining water is . The drag force exerted by the surrounding water on the octopus is , where is a positive constant.
Show that, during ejection of water, the equation of motion is
Once all the water has been ejected, at time , the octopus has attained a velocity . Use dimensional analysis to show that
where and are two dimensionless quantities and is an unknown function. Solve equation (1) to find an explicit expression for , and verify that your answer is of the form given in equation (2).
Paper 4, Section I, C
Sketch the graph of .
A particle of unit mass moves along the axis in the potential . Sketch the phase plane, and describe briefly the motion of the particle on the different trajectories.
Paper 4, Section I, C
A rocket, moving vertically upwards, ejects gas vertically downwards at speed relative to the rocket. Derive, giving careful explanations, the equation of motion
where and are the speed and total mass of the rocket (including fuel) at time .
If is constant and the rocket starts from rest with total mass , show that
Paper 4, Section II,
The th particle of a system of particles has mass and, at time , position vector with respect to an origin . It experiences an external force , and also an internal force due to the th particle (for each ), where is parallel to and Newton's third law applies.
(i) Show that the position of the centre of mass, , satisfies
where is the total mass of the system and is the sum of the external forces.
(ii) Show that the total angular momentum of the system about the origin, , satisfies
where is the total moment about the origin of the external forces.
(iii) Show that can be expressed in the form
where is the velocity of the centre of mass, is the position vector of the th particle relative to the centre of mass, and is the velocity of the th particle relative to the centre of mass.
(iv) In the case when the internal forces are derived from a potential , where , and there are no external forces, show that
where is the total kinetic energy of the system.
Paper 4, Section II, C
A particle moves in the gravitational field of the Sun. The angular momentum per unit mass of the particle is and the mass of the Sun is . Assuming that the particle moves in a plane, write down the equations of motion in polar coordinates, and derive the equation
where and .
Write down the equation of the orbit ( as a function of ), given that the particle moves with the escape velocity and is at the perihelion of its orbit, a distance from the Sun, when . Show that
and hence that the particle reaches a distance from the Sun at time .
Paper 4, Section II, C
A particle of mass experiences, at the point with position vector , a force given by
where and are positive constants and is a constant, uniform, vector field.
(i) Show that is constant. Give a physical interpretation of each term and a physical explanation of the fact that does not arise in this expression.
(ii) Show that is constant.
(iii) Given that the particle was initially at rest at , derive an expression for at time .
Paper 4, Section II, C
A small ring of mass is threaded on a smooth rigid wire in the shape of a parabola given by , where measures horizontal distance and measures distance vertically upwards. The ring is held at height , then released.
(i) Show by dimensional analysis that the period of oscillations, , can be written in the form
for some function .
(ii) Show that is given by
and find, to first order in , the period of small oscillations.
4.I.3C
A car is at rest on a horizontal surface. The engine is switched on and suddenly sets the wheels spinning at a constant angular velocity . The wheels have radius and the coefficient of friction between the ground and the surface of the wheels is . Calculate the time when the wheels start rolling without slipping. If the car is started on an upward slope in a similar manner, explain whether is increased or decreased relative to the case where the car starts on a horizontal surface.
4.I.4C
For the dynamical system
find the stable and unstable fixed points and the equation determining the separatrix. Sketch the phase diagram. If the system starts on the separatrix at , write down an integral determining the time taken for the velocity to reach zero. Show that the integral is infinite.
4.II.10C
A particle of mass bounces back and forth between two walls of mass moving towards each other in one dimension. The walls are separated by a distance . The wall on the left has velocity and the wall on the right has velocity . The particle has speed . Friction is negligible and the particle-wall collisions are elastic.
Consider a collision between the particle and the wall on the right. Show that the centre-of-mass velocity of the particle-wall system is . Calculate the particle's speed following the collision.
Assume that the particle is much lighter than the walls, i.e., . Show that the particle's speed increases by approximately every time it collides with a wall.
Assume also that (so that particle-wall collisions are frequent) and that the velocities of the two walls remain nearly equal and opposite. Show that in a time interval , over which the change in is negligible, the wall separation changes by . Show that the number of particle-wall collisions during is approximately and that the particle's speed increases by during this time interval.
Hence show that under the given conditions the particle speed is approximately proportional to .
4.II.11C
Two light, rigid rods of length have a mass attached to each end. Both are free to move in two dimensions. The two rods are placed so that their two ends are located at , and respectively, where is positive. They are set in motion with no rotation, with centre-of-mass velocities and , so that the lower mass on the first rod collides head on with the upper mass on the second rod at the origin . [You may assume that the impulse is directed along the -axis.]
Assuming the collision is elastic, calculate the centre of-mass velocity and the angular velocity of each rod immediately after the collision.
Assuming a coefficient of restitution , compute and for each rod after the collision.
4.II.12C
A particle of mass and charge moves in a time-dependent magnetic field .
Write down the equations of motion governing the particle's and coordinates.
Show that the speed of the particle in the plane, , is a constant.
Show that the general solution of the equations of motion is
and interpret each of the six constants of integration, and . [Hint: Solve the equations for the particle's velocity in cylindrical polars.]
Let , where is a positive constant. Assuming that and , calculate the position of the particle in the limit (you may assume this limit exists). [Hint: You may use the results
4.II.9C
A motorcycle of mass moves on a bowl-shaped surface specified by its height where is the radius in cylindrical polar coordinates . The torque exerted by the motorcycle engine on the rear wheel results in a force pushing the motorcycle forward. Assuming is directed along the motorcycle's velocity and that the motorcycle's vertical velocity and acceleration are small, show that the motion is described by
where dots denote time derivatives, and is the acceleration due to gravity.
The motorcycle rider can adjust to produce the desired trajectory. If the rider wants to move on a curve , show that must obey
Now assume that , with a constant, and with a positive constant, and so that the desired trajectory is a spiral curve. Assuming that tends to infinity as tends to infinity, show that tends to and tends to as tends to infinity.
4.I.3C
Planetary Explorers Ltd. want to put a communications satellite of mass into geostationary orbit around the spherical planet Zog (i.e. with the satellite always above the same point on the surface of Zog). The mass of Zog is , the length of its day is and is the gravitational constant.
Write down the equations of motion for a general orbit of the satellite and determine the radius and speed of the geostationary orbit.
Describe briefly how the orbit is modified if the satellite is released at the correct radius and on the correct trajectory for a geostationary orbit, but with a little too much speed. Comment on how the satellite's speed varies around such an orbit.
4.I.4C
A car of mass travelling at speed on a smooth, horizontal road attempts an emergency stop. The car skids in a straight line with none of its wheels able to rotate.
Calculate the stopping distance and time on a dry road where the dry friction coefficient between the tyres and the road is .
At high speed on a wet road the grip of each of the four tyres changes from dry friction to a lubricated drag equal to for each tyre, where is the drag coefficient and the instantaneous speed of the car. However, the tyres regain their dry-weather grip when the speed falls below . Calculate the stopping distance and time under these conditions.
4.II.10C
A keen cyclist wishes to analyse her performance on training rollers. She decides that the key components are her bicycle's rear wheel and the roller on which the wheel sits. The wheel, of radius , has its mass entirely at its outer edge. The roller, which is driven by the wheel without any slippage, is a solid cylinder of radius and mass . The angular velocities of the wheel and roller are and , respectively.
Determine and , the moments of inertia of the wheel and roller, respectively. Find the ratio of the angular velocities of the wheel and roller. Show that the combined total kinetic energy of the wheel and roller is , where
is the effective combined moment of inertia of the wheel and roller.
Why should be used instead of just or in the equation connecting torque with angular acceleration? The cyclist believes the torque she can produce at the back wheel is where and are dimensional constants. Determine the angular velocity of the wheel, starting from rest, as a function of time.
In an attempt to make the ride more realistic, the cyclist adds a fan (of negligible mass) to the roller. The fan imposes a frictional torque on the roller, where is a dimensional constant. Determine the new maximum speed for the wheel.
4.II.11C
A puck of mass located at slides without friction under the influence of gravity on a surface of height . Show that the equations of motion can be approximated by
where is the gravitational acceleration and the small slope approximation is used.
Determine the motion of the puck when .
Sketch the surface
as a function of , where . Write down the equations of motion of the puck on this surface in polar coordinates under the assumption that the small slope approximation can be used. Show that , the angular momentum per unit mass about the origin, is conserved. Show also that the initial kinetic energy per unit mass of the puck is if the puck is released at radius with negligible radial velocity. Determine and sketch as a function of for this release condition. What condition relating and must be satisfied for the orbit to be bounded?
4.II.12C
In an experiment a ball of mass is released from a height above a flat, horizontal plate. Assuming the gravitational acceleration is constant and the ball falls through a vacuum, find the speed of the ball on impact.
Determine the speed at which the ball rebounds if the coefficient of restitution for the collision is . What fraction of the impact energy is dissipated during the collision? Determine also the maximum height the ball reaches after the bounce, and the time between the and bounce. What is the total distance travelled by the ball before it comes to rest if ?
If the experiment is repeated in an atmosphere then the ball experiences a drag force , where is a dimensional constant and the instantaneous velocity of the ball. Write down and solve the modified equation for before the ball first hits the plate.
4.II.9C
A particle of mass and charge moving in a vacuum through a magnetic field and subject to no other forces obeys
where is the location of the particle.
For with constant , and using cylindrical polar coordinates , or otherwise, determine the motion of the particle in the plane if its initial speed is with . [Hint: Choose the origin so that and at .]
Due to a leak, a small amount of gas enters the system, causing the particle to experience a drag force , where . Write down the new governing equations and show that the speed of the particle decays exponentially. Sketch the path followed by the particle. [Hint: Consider the equations for the velocity in Cartesian coordinates; you need not apply any initial conditions.]
4.I.3A
A lecturer driving his car of mass along the flat at speed accidentally collides with a stationary vehicle of mass . As both vehicles are old and very solidly built, neither suffers damage in the collision: they simply bounce elastically off each other in a straight line. Determine how both vehicles are moving after the collision if neither driver applied their brakes. State any assumptions made and consider all possible values of the mass ratio . You may neglect friction and other such losses.
An undergraduate drives into a rigid rock wall at speed . The undergraduate's car of mass is modern and has a crumple zone of length at its front. As this zone crumples upon impact, it exerts a net force on the car, where is the amount the zone has crumpled. Determine the value of at the point the car stops moving forwards as a function of , where .
4.I.4A
A small spherical bubble of radius a containing carbon dioxide rises in water due to a buoyancy force , where is the density of water, is gravitational attraction and is the volume of the bubble. The drag on a bubble moving at speed is , where is the dynamic viscosity of water, and an accelerating bubble acts like a particle of mass , for some constant . Find the location at time of a bubble released from rest at and show the bubble approaches a steady rise speed
Under some circumstances the carbon dioxide gradually dissolves in the water, which leads to the bubble radius varying as , where is the bubble radius at and is a constant. Under the assumption that the bubble rises at speed given by , determine the height to which it rises before it disappears.
4.II.10A
A small probe of mass is in low orbit about a planet of mass . If there is no drag on the probe then its orbit is governed by
where is the location of the probe relative to the centre of the planet and is the gravitational constant. Show that the basic orbital trajectory is elliptical. Determine the orbital period for the probe if it is in a circular orbit at a distance from the centre of the planet.
Data returned by the probe shows that the planet has a very extensive but diffuse atmosphere. This atmosphere induces a drag on the probe that may be approximated by the linear law , where is the drag force and is a constant. Show that the angular momentum of the probe about the planet decays exponentially.
4.II.11A
A particle of mass and charge moves through a magnetic field . There is no electric field or external force so that the particle obeys
where is the location of the particle. Prove that the kinetic energy of the particle is preserved.
Consider an axisymmetric magnetic field described by in cylindrical polar coordinates . Determine the angular velocity of a circular orbit centred on .
For a general orbit when , show that the angular momentum about the -axis varies as , where is the angular momentum at radius . Determine and sketch the relationship between and . [Hint: Use conservation of energy.] What is the escape velocity for the particle?
4.II.12A
A circular cylinder of radius , length and mass is rolling along a surface. Show that its moment of inertia is given by .
At the cylinder is at the bottom of a slope making an angle to the horizontal, and is rolling with velocity and angular velocity . Assuming slippage does not occur, determine the position of the cylinder as a function of time. What is the maximum height that the cylinder reaches?
The frictional force between the cylinder and surface is given by , where is the friction coefficient. Show that the cylinder begins to slip rather than roll if . Determine as a function of time the location, speed and angular velocity of the cylinder on the slope if this condition is satisfied. Show that slipping continues as the cylinder ascends and descends the slope. Find also the maximum height the cylinder reaches, and its speed and angular velocity when it returns to the bottom of the slope.
4.II.9A
A horizontal table oscillates with a displacement , where is the amplitude vector and the angular frequency in an inertial frame of reference with the axis vertically upwards, normal to the table. A block sitting on the table has mass and linear friction that results in a force , where is a constant and is the velocity difference between the block and the table. Derive the equations of motion for this block in the frame of reference of the table using axes on the table parallel to the axes in the inertial frame.
For the case where , show that at late time the block will approach the steady orbit
where
and is a constant.
Given that there are no attractive forces between block and table, show that the block will only remain in contact with the table if .
4.I.3E
Because of an accident on launching, a rocket of unladen mass lies horizontally on the ground. It initially contains fuel of mass , which ignites and is emitted horizontally at a constant rate and at uniform speed relative to the rocket. The rocket is initially at rest. If the coefficient of friction between the rocket and the ground is , and the fuel is completely burnt in a total time , show that the final speed of the rocket is
4.I.4E
Write down an expression for the total momentum and angular momentum with respect to an origin of a system of point particles of masses , position vectors (with respect to , and velocities .
Show that with respect to a new origin the total momentum and total angular momentum are given by
and hence
where is the constant vector displacement of with respect to . How does change under change of origin?
Hence show that either
(1) the total momentum vanishes and the total angular momentum is independent of origin, or
(2) by choosing in a way that should be specified, the total angular momentum with respect to can be made parallel to the total momentum.
4.II.10E
Write down the equations of motion for a system of gravitating particles with masses , and position vectors .
The particles undergo a motion for which , where the vectors are independent of time . Show that the equations of motion will be satisfied as long as the function satisfies
where is a constant and the vectors satisfy
Show that has as first integral
where is another constant. Show that
where is the gradient operator with respect to and
Using Euler's theorem for homogeneous functions (see below), or otherwise, deduce that
Hence show that all solutions of satisfy
where
Deduce that must be positive and that the total kinetic energy plus potential energy of the system of particles is equal to .
[Euler's theorem states that if
then
4.II.11E
State the parallel axis theorem and use it to calculate the moment of inertia of a uniform hemisphere of mass and radius about an axis through its centre of mass and parallel to the base.
[You may assume that the centre of mass is located at a distance a from the flat face of the hemisphere, and that the moment of inertia of a full sphere about its centre is , with .]
The hemisphere initially rests on a rough horizontal plane with its base vertical. It is then released from rest and subsequently rolls on the plane without slipping. Let be the angle that the base makes with the horizontal at time . Express the instantaneous speed of the centre of mass in terms of and the rate of change of , where is the instantaneous distance from the centre of mass to the point of contact with the plane. Hence write down expressions for the kinetic energy and potential energy of the hemisphere and deduce that
4.II.12E
Let be plane polar coordinates and and unit vectors in the direction of increasing and respectively. Show that the velocity of a particle moving in the plane with polar coordinates is given by
and that the unit normal to the particle path is parallel to
Deduce that the perpendicular distance from the origin to the tangent of the curve is given by
The particle, whose mass is , moves under the influence of a central force with potential . Use the conservation of energy and angular momentum to obtain the equation
Hence express as a function of as the integral
where
Evaluate the integral and describe the orbit when , with a positive constant.
4.II.9E
Write down the equation of motion for a point particle with mass , charge , and position vector moving in a time-dependent magnetic field with vanishing electric field, and show that the kinetic energy of the particle is constant. If the magnetic field is constant in direction, show that the component of velocity in the direction of is constant. Show that, in general, the angular momentum of the particle is not conserved.
Suppose that the magnetic field is independent of time and space and takes the form and that is the rate of change of area swept out by a radius vector joining the origin to the projection of the particle's path on the plane. Obtain the equation
where are plane polar coordinates. Hence obtain an equation replacing the equation of conservation of angular momentum.
Show further, using energy conservation and , that the equations of motion in plane polar coordinates may be reduced to the first order non-linear system
where and are constants.
4.I.3E
The position of the leading edge of an avalanche moving down a mountain side making a positive angle to the horizontal satisfies the equation
where is the acceleration due to gravity.
By multiplying the equation by , obtain the first integral
where is an arbitrary constant of integration and the dot denotes differentiation with respect to time.
Sketch the positive quadrant of the phase plane. Show that all solutions approach the trajectory
Hence show that, independent of initial conditions, the avalanche ultimately has acceleration .
4.I.4E
An inertial reference frame and another reference frame have a common origin O. rotates with constant angular velocity with respect to . Assuming the result that
for an arbitrary vector , show that
where is the position vector of a point measured from the origin.
A system of electrically charged particles, all with equal masses and charges , moves under the influence of mutual central forces of the form
In addition each particle experiences a Lorentz force due to a constant weak magnetic field given by
Transform the equations of motion to the rotating frame . Show that if the angular velocity is chosen to satisfy
and if terms of second order in are neglected, then the equations of motion in the rotating frame are identical to those in the non-rotating frame in the absence of the magnetic field B.
4.II.10E
Derive the equation
for the orbit of a particle of mass and angular momentum moving under a central force directed towards a fixed point . Give an interpretation of in terms of the area swept out by a radius vector.
If the orbits are found to be circles passing through , then deduce that the force varies inversely as the fifth power of the distance, , where is a constant. Is the force attractive or repulsive?
Show that, for fixed mass, the radius of the circle varies inversely as the angular momentum of the particle, and hence that the time taken to traverse a complete circle is proportional to .
[You may assume, if you wish, the expressions for radial and transverse acceleration in the forms .]
4.II.11E
An electron of mass moving with velocity in the vicinity of the North Pole experiences a force
where is a constant and the position vector of the particle is with respect to an origin located at the North Pole. Write down the equation of motion of the electron, neglecting gravity. By taking the dot product of the equation with show that the speed of the electron is constant. By taking the cross product of the equation with show that
where is a constant vector. By taking the dot product of this equation with , show that the electron moves on a cone centred on the North Pole.
4.II.12E
Calculate the moment of inertia of a uniform rod of length and mass about an axis through its centre and perpendicular to its length. Assuming it moves in a plane, give an expression for the kinetic energy of the rod in terms of the speed of the centre and the angle that it makes with a fixed direction.
Two such rods are freely hinged together at one end and the other two ends slide on a perfectly smooth horizontal floor. The rods are initially at rest and lie in a vertical plane, each making an angle to the horizontal. The rods subsequently move under gravity. Calculate the speed with which the hinge strikes the ground.
4.II.9E
Write down the equations of motion for a system of gravitating point particles with masses and position vectors .
Assume that , where the vectors are independent of time . Obtain a system of equations for the vectors which does not involve the time variable .
Show that the constant vectors must be located at stationary points of the function
Show that for this system, the total angular momentum about the origin and the total momentum both vanish. What is the angular momentum about any other point?
4.I.3A
Derive the equation
for the motion of a particle of mass under an attractive central force , where and is the distance of the particle from the centre of force, and where is the angular momentum of the particle about the centre of force.
[Hint: you may assume the expressions for the radial and transverse accelerations in the form .]
4.I.4A
Two particles of masses and at positions and are subject to forces . Show that the centre of mass moves at a constant velocity. Obtain the equation of motion for the relative position of the particles. How does the reduced mass
of the system enter?
4.II.10A
A spherical raindrop of radius and density falls down at a velocity through a fine stationary mist. As the raindrop falls its volume grows at the rate with constant . The raindrop is subject to the gravitational force and a resistive force with a positive constant. Show and satisfy
Find an expression for , and deduce that as time increases tends to the constant value , and thence the raindrop tends to a constant acceleration which is less than .
4.II.11A
A spacecraft of mass moves under the gravitational influence of the Sun of mass and with universal gravitation constant . After a disastrous manoeuvre, the unfortunate spacecraft finds itself exactly in a parabolic orbit about the Sun: the orbit with zero total energy. Using the conservation of energy and angular momentum, or otherwise, show that in the subsequent motion the distance of the spacecraft from the Sun satisfies
with constants and .
4.II.12A
Find the moment of inertia of a uniform solid cylinder of radius , length and total mass about its axis.
The cylinder is released from rest at the top of an inclined plane of length and inclination to the horizontal. The first time the plane is perfectly smooth and the cylinder slips down the plane without rotating. The experiment is then repeated after the plane has been roughened, so that the cylinder now rolls without slipping at the point of contact. Show that the time taken to roll down the roughened plane is times the time taken to slip down the smooth plane.
4.II.9A
The position and velocity of a particle of mass are measured in a frame which rotates at constant angular velocity with respect to an inertial frame. Write down the equation of motion of the particle under a force .
Find the motion of the particle in coordinates with initial condition
where . Show that the particle has a maximum speed at , and find this speed.
[Hint: you may find it useful to consider the combination .]