Dynamics And Relativity
Dynamics And Relativity
Jump to year
Paper 4, Section I, C
A rigid body composed of particles with positions , and masses , rotates about the -axis with constant angular speed . Show that the body's kinetic energy is , where you should give an expression for the moment of inertia in terms of the particle masses and positions.
Consider a solid cuboid of uniform density, mass , and dimensions . Choose coordinate axes so that the cuboid is described by the points with , and . In terms of , , and , find the cuboid's moment of inertia for rotations about the -axis.
Paper 4, Section I, C
A trolley travels with initial speed along a frictionless, horizontal, linear track. It slows down by ejecting gas in the direction of motion. The gas is emitted at a constant mass ejection rate and with constant speed relative to the trolley. The trolley and its supply of gas initially have a combined mass of . How much time is spent ejecting gas before the trolley stops? [Assume that the trolley carries sufficient gas.]
Paper 4, Section II, 10C
(a) A mass is acted upon by a central force
where is a positive constant and is the displacement of the mass from the origin. Show that the angular momentum and energy of the mass are conserved.
(b) Working in plane polar coordinates , or otherwise, show that the distance between the mass and the origin obeys the following differential equation
where is the angular momentum per unit mass.
(c) A satellite is initially in a circular orbit of radius and experiences the force described above. At and time , the satellite emits a short rocket burst putting it on an elliptical orbit with its closest distance to the centre and farthest distance . When and the time is , the satellite reaches the farthest distance and a second short rocket burst puts the rocket on a circular orbit of radius . (See figure.) [Assume that the duration of the rocket bursts is negligible.]

(i) Show that the satellite's angular momentum per unit mass while in the elliptical orbit is
where is a number you should determine.
(ii) What is the change in speed as a result of the rocket burst at time ? And what is the change in speed at ?
(iii) Given that the elliptical orbit can be described by
where is the eccentricity of the orbit, find in terms of , and . [Hint: The area of an ellipse is equal to , where and b are its semi-major and semi-minor axes; these are related to the eccentricity by
Paper 4, Section II, C
Write down the expression for the momentum of a particle of rest mass , moving with velocity where is near the speed of light . Write down the corresponding 4-momentum.
Such a particle experiences a force . Why is the following expression for the particle's acceleration,
not generally correct? Show that the force can be written as follows
Invert this expression to find the particle's acceleration as the sum of two vectors, one parallel to and one parallel to .
A particle with rest mass and charge is in the presence of a constant electric field which exerts a force on the particle. If the particle is at rest at , its motion will be in the direction of for . Determine the particle's speed for . How does the velocity behave as ?
[Hint: You may find that trigonometric substitution is helpful in evaluating an integral.]
Paper 4, Section II, C
Consider an inertial frame of reference and a frame of reference which is rotating with constant angular velocity relative to . Assume that the two frames have a common origin .
Let be any vector. Explain why the derivative of in frame is related to its derivative in by the following equation
[Hint: It may be useful to use Cartesian basis vectors in both frames.]
Let be the position vector of a particle, measured from . Derive the expression relating the particle's acceleration as observed in , to the acceleration observed in , written in terms of and
A small bead of mass is threaded on a smooth, rigid, circular wire of radius . At any given instant, the wire hangs in a vertical plane with respect to a downward gravitational acceleration . The wire is rotating with constant angular velocity about its vertical diameter. Let be the angle between the downward vertical and the radial line going from the centre of the hoop to the bead.
(i) Show that satisfies the following equation of motion
(ii) Find any equilibrium angles and determine their stability.
(iii) Find the force of the wire on the bead as a function of and .
Paper 4, Section II, C
A particle of mass follows a one-dimensional trajectory in the presence of a variable force . Write down an expression for the work done by this force as the particle moves from to . Assuming that this is the only force acting on the particle, show that the work done by the force is equal to the change in the particle's kinetic energy.
What does it mean if a force is said to be conservative?
A particle moves in a force field given by
where and are positive constants. The particle starts at the origin with initial velocity . Show that, as the particle's position increases from to larger , the particle's velocity at position is given by
where you should determine . What determines whether the particle will escape to infinity or oscillate about the origin? Sketch versus for each of these cases, carefully identifying any significant velocities or positions.
In the case of oscillatory motion, find the period of oscillation in terms of , and . [Hint: You may use the fact that
for .]
Paper 2, Section I, C
A particle with unit mass moves in a central potential where . Initially is a distance away from the origin moving with speed on a trajectory which, in the absence of any force, would be a straight line whose shortest distance from the origin is . The shortest distance between 's actual trajectory and the origin is , with , at which point it is moving with speed .
(i) Assuming , find in terms of and .
(ii) Assuming , find an expression for 's farthest distance from the origin in the form
where , and depend only on , and the angular momentum .
[You do not need to prove that energy and angular momentum are conserved.]
Paper 2, Section II, C
(a) A moving particle with rest mass decays into two particles (photons) with zero rest mass. Derive an expression for , where is the angle between the spatial momenta of the final state particles, and show that it depends only on and the energies of the massless particles. ( is the speed of light in vacuum.)
(b) A particle with rest mass decays into two particles: a particle with rest mass and another particle with zero rest mass. Using dimensional analysis explain why the speed of in the rest frame of can be expressed as
and a dimensionless function of . Determine the function .
Choose coordinates in the rest frame of such that is emitted at from the origin in the -direction. The particle decays after a time , measured in its own rest frame. Determine the spacetime coordinates , in the rest frame of , corresponding to this event.
Paper 2, Section II, C
An axially symmetric pulley of mass rotates about a fixed, horizontal axis, say the -axis. A string of fixed length and negligible mass connects two blocks with masses and . The string is hung over the pulley, with one mass on each side. The tensions in the string due to masses and can respectively be labelled and . The moment of inertia of the pulley is , where is a number and is the radius of the
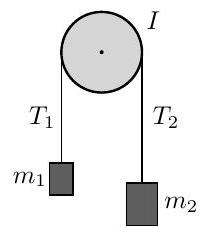
The motion of the pulley is opposed by a frictional torque of magnitude , where is the angular velocity of the pulley and is a real positive constant. Obtain a first-order differential equation for and, from it, find given that the system is released from rest.
The surface of the pulley is defined by revolving the function about the -axis, with
Find a value for the constant given that the pulley has uniform mass density .
Paper 4, Section I, A
Galileo releases a cannonball of mass from the top of the leaning tower of Pisa, a vertical height above the ground. Ignoring the rotation of the Earth but assuming that the cannonball experiences a quadratic drag force whose magnitude is (where is the speed of the cannonball), find the time for it to hit the ground in terms of and , the acceleration due to gravity. [You may assume that is constant.]
Paper 4, Section I, A
A rocket of mass moving at speed and ejecting fuel behind it at a constant speed relative to the rocket, is subject to an external force . Considering a small time interval , derive the rocket equation
In deep space where , how much faster does the rocket go if it burns half of its mass in fuel?
Paper 4, Section II, A
An inertial frame and another reference frame have a common origin , and rotates with angular velocity vector with respect to . Derive the results (a) and (b) below, where dot denotes a derivative with respect to time :
(a) The rates of change of an arbitrary vector in frames and are related by
(b) The accelerations in and are related by
where is the position vector relative to .
Just after passing the South Pole, a ski-doo of mass is travelling on a constant longitude with speed . Find the magnitude and direction of the sideways component of apparent force experienced by the ski-doo. [The sideways component is locally along the surface of the Earth and perpendicular to the motion of the ski-doo.]
Paper 4, Section II, A
(a) Writing a mass dimension as , a time dimension as , a length dimension as and a charge dimension as , write, using relations that you know, the dimensions of:
(i) force
(ii) electric field
(b) In the Large Hadron Collider at CERN, a proton of rest mass and charge is accelerated by a constant electric field . At time , the particle is at rest at the origin.
Writing the proton's position as and including relativistic effects, calculate . Use your answers to part (a) to check that the dimensions in your expression are correct.
Sketch a graph of versus , commenting on the limit.
Calculate as an explicit function of and find the non-relativistic limit at small times . What kind of motion is this?
(c) At a later time , an observer in the laboratory frame sees a cosmic microwave photon of energy hit the accelerated proton, leaving only a particle of mass in the final state. In its rest frame, the takes a time to decay. How long does it take to decay in the laboratory frame as a function of and , the speed of light in a vacuum?
Paper 4, Section II, A
(a) A particle of mass and positive charge moves with velocity in a region in which the magnetic field is constant and no other forces act, where . Initially, the particle is at position and . Write the equation of motion of the particle and then solve it to find as a function of time . Sketch its path in .
(b) For , three point particles, each of charge , are fixed at , and , respectively. Another point particle of mass and charge is constrained to move in the plane and suffers Coulomb repulsion from each fixed charge. Neglecting any magnetic fields,
(i) Find the position of an equilibrium point.
(ii) By finding the form of the electric potential near this point, deduce that the equilibrium is stable.
(iii) Consider small displacements of the point particle from the equilibrium point. By resolving forces in the directions and , show that the frequency of oscillation is
where is a constant which you should find.
[You may assume that if two identical charges are separated by a distance then the repulsive Coulomb force experienced by each of the charges is , where is a constant.]
Paper 4, Section II, A
In an alien invasion, a flying saucer hovers at a fixed point , a height far above the White House, which is at point . A wrecking ball of mass is attached to one end of a light inextensible rod, also of length . The other end of the rod is attached to the flying saucer. The wrecking ball is initially at rest at point , and the angle is . At , the acceleration due to gravity is . Assume that the rotation of the Earth can be neglected and that the only force acting is Earth's gravity.
(a) Under the approximations that gravity acts everywhere parallel to the line and that the acceleration due to Earth's gravity is constant throughout the space through which the wrecking ball is travelling, find the speed with which the wrecking ball hits the White House, in terms of the constants introduced above.
(b) Taking into account the fact that gravity is non-uniform and acts toward the centre of the Earth, find the speed with which the wrecking ball hits the White House in terms of the constants introduced above and , where is the radius of the Earth, which you may assume is exactly spherical.
(c) Finally, show that
where and are constants, which you should determine.
Paper 4, Section I, 3A
(a) Define an inertial frame.
(b) Specify three different types of Galilean transformation on inertial frames whose space coordinates are and whose time coordinate is .
(c) State the Principle of Galilean Relativity.
(d) Write down the equation of motion for a particle in one dimension in a potential . Prove that energy is conserved. A particle is at position at time . Find an expression for time as a function of in terms of an integral involving .
(e) Write down the values of any equilibria and state (without justification) whether they are stable or unstable for:
(i)
(ii) for and .
Paper 4, Section I, A
Explain what is meant by a central force acting on a particle moving in three dimensions.
Show that the angular momentum of a particle about the origin for a central force is conserved, and hence that its path lies in a plane.
Show that, in the approximation in which the Sun is regarded as fixed and only its gravitational field is considered, a straight line joining the Sun and an orbiting planet sweeps out equal areas in equal time (Kepler's second law).
Paper 4, Section II, A
The position and velocity of a particle of mass are measured in a frame which rotates at constant angular velocity with respect to an inertial frame. The particle is subject to a force . What is the equation of motion of the particle?
Find the trajectory of the particle in the coordinates if and at and .
Find the maximum value of the speed of the particle and the times at which it travels at this speed.
[Hint: You may find using the variable helpful.]
Paper 4, Section II, A
Write down the Lorentz force law for a charge travelling at velocity in an electric field and magnetic field .
In a space station which is in an inertial frame, an experiment is performed in vacuo where a ball is released from rest a distance from a wall. The ball has charge and at time , it is a distance from the wall. A constant electric field of magnitude points toward the wall in a perpendicular direction, but there is no magnetic field. Find the speed of the ball on its first impact.
Every time the ball bounces, its speed is reduced by a factor . Show that the total distance travelled by the ball before it comes to rest is
where and are quadratic functions which you should find explicitly.
A gas leak fills the apparatus with an atmosphere and the experiment is repeated. The ball now experiences an additional drag force , where is the instantaneous velocity of the ball and . Solve the system before the first bounce, finding an explicit solution for the distance between the ball and the wall as a function of time of the form
where is a function and and are dimensional constants, all of which you should find explicitly.
Paper 4, Section II, A
Define the 4-momentum of a particle of rest mass and velocity . Calculate the power series expansion of the component for small (where is the speed of light in vacuo) up to and including terms of order , and interpret the first two terms.
(a) At CERN, anti-protons are made by colliding a moving proton with another proton at rest in a fixed target. The collision in question produces three protons and an anti-proton. Assume that the rest mass of a proton is identical to the rest mass of an anti-proton. What is the smallest possible speed of the incoming proton (measured in the laboratory frame)?
(b) A moving particle of rest mass decays into particles with 4 -momenta , and rest masses , where . Show that
Thus, show that
(c) A particle decays into particle and a massless particle 1 . Particle subsequently decays into particle and a massless particle 2 . Show that
where and are the 4-momenta of particles 1 and 2 respectively and are the masses of particles and respectively.
Paper 4, Section II, A
Consider a rigid body, whose shape and density distribution are rotationally symmetric about a horizontal axis. The body has mass , radius and moment of inertia about its axis of rotational symmetry and is rolling down a non-slip slope inclined at an angle to the horizontal. By considering its energy, calculate the acceleration of the disc down the slope in terms of the quantities introduced above and , the acceleration due to gravity.
(a) A sphere with density proportional to (where is distance to the sphere's centre and is a positive constant) is launched up a non-slip slope of constant incline at the same time, level and speed as a vertical disc of constant density. Find such that the sphere and the disc return to their launch points at the same time.
(b) Two spherical glass marbles of equal radius are released from rest at time on an inclined non-slip slope of constant incline from the same level. The glass in each marble is of constant and equal density, but the second marble has two spherical air bubbles in it whose radii are half the radius of the marbles, initially centred directly above and below the marble's centre, respectively. Each bubble is centred half-way between the centre of the marble and its surface. At a later time , find the ratio of the distance travelled by the first marble and the second. [ You may state without proof any theorems that you use and neglect the mass of air in the bubbles. ]
Paper 4, Section I, A
A tennis ball of mass is projected vertically upwards with initial speed and reaches its highest point at time . In addition to uniform gravity, the ball experiences air resistance, which produces a frictional force of magnitude , where is the ball's speed and is a positive constant. Show by dimensional analysis that can be written in the form
for some function of a dimensionless quantity .
Use the equation of motion of the ball to find .
Paper 4, Section I, A
Consider a system of particles with masses and position vectors . Write down the definition of the position of the centre of mass of the system. Let be the total kinetic energy of the system. Show that
where is the total mass and is the position vector of particle with respect to .
The particles are connected to form a rigid body which rotates with angular speed about an axis through , where . Show that
where and is the moment of inertia of particle about .
Paper 4, Section II, A
(a) A rocket moves in a straight line with speed and is subject to no external forces. The rocket is composed of a body of mass and fuel of mass , which is burnt at constant rate and the exhaust is ejected with constant speed relative to the rocket. Show that
Show that the speed of the rocket when all its fuel is burnt is
where and are the speed of the rocket and the mass of the fuel at .
(b) A two-stage rocket moves in a straight line and is subject to no external forces. The rocket is initially at rest. The masses of the bodies of the two stages are and , with , and they initially carry masses and of fuel. Both stages burn fuel at a constant rate when operating and the exhaust is ejected with constant speed relative to the rocket. The first stage operates first, until all its fuel is burnt. The body of the first stage is then detached with negligible force and the second stage ignites.
Find the speed of the second stage when all its fuel is burnt. For compare it with the speed of the rocket in part (a) in the case . Comment on the case .
Paper 4, Section II, A
(a) Consider an inertial frame , and a frame which rotates with constant angular velocity relative to . The two frames share a common origin. Identify each term in the equation
(b) A small bead of unit mass can slide without friction on a circular hoop of radius . The hoop is horizontal and rotating with constant angular speed about a fixed vertical axis through a point on its circumference.
(i) Using Cartesian axes in the rotating frame , with origin at and -axis along the diameter of the hoop through , write down the position vector of in terms of and the angle shown in the diagram .

(ii) Working again in the rotating frame, find, in terms of and , an expression for the horizontal component of the force exerted by the hoop on the bead.
(iii) For what value of is the bead in stable equilibrium? Find the frequency of small oscillations of the bead about that point.
Paper 4, Section II, A
A particle of unit mass moves under the influence of a central force. By considering the components of the acceleration in polar coordinates prove that the magnitude of the angular momentum is conserved. [You may use . ]
Now suppose that the central force is derived from the potential , where is a constant.
(a) Show that the total energy of the particle can be written in the form
Sketch in the cases and .
(b) The particle is projected from a very large distance from the origin with speed and impact parameter . [The impact parameter is the distance of closest approach to the origin in absence of any force.]
(i) In the case , sketch the particle's trajectory and find the shortest distance between the particle and the origin, and the speed of the particle when .
(ii) In the case , sketch the particle's trajectory and find the corresponding shortest distance between the particle and the origin, and the speed of the particle when .
(iii) Find and in terms of and . [In answering part (iii) you should assume that is the same in parts (i) and (ii).]
Paper 4, Section II, A
(a) A photon with energy in the laboratory frame collides with an electron of rest mass that is initially at rest in the laboratory frame. As a result of the collision the photon is deflected through an angle as measured in the laboratory frame and its energy changes to .
Derive an expression for in terms of and .
(b) A deuterium atom with rest mass and energy in the laboratory frame collides with another deuterium atom that is initially at rest in the laboratory frame. The result of this collision is a proton of rest mass and energy , and a tritium atom of rest mass . Show that, if the proton is emitted perpendicular to the incoming trajectory of the deuterium atom as measured in the laboratory frame, then
Paper 4, Section , B
The radial equation of motion of a particle moving under the influence of a central force is
where is the angular momentum per unit mass of the particle, is a constant, and is a positive constant.
Show that circular orbits with are possible for any positive value of , and that they are stable to small perturbations that leave unchanged if .
Paper 4, Section I, B
With the help of definitions or equations of your choice, determine the dimensions, in terms of mass , length , time and charge , of the following quantities:
(i) force;
(ii) moment of a force (i.e. torque);
(iii) energy;
(iv) Newton's gravitational constant ;
(v) electric field ;
(vi) magnetic field ;
(vii) the vacuum permittivity .
Paper 4, Section II, B
State what the vectors and represent in the following equation:
where is the acceleration due to gravity.
Assume that the radius of the Earth is , that , and that there are seconds in a day. Use these data to determine roughly the order of magnitude of each term on the right hand side of in the case of a particle dropped from a point at height above the surface of the Earth.
Taking again , find the time of the particle's fall in the absence of rotation.
Use a suitable approximation scheme to show that
where is the position vector of the point at which the particle lands, and is the position vector of the point at which the particle would have landed in the absence of rotation.
The particle is dropped at latitude . Find expressions for the approximate northerly and easterly displacements of from in terms of (the magnitudes of and , respectively), and . You should ignore the curvature of the Earth's surface.
Paper 4, Section II, B
(a) Alice travels at constant speed to Alpha Centauri, which is at distance from Earth. She then turns around (taking very little time to do so), and returns at speed . Bob stays at home. By how much has Bob aged during the journey? By how much has Alice aged? [No justification is required.]
Briefly explain what is meant by the twin paradox in this context. Why is it not a paradox?
(b) Suppose instead that Alice's world line is given by
where is a positive constant. Bob stays at home, at , where . Alice and Bob compare their ages on both occasions when they meet. By how much does Bob age? Show that Alice ages by .
Paper 4, Section II, B
A particle of unit mass moves with angular momentum in an attractive central force field of magnitude , where is the distance from the particle to the centre and is a constant. You may assume that the equation of its orbit can be written in plane polar coordinates in the form
where and is the eccentricity. Show that the energy of the particle is
A comet moves in a parabolic orbit about the Sun. When it is at its perihelion, a distance from the Sun, and moving with speed , it receives an impulse which imparts an additional velocity of magnitude directly away from the Sun. Show that the eccentricity of its new orbit is , and sketch the two orbits on the same axes.
Paper 4, Section II, B
(a) A rocket, moving non-relativistically, has speed and mass at a time after it was fired. It ejects mass with constant speed relative to the rocket. Let the total momentum, at time , of the system (rocket and ejected mass) in the direction of the motion of the rocket be . Explain carefully why can be written in the form
If the rocket experiences no external force, show that
Derive the expression corresponding to for the total kinetic energy of the system at time . Show that kinetic energy is not necessarily conserved.
(b) Explain carefully how should be modified for a rocket moving relativistically, given that there are no external forces. Deduce that
where and hence that
(c) Show that and agree in the limit . Briefly explain the fact that kinetic energy is not conserved for the non-relativistic rocket, but relativistic energy is conserved for the relativistic rocket.
Paper 4, Section I, C
Write down the 4-momentum of a particle with energy and 3-momentum p. State the relationship between the energy and wavelength of a photon.
An electron of mass is at rest at the origin of the laboratory frame: write down its 4 -momentum. The electron is scattered by a photon of wavelength travelling along the -axis: write down the initial 4-momentum of the photon. Afterwards, the photon has wavelength and has been deflected through an angle . Show that
where is the speed of light and is Planck's constant.
Paper 4, Section I, C
Find the moment of inertia of a uniform sphere of mass and radius about an axis through its centre.
The kinetic energy of any rigid body with total mass , centre of mass , moment of inertia about an axis of rotation through , and angular velocity about that same axis, is given by . What physical interpretation can be given to the two parts of this expression?
A spherical marble of uniform density and mass rolls without slipping at speed along a flat surface. Explaining any relationship that you use between its speed and angular velocity, show that the kinetic energy of the marble is .
Paper 4, Section II,
A particle is projected vertically upwards at speed from the surface of the Earth, which may be treated as a perfect sphere. The variation of gravity with height should not be ignored, but the rotation of the Earth should be. Show that the height of the particle obeys
where is the radius of the Earth and is the acceleration due to gravity measured at the Earth's surface.
Using dimensional analysis, show that the maximum height of the particle and the time taken to reach that height are given by
where and are functions of .
Write down the equation of conservation of energy and deduce that
Hence or otherwise show that
Paper 4, Section II, C
Write down the Lorentz transform relating the components of a 4-vector between two inertial frames.
A particle moves along the -axis of an inertial frame. Its position at time is , its velocity is , and its 4 -position is , where is the speed of light. The particle's 4-velocity is given by and its 4 -acceleration is , where proper time is defined by . Show that
where and .
The proper 3-acceleration a of the particle is defined to be the spatial component of its 4-acceleration measured in the particle's instantaneous rest frame. By transforming to the rest frame, or otherwise, show that
Given that the particle moves with constant proper 3 -acceleration starting from rest at the origin, show that
and that, if , then .
Paper 4, Section II, C
Consider a particle with position vector moving in a plane described by polar coordinates . Obtain expressions for the radial and transverse components of the velocity and acceleration .
A charged particle of unit mass moves in the electric field of another charge that is fixed at the origin. The electrostatic force on the particle is in the radial direction, where is a positive constant. The motion takes place in an unusual medium that resists radial motion but not tangential motion, so there is an additional radial force where is a positive constant. Show that the particle's motion lies in a plane. Using polar coordinates in that plane, show also that its angular momentum is constant.
Obtain the equation of motion
where , and find its general solution assuming that . Show that so long as the motion remains bounded it eventually becomes circular with radius .
Obtain the expression
for the particle's total energy, that is, its kinetic energy plus its electrostatic potential energy. Hence, or otherwise, show that the energy is a decreasing function of time.
Paper 4, Section II, C
A particle of mass and charge has position vector and moves in a constant, uniform magnetic field so that its equation of motion is
Let be the particle's angular momentum. Show that
is a constant of the motion. Explain why the kinetic energy is also constant, and show that it may be written in the form
where and .
[Hint: Consider u
Paper 4, Section I,
A particle of mass has charge and moves in a constant magnetic field B. Show that the particle's path describes a helix. In which direction is the axis of the helix, and what is the particle's rotational angular frequency about that axis?
Paper 4, Section I,
What is a 4-vector? Define the inner product of two 4-vectors and give the meanings of the terms timelike, null and spacelike. How do the four components of a 4-vector change under a Lorentz transformation of speed ? [Without loss of generality, you may take the velocity of the transformation to be along the positive -axis.]
Show that a 4-vector that is timelike in one frame of reference is also timelike in a second frame of reference related by a Lorentz transformation. [Again, you may without loss of generality take the velocity of the transformation to be along the positive -axis.]
Show that any null 4-vector may be written in the form where is real and is a unit 3-vector. Given any two null 4-vectors that are future-pointing, that is, which have positive time-components, show that their sum is either null or timelike.
Paper 4, Section II, C
Define the 4-momentum of a particle and describe briefly the principle of conservation of 4-momentum.
A photon of angular frequency is absorbed by a particle of rest mass that is stationary in the laboratory frame of reference. The particle then splits into two equal particles, each of rest mass .
Find the maximum possible value of as a function of . Verify that as , this maximum value tends to . For general , show that when the maximum value of is achieved, the resulting particles are each travelling at speed in the laboratory frame.
Paper 4, Section II, C
A thin flat disc of radius has density (mass per unit area) where are plane polar coordinates on the disc and is a constant. The disc is free to rotate about a light, thin rod that is rigidly fixed in space, passing through the centre of the disc orthogonal to it. Find the moment of inertia of the disc about the rod.
The section of the disc lying in is cut out and removed. Starting from rest, a constant torque is applied to the remaining part of the disc until its angular speed about the axis reaches . Show that this takes a time
After this time, no further torque is applied and the partial disc continues to rotate at constant angular speed . Given that the total mass of the partial disc is , where is a constant that you need not determine, find the position of the centre of mass, and hence its acceleration. From where does the force required to produce this acceleration arise?
Paper 4, Section II, C
A reference frame rotates with constant angular velocity relative to an inertial frame that has the same origin as . A particle of mass at position vector is subject to a force . Derive the equation of motion for the particle in .
A marble moves on a smooth plane which is inclined at an angle to the horizontal. The whole plane rotates at constant angular speed about a vertical axis through a point fixed in the plane. Coordinates are defined with respect to axes fixed in the plane: horizontal and up the line of greatest slope in the plane. Ensuring that you account for the normal reaction force, show that the motion of the marble obeys
By considering the marble's kinetic energy as measured on the plane in the rotating frame, or otherwise, find a constant of the motion.
[You may assume that the marble never leaves the plane.]
Paper 4, Section II, C
A rocket of mass , which includes the mass of its fuel and everything on board, moves through free space in a straight line at speed . When its engines are operational, they burn fuel at a constant mass rate and eject the waste gases behind the rocket at a constant speed relative to the rocket. Obtain the rocket equation
The rocket is initially at rest in a cloud of space dust which is also at rest. The engines are started and, as the rocket travels through the cloud, it collects dust which it stores on board for research purposes. The mass of dust collected in a time is given by , where is the distance travelled in that time and is a constant. Obtain the new equations
By eliminating , or otherwise, obtain the relationship
where is the initial mass of the rocket and .
If , show that the fuel will be exhausted before the speed of the rocket can reach . Comment on the case when , giving a physical interpretation of your answer.
Paper 4 , Section II, B
(i) An inertial frame has orthonormal coordinate basis vectors . A second frame rotates with angular velocity relative to and has coordinate basis vectors . The motion of is characterised by the equations and at the two coordinate frames coincide.
If a particle has position vector show that where and are the velocity vectors of as seen by observers fixed respectively in and .
(ii) For the remainder of this question you may assume that where and are the acceleration vectors of as seen by observers fixed respectively in and , and that is constant.
Consider again the frames and in (i). Suppose that with constant. A particle of mass moves under a force . When viewed in its position and velocity at time are and . Find the motion of the particle in the coordinates of . Show that for an observer fixed in , the particle achieves its maximum speed at time and determine that speed. [Hint: you may find it useful to consider the combination .]
Paper 4, Section , B
A frame moves with constant velocity along the axis of an inertial frame of Minkowski space. A particle moves with constant velocity along the axis of . Find the velocity of in .
The rapidity of any velocity is defined by . Find a relation between the rapidities of and .
Suppose now that is initially at rest in and is subsequently given successive velocity increments of (each delivered in the instantaneous rest frame of the particle). Show that the resulting velocity of in is
where .
[You may use without proof the addition formulae and .]
Paper 4, Section I, B
A hot air balloon of mass is equipped with a bag of sand of mass which decreases in time as the sand is gradually released. In addition to gravity the balloon experiences a constant upwards buoyancy force and we neglect air resistance effects. Show that if is the upward speed of the balloon then
Initially at the mass of sand is and the balloon is at rest in equilibrium. Subsequently the sand is released at a constant rate and is depleted in a time . Show that the speed of the balloon at time is
[You may use without proof the indefinite integral ]
Paper 4, Section II, B
(a) Let with coordinates and with coordinates be inertial frames in Minkowski space with two spatial dimensions. moves with velocity along the -axis of and they are related by the standard Lorentz transformation:
A photon is emitted at the spacetime origin. In it has frequency and propagates at angle to the -axis.
Write down the 4 -momentum of the photon in the frame .
Hence or otherwise find the frequency of the photon as seen in . Show that it propagates at angle to the -axis in , where
A light source in emits photons uniformly in all directions in the -plane. Show that for large , in half of the light is concentrated into a narrow cone whose semi-angle is given by .
(b) The centre-of-mass frame for a system of relativistic particles in Minkowski space is the frame in which the total relativistic 3-momentum is zero.
Two particles and of rest masses and move collinearly with uniform velocities and respectively, along the -axis of a frame . They collide, coalescing to form a single particle .
Determine the velocity of the centre-of-mass frame of the system comprising and .
Find the speed of in and show that its rest mass is given by
where
Paper 4, Section II, B
(a) A rigid body is made up of particles of masses at positions . Let denote the position of its centre of mass. Show that the total kinetic energy of may be decomposed into , the kinetic energy of the centre of mass, plus a term representing the kinetic energy about the centre of mass.
Suppose now that is rotating with angular velocity about its centre of mass. Define the moment of inertia of (about the axis defined by ) and derive an expression for in terms of and .
(b) Consider a uniform rod of length and mass . Two such rods and are freely hinged together at . The end is attached to a fixed point on a perfectly smooth horizontal floor and is able to rotate freely about . The rods are initially at rest, lying in a vertical plane with resting on the floor and each rod making angle with the horizontal. The rods subsequently move under gravity in their vertical plane.
Find an expression for the angular velocity of rod when it makes angle with the floor. Determine the speed at which the hinge strikes the floor.
Paper 4, Section II, B
(a) A particle of unit mass moves in a plane with polar coordinates . You may assume that the radial and angular components of the acceleration are given by , where the dot denotes . The particle experiences a central force corresponding to a potential .
(i) Prove that is constant in time and show that the time dependence of the radial coordinate is equivalent to the motion of a particle in one dimension in a potential given by
(ii) Now suppose that . Show that if then two circular orbits are possible with radii and . Determine whether each orbit is stable or unstable.
(b) Kepler's first and second laws for planetary motion are the following statements:
K1: the planet moves on an ellipse with a focus at the Sun;
K2: the line between the planet and the Sun sweeps out equal areas in equal times.
Show that K2 implies that the force acting on the planet is a central force.
Show that K2 together with implies that the force is given by the inverse square law.
[You may assume that an ellipse with a focus at the origin has polar equation with and .]
Paper 4, Section I, B
Let and be inertial frames in 2-dimensional spacetime with coordinate systems and respectively. Suppose that moves with positive velocity relative to and the spacetime origins of and coincide. Write down the Lorentz transformation relating the coordinates of any event relative to the two frames.
Show that events which occur simultaneously in are not generally seen to be simultaneous when viewed in .
In two light sources and are at rest and placed a distance apart. They simultaneously each emit a photon in the positive direction. Show that in the photons are separated by a constant distance .
Paper 4, Section I, B
Two particles of masses and have position vectors and respectively. Particle 2 exerts a force ) on particle 1 (where ) and there are no external forces.
Prove that the centre of mass of the two-particle system will move at constant speed along a straight line.
Explain how the two-body problem of determining the motion of the system may be reduced to that of a single particle moving under the force .
Suppose now that and that
is gravitational attraction. Let be a circle fixed in space. Is it possible (by suitable choice of initial conditions) for the two particles to be traversing at the same constant angular speed? Give a brief reason for your answer.
Paper 4, Section II, B
(a) Define the 4-momentum of a particle of rest mass and 3 -velocity , and the 4-momentum of a photon of frequency (having zero rest mass) moving in the direction of the unit vector .
Show that if and are timelike future-pointing 4-vectors then (where the dot denotes the Lorentz-invariant scalar product). Hence or otherwise show that the law of conservation of 4 -momentum forbids a photon to spontaneously decay into an electron-positron pair. [Electrons and positrons have equal rest masses .]
(b) In the laboratory frame an electron travelling with velocity u collides with a positron at rest. They annihilate, producing two photons of frequencies and that move off at angles and to , in the directions of the unit vectors and respectively. By considering 4-momenta in the laboratory frame, or otherwise, show that
where
Paper 4, Section II, B
(a) State the parallel axis theorem for moments of inertia.
(b) A uniform circular disc of radius and total mass can turn frictionlessly about a fixed horizontal axis that passes through a point on its circumference and is perpendicular to its plane. Initially the disc hangs at rest (in constant gravity ) with its centre being vertically below . Suppose the disc is disturbed and executes free oscillations. Show that the period of small oscillations is .
(c) Suppose now that the disc is released from rest when the radius is vertical with directly above . Find the angular velocity and angular acceleration of about when the disc has turned through angle . Let denote the reaction force at on the disc. Find the acceleration of the centre of mass of the disc. Hence, or otherwise, show that the component of parallel to is .
Paper 4, Section II, B
For any frame and vector , let denote the derivative of relative to . A frame of reference rotates with constant angular velocity with respect to an inertial frame and the two frames have a common origin . [You may assume that for any vector
(a) If is the position vector of a point from , show that
where is the velocity in .
Suppose now that is the position vector of a particle of mass moving under a conservative force and a force that is always orthogonal to the velocity in . Show that the quantity
is a constant of the motion. [You may assume that .]
(b) A bead slides on a frictionless circular hoop of radius which is forced to rotate with constant angular speed about a vertical diameter. Let denote the angle between the line from the centre of the hoop to the bead and the downward vertical. Using the results of (a), or otherwise, show that
Deduce that if there are two equilibrium positions off the axis of rotation, and show that these are stable equilibria.
Paper 4, Section II, B
Let be polar coordinates in the plane. A particle of mass moves in the plane under an attractive force of towards the origin . You may assume that the acceleration a is given by
where and are the unit vectors in the directions of increasing and respectively, and the dot denotes .
(a) Show that is a constant of the motion. Introducing show that and derive the geometric orbit equation
(b) Suppose now that
and that initially the particle is at distance from , moving with speed in a direction making angle with the radial vector pointing towards .
Show that and find as a function of . Hence or otherwise show that the particle returns to its original position after one revolution about and then flies off to infinity.
Paper 4, Section I, B
Inertial frames and in two-dimensional space-time have coordinates and , respectively. These coordinates are related by a Lorentz transformation with the velocity of relative to . Show that if and then the Lorentz transformation can be expressed in the form
Deduce that .
Use the form to verify that successive Lorentz transformations with velocities and result in another Lorentz transformation with velocity , to be determined in terms of and .
Paper 4, Section I, B
The motion of a planet in the gravitational field of a star of mass obeys
where and are polar coordinates in a plane and is a constant. Explain one of Kepler's Laws by giving a geometrical interpretation of .
Show that circular orbits are possible, and derive another of Kepler's Laws relating the radius and the period of such an orbit. Show that any circular orbit is stable under small perturbations that leave unchanged.
Paper 4, Section II, B
(a) Write down the relativistic energy of a particle of rest mass and speed . Find the approximate form for when is small compared to , keeping all terms up to order . What new physical idea (when compared to Newtonian Dynamics) is revealed in this approximation?
(b) A particle of rest mass is fired at an identical particle which is at rest in the laboratory frame. Let be the relativistic energy and the speed of the incident particle in this frame. After the collision, there are particles in total, each with rest mass . Assuming that four-momentum is conserved, find a lower bound on and hence show that
Paper 4, Section II, B
A rocket carries equipment to collect samples from a stationary cloud of cosmic dust. The rocket moves in a straight line, burning fuel and ejecting gas at constant speed relative to itself. Let be the speed of the rocket, its total mass, including fuel and any dust collected, and the total mass of gas that has been ejected. Show that
assuming that all external forces are negligible.
(a) If no dust is collected and the rocket starts from rest with mass , deduce that
(b) If cosmic dust is collected at a constant rate of units of mass per unit time and fuel is consumed at a constant rate , show that, with the same initial conditions as in (a),
Verify that the solution in (a) is recovered in the limit .
Paper 4, Section II, B
The trajectory of a particle is observed in a frame which rotates with constant angular velocity relative to an inertial frame . Given that the time derivative in of any vector is
where a dot denotes a time derivative in , show that
where is the force on the particle and is its mass.
Let be the frame that rotates with the Earth. Assume that the Earth is a sphere of radius . Let be a point on its surface at latitude , and define vertical to be the direction normal to the Earth's surface at .
(a) A particle at is released from rest in and is acted on only by gravity. Show that its initial acceleration makes an angle with the vertical of approximately
working to lowest non-trivial order in .
(b) Now consider a particle fired vertically upwards from with speed . Assuming that terms of order and higher can be neglected, show that it falls back to Earth under gravity at a distance
from . [You may neglect the curvature of the Earth's surface and the vertical variation of gravity.]
Paper 4, Section II, B
A particle with mass and position is subject to a force
(a) Suppose that . Show that
is constant, and interpret this result, explaining why the field plays no role.
(b) Suppose, in addition, that and that both and depend only on . Show that
is independent of time if , for any constant .
(c) Now specialise further to the case . Explain why the result in (b) implies that the motion of the particle is confined to a plane. Show also that
is constant provided takes a certain form, to be determined.
[ Recall that and that if depends only on then
Paper 4 , Section II, B
A sphere of uniform density has mass and radius . Find its moment of inertia about an axis through its centre.
A marble of uniform density is released from rest on a plane inclined at an angle to the horizontal. Let the time taken for the marble to travel a distance down the plane be: (i) if the plane is perfectly smooth; or (ii) if the plane is rough and the marble rolls without slipping.
Explain, with a clear discussion of the forces acting on the marble, whether or not its energy is conserved in each of the cases (i) and (ii). Show that .
Suppose that the original marble is replaced by a new one with the same mass and radius but with a hollow centre, so that its moment of inertia is for some constant . What is the new value for ?
Paper 4, Section , B
Let be an inertial frame with coordinates in two-dimensional spacetime. Write down the Lorentz transformation giving the coordinates in a second inertial frame moving with velocity relative to . If a particle has constant velocity in , find its velocity in . Given that and , show that .
Paper 4, Section I, B
A particle of mass and charge moves with trajectory in a constant magnetic field . Write down the Lorentz force on the particle and use Newton's Second Law to deduce that
where is a constant vector and is to be determined. Find and hence for the initial conditions
where and are constants. Sketch the particle's trajectory in the case .
[Unit vectors correspond to a set of Cartesian coordinates. ]
Paper 4, Section II, B
A particle of rest mass is fired at an identical particle which is stationary in the laboratory. On impact, and annihilate and produce two massless photons whose energies are equal. Assuming conservation of four-momentum, show that the angle between the photon trajectories is given by
where is the relativistic energy of .
Let be the speed of the incident particle . For what value of will the photons move in perpendicular directions? If is very small compared with , show that
[All quantities referred to are measured in the laboratory frame.]
Paper 4, Section II, B
Consider a set of particles with position vectors and masses , where . Particle experiences an external force and an internal force from particle , for each . Stating clearly any assumptions you need, show that
where is the total momentum, is the total external force, is the total angular momentum about a fixed point , and is the total external torque about .
Does the result still hold if the fixed point is replaced by the centre of mass of the system? Justify your answer.
Suppose now that the external force on particle is and that all the particles have the same mass . Show that
Paper 4, Section II, B
A particle of unit mass moves in a plane with polar coordinates and components of acceleration . The particle experiences a force corresponding to a potential . Show that
are constants of the motion, where
Sketch the graph of in the cases and .
(a) Assuming and , for what range of values of do bounded orbits exist? Find the minimum and maximum distances from the origin, and , on such an orbit and show that
Prove that the minimum and maximum values of the particle's speed, and , obey
(b) Now consider trajectories with and of either sign. Find the distance of closest approach, , in terms of the impact parameter, , and , the limiting value of the speed as . Deduce that if then, to leading order,
Paper 4, Section I, A
(a) Explain what is meant by a central force acting on a particle moving in three dimensions.
(b) Show that the orbit of a particle experiencing a central force lies in a plane.
(c) Show that, in the approximation in which the Sun is regarded as fixed and only its gravitational field is considered, a straight line joining the Sun and an orbiting planet sweeps out equal areas in equal times (Kepler's second law).
[With respect to the basis vectors of plane polar coordinates, the velocity and acceleration of a particle are given by and .]
Paper 4, Section I, A
A rocket moves vertically upwards in a uniform gravitational field and emits exhaust gas downwards with time-dependent speed relative to the rocket. Derive the rocket equation
where and are respectively the rocket's mass and upward vertical speed at time . Suppose now that and . What is the condition for the rocket to lift off at ? Assuming that this condition is satisfied, find .
State the dimensions of all the quantities involved in your expression for , and verify that the expression is dimensionally consistent.
[ You may assume that all speeds are small compared with the speed of light and neglect any relativistic effects.]
Paper 4, Section II, A
(a) A particle of charge moves with velocity in a constant magnetic field B. Give an expression for the Lorentz force experienced by the particle. If no other forces act on the particle, show that its kinetic energy is independent of time.
(b) Four point particles, each of positive charge , are fixed at the four corners of a square with sides of length . Another point particle, of positive charge , is constrained to move in the plane of the square but is otherwise free.
By considering the form of the electrostatic potential near the centre of the square, show that the state in which the particle of charge is stationary at the centre of the square is a stable equilibrium. Obtain the frequency of small oscillations about this equilibrium.
[The Coulomb potential for two point particles of charges and separated by distance is
Paper 4, Section II, A
Obtain the moment of inertia of a uniform disc of radius and mass about its axis of rotational symmetry. A uniform rigid body of mass takes the form of a disc of radius with a concentric circular hole of radius cut out. Calculate the body's moment of inertia about its axis of rotational symmetry.
The body rolls without slipping, with its axis of symmetry horizontal, down a plane inclined at angle to the horizontal. Determine its acceleration and the frictional and normal-reaction forces resulting from contact with the plane.
Paper 4, Section II, A
(a) Write down expressions for the relativistic 3 -momentum and energy of a particle of rest mass and velocity . Show that these expressions are consistent with
Define the 4-momentum for such a particle and obtain by considering the invariance properties of .
(b) Two particles, each with rest mass and energy , moving in opposite directions, collide head on. Show that it is consistent with the conservation of 4 -momentum for the collision to result in a set of particles of rest masses (for only if
(c) A particle of rest mass and energy is fired at a stationary particle of rest mass . Show that it is consistent with the conservation of 4 -momentum for the collision to result in a set of particles of rest masses (for ) only if
Deduce the minimum frequency required for a photon fired at a stationary particle of rest mass to result in the same set of particles, assuming that the conservation of 4 -momentum is the only relevant constraint.
Paper 4, Section II, A
Davros departs on a rocket voyage from the planet Skaro, travelling at speed (where ) in the positive direction in Skaro's rest frame. After travelling a distance in Skaro's rest frame, he jumps onto another rocket travelling at speed (where ) in the positive direction in the first rocket's rest frame. After travelling a further distance in Skaro's rest frame, he jumps onto a third rocket, travelling at speed where ) in the negative direction in the second rocket's rest frame.
Let and be Davros' speed on the second and third rockets, respectively, in Skaro's rest frame. Show that
Express in terms of and .
How large must be, expressed in terms of and , to ensure that Davros eventually returns to Skaro?
Supposing that satisfies this condition, draw a spacetime diagram illustrating Davros' journey. Label clearly each point where he boards a rocket and the point of his return to Skaro, and give the coordinates of each point in Skaro's rest frame, expressed in terms of and .
Hence, or otherwise, calculate how much older Davros will be on his return, and how much time will have elapsed on Skaro during his voyage, giving your answers in terms of and .
[You may neglect any effects due to gravity and any corrections arising from Davros' brief accelerations when getting onto or leaving rockets.