Part II, 2021, Paper 2

Algebraic Geometry

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2021

  Let $k$ be an algebraically closed field and $n \geqslant 1$. Exhibit $G L(n, k)$ as an open subset of affine space $\mathbb{A}_{k}^{n^{2}}$. Deduce that $G L(n, k)$ is smooth. Prove that it is also irreducible.

  Prove that $G L(n, k)$ is isomorphic to a closed subvariety in an affine space.

  Show that the matrix multiplication map

  $$G L(n, k) \times G L(n, k) \rightarrow G L(n, k)$$

  that sends a pair of matrices to their product is a morphism.

  Prove that any morphism from $\mathbb{A}_{k}^{n}$ to $\mathbb{A}_{k}^{1}\setminus\{0\}$ is constant.

  Prove that for $n \geqslant 2$ any morphism from $\mathbb{P}_{k}^{n}$ to $\mathbb{P}_{k}^{1}$ is constant.

  comment

Algebraic Topology

• Paper 2, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) State a suitable version of the Seifert-van Kampen theorem and use it to calculate the fundamental groups of the torus $T^{2}:=S^{1} \times S^{1}$ and of the real projective plane $\mathbb{R P}^{2}$.

  (b) Show that there are no covering maps $T^{2} \rightarrow \mathbb{R} \mathbb{P}^{2}$ or $\mathbb{R P}^{2} \rightarrow T^{2}$.

  (c) Consider the following covering space of $S^{1} \vee S^{1}$ :

  

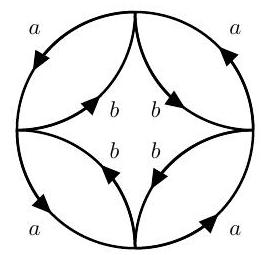
  Here the line segments labelled $a$ and $b$ are mapped to the two different copies of $S^{1}$ contained in $S^{1} \vee S^{1}$, with orientations as indicated.

  Using the Galois correspondence with basepoints, identify a subgroup of

  $$\pi_{1}\left(S^{1} \vee S^{1}, x_{0}\right)=F_{2}$$

  (where $x_{0}$ is the wedge point) that corresponds to this covering space.

  comment

Analysis of Functions

• Paper 2, Section II, H

  Analysis of Functions | Part II, 2021

  Define the Schwartz space, $\mathscr{S}\left(\mathbb{R}^{n}\right)$, and the space of tempered distributions, $\mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$, stating what it means for a sequence to converge in each space.

  For a $C^{k}$ function $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$, and non-negative integers $N, k$, we say $f \in X_{N, k}$ if

  $$\|f\|_{N, k}:=\sup _{x \in \mathbb{R}^{n} ;|\alpha| \leqslant k}\left|\left(1+|x|^{2}\right)^{\frac{N}{2}} D^{\alpha} f(x)\right|<\infty$$

  You may assume that $X_{N, k}$ equipped with $\|\cdot\|_{N, k}$ is a Banach space in which $\mathscr{S}\left(\mathbb{R}^{n}\right)$ is dense.

  (a) Show that if $u \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ there exist $N, k \in \mathbb{Z}_{\geqslant 0}$ and $C>0$ such that

  $$|u[\phi]| \leqslant C\|\phi\|_{N, k} \text { for all } \phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$$

  Deduce that there exists a unique $\tilde{u} \in X_{N, k}^{\prime}$ such that $\tilde{u}[\phi]=u[\phi]$ for all $\phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$.

  (b) Recall that $v \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ is positive if $v[\phi] \geqslant 0$ for all $\phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$ satisfying $\phi \geqslant 0$. Show that if $v \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ is positive, then there exist $M \in \mathbb{Z}_{\geqslant 0}$ and $K>0$ such that

  $$|v[\phi]| \leqslant K\|\phi\|_{M, 0}, \quad \text { for all } \phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$$

  $\left[\right.$ Hint: Note that $\left.|\phi(x)| \leqslant\|\phi\|_{M, 0}\left(1+|x|^{2}\right)^{-\frac{M}{2}} \cdot\right]$

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, 36B

  Applications of Quantum Mechanics | Part II, 2021

  (a) The $s$-wave solution $\psi_{0}$ for the scattering problem of a particle of mass $m$ and momentum $\hbar k$ has the asymptotic form

  $$\psi_{0}(r) \sim \frac{A}{r}[\sin (k r)+g(k) \cos (k r)]$$

  Define the phase shift $\delta_{0}$ and verify that $\tan \delta_{0}=g(k)$.

  (b) Define the scattering amplitude $f$. For a spherically symmetric potential of finite range, starting from $\sigma_{T}=\int|f|^{2} d \Omega$, derive the expression

  $$\sigma_{T}=\frac{4 \pi}{k^{2}} \sum_{l=0}^{\infty}(2 l+1) \sin ^{2} \delta_{l}$$

  giving the cross-section $\sigma_{T}$ in terms of the phase shifts $\delta_{l}$ of the partial waves.

  (c) For $g(k)=-k / K$ with $K>0$, show that a bound state exists and compute its energy. Neglecting the contributions from partial waves with $l>0$, show that

  $$\sigma_{T} \approx \frac{4 \pi}{K^{2}+k^{2}}$$

  (d) For $g(k)=\gamma /\left(K_{0}-k\right)$ with $K_{0}>0, \gamma>0$ compute the $s$-wave contribution to $\sigma_{T}$. Working to leading order in $\gamma \ll K_{0}$, show that $\sigma_{T}$ has a local maximum at $k=K_{0}$. Interpret this fact in terms of a resonance and compute its energy and decay width.

  comment

Applied Probability

• Paper 2, Section II, $28 K$

  Applied Probability | Part II, 2021

  Let $X$ be an irreducible, non-explosive, continuous-time Markov process on the state space $\mathbb{Z}$ with generator $Q=\left(q_{x, y}\right)_{x, y \in \mathbb{Z}}$.

  (a) Define its jump chain $Y$ and prove that it is a discrete-time Markov chain.

  (b) Define what it means for $X$ to be recurrent and prove that $X$ is recurrent if and only if its jump chain $Y$ is recurrent. Prove also that this is the case if the transition semigroup $\left(p_{x, y}(t)\right)$ satisfies

  $$\int_{0}^{\infty} p_{0,0}(t) d t=\infty$$

  (c) Show that $X$ is recurrent for at least one of the following generators:

  $$\begin{array}{cc} q_{x, y}=(1+|x|)^{-2} e^{-|x-y|^{2}} & (x \neq y), \\ q_{x, y}=(1+|x-y|)^{-2} e^{-|x|^{2}} & (x \neq y) . \end{array}$$

  [Hint: You may use that the semigroup associated with a $Q$-matrix on $\mathbb{Z}$ such that $q_{x, y}$ depends only on $x-y$ (and has sufficient decay) can be written as

  $$p_{x, y}(t)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} e^{-t \lambda(k)} e^{i k(x-y)} d k$$

  where $\lambda(k)=\sum_{y} q_{0, y}\left(1-e^{i k y}\right)$. You may also find the bound $1-\cos x \leqslant x^{2} / 2$ useful. $]$

  comment

Asymptotic Methods

• Paper 2, Section II, 32A

  Asymptotic Methods | Part II, 2021

  (a) Let $x(t)$ and $\phi_{n}(t)$, for $n=0,1,2, \ldots$, be real-valued functions on $\mathbb{R}$.

  (i) Define what it means for the sequence $\left\{\phi_{n}(t)\right\}_{n=0}^{\infty}$ to be an asymptotic sequence as $t \rightarrow \infty$.

  (ii) Define what it means for $x(t)$ to have the asymptotic expansion

  $$x(t) \sim \sum_{n=0}^{\infty} a_{n} \phi_{n}(t) \quad \text { as } \quad t \rightarrow \infty$$

  (b) Use the method of stationary phase to calculate the leading-order asymptotic approximation as $x \rightarrow \infty$ of

  $$I(x)=\int_{0}^{1} \sin \left(x\left(2 t^{4}-t^{2}\right)\right) d t$$

  [You may assume that $\int_{-\infty}^{\infty} e^{i u^{2}} d u=\sqrt{\pi} e^{i \pi / 4}$.]

  (c) Use Laplace's method to calculate the leading-order asymptotic approximation as $x \rightarrow \infty$ of

  $$J(x)=\int_{0}^{1} \sinh \left(x\left(2 t^{4}-t^{2}\right)\right) d t$$

  [In parts (b) and (c) you should include brief qualitative reasons for the origin of the leading-order contributions, but you do not need to give a formal justification.]

  comment

Automata and Formal Languages

• Paper 2, Section I, F

  Automata and Formal Languages | Part II, 2021

  Assuming the definition of a deterministic finite-state automaton (DFA) $D=$ $\left(Q, \Sigma, \delta, q_{0}, F\right)$, what is the extended transition function $\hat{\delta}$ for $D$ ? Also assuming the definition of a nondeterministic finite-state automaton (NFA) $N$, what is $\hat{\delta}$ in this case?

  Define the languages accepted by $D$ and $N$, respectively, in terms of $\hat{\delta}$.

  Given an NFA $N$ as above, describe the subset construction and show that the resulting DFA $\bar{N}$ accepts the same language as $N$. If $N$ has one accept state then how many does $\bar{N}$ have?

  comment

Classical Dynamics

• Paper 2, Section I, D

  Classical Dynamics | Part II, 2021

  Show that, in a uniform gravitational field, the net gravitational torque on a system of particles, about its centre of mass, is zero.

  Let $S$ be an inertial frame of reference, and let $S^{\prime}$ be the frame of reference with the same origin and rotating with angular velocity $\boldsymbol{\omega}(t)$ with respect to $S$. You may assume that the rates of change of a vector $v$ observed in the two frames are related by

  $$\left(\frac{d \mathbf{v}}{d t}\right)_{S}=\left(\frac{d \mathbf{v}}{d t}\right)_{S^{\prime}}+\omega \times \mathbf{v} .$$

  Derive Euler's equations for the torque-free motion of a rigid body.

  Show that the general torque-free motion of a symmetric top involves precession of the angular-velocity vector about the symmetry axis of the body. Determine how the direction and rate of precession depend on the moments of inertia of the body and its angular velocity.

  comment

• Paper 2, Section II, D

  Classical Dynamics | Part II, 2021

  (a) Show that the Hamiltonian

  $$H=\frac{1}{2} p^{2}+\frac{1}{2} \omega^{2} q^{2},$$

  where $\omega$ is a positive constant, describes a simple harmonic oscillator with angular frequency $\omega$. Show that the energy $E$ and the action $I$ of the oscillator are related by $E=\omega I$.

  (b) Let $0<\epsilon<2$ be a constant. Verify that the differential equation

  $$\ddot{x}+\frac{x}{(\epsilon t)^{2}}=0 \quad \text { subject to } \quad x(1)=0, \quad \dot{x}(1)=1$$

  is solved by

  $$x(t)=\frac{\sqrt{t}}{k} \sin (k \log t)$$

  when $t>1$, where $k$ is a constant you should determine in terms of $\epsilon$.

  (c) Show that the solution in part (b) obeys

  $$\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \frac{x^{2}}{(\epsilon t)^{2}}=\frac{1-\cos (2 k \log t)+2 k \sin (2 k \log t)+4 k^{2}}{8 k^{2} t}$$

  Hence show that the fractional variation of the action in the limit $\epsilon \ll 1$ is $O(\epsilon)$, but that these variations do not accumulate. Comment on this behaviour in relation to the theory of adiabatic invariance.

  comment

Coding and Cryptography

• Paper 2, Section I, K

  Coding and Cryptography | Part II, 2021

  State Shannon's noisy coding theorem for a binary symmetric channel, defining the terms involved.

  Suppose a channel matrix, with output alphabet of size $n$, is such that the entries in each row are the elements of the set $\left\{p_{1}, \ldots, p_{n}\right\}$ in some order. Further suppose that all columns are permutations of one another. Show that the channel's information capacity $C$ is given by

  $$C=\log n+\sum_{i=1}^{n} p_{i} \log p_{i}$$

  Show that the information capacity of the channel matrix

  $$\left(\begin{array}{cccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{6} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} \end{array}\right)$$

  is given by $C=\frac{5}{3}-\log 3$.

  comment

• Paper 2, Section II, $12 K$

  Coding and Cryptography | Part II, 2021

  (a) Define what it means to say that $C$ is a binary cyclic code. Explain the bijection between the set of binary cyclic codes of length $n$ and the factors of $X^{n}-1$ in $\mathbb{F}_{2}[X]$.

  (b) What is a linear feedback shift register?

  Suppose that $M: \mathbb{F}_{2}^{d} \rightarrow \mathbb{F}_{2}^{d}$ is a linear feedback shift register. Further suppose $\mathbf{0} \neq \mathbf{x} \in \mathbb{F}_{2}^{d}$ and $k$ is a positive integer such that $M^{k} \mathbf{x}=\mathbf{x}$. Let $H$ be the $d \times k$ matrix $\left(\mathbf{x}, M \mathbf{x}, \ldots, M^{k-1} \mathbf{x}\right)$. Considering $H$ as a parity check matrix of a code $C$, show that $C$ is a binary cyclic code.

  (c) Suppose that $C$ is a binary cyclic code. Prove that, if $C$ does not contain the codeword $11 . . .1$, then all codewords in $C$ have even weight.

  comment

Cosmology

• Paper 2, Section I, 9B

  Cosmology | Part II, 2021

  (a) The generalised Boltzmann distribution $P(\mathbf{p})$ is given by

  $$P(\mathbf{p})=\frac{e^{-\beta\left(E_{\mathbf{p}} n_{\mathbf{p}}-\mu n_{\mathbf{p}}\right)}}{\mathcal{Z}_{\mathbf{p}}}$$

  where $\beta=\left(k_{B} T\right)^{-1}, \mu$ is the chemical potential,

  $$\mathcal{Z}_{\mathbf{p}}=\sum_{n_{\mathbf{p}}} e^{-\beta\left(E_{\mathbf{p}} n_{\mathbf{p}}-\mu n_{\mathbf{p}}\right)}, \quad E_{\mathbf{p}}=\sqrt{m^{2} c^{4}+p^{2} c^{2}} \quad \text { and } \quad p=|\mathbf{p}|$$

  Find the average particle number $\langle N(\mathbf{p})\rangle$ with momentum $\mathbf{p}$, assuming that all particles have rest mass $m$ and are either

  (i) bosons, or

  (ii) fermions .

  (b) The photon total number density $n_{\gamma}$ is given by

  $$n_{\gamma}=\frac{2 \zeta(3)}{\pi^{2} \hbar^{3} c^{3}}\left(k_{B} T\right)^{3}$$

  where $\zeta(3) \approx 1.2$. Consider now the fractional ionisation of hydrogen

  $$X_{e}=\frac{n_{e}}{n_{e}+n_{H}}$$

  In our universe $n_{e}+n_{H}=n_{p}+n_{H} \approx \eta n_{\gamma}$, where $\eta \sim 10^{-9}$ is the baryon-to-photon number density. Find an expression for the ratio

  $$\frac{1-X_{e}}{X_{e}^{2}}$$

  in terms of $\eta,\left(k_{B} T\right)$, the electron mass $m_{e}$, the speed of light $c$ and the ionisation energy of hydrogen $I \approx 13.6 \mathrm{eV}$.

  One might expect neutral hydrogen to form at a temperature $k_{B} T \sim I$, but instead in our universe it happens at the much lower temperature $k_{B} T \approx 0.3 \mathrm{eV}$. Briefly explain why this happens.

  [You may use without proof the Saha equation

  $$\frac{n_{H}}{n_{e}^{2}}=\left(\frac{2 \pi \hbar^{2}}{m_{e} k_{B} T}\right)^{3 / 2} e^{\beta I}$$

  for chemical equilibrium in the reaction $\left.e^{-}+p^{+} \leftrightarrow H+\gamma .\right]$

  comment

Differential Geometry

• Paper 2, Section II, $26 \mathbf{F}$

  Differential Geometry | Part II, 2021

  Let $U$ be a domain in $\mathbb{R}^{2}$, and let $\phi: U \rightarrow \mathbb{R}^{3}$ be a smooth map. Define what it means for $\phi$ to be an immersion. What does it mean for an immersion to be isothermal?

  Write down a formula for the mean curvature of an immersion in terms of the first and second fundamental forms. What does it mean for an immersed surface to be minimal? Assume that $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$ is an isothermal immersion. Prove that it is minimal if and only if $x, y, z$ are harmonic functions of $u, v$.

  For $u \in \mathbb{R}, v \in[0,2 \pi]$, and smooth functions $f, g: \mathbb{R} \rightarrow \mathbb{R}$, assume that

  $$\phi(u, v)=(f(u) \cos v, f(u) \sin v, g(u))$$

  is an isothermal immersion. Find all possible pairs $(f, g)$ such that this immersion is minimal.

  comment

Dynamical Systems

• Paper 2, Section II, A

  Dynamical Systems | Part II, 2021

  Consider a modified van der Pol system defined by

  $$\begin{aligned} &\dot{x}=y-\mu\left(\frac{1}{3} x^{3}-x\right) \\ &\dot{y}=-x+F \end{aligned}$$

  where $\mu>0$ and $F$ are constants.

  (a) A parallelogram PQRS of width $2 L$ is defined by

  $$\begin{array}{ll} P=(L, \mu f(L)), & Q=(L, 2 L-\mu f(L)) \\ R=(-L,-\mu f(L)), & S=(-L, \mu f(L)-2 L) \end{array}$$

  where $f(L)=\frac{1}{3} L^{3}-L$. Show that if $L$ is sufficiently large then trajectories never leave the region inside the parallelogram.

  Hence show that if $F^{2}<1$ there must be a periodic orbit. Explain your reasoning carefully.

  (b) Use the energy-balance method to analyse the behaviour of the system for $\mu \ll 1$, identifying the difference in behaviours between $F^{2}<1$ and $F^{2}>1$.

  (c) Describe the behaviour of the system for $\mu \gg 1$, using sketches of the phase plane to illustrate your arguments for the cases $0<F<1$ and $F>1$.

  comment

Fluid Dynamics II

• Paper 2, Section II, 39A

  Fluid Dynamics II | Part II, 2021

  (a) Incompressible fluid of viscosity $\mu$ fills the thin, slowly varying gap between rigid boundaries at $z=0$ and $z=h(x, y)>0$. The boundary at $z=0$ translates in its own plane with a constant velocity $\mathbf{U}=(U, 0,0)$, while the other boundary is stationary. If $h$ has typical magnitude $H$ and varies on a lengthscale $L$, state conditions for the lubrication approximation to be appropriate.

  Write down the lubrication equations for this problem and show that the horizontal volume flux $\mathbf{q}=\left(q_{x}, q_{y}, 0\right)$ is given by

  $$\mathbf{q}=\frac{\mathbf{U} h}{2}-\frac{h^{3}}{12 \mu} \nabla p$$

  where $p(x, y)$ is the pressure.

  Explain why $\mathbf{q}=\nabla \wedge(0,0, \psi)$ for some function $\psi(x, y)$. Deduce that $\psi$ satisfies the equation

  $$\nabla \cdot\left(\frac{1}{h^{3}} \nabla \psi\right)=-\frac{U}{h^{3}} \frac{\partial h}{\partial y}$$

  (b) Now consider the case $\mathbf{U}=\mathbf{0}, h=h_{0}$ for $r>a$ and $h=h_{1}$ for $r<a$, where $h_{0}, h_{1}$ and $a$ are constants, and $(r, \theta)$ are polar coordinates. A uniform pressure gradient $\nabla p=-G \mathbf{e}_{x}$ is applied at infinity. Show that $\psi \sim A r \sin \theta$ as $r \rightarrow \infty$, where the constant $A$ is to be determined.

  Given that $a \gg h_{0}, h_{1}$, you may assume that the equations of part (a) apply for $r<a$ and $r>a$, and are subject to conditions that the radial component $q_{r}$ of the volume flux and the pressure $p$ are both continuous across $r=a$. Show that these continuity conditions imply that

  $$\left[\frac{\partial \psi}{\partial \theta}\right]_{-}^{+}=0 \quad \text { and }\left[\frac{1}{h^{3}} \frac{\partial \psi}{\partial r}\right]_{-}^{+}=0$$

  respectively, where []$_{-}^{+}$denotes the jump across $r=a$.

  Hence determine $\psi(r, \theta)$ and deduce that the total flux through $r=a$ is given by

  $$\frac{4 A a h_{1}^{3}}{h_{0}^{3}+h_{1}^{3}}$$

  comment

Further Complex Methods

• Paper 2, Section I, 7E

  Further Complex Methods | Part II, 2021

  The function $w(z)$ satisfies the differential equation

  $$\tag{†} \frac{d^{2} w}{d z^{2}}+p(z) \frac{d w}{d z}+q(z) w=0$$

  where $p(z)$ and $q(z)$ are complex analytic functions except, possibly, for isolated singularities in $\overline{\mathbb{C}}=\mathbb{C} \cup\{\infty\}$ (the extended complex plane).

  (a) Given equation $(†)$, state the conditions for a point $z_{0} \in \mathbb{C}$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  (b) Now consider $z_{0}=\infty$ and use a suitable change of variables $z \rightarrow t$, with $y(t)=w(z)$, to rewrite $(†)$ as a differential equation that is satisfied by $y(t)$. Hence, deduce the conditions for $z_{0}=\infty$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  [In each case, you should express your answer in terms of the functions $p$ and $q$.]

  (c) Use the results above to prove that any equation of the form ( $\dagger$ ) must have at least one singular point in $\overline{\mathbb{C}}$.

  comment

• Paper 2, Section II, 13E

  Further Complex Methods | Part II, 2021

  The temperature $T(x, t)$ in a semi-infinite bar $(0 \leqslant x<\infty)$ satisfies the heat equation

  $$\frac{\partial T}{\partial t}=\kappa \frac{\partial^{2} T}{\partial x^{2}}, \quad \text { for } x>0 \text { and } t>0$$

  where $\kappa$ is a positive constant.

  For $t<0$, the bar is at zero temperature. For $t \geqslant 0$, the temperature is subject to the boundary conditions

  $$T(0, t)=a\left(1-e^{-b t}\right),$$

  where $a$ and $b$ are positive constants, and $T(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (a) Show that the Laplace transform of $T(x, t)$ with respect to $t$ takes the form

  $$\hat{T}(x, p)=\hat{f}(p) e^{-x \sqrt{p / \kappa}}$$

  and find $\hat{f}(p)$. Hence write $\hat{T}(x, p)$ in terms of $a, b, \kappa, p$ and $x$.

  (b) By performing the inverse Laplace transform using contour integration, show that for $t \geqslant 0$

  $$T(x, t)=a\left[1-e^{-b t} \cos \left(\sqrt{\frac{b}{\kappa}} x\right)\right]+\frac{2 a b}{\pi} \mathcal{P} \int_{0}^{\infty} \frac{e^{-v^{2} t} \sin (x v / \sqrt{\kappa})}{v\left(v^{2}-b\right)} d v$$

  comment

Galois Theory

• Paper 2, Section II, 18I

  Galois Theory | Part II, 2021

  (a) Let $f(x) \in \mathbb{F}_{q}[x]$ be a polynomial of degree $n$, and let $L$ be its splitting field.

  (i) Suppose that $f$ is irreducible. Compute $\operatorname{Gal}(f)$, carefully stating any theorems you use.

  (ii) Now suppose that $f(x)$ factors as $f=h_{1} \cdots h_{r}$ in $\mathbb{F}_{q}[x]$, with each $h_{i}$ irreducible, and $h_{i} \neq h_{j}$ if $i \neq j$. Compute $\operatorname{Gal}(f)$, carefully stating any theorems you use.

  (iii) Explain why $L / \mathbb{F}_{q}$ is a cyclotomic extension. Define the corresponding homomorphism $\operatorname{Gal}\left(L / \mathbb{F}_{q}\right) \hookrightarrow(\mathbb{Z} / m \mathbb{Z})^{*}$ for this extension (for a suitable integer $m$ ), and compute its image.

  (b) Compute $\operatorname{Gal}(f)$ for the polynomial $f=x^{4}+8 x+12 \in \mathbb{Q}[x]$. [You may assume that $f$ is irreducible and that its discriminant is $576^{2}$.]

  comment

General Relativity

• Paper 2, Section II, 38C

  General Relativity | Part II, 2021

  Consider the following metric for a 3-dimensional, static and rotationally symmetric Lorentzian manifold:

  $$d s^{2}=r^{-2}\left(-d t^{2}+d r^{2}\right)+r^{2} d \theta^{2}$$

  (a) Write down a Lagrangian $\mathcal{L}$ for arbitrary geodesics in this metric, if the geodesic is affinely parameterized with respect to $\lambda$. What condition may be imposed to distinguish spacelike, timelike, and null geodesics?

  (b) Find the three constants of motion for any geodesic.

  (c) Two observation stations are sitting at radii $r=R$ and $r=2 R$ respectively, and at the same angular coordinate. Each is accelerating so as to remain stationary with respect to time translations. At $t=0$ a photon is emitted from the naked singularity at $r=0$.

  (i) At what time $t_{1}$ does the photon reach the inner station?

  (ii) Express the frequency $\nu_{2}$ of the photon at the outer station in terms of the frequency $\nu_{1}$ at the inner station. Explain whether the photon is redshifted or blueshifted as it travels.

  (d) Consider a complete (i.e. infinite in both directions) spacelike geodesic on a constant- $t$ slice with impact parameter $b=r_{\min }>0$. What is the angle $\Delta \theta$ between the two asymptotes of the geodesic at $r=\infty$ ? [You need not be concerned with the sign of $\Delta \theta$ or the periodicity of the $\theta$ coordinate.]

  [Hint: You may find integration by substitution useful.]

  comment

Graph Theory

• Paper 2, Section II, 17 G

  Graph Theory | Part II, 2021

  (a) Define a tree and what it means for a graph to be acyclic. Show that if $G$ is an acyclic graph on $n$ vertices then $e(G) \leqslant n-1$. [You may use the fact that a spanning tree on $n$ vertices has $n-1$ edges.]

  (b) Show that any 3-regular graph on $n$ vertices contains a cycle of length $\leqslant$ $100 \log n$. Hence show that there exists $n_{0}$ such that every 3-regular graph on more than $n_{0}$ vertices must contain two cycles $C_{1}, C_{2}$ with disjoint vertex sets.

  (c) An unfriendly partition of a graph $G=(V, E)$ is a partition $V=A \cup B$, where $A, B \neq \emptyset$, such that every vertex $v \in A$ has $|N(v) \cap B| \geqslant|N(v) \cap A|$ and every $v \in B$ has $|N(v) \cap A| \geqslant|N(v) \cap B|$. Show that every graph $G$ with $|G| \geqslant 2$ has an unfriendly partition.

  (d) A friendly partition of a graph $G=(V, E)$ is a partition $V=S \cup T$, where $S, T \neq \emptyset$, such that every vertex $v \in S$ has $|N(v) \cap S| \geqslant|N(v) \cap T|$ and every $v \in T$ has $|N(v) \cap T| \geqslant|N(v) \cap S|$. Give an example of a 3-regular graph (on at least 1 vertex) that does not have a friendly partition. Using part (b), show that for large enough $n_{0}$ every 3-regular graph $G$ with $|G| \geqslant n_{0}$ has a friendly partition.

  comment

Integrable Systems

• Paper 2, Section II, 34D

  Integrable Systems | Part II, 2021

  (a) Explain briefly how the linear operators $L=-\partial_{x}^{2}+u(x, t)$ and $A=4 \partial_{x}^{3}-3 u \partial_{x}-$ $3 \partial_{x} u$ can be used to give a Lax-pair formulation of the $\mathrm{KdV}$ equation $u_{t}+u_{x x x}-6 u u_{x}=0$.

  (b) Give a brief definition of the scattering data

  $$\mathcal{S}_{u(t)}=\left\{\{R(k, t)\}_{k \in \mathbb{R}},\left\{-\kappa_{n}(t)^{2}, c_{n}(t)\right\}_{n=1}^{N}\right\}$$

  attached to a smooth solution $u=u(x, t)$ of the KdV equation at time $t$. [You may assume $u(x, t)$ to be rapidly decreasing in $x$.] State the time dependence of $\kappa_{n}(t)$ and $c_{n}(t)$, and derive the time dependence of $R(k, t)$ from the Lax-pair formulation.

  (c) Show that

  $$F(x, t)=\sum_{n=1}^{N} c_{n}(t)^{2} e^{-\kappa_{n}(t) x}+\frac{1}{2 \pi} \int_{-\infty}^{\infty} R(k, t) e^{i k x} d k$$

  satisfies $\partial_{t} F+8 \partial_{x}^{3} F=0$. Now let $K(x, y, t)$ be the solution of the equation

  $$K(x, y, t)+F(x+y, t)+\int_{x}^{\infty} K(x, z, t) F(z+y, t) d z=0$$

  and let $u(x, t)=-2 \partial_{x} \phi(x, t)$, where $\phi(x, t)=K(x, x, t)$. Defining $G(x, y, t)$ by $G=$ $\left(\partial_{x}^{2}-\partial_{y}^{2}-u(x, t)\right) K(x, y, t)$, show that

  $$G(x, y, t)+\int_{x}^{\infty} G(x, z, t) F(z+y, t) d z=0$$

  (d) Given that $K(x, y, t)$ obeys the equations

  $$\begin{aligned} \left(\partial_{x}^{2}-\partial_{y}^{2}\right) K-u K &=0 \\ \left(\partial_{t}+4 \partial_{x}^{3}+4 \partial_{y}^{3}\right) K-3\left(\partial_{x} u\right) K-6 u \partial_{x} K &=0 \end{aligned}$$

  where $u=u(x, t)$, deduce that

  $$\partial_{t} K+\left(\partial_{x}+\partial_{y}\right)^{3} K-3 u\left(\partial_{x}+\partial_{y}\right) K=0$$

  and hence that $u$ solves the $\mathrm{KdV}$ equation.

  comment

Linear Analysis

• Paper 2, Section II, 22H

  Linear Analysis | Part II, 2021

  (a) Let $V$ be a real normed vector space. Show that any proper subspace of $V$ has empty interior.

  Assuming $V$ to be infinite-dimensional and complete, prove that any algebraic basis of $V$ is uncountable. [The Baire category theorem can be used if stated properly.] Deduce that the vector space of polynomials with real coefficients cannot be equipped with a complete norm, i.e. a norm that makes it complete.

  (b) Suppose that $\|\cdot\|_{1}$ and $\|\cdot\|_{2}$ are norms on a vector space $V$ such that $\left(V,\|\cdot\|_{1}\right)$ and $\left(V,\|\cdot\|_{2}\right)$ are both complete. Prove that if there exists $C_{1}>0$ such that $\|x\|_{2} \leqslant C_{1}\|x\|_{1}$ for all $x \in V$, then there exists $C_{2}>0$ such that $\|x\|_{1} \leqslant C_{2}\|x\|_{2}$ for all $x \in V$. Is this still true without the assumption that $\left(V,\|\cdot\|_{1}\right)$ and $\left(V,\|\cdot\|_{2}\right)$ are both complete? Justify your answer.

  (c) Let $V$ be a real normed vector space (not necessarily complete) and $V^{*}$ be the set of linear continuous forms $f: V \rightarrow \mathbb{R}$. Let $\left(x_{n}\right)_{n \geqslant 1}$ be a sequence in $V$ such that $\sum_{n \geqslant 1}\left|f\left(x_{n}\right)\right|<\infty$ for all $f \in V^{*}$. Prove that

  $$\sup _{\|f\|_{V^{*} \leqslant 1}} \sum_{n \geqslant 1}\left|f\left(x_{n}\right)\right|<\infty .$$

  comment

Logic and Set Theory

• Paper 2, Section II, G

  Logic and Set Theory | Part II, 2021

  Write down the inductive definition of ordinal exponentiation. Show that $\omega^{\alpha} \geqslant \alpha$ for every ordinal $\alpha$. Deduce that, for every ordinal $\alpha$, there is a least ordinal $\alpha^{*}$ with $\omega^{\alpha^{*}}>\alpha$. Show that, if $\alpha \neq 0$, then $\alpha^{*}$ must be a successor ordinal.

  Now let $\alpha$ be a non-zero ordinal. Show that there exist ordinals $\beta$ and $\gamma$, where $\gamma<\alpha$, and a positive integer $n$ such that $\alpha=\omega^{\beta} n+\gamma$. Hence, or otherwise, show that $\alpha$ can be written in the form

  $$\alpha=\omega^{\beta_{1}} n_{1}+\omega^{\beta_{2}} n_{2}+\cdots+\omega^{\beta_{k}} n_{k}$$

  where $k, n_{1}, n_{2}, \ldots, n_{k}$ are positive integers and $\beta_{1}>\beta_{2}>\cdots>\beta_{k}$ are ordinals. [We call this the Cantor normal form of $\alpha$, and you may henceforth assume that it is unique.]

  Given ordinals $\delta_{1}, \delta_{2}$ and positive integers $m_{1}, m_{2}$ find the Cantor normal form of $\omega^{\delta_{1}} m_{1}+\omega^{\delta_{2}} m_{2}$. Hence, or otherwise, given non-zero ordinals $\alpha$ and $\alpha^{\prime}$, find the Cantor normal form of $\alpha+\alpha^{\prime}$ in terms of the Cantor normal forms

  $$\alpha=\omega^{\beta_{1}} n_{1}+\omega^{\beta_{2}} n_{2}+\cdots+\omega^{\beta_{k}} n_{k}$$

  and

  $$\alpha^{\prime}=\omega^{\beta_{1}^{\prime}} n_{1}^{\prime}+\omega^{\beta_{2}^{\prime}} n_{2}^{\prime}+\cdots+\omega^{\beta_{k^{\prime}}^{\prime}} n_{k^{\prime}}^{\prime}$$

  of $\alpha$ and $\alpha^{\prime}$.

  comment

Mathematical Biology

• Paper 2, Section I, E

  Mathematical Biology | Part II, 2021

  Consider a stochastic birth-death process in a population of size $n(t)$, where deaths occur in pairs for $n \geqslant 2$. The probability per unit time of a birth, $n \rightarrow n+1$ for $n \geqslant 0$, is $b$, that of a pair of deaths, $n \rightarrow n-2$ for $n \geqslant 2$, is $d n$, and that of the death of a lonely singleton, $1 \rightarrow 0$, is $D$.

  (a) Write down the master equation for $p_{n}(t)$, the probability of a population of size $n$ at time $t$, distinguishing between the cases $n \geqslant 2, n=0$ and $n=1$.

  (b) For a function $f(n), n \geqslant 0$, show carefully that

  $$\frac{d}{d t}\langle f(n)\rangle=b \sum_{n=0}^{\infty}\left(f_{n+1}-f_{n}\right) p_{n}-d \sum_{n=2}^{\infty}\left(f_{n}-f_{n-2}\right) n p_{n}-D\left(f_{1}-f_{0}\right) p_{1}$$

  where $f_{n}=f(n)$.

  (c) Deduce the evolution equation for the mean $\mu(t)=\langle n\rangle$, and simplify it for the case $D=2 d$.

  (d) For the same value of $D$, show that

  $$\frac{d}{d t}\left\langle n^{2}\right\rangle=b(2 \mu+1)-4 d\left(\left\langle n^{2}\right\rangle-\mu\right)-2 d p_{1}$$

  Deduce that the variance $\sigma^{2}$ in the stationary state for $b, d>0$ satisfies

  $$\frac{3 b}{4 d}-\frac{1}{2}<\sigma^{2}<\frac{3 b}{4 d}$$

  comment

Mathematics of Machine Learning

• Paper 2, Section II, J

  Mathematics of Machine Learning | Part II, 2021

  (a) What is meant by the subdifferential $\partial f(x)$ of a convex function $f: \mathbb{R}^{d} \rightarrow \mathbb{R}$ at $x \in \mathbb{R}^{d}$ ? Write down the subdifferential $\partial f(x)$ of the function $f: \mathbb{R} \rightarrow \mathbb{R}$ given by $f(x)=\gamma|x|$, where $\gamma>0$.

  Show that $x$ minimises $f$ if and only if $0 \in \partial f(x)$.

  What does it mean for a function $f: \mathbb{R}^{d} \rightarrow \mathbb{R}$ to be strictly convex? Show that any minimiser of a strictly convex function must be unique.

  (b) Suppose we have input-output pairs $\left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right) \in\{-1,1\}^{p} \times\{-1,1\}$ with $p \geqslant 2$. Consider the objective function

  $$f(\beta)=\frac{1}{n} \sum_{i=1}^{n} \exp \left(-y_{i} x_{i}^{T} \beta\right)+\gamma\|\beta\|_{1}$$

  where $\beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{T}$ and $\gamma>0$. Assume that $\left(y_{i}\right)_{i=1}^{n} \neq\left(x_{i 1}\right)_{i=1}^{n}$. Fix $\beta_{2}, \ldots, \beta_{p}$ and define

  $$\kappa_{1}=\sum_{\substack{1 \leqslant i \leqslant n: \\ x_{i 1} \neq y_{i}}} \exp \left(-y_{i} \eta_{i}\right) \quad \text { and } \quad \kappa_{2}=\sum_{i=1}^{n} \exp \left(-y_{i} \eta_{i}\right)$$

  where $\eta_{i}=\sum_{j=2}^{p} x_{i j} \beta_{j}$ for $i=1, \ldots, n$. Show that if $\left|2 \kappa_{1}-\kappa_{2}\right| \leqslant \gamma$, then

  $$\operatorname{argmin}_{\beta_{1} \in \mathbb{R}} f\left(\beta_{1}, \beta_{2}, \ldots, \beta_{p}\right)=0 .$$

  [You may use any results from the course without proof, other than those whose proof is asked for directly.]

  comment

Number Fields

• Paper 2, Section II, 20G

  Number Fields | Part II, 2021

  Let $K$ be a field containing $\mathbb{Q}$. What does it mean to say that an element of $K$ is algebraic? Show that if $\alpha \in K$ is algebraic and non-zero, then there exists $\beta \in \mathbb{Z}[\alpha]$ such that $\alpha \beta$ is a non-zero (rational) integer.

  Now let $K$ be a number field, with ring of integers $\mathcal{O}_{K}$. Let $R$ be a subring of $\mathcal{O}_{K}$ whose field of fractions equals $K$. Show that every element of $K$ can be written as $r / m$, where $r \in R$ and $m$ is a positive integer.

  Prove that $R$ is a free abelian group of $\operatorname{rank}[K: \mathbb{Q}]$, and that $R$ has finite index in $\mathcal{O}_{K}$. Show also that for every nonzero ideal $I$ of $R$, the index $(R: I)$ of $I$ in $R$ is finite, and that for some positive integer $m, m \mathcal{O}_{K}$ is an ideal of $R$.

  Suppose that for every pair of non-zero ideals $I, J \subset R$, we have

  $$(R: I J)=(R: I)(R: J) .$$

  Show that $R=\mathcal{O}_{K}$.

  [You may assume without proof that $\mathcal{O}_{K}$ is a free abelian group of rank $[K: \mathbb{Q}]$ ] ]

  comment

Number Theory

• Paper 2, Section $I$, I

  Number Theory | Part II, 2021

  Define the Möbius function $\mu$, and explain what it means for it to be multiplicative.

  Show that for every positive integer $n$

  $$\sum_{d \mid n} \frac{\mu(d)^{2}}{\phi(d)}=\frac{n}{\phi(n)}$$

  where $\phi$ is the Euler totient function.

  Fix an integer $k \geqslant 1$. Use the Chinese remainder theorem to show that there are infinitely many positive integers $n$ for which

  $$\mu(n)=\mu(n+1)=\cdots=\mu(n+k)$$

  comment

Numerical Analysis

• Paper 2, Section II, 41E

  Numerical Analysis | Part II, 2021

  (a) Let $\mathbf{x} \in \mathbb{R}^{N}$ and define $\mathbf{y} \in \mathbb{R}^{2 N}$ by

  $$y_{n}= \begin{cases}x_{n}, & 0 \leqslant n \leqslant N-1 \\ x_{2 N-n-1}, & N \leqslant n \leqslant 2 N-1\end{cases}$$

  Let $\mathbf{Y} \in \mathbb{C}^{2 N}$ be defined as the discrete Fourier transform (DFT) of $\mathbf{y}$, i.e.

  $$Y_{k}=\sum_{n=0}^{2 N-1} y_{n} \omega_{2 N}^{n k}, \quad \omega_{2 N}=\exp (-\pi i / N), \quad 0 \leqslant k \leqslant 2 N-1$$

  Show that

  $$Y_{k}=2 \omega_{2 N}^{-k / 2} \sum_{n=0}^{N-1} x_{n} \cos \left[\frac{\pi}{N}\left(n+\frac{1}{2}\right) k\right], \quad 0 \leqslant k \leqslant 2 N-1$$

  (b) Define the discrete cosine transform $(\mathrm{DCT}) \mathcal{C}_{N}: \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$ by

  $$\mathbf{z}=\mathcal{C}_{N} \mathbf{x}, \text { where } z_{k}=\sum_{n=0}^{N-1} x_{n} \cos \left[\frac{\pi}{N}\left(n+\frac{1}{2}\right) k\right], \quad k=0, \ldots, N-1$$

  For $N=2^{p}$ with $p \in \mathbb{N}$, show that, similar to the Fast Fourier Transform (FFT), there exists an algorithm that computes the DCT of a vector of length $N$, where the number of multiplications required is bounded by $C N \log N$, where $C$ is some constant independent of $N$.

  [You may not assume that the FFT algorithm requires $\mathcal{O}(N \log N)$ multiplications to compute the DFT of a vector of length $N$. If you use this, you must prove it.]

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, B

  Principles of Quantum Mechanics | Part II, 2021

  (a) Let $\{|n\rangle\}$ be a basis of eigenstates of a non-degenerate Hamiltonian $H$, with corresponding eigenvalues $\left\{E_{n}\right\}$. Write down an expression for the energy levels of the perturbed Hamiltonian $H+\lambda \Delta H$, correct to second order in the dimensionless constant $\lambda \ll 1$.

  (b) A particle travels in one dimension under the influence of the potential

  $$V(X)=\frac{1}{2} m \omega^{2} X^{2}+\lambda \hbar \omega \frac{X^{3}}{L^{3}}$$

  where $m$ is the mass, $\omega$ a frequency and $L=\sqrt{\hbar / 2 m \omega}$ a length scale. Show that, to first order in $\lambda$, all energy levels coincide with those of the harmonic oscillator. Calculate the energy of the ground state to second order in $\lambda$.

  Does perturbation theory in $\lambda$ converge for this potential? Briefly explain your answer.

  comment

Principles of Statistics

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2021

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. random observations taking values in $[0,1]$ with a continuous distribution function $F$. Let $\hat{F}_{n}(x)=n^{-1} \sum_{i=1}^{n} \mathbf{1}_{\left\{X_{i} \leqslant x\right\}}$ for each $x \in[0,1]$.

  (a) State the Kolmogorov-Smirnov theorem. Explain how this theorem may be used in a goodness-of-fit test for the null hypothesis $H_{0}: F=F_{0}$, with $F_{0}$ continuous.

  (b) Suppose you do not have access to the quantiles of the sampling distribution of the Kolmogorov-Smirnov test statistic. However, you are given i.i.d. samples $Z_{1}, \ldots, Z_{n m}$ with distribution function $F_{0}$. Describe a test of $H_{0}: F=F_{0}$ with size exactly $1 /(m+1)$.

  (c) Now suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. taking values in $[0, \infty)$ with probability density function $f$, with $\sup _{x \geqslant 0}\left(|f(x)|+\left|f^{\prime}(x)\right|\right)<1$. Define the density estimator

  $$\left.\hat{f}_{n}(x)=n^{-2 / 3} \sum_{i=1}^{n} \mathbf{1}_{\left\{X_{i}\right.}-\frac{1}{2 n^{1 / 3}} \leqslant x \leqslant X_{i}+\frac{1}{2 n^{1 / 3}}\right\}, \quad x \geqslant 0 .$$

  Show that for all $x \geqslant 0$ and all $n \geqslant 1$,

  $$\mathbb{E}\left[\left(\hat{f}_{n}(x)-f(x)\right)^{2}\right] \leqslant \frac{2}{n^{2 / 3}} .$$

  comment

Probability and Measure

• Paper 2, Section II, H

  Probability and Measure | Part II, 2021

  Let $(E, \mathcal{E}, \mu)$ be a measure space. A function $f$ is simple if it is of the form $f=\sum_{i=1}^{N} a_{i} 1_{A_{i}}$, where $a_{i} \in \mathbb{R}, N \in \mathbb{N}$ and $A_{i} \in \mathcal{E}$.

  Now let $f:(E, \mathcal{E}, \mu) \rightarrow[0, \infty]$ be a Borel-measurable map. Show that there exists a sequence $f_{n}$ of simple functions such that $f_{n}(x) \rightarrow f(x)$ for all $x \in E$ as $n \rightarrow \infty$.

  Next suppose $f$ is also $\mu$-integrable. Construct a sequence $f_{n}$ of simple $\mu$-integrable functions such that $\int_{E}\left|f_{n}-f\right| d \mu \rightarrow 0$ as $n \rightarrow \infty$.

  Finally, suppose $f$ is also bounded. Show that there exists a sequence $f_{n}$ of simple functions such that $f_{n} \rightarrow f$ uniformly on $E$ as $n \rightarrow \infty$.

  comment

Quantum Information and Computation

• Paper 2, Section I, 10D

  Quantum Information and Computation | Part II, 2021

  Let $\mathcal{B}_{n}$ denote the set of all $n$-bit strings and let $f: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ be a Boolean function which obeys either

  (I) $f(x)=0$ for all $x \in \mathcal{B}_{n}$, or

  (II) $f(x)=0$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Suppose we are given the $n$-qubit state

  $$|\xi\rangle=\frac{1}{\sqrt{2^{n}}} \sum_{x \in \mathcal{B}_{n}}(-1)^{f(x)}|x\rangle$$

  Show how we may determine with certainty whether $f$ is of case (I) or case (II).

  Suppose now that Alice and Bob are separated in space. Alice possesses a quantum oracle for a Boolean function $f_{A}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ and Bob similarly possess a quantum oracle for a Boolean function $f_{B}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$. These functions are arbitrary, except that either

  (1) $f_{A}(x)=f_{B}(x)$ for all $x \in \mathcal{B}_{n}$, or

  (2) $f_{A}(x)=f_{B}(x)$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Alice and Bob each have available a supply of qubits in state $|0\rangle$ and each can apply local quantum operations (including their own function oracle) to any qubits in their possession. Additionally, they can send qubits to each other.

  Show how Bob may decide with certainty which case applies, after he has received $n$ qubits from Alice. [Hint: You may find it helpful to consider the function $h(x)=$ $f_{A}(x) \oplus f_{B}(x)$, where $\oplus$ denotes addition mod 2.]

  comment

• Paper 2, Section II, D

  Quantum Information and Computation | Part II, 2021

  Alice and Bob are separated in space and can communicate only over a noiseless public classical channel, i.e. they can exchange bit string messages perfectly, but the messages can be read by anyone. An eavesdropper Eve constantly monitors the channel, but cannot alter any passing messages. Alice wishes to communicate an $m$-bit string message to Bob whilst keeping it secret from Eve.

  (a) Explain how Alice can do this by the one-time pad method, specifying clearly any additional resource that Alice and Bob need. Explain why in this method, Alice's message does, in fact, remain secure against eavesdropping.

  (b) Suppose now that Alice and Bob do not possess the additional resource needed in part (a) for the one-time pad, but that they instead possess $n$ pairs of qubits, where $n \gg 1$, with each pair being in the state

  $$|\psi\rangle_{A B}=t|00\rangle_{A B}+s|11\rangle_{A B},$$

  where the real parameters $(t, s)$ are known to Alice and Bob and obey $t>s>0$ and $t^{2}+s^{2}=1$. For each qubit pair in state $|\psi\rangle_{A B}$, Alice possesses qubit $A$ and Bob possesses qubit $B$. They each also have available a supply of ancilla qubits, each in state $|0\rangle$, and they can each perform local quantum operations on qubits in their possession.

  Show how Alice, using only local quantum operations, can convert each $|\psi\rangle_{A B}$ state into $\left|\phi^{+}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}+|11\rangle_{A B}\right)$ by a process that succeeds with non-zero probability. [Hint: It may be useful for Alice to start by adjoining an ancilla qubit $|0\rangle_{A^{\prime}}$ and work locally on her two qubits in $\left.|0\rangle_{A^{\prime}}|\psi\rangle_{A B \cdot}\right]$

  Hence, or otherwise, show how Alice can communicate a bit string of expected length $\left(2 s^{2}\right) n$ to Bob in a way that keeps it secure against eavesdropping by Eve.

  comment

Representation Theory

• Paper 2, Section II, I

  Representation Theory | Part II, 2021

  Let $G$ be a finite group and work over $\mathbb{C}$.

  (a) Let $\chi$ be a faithful character of $G$, and suppose that $\chi(g)$ takes precisely $r$ different values as $g$ varies over all the elements of $G$. Show that every irreducible character of $G$ is a constituent of one of the powers $\chi^{0}, \chi^{1}, \ldots, \chi^{r-1}$. [Standard properties of the Vandermonde matrix may be assumed if stated correctly.]

  (b) Assuming that the number of irreducible characters of $G$ is equal to the number of conjugacy classes of $G$, show that the irreducible characters of $G$ form a basis of the complex vector space of all class functions on $G$. Deduce that $g, h \in G$ are conjugate if and only if $\chi(g)=\chi(h)$ for all characters $\chi$ of $G$.

  (c) Let $\chi$ be a character of $G$ which is not faithful. Show that there is some irreducible character $\psi$ of $G$ such that $\left\langle\chi^{n}, \psi\right\rangle=0$ for all integers $n \geqslant 0$.

  comment

Riemann Surfaces

• Paper 2, Section II, F

  Riemann Surfaces | Part II, 2021

  Let $D \subseteq \mathbb{C}$ be a domain, let $(f, U)$ be a function element in $D$, and let $\alpha:[0,1] \rightarrow D$ be a path with $\alpha(0) \in U$. Define what it means for a function element $(g, V)$ to be an analytic continuation of $(f, U)$ along $\alpha$.

  Suppose that $\beta:[0,1] \rightarrow D$ is a path homotopic to $\alpha$ and that $(h, V)$ is an analytic continuation of $(f, U)$ along $\beta$. Suppose, furthermore, that $(f, U)$ can be analytically continued along any path in $D$. Stating carefully any theorems that you use, prove that $g(\alpha(1))=h(\beta(1))$.

  Give an example of a function element $(f, U)$ that can be analytically continued to every point of $\mathbb{C}_{*}$ and a pair of homotopic paths $\alpha, \beta$ in $\mathbb{C}_{*}$ starting in $U$ such that the analytic continuations of $(f, U)$ along $\alpha$ and $\beta$ take different values at $\alpha(1)=\beta(1)$.

  comment

Statistical Modelling

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2021

  Define a generalised linear model for a sample $Y_{1}, \ldots, Y_{n}$ of independent random variables. Define further the concept of the link function. Define the binomial regression model (without the dispersion parameter) with logistic and probit link functions. Which of these is the canonical link function?

  comment

Statistical Physics

• Paper 2, Section II, $37 \mathrm{C}$

  Statistical Physics | Part II, 2021

  (a) What systems are described by microcanonical, canonical and grand canonical ensembles? Under what conditions is the choice of ensemble irrelevant?

  (b) In a simple model a meson consists of two quarks bound in a linear potential, $U(\mathbf{r})=\alpha|\mathbf{r}|$, where $\mathbf{r}$ is the relative displacement of the two quarks and $\alpha$ is a positive constant. You are given that the classical (non-relativistic) Hamiltonian for the meson is

  $$H(\mathbf{P}, \mathbf{R}, \mathbf{p}, \mathbf{r})=\frac{|\mathbf{P}|^{2}}{2 M}+\frac{|\mathbf{p}|^{2}}{2 \mu}+\alpha|\mathbf{r}|$$

  where $M=2 m$ is the total mass, $\mu=m / 2$ is the reduced mass, $\mathbf{P}$ is the total momentum, $\mathbf{p}=\mu d \mathbf{r} / d t$ is the internal momentum, and $\mathbf{R}$ is the centre of mass position.

  (i) Show that the partition function for a single meson in thermal equilibrium at temperature $T$ in a three-dimensional volume $V$ can be written as $Z_{1}=Z_{\text {trans }} Z_{\text {int }}$, where

  $$Z_{\text {trans }}=\frac{V}{(2 \pi \hbar)^{3}} \int d^{3} P e^{-\beta|\mathbf{P}|^{2} /(2 M)}, \quad Z_{\text {int }}=\frac{1}{(2 \pi \hbar)^{3}} \int d^{3} r d^{3} p e^{-\beta|\mathbf{p}|^{2} /(2 \mu)} e^{-\beta \alpha|\mathbf{r}|}$$

  and $\beta=1 /\left(k_{\mathrm{B}} T\right)$

  Evaluate $Z_{\text {trans }}$ and evaluate $Z_{\text {int }}$ in the large-volume limit $\left(\beta \alpha V^{1 / 3} \gg 1\right)$.

  What is the average separation of the quarks within the meson at temperature $T$ ?

  $\left[\right.$ You may assume that $\int_{-\infty}^{\infty} e^{-c x^{2}} d x=\sqrt{\pi / c}$ for $c>0$ ]

  (ii) Now consider an ideal gas of $N$ such mesons in a three-dimensional volume $V$.

  Calculate the total partition function of the gas.

  What is the heat capacity $C_{V} ?$

  comment

Stochastic Financial Models

• Paper 2, Section II, 30K

  Stochastic Financial Models | Part II, 2021

  Consider a one-period market model with $d$ risky assets and one risk-free asset. Let $S_{t}$ denote the vector of prices of the risky assets at time $t \in\{0,1\}$ and let $r$ be the interest rate.

  (a) What does it mean to say a portfolio $\varphi \in \mathbb{R}^{d}$ is an arbitrage for this market?

  (b) An investor wishes to maximise their expected utility of time-1 wealth $X_{1}$ attainable by investing in the market with their time- 0 wealth $X_{0}=x$. The investor's utility function $U$ is increasing and concave. Show that, if there exists an optimal solution $X_{1}^{*}$ to the investor's expected utility maximisation problem, then the market has no arbitrage. [Assume that $U\left(X_{1}\right)$ is integrable for any attainable time-1 wealth $X_{1}$.]

  (c) Now introduce a contingent claim with time-1 bounded payout $Y$. How does the investor in part (b) calculate an indifference bid price $\pi(Y)$ for the claim? Assuming each such claim has a unique indifference price, show that the map $Y \mapsto \pi(Y)$ is concave. [Assume that any relevant utility maximisation problem that you consider has an optimal solution.]

  (d) Consider a contingent claim with time-1 bounded payout $Y$. Let $I \subseteq \mathbb{R}$ be the set of initial no-arbitrage prices for the claim; that is, the set $I$ consists of all $p$ such that the market augmented with the contingent claim with time- 0 price $p$ has no arbitrage. Show that $\pi(Y) \leqslant \sup \{p \in I\}$. [Assume that any relevant utility maximisation problem that you consider has an optimal solution. You may use results from lectures without proof, such as the fundamental theorem of asset pricing or the existence of marginal utility prices, as long as they are clearly stated.]

  comment

Topics in Analysis

• Paper 2, Section I, $2 H$

  Topics in Analysis | Part II, 2021

  Let $\Omega$ be a non-empty bounded open set in $\mathbb{R}^{2}$ with closure $\bar{\Omega}$ and boundary $\partial \Omega$ and let $\phi: \bar{\Omega} \rightarrow \mathbb{R}$ be a continuous function. Give a proof or a counterexample for each of the following assertions.

  (i) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})>0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (ii) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})<0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (iii) If $\phi$ is four times differentiable on $\Omega$ with

  $$\frac{\partial^{4} \phi}{\partial x^{4}}(\mathbf{x})+\frac{\partial^{4} \phi}{\partial y^{4}}(\mathbf{x})>0$$

  for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (iv) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})=0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  comment

• Paper 2, Section II, H

  Topics in Analysis | Part II, 2021

  Let $r:[-1,1] \rightarrow \mathbb{R}$ be a continuous function with $r(x)>0$ for all but finitely many values of $x$.

  (a) Show that

  $$\langle u, v\rangle=\int_{-1}^{1} u(x) v(x) r(x) d x$$

  defines an inner product on $C([-1,1])$.

  (b) Show that for each $n$ there exists a polynomial $P_{n}$ of degree exactly $n$ which is orthogonal, with respect to the inner product $(*)$, to all polynomials of lower degree.

  (c) Show that $P_{n}$ has $n$ simple zeros $\omega_{1}(n), \omega_{2}(n), \ldots, \omega_{n}(n)$ on $[-1,1]$.

  (d) Show that for each $n$ there exist unique real numbers $A_{j}(n), 1 \leqslant j \leqslant n$, such that whenever $Q$ is a polynomial of degree at most $2 n-1$,

  $$\int_{-1}^{1} Q(x) r(x) d x=\sum_{j=1}^{n} A_{j}(n) Q\left(\omega_{j}(n)\right)$$

  (e) Show that

  $$\sum_{j=1}^{n} A_{j}(n) f\left(\omega_{j}(n)\right) \rightarrow \int_{-1}^{1} f(x) r(x) d x$$

  as $n \rightarrow \infty$ for all $f \in C([-1,1])$.

  (f) If $R>1, K>0, a_{m}$ is real with $\left|a_{m}\right| \leqslant K R^{-m}$ and $f(x)=\sum_{m=1}^{\infty} a_{m} x^{m}$, show that

  $$\left|\int_{-1}^{1} f(x) r(x) d x-\sum_{j=1}^{n} A_{j}(n) f\left(\omega_{j}(n)\right)\right| \leqslant \frac{2 K R^{-2 n+1}}{R-1} \int_{-1}^{1} r(x) d x$$

  (g) If $r(x)=\left(1-x^{2}\right)^{1 / 2}$ and $P_{n}(0)=1$, identify $P_{n}$ (giving brief reasons) and the $\omega_{j}(n)$. [Hint: A change of variable may be useful.]

  comment

Waves

• Paper 2, Section II, 40A

  Waves | Part II, 2021

  A semi-infinite elastic medium with shear modulus $\mu$ and shear-wave speed $c_{s}$ lies in $z \leqslant 0$. Above it, there is a layer $0 \leqslant z \leqslant h$ of a second elastic medium with shear modulus $\bar{\mu}$ and shear-wave speed $\bar{c}_{s}<c_{s}$. The top boundary is stress-free. Consider a monochromatic SH-wave propagating in the $x$-direction at speed $c$ with wavenumber $k>0$.

  (a) Derive the dispersion relation

  $$\tan \left[k h \sqrt{c^{2} / \bar{c}_{s}^{2}-1}\right]=\frac{\mu}{\bar{\mu}} \frac{\sqrt{1-c^{2} / c_{s}^{2}}}{\sqrt{c^{2} / \bar{c}_{s}^{2}-1}}$$

  for trapped modes with no disturbance as $z \rightarrow-\infty$.

  (b) Show graphically that there is always a zeroth mode, and show that the other modes have cut-off frequencies

  $$\omega_{c}^{(n)}=\frac{n \pi \bar{c}_{s} c_{s}}{h \sqrt{c_{s}^{2}-\bar{c}_{s}^{2}}}$$

  where $n$ is a positive integer. Sketch a graph of frequency $\omega$ against $k$ for the $n=1$ mode showing the behaviour near cut-off and for large $k$.

  comment