(a) State a suitable version of the Seifert-van Kampen theorem and use it to calculate the fundamental groups of the torus $T^{2}:=S^{1} \times S^{1}$ and of the real projective plane $\mathbb{R P}^{2}$.

(b) Show that there are no covering maps $T^{2} \rightarrow \mathbb{R} \mathbb{P}^{2}$ or $\mathbb{R P}^{2} \rightarrow T^{2}$.

(c) Consider the following covering space of $S^{1} \vee S^{1}$ :

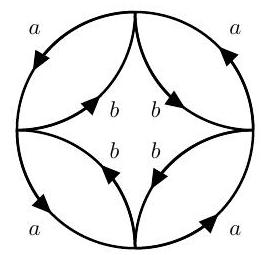
Here the line segments labelled $a$ and $b$ are mapped to the two different copies of $S^{1}$ contained in $S^{1} \vee S^{1}$, with orientations as indicated.

Using the Galois correspondence with basepoints, identify a subgroup of

$$\pi_{1}\left(S^{1} \vee S^{1}, x_{0}\right)=F_{2}$$

(where $x_{0}$ is the wedge point) that corresponds to this covering space.