Part II, 2018, Paper 4

Algebraic Geometry

• Paper 4, Section II, I

  Algebraic Geometry | Part II, 2018

  State a theorem which describes the canonical divisor of a smooth plane curve $C$ in terms of the divisor of a hyperplane section. Express the degree of the canonical divisor $K_{C}$ and the genus of $C$ in terms of the degree of $C$. [You need not prove these statements.]

  From now on, we work over $\mathbb{C}$. Consider the curve in $\mathbf{A}^{2}$ defined by the equation

  $$y+x^{3}+x y^{3}=0$$

  Let $C$ be its projective completion. Show that $C$ is smooth.

  Compute the genus of $C$ by applying the Riemann-Hurwitz theorem to the morphism $C \rightarrow \mathbf{P}^{1}$ induced from the rational map $(x, y) \mapsto y$. [You may assume that the discriminant of $x^{3}+a x+b$ is $-4 a^{3}-27 b^{2}$.]

  comment

Algebraic Topology

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State the Mayer-Vietoris theorem for a union of simplicial complexes

  $$K=M \cup N$$

  with $L=M \cap N$.

  (b) Construct the map $\partial_{*}: H_{k}(K) \rightarrow H_{k-1}(L)$ that appears in the statement of the theorem. [You do not need to prove that the map is well defined, or a homomorphism.]

  (c) Let $K$ be a simplicial complex with $|K|$ homeomorphic to the $n$-dimensional sphere $S^{n}$, for $n \geqslant 2$. Let $M \subseteq K$ be a subcomplex with $|M|$ homeomorphic to $S^{n-1} \times[-1,1]$. Suppose that $K=M \cup N$, such that $L=M \cap N$ has polyhedron $|L|$ identified with $S^{n-1} \times\{-1,1\} \subseteq S^{n-1} \times[-1,1]$. Prove that $|N|$ has two path components.

  comment

Analysis of Functions

• Paper 4, Section II, 23F

  Analysis of Functions | Part II, 2018

  Here and below, $\Phi: \mathbb{R} \rightarrow \mathbb{R}$ is smooth such that $\int_{\mathbb{R}} e^{-\Phi(x)} \mathrm{d} x=1$ and

  $$\lim _{|x| \rightarrow+\infty}\left(\frac{\left|\Phi^{\prime}(x)\right|^{2}}{4}-\frac{\Phi^{\prime \prime}(x)}{2}\right)=\ell \in(0,+\infty)$$

  $C_{c}^{1}(\mathbb{R})$ denotes the set of continuously differentiable complex-valued functions with compact support on $\mathbb{R}$.

  (a) Prove that there are constants $R_{0}>0, \lambda_{1}>0$ and $K_{1}>0$ so that for any $R \geqslant R_{0}$ and $h \in C_{c}^{1}(\mathbb{R})$ :

  $$\int_{\mathbb{R}}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{1} \int_{\{|x| \geqslant R\}}|h(x)|^{2} e^{-\Phi(x)} d x-K_{1} \int_{\{|x| \leqslant R\}}|h(x)|^{2} e^{-\Phi(x)} d x$$

  [Hint: Denote $g:=h e^{-\Phi / 2}$, expand the square and integrate by parts.]

  (b) Prove that, given any $R>0$, there is a $C_{R}>0$ so that for any $h \in C^{1}([-R, R])$ with $\int_{-R}^{+R} h(x) e^{-\Phi(x)} d x=0$ :

  $$\max _{x \in[-R, R]}|h(x)|+\operatorname{sip}_{\{x, y \in[-R, R], x \neq y\}} \frac{|h(x)-h(y)|}{|x-y|^{1 / 2}} \leqslant C_{R}\left(\int_{-R}^{+R}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x\right)^{1 / 2}$$

  [Hint: Use the fundamental theorem of calculus to control the second term of the left-hand side, and then compare $h$ to its weighted mean to control the first term of the left-hand side.]

  (c) Prove that, given any $R>0$, there is a $\lambda_{R}>0$ so that for any $h \in C^{1}([-R, R])$ :

  $$\int_{-R}^{+R}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{R} \int_{-R}^{+R}\left|h(x)-\frac{\int_{-R}^{+R} h(y) e^{-\Phi(y)} d y}{\int_{-R}^{+R} e^{-\Phi(y)} d y}\right|^{2} e^{-\Phi(x)} d x$$

  [Hint: Show first that one can reduce to the case $\int_{-R}^{+R} h e^{-\Phi}=0$. Then argue by contradiction with the help of the Arzelà-Ascoli theorem and part (b).]

  (d) Deduce that there is a $\lambda_{0}>0$ so that for any $h \in C_{c}^{1}(\mathbb{R})$ :

  $$\int_{\mathbb{R}}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{0} \int_{\mathbb{R}}\left|h(x)-\left(\int_{\mathbb{R}} h(y) e^{-\Phi(y)} d y\right)\right|^{2} e^{-\Phi(x)} d x$$

  [Hint: Show first that one can reduce to the case $\int_{\mathbb{R}} h e^{-\Phi}=0$. Then combine the inequality (a), multiplied by a constant of the form $\epsilon=\epsilon_{0} \lambda_{R}$ (where $\epsilon_{0}>0$ is chosen so that $\epsilon$ be sufficiently small), and the inequality (c).]

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  Define a Bravais lattice $\Lambda$ in three dimensions. Define the reciprocal lattice $\Lambda^{\star}$. Define the Brillouin zone.

  An FCC lattice has a basis of primitive vectors given by

  $$\mathbf{a}_{1}=\frac{a}{2}\left(\mathbf{e}_{2}+\mathbf{e}_{3}\right), \quad \mathbf{a}_{2}=\frac{a}{2}\left(\mathbf{e}_{1}+\mathbf{e}_{3}\right), \quad \mathbf{a}_{3}=\frac{a}{2}\left(\mathbf{e}_{1}+\mathbf{e}_{2}\right),$$

  where $\mathbf{e}_{i}$ is an orthonormal basis of $\mathbb{R}^{3}$. Find a basis of reciprocal lattice vectors. What is the volume of the Brillouin zone?

  The asymptotic wavefunction for a particle, of wavevector $\mathbf{k}$, scattering off a potential $V(\mathbf{r})$ is

  $$\psi(\mathbf{r}) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+f_{\mathrm{V}}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right) \frac{e^{i k r}}{r}$$

  where $\mathbf{k}^{\prime}=k \hat{\mathbf{r}}$ and $f_{\mathrm{V}}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right)$ is the scattering amplitude. Give a formula for the Born approximation to the scattering amplitude.

  Scattering of a particle off a single atom is modelled by a potential $V(\mathbf{r})=V_{0} \delta(r-d)$ with $\delta$-function support on a spherical shell, $r=|\mathbf{r}|=d$ centred at the origin. Calculate the Born approximation to the scattering amplitude, denoting the resulting expression as $\tilde{f}_{V}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right)$.

  Scattering of a particle off a crystal consisting of atoms located at the vertices of a lattice $\Lambda$ is modelled by a potential

  $$V_{\Lambda}=\sum_{\mathbf{R} \in \Lambda} V(\mathbf{r}-\mathbf{R})$$

  where $V(\mathbf{r})=V_{0} \delta(r-d)$ as above. Calculate the Born approximation to the scattering amplitude giving your answer in terms of your approximate expression $\tilde{f}_{\mathrm{V}}$ for scattering off a single atom. Show that the resulting amplitude vanishes unless the momentum transfer $\mathbf{q}=\mathbf{k}-\mathbf{k}^{\prime}$ lies in the reciprocal lattice $\Lambda^{\star}$.

  For the particular FCC lattice considered above, show that, when $k=|\mathbf{k}|>2 \pi / a$, scattering occurs for two values of the scattering angle, $\theta_{1}$ and $\theta_{2}$, related by

  $$\frac{\sin \left(\frac{\theta_{1}}{2}\right)}{\sin \left(\frac{\theta_{2}}{2}\right)}=\frac{2}{\sqrt{3}}$$

  comment

Applied Probability

• Paper 4, Section II, J

  Applied Probability | Part II, 2018

  Let $X_{1}, X_{2}, \ldots$ be independent, identically distributed random variables with finite mean $\mu$. Explain what is meant by saying that the random variable $M$ is a stopping time with respect to the sequence $\left(X_{i}: i=1,2, \ldots\right)$.

  Let $M$ be a stopping time with finite mean $\mathbb{E}(M)$. Prove Wald's equation:

  $$\mathbb{E}\left(\sum_{i=1}^{M} X_{i}\right)=\mu \mathbb{E}(M)$$

  [Here and in the following, you may use any standard theorem about integration.]

  Suppose the $X_{i}$ are strictly positive, and let $N$ be the renewal process with interarrival times $\left(X_{i}: i=1,2, \ldots\right)$. Prove that $m(t)=\mathbb{E}\left(N_{t}\right)$ satisfies the elementary renewal theorem:

  $$\frac{1}{t} m(t) \rightarrow \frac{1}{\mu} \quad \text { as } t \rightarrow \infty .$$

  A computer keyboard contains 100 different keys, including the lower and upper case letters, the usual symbols, and the space bar. A monkey taps the keys uniformly at random. Find the mean number of keys tapped until the first appearance of the sequence 'lava' as a sequence of 4 consecutive characters.

  Find the mean number of keys tapped until the first appearance of the sequence 'aa' as a sequence of 2 consecutive characters.

  comment

Asymptotic Methods

• Paper 4, Section II, B

  Asymptotic Methods | Part II, 2018

  Show that

  $$I_{0}(x)=\frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} d \theta$$

  is a solution to the equation

  $$x y^{\prime \prime}+y^{\prime}-x y=0,$$

  and obtain the first two terms in the asymptotic expansion of $I_{0}(x)$ as $x \rightarrow+\infty$.

  For $x>0$, define a new dependent variable $w(x)=x^{\frac{1}{2}} y(x)$, and show that if $y$ solves the preceding equation then

  $$w^{\prime \prime}+\left(\frac{1}{4 x^{2}}-1\right) w=0 .$$

  Obtain the Liouville-Green approximate solutions to this equation for large positive $x$, and compare with your asymptotic expansion for $I_{0}(x)$ at the leading order.

  comment

Automata and Formal Languages

• Paper 4, Section I, 4G

  Automata and Formal Languages | Part II, 2018

  (a) State the $s-m-n$ theorem, the recursion theorem, and Rice's theorem.

  (b) Show that if $g: \mathbb{N}^{2} \rightarrow \mathbb{N}$ is partial recursive, then there is some $e \in \mathbb{N}$ such that

  $$f_{e, 1}(y)=g(e, y) \quad \forall y \in \mathbb{N}$$

  (c) By considering the partial function $g: \mathbb{N}^{2} \rightarrow \mathbb{N}$ given by

  $$g(x, y)= \begin{cases}0 & \text { if } y<x \\ \uparrow & \text { otherwise }\end{cases}$$

  show there exists some $m \in \mathbb{N}$ such that $W_{m}$ has exactly $m$ elements.

  (d) Given $n \in \mathbb{N}$, is it possible to compute whether or not $W_{n}$ has exactly 9 elements? Justify your answer.

  [Note that we define $\mathbb{N}=\{0,1, \ldots\}$. Any use of Church's thesis in your answers should be explicitly stated.]

  comment

Classical Dynamics

• Paper 4, Section I, B

  Classical Dynamics | Part II, 2018

  State and prove Noether's theorem in Lagrangian mechanics.

  Consider a Lagrangian

  $$\mathcal{L}=\frac{1}{2} \frac{\dot{x}^{2}+\dot{y}^{2}}{y^{2}}-V\left(\frac{x}{y}\right)$$

  for a particle moving in the upper half-plane $\left\{(x, y) \in \mathbb{R}^{2}, y>0\right\}$ in a potential $V$ which only depends on $x / y$. Find two independent first integrals.

  comment

• Paper 4, Section II, B

  Classical Dynamics | Part II, 2018

  Given a Lagrangian $\mathcal{L}\left(q_{i}, \dot{q}_{i}, t\right)$ with degrees of freedom $q_{i}$, define the Hamiltonian and show how Hamilton's equations arise from the Lagrange equations and the Legendre transform.

  Consider the Lagrangian for a symmetric top moving in constant gravity:

  $$\mathcal{L}=\frac{1}{2} A\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} B(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  where $A, B, M, g$ and $l$ are constants. Construct the corresponding Hamiltonian, and find three independent Poisson-commuting first integrals of Hamilton's equations.

  comment

Coding and Cryptography

• Paper 4, Section I, H

  Coding and Cryptography | Part II, 2018

  What is a linear feedback shift register? Explain the Berlekamp-Massey method for recovering a feedback polynomial of a linear feedback shift register from its output. Illustrate the method in the case when we observe output

  $010111100010 \ldots$

  comment

Cosmology

• Paper 4, Section I, B

  Cosmology | Part II, 2018

  A constant overdensity is created by taking a spherical region of a flat matterdominated universe with radius $\bar{R}$ and compressing it into a region with radius $R<\bar{R}$. The evolution is governed by the parametric equations

  $$R=A R_{0}(1-\cos \theta), \quad t=B(\theta-\sin \theta)$$

  where $R_{0}$ is a constant and

  $$A=\frac{\Omega_{m, 0}}{2\left(\Omega_{m, 0}-1\right)}, \quad B=\frac{\Omega_{m, 0}}{2 H_{0}\left(\Omega_{m, 0}-1\right)^{3 / 2}}$$

  where $H_{0}$ is the Hubble constant and $\Omega_{m, 0}$ is the fractional overdensity at time $t_{0}$.

  Show that, as $t \rightarrow 0^{+}$,

  $$R(t)=R_{0} \Omega_{m, 0}^{1 / 3} a(t)\left(1-\frac{1}{20}\left(\frac{6 t}{B}\right)^{2 / 3}+\ldots\right)$$

  where the scale factor is given by $a(t)=\left(3 H_{0} t / 2\right)^{2 / 3}$.

  that, when the spherical overdensity has collapsed to zero radius, the linear perturbation has value $\delta_{\text {linear }}=\frac{3}{20}(12 \pi)^{2 / 3}$.

  comment

Differential Geometry

• Paper 4, Section II, I

  Differential Geometry | Part II, 2018

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define what it means for a curve $\gamma: I \rightarrow S$ to be a geodesic, where $I=(a, b)$ and $-\infty \leqslant a<b \leqslant \infty$.

  (b) A geodesic $\gamma: I \rightarrow S$ is said to be maximal if any geodesic $\widetilde{\gamma}: \tilde{I} \rightarrow S$ with $I \subset \tilde{I}$ and $\left.\tilde{\gamma}\right|_{I}=\gamma$ satisfies $I=\tilde{I}$. A surface is said to be geodesically complete if all maximal geodesics are defined on $I=(-\infty, \infty)$, otherwise, the surface is said to be geodesically incomplete. Give an example, with justification, of a non-compact geodesically complete surface $S$ which is not a plane.

  (c) Assume that along any maximal geodesic

  $$\gamma:\left(-T_{-}, T_{+}\right) \rightarrow S$$

  the following holds:

  $$\tag{*} T_{\pm}<\infty \Longrightarrow \limsup _{s \rightarrow T_{\pm}}|K(\gamma(\pm s))|=\infty$$

  Here $K$ denotes the Gaussian curvature of $S$.

  (i) Show that $S$ is inextendible, i.e. if $\widetilde{S} \subset \mathbb{R}^{3}$ is a connected surface with $S \subset \widetilde{S}$, then $\widetilde{S}=S$.

  (ii) Give an example of a surface $S$ which is geodesically incomplete and satisfies $(*)$. Do all geodesically incomplete inextendible surfaces satisfy $(*)$ ? Justify your answer.

  [You may use facts about geodesics from the course provided they are clearly stated.]

  comment

Dynamical Systems

• Paper 4, Section II, E

  Dynamical Systems | Part II, 2018

  Let $F: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. Define what it means (i) for $F$ to have a horseshoe (ii) for $F$ to be chaotic. [Glendinning's definition should be used throughout this question.]

  Prove that if $F$ has a 3 -cycle $x_{1}<x_{2}<x_{3}$ then $F$ is chaotic. [You may assume the intermediate value theorem and any corollaries of it.]

  State Sharkovsky's theorem.

  Use the above results to deduce that if $F$ has an $N$-cycle, where $N$ is any integer that is not a power of 2 , then $F$ is chaotic.

  Explain briefly why if $F$ is chaotic then $F$ has $N$-cycles for many values of $N$ that are not powers of 2. [You may assume that a map with a horseshoe acts on some set $\Lambda$ like the Bernoulli shift map acts on $[0,1)$.]

  The logistic map is not chaotic when $\mu<\mu_{\infty} \approx 3.57$ and it has 3 -cycles when $\mu>1+\sqrt{8} \approx 3.84$. What can be deduced from these statements about the values of $\mu$ for which the logistic map has a 10-cycle?

  comment

Electrodynamics

• Paper 4 , Section II, D

  Electrodynamics | Part II, 2018

  (a) Define the polarisation of a dielectric material and explain what is meant by the term bound charge.

  Consider a sample of material with spatially dependent polarisation $\mathbf{P}(\mathbf{x})$ occupying a region $V$ with surface $S$. Show that, in the absence of free charge, the resulting scalar potential $\phi(\mathbf{x})$ can be ascribed to bulk and surface densities of bound charge.

  Consider a sphere of radius $R$ consisting of a dielectric material with permittivity $\epsilon$ surrounded by a region of vacuum. A point-like electric charge $q$ is placed at the centre of the sphere. Determine the density of bound charge on the surface of the sphere.

  (b) Define the magnetization of a material and explain what is meant by the term bound current.

  Consider a sample of material with spatially-dependent magnetization $\mathbf{M}(\mathbf{x})$ occupying a region $V$ with surface $S$. Show that, in the absence of free currents, the resulting vector potential $\mathbf{A}(\mathbf{x})$ can be ascribed to bulk and surface densities of bound current.

  Consider an infinite cylinder of radius $r$ consisting of a material with permeability $\mu$ surrounded by a region of vacuum. A thin wire carrying current $I$ is placed along the axis of the cylinder. Determine the direction and magnitude of the resulting bound current density on the surface of the cylinder. What is the magnetization $\mathbf{M}(\mathbf{x})$ on the surface of the cylinder?

  comment

Fluid Dynamics II

• Paper 4, Section II, C

  Fluid Dynamics II | Part II, 2018

  A cylinder of radius $a$ rotates about its axis with angular velocity $\Omega$ while its axis is fixed parallel to and at a distance $a+h_{0}$ from a rigid plane, where $h_{0} \ll a$. Fluid of kinematic viscosity $\nu$ fills the space between the cylinder and the plane. Determine the gap width $h$ between the cylinder and the plane as a function of a coordinate $x$ parallel to the surface of the wall and orthogonal to the axis of the cylinder. What is the characteristic length scale, in the $x$ direction, for changes in the gap width? Taking an appropriate approximation for $h(x)$, valid in the region where the gap width $h$ is small, use lubrication theory to determine that the volume flux between the wall and the cylinder (per unit length along the axis) has magnitude $\frac{2}{3} a \Omega h_{0}$, and state its direction.

  Evaluate the tangential shear stress $\tau$ on the surface of the cylinder. Approximating the torque on the cylinder (per unit length along the axis) in the form of an integral $T=a \int_{-\infty}^{\infty} \tau d x$, find the torque $T$ to leading order in $h_{0} / a \ll 1$.

  Explain the restriction $a^{1 / 2} \Omega h_{0}^{3 / 2} / \nu \ll 1$ for the theory to be valid.

  [You may use the facts that $\int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{2}}=\frac{\pi}{2}$ and $\left.\int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{3}}=\frac{3 \pi}{8} .\right]$

  comment

Further Complex Methods

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2018

  State the conditions for a point $z=z_{0}$ to be a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane.

  Find all singular points of the Bessel equation

  $$z^{2} y^{\prime \prime}(z)+z y^{\prime}(z)+\left(z^{2}-\frac{1}{4}\right) y(z)=0$$

  and determine whether they are regular or irregular.

  By writing $y(z)=f(z) / \sqrt{z}$, find two linearly independent solutions of $(*)$. Comment on the relationship of your solutions to the nature of the singular points.

  comment

Galois Theory

• Paper 4, Section II, I

  Galois Theory | Part II, 2018

  Let $K$ be a field of characteristic $p>0$ and let $L$ be the splitting field of the polynomial $f(t)=t^{p}-t+a$ over $K$, where $a \in K$. Let $\alpha \in L$ be a root of $f(t)$.

  If $L \neq K$, show that $f(t)$ is irreducible over $K$, that $L=K(\alpha)$, and that $L$ is a Galois extension of $K$. What is $\operatorname{Gal}(L / K)$ ?

  comment

General Relativity

• Paper 4, Section II, E

  General Relativity | Part II, 2018

  (a) In the Newtonian weak-field limit, we can write the spacetime metric in the form

  $$d s^{2}=-(1+2 \Phi) d t^{2}+(1-2 \Phi) \delta_{i j} d x^{i} d x^{j},$$

  where $\delta_{i j} d x^{i} d x^{j}=d x^{2}+d y^{2}+d z^{2}$ and the potential $\Phi(t, x, y, z)$, as well as the velocity $v$ of particles moving in the gravitational field are assumed to be small, i.e.,

  $$\Phi, \partial_{t} \Phi, \partial_{x^{i}} \Phi, v^{2} \ll 1$$

  Use the geodesic equation for this metric to derive the equation of motion for a massive point particle in the Newtonian limit.

  (b) The far-field limit of the Schwarzschild metric is a special case of (*) given, in spherical coordinates, by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1+\frac{2 M}{r}\right)\left(d r^{2}+r^{2} d \theta^{2}+r^{2} \sin ^{2} \theta d \varphi^{2}\right)$$

  where now $M / r \ll 1$. For the following questions, state your results to first order in $M / r$, i.e. neglecting terms of $\mathcal{O}\left((M / r)^{2}\right)$.

  (i) Let $r_{1}, r_{2} \gg M$. Calculate the proper length $S$ along the radial curve from $r_{1}$ to $r_{2}$ at fixed $t, \theta, \varphi$.

  (ii) Consider a massless particle moving radially from $r=r_{1}$ to $r=r_{2}$. According to an observer at rest at $r_{2}$, what time $T$ elapses during this motion?

  (iii) The effective velocity of the particle as seen by the observer at $r_{2}$ is defined as $v_{\text {eff }}:=S / T$. Evaluate $v_{\text {eff }}$ and then take the limit of this result as $r_{1} \rightarrow r_{2}$. Briefly discuss the value of $v_{\text {eff }}$ in this limit.

  comment

Graph Theory

• Paper 4, Section II, I

  Graph Theory | Part II, 2018

  Let $s \geqslant 3$. Define the Ramsey number $R(s)$. Show that $R(s)$ exists and that $R(s) \leqslant 4^{s}$.

  Show that $R(3)=6$. Show that (up to relabelling the vertices) there is a unique way to colour the edges of the complete graph $K_{5}$ blue and yellow with no monochromatic triangle.

  What is the least positive integer $n$ such that the edges of the complete graph $K_{6}$ can be coloured blue and yellow in such a way that there are precisely $n$ monochromatic triangles?

  comment

Linear Analysis

• Paper 4, Section II, F

  Linear Analysis | Part II, 2018

  (a) Let $X$ be a separable normed space. For any sequence $\left(f_{n}\right)_{n \in \mathbb{N}} \subset X^{*}$ with $\left\|f_{n}\right\| \leqslant 1$ for all $n$, show that there is $f \in X^{*}$ and a subsequence $\Lambda \subset \mathbb{N}$ such that $f_{n}(x) \rightarrow f(x)$ for all $x \in X$ as $n \in \Lambda, n \rightarrow \infty$. [You may use without proof the fact that $X^{*}$ is complete and that any bounded linear map $f: D \rightarrow \mathbb{R}$, where $D \subset X$ is a dense linear subspace, can be extended uniquely to an element $f \in X^{*}$.]

  (b) Let $H$ be a Hilbert space and $U: H \rightarrow H$ a unitary map. Let

  $$I=\{x \in H: U x=x\}, \quad W=\{U x-x: x \in H\}$$

  Prove that $I$ and $W$ are orthogonal, $H=I \oplus \bar{W}$, and that for every $x \in H$,

  $$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=0}^{n-1} U^{i} x=P x$$

  where $P$ is the orthogonal projection onto the closed subspace $I$.

  (c) Let $T: C\left(S^{1}\right) \rightarrow C\left(S^{1}\right)$ be a linear map, where $S^{1}=\left\{e^{i \theta} \in \mathbb{C}: \theta \in \mathbb{R}\right\}$ is the unit circle, induced by a homeomorphism $\tau: S^{1} \rightarrow S^{1}$ by $(T f) e^{i \theta}=f\left(\tau\left(e^{i \theta}\right)\right)$. Prove that there exists $\mu \in C\left(S^{1}\right)^{*}$ with $\mu\left(1_{S^{1}}\right)=1$ such that $\mu(T f)=\mu(f)$ for all $f \in C\left(S^{1}\right)$. (Here $1_{S^{1}}$ denotes the function on $S^{1}$ which returns 1 identically.) If $T$ is not the identity map, does it follow that $\mu$ as above is necessarily unique? Justify your answer.

  comment

Logic and Set Theory

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2018

  State and prove the $\epsilon$-Recursion Theorem. [You may assume the Principle of $\epsilon-$ Induction.]

  What does it mean to say that a relation $r$ on a set $x$ is well-founded and extensional? State and prove Mostowski's Collapsing Theorem. [You may use any recursion theorem from the course, provided you state it precisely.]

  For which sets $x$ is it the case that every well-founded extensional relation on $x$ is isomorphic to the relation $\epsilon$ on some transitive subset of $V_{\omega}$ ?

  comment

Mathematical Biology

• Paper 4, Section I, C

  Mathematical Biology | Part II, 2018

  Consider a model of a population $N_{\tau}$ in discrete time

  $$N_{\tau+1}=\frac{r N_{\tau}}{\left(1+b N_{\tau}\right)^{2}}$$

  where $r, b>0$ are constants and $\tau=1,2,3, \ldots$ Interpret the constants and show that for $r>1$ there is a stable fixed point.

  Suppose the initial condition is $N_{1}=1 / b$ and that $r>4$. Show, using a cobweb diagram, that the population $N_{\tau}$ is bounded as

  $$\frac{4 r^{2}}{(4+r)^{2} b} \leqslant N_{\tau} \leqslant \frac{r}{4 b}$$

  and attains the bounds.

  comment

• Paper 4, Section II, C

  Mathematical Biology | Part II, 2018

  An activator-inhibitor reaction diffusion system is given, in dimensionless form, by

  $$\frac{\partial u}{\partial t}=d \frac{\partial^{2} u}{\partial x^{2}}+\frac{u^{2}}{v}-2 b u, \quad \frac{\partial v}{\partial t}=\frac{\partial^{2} v}{\partial x^{2}}+u^{2}-v$$

  where $d$ and $b$ are positive constants. Which symbol represents the concentration of activator and which the inhibitor? Determine the positive steady states and show, by an examination of the eigenvalues in a linear stability analysis of the spatially uniform situation, that the reaction kinetics are stable if $b<\frac{1}{2}$.

  Determine the conditions for the steady state to be driven unstable by diffusion, and sketch the $(b, d)$ parameter space in which the diffusion-driven instability occurs. Find the critical wavenumber $k_{c}$ at the bifurcation to such a diffusion-driven instability.

  comment

Number Fields

• Paper 4, Section II, G

  Number Fields | Part II, 2018

  Let $m \geqslant 2$ be a square-free integer, and let $n \geqslant 2$ be an integer. Let $L=\mathbb{Q}(\sqrt[n]{m})$.

  (a) By considering the factorisation of $(m)$ into prime ideals, show that $[L: \mathbb{Q}]=n$.

  (b) Let $T: L \times L \rightarrow \mathbb{Q}$ be the bilinear form defined by $T(x, y)=\operatorname{tr}_{L / \mathbb{Q}}(x y)$. Let $\beta_{i}=\sqrt[n]{m} i, i=0, \ldots, n-1$. Calculate the dual basis $\beta_{0}^{*}, \ldots, \beta_{n-1}^{*}$ of $L$ with respect to $T$, and deduce that $\mathcal{O}_{L} \subset \frac{1}{n m} \mathbb{Z}[\sqrt[n]{m}]$.

  (c) Show that if $p$ is a prime and $n=m=p$, then $\mathcal{O}_{L}=\mathbb{Z}[\sqrt[p]{p}]$.

  comment

Number Theory

• Paper 4, Section I, G

  Number Theory | Part II, 2018

  Show that if a continued fraction is periodic, then it represents a quadratic irrational. What number is represented by the continued fraction $[7,7,7, \ldots]$ ?

  Compute the continued fraction expansion of $\sqrt{23}$. Hence or otherwise find a solution in positive integers to the equation $x^{2}-23 y^{2}=1$.

  comment

• Paper 4, Section II, G

  Number Theory | Part II, 2018

  (a) State and prove the Fermat-Euler theorem. Let $p$ be a prime and $k$ a positive integer. Show that $b^{k} \equiv b(\bmod p)$ holds for every integer $b$ if and only if $k \equiv 1(\bmod p-1)$.

  (b) Let $N \geqslant 3$ be an odd integer and $b$ be an integer with $(b, N)=1$. What does it mean to say that $N$ is a Fermat pseudoprime to base $b$ ? What does it mean to say that $N$ is a Carmichael number?

  Show that every Carmichael number is squarefree, and that if $N$ is squarefree, then $N$ is a Carmichael number if and only if $N \equiv 1(\bmod p-1)$ for every prime divisor $p$ of $N$. Deduce that a Carmichael number is a product of at least three primes.

  (c) Let $r$ be a fixed odd prime. Show that there are only finitely many pairs of primes $p, q$ for which $N=p q r$ is a Carmichael number.

  [You may assume throughout that $\left(\mathbb{Z} / p^{n} \mathbb{Z}\right)^{*}$ is cyclic for every odd prime $p$ and every integer $n \geqslant 1 .]$

  comment

Numerical Analysis

• Paper 4, Section II, E

  Numerical Analysis | Part II, 2018

  The inverse discrete Fourier transform $\mathcal{F}_{n}^{-1}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is given by the formula

  $$\boldsymbol{x}=\mathcal{F}_{n}^{-1} \boldsymbol{y}, \quad \text { where } \quad x_{\ell}=\sum_{j=0}^{n-1} \omega_{n}^{j \ell} y_{j}, \quad \ell=0, \ldots, n-1$$

  Here, $\omega_{n}=\exp \frac{2 \pi i}{n}$ is the primitive root of unity of degree $n$ and $n=2^{p}, p=1,2, \ldots$

  (a) Show how to assemble $\boldsymbol{x}=\mathcal{F}_{2 m}^{-1} \boldsymbol{y}$ in a small number of operations if the Fourier transforms of the even and odd parts of $\boldsymbol{y}$,

  $$\boldsymbol{x}^{(\mathrm{E})}=\mathcal{F}_{m}^{-1} \boldsymbol{y}^{(\mathrm{E})}, \quad \boldsymbol{x}^{(\mathrm{O})}=\mathcal{F}_{m}^{-1} \boldsymbol{y}^{(\mathrm{O})}$$

  are already known.

  (b) Describe the Fast Fourier Transform (FFT) method for evaluating $\boldsymbol{x}$, and draw a diagram to illustrate the method for $n=8$.

  (c) Find the cost of the FFT method for $n=2^{p}$ (only multiplications count).

  (d) For $n=4$ use the FFT method to find $\boldsymbol{x}=\mathcal{F}_{n}^{-1} \boldsymbol{y}$ when: (i) $\boldsymbol{y}=(1,-1,1,-1)$, (ii) $\boldsymbol{y}=(1,1,-1,-1)$.

  comment

Optimisation and Control

• Paper 4, Section II, $30 K$

  Optimisation and Control | Part II, 2018

  Consider the deterministic system

  $$\dot{x}_{t}=u_{t}$$

  where $x_{t}$ and $u_{t}$ are scalars. Here $x_{t}$ is the state variable and the control variable $u_{t}$ is to be chosen to minimise, for a fixed $h>0$, the cost

  $$x_{h}^{2}+\int_{0}^{h} c_{t} u_{t}^{2} \mathrm{~d} t$$

  where $c_{t}$ is known and $c_{t}>c>0$ for all $t$. Let $F(x, t)$ be the minimal cost from state $x$ and time $t$.

  (a) By writing the dynamic programming equation in infinitesimal form and taking the appropriate limit show that $F(x, t)$ satisfies

  $$\frac{\partial F}{\partial t}=-\inf _{u}\left[c_{t} u^{2}+\frac{\partial F}{\partial x} u\right], \quad t<h$$

  with boundary condition $F(x, h)=x^{2}$.

  (b) Determine the form of the optimal control in the special case where $c_{t}$ is constant, and also in general.

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  The spin operators obey the commutation relations $\left[S_{i}, S_{j}\right]=i \hbar \epsilon_{i j k} S_{k}$. Let $|s, \sigma\rangle$ be an eigenstate of the spin operators $S_{z}$ and $\mathbf{S}^{2}$, with $S_{z}|s, \sigma\rangle=\sigma \hbar|s, \sigma\rangle$ and $\mathbf{S}^{2}|s, \sigma\rangle=s(s+1) \hbar^{2}|s, \sigma\rangle$. Show that

  $$S_{\pm}|s, \sigma\rangle=\sqrt{s(s+1)-\sigma(\sigma \pm 1)} \hbar|s, \sigma \pm 1\rangle,$$

  where $S_{\pm}=S_{x} \pm i S_{y}$. When $s=1$, use this to derive the explicit matrix representation

  $$S_{x}=\frac{\hbar}{\sqrt{2}}\left(\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right)$$

  in a basis in which $S_{z}$ is diagonal.

  A beam of atoms, each with spin 1 , is polarised to have spin $+\hbar$ along the direction $\mathbf{n}=(\sin \theta, 0, \cos \theta)$. This beam enters a Stern-Gerlach filter that splits the atoms according to their spin along the $\hat{\mathbf{z}}$-axis. Show that $N_{+} / N_{-}=\cot ^{4}(\theta / 2)$, where $N_{+}$(respectively, $N_{-}$) is the number of atoms emerging from the filter with spins parallel (respectively, anti-parallel) to $\hat{\mathbf{z}}$.

  comment

Principles of Statistics

• Paper 4, Section II, $28 \mathrm{~K}$

  Principles of Statistics | Part II, 2018

  Let $g: \mathbb{R} \rightarrow \mathbb{R}$ be an unknown function, twice continuously differentiable with $\left|g^{\prime \prime}(x)\right| \leqslant M$ for all $x \in \mathbb{R}$. For some $x_{0} \in \mathbb{R}$, we know the value $g\left(x_{0}\right)$ and we wish to estimate its derivative $g^{\prime}\left(x_{0}\right)$. To do so, we have access to a pseudo-random number generator that gives $U_{1}^{*}, \ldots, U_{N}^{*}$ i.i.d. uniform over $[0,1]$, and a machine that takes input $x_{1}, \ldots, x_{N} \in \mathbb{R}$ and returns $g\left(x_{i}\right)+\varepsilon_{i}$, where the $\varepsilon_{i}$ are i.i.d. $\mathcal{N}\left(0, \sigma^{2}\right)$.

  (a) Explain how this setup allows us to generate $N$ independent $X_{i}=x_{0}+h Z_{i}$, where the $Z_{i}$ take value 1 or $-1$ with probability $1 / 2$, for any $h>0$.

  (b) We denote by $Y_{i}$ the output $g\left(X_{i}\right)+\varepsilon_{i}$. Show that for some independent $\xi_{i} \in \mathbb{R}$

  $$Y_{i}-g\left(x_{0}\right)=h Z_{i} g^{\prime}\left(x_{0}\right)+\frac{h^{2}}{2} g^{\prime \prime}\left(\xi_{i}\right)+\varepsilon_{i}$$

  (c) Using the intuition given by the least-squares estimator, justify the use of the estimator $\hat{g}_{N}$ given by

  $$\hat{g}_{N}=\frac{1}{N} \sum_{i=1}^{N} \frac{Z_{i}\left(Y_{i}-g\left(x_{0}\right)\right)}{h}$$

  (d) Show that

  $$\mathbb{E}\left[\left|\hat{g}_{N}-g^{\prime}\left(x_{0}\right)\right|^{2}\right] \leqslant \frac{h^{2} M^{2}}{4}+\frac{\sigma^{2}}{N h^{2}} .$$

  Show that for some choice $h_{N}$ of parameter $h$, this implies

  $$\mathbb{E}\left[\left|\hat{g}_{N}-g^{\prime}\left(x_{0}\right)\right|^{2}\right] \leqslant \frac{\sigma M}{\sqrt{N}}$$

  comment

Probability and Measure

• Paper 4, Section II, J

  Probability and Measure | Part II, 2018

  Let $(X, \mathcal{A})$ be a measurable space. Let $T: X \rightarrow X$ be a measurable map, and $\mu$ a probability measure on $(X, \mathcal{A})$.

  (a) State the definition of the following properties of the system $(X, \mathcal{A}, \mu, T)$ :

  (i) $\mu$ is T-invariant.

  (ii) $T$ is ergodic with respect to $\mu$.

  (b) State the pointwise ergodic theorem.

  (c) Give an example of a probability measure preserving system $(X, \mathcal{A}, \mu, T)$ in which $\operatorname{Card}\left(T^{-1}\{x\}\right)>1$ for $\mu$-a.e. $x$.

  (d) Assume $X$ is finite and $\mathcal{A}$ is the boolean algebra of all subsets of $X$. Suppose that $\mu$ is a $T$-invariant probability measure on $X$ such that $\mu(\{x\})>0$ for all $x \in X$. Show that $T$ is a bijection.

  (e) Let $X=\mathbb{N}$, the set of positive integers, and $\mathcal{A}$ be the $\sigma$-algebra of all subsets of $X$. Suppose that $\mu$ is a $T$-invariant ergodic probability measure on $X$. Show that there is a finite subset $Y \subseteq X$ with $\mu(Y)=1$.

  comment

Quantum Information and Computation

• Paper 4, Section I, 10D

  Quantum Information and Computation | Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. Suppose we are given a 2-qubit quantum gate $I_{x_{0}}$ which is promised to be of the form

  $$I_{x_{0}}|x\rangle=\left\{\begin{array}{rr} |x\rangle & x \neq x_{0} \\ -|x\rangle & x=x_{0} \end{array}\right.$$

  but the 2-bit string $x_{0}$ is unknown to us. We wish to determine $x_{0}$ with the least number of queries to $I_{x_{0}}$. Define $A=I-2|\psi\rangle\langle\psi|$, where $I$ is the identity operator and $|\psi\rangle=\frac{1}{2} \sum_{x \in B_{2}}|x\rangle$.

  (a) Is $A$ unitary? Justify your answer.

  (b) Compute the action of $I_{x_{0}}$ on $|\psi\rangle$, and the action of $|\psi\rangle\langle\psi|$ on $\left|x_{0}\right\rangle$, in each case expressing your answer in terms of $|\psi\rangle$ and $\left|x_{0}\right\rangle$. Hence or otherwise show that $x_{0}$ may be determined with certainty using only one application of the gate $I_{x_{0}}$, together with any other gates that are independent of $x_{0}$.

  (c) Let $f_{x_{0}}: B_{2} \rightarrow B_{1}$ be the function having value 0 for all $x \neq x_{0}$ and having value 1 for $x=x_{0}$. It is known that a single use of $I_{x_{0}}$ can be implemented with a single query to a quantum oracle for the function $f_{x_{0}}$. But suppose instead that we have a classical oracle for $f_{x_{0}}$, i.e. a black box which, on input $x$, outputs the value of $f_{x_{0}}(x)$. Can we determine $x_{0}$ with certainty using a single query to the classical oracle? Justify your answer.

  comment

Representation Theory

• Paper 4, Section II, I

  Representation Theory | Part II, 2018

  Define $G=\mathrm{SU}(2)$ and write down a complete list

  $$\left\{V_{n}: n=0,1,2, \ldots\right\}$$

  of its continuous finite-dimensional irreducible representations. You should define all the terms you use but proofs are not required. Find the character $\chi_{V_{n}}$ of $V_{n}$. State the Clebsch-Gordan formula.

  (a) Stating clearly any properties of symmetric powers that you need, decompose the following spaces into irreducible representations of $G$ :

  (i) $V_{4} \otimes V_{3}, V_{3} \otimes V_{3}, S^{2} V_{3}$;

  (ii) $V_{1} \otimes \cdots \otimes V_{1}$ (with $n$ multiplicands);

  (iii) $S^{3} V_{2}$.

  (b) Let $G$ act on the space $M_{3}(\mathbb{C})$ of $3 \times 3$ complex matrices by

  $$A: X \mapsto A_{1} X A_{1}^{-1}$$

  where $A_{1}$ is the block matrix $\left(\begin{array}{cc}A & 0 \\ 0 & 1\end{array}\right)$. Show that this gives a representation of $G$ and decompose it into irreducible summands.

  comment

Statistical Modelling

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2018

  A scientist is studying the effects of a drug on the weight of mice. Forty mice are divided into two groups, control and treatment. The mice in the treatment group are given the drug, and those in the control group are given water instead. The mice are kept in 8 different cages. The weight of each mouse is monitored for 10 days, and the results of the experiment are recorded in the data frame Weight.data. Consider the following $R$ code and its output.

  head (Weight.data)

  Time Group Cage Mouse Weight

  11 Control 1 1 $24.77578$

  $2 \quad 2$ Control 1 1 $24.68766$

  $3 \quad 3$ Control $1 \quad 124.79008$

  44 Control $1 \quad 124.77005$

  $5 \quad 5$ Control 1 1 $24.65092$

  $6 \quad 6$ Control $1 \quad 124.38436$

  $>\bmod 1=\operatorname{lm}$ (Weight $\sim$ Time*Group $+$ Cage, data=Weight. data)

  $>\operatorname{summary}(\bmod 1)$

  Call:

  $\operatorname{lm}$ (formula $=$ Weight $~$Time $*$ Group $+$ Cage, data $=$ Weight. data)

  Residuals:

  Min $1 Q$ Median $3 Q$ Max

  $-1.36903-0.33527-0.01719 \quad 0.38807 \quad 1.24368$

  Coefficients:

  Estimate Std. Error t value $\operatorname{Pr}(>|t|)$

  $\begin{array}{lllll}\text { Time } & -0.006023 & 0.012616 & -0.477 & 0.63334\end{array}$

  GroupTreatment $\quad 0.321837 \quad 0.121993 \quad 2.638 \quad 0.00867 *$

  Cage2 $\quad-0.400228 \quad 0.095875-4.1743 .68 \mathrm{e}-05 * * *$

  $\begin{array}{lllll}\text { Cage3 } & 0.286941 & 0.102494 & 2.800 & 0.00537 *\end{array}$

  $\begin{array}{lllll}\text { Cage4 } & 0.007535 & 0.095875 & 0.079 & 0.93740\end{array}$

  $\begin{array}{rrrrr}\text { Cage6 } & 0.124767 & 0.125530 & 0.994 & 0.32087\end{array}$

  $\begin{array}{lllll}\text { Cage8 } & -0.295168 & 0.125530 & -2.351 & 0.01920 * \\ \text { Time:GroupTreatment } & -0.173515 & 0.017842 & -9.725 & <2 e-16 * * *\end{array}$

  Time: GroupTreatment $-0.173515 \quad 0.017842-9.725<2 \mathrm{e}-16 * * *$

  Signif. codes: 0 '' $0.001$ '' $0.01$ '' $0.05$ '., $0.1$ ', 1

  Residual standard error: $0.5125$ on 391 degrees of freedom

  Multiple R-squared: $0.5591$, Adjusted R-squared: $0.55$

  F-statistic: $61.97$ on 8 and 391 DF, p-value: $<2.2 \mathrm{e}-16$

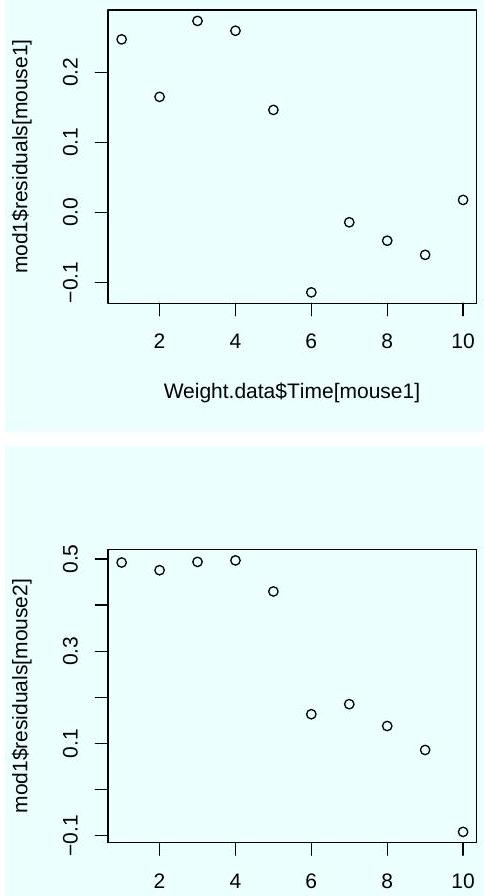
  Which parameters describe the rate of weight loss with time in each group? According to the $\mathrm{R}$ output, is there a statistically significant weight loss with time in the control group?

  Three diagnostic plots were generated using the following $R$ code.

  Weight.data$Time[mouse1]

  

  Weight.data$Time[mouse2]

  

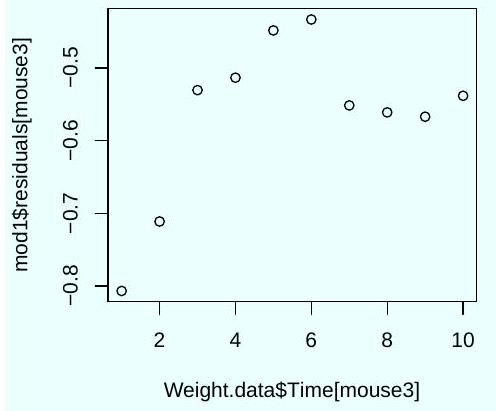
  Based on these plots, should you trust the significance tests shown in the output of the command summary (mod1)? Explain.

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2018

  Bridge is a card game played by 2 teams of 2 players each. A bridge club records the outcomes of many games between teams formed by its $m$ members. The outcomes are modelled by

  $$\mathbb{P}(\text { team }\{i, j\} \text { wins against team }\{k, \ell\})=\frac{\exp \left(\beta_{i}+\beta_{j}+\beta_{\{i, j\}}-\beta_{k}-\beta_{\ell}-\beta_{\{k, \ell\}}\right)}{1+\exp \left(\beta_{i}+\beta_{j}+\beta_{\{i, j\}}-\beta_{k}-\beta_{\ell}-\beta_{\{k, \ell\}}\right)},$$

  where $\beta_{i} \in \mathbb{R}$ is a parameter representing the skill of player $i$, and $\beta_{\{i, j\}} \in \mathbb{R}$ is a parameter representing how well-matched the team formed by $i$ and $j$ is.

  (a) Would it make sense to include an intercept in this logistic regression model? Explain your answer.

  (b) Suppose that players 1 and 2 always play together as a team. Is there a unique maximum likelihood estimate for the parameters $\beta_{1}, \beta_{2}$ and $\beta_{\{1,2\}}$ ? Explain your answer.

  (c) Under the model defined above, derive the asymptotic distribution (including the values of all relevant parameters) for the maximum likelihood estimate of the probability that team $\{i, j\}$ wins a game against team $\{k, \ell\}$. You can state it as a function of the true vector of parameters $\beta$, and the Fisher information matrix $i_{N}(\beta)$ with $N$ games. You may assume that $i_{N}(\beta) / N \rightarrow I(\beta)$ as $N \rightarrow \infty$, and that $\beta$ has a unique maximum likelihood estimate for $N$ large enough.

  comment

Statistical Physics

• Paper 4, Section II, A

  Statistical Physics | Part II, 2018

  The one-dimensional Ising model consists of a set of $N$ spins $s_{i}$ with Hamiltonian

  $$H=-J \sum_{i=1}^{N} s_{i} s_{i+1}-\frac{B}{2} \sum_{i=1}^{N}\left(s_{i}+s_{i+1}\right)$$

  where periodic boundary conditions are imposed so $s_{N+1}=s_{1}$. Here $J$ is a positive coupling constant and $B$ is an external magnetic field. Define a $2 \times 2$ matrix $M$ with elements

  $$M_{s t}=\exp \left[\beta J s t+\frac{\beta B}{2}(s+t)\right]$$

  where indices $s, t$ take values $\pm 1$ and $\beta=(k T)^{-1}$ with $k$ Boltzmann's constant and $T$ temperature.

  (a) Prove that the partition function of the Ising model can be written as

  $$Z=\operatorname{Tr}\left(M^{N}\right)$$

  Calculate the eigenvalues of $M$ and hence determine the free energy in the thermodynamic limit $N \rightarrow \infty$. Explain why the Ising model does not exhibit a phase transition in one dimension.

  (b) Consider the case of zero magnetic field $B=0$. The correlation function $\left\langle s_{i} s_{j}\right\rangle$ is defined by

  $$\left\langle s_{i} s_{j}\right\rangle=\frac{1}{Z} \sum_{\left\{s_{k}\right\}} s_{i} s_{j} e^{-\beta H}$$

  (i) Show that, for $i>1$,

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{1}{Z} \sum_{s, t} s t\left(M^{i-1}\right)_{s t}\left(M^{N-i+1}\right)_{t s}$$

  (ii) By diagonalizing $M$, or otherwise, calculate $M^{p}$ for any positive integer $p$. Hence show that

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{\tanh ^{i-1}(\beta J)+\tanh ^{N-i+1}(\beta J)}{1+\tanh ^{N}(\beta J)}$$

  comment

Stochastic Financial Models

• Paper 4, Section II, K

  Stochastic Financial Models | Part II, 2018

  Consider a utility function $U: \mathbb{R} \rightarrow \mathbb{R}$, which is assumed to be concave, strictly increasing and twice differentiable. Further, $U$ satisfies

  $$\left|U^{\prime}(x)\right| \leqslant c|x|^{\alpha}, \quad \forall x \in \mathbb{R},$$

  for some positive constants $c$ and $\alpha$. Let $X$ be an $\mathcal{N}\left(\mu, \sigma^{2}\right)$-distributed random variable and set $f(\mu, \sigma):=\mathbb{E}[U(X)]$.

  (a) Show that

  $$\mathbb{E}\left[U^{\prime}(X)(X-\mu)\right]=\sigma^{2} \mathbb{E}\left[U^{\prime \prime}(X)\right]$$

  (b) Show that $\frac{\partial f}{\partial \mu}>0$ and $\frac{\partial f}{\partial \sigma} \leqslant 0$. Discuss this result in the context of meanvariance analysis.

  (c) Show that $f$ is concave in $\mu$ and $\sigma$, i.e. check that the matrix of second derivatives is negative semi-definite. [You may use without proof the fact that if a $2 \times 2$ matrix has nonpositive diagonal entries and a non-negative determinant, then it is negative semi-definite.]

  comment

Topics in Analysis

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  Let $0 \leqslant \alpha<1$ and $A>0$. If we have an infinite sequence of integers $m_{n}$ with $1 \leqslant m_{n} \leqslant A n^{\alpha}$, show that

  $$\sum_{n=1}^{\infty} \frac{m_{n}}{n !}$$

  is irrational.

  Does the result remain true if the $m_{n}$ are not restricted to integer values? Justify your answer.

  comment

• Paper 4, Section II, F

  Topics in Analysis | Part II, 2018

  We work in $\mathbb{C}$. Consider

  $$K=\{z:|z-2| \leqslant 1\} \cup\{z:|z+2| \leqslant 1\}$$

  and

  $$\Omega=\{z:|z-2|<3 / 2\} \cup\{z:|z+2|<3 / 2\}$$

  Show that if $f: \Omega \rightarrow \mathbb{C}$ is analytic, then there is a sequence of polynomials $p_{n}$ such that $p_{n}(z) \rightarrow f(z)$ uniformly on $K$.

  Show that there is a sequence of polynomials $P_{n}$ such that $P_{n}(z) \rightarrow 0$ uniformly for $|z-2| \leqslant 1$ and $P_{n}(z) \rightarrow 1$ uniformly for $|z+2| \leqslant 1$.

  Give two disjoint non-empty bounded closed sets $K_{1}$ and $K_{2}$ such that there does not exist a sequence of polynomials $Q_{n}$ with $Q_{n}(z) \rightarrow 0$ uniformly on $K_{1}$ and $Q_{n}(z) \rightarrow 1$ uniformly on $K_{2}$. Justify your answer.

  comment

Waves

• Paper 4, Section II, C

  Waves | Part II, 2018

  A physical system permits one-dimensional wave propagation in the $x$-direction according to the equation

  $$\left(1-2 \frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{4}}{\partial x^{4}}\right) \frac{\partial^{2} \varphi}{\partial t^{2}}+\frac{\partial^{4} \varphi}{\partial x^{4}}=0$$

  Derive the corresponding dispersion relation and sketch graphs of frequency, phase velocity and group velocity as functions of the wavenumber. Waves of what wavenumber are at the front of a dispersing wave train arising from a localised initial disturbance? For waves of what wavenumbers do wave crests move faster or slower than a packet of waves?

  Find the solution of the above equation for the initial disturbance given by

  $$\varphi(x, 0)=\int_{-\infty}^{\infty} 2 A(k) e^{i k x} d k, \quad \frac{\partial \varphi}{\partial t}(x, 0)=0$$

  where $A^{*}(-k)=A(k)$, and $A^{*}$ is the complex conjugate of $A$. Let $V=x / t$ be held fixed. Use the method of stationary phase to obtain a leading-order approximation to this solution for large $t$ when $0<V<V_{m}=(3 \sqrt{3}) / 8$, where the solutions for the stationary points should be left in implicit form.

  Very briefly discuss the nature of the solutions for $-V_{m}<V<0$ and $|V|>V_{m}$.

  [Hint: You may quote the result that the large time behaviour of

  $$\Phi(x, t)=\int_{-\infty}^{\infty} A(k) e^{i k x-i \omega(k) t} d k$$

  due to a stationary point $k=\alpha$, is given by

  $$\Phi(x, t) \sim\left(\frac{2 \pi}{\left|\omega^{\prime \prime}(\alpha)\right| t}\right)^{\frac{1}{2}} A(\alpha) e^{i \alpha x-i \omega(\alpha) t+i \sigma \pi / 4}$$

  where $\left.\sigma=-\operatorname{sgn}\left(\omega^{\prime \prime}(\alpha)\right) .\right]$

  comment