Part II, 2018, Paper 1

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2018

  (a) Let $k$ be an uncountable field, $\mathcal{M} \subseteq k\left[x_{1}, \ldots, x_{n}\right]$ a maximal ideal and $A=k\left[x_{1}, \ldots, x_{n}\right] / \mathcal{M} .$

  Show that every element of $A$ is algebraic over $k$.

  (b) Now assume that $k$ is algebraically closed. Suppose that $J \subset k\left[x_{1}, \ldots, x_{n}\right]$ is an ideal, and that $f \in k\left[x_{1}, \ldots, x_{n}\right]$ vanishes on $Z(J)$. Using the result of part (a) or otherwise, show that $f^{N} \in J$ for some $N \geqslant 1$.

  (c) Let $f: X \rightarrow Y$ be a morphism of affine algebraic varieties. Show $\overline{f(X)}=Y$ if and only if the map $f^{*}: k[Y] \rightarrow k[X]$ is injective.

  Suppose now that $\overline{f(X)}=Y$, and that $X$ and $Y$ are irreducible. Define the dimension of $X, \operatorname{dim} X$, and show $\operatorname{dim} X \geqslant \operatorname{dim} Y$. [You may use whichever definition of $\operatorname{dim} X$ you find most convenient.]

  comment

Algebraic Topology

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2018

  (a) Let $V$ be the vector space of 3-dimensional upper-triangular matrices with real entries:

  $$V=\left\{\left(\begin{array}{ccc} 1 & x & y \\ 0 & 1 & z \\ 0 & 0 & 1 \end{array}\right) \mid x, y, z \in \mathbb{R}\right\}$$

  Let $\Gamma$ be the set of elements of $V$ for which $x, y, z$ are integers. Notice that $\Gamma$ is a subgroup of $G L_{3}(\mathbb{R})$; let $\Gamma$ act on $V$ by left-multiplication and let $N=\Gamma \backslash V$. Show that the quotient $\operatorname{map} V \rightarrow N$ is a covering map.

  (b) Consider the unit circle $S^{1} \subseteq \mathbb{C}$, and let $T=S^{1} \times S^{1}$. Show that the map $f: T \rightarrow T$ defined by

  $$f(z, w)=(z w, w)$$

  is a homeomorphism.

  (c) Let $M=[0,1] \times T / \sim$, where $\sim$ is the smallest equivalence relation satisfying

  $$(1, x) \sim(0, f(x))$$

  for all $x \in T$. Prove that $N$ and $M$ are homeomorphic by exhibiting a homeomorphism $M \rightarrow N$. [You may assume without proof that $N$ is Hausdorff.]

  (d) Prove that $\pi_{1}(M) \cong \Gamma$.

  comment

Analysis of Functions

• Paper 1, Section II, F

  Analysis of Functions | Part II, 2018

  (a) Consider a measure space $(X, \mathcal{A}, \mu)$ and a complex-valued measurable function $F$ on $X$. Prove that for any $\varphi:[0,+\infty) \rightarrow[0,+\infty)$ differentiable and increasing such that $\varphi(0)=0$, then

  $$\int_{X} \varphi(|F(x)|) \mathrm{d} \mu(x)=\int_{0}^{+\infty} \varphi^{\prime}(s) \mu(\{|F|>s\}) \mathrm{d} \lambda(s)$$

  where $\lambda$ is the Lebesgue measure.

  (b) Consider a complex-valued measurable function $f \in L^{1}\left(\mathbb{R}^{n}\right) \cap L^{\infty}\left(\mathbb{R}^{n}\right)$ and its maximal function $M f(x)=\sup _{r>0} \frac{1}{|B(x, r)|} \int_{B(x, r)}|f| \mathrm{d} \lambda$. Prove that for $p \in(1,+\infty)$ there is a constant $c_{p}>0$ such that $\|M f\|_{L^{p}\left(\mathbb{R}^{n}\right)} \leqslant c_{p}\|f\|_{L^{p}\left(\mathbb{R}^{n}\right)}$.

  [Hint: Split $f=f_{0}+f_{1}$ with $f_{0}=f \chi_{\{|f|>s / 2\}}$ and $f_{1}=f \chi_{\{|f| \leqslant s / 2\}}$ and prove that $\lambda(\{M f>s\}) \leqslant \lambda\left(\left\{M f_{0}>s / 2\right\}\right)$. Then use the maximal inequality $\lambda(\{M f>s\}) \leqslant$ $\frac{C_{1}}{s}\|f\|_{L^{1}\left(\mathbb{R}^{n}\right)}$ for some constant $\left.C_{1}>0 .\right]$

  (c) Consider $p, q \in(1,+\infty)$ with $p<q$ and $\alpha \in(0, n)$ such that $1 / q=1 / p-\alpha / n$. Define $I_{\alpha}|f|(x):=\int_{\mathbb{R}^{n}} \frac{|f(y)|}{|x-y|^{n-\alpha}} \mathrm{d} \lambda(y)$ and prove $I_{\alpha}|f|(x) \leqslant\|f\|_{L^{p}\left(\mathbb{R}^{n}\right)}^{\alpha p / n} M f(x)^{1-\alpha p / n}$.

  [Hint: Split the integral into $|x-y| \geqslant r$ and $|x-y| \in\left[2^{-k-1} r, 2^{-k} r\right)$ for all $k \geqslant 0$, given some suitable $r>0 .]$

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  A particle of mass $m$ moves in one dimension in a periodic potential $V(x)$ satisfying $V(x+a)=V(x)$. Define the Floquet matrix $F$. Show that $\operatorname{det} F=1$ and explain why Tr $F$ is real. Show that allowed bands occur for energies such that $(\operatorname{Tr} F)^{2}<4$. Consider the potential

  $$V(x)=-\frac{\hbar^{2} \lambda}{m} \sum_{n=-\infty}^{+\infty} \delta(x-n a)$$

  For states of negative energy, construct the Floquet matrix with respect to the basis of states $e^{\pm \mu x}$. Derive an inequality for the values of $\mu$ in an allowed energy band.

  For states of positive energy, construct the Floquet matrix with respect to the basis of states $e^{\pm i k x}$. Derive an inequality for the values of $k$ in an allowed energy band.

  Show that the state with zero energy lies in a forbidden region for $\lambda a>2$.

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2018

  Let $\lambda:[0, \infty) \rightarrow(0, \infty)$ be a continuous function. Explain what is meant by an inhomogeneous Poisson process with intensity function $\lambda$.

  Let $\left(N_{t}: t \geqslant 0\right)$ be such an inhomogeneous Poisson process, and let $M_{t}=N_{g(t)}$ where $g:[0, \infty) \rightarrow[0, \infty)$ is strictly increasing, differentiable and satisfies $g(0)=0$. Show that $M$ is a homogeneous Poisson process with intensity 1 if $\Lambda(g(t))=t$ for all $t$, where $\Lambda(t)=\int_{0}^{t} \lambda(u) d u$. Deduce that $N_{t}$ has the Poisson distribution with mean $\Lambda(t)$.

  Bicycles arrive at the start of a long road in the manner of a Poisson process $N=\left(N_{t}: t \geqslant 0\right)$ with constant intensity $\lambda$. The $i$ th bicycle has constant velocity $V_{i}$, where $V_{1}, V_{2}, \ldots$ are independent, identically distributed random variables, which are independent of $N$. Cyclists can overtake one another freely. Show that the number of bicycles on the first $x$ miles of the road at time $t$ has the Poisson distribution with parameter $\lambda \mathbb{E}\left(V^{-1} \min \{x, V t\}\right)$.

  comment

Automata and Formal Languages

• Paper 1, Section I, G

  Automata and Formal Languages | Part II, 2018

  (a) State the pumping lemma for context-free languages (CFLs).

  (b) Which of the following are CFLs? Justify your answers.

  (i) $\left\{w w \mid w \in\{a, b, c\}^{*}\right\}$

  (ii) $\left\{a^{m} b^{n} c^{k} d^{l} \mid 3 m=4 n\right.$ and $\left.2 k=5 l\right\}$

  (iii) $\left\{a^{3^{n}} \mid n \geqslant 0\right\}$

  (c) Let $L$ be a CFL. Show that $L^{*}$ is also a CFL.

  comment

• Paper 1, Section II, G

  Automata and Formal Languages | Part II, 2018

  (a) Define the halting set $\mathbb{K}$. Prove that $\mathbb{K}$ is recursively enumerable, but not recursive.

  (b) Given $A, B \subseteq \mathbb{N}$, define a many-one reduction of $A$ to $B$. Show that if $B$ is recursively enumerable and $A \leqslant_{m} B$, then $A$ is also recursively enumerable.

  (c) Show that each of the functions $f(n)=2 n$ and $g(n)=2 n+1$ are both partial recursive and total, by building them up as partial recursive functions.

  (d) Let $X, Y \subseteq \mathbb{N}$. We define the set $X \oplus Y$ via

  $$X \oplus Y:=\{2 x \mid x \in X\} \cup\{2 y+1 \mid y \in Y\}$$

  (i) Show that both $X \leqslant_{m} X \oplus Y$ and $Y \leqslant_{m} X \oplus Y$.

  (ii) Using the above, or otherwise, give an explicit example of a subset $C$ of $\mathbb{N}$ for which neither $C$ nor $\mathbb{N} \backslash C$ are recursively enumerable.

  (iii) For every $Z \subseteq \mathbb{N}$, show that if $X \leqslant_{m} Z$ and $Y \leqslant_{m} Z$ then $X \oplus Y \leqslant_{m} Z$.

  [Note that we define $\mathbb{N}=\{0,1, \ldots\}$. Any use of Church's thesis in your answers should be explicitly stated.]

  comment

Classical Dynamics

• Paper 1, Section I, B

  Classical Dynamics | Part II, 2018

  Derive Hamilton's equations from an action principle.

  Consider a two-dimensional phase space with the Hamiltonian $H=p^{2}+q^{-2}$. Show that $F=p q-c t H$ is the first integral for some constant $c$ which should be determined. By considering the surfaces of constant $F$ in the extended phase space, solve Hamilton's equations, and sketch the orbits in the phase space.

  comment

Coding and Cryptography

• Paper 1, Section I, H

  Coding and Cryptography | Part II, 2018

  State and prove Shannon's noiseless coding theorem. [You may use Gibbs' and Kraft's inequalities as long as they are clearly stated.]

  comment

• Paper 1, Section II, H

  Coding and Cryptography | Part II, 2018

  Define the bar product $C_{1} \mid C_{2}$ of binary linear codes $C_{1}$ and $C_{2}$, where $C_{2}$ is a subcode of $C_{1}$. Relate the rank and minimum distance of $C_{1} \mid C_{2}$ to those of $C_{1}$ and $C_{2}$ and justify your answer.

  What is a parity check matrix for a linear code? If $C_{1}$ has parity check matrix $P_{1}$ and $C_{2}$ has parity check matrix $P_{2}$, find a parity check matrix for $C_{1} \mid C_{2}$.

  Using the bar product construction, or otherwise, define the Reed-Muller code $R M(d, r)$ for $0 \leqslant r \leqslant d$. Compute the rank of $R M(d, r)$. Show that all but two codewords in $R M(d, 1)$ have the same weight. Given $d$, for which $r$ is it true that all elements of $R M(d, r)$ have even weight? Justify your answer.

  comment

Cosmology

• Paper 1, Section I, B

  Cosmology | Part II, 2018

  For a homogeneous and isotropic universe filled with pressure-free matter $(P=0)$, the Friedmann and Raychaudhuri equations are, respectively,

  $$\left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho \quad \text { and } \quad \frac{\ddot{a}}{a}=-\frac{4 \pi G}{3} \rho,$$

  with mass density $\rho$, curvature $k$, and where $\dot{a} \equiv d a / d t$. Using conformal time $\tau$ with $d \tau=d t / a$, show that the relative density parameter can be expressed as

  $$\Omega(t) \equiv \frac{\rho}{\rho_{\text {crit }}}=\frac{8 \pi G \rho a^{2}}{3 \mathcal{H}^{2}}$$

  where $\mathcal{H}=\frac{1}{a} \frac{d a}{d \tau}$ and $\rho_{\text {crit }}$ is the critical density of a flat $k=0$ universe (Einstein-de Sitter). Use conformal time $\tau$ again to show that the Friedmann and Raychaudhuri equations can be re-expressed as

  $$\frac{k c^{2}}{\mathcal{H}^{2}}=\Omega-1 \quad \text { and } \quad 2 \frac{d \mathcal{H}}{d \tau}+\mathcal{H}^{2}+k c^{2}=0$$

  From these derive the evolution equation for the density parameter $\Omega$ :

  $$\frac{d \Omega}{d \tau}=\mathcal{H} \Omega(\Omega-1)$$

  Plot the qualitative behaviour of $\Omega$ as a function of time relative to the expanding Einsteinde Sitter model with $\Omega=1$ (i.e., include curves initially with $\Omega>1$ and $\Omega<1$ ).

  comment

• Paper 1, Section II, B

  Cosmology | Part II, 2018

  A flat $(k=0)$ homogeneous and isotropic universe with scale factor $a(t)$ is filled with a scalar field $\phi(t)$ with potential $V(\phi)$. Its evolution satisfies the Friedmann and scalar field equations,

  $$H^{2}=\frac{1}{3 M_{\mathrm{Pl}}^{2}}\left(\frac{1}{2} \dot{\phi}^{2}+c^{2} V(\phi)\right), \quad \ddot{\phi}+3 H \dot{\phi}+c^{2} \frac{d V}{d \phi}=0$$

  where $H(t)=\frac{\dot{a}}{a}$ is the Hubble parameter, $M_{\mathrm{Pl}}$ is the reduced Planck mass, and dots denote derivatives with respect to cosmic time $t$, e.g. $\dot{\phi} \equiv d \phi / d t$.

  (a) Use these equations to derive the Raychaudhuri equation, expressed in the form:

  $$\dot{H}=-\frac{1}{2 M_{\mathrm{Pl}}^{2}} \dot{\phi}^{2}$$

  (b) Consider the following ansatz for the scalar field evolution,

  $$\phi(t)=\phi_{0} \ln \tanh (\lambda t)$$

  where $\lambda, \phi_{0}$ are constants. Find the specific cosmological solution,

  $$\begin{aligned} H(t) &=\lambda \frac{\phi_{0}^{2}}{M_{\mathrm{Pl}}^{2}} \operatorname{coth}(2 \lambda t) \\ a(t) &=a_{0}[\sinh (2 \lambda t)]^{\phi_{0}^{2} / 2 M_{\mathrm{Pl}}^{2}}, \quad a_{0} \text { constant. } \end{aligned}$$

  (c) Hence, show that the Hubble parameter can be expressed in terms of $\phi$ as

  $$H(\phi)=\lambda \frac{\phi_{0}^{2}}{M_{\mathrm{P} 1}^{2}} \cosh \left(\frac{\phi}{\phi_{0}}\right),$$

  and that the scalar field ansatz solution ( $\dagger$ ) requires the following form for the potential:

  $$V(\phi)=\frac{2 \lambda^{2} \phi_{0}^{2}}{c^{2}}\left[\left(\frac{3 \phi_{0}^{2}}{2 M_{\mathrm{Pl}}^{2}}-1\right) \cosh ^{2}\left(\frac{\phi}{\phi_{0}}\right)+1\right]$$

  (d) Assume that the given parameters in $V(\phi)$ are such that $2 / 3<\phi_{0}^{2} / M_{\mathrm{Pl}}^{2}<2$. Show that the asymptotic limit for the cosmological solution as $t \rightarrow 0$ exhibits decelerating power law evolution and that there is an accelerating solution as $t \rightarrow \infty$, that is,

  $$\begin{array}{lll} t \rightarrow 0, & \phi \rightarrow-\infty, & a(t) \sim t^{\phi_{0}^{2} / 2 M_{\mathrm{Pl}}^{2}} \\ t \rightarrow \infty, & \phi \rightarrow 0, & a(t) \sim \exp \left(\lambda \phi_{0}^{2} t / M_{\mathrm{Pl}}^{2}\right) . \end{array}$$

  Find the time $t_{\mathrm{acc}}$ at which the solution transitions from deceleration to acceleration.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2018

  (a) Let $X \subset \mathbb{R}^{n}$ be a manifold and $p \in X$. Define the tangent space $T_{p} X$ and show that it is a vector subspace of $\mathbb{R}^{n}$, independent of local parametrization, of dimension equal to $\operatorname{dim} X$.

  (b) Now show that $T_{p} X$ depends continuously on $p$ in the following sense: if $p_{i}$ is a sequence in $X$ such that $p_{i} \rightarrow p \in X$, and $w_{i} \in T_{p_{i}} X$ is a sequence such that $w_{i} \rightarrow w \in \mathbb{R}^{n}$, then $w \in T_{p} X$. If $\operatorname{dim} X>0$, show that all $w \in T_{p} X$ arise as such limits where $p_{i}$ is a sequence in $X \backslash p$.

  (c) Consider the set $X_{a} \subset \mathbb{R}^{4}$ defined by $X_{a}=\left\{x_{1}^{2}+2 x_{2}^{2}=a^{2}\right\} \cap\left\{x_{3}=a x_{4}\right\}$, where $a \in \mathbb{R}$. Show that, for all $a \in \mathbb{R}$, the set $X_{a}$ is a smooth manifold. Compute its dimension.

  (d) For $X_{a}$ as above, does $T_{p} X_{a}$ depend continuously on $p$ and $a$ for all $a \in \mathbb{R}$ ? In other words, let $a_{i} \in \mathbb{R}, p_{i} \in X_{a_{i}}$ be sequences with $a_{i} \rightarrow a \in \mathbb{R}, p_{i} \rightarrow p \in X_{a}$. Suppose that $w_{i} \in T_{p_{i}} X_{a_{i}}$ and $w_{i} \rightarrow w \in \mathbb{R}^{4}$. Is it necessarily the case that $w \in T_{p} X_{a}$ ? Justify your answer.

  comment

Dynamical Systems

• Paper 1, Section II, E

  Dynamical Systems | Part II, 2018

  Consider the system

  $$\dot{x}=-2 a x+2 x y, \quad \dot{y}=1-x^{2}-y^{2}$$

  where $a$ is a constant.

  (a) Find and classify the fixed points of the system. For $a=0$ show that the linear classification of the non-hyperbolic fixed points is nonlinearly correct. For $a \neq 0$ show that there are no periodic orbits. [Standard results for periodic orbits may be quoted without proof.]

  (b) Sketch the phase plane for the cases (i) $a=0$, (ii) $a=\frac{1}{2}$, and (iii) $a=\frac{3}{2}$, showing any separatrices clearly.

  (c) For what values of a do stationary bifurcations occur? Consider the bifurcation with $a>0$. Let $y_{0}, a_{0}$ be the values of $y, a$ at which the bifurcation occurs, and define $Y=y-y_{0}, \mu=a-a_{0}$. Assuming that $\mu=O\left(x^{2}\right)$, find the extended centre manifold $Y=Y(x, \mu)$ to leading order. Further, determine the evolution equation on the centre manifold to leading order. Hence identify the type of bifurcation.

  comment

Electrodynamics

• Paper 1, Section II, D

  Electrodynamics | Part II, 2018

  Define the field strength tensor $F^{\mu \nu}(x)$ for an electromagnetic field specified by a 4-vector potential $A^{\mu}(x)$. How do the components of $F^{\mu \nu}$ change under a Lorentz transformation? Write down two independent Lorentz-invariant quantities which are quadratic in the field strength tensor.

  [Hint: The alternating tensor $\varepsilon^{\mu \nu \rho \sigma}$ takes the values $+1$ and $-1$ when $(\mu, \nu, \rho, \sigma)$ is an even or odd permutation of $(0,1,2,3)$ respectively and vanishes otherwise. You may assume this is an invariant tensor of the Lorentz group. In other words, its components are the same in all inertial frames.]

  In an inertial frame with spacetime coordinates $x^{\mu}=(c t, \mathbf{x})$, the 4-vector potential has components $A^{\mu}=(\phi / c, \mathbf{A})$ and the electric and magnetic fields are given as

  $$\begin{aligned} \mathbf{E} &=-\nabla \phi-\frac{\partial \mathbf{A}}{\partial t} \\ \mathbf{B} &=\nabla \times \mathbf{A} \end{aligned}$$

  Evaluate the components of $F^{\mu \nu}$ in terms of the components of $\mathbf{E}$ and $\mathbf{B}$. Show that the quantities

  $$S=|\mathbf{B}|^{2}-\frac{1}{c^{2}}|\mathbf{E}|^{2} \quad \text { and } \quad T=\mathbf{E} \cdot \mathbf{B}$$

  are the same in all inertial frames.

  A relativistic particle of mass $m$, charge $q$ and 4 -velocity $u^{\mu}(\tau)$ moves according to the Lorentz force law,

  $$\frac{d u^{\mu}}{d \tau}=\frac{q}{m} F_{\nu}^{\mu} u^{\nu}$$

  Here $\tau$ is the proper time. For the case of a constant, uniform field, write down a solution of $(*)$ giving $u^{\mu}(\tau)$ in terms of its initial value $u^{\mu}(0)$ as an infinite series in powers of the field strength.

  Suppose further that the fields are such that both $S$ and $T$ defined above are zero. Work in an inertial frame with coordinates $x^{\mu}=(c t, x, y, z)$ where the particle is at rest at the origin at $t=0$ and the magnetic field points in the positive $z$-direction with magnitude $|\mathbf{B}|=B$. The electric field obeys $\mathbf{E} \cdot \hat{\mathbf{y}}=0$. Show that the particle moves on the curve $y^{2}=A x^{3}$ for some constant $A$ which you should determine.

  comment

Fluid Dynamics II

• Paper 1, Section II, C

  Fluid Dynamics II | Part II, 2018

  A two-dimensional layer of very viscous fluid of uniform thickness $h(t)$ sits on a stationary, rigid surface $y=0$. It is impacted by a stream of air (which can be assumed inviscid) such that the air pressure at $y=h$ is $p_{0}-\frac{1}{2} \rho_{a} E^{2} x^{2}$, where $p_{0}$ and $E$ are constants, $\rho_{a}$ is the density of the air, and $x$ is the coordinate parallel to the surface.

  What boundary conditions apply to the velocity $\mathbf{u}=(u, v)$ and stress tensor $\sigma$ of the viscous fluid at $y=0$ and $y=h$ ?

  By assuming the form $\psi=x f(y)$ for the stream function of the flow, or otherwise, solve the Stokes equations for the velocity and pressure fields. Show that the layer thins at a rate

  $$V=-\frac{\mathrm{d} h}{\mathrm{~d} t}=\frac{1}{3} \frac{\rho_{a}}{\mu} E^{2} h^{3}$$

  comment

Further Complex Methods

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2018

  The Beta and Gamma functions are defined by

  $$\begin{aligned} B(p, q) &=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t \\ \Gamma(p) &=\int_{0}^{\infty} e^{-t} t^{p-1} d t \end{aligned}$$

  where $\operatorname{Re} p>0, \operatorname{Re} q>0$.

  (a) By using a suitable substitution, or otherwise, prove that

  $$B(z, z)=2^{1-2 z} B\left(z, \frac{1}{2}\right)$$

  for $\operatorname{Re} z>0$. Extending $B$ by analytic continuation, for which values of $z \in \mathbb{C}$ does this result hold?

  (b) Prove that

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  for $\operatorname{Re} p>0, \operatorname{Re} q>0$

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2018

  The equation

  $$\tag{†} z w^{\prime \prime}+2 a w^{\prime}+z w=0,$$

  where $a$ is a constant with $\operatorname{Re} a>0$, has solutions of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  for suitably chosen contours $\gamma$ and some suitable function $f(t)$.

  (a) Find $f(t)$ and determine the condition on $\gamma$, which you should express in terms of $z, t$ and $a$.

  (b) Use the results of part (a) to show that $\gamma$ can be a finite contour and specify two possible finite contours with the help of a clearly labelled diagram. Hence, find the corresponding solution of the equation $(†)$ in the case $a=1$.

  (c) In the case $a=1$ and real $z$, show that $\gamma$ can be an infinite contour and specify two possible infinite contours with the help of a clearly labelled diagram. [Hint: Consider separately the cases $z>0$ and $z<0$.] Hence, find a second, linearly independent solution of the equation ( $\dagger$ ) in this case.

  comment

Galois Theory

• Paper 1, Section II, I

  Galois Theory | Part II, 2018

  Let $f(t)=t^{4}+b t^{2}+c t+d$ be an irreducible quartic with rational coefficients. Explain briefly why it is that if the cubic $g(t)=t^{3}+2 b t^{2}+\left(b^{2}-4 d\right) t-c^{2}$ has $S_{3}$ as its Galois group then the Galois group of $f(t)$ is $S_{4}$.

  For which prime numbers $p$ is the Galois group of $t^{4}+p t+p$ a proper subgroup of $S_{4}$ ? [You may assume that the discriminant of $t^{3}+\lambda t+\mu$ is $-4 \lambda^{3}-27 \mu^{2}$.]

  comment

General Relativity

• Paper 1, Section II, 37E

  General Relativity | Part II, 2018

  Consider the de Sitter metric

  $$d s^{2}=-d t^{2}+e^{2 H t}\left(d x^{2}+d y^{2}+d z^{2}\right)$$

  where $H>0$ is a constant.

  (a) Write down the Lagrangian governing the geodesics of this metric. Use the Euler-Lagrange equations to determine all non-vanishing Christoffel symbols.

  (b) Let $\mathcal{C}$ be a timelike geodesic parametrized by proper time $\tau$ with initial conditions at $\tau=0$,

  $$t=0, \quad x=y=z=0, \quad \dot{x}=v_{0}>0, \quad \dot{y}=\dot{z}=0,$$

  where the dot denotes differentiation with respect to $\tau$ and $v_{0}$ is a constant. Assuming both $t$ and $\tau$ to be future oriented, show that at $\tau=0$,

  $$\dot{t}=\sqrt{1+v_{0}^{2}}$$

  (c) Find a relation between $\tau$ and $t$ along the geodesic of part (b) and show that $t \rightarrow-\infty$ for a finite value of $\tau$. [You may use without proof that

  $$\left.\int \frac{1}{\sqrt{1+a e^{-b u}}} d u=\frac{1}{b} \ln \frac{\sqrt{1+a e^{-b u}}+1}{\sqrt{1+a e^{-b u}}-1}+\text { constant }, \quad a, b>0 .\right]$$

  (d) Briefly interpret this result.

  comment

Graph Theory

• Paper 1, Section II, I

  Graph Theory | Part II, 2018

  (a) Define ex $(n, H)$ where $H$ is a graph with at least one edge and $n \geqslant|H|$. Show that, for any such $H$, the $\operatorname{limit}_{n \rightarrow \infty} \lim (n, H) /\left(\begin{array}{c}n \\ 2\end{array}\right)$ exists.

  [You may not assume the Erdős-Stone theorem.]

  (b) State the Erdős-Stone theorem. Use it to deduce that if $H$ is bipartite then $\lim _{n \rightarrow \infty} \operatorname{ex}(n, H) /\left(\begin{array}{l}n \\ 2\end{array}\right)=0 .$

  (c) Let $t \geqslant 2$. Show that ex $\left(n, K_{t, t}\right)=O\left(n^{2-\frac{1}{t}}\right)$.

  We say $A \subset \mathbb{Z}_{n}$ is nice if whenever $a, b, c, d \in A$ with $a+b=c+d$ then either $a=c, b=d$ or $a=d, b=c$. Let $f(n)=\max \left\{|A|: A \subset \mathbb{Z}_{n}, A\right.$ is nice $\}$. Show that $f(n)=O(\sqrt{n}) .$

  $\left[\mathbb{Z}_{n}\right.$ denotes the set of integers modulo $n$, i.e. $\mathbb{Z}_{n}=\{0,1,2, \ldots, n-1\}$ with addition modulo $n .]$

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2018

  Let $M=\mathbb{R}^{2 n}=\left\{(\mathbf{q}, \mathbf{p}) \mid \mathbf{q}, \mathbf{p} \in \mathbb{R}^{n}\right\}$ be equipped with the standard symplectic form so that the Poisson bracket is given by:

  $$\{f, g\}=\frac{\partial f}{\partial q_{j}} \frac{\partial g}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial g}{\partial q_{j}}$$

  for $f, g$ real-valued functions on $M$. Let $H=H(\mathbf{q}, \mathbf{p})$ be a Hamiltonian function.

  (a) Write down Hamilton's equations for $(M, H)$, define a first integral of the system and state what it means that the system is integrable.

  (b) State the Arnol'd-Liouville theorem.

  (c) Define complex coordinates $z_{j}$ by $z_{j}=q_{j}+i p_{j}$, and show that if $f, g$ are realvalued functions on $M$ then:

  $$\{f, g\}=-2 i \frac{\partial f}{\partial z_{j}} \frac{\partial g}{\partial \overline{z_{j}}}+2 i \frac{\partial g}{\partial z_{j}} \frac{\partial f}{\partial \bar{z}_{j}}$$

  (d) For an $n \times n$ anti-Hermitian matrix $A$ with components $A_{j k}$, let $I_{A}:=\frac{1}{2 i} \overline{z_{j}} A_{j k} z_{k}$. Show that:

  $$\left\{I_{A}, I_{B}\right\}=-I_{[A, B]},$$

  where $[A, B]=A B-B A$ is the usual matrix commutator.

  (e) Consider the Hamiltonian:

  $$H=\frac{1}{2} \overline{z_{j}} z_{j}$$

  Show that $(M, H)$ is integrable and describe the invariant tori.

  [In this question $j, k=1, \ldots, n$, and the summation convention is understood for these indices.]

  comment

Linear Analysis

• Paper 1, Section II, F

  Linear Analysis | Part II, 2018

  Let $K$ be a compact Hausdorff space.

  (a) State the Arzelà-Ascoli theorem, and state both the real and complex versions of the Stone-Weierstraß theorem. Give an example of a compact space $K$ and a bounded set of functions in $C(K)$ that is not relatively compact.

  (b) Let $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ be continuous. Show that there exists a sequence of polynomials $\left(p_{i}\right)$ in $n$ variables such that

  $$B \subset \mathbb{R}^{n} \text { compact }\left.\left.\Rightarrow \quad p_{i}\right|_{B} \rightarrow f\right|_{B} \text { uniformly }$$

  Characterize the set of continuous functions $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ for which there exists a sequence of polynomials $\left(p_{i}\right)$ such that $p_{i} \rightarrow f$ uniformly on $\mathbb{R}^{n}$.

  (c) Prove that if $C(K)$ is equicontinuous then $K$ is finite. Does this implication remain true if we drop the requirement that $K$ be compact? Justify your answer.

  comment

Logic and Set Theory

• Paper 1, Section II, G

  Logic and Set Theory | Part II, 2018

  Give the inductive definition of ordinal exponentiation. Use it to show that $\alpha^{\beta} \leqslant \alpha^{\gamma}$ whenever $\beta \leqslant \gamma$ (for $\alpha \geqslant 1$ ), and also that $\alpha^{\beta}<\alpha^{\gamma}$ whenever $\beta<\gamma($ for $\alpha \geqslant 2)$.

  Give an example of ordinals $\alpha$ and $\beta$ with $\omega<\alpha<\beta$ such that $\alpha^{\omega}=\beta^{\omega}$.

  Show that $\alpha^{\beta+\gamma}=\alpha^{\beta} \alpha^{\gamma}$, for any ordinals $\alpha, \beta, \gamma$, and give an example to show that we need not have $(\alpha \beta)^{\gamma}=\alpha^{\gamma} \beta^{\gamma}$.

  For which ordinals $\alpha$ do we have $\alpha^{\omega_{1}} \geqslant \omega_{1}$ ? And for which do we have $\alpha^{\omega_{1}} \geqslant \omega_{2}$ ? Justify your answers.

  [You may assume any standard results not concerning ordinal exponentiation.]

  comment

Mathematical Biology

• Paper 1, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2018

  Consider a birth-death process in which the birth and death rates in a population of size $n$ are, respectively, $B n$ and $D n$, where $B$ and $D$ are per capita birth and death rates.

  (a) Write down the master equation for the probability, $p_{n}(t)$, of the population having size $n$ at time $t$.

  (b) Obtain the differential equations for the rates of change of the mean $\mu(t)=\langle n\rangle$ and the variance $\sigma^{2}(t)=\left\langle n^{2}\right\rangle-\langle n\rangle^{2}$ in terms of $\mu, \sigma, B$ and $D$.

  (c) Compare the equations obtained above with the deterministic description of the evolution of the population size, $d n / d t=(B-D) n$. Comment on why $B$ and $D$ cannot be uniquely deduced from the deterministic model but can be deduced from the stochastic description.

  comment

Number Fields

• Paper 1, Section II, G

  Number Fields | Part II, 2018

  (a) Let $m \geqslant 2$ be an integer such that $p=4 m-1$ is prime. Suppose that the ideal class group of $L=\mathbb{Q}(\sqrt{-p})$ is trivial. Show that if $n \geqslant 0$ is an integer and $n^{2}+n+m<m^{2}$, then $n^{2}+n+m$ is prime.

  (b) Show that the ideal class group of $\mathbb{Q}(\sqrt{-163})$ is trivial.

  comment

Number Theory

• Paper 1, Section I, G

  Number Theory | Part II, 2018

  (a) State and prove the Chinese remainder theorem.

  (b) An integer $n$ is squarefull if whenever $p$ is prime and $p \mid n$, then $p^{2} \mid n$. Show that there exist 1000 consecutive positive integers, none of which are squarefull.

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2018

  (a) Suppose that $A$ is a real $n \times n$ matrix, and $\boldsymbol{w} \in \mathbb{R}^{n}$ and $\lambda_{1} \in \mathbb{R}$ are given so that $A \boldsymbol{w}=\lambda_{1} \boldsymbol{w}$. Further, let $S$ be a non-singular matrix such that $S \boldsymbol{w}=c e^{(1)}$, where $e^{(1)}$ is the first coordinate vector and $c \neq 0$.

  Let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are $\lambda_{1}$ together with the eigenvalues of the bottom right $(n-1) \times(n-1)$ submatrix of $\widehat{A}$.

  Explain briefly how, given a vector $\boldsymbol{w}$, an orthogonal matrix $S$ such that $S \boldsymbol{w}=c e^{(1)}$ can be constructed.

  (b) Suppose that $A$ is a real $n \times n$ matrix, and two linearly independent vectors $\boldsymbol{v}, \boldsymbol{w} \in \mathbb{R}^{n}$ are given such that the linear subspace $L\{\boldsymbol{v}, \boldsymbol{w}\}$ spanned by $\boldsymbol{v}$ and $\boldsymbol{w}$ is invariant under the action of $A$, i.e.,

  $$x \in L\{\boldsymbol{v}, \boldsymbol{w}\} \quad \Rightarrow \quad A x \in L\{\boldsymbol{v}, \boldsymbol{w}\}$$

  Denote by $V$ an $n \times 2$ matrix whose two columns are the vectors $\boldsymbol{v}$ and $\boldsymbol{w}$, and let $S$ be a non-singular matrix such that $R=S V$ is upper triangular:

  $$S V=S \times\left[\begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \\ v_{3} & w_{3} \\ : & : \\ v_{n} & w_{n} \end{array}\right]=\left[\begin{array}{cc} r_{11} & r_{12} \\ 0 & r_{22} \\ 0 & 0 \\ : & : \\ 0 & 0 \end{array}\right]$$

  Again, let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are the eigenvalues of the top left $2 \times 2$ submatrix of $\widehat{A}$together with the eigenvalues of the bottom right $(n-2) \times(n-2)$ submatrix of $\widehat{A}$.

  Explain briefly how, for given vectors $\boldsymbol{v}, \boldsymbol{w}$, an orthogonal matrix $S$ which satisfies (*) can be constructed.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  A one-dimensional harmonic oscillator has Hamiltonian

  $$H=\hbar \omega\left(A^{\dagger} A+\frac{1}{2}\right)$$

  where $\left[A, A^{\dagger}\right]=1$. Show that $A|n\rangle=\sqrt{n}|n-1\rangle$, where $H|n\rangle=\left(n+\frac{1}{2}\right) \hbar \omega|n\rangle$ and $\langle n \mid n\rangle=1$.

  This oscillator is perturbed by adding a new term $\lambda X^{4}$ to the Hamiltonian. Given that

  $$A=\frac{m \omega X-i P}{\sqrt{2 m \hbar \omega}}$$

  show that the ground state of the perturbed system is

  $$\left|0_{\lambda}\right\rangle=|0\rangle-\frac{\hbar \lambda}{4 m^{2} \omega^{3}}\left(3 \sqrt{2}|2\rangle+\sqrt{\frac{3}{2}}|4\rangle\right)$$

  to first order in $\lambda$. [You may use the fact that, in non-degenerate perturbation theory, a perturbation $\Delta$ causes the first-order shift

  $$\left|m^{(1)}\right\rangle=\sum_{n \neq m} \frac{\langle n|\Delta| m\rangle}{E_{m}-E_{n}}|n\rangle$$

  in the $m^{\text {th }}$energy level.]

  comment

Principles of Statistics

• Paper 1, Section II, $29 \mathrm{~K}$

  Principles of Statistics | Part II, 2018

  A scientist wishes to estimate the proportion $\theta \in(0,1)$ of presence of a gene in a population of flies of size $n$. Every fly receives a chromosome from each of its two parents, each carrying the gene $A$ with probability $(1-\theta)$ or the gene $B$ with probability $\theta$, independently. The scientist can observe if each fly has two copies of the gene A (denoted by AA), two copies of the gene $B$ (denoted by BB) or one of each (denoted by AB). We let $n_{\mathrm{AA}}, n_{\mathrm{BB}}$, and $n_{\mathrm{AB}}$ denote the number of each observation among the $n$ flies.

  (a) Give the probability of each observation as a function of $\theta$, denoted by $f(X, \theta)$, for all three values $X=\mathrm{AA}, \mathrm{BB}$, or $\mathrm{AB}$.

  (b) For a vector $w=\left(w_{\mathrm{AA}}, w_{\mathrm{BB}}, w_{\mathrm{AB}}\right)$, we let $\hat{\theta}_{w}$ denote the estimator defined by

  $$\hat{\theta}_{w}=w_{\mathrm{AA}} \frac{n_{\mathrm{AA}}}{n}+w_{\mathrm{BB}} \frac{n_{\mathrm{BB}}}{n}+w_{\mathrm{AB}} \frac{n_{\mathrm{AB}}}{n} .$$

  Find the unique vector $w^{*}$ such that $\hat{\theta}_{w^{*}}$ is unbiased. Show that $\hat{\theta}_{w^{*}}$ is a consistent estimator of $\theta$.

  (c) Compute the maximum likelihood estimator of $\theta$ in this model, denoted by $\hat{\theta}_{M L E}$. Find the limiting distribution of $\sqrt{n}\left(\hat{\theta}_{M L E}-\theta\right)$. [You may use results from the course, provided that you state them clearly.]

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2018

  (a) Let $X$ be a real random variable with $\mathbb{E}\left(X^{2}\right)<\infty$. Show that the variance of $X$ is equal to $\inf _{a \in \mathbb{R}}\left(\mathbb{E}(X-a)^{2}\right)$.

  (b) Let $f(x)$ be the indicator function of the interval $[-1,1]$ on the real line. Compute the Fourier transform of $f$.

  (c) Show that

  $$\int_{0}^{+\infty}\left(\frac{\sin x}{x}\right)^{2} d x=\frac{\pi}{2}$$

  (d) Let $X$ be a real random variable and $\widehat{\mu_{X}}$ be its characteristic function.

  (i) Assume that $\left|\widehat{\mu_{X}}(u)\right|=1$ for some $u \in \mathbb{R}$. Show that there exists $\theta \in \mathbb{R}$ such that almost surely:

  $$u X \in \theta+2 \pi \mathbb{Z}$$

  (ii) Assume that $\left|\widehat{\mu_{X}}(u)\right|=\left|\widehat{\mu_{X}}(v)\right|=1$ for some real numbers $u$, $v$ not equal to 0 and such that $u / v$ is irrational. Prove that $X$ is almost surely constant. [Hint: You may wish to consider an independent copy of $X$.]

  comment

Quantum Information and Computation

• Paper 1, Section I, D

  Quantum Information and Computation | Part II, 2018

  (a) Define what it means for a 2-qubit state $|\psi\rangle_{A B}$ of a composite quantum system $A B$ to be entangled.

  Consider the 2-qubit state

  $$|\alpha\rangle=\frac{1}{\sqrt{3}}(2|00\rangle-H \otimes H|11\rangle)$$

  where $H$ is the Hadamard gate. From the definition of entanglement, show that $|\alpha\rangle$ is an entangled state.

  (b) Alice and Bob are distantly separated in space. Initially they each hold one qubit of the 2-qubit entangled state

  $$\left|\phi^{+}\right\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$$

  They are able to perform local quantum operations (unitary gates and measurements) on quantum systems they hold. Alice wants to communicate two classical bits of information to Bob. Explain how she can achieve this (within their restricted operational resources) by sending him a single qubit.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2018

  (a) Define the derived subgroup, $G^{\prime}$, of a finite group $G$. Show that if $\chi$ is a linear character of $G$, then $G^{\prime} \leqslant$ ker $\chi$. Prove that the linear characters of $G$ are precisely the lifts to $G$ of the irreducible characters of $G / G^{\prime}$. [You should state clearly any additional results that you require.]

  (b) For $n \geqslant 1$, you may take as given that the group

  $$G_{6 n}:=\left\langle a, b: a^{2 n}=b^{3}=1, a^{-1} b a=b^{-1}\right\rangle$$

  has order $6 n$.

  (i) Let $\omega=e^{2 \pi i / 3}$. Show that if $\varepsilon$ is any $(2 n)$-th root of unity in $\mathbb{C}$, then there is a representation of $G_{6 n}$ over $\mathbb{C}$ which sends

  $$a \mapsto\left(\begin{array}{ll} 0 & \varepsilon \\ \varepsilon & 0 \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} \omega & 0 \\ 0 & \omega^{2} \end{array}\right)$$

  (ii) Find all the irreducible representations of $G_{6 n}$.

  (iii) Find the character table of $G_{6 n}$.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2018

  Given a complete analytic function $\mathcal{F}$ on a domain $G \subset \mathbb{C}$, define the germ of a function element $(f, D)$ of $\mathcal{F}$ at $z \in D$. Let $\mathcal{G}$ be the set of all germs of function elements in $G$. Describe without proofs the topology and complex structure on $\mathcal{G}$ and the natural covering map $\pi: \mathcal{G} \rightarrow G$. Prove that the evaluation map $\mathcal{E}: \mathcal{G} \rightarrow \mathbb{C}$ defined by

  $$\mathcal{E}\left([f]_{z}\right)=f(z)$$

  is analytic on each component of $\mathcal{G}$.

  Suppose $f: R \rightarrow S$ is an analytic map of compact Riemann surfaces with $B \subset S$ the set of branch points. Show that $f: R \backslash f^{-1}(B) \rightarrow S \backslash B$ is a regular covering map.

  Given $P \in S \backslash B$, explain how any closed curve in $S \backslash B$ with initial and final points $P$ yields a permutation of the set $f^{-1}(P)$. Show that the group $H$ obtained from all such closed curves is a transitive subgroup of the group of permutations of $f^{-1}(P)$.

  Find the group $H$ for the analytic map $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ where $f(z)=z^{2}+z^{-2}$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2018

  The data frame Ambulance contains data on the number of ambulance requests from a Cambridgeshire hospital on different days. In addition to the number of ambulance requests on each day, the dataset records whether each day fell in the winter season, on a weekend, or on a bank holiday, as well as the pollution level on each day.

  A health researcher fitted two models to the dataset above using $R$. Consider the following code and its output.

  

  $$\begin{aligned} & \text { > head (Ambulance) } \\ & \text { Winter Weekend Bank. holiday Pollution. level Ambulance.requests } \\ & 1 \text { Yes Yes No High } 16 \end{aligned}$$

  

  $$\begin{aligned} & 3 \text { No No No High } 22 \\ & 4 \text { No } \quad \text { Yes } \quad \text { No } \quad \text { Medium } \quad 11 \end{aligned}$$

  

  

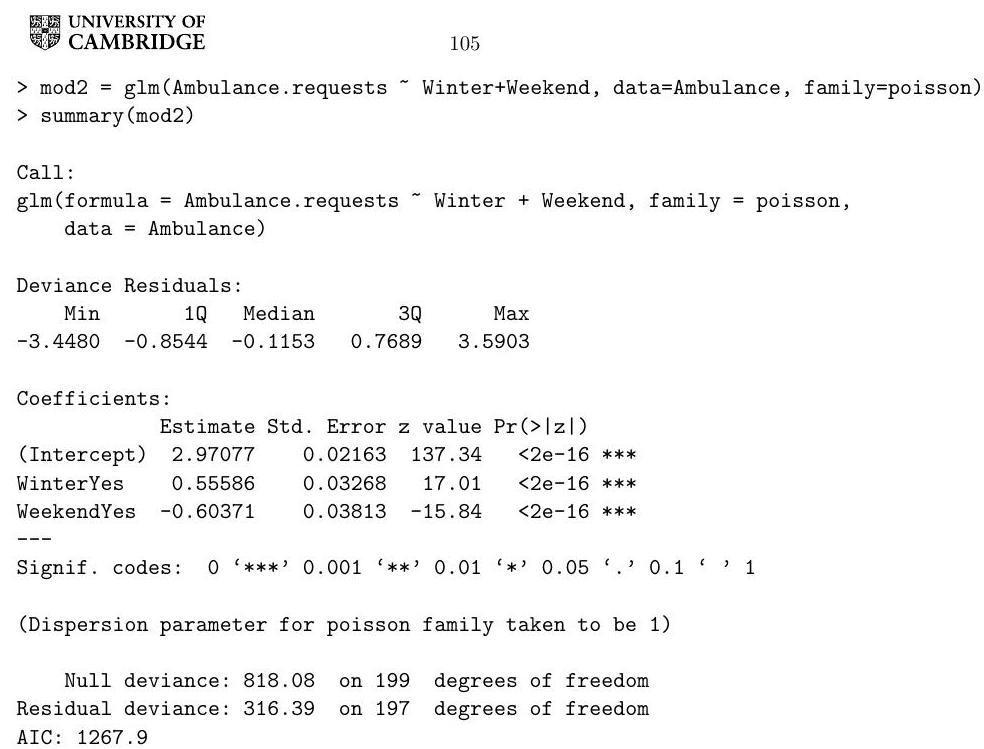
  Define the two models fitted by this code and perform a hypothesis test with level $1 \%$ in which one of the models is the null hypothesis and the other is the alternative. State the theorem used in this hypothesis test. You may use the information generated by the following commands.

  

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2018

  A clinical study follows a number of patients with an illness. Let $Y_{i} \in[0, \infty)$ be the length of time that patient $i$ lives and $x_{i} \in \mathbb{R}^{p}$ a vector of predictors, for $i \in\{1, \ldots, n\}$. We shall assume that $Y_{1}, \ldots, Y_{n}$ are independent. Let $f_{i}$ and $F_{i}$ be the probability density function and cumulative distribution function, respectively, of $Y_{i}$. The hazard function $h_{i}$ is defined as

  $$h_{i}(t)=\frac{f_{i}(t)}{1-F_{i}(t)} \quad \text { for } t \geqslant 0 .$$

  We shall assume that $h_{i}(t)=\lambda(t) \exp \left(\beta^{\top} x_{i}\right)$, where $\beta \in \mathbb{R}^{p}$ is a vector of coefficients and $\lambda(t)$ is some fixed hazard function.

  (a) Prove that $F_{i}(t)=1-\exp \left(-\int_{0}^{t} h_{i}(s) d s\right)$.

  (b) Using the equation in part (a), write the log-likelihood function for $\beta$ in terms of $\lambda, \beta, x_{i}$ and $Y_{i}$ only.

  (c) Show that the maximum likelihood estimate of $\beta$ can be obtained through a surrogate Poisson generalised linear model with an offset.

  comment

Statistical Physics

• Paper 1, Section II, A

  Statistical Physics | Part II, 2018

  (a) A macroscopic system has volume $V$ and contains $N$ particles. Let $\Omega(E, V, N ; \delta E)$ denote the number of states of the system which have energy in the range $(E, E+\delta E)$ where $\delta E \ll E$ represents experimental uncertainty. Define the entropy $S$ of the system and explain why the dependence of $S$ on $\delta E$ is usually negligible. Define the temperature and pressure of the system and hence obtain the fundamental thermodynamic relation.

  (b) A one-dimensional model of rubber consists of a chain of $N$ links, each of length a. The chain lies along the $x$-axis with one end fixed at $x=0$ and the other at $x=L$ where $L<N a$. The chain can "fold back" on itself so $x$ may not increase monotonically along the chain. Let $N_{\rightarrow}$ and $N_{\leftarrow}$ denote the number of links along which $x$ increases and decreases, respectively. All links have the same energy.

  (i) Show that $N_{\rightarrow}$ and $N_{\leftarrow}$ are uniquely determined by $L$ and $N$. Determine $\Omega(L, N)$, the number of different arrangements of the chain, as a function of $N_{\rightarrow}$ and $N_{\leftarrow}$. Hence show that, if $N_{\rightarrow} \gg 1$ and $N_{\leftarrow} \gg 1$ then the entropy of the chain is

  $$\begin{aligned} S(L, N)=k N & {\left[\log 2-\frac{1}{2}\left(1+\frac{L}{N a}\right) \log \left(1+\frac{L}{N a}\right)\right.} \\ &\left.-\frac{1}{2}\left(1-\frac{L}{N a}\right) \log \left(1-\frac{L}{N a}\right)\right] \end{aligned}$$

  where $k$ is Boltzmann's constant. [You may use Stirling's approximation: $n$ ! $\approx$ $\sqrt{2 \pi} n^{n+1 / 2} e^{-n}$ for $\left.n \gg 1 .\right]$

  (ii) Let $f$ denote the force required to hold the end of the chain fixed at $x=L$. This force does work $f d L$ on the chain if the length is increased by $d L$. Write down the fundamental thermodynamic relation for this system and hence calculate $f$ as a function of $L$ and the temperature $T$.

  Assume that $N a \gg L$. Show that the chain satisfies Hooke's law $f \propto L$. What happens if $f$ is held constant and $T$ is increased?

  comment

Stochastic Financial Models

• Paper 1, Section II, K

  Stochastic Financial Models | Part II, 2018

  (a) What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $Y_{1}, Y_{2}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $Y_{i}>0 \mathbb{P}$-a.s. and $\mathbb{E}\left[Y_{i}\right]=1, i \geqslant 1$. Further, let

  $$M_{0}=1 \quad \text { and } \quad M_{n}=\prod_{i=1}^{n} Y_{i}, \quad n \geqslant 1$$

  Show that $\left(M_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the filtration $\mathcal{F}_{n}=\sigma\left(Y_{1}, \ldots, Y_{n}\right)$.

  (c) Let $X=\left(X_{n}\right)_{n \geqslant 0}$ be an adapted process with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ such that $\mathbb{E}\left[\left|X_{n}\right|\right]<\infty$ for every $n$. Show that $X$ admits a unique decomposition

  $$X_{n}=M_{n}+A_{n}, \quad n \geqslant 0,$$

  where $M=\left(M_{n}\right)_{n \geqslant 0}$ is a martingale and $A=\left(A_{n}\right)_{n \geqslant 0}$ is a previsible process with $A_{0}=0$, which can recursively be constructed from $X$ as follows,

  $$A_{0}:=0, \quad A_{n+1}-A_{n}:=\mathbb{E}\left[X_{n+1}-X_{n} \mid \mathcal{F}_{n}\right]$$

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a super-martingale. Show that the following are equivalent:

  (i) $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale.

  (ii) $\mathbb{E}\left[X_{n}\right]=\mathbb{E}\left[X_{0}\right]$ for all $n \in \mathbb{N}$.

  comment

Topics in Analysis

• Paper 1, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  State and prove Sperner's lemma concerning colourings of points in a triangular grid.

  Suppose that $\triangle$ is a non-degenerate closed triangle with closed edges $\alpha_{1}, \alpha_{2}$ and $\alpha_{3}$. Show that we cannot find closed sets $A_{j}$ with $A_{j} \supseteq \alpha_{j}$, for $j=1,2,3$, such that

  $$\bigcup_{j=1}^{3} A_{j}=\Delta, \text { but } \bigcap_{j=1}^{3} A_{j}=\emptyset$$

  comment

Waves

• Paper 1, Section II, 39C

  Waves | Part II, 2018

  Derive the wave equation governing the velocity potential for linearised sound waves in a perfect gas. How is the pressure disturbance related to the velocity potential?

  A high pressure gas with unperturbed density $\rho_{0}$ is contained within a thin metal spherical shell which makes small amplitude spherically symmetric vibrations. Let the metal shell have radius $a$, mass $m$ per unit surface area, and an elastic stiffness which tries to restore the radius to its equilibrium value $a_{0}$ with a force $\kappa\left(a-a_{0}\right)$ per unit surface area. Assume that there is a vacuum outside the spherical shell. Show that the frequencies $\omega$ of vibration satisfy

  $$\theta^{2}\left(1+\frac{\alpha}{\theta \cot \theta-1}\right)=\frac{\kappa a_{0}^{2}}{m c_{0}^{2}}$$

  where $\theta=\omega a_{0} / c_{0}, \alpha=\rho_{0} a_{0} / m$, and $c_{0}$ is the speed of sound in the undisturbed gas. Briefly comment on the existence of solutions.

  [Hint: In terms of spherical polar coordinates you may assume that for a function $\psi \equiv \psi(r)$,

  $$\nabla^{2} \psi=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \psi)$$

  comment