Part II, 2016, Paper 3

Algebraic Geometry

• Paper 3, Section II, H

  Algebraic Geometry | Part II, 2016

  (a) Let $X$ be an affine variety. Define the tangent space of $X$ at a point $P$. Say what it means for the variety to be singular at $P$.

  Define the dimension of $X$ in terms of (i) the tangent spaces of $X$, and (ii) Krull dimension.

  (b) Consider the ideal $I$ generated by the set $\left\{y, y^{2}-x^{3}+x y^{3}\right\} \subseteq k[x, y]$. What is $Z(I) \subseteq \mathbb{A}^{2} ?$

  Using the generators of the ideal, calculate the tangent space of a point in $Z(I)$. What has gone wrong? [A complete argument is not necessary.]

  (c) Calculate the dimension of the tangent space at each point $p \in X$ for $X=$ $Z\left(x-y^{2}, x-z w\right) \subseteq \mathbb{A}^{4}$, and determine the location of the singularities of $X .$

  comment

Algebraic Topology

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2016

  Construct a space $X$ as follows. Let $Z_{1}, Z_{2}, Z_{3}$ each be homeomorphic to the standard 2-sphere $S^{2} \subseteq \mathbb{R}^{3}$. For each $i$, let $x_{i} \in Z_{i}$ be the North pole $(1,0,0)$ and let $y_{i} \in Z_{i}$ be the South pole $(-1,0,0)$. Then

  $$X=\left(Z_{1} \sqcup Z_{2} \sqcup Z_{3}\right) / \sim$$

  where $x_{i+1} \sim y_{i}$ for each $i$ (and indices are taken modulo 3 ).

  (a) Describe the universal cover of $X$.

  (b) Compute the fundamental group of $X$ (giving your answer as a well-known group).

  (c) Show that $X$ is not homotopy equivalent to the circle $S^{1}$.

  comment

Applications of Quantum Mechanics

• Paper 3, Section II, A

  Applications of Quantum Mechanics | Part II, 2016

  (a) A spinless charged particle moves in an electromagnetic field defined by vector and scalar potentials $\mathbf{A}(\mathbf{x}, t)$ and $\phi(\mathbf{x}, t)$. The wavefunction $\psi(\mathbf{x}, t)$ for the particle satisfies the time-dependent Schrödinger equation with Hamiltonian

  $$\hat{H}_{0}=\frac{1}{2 m}(-i \hbar \boldsymbol{\nabla}+e \mathbf{A}) \cdot(-i \hbar \boldsymbol{\nabla}+e \mathbf{A})-e \phi .$$

  Consider a gauge transformation

  $$\mathbf{A} \rightarrow \tilde{\mathbf{A}}=\mathbf{A}+\nabla f, \quad \phi \rightarrow \tilde{\phi}=\phi-\frac{\partial f}{\partial t}, \quad \psi \rightarrow \tilde{\psi}=\exp \left(-\frac{i e f}{\hbar}\right) \psi$$

  for some function $f(\mathbf{x}, t)$. Define covariant derivatives with respect to space and time, and show that $\tilde{\psi}$ satisfies the Schrödinger equation with potentials $\tilde{\mathbf{A}}$ and $\tilde{\phi}$.

  (b) Suppose that in part (a) the magnetic field has the form $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}=(0,0, B)$, where $B$ is a constant, and that $\phi=0$. Find a suitable $\mathbf{A}$ with $A_{y}=A_{z}=0$ and determine the energy levels of the Hamiltonian $\hat{H}_{0}$ when the $z$-component of the momentum of the particle is zero. Suppose in addition that the particle is constrained to lie in a rectangular region of area $\mathcal{A}$ in the $(x, y)$-plane. By imposing periodic boundary conditions in the $x$-direction, estimate the degeneracy of each energy level. [You may use without proof results for a quantum harmonic oscillator, provided they are clearly stated.]

  (c) An electron is a charged particle of spin $\frac{1}{2}$ with a two-component wavefunction $\psi(\mathbf{x}, t)$ governed by the Hamiltonian

  $$\hat{H}=\hat{H}_{0} \mathbb{I}_{2}+\frac{e \hbar}{2 m} \mathbf{B} \cdot \boldsymbol{\sigma}$$

  where $\mathbb{I}_{2}$ is the $2 \times 2$ unit matrix and $\sigma=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ denotes the Pauli matrices. Find the energy levels for an electron in the constant magnetic field defined in part (b), assuming as before that the $z$-component of the momentum of the particle is zero.

  Consider $N$ such electrons confined to the rectangular region defined in part (b). Ignoring interactions between the electrons, show that the ground state energy of this system vanishes for $N$ less than some integer $N_{\max }$ which you should determine. Find the ground state energy for $N=(2 p+1) N_{\max }$, where $p$ is a positive integer.

  comment

Applied Probability

• Paper 3, Section II, J

  Applied Probability | Part II, 2016

  (a) State the thinning and superposition properties of a Poisson process on $\mathbb{R}_{+}$. Prove the superposition property.

  (b) A bi-infinite Poisson process $\left(N_{t}: t \in \mathbb{R}\right)$ with $N_{0}=0$ is a process with independent and stationary increments over $\mathbb{R}$. Moreover, for all $-\infty<s \leqslant t<\infty$, the increment $N_{t}-N_{s}$ has the Poisson distribution with parameter $\lambda(t-s)$. Prove that such a process exists.

  (c) Let $N$ be a bi-infinite Poisson process on $\mathbb{R}$ of intensity $\lambda$. We identify it with the set of points $\left(S_{n}\right)$ of discontinuity of $N$, i.e., $N[s, t]=\sum_{n} \mathbf{l}\left(S_{n} \in[s, t]\right)$. Show that if we shift all the points of $N$ by the same constant $c$, then the resulting process is also a Poisson process of intensity $\lambda$.

  Now suppose we shift every point of $N$ by $+1$ or $-1$ with equal probability. Show that the final collection of points is still a Poisson process of intensity $\lambda$. [You may assume the thinning and superposition properties for the bi-infinite Poisson process.]

  comment

Asymptotic Methods

• Paper 3, Section II, C

  Asymptotic Methods | Part II, 2016

  Consider the integral

  $$I(x)=\int_{0}^{1} \frac{1}{\sqrt{t(1-t)}} \exp [i x f(t)] d t$$

  for real $x>0$, where $f(t)=t^{2}+t$. Find and sketch, in the complex $t$-plane, the paths of steepest descent through the endpoints $t=0$ and $t=1$ and through any saddle point(s). Obtain the leading order term in the asymptotic expansion of $I(x)$ for large positive $x$. What is the order of the next term in the expansion? Justify your answer.

  comment

Automata and Formal Languages

• Paper 3, Section I, $4 F$

  Automata and Formal Languages | Part II, 2016

  (a) Define what it means for a context-free grammar (CFG) to be in Chomsky normal form (CNF). Can a CFG in CNF ever define a language containing $\epsilon$ ? If $G_{\text {Chom }}$ denotes the result of converting an arbitrary CFG $G$ into one in CNF, state the relationship between $\mathcal{L}(G)$ and $\mathcal{L}\left(G_{\text {Chom }}\right)$.

  (b) Let $G$ be a CFG in CNF, and let $w \in \mathcal{L}(G)$ be a word of length $|w|=n>0$. Show that every derivation of $w$ in $G$ requires precisely $2 n-1$ steps. Using this, give an algorithm that, on input of any word $v$ on the terminals of $G$, decides if $v \in \mathcal{L}(G)$ or not.

  (c) Convert the following CFG $G$ into a grammar in CNF:

  $$S \rightarrow a S b|S S| \epsilon$$

  Does $\mathcal{L}(G)=\mathcal{L}\left(G_{\text {Chom }}\right)$ in this case? Justify your answer.

  comment

• Paper 3, Section II, F

  Automata and Formal Languages | Part II, 2016

  (a) Let $D=\left(Q, \Sigma, \delta, q_{0}, F\right)$ be a deterministic finite-state automaton. Define the extended transition function $\hat{\delta}: Q \times \Sigma^{*} \rightarrow Q$, and the language accepted by $D$, denoted $\mathcal{L}(D)$. Let $u, v \in \Sigma^{*}$, and $p \in Q$. Prove that $\hat{\delta}(p, u v)=\hat{\delta}(\hat{\delta}(p, u), v)$.

  (b) Let $\sigma_{1}, \sigma_{2}, \ldots, \sigma_{k} \in \Sigma$ where $k \geqslant|Q|$, and let $p \in Q$.

  (i) Show that there exist $0 \leqslant i<j \leqslant k$ such that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{j}\right)$, where we interpret $\sigma_{1} \cdots \sigma_{i}$ as $\epsilon$ if $i=0$.

  (ii) Show that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i} \sigma_{j+1} \cdots \sigma_{k}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{k}\right)$.

  (iii) Show that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i}\left(\sigma_{i+1} \cdots \sigma_{j}\right)^{t} \sigma_{j+1} \cdots \sigma_{k}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{k}\right)$ for all $t \geqslant 1$.

  (c) Prove the following version of the pumping lemma. Suppose $w \in \mathcal{L}(D)$, with $|w| \geqslant|Q|$. Then $w$ can be broken up into three words $w=x y z$ such that $y \neq \epsilon,|x y| \leqslant|Q|$, and for all $t \geqslant 0$, the word $x y^{t} z$ is also in $\mathcal{L}(D)$.

  (d) Hence show that

  (i) if $\mathcal{L}(D)$ contains a word of length at least $|Q|$, then it contains infinitely many words;

  (ii) if $\mathcal{L}(D) \neq \emptyset$, then it contains a word of length less than $|Q|$;

  (iii) if $\mathcal{L}(D)$ contains all words in $\Sigma^{*}$ of length less than $|Q|$, then $\mathcal{L}(D)=\Sigma^{*}$.

  comment

Classical Dynamics

• Paper 3, Section I, E

  Classical Dynamics | Part II, 2016

  Consider a six-dimensional phase space with coordinates $\left(q_{i}, p_{i}\right)$ for $i=1,2,3$. Compute the Poisson brackets $\left\{L_{i}, L_{j}\right\}$, where $L_{i}=\epsilon_{i j k} q_{j} p_{k}$.

  Consider the Hamiltonian

  $$H=\frac{1}{2}|\mathbf{p}|^{2}+V(|\mathbf{q}|)$$

  and show that the resulting Hamiltonian system admits three Poisson-commuting independent first integrals.

  comment

Coding and Cryptography

• Paper 3, Section I, $3 G$

  Coding and Cryptography | Part II, 2016

  Describe in words the unicity distance of a cryptosystem.

  Denote the cryptosystem by $\langle M, K, C\rangle$, in the usual way, and let $m \in M$ and $k \in K$ be random variables and $c=e(m, k)$. The unicity distance $U$ is formally defined to be the least $n>0$ such that $H\left(k \mid c^{(n)}\right)=0$. Derive the formula

  $$U=\frac{\log |K|}{\log |\Sigma|-H}$$

  where $H=H(m)$, and $\Sigma$ is the alphabet of the ciphertext. Make clear any assumptions you make.

  The redundancy of a language is given by $R=1-\frac{H}{\log |\Sigma|}$. If a language has zero redundancy what is the unicity of any cryptosystem?

  comment

Cosmology

• Paper 3, Section I, C

  Cosmology | Part II, 2016

  A universe contains baryonic matter with background density $\rho_{B}(t)$ and density inhomogeneity $\delta_{B}(\mathbf{x}, t)$, together with non-baryonic dark matter with background density $\rho_{D}(t)$ and density inhomogeneity $\delta_{D}(\mathbf{x}, t)$. After the epoch of radiation-matter density equality, $t_{\mathrm{eq}}$, the background dynamics are governed by

  $$H=\frac{2}{3 t} \quad \text { and } \quad \rho_{D}=\frac{1}{6 \pi G t^{2}}$$

  where $H$ is the Hubble parameter.

  The dark-matter density is much greater than the baryonic density $\left(\rho_{D} \gg \rho_{B}\right)$ and so the time-evolution of the coupled density perturbations, at any point $\mathbf{x}$, is described by the equations

  $$\begin{aligned} &\ddot{\delta}_{B}+2 H \dot{\delta}_{B}=4 \pi G \rho_{D} \delta_{D} \\ &\ddot{\delta}_{D}+2 H \dot{\delta}_{D}=4 \pi G \rho_{D} \delta_{D} \end{aligned}$$

  Show that

  $$\delta_{D}=\frac{\alpha}{t}+\beta t^{2 / 3}$$

  where $\alpha$ and $\beta$ are independent of time. Neglecting modes in $\delta_{D}$ and $\delta_{B}$ that decay with increasing time, show that the baryonic density inhomogeneity approaches

  $$\delta_{B}=\beta t^{2 / 3}+\gamma$$

  where $\gamma$ is independent of time.

  Briefly comment on the significance of your calculation for the growth of baryonic density inhomogeneities in the early universe.

  comment

• Paper 3, Section II, C

  Cosmology | Part II, 2016

  The early universe is described by equations (with units such that $c=8 \pi G=\hbar=1$ )

  $$3 H^{2}=\rho, \quad \dot{\rho}+3 H(\rho+p)=0$$

  where $H=\dot{a} / a$. The universe contains only a self-interacting scalar field $\phi$ with interaction potential $V(\phi)$ so that the density and pressure are given by

  $$\begin{aligned} \rho &=\frac{1}{2} \dot{\phi}^{2}+V(\phi) \\ p &=\frac{1}{2} \dot{\phi}^{2}-V(\phi) . \end{aligned}$$

  Show that

  $$\ddot{\phi}+3 H \dot{\phi}+V^{\prime}(\phi)=0$$

  Explain the slow-roll approximation and apply it to equations (1) and (2) to show that it leads to

  $$\sqrt{3} \int \frac{\sqrt{V}}{V^{\prime}} d \phi=-t+\text { const. }$$

  If $V(\phi)=\frac{1}{4} \lambda \phi^{4}$ with $\lambda$ a positive constant and $\phi(0)=\phi_{0}$, show that

  $$\phi(t)=\phi_{0} \exp \left[-\sqrt{\frac{4 \lambda}{3}} t\right]$$

  and that, for small $t$, the scale factor $a(t)$ expands to leading order in $t$ as

  $$a(t) \propto \exp \left[\sqrt{\frac{\lambda}{12}} \phi_{0}^{2} t\right]$$

  Comment on the relevance of this result for inflationary cosmology.

  comment

Differential Geometry

• Paper 3, Section II, G

  Differential Geometry | Part II, 2016

  Explain what it means for an embedded surface $S$ in $\mathbf{R}^{3}$ to be minimal. What is meant by an isothermal parametrization $\phi: U \rightarrow V \subset \mathbf{R}^{3}$ of an embedded surface $V \subset \mathbf{R}^{3}$ ? Prove that if $\phi$ is isothermal then $\phi(U)$ is minimal if and only if the components of $\phi$ are harmonic functions on $U$. [You may assume the formula for the mean curvature of a parametrized embedded surface,

  $$H=\frac{e G-2 f F+g E}{2\left(E G-F^{2}\right)}$$

  where $E, F, G$ (respectively $e, f, g$ ) are the coefficients of the first (respectively second) fundamental forms.]

  Let $S$ be an embedded connected minimal surface in $\mathbf{R}^{3}$ which is closed as a subset of $\mathbf{R}^{3}$, and let $\Pi \subset \mathbf{R}^{3}$ be a plane which is disjoint from $S$. Assuming that local isothermal parametrizations always exist, show that if the Euclidean distance between $S$ and $\Pi$ is attained at some point $P \in S$, i.e. $d(P, \Pi)=\inf _{Q \in S} d(Q, \Pi)$, then $S$ is a plane parallel to $\Pi$.

  comment

Dynamical Systems

• Paper 3, Section II, E

  Dynamical Systems | Part II, 2016

  Consider the dependence of the system

  $$\begin{aligned} \dot{x} &=\left(a-x^{2}\right)\left(a^{2}-y\right) \\ \dot{y} &=x-y \end{aligned}$$

  on the parameter $a$. Find the fixed points and plot their location in the $(a, x)$-plane. Hence, or otherwise, deduce that there are bifurcations at $a=0$ and $a=1$.

  Investigate the bifurcation at $a=1$ by making the substitutions $u=x-1, v=y-1$ and $\mu=a-1$. Find the extended centre manifold in the form $v(u, \mu)$ correct to second order. Find the evolution equation on the extended centre manifold to second order, and determine the stability of its fixed points.

  Use a plot to show which branches of fixed points in the $(a, x)$-plane are stable and which are unstable, and state, without calculation, the type of bifurcation at $a=0$. Hence sketch the structure of the $(x, y)$ phase plane very close to the origin for $|a| \ll 1$ in the cases (i) $a<0$ and (ii) $a>0$.

  comment

Electrodynamics

• Paper 3, Section II, E

  Electrodynamics | Part II, 2016

  The current density in an antenna lying along the $z$-axis takes the form

  $$\mathbf{J}(t, \mathbf{x})=\left\{\begin{array}{ll} \hat{\mathbf{z}} I_{0} \sin (k d-k|z|) e^{-i \omega t} \delta(x) \delta(y) & |z| \leqslant d \\ \mathbf{0} & |z|>d \end{array},\right.$$

  where $I_{0}$ is a constant and $\omega=c k$. Show that at distances $r=|\mathbf{x}|$ for which both $r \gg d$ and $r \gg k d^{2} /(2 \pi)$, the retarded vector potential in Lorenz gauge is

  $$\mathbf{A}(t, \mathbf{x}) \approx \hat{\mathbf{z}} \frac{\mu_{0} I_{0}}{4 \pi r} e^{-i \omega(t-r / c)} \int_{-d}^{d} \sin \left(k d-k\left|z^{\prime}\right|\right) e^{-i k z^{\prime} \cos \theta} d z^{\prime}$$

  where $\cos \theta=\hat{\mathbf{r}} \cdot \hat{\mathbf{z}}$ and $\hat{\mathbf{r}}=\mathbf{x} /|\mathbf{x}|$. Evaluate the integral to show that

  $$\mathbf{A}(t, \mathbf{x}) \approx \hat{\mathbf{z}} \frac{\mu_{0} I_{0}}{2 \pi k r}\left(\frac{\cos (k d \cos \theta)-\cos (k d)}{\sin ^{2} \theta}\right) e^{-i \omega(t-r / c)}$$

  In the far-field, where $k r \gg 1$, the electric and magnetic fields are given by

  $$\begin{aligned} &\mathbf{E}(t, \mathbf{x}) \approx-i \omega \hat{\mathbf{r}} \times[\hat{\mathbf{r}} \times \mathbf{A}(t, \mathbf{x})] \\ &\mathbf{B}(t, \mathbf{x}) \approx i k \hat{\mathbf{r}} \times \mathbf{A}(t, \mathbf{x}) \end{aligned}$$

  By calculating the Poynting vector, show that the time-averaged power radiated per unit solid angle is

  $$\frac{d \mathcal{P}}{d \Omega}=\frac{c \mu_{0} I_{0}^{2}}{8 \pi^{2}}\left(\frac{\cos (k d \cos \theta)-\cos (k d)}{\sin \theta}\right)^{2}$$

  [You may assume that in Lorenz gauge, the retarded potential due to a localised current distribution is

  $$\mathbf{A}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} d^{3} \mathbf{x}^{\prime}$$

  where the retarded time $\left.t_{\text {ret }}=t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right| / c .\right]$

  comment

Fluid Dynamics II

• Paper 3, Section II, B

  Fluid Dynamics II | Part II, 2016

  A cylindrical pipe of radius $a$ and length $L \gg a$ contains two viscous fluids arranged axisymmetrically with fluid 1 of viscosity $\mu_{1}$ occupying the central region $r<\beta a$, where $0<\beta<1$, and fluid 2 of viscosity $\mu_{2}$ occupying the surrounding annular region $\beta a<r<a$. The flow in each fluid is assumed to be steady and unidirectional, with velocities $u_{1}(r) \mathbf{e}_{z}$ and $u_{2}(r) \mathbf{e}_{z}$ respectively, with respect to cylindrical coordinates $(r, \theta, z)$ aligned with the pipe. A fixed pressure drop $\Delta p$ is applied between the ends of the pipe.

  Starting from the Navier-Stokes equations, derive the equations satisfied by $u_{1}(r)$ and $u_{2}(r)$, and state all the boundary conditions. Show that the pressure gradient is constant.

  Solve for the velocity profile in each fluid and calculate the corresponding flow rates, $Q_{1}$ and $Q_{2}$.

  Derive the relationship between $\beta$ and $\mu_{2} / \mu_{1}$ that yields the same flow rate in each fluid. Comment on the behaviour of $\beta$ in the limits $\mu_{2} / \mu_{1} \gg 1$ and $\mu_{2} / \mu_{1} \ll 1$, illustrating your comment by sketching the flow profiles.

  $[$ Hint: In cylindrical coordinates $(r, \theta, z)$,

  $$\nabla^{2} u=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}+\frac{\partial^{2} u}{\partial z^{2}}, \quad e_{r z}=\frac{1}{2}\left(\frac{\partial u_{r}}{\partial z}+\frac{\partial u_{z}}{\partial r}\right)$$

  comment

Further Complex Methods

• Paper 3, Section I, A

  Further Complex Methods | Part II, 2016

  The functions $f(x)$ and $g(x)$ have Laplace transforms $F(p)$ and $G(p)$ respectively, and $f(x)=g(x)=0$ for $x \leqslant 0$. The convolution $h(x)$ of $f(x)$ and $g(x)$ is defined by

  $$h(x)=\int_{0}^{x} f(y) g(x-y) d y \quad \text { for } \quad x>0 \quad \text { and } \quad h(x)=0 \quad \text { for } \quad x \leqslant 0$$

  Express the Laplace transform $H(p)$ of $h(x)$ in terms of $F(p)$ and $G(p)$.

  Now suppose that $f(x)=x^{\alpha}$ and $g(x)=x^{\beta}$ for $x>0$, where $\alpha, \beta>-1$. Find expressions for $F(p)$ and $G(p)$ by using a standard integral formula for the Gamma function. Find an expression for $h(x)$ by using a standard integral formula for the Beta function. Hence deduce that

  $$\frac{\Gamma(z) \Gamma(w)}{\Gamma(z+w)}=\mathrm{B}(z, w)$$

  for all $\operatorname{Re}(z)>0, \operatorname{Re}(w)>0$.

  comment

Galois Theory

• Paper 3, Section II, H

  Galois Theory | Part II, 2016

  (a) Let $L$ be the 13 th cyclotomic extension of $\mathbb{Q}$, and let $\mu$ be a 13 th primitive root of unity. What is the minimal polynomial of $\mu$ over $\mathbb{Q}$ ? What is the Galois group $\operatorname{Gal}(L / \mathbb{Q})$ ? Put $\lambda=\mu+\frac{1}{\mu}$. Show that $\mathbb{Q} \subseteq \mathbb{Q}(\lambda)$ is a Galois extension and find $\operatorname{Gal}(\mathbb{Q}(\lambda) / \mathbb{Q})$.

  (b) Define what is meant by a Kummer extension. Let $K$ be a field of characteristic zero and let $L$ be the $n$th cyclotomic extension of $K$. Show that there is a sequence of Kummer extensions $K=F_{1} \subseteq F_{2} \subseteq \cdots \subseteq F_{r}$ such that $L$ is contained in $F_{r}$.

  comment

General Relativity

• Paper 3, Section II, D

  General Relativity | Part II, 2016

  For a spacetime that is nearly flat, the metric $g_{a b}$ can be expressed in the form

  $$g_{a b}=\eta_{a b}+h_{a b}$$

  where $\eta_{a b}$ is a flat metric (not necessarily diagonal) with constant components, and the components of $h_{a b}$ and their derivatives are small. Show that

  $$2 R_{b d} \approx h_{d}^{a}, b a+h_{b}^{a}, d a-h_{a, b d}^{a}-h_{b d, a c} \eta^{a c}$$

  where indices are raised and lowered using $\eta_{a b}$.

  [You may assume that $\left.R_{b c d}^{a}=\Gamma_{b d, c}^{a}-\Gamma_{b c, d}^{a}+\Gamma_{c e}^{a} \Gamma_{d b}^{e}-\Gamma_{d e}^{a} \Gamma_{c b}^{e} .\right]$

  For the line element

  $$d s^{2}=2 d u d v+d x^{2}+d y^{2}+H(u, x, y) d u^{2},$$

  where $H$ and its derivatives are small, show that the linearised vacuum field equations reduce to $\nabla^{2} H=0$, where $\nabla^{2}$ is the two-dimensional Laplacian operator in $x$ and $y$.

  comment

Graph Theory

• Paper 3, Section II, G

  Graph Theory | Part II, 2016

  Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that if $G$ has $n$ vertices and $m$ edges then

  $$p_{G}(t)=a_{n} t^{n}-a_{n-1} t^{n-1}+a_{n-2} t^{n-2}-\ldots+(-1)^{n} a_{0}$$

  where $a_{n}=1, a_{n-1}=m$ and $a_{i} \geqslant 0$ for all $i$. [You may assume the deletion-contraction relation, provided that you state it clearly.]

  Show that for every graph $G$ (with $n>0$ ) we have $a_{0}=0$. Show also that $a_{1}=0$ if and only if $G$ is disconnected.

  Explain why $t^{4}-2 t^{3}+3 t^{2}-t$ is not the chromatic polynomial of any graph.

  comment

Integrable Systems

• Paper 3, Section II, D

  Integrable Systems | Part II, 2016

  What is meant by an auto-Bäcklund transformation?

  The sine-Gordon equation in light-cone coordinates is

  $$\frac{\partial^{2} \varphi}{\partial \xi \partial \tau}=\sin \varphi$$

  where $\xi=\frac{1}{2}(x-t), \tau=\frac{1}{2}(x+t)$ and $\varphi$ is to be understood modulo $2 \pi$. Show that the pair of equations

  $$\partial_{\xi}\left(\varphi_{1}-\varphi_{0}\right)=2 \epsilon \sin \left(\frac{\varphi_{1}+\varphi_{0}}{2}\right), \quad \partial_{\tau}\left(\varphi_{1}+\varphi_{0}\right)=\frac{2}{\epsilon} \sin \left(\frac{\varphi_{1}-\varphi_{0}}{2}\right)$$

  constitute an auto-Bäcklund transformation for (1).

  By noting that $\varphi=0$ is a solution to (1), use the transformation (2) to derive the soliton (or 'kink') solution to the sine-Gordon equation. Show that this solution can be expressed as

  $$\varphi(x, t)=4 \arctan \left[\exp \left(\pm \frac{x-c t}{\sqrt{1-c^{2}}}+x_{0}\right)\right]$$

  for appropriate constants $c$ and $x_{0}$.

  [Hint: You may use the fact that $\int \operatorname{cosec} x \mathrm{~d} x=\log \tan (x / 2)+$ const.]

  The following function is a solution to the sine-Gordon equation:

  $$\varphi(x, t)=4 \arctan \left[c \frac{\sinh \left(x / \sqrt{1-c^{2}}\right)}{\cosh \left(c t / \sqrt{1-c^{2}}\right)}\right] \quad(c>0) .$$

  Verify that this represents two solitons travelling towards each other at the same speed by considering $x \pm c t=$ constant and taking an appropriate limit.

  comment

Linear Analysis

• Paper 3, Section II, I

  Linear Analysis | Part II, 2016

  (a) Define Banach spaces and Euclidean spaces over $\mathbb{R}$. [You may assume the definitions of vector spaces and inner products.]

  (b) Let $X$ be the space of sequences of real numbers with finitely many non-zero entries. Does there exist a norm $\|\cdot\|$ on $X$ such that $(X,\|\cdot\|)$ is a Banach space? Does there exist a norm such that $(X,\|\cdot\|)$ is Euclidean? Justify your answers.

  (c) Let $(X,\|\cdot\|)$ be a normed vector space over $\mathbb{R}$ satisfying the parallelogram law

  $$\|x+y\|^{2}+\|x-y\|^{2}=2\|x\|^{2}+2\|y\|^{2}$$

  for all $x, y \in X$. Show that $\langle x, y\rangle=\frac{1}{4}\left(\|x+y\|^{2}-\|x-y\|^{2}\right)$ is an inner product on $X$. [You may use without proof the fact that the vector space operations $+$ and are continuous with respect to $\|\cdot\|$. To verify the identity $\langle a+b, c\rangle=\langle a, c\rangle+\langle b, c\rangle$, you may find it helpful to consider the parallelogram law for the pairs $(a+c, b),(b+c, a),(a-c, b)$ and $(b-c, a) .]$

  (d) Let $\left(X,\|\cdot\|_{X}\right)$ be an incomplete normed vector space over $\mathbb{R}$ which is not a Euclidean space, and let $\left(X^{*},\|\cdot\|_{X^{*}}\right)$ be its dual space with the dual norm. Is $\left(X^{*},\|\cdot\|_{X^{*}}\right)$ a Banach space? Is it a Euclidean space? Justify your answers.

  comment

Logic and Set Theory

• Paper 3, Section II, F

  Logic and Set Theory | Part II, 2016

  State the Completeness Theorem for the first-order predicate calculus, and deduce the Compactness Theorem.

  Let $\mathbb{T}$ be a first-order theory over a signature $\Sigma$ whose axioms all have the form $(\forall \vec{x}) \phi$ where $\vec{x}$is a (possibly empty) string of variables and $\phi$ is quantifier-free. Show that every substructure of a $\mathbb{T}$-model is a $\mathbb{T}$-model, and deduce that if $\mathbb{T}$ is consistent then it has a model in which every element is the interpretation of a closed term of $\mathcal{L}(\Sigma)$. $[$ You may assume the result that if $B$ is a substructure of $A$ and $\phi$ is a quantifier-free formula with $n$ free variables, then $\llbracket \phi \rrbracket_{B}=\llbracket \phi \rrbracket_{A} \cap B^{n}$.]

  Now suppose $\mathbb{T} \vdash(\exists x) \psi$ where $\psi$ is a quantifier-free formula with one free variable $x$. Show that there is a finite list $\left(t_{1}, t_{2}, \ldots, t_{n}\right)$ of closed terms of $\mathcal{L}(\Sigma)$ such that

  $$\mathbb{T} \vdash\left(\psi\left[t_{1} / x\right] \vee \psi\left[t_{2} / x\right] \vee \cdots \vee \psi\left[t_{n} / x\right]\right)$$

  comment

Mathematical Biology

• Paper 3, Section $\mathbf{I}$, B

  Mathematical Biology | Part II, 2016

  A delay model for a population of size $N_{t}$ at discrete time $t$ is given by

  $$N_{t+1}=\max \left\{\left(r-N_{t-1}^{2}\right) N_{t}, 0\right\}$$

  Show that for $r>1$ there is a non-trivial equilibrium, and analyse its stability. Show that, as $r$ is increased from 1 , the equilibrium loses stability at $r=3 / 2$ and find the approximate periodicity close to equilibrium at this point.

  comment

• Paper 3, Section II, B

  Mathematical Biology | Part II, 2016

  The Fitzhugh-Nagumo model is given by

  $$\begin{aligned} \dot{u} &=c\left(v+u-\frac{1}{3} u^{3}+z(t)\right) \\ \dot{v} &=-\frac{1}{c}(u-a+b v) \end{aligned}$$

  where $\left(1-\frac{2}{3} b\right)<a<1,0<b \leqslant 1$ and $c \gg 1$.

  For $z(t)=0$, by considering the nullclines in the $(u, v)$-plane, show that there is a unique equilibrium. Sketch the phase diagram

  At $t=0$ the system is at the equilibrium, and $z(t)$ is then 'switched on' to be $z(t)=-V_{0}$ for $t>0$, where $V_{0}$ is a constant. Describe carefully how suitable choices of $V_{0}>0$ can represent a system analogous to (i) a neuron firing once, and (ii) a neuron firing repeatedly. Illustrate your answer with phase diagrams and also plots of $v$ against $t$ for each case. Find the threshold for $V_{0}$ that separates these cases. Comment briefly from a biological perspective on the behaviour of the system when $a=1-\frac{2}{3} b+\epsilon b$ and $0<\epsilon \ll 1$.

  comment

Number Theory

• Paper 3, Section I, I

  Number Theory | Part II, 2016

  Show that the exact power of a prime $p$ dividing $N !$ is $\sum_{j=1}^{\infty}\left\lfloor\frac{N}{p^{j}}\right\rfloor$. By considering the prime factorisation of $\left(\begin{array}{c}2 n \\ n\end{array}\right)$, show that

  $$\frac{4^{n}}{2 n+1} \leqslant\left(\begin{array}{c} 2 n \\ n \end{array}\right) \leqslant(2 n)^{\pi(2 n)}$$

  Setting $n=\left\lfloor\frac{x}{2}\right\rfloor$, deduce that for $x$ sufficiently large

  $$\pi(x)>\frac{\left\lfloor\frac{x}{2}\right\rfloor \log 3}{\log x}>\frac{x}{2 \log x}$$

  comment

• Paper 3, Section II, I

  Number Theory | Part II, 2016

  What does it mean for a positive definite binary quadratic form to be reduced?

  Prove that every positive definite binary quadratic form is equivalent to a reduced form, and that there are only finitely many reduced forms with given discriminant.

  State a criterion for a positive integer $n$ to be represented by a positive definite binary quadratic form with discriminant $d<0$, and hence determine which primes $p$ are represented by $x^{2}+x y+7 y^{2}$.

  comment

Numerical Analysis

• Paper 3, Section II, B

  Numerical Analysis | Part II, 2016

  (a) Define the Jacobi and Gauss-Seidel iteration schemes for solving a linear system of the form $A \mathbf{u}=\mathbf{b}$, where $\mathbf{u}, \mathbf{b} \in \mathbb{R}^{M}$ and $A \in \mathbb{R}^{M \times M}$, giving formulae for the corresponding iteration matrices $H_{J}$ and $H_{G S}$ in terms of the usual decomposition $A=L_{0}+D+U_{0}$.

  Show that both iteration schemes converge when $A$ results from discretization of Poisson's equation on a square with the five-point formula, that is when

  $$A=\left[\begin{array}{rrrrr} S & I & & & \\ I & S & I & & \\ & \ddots & \ddots & \ddots & \\ & & I & S & I \\ & & & I & S \end{array}\right], \quad S=\left[\begin{array}{rrrrr} -4 & 1 & & & \\ 1 & -4 & 1 & & \\ & \ddots & \ddots & \ddots & \\ & & 1 & -4 & 1 \\ & & & 1 & -4 \end{array}\right] \in \mathbb{R}^{m \times m}$$

  and $M=m^{2}$. [You may state the Householder-John theorem without proof.]

  (b) For the matrix $A$ given in $(*)$ :

  (i) Calculate the eigenvalues of $H_{J}$ and deduce its spectral radius $\rho\left(H_{J}\right)$.

  (ii) Show that each eigenvector $\mathbf{q}$ of $H_{G S}$ is related to an eigenvector $\mathbf{p}$ of $H_{J}$ by a transformation of the form $q_{i, j}=\alpha^{i+j} p_{i, j}$ for a suitable value of $\alpha$.

  (iii) Deduce that $\rho\left(H_{G S}\right)=\rho^{2}\left(H_{J}\right)$. What is the significance of this result for the two iteration schemes?

  [Hint: You may assume that the eigenvalues of the matrix $A$ in $(*)$ are

  $$\lambda_{k, \ell}=-4\left(\sin ^{2} \frac{x}{2}+\sin ^{2} \frac{y}{2}\right), \quad \text { where } x=\frac{k \pi h}{m+1}, y=\frac{\ell \pi h}{m+1}, \quad k, \ell=1, \ldots, m,$$

  with corresponding eigenvectors $\left.\mathbf{v}=\left(v_{i, j}\right), \quad v_{i, j}=\sin i x \sin j y, \quad i, j=1, \ldots, m . \quad\right]$

  comment

Optimization and Control

• Paper 3, Section II, K

  Optimization and Control | Part II, 2016

  Consider the system in scalar variables, for $t=1,2, \ldots, h$ :

  $$\begin{aligned} x_{t} &=x_{t-1}+u_{t-1} \\ y_{t} &=x_{t-1}+\eta_{t} \\ \hat{x}_{0} &=x_{0}+\eta_{0} \end{aligned}$$

  where $\hat{x}_{0}$ is given, $y_{t}, u_{t}$ are observed at $t$, but $x_{0}, x_{1}, \ldots$ and $\eta_{0}, \eta_{1}, \ldots$ are unobservable, and $\eta_{0}, \eta_{1}, \ldots$ are independent random variables with mean 0 and variance $v$. Define $\hat{x}_{t-1}$ to be the estimator of $x_{t-1}$ with minimum variance amongst all estimators that are unbiased and linear functions of $W_{t-1}=\left(\hat{x}_{0}, y_{1}, \ldots, y_{t-1}, u_{0}, \ldots, u_{t-2}\right)$. Suppose $\hat{x}_{t-1}=a^{T} W_{t-1}$ and its variance is $V_{t-1}$. After observation at $t$ of $\left(y_{t}, u_{t-1}\right)$, a new unbiased estimator of $x_{t-1}$, linear in $W_{t}$, is expressed

  $$x_{t-1}^{*}=(1-H) b^{T} W_{t-1}+H y_{t}$$

  Find $b$ and $H$ to minimize the variance of $x_{t-1}^{*}$. Hence find $\hat{x}_{t}$ in terms of $\hat{x}_{t-1}, y_{t}, u_{t-1}$, $V_{t-1}$ and $v$. Calculate $V_{h}$.

  Suppose $\eta_{0}, \eta_{1}, \ldots$ are Gaussian and thus $\hat{x}_{t}=E\left[x_{t} \mid W_{t}\right]$. Consider minimizing $E\left[x_{h}^{2}+\sum_{t=0}^{h-1} u_{t}^{2}\right]$, under the constraint that the control $u_{t}$ can only depend on $W_{t}$. Show that the value function of dynamic programming for this problem can be expressed

  $$F\left(W_{t}\right)=\Pi_{t} \hat{x}_{t}^{2}+\cdots$$

  where $F\left(W_{h}\right)=\hat{x}_{h}^{2}+V_{h}$ and $+\cdots$ is independent of $W_{t}$ and linear in $v$.

  comment

Principles of Quantum Mechanics

• Paper 3, Section II, 31 A

  Principles of Quantum Mechanics | Part II, 2016

  A three-dimensional oscillator has Hamiltonian

  $$H=\frac{1}{2 m}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}+\hat{p}_{3}^{2}\right)+\frac{1}{2} m \omega^{2}\left(\alpha^{2} \hat{x}_{1}^{2}+\beta^{2} \hat{x}_{2}^{2}+\gamma^{2} \hat{x}_{3}^{2}\right),$$

  where the constants $m, \omega, \alpha, \beta, \gamma$ are real and positive. Assuming a unique ground state, construct the general normalised eigenstate of $H$ and give a formula for its energy eigenvalue. [You may quote without proof results for a one-dimensional harmonic oscillator of mass $m$ and frequency $\omega$ that follow from writing $\hat{x}=(\hbar / 2 m \omega)^{1 / 2}\left(a+a^{\dagger}\right)$ and $\left.\hat{p}=(\hbar m \omega / 2)^{1 / 2} i\left(a^{\dagger}-a\right) .\right]$

  List all states in the four lowest energy levels of $H$ in the cases:

  (i) $\alpha<\beta<\gamma<2 \alpha$;

  (ii) $\alpha=\beta$ and $\gamma=\alpha+\epsilon$, where $0<\epsilon \ll \alpha$.

  Now consider $H$ with $\alpha=\beta=\gamma=1$ subject to a perturbation

  $$\lambda m \omega^{2}\left(\hat{x}_{1} \hat{x}_{2}+\hat{x}_{2} \hat{x}_{3}+\hat{x}_{3} \hat{x}_{1}\right),$$

  where $\lambda$ is small. Compute the changes in energies for the ground state and the states at the first excited level of the original Hamiltonian, working to the leading order at which nonzero corrections occur. [You may quote without proof results from perturbation theory.]

  Explain briefly why some energy levels of the perturbed Hamiltonian will be exactly degenerate. [Hint: Compare with (ii) above.]

  comment

Principles of Statistics

• Paper 3, Section II, J

  Principles of Statistics | Part II, 2016

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. random variables from a $N(\theta, 1)$ distribution, $\theta \in \mathbb{R}$, and consider a Bayesian model $\theta \sim N\left(0, v^{2}\right)$ for the unknown parameter, where $v>0$ is a fixed constant.

  (a) Derive the posterior distribution $\Pi\left(\cdot \mid X_{1}, \ldots, X_{n}\right)$ of $\theta \mid X_{1}, \ldots, X_{n}$.

  (b) Construct a credible set $C_{n} \subset \mathbb{R}$ such that

  (i) $\Pi\left(C_{n} \mid X_{1}, \ldots, X_{n}\right)=0.95$ for every $n \in \mathbb{N}$, and

  (ii) for any $\theta_{0} \in \mathbb{R}$,

  $$P_{\theta_{0}}^{\mathbb{N}}\left(\theta_{0} \in C_{n}\right) \rightarrow 0.95 \quad \text { as } n \rightarrow \infty,$$

  where $P_{\theta}^{\mathbb{N}}$ denotes the distribution of the infinite sequence $X_{1}, X_{2}, \ldots$ when drawn independently from a fixed $N(\theta, 1)$ distribution.

  [You may use the central limit theorem.]

  comment

Probability and Measure

• Paper 3, Section II, J

  Probability and Measure | Part II, 2016

  (a) Define the Borel $\sigma$-algebra $\mathcal{B}$ and the Borel functions.

  (b) Give an example with proof of a set in $[0,1]$ which is not Lebesgue measurable.

  (c) The Cantor set $\mathcal{C}$ is given by

  $$\mathcal{C}=\left\{\sum_{k=1}^{\infty} \frac{a_{k}}{3^{k}}:\left(a_{k}\right) \text { is a sequence with } a_{k} \in\{0,2\} \text { for all } k\right\}$$

  (i) Explain why $\mathcal{C}$ is Lebesgue measurable.

  (ii) Compute the Lebesgue measure of $\mathcal{C}$.

  (iii) Is every subset of $\mathcal{C}$ Lebesgue measurable?

  (iv) Let $f:[0,1] \rightarrow \mathcal{C}$ be the function given by

  $$f(x)=\sum_{k=1}^{\infty} \frac{2 a_{k}}{3^{k}} \quad \text { where } \quad a_{k}=\left\lfloor 2^{k} x\right\rfloor-2\left\lfloor 2^{k-1} x\right\rfloor$$

  Explain why $f$ is a Borel function.

  (v) Using the previous parts, prove the existence of a Lebesgue measurable set which is not Borel.

  comment

Representation Theory

• Paper 3, Section II, I

  Representation Theory | Part II, 2016

  (a) Let the finite group $G$ act on a finite set $X$ and let $\pi$ be the permutation character. If $G$ is 2 -transitive on $X$, show that $\pi=1_{G}+\chi$, where $\chi$ is an irreducible character of $G$.

  (b) Let $n \geqslant 4$, and let $G$ be the symmetric group $S_{n}$ acting naturally on the set $X=\{1, \ldots, n\}$. For any integer $r \leqslant n / 2$, write $X_{r}$ for the set of all $r$-element subsets of $X$, and let $\pi_{r}$ be the permutation character of the action of $G$ on $X_{r}$. Compute the degree of $\pi_{r}$. If $0 \leqslant \ell \leqslant k \leqslant n / 2$, compute the character inner product $\left\langle\pi_{k}, \pi_{\ell}\right\rangle$.

  Let $m=n / 2$ if $n$ is even, and $m=(n-1) / 2$ if $n$ is odd. Deduce that $S_{n}$ has distinct irreducible characters $\chi^{(n)}=1_{G}, \chi^{(n-1,1)}, \chi^{(n-2,2)}, \ldots, \chi^{(n-m, m)}$ such that for all $r \leqslant m$,

  $$\pi_{r}=\chi^{(n)}+\chi^{(n-1,1)}+\chi^{(n-2,2)}+\cdots+\chi^{(n-r, r)}$$

  (c) Let $\Omega$ be the set of all ordered pairs $(i, j)$ with $i, j \in\{1,2, \ldots, n\}$ and $i \neq j$. Let $S_{n}$ act on $\Omega$ in the obvious way. Write $\pi^{(n-2,1,1)}$ for the permutation character of $S_{n}$ in this action. By considering inner products, or otherwise, prove that

  $$\pi^{(n-2,1,1)}=1+2 \chi^{(n-1,1)}+\chi^{(n-2,2)}+\psi$$

  where $\psi$ is an irreducible character. Calculate the degree of $\psi$, and calculate its value on the elements $\left(\begin{array}{ll}1 & 2\end{array}\right)$ and $\left(\begin{array}{lll}1 & 2 & 3)\end{array}\right)$ of $S_{n}$.

  comment

Riemann Surfaces

• Paper 3, Section II, H

  Riemann Surfaces | Part II, 2016

  Let $f$ be a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$. Let $P \subset \mathbb{C}$ be a fundamental parallelogram and let the degree of $f$ be $n$. Let $a_{1}, \ldots, a_{n}$ denote the zeros of $f$ in $P$, and let $b_{1}, \ldots, b_{n}$ denote the poles (both with possible repeats). By considering the integral (if required, also slightly perturbing $P$ )

  $$\frac{1}{2 \pi i} \int_{\partial P} z \frac{f^{\prime}(z)}{f(z)} d z$$

  show that

  $$\sum_{j=1}^{n} a_{j}-\sum_{j=1}^{n} b_{j} \in \Lambda$$

  Let $\wp(z)$ denote the Weierstrass $\wp$-function with respect to $\Lambda$. For $v, w \notin \Lambda$ with $\wp(v) \neq \wp(w)$ we set

  $$f(z)=\operatorname{det}\left(\begin{array}{ccc} 1 & 1 & 1 \\ \wp(z) & \wp(v) & \wp(w) \\ \wp^{\prime}(z) & \wp^{\prime}(v) & \wp^{\prime}(w) \end{array}\right)$$

  an elliptic function with periods $\Lambda$. Suppose $z \notin \Lambda, z-v \notin \Lambda$ and $z-w \notin \Lambda$. Prove that $f(z)=0$ if and only if $z+v+w \in \Lambda$. [You may use standard properties of the Weierstrass $\wp$-function provided they are clearly stated.]

  comment

Statistical Modelling

• Paper 3, Section I, K

  Statistical Modelling | Part II, 2016

  The $R$ command

  $>\operatorname{boxcox}($ rainfall $\sim$ month+elnino+month:elnino)

  performs a Box-Cox transform of the response at several values of the parameter $\lambda$, and produces the following plot:

  

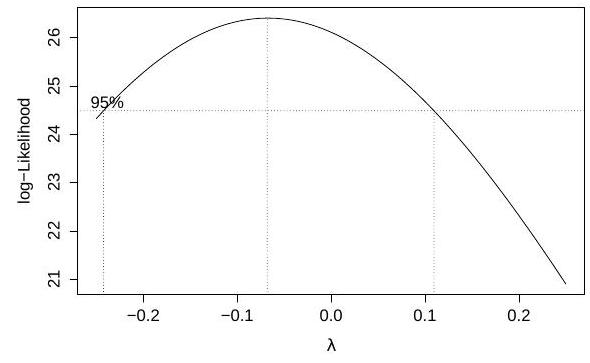
  We fit two linear models and obtain the Q-Q plots for each fit, which are shown below in no particular order:

  

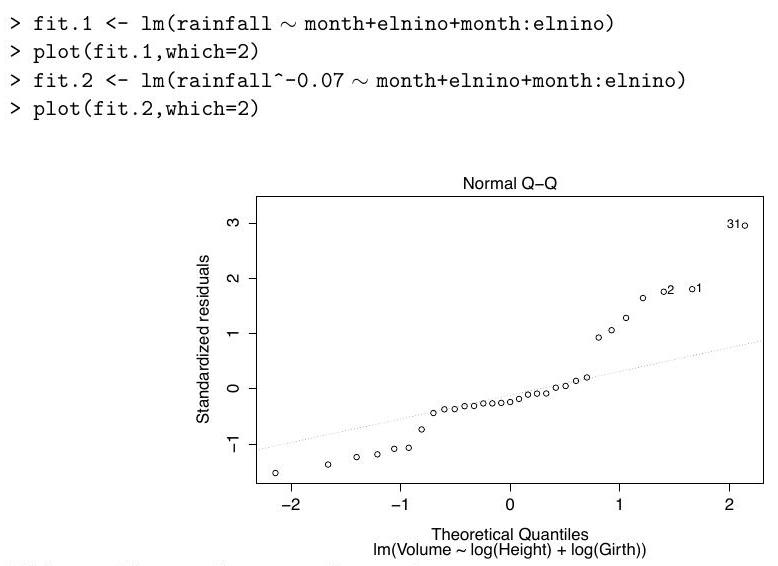
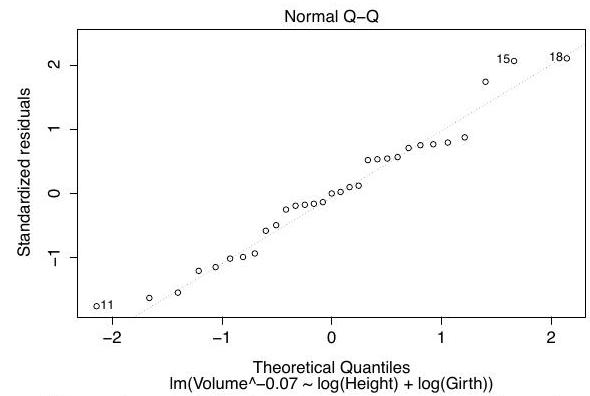
  Define the variable on the $y$-axis in the output of boxcox, and match each Q-Q plot to one of the models.

  After choosing the model fit.2, the researcher calculates Cook's distance for the $i$ th sample, which has high leverage, and compares it to the upper $0.01$-point of an $F_{p, n-p}$ distribution, because the design matrix is of size $n \times p$. Provide an interpretation of this comparison in terms of confidence sets for $\hat{\beta}$. Is this confidence statement exact?

  comment

Statistical Physics

• Paper 3, Section II, C

  Statistical Physics | Part II, 2016

  (a) Consider an ideal gas consisting of $N$ identical classical particles of mass $m$ moving freely in a volume $V$ with Hamiltonian $H=|\mathbf{p}|^{2} / 2 m$. Show that the partition function of the gas has the form

  $$Z_{\text {ideal }}=\frac{V^{N}}{\lambda^{3 N} N !}$$

  and find $\lambda$ as a function of the temperature $T$.

  [You may assume that $\int_{-\infty}^{\infty} e^{-a x^{2}} d x=\sqrt{\pi / a}$ for $a>0$.]

  (b) A monatomic gas of interacting particles is a modification of an ideal gas where any pair of particles with separation $r$ interact through a potential energy $U(r)$. The partition function for this gas can be written as

  $$Z=Z_{\text {ideal }}\left[1+\frac{2 \pi N}{V} \int_{0}^{\infty} f(r) r^{2} d r\right]^{N}$$

  where $f(r)=e^{-\beta U(r)}-1, \quad \beta=1 /\left(k_{B} T\right)$. The virial expansion of the equation of state for small densities $N / V$ is

  $$\frac{p}{k_{B} T}=\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}+\mathcal{O}\left(\frac{N^{3}}{V^{3}}\right)$$

  Using the free energy, show that

  $$B_{2}(T)=-2 \pi \int_{0}^{\infty} f(r) r^{2} d r$$

  (c) The Lennard-Jones potential is

  $$U(r)=\epsilon\left(\frac{r_{0}^{12}}{r^{12}}-2 \frac{r_{0}^{6}}{r^{6}}\right)$$

  where $\epsilon$ and $r_{0}$ are positive constants. Find the separation $\sigma$ where $U(\sigma)=0$ and the separation $r_{\min }$ where $U(r)$ has its minimum. Sketch the graph of $U(r)$. Calculate $B_{2}(T)$ for this potential using the approximations

  $$f(r)=e^{-\beta U(r)}-1 \simeq \begin{cases}-1 & \text { for } \quad r<\sigma \\ -\beta U(r) & \text { for } r \geqslant \sigma\end{cases}$$

  comment

Stochastic Financial Models

• Paper 3, Section II, K

  Stochastic Financial Models | Part II, 2016

  Consider the following two-period market model. There is a risk-free asset which pays interest at rate $r=1 / 4$. There is also a risky stock with prices $\left(S_{t}\right)_{t \in\{0,1,2\}}$ given by

  

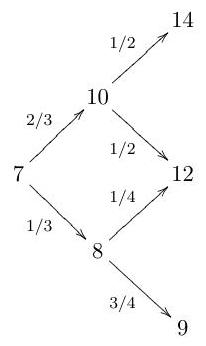
  The above diagram should be read as

  $$\mathbb{P}\left(S_{1}=10 \mid S_{0}=7\right)=2 / 3, \quad \mathbb{P}\left(S_{2}=14 \mid S_{1}=10\right)=1 / 2$$

  and so forth.

  (a) Find the risk-neutral probabilities.

  (b) Consider a European put option with strike $K=10$ expiring at time $T=2$. What is the initial no-arbitrage price of the option? How many shares should be held in each period to replicate the payout?

  (c) Now consider an American put option with the same strike and expiration date. Find the optimal exercise policy, assuming immediate exercise is not allowed. Would your answer change if you were allowed to exercise the option at time 0 ?

  comment

Topics in Analysis

• Paper 3, Section I, $2 \mathrm{H}$

  Topics in Analysis | Part II, 2016

  In the game of 'Chicken', $A$ and $B$ drive fast cars directly at each other. If they both swerve, they both lose 10 status points; if neither swerves, they both lose 100 status points. If one swerves and the other does not, the swerver loses 20 status points and the non-swerver gains 40 status points. Find all the pairs of probabilistic strategies such that, if one driver maintains their strategy, it is not in the interest of the other to change theirs.

  comment

Waves

• Paper 3, Section II, $37 \mathrm{D}$

  Waves | Part II, 2016

  Small disturbances in a homogeneous elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \times(\boldsymbol{\nabla} \times \mathbf{u})$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement. Show that a harmonic plane-wave solution

  $$\mathbf{u}=\operatorname{Re}\left[\mathbf{A} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  must satisfy

  $$\omega^{2} \mathbf{A}=c_{P}^{2} \mathbf{k}(\mathbf{k} \cdot \mathbf{A})-c_{S}^{2} \mathbf{k} \times(\mathbf{k} \times \mathbf{A}),$$

  where the wavespeeds $c_{P}$ and $c_{S}$ are to be identified. Describe mathematically how such plane-wave solutions can be classified into longitudinal $P$-waves and transverse $S V$ - and $S H$-waves (taking the $y$-direction as the vertical direction).

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with a homogeneous elastic solid with Lamé moduli $\bar{\lambda}$ and $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a rigid boundary at $y=h$. A harmonic plane $S H$-wave propagates from $y<0$ towards the interface $y=0$, with displacement

  $$\operatorname{Re}\left[A e^{i(\ell x+m y-\omega t)}\right](0,0,1)$$

  How are $\ell, m$ and $\omega$ related? The total displacement in $y<0$ is the sum of $(*)$ and that of the reflected $S H$-wave,

  $$\operatorname{Re}\left[R A e^{i(\ell x-m y-\omega t)}\right](0,0,1)$$

  Write down the form of the displacement in $0<y<h$, and determine the (complex) reflection coefficient $R$. Verify that $|R|=1$ regardless of the parameter values, and explain this physically.

  comment

• Paper 3, Section II, $37 \mathrm{D}$

  Waves | Part II, 2016

  Small disturbances in a homogeneous elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \times(\boldsymbol{\nabla} \times \mathbf{u})$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement. Show that a harmonic plane-wave solution

  $$\mathbf{u}=\operatorname{Re}\left[\mathbf{A} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  must satisfy

  $$\omega^{2} \mathbf{A}=c_{P}^{2} \mathbf{k}(\mathbf{k} \cdot \mathbf{A})-c_{S}^{2} \mathbf{k} \times(\mathbf{k} \times \mathbf{A}),$$

  where the wavespeeds $c_{P}$ and $c_{S}$ are to be identified. Describe mathematically how such plane-wave solutions can be classified into longitudinal $P$-waves and transverse $S V$ - and $S H$-waves (taking the $y$-direction as the vertical direction).

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with a homogeneous elastic solid with Lamé moduli $\bar{\lambda}$ and $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a rigid boundary at $y=h$. A harmonic plane $S H$-wave propagates from $y<0$ towards the interface $y=0$, with displacement

  $$\operatorname{Re}\left[A e^{i(\ell x+m y-\omega t)}\right](0,0,1)$$

  How are $\ell, m$ and $\omega$ related? The total displacement in $y<0$ is the sum of $(*)$ and that of the reflected $S H$-wave,

  $$\operatorname{Re}\left[R A e^{i(\ell x-m y-\omega t)}\right](0,0,1)$$

  Write down the form of the displacement in $0<y<h$, and determine the (complex) reflection coefficient $R$. Verify that $|R|=1$ regardless of the parameter values, and explain this physically.

  comment