Part II, 2016, Paper 1

Algebraic Geometry

• Paper 1, Section II, H

  Algebraic Geometry | Part II, 2016

  Let $k$ be an algebraically closed field.

  (a) Let $X$ and $Y$ be affine varieties defined over $k$. Given a map $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of affine varieties.

  (b) Let $f: \mathbb{A}^{1} \rightarrow \mathbb{A}^{3}$ be the map given by

  $$f(t)=\left(t, t^{2}, t^{3}\right)$$

  Show that $f$ is a morphism. Show that the image of $f$ is a closed subvariety of $\mathbb{A}^{3}$ and determine its ideal.

  (c) Let $g: \mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1} \rightarrow \mathbb{P}^{7}$ be the map given by

  $g\left(\left(s_{1}, t_{1}\right),\left(s_{2}, t_{2}\right),\left(s_{3}, t_{3}\right)\right)=\left(s_{1} s_{2} s_{3}, s_{1} s_{2} t_{3}, s_{1} t_{2} s_{3}, s_{1} t_{2} t_{3}, t_{1} s_{2} s_{3}, t_{1} s_{2} t_{3}, t_{1} t_{2} s_{3}, t_{1} t_{2} t_{3}\right) .$

  Show that the image of $g$ is a closed subvariety of $\mathbb{P}^{7}$.

  comment

Algebraic Topology

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2016

  Let $T=S^{1} \times S^{1}$ be the 2-dimensional torus. Let $\alpha: S^{1} \rightarrow T$ be the inclusion of the coordinate circle $S^{1} \times\{1\}$, and let $X$ be the result of attaching a 2-cell along $\alpha$.

  (a) Write down a presentation for the fundamental group of $X$ (with respect to some basepoint), and identify it with a well-known group.

  (b) Compute the simplicial homology of any triangulation of $X$.

  (c) Show that $X$ is not homotopy equivalent to any compact surface.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, A

  Applications of Quantum Mechanics | Part II, 2016

  A particle in one dimension of mass $m$ and energy $E=\hbar^{2} k^{2} / 2 m(k>0)$ is incident from $x=-\infty$ on a potential $V(x)$ with $V(x) \rightarrow 0$ as $x \rightarrow-\infty$ and $V(x)=\infty$ for $x>0$. The relevant solution of the time-independent Schrödinger equation has the asymptotic form

  $$\psi(x) \sim \exp (i k x)+r(k) \exp (-i k x), \quad x \rightarrow-\infty$$

  Explain briefly why a pole in the reflection amplitude $r(k)$ at $k=i \kappa$ with $\kappa>0$ corresponds to the existence of a stable bound state in this potential. Indicate why a pole in $r(k)$ just below the real $k$-axis, at $k=k_{0}-i \rho$ with $k_{0} \gg \rho>0$, corresponds to a quasi-stable bound state. Find an approximate expression for the lifetime $\tau$ of such a quasi-stable state.

  Now suppose that

  $$V(x)= \begin{cases}\left(\hbar^{2} U / 2 m\right) \delta(x+a) & \text { for } x<0 \\ \infty & \text { for } x>0\end{cases}$$

  where $U>0$ and $a>0$ are constants. Compute the reflection amplitude $r(k)$ in this case and deduce that there are quasi-stable bound states if $U$ is large. Give expressions for the wavefunctions and energies of these states and compute their lifetimes, working to leading non-vanishing order in $1 / U$ for each expression.

  [ You may assume $\psi=0$ for $x \geqslant 0$ and $\lim _{\epsilon \rightarrow 0+}\left\{\psi^{\prime}(-a+\epsilon)-\psi^{\prime}(-a-\epsilon)\right\}=U \psi(-a)$.]

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2016

  (a) Define a continuous-time Markov chain $X$ with infinitesimal generator $Q$ and jump chain $Y$.

  (b) Prove that if a state $x$ is transient for $Y$, then it is transient for $X$.

  (c) Prove or provide a counterexample to the following: if $x$ is positive recurrent for $X$, then it is positive recurrent for $Y$.

  (d) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ on $\mathbb{Z}$ with non-zero transition rates given by

  $$q(i, i+1)=2 \cdot 3^{|i|}, \quad q(i, i)=-3^{|i|+1} \quad \text { and } \quad q(i, i-1)=3^{|i|}$$

  Determine whether $X$ is transient or recurrent. Let $T_{0}=\inf \left\{t \geqslant J_{1}: X_{t}=0\right\}$, where $J_{1}$ is the first jump time. Does $X$ have an invariant distribution? Justify your answer. Calculate $\mathbb{E}_{0}\left[T_{0}\right]$.

  (e) Let $X$ be a continuous-time random walk on $\mathbb{Z}^{d}$ with $q(x)=\|x\|^{\alpha} \wedge 1$ and $q(x, y)=q(x) /(2 d)$ for all $y \in \mathbb{Z}^{d}$ with $\|y-x\|=1$. Determine for which values of $\alpha$ the walk is transient and for which it is recurrent. In the recurrent case, determine the range of $\alpha$ for which it is also positive recurrent. [Here $\|x\|$ denotes the Euclidean norm of $x$.]

  comment

Automata and Formal Languages

• Paper 1, Section I, $4 \mathrm{~F}$

  Automata and Formal Languages | Part II, 2016

  State the pumping lemma for context-free languages (CFLs). Which of the following are CFLs? Justify your answers.

  (i) $\left\{a^{2 n} b^{3 n} \mid n \geqslant 3\right\}$.

  (ii) $\left\{a^{2 n} b^{3 n} c^{5 n} \mid n \geqslant 0\right\}$.

  (iii) $\left\{a^{p} \mid p\right.$ is a prime $\}$.

  Let $L, M$ be CFLs. Show that $L \cup M$ is also a CFL.

  comment

• Paper 1, Section II, F

  Automata and Formal Languages | Part II, 2016

  (a) Define a recursive set and a recursively enumerable (r.e.) set. Prove that $E \subseteq \mathbb{N}$ is recursive if and only if both $E$ and $\mathbb{N} \backslash E$ are r.e.

  (b) Define the halting set $\mathbb{K}$. Prove that $\mathbb{K}$ is r.e. but not recursive.

  (c) Let $E_{1}, E_{2}, \ldots, E_{n}$ be r.e. sets. Prove that $\bigcup_{i=1}^{n} E_{i}$ and $\bigcap_{i=1}^{n} E_{i}$ are r.e. Show by an example that the union of infinitely many r.e. sets need not be r.e.

  (d) Let $E$ be a recursive set and $f: \mathbb{N} \rightarrow \mathbb{N}$ a (total) recursive function. Prove that the set $\{f(n) \mid n \in E\}$ is r.e. Is it necessarily recursive? Justify your answer.

  [Any use of Church's thesis in your answer should be explicitly stated.]

  comment

Classical Dynamics

• Paper 1, Section I, E

  Classical Dynamics | Part II, 2016

  Consider a one-parameter family of transformations $q_{i}(t) \mapsto Q_{i}(s, t)$ such that $Q_{i}(0, t)=q_{i}(t)$ for all time $t$, and

  $$\frac{\partial}{\partial s} L\left(Q_{i}, \dot{Q}_{i}, t\right)=0$$

  where $L$ is a Lagrangian and a dot denotes differentiation with respect to $t$. State and prove Noether's theorem.

  Consider the Lagrangian

  $$L=\frac{1}{2}\left(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}\right)-V(x+y, y+z),$$

  where the potential $V$ is a function of two variables. Find a continuous symmetry of this Lagrangian and construct the corresponding conserved quantity. Use the Euler-Lagrange equations to explicitly verify that the function you have constructed is independent of $t$.

  comment

Coding and Cryptography

• Paper 1, Section I, G

  Coding and Cryptography | Part II, 2016

  Find the average length of an optimum decipherable binary code for a source that emits five words with probabilities

  $$0.25,0.15,0.15,0.2,0.25$$

  Show that, if a source emits $N$ words (with $N \geqslant 2$ ), and if $l_{1}, \ldots, l_{N}$ are the lengths of the codewords in an optimum encoding over the binary alphabet, then

  $$l_{1}+\cdots+l_{N} \leqslant \frac{1}{2}\left(N^{2}+N-2\right) .$$

  [You may assume that an optimum encoding can be given by a Huffman encoding.]

  comment

• Paper 1, Section II, G

  Coding and Cryptography | Part II, 2016

  What does it mean to say a binary code $C$ has length $n$, size $m$ and minimum distance d?

  Let $A(n, d)$ be the largest value of $m$ for which there exists an $[n, m, d]$-code. Prove that

  $$\frac{2^{n}}{V(n, d-1)} \leqslant A(n, d) \leqslant \frac{2^{n}}{V(n,\lfloor(d-1) / 2\rfloor)}$$

  where

  $$V(n, r)=\sum_{j=0}^{r}\left(\begin{array}{l} n \\ j \end{array}\right)$$

  Another bound for $A(n, d)$ is the Singleton bound given by

  $$A(n, d) \leqslant 2^{n-d+1}$$

  Prove the Singleton bound and give an example of a linear code of length $n>1$ that satisfies $A(n, d)=2^{n-d+1}$.

  comment

Cosmology

• Paper 1, Section I, C

  Cosmology | Part II, 2016

  The expansion scale factor, $a(t)$, for an isotropic and spatially homogeneous universe containing material with pressure $p$ and mass density $\rho$ obeys the equations

  $$\begin{gathered} \dot{\rho}+3(\rho+p) \frac{\dot{a}}{a}=0, \\ \left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G \rho}{3}-\frac{k}{a^{2}}+\frac{\Lambda}{3}, \end{gathered}$$

  where the speed of light is set equal to unity, $G$ is Newton's constant, $k$ is a constant equal to 0 or $\pm 1$, and $\Lambda$ is the cosmological constant. Explain briefly the interpretation of these equations.

  Show that these equations imply

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G(\rho+3 p)}{3}+\frac{\Lambda}{3} .$$

  Hence show that a static solution with constant $a=a_{\mathrm{s}}$ exists when $p=0$ if

  $$\Lambda=4 \pi G \rho=\frac{k}{a_{\mathrm{s}}^{2}}$$

  What must the value of $k$ be, if the density $\rho$ is non-zero?

  comment

• Paper 1, Section II, C

  Cosmology | Part II, 2016

  The distribution function $f(\mathbf{x}, \mathbf{p}, t)$ gives the number of particles in the universe with position in $(\mathbf{x}, \mathbf{x}+\delta \mathbf{x})$ and momentum in $(\mathbf{p}, \mathbf{p}+\delta \mathbf{p})$ at time $t$. It satisfies the boundary condition that $f \rightarrow 0$ as $|\mathbf{x}| \rightarrow \infty$ and as $|\mathbf{p}| \rightarrow \infty$. Its evolution obeys the Boltzmann equation

  $$\frac{\partial f}{\partial t}+\frac{\partial f}{\partial \mathbf{p}} \cdot \frac{d \mathbf{p}}{d t}+\frac{\partial f}{\partial \mathbf{x}} \cdot \frac{d \mathbf{x}}{d t}=\left[\frac{d f}{d t}\right]_{\mathrm{col}}$$

  where the collision term $\left[\frac{d f}{d t}\right]_{c o l}$ describes any particle production and annihilation that occurs.

  The universe expands isotropically and homogeneously with expansion scale factor $a(t)$, so the momenta evolve isotropically with magnitude $p \propto a^{-1}$. Show that the Boltzmann equation simplifies to

  $$\frac{\partial f}{\partial t}-\frac{\dot{a}}{a} \mathbf{p} \cdot \frac{\partial f}{\partial \mathbf{p}}=\left[\frac{d f}{d t}\right]_{\mathrm{col}}$$

  The number densities $n$ of particles and $\bar{n}$ of antiparticles are defined in terms of their distribution functions $f$ and $\bar{f}$, and momenta $p$ and $\bar{p}$, by

  $$n=\int_{0}^{\infty} f 4 \pi p^{2} d p \quad \text { and } \quad \bar{n}=\int_{0}^{\infty} \bar{f} 4 \pi \bar{p}^{2} d \bar{p}$$

  and the collision term may be assumed to be of the form

  $$\left[\frac{d f}{d t}\right]_{\mathrm{col}}=-\langle\sigma v\rangle \int_{0}^{\infty} \bar{f} f 4 \pi \bar{p}^{2} d \bar{p}+R$$

  where $\langle\sigma v\rangle$ determines the annihilation cross-section of particles by antiparticles and $R$ is the production rate of particles.

  By integrating equation $(*)$ with respect to the momentum $\mathbf{p}$ and assuming that $\langle\sigma v\rangle$ is a constant, show that

  $$\frac{d n}{d t}+3 \frac{\dot{a}}{a} n=-\langle\sigma v\rangle n \bar{n}+Q$$

  where $Q=\int_{0}^{\infty} R 4 \pi p^{2} d p$. Assuming the same production rate $R$ for antiparticles, write down the corresponding equation satisfied by $\bar{n}$ and show that

  $$(n-\bar{n}) a^{3}=\mathrm{constant}$$

  comment

Differential Geometry

• Paper 1, Section II, G

  Differential Geometry | Part II, 2016

  Define what is meant by the regular values and critical values of a smooth map $f: X \rightarrow Y$ of manifolds. State the Preimage Theorem and Sard's Theorem.

  Suppose now that $\operatorname{dim} X=\operatorname{dim} Y$. If $X$ is compact, prove that the set of regular values is open in $Y$, but show that this may not be the case if $X$ is non-compact.

  Construct an example with $\operatorname{dim} X=\operatorname{dim} Y$ and $X$ compact for which the set of critical values is not a submanifold of $Y$.

  [Hint: You may find it helpful to consider the case $X=S^{1}$ and $Y=\mathbf{R}$. Properties of bump functions and the function $e^{-1 / x^{2}}$ may be assumed in this question.]

  comment

Dynamical Systems

• Paper 1, Section II, E

  Dynamical Systems | Part II, 2016

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=x(y-a), \\ &\dot{y}=1-x-y^{2}, \end{aligned}$$

  where $-1<a<1$. Find and classify the fixed points of the system.

  Use Dulac's criterion with a weighting function of the form $\phi=x^{p}$ and a suitable choice of $p$ to show that there are no periodic orbits for $a \neq 0$. For the case $a=0$ use the same weighting function to find a function $V(x, y)$ which is constant on trajectories. [Hint: $\phi \dot{\mathbf{x}}$ is Hamiltonian.]

  Calculate the stable manifold at $(0,-1)$ correct to quadratic order in $x$.

  Sketch the phase plane for the cases (i) $a=0$ and (ii) $a=\frac{1}{2}$.

  comment

Electrodynamics

• Paper 1, Section II, E

  Electrodynamics | Part II, 2016

  A point particle of charge $q$ and mass $m$ moves in an electromagnetic field with 4 -vector potential $A_{\mu}(x)$, where $x^{\mu}$ is position in spacetime. Consider the action

  $$S=-m c \int\left(-\eta_{\mu \nu} \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda}\right)^{1 / 2} d \lambda+q \int A_{\mu} \frac{d x^{\mu}}{d \lambda} d \lambda$$

  where $\lambda$ is an arbitrary parameter along the particle's worldline and $\eta_{\mu \nu}=\operatorname{diag}(-1,+1,+1,+1)$ is the Minkowski metric.

  (a) By varying the action with respect to $x^{\mu}(\lambda)$, with fixed endpoints, obtain the equation of motion

  $$m \frac{d u^{\mu}}{d \tau}=q F_{\nu}^{\mu} u^{\nu} \text {, }$$

  where $\tau$ is the proper time, $u^{\mu}=d x^{\mu} / d \tau$ is the velocity 4-vector, and $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ is the field strength tensor.

  (b) This particle moves in the field generated by a second point charge $Q$ that is held at rest at the origin of some inertial frame. By choosing a suitable expression for $A_{\mu}$ and expressing the first particle's spatial position in spherical polar coordinates $(r, \theta, \phi)$, show from the action $(*)$ that

  $$\begin{aligned} \mathcal{E} & \equiv \dot{t}-\Gamma / r \\ \ell c & \equiv r^{2} \dot{\phi} \sin ^{2} \theta \end{aligned}$$

  are constants, where $\Gamma=-q Q /\left(4 \pi \epsilon_{0} m c^{2}\right)$ and overdots denote differentiation with respect to $\tau$.

  (c) Show that when the motion is in the plane $\theta=\pi / 2$,

  $$\mathcal{E}+\frac{\Gamma}{r}=\sqrt{1+\frac{\dot{r}^{2}}{c^{2}}+\frac{\ell^{2}}{r^{2}}}$$

  Hence show that the particle's orbit is bounded if $\mathcal{E}<1$, and that the particle can reach the origin in finite proper time if $\Gamma>|\ell|$.

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2016

  State the vorticity equation and interpret the meaning of each term.

  A planar vortex sheet is diffusing in the presence of a perpendicular straining flow. The flow is everywhere of the form $\mathbf{u}=(U(y, t),-E y, E z)$, where $U \rightarrow \pm U_{0}$ as $y \rightarrow \pm \infty$, and $U_{0}$ and $E>0$ are constants. Show that the vorticity has the form $\boldsymbol{\omega}=\omega(y, t) \mathbf{e}_{z}$, and obtain a scalar equation describing the evolution of $\omega$.

  Explain physically why the solution approaches a steady state in which the vorticity is concentrated near $y=0$. Use scaling to estimate the thickness $\delta$ of the steady vorticity layer as a function of $E$ and the kinematic viscosity $\nu$.

  Determine the steady vorticity profile, $\omega(y)$, and the steady velocity profile, $U(y)$.

  $\left[\right.$ Hint: $\left.\quad \operatorname{erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-u^{2}} \mathrm{~d} u .\right]$

  State, with a brief physical justification, why you might expect this steady flow to be unstable to long-wavelength perturbations, defining what you mean by long.

  comment

Further Complex Methods

• Paper 1, Section I, A

  Further Complex Methods | Part II, 2016

  Evaluate the integral

  $$f(p)=\mathcal{P} \int_{-\infty}^{\infty} d x \frac{e^{i p x}}{x^{4}-1}$$

  where $p$ is a real number, for (i) $p>0$ and (ii) $p<0$.

  comment

• Paper 1, Section II, A

  Further Complex Methods | Part II, 2016

  (a) Legendre's equation for $w(z)$ is

  $$\left(z^{2}-1\right) w^{\prime \prime}+2 z w^{\prime}-\ell(\ell+1) w=0, \quad \text { where } \quad \ell=0,1,2, \ldots$$

  Let $\mathcal{C}$ be a closed contour. Show by direct substitution that for $z$ within $\mathcal{C}$

  $$\int_{\mathcal{C}} d t \frac{\left(t^{2}-1\right)^{\ell}}{(t-z)^{\ell+1}}$$

  is a non-trivial solution of Legendre's equation.

  (b) Now consider

  $$Q_{\nu}(z)=\frac{1}{4 i \sin \nu \pi} \int_{\mathcal{C}^{\prime}} d t \frac{\left(t^{2}-1\right)^{\nu}}{(t-z)^{\nu+1}}$$

  for real $\nu>-1$ and $\nu \neq 0,1,2, \ldots$. The closed contour $\mathcal{C}^{\prime}$ is defined to start at the origin, wind around $t=1$ in a counter-clockwise direction, then wind around $t=-1$ in a clockwise direction, then return to the origin, without encircling the point $z$. Assuming that $z$ does not lie on the real interval $-1 \leqslant x \leqslant 1$, show by deforming $\mathcal{C}^{\prime}$ onto this interval that functions $Q_{\ell}(z)$ may be defined as limits of $Q_{\nu}(z)$ with $\nu \rightarrow \ell=0,1,2, \ldots$.

  Find an explicit expression for $Q_{0}(z)$ and verify that it satisfies Legendre's equation with $\ell=0$.

  comment

Galois Theory

• Paper 1, Section II, H

  Galois Theory | Part II, 2016

  (a) Prove that if $K$ is a field and $f \in K[t]$, then there exists a splitting field $L$ of $f$ over $K$. [You do not need to show uniqueness of $L$.]

  (b) Let $K_{1}$ and $K_{2}$ be algebraically closed fields of the same characteristic. Show that either $K_{1}$ is isomorphic to a subfield of $K_{2}$ or $K_{2}$ is isomorphic to a subfield of $K_{1}$. [For subfields $F_{i}$ of $K_{1}$ and field homomorphisms $\psi_{i}: F_{i} \rightarrow K_{2}$ with $i=1$, 2, we say $\left(F_{1}, \psi_{1}\right) \leqslant\left(F_{2}, \psi_{2}\right)$ if $F_{1}$ is a subfield of $F_{2}$ and $\left.\psi_{2}\right|_{F_{1}}=\psi_{1}$. You may assume the existence of a maximal pair $(F, \psi)$ with respect to the partial order just defined.]

  (c) Give an example of a finite field extension $K \subseteq L$ such that there exist $\alpha, \beta \in L \backslash K$ where $\alpha$ is separable over $K$ but $\beta$ is not separable over $K .$

  comment

General Relativity

• Paper 1, Section II, D

  General Relativity | Part II, 2016

  Consider a family of geodesics with $s$ an affine parameter and $V^{a}$ the tangent vector on each curve. The equation of geodesic deviation for a vector field $W^{a}$ is

  $$\frac{D^{2} W^{a}}{D s^{2}}=R_{b c d}^{a} V^{b} V^{c} W^{d}$$

  where $\frac{D}{D s}$ denotes the directional covariant derivative $V^{b} \nabla_{b}$.

  (i) Show that if

  $$V^{b} \frac{\partial W^{a}}{\partial x^{b}}=W^{b} \frac{\partial V^{a}}{\partial x^{b}}$$

  then $W^{a}$ satisfies $(*)$.

  (ii) Show that $V^{a}$ and $s V^{a}$ satisfy $(*)$.

  (iii) Show that if $W^{a}$ is a Killing vector field, meaning that $\nabla_{b} W_{a}+\nabla_{a} W_{b}=0$, then $W^{a}$ satisfies $(*)$.

  (iv) Show that if $W^{a}=w U^{a}$ satisfies $(*)$, where $w$ is a scalar field and $U^{a}$ is a time-like unit vector field, then

  $$\begin{gathered} \frac{d^{2} w}{d s^{2}}=\left(\Omega^{2}-K\right) w \\ -\frac{D U^{a}}{D s} \frac{D U_{a}}{D s} \quad \text { and } \quad K=R_{a b c d} U^{a} V^{b} V^{c} U^{d} \end{gathered}$$

  $$\begin{aligned} & \text { where } \quad \Omega^{2}=-\frac{D U^{a}}{D s} \frac{D U_{a}}{D s} \text { and } \quad K=R_{a b c d} U^{a} V^{b} V^{c} U^{d} \text {. } \end{aligned}$$

  [You may use: $\nabla_{b} \nabla_{c} X^{a}-\nabla_{c} \nabla_{b} X^{a}=R_{d b c}^{a} X^{d}$ for any vector field $\left.X^{a} .\right]$

  comment

Graph Theory

• Paper 1, Section II, 16G

  Graph Theory | Part II, 2016

  (a) Show that if $G$ is a planar graph then $\chi(G) \leqslant 5$. [You may assume Euler's formula, provided that you state it precisely.]

  (b) (i) Prove that if $G$ is a triangle-free planar graph then $\chi(G) \leqslant 4$.

  (ii) Prove that if $G$ is a planar graph of girth at least 6 then $\chi(G) \leqslant 3$.

  (iii) Does there exist a constant $g$ such that, if $G$ is a planar graph of girth at least $g$, then $\chi(G) \leqslant 2 ?$ Justify your answer.

  comment

Integrable Systems

• Paper 1, Section II, D

  Integrable Systems | Part II, 2016

  What does it mean for an evolution equation $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ to be in Hamiltonian form? Define the associated Poisson bracket.

  An evolution equation $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ is said to be bi-Hamiltonian if it can be written in Hamiltonian form in two distinct ways, i.e.

  $$K=\mathcal{J} \delta H_{0}=\mathcal{E} \delta H_{1}$$

  for Hamiltonian operators $\mathcal{J}, \mathcal{E}$ and functionals $H_{0}, H_{1}$. By considering the sequence $\left\{H_{m}\right\}_{m \geqslant 0}$ defined by the recurrence relation

  $$\mathcal{E} \delta H_{m+1}=\mathcal{J} \delta H_{m}$$

  show that bi-Hamiltonian systems possess infinitely many first integrals in involution. [You may assume that $(*)$ can always be solved for $H_{m+1}$, given $H_{m}$.]

  The Harry Dym equation for the function $u=u(x, t)$ is

  $$u_{t}=\frac{\partial^{3}}{\partial x^{3}}\left(u^{-1 / 2}\right)$$

  This equation can be written in Hamiltonian form $u_{t}=\mathcal{E} \delta H_{1}$ with

  $$\mathcal{E}=2 u \frac{\partial}{\partial x}+u_{x}, \quad H_{1}[u]=\frac{1}{8} \int u^{-5 / 2} u_{x}^{2} \mathrm{~d} x$$

  Show that the Harry Dym equation possesses infinitely many first integrals in involution. [You need not verify the Jacobi identity if your argument involves a Hamiltonian operator.]

  comment

Linear Analysis

• Paper 1, Section II, I

  Linear Analysis | Part II, 2016

  (a) State the closed graph theorem.

  (b) Prove the closed graph theorem assuming the inverse mapping theorem.

  (c) Let $X, Y, Z$ be Banach spaces and $T: X \rightarrow Y, S: Y \rightarrow Z$ be linear maps. Suppose that $S \circ T$ is bounded and $S$ is both bounded and injective. Show that $T$ is bounded.

  comment

Logic and Set Theory

• Paper 1, Section II, F

  Logic and Set Theory | Part II, 2016

  Which of the following statements are true? Justify your answers. (a) Every ordinal is of the form $\alpha+n$, where $\alpha$ is a limit ordinal and $n \in \omega$. (b) Every ordinal is of the form $\omega^{\alpha} \cdot m+n$, where $\alpha$ is an ordinal and $m, n \in \omega$. (c) If $\alpha=\omega \cdot \alpha$, then $\alpha=\omega^{\omega} \cdot \beta$ for some $\beta$. (d) If $\alpha=\omega^{\alpha}$, then $\alpha$ is uncountable. (e) If $\alpha>1$ and $\alpha=\alpha^{\omega}$, then $\alpha$ is uncountable.

  [Standard laws of ordinal arithmetic may be assumed, but if you use the Division Algorithm you should prove it.]

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2016

  Consider an epidemic model where susceptibles are vaccinated at per capita rate $v$, but immunity (from infection or vaccination) is lost at per capita rate $b$. The system is given by

  $$\begin{aligned} &\frac{d S}{d t}=-r I S+b(N-I-S)-v S \\ &\frac{d I}{d t}=r I S-a I \end{aligned}$$

  where $S(t)$ are the susceptibles, $I(t)$ are the infecteds, $N$ is the total population size and all parameters are positive. The basic reproduction ratio $R_{0}=r N / a$ satisfies $R_{0}>1$.

  Find the critical vaccination rate $v_{c}$, in terms of $b$ and $R_{0}$, such that the system has an equilibrium with the disease present if $v<v_{c}$. Show that this equilibrium is stable when it exists.

  Find the long-term outcome for $S$ and $I$ if $v>v_{c}$.

  comment

Number Fields

• Paper 1, Section II, F

  Number Fields | Part II, 2016

  (a) Let $f(X) \in \mathbb{Q}[X]$ be an irreducible polynomial of degree $n, \theta \in \mathbb{C}$ a root of $f$, and $K=\mathbb{Q}(\theta)$. Show that $\operatorname{disc}(f)=\pm N_{K / \mathbb{Q}}\left(f^{\prime}(\theta)\right)$.

  (b) Now suppose $f(X)=X^{n}+a X+b$. Write down the matrix representing multiplication by $f^{\prime}(\theta)$ with respect to the basis $1, \theta, \ldots, \theta^{n-1}$ for $K$. Hence show that

  $$\operatorname{disc}(f)=\pm\left((1-n)^{n-1} a^{n}+n^{n} b^{n-1}\right)$$

  (c) Suppose $f(X)=X^{4}+X+1$. Determine $\mathcal{O}_{K}$. [You may quote any standard result, as long as you state it clearly.]

  comment

Number Theory

• Paper 1, Section I, I

  Number Theory | Part II, 2016

  Define the Riemann zeta function $\zeta(s)$ for $\operatorname{Re}(s)>1$. State and prove the alternative formula for $\zeta(s)$ as an Euler product. Hence or otherwise show that $\zeta(s) \neq 0$ for $\operatorname{Re}(s)>1$.

  comment

Numerical Analysis

• Paper 1, Section II, B

  Numerical Analysis | Part II, 2016

  (a) Consider the periodic function

  $$f(x)=5+2 \cos \left(2 \pi x-\frac{\pi}{2}\right)+3 \cos (4 \pi x)$$

  on the interval $[0,1]$. The $N$-point discrete Fourier transform of $f$ is defined by

  $$F_{N}(n)=\frac{1}{N} \sum_{k=0}^{N-1} f_{k} \omega_{N}^{-n k}, \quad n=0,1, \ldots, N-1$$

  where $\omega_{N}=e^{2 \pi i / N}$ and $f_{k}=f(k / N)$. Compute $F_{4}(n), n=0, \ldots, 3$, using the Fast Fourier Transform (FFT). Compare your result with what you get by computing $F_{4}(n)$ directly from $(*)$. Carefully explain all your computations.

  (b) Now let $f$ be any analytic function on $\mathbb{R}$ that is periodic with period 1 . The continuous Fourier transform of $f$ is defined by

  $$\hat{f}_{n}=\int_{0}^{1} f(\tau) e^{-2 \pi i n \tau} d \tau, \quad n \in \mathbb{Z}$$

  Use integration by parts to show that the Fourier coefficients $\hat{f}_{n}$ decay spectrally.

  Explain what it means for the discrete Fourier transform of $f$ to approximate the continuous Fourier transform with spectral accuracy. Prove that it does so.

  What can you say about the behaviour of $F_{N}(N-n)$ as $N \rightarrow \infty$ for fixed $n$ ?

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, A

  Principles of Quantum Mechanics | Part II, 2016

  A particle in one dimension has position and momentum operators $\hat{x}$ and $\hat{p}$ whose eigenstates obey

  $$\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right), \quad\langle x \mid p\rangle=(2 \pi \hbar)^{-1 / 2} e^{i x p / \hbar}$$

  For a state $|\psi\rangle$, define the position-space and momentum-space wavefunctions $\psi(x)$ and $\tilde{\psi}(p)$ and show how each of these can be expressed in terms of the other.

  Write down the translation operator $U(\alpha)$ and check that your expression is consistent with the property $U(\alpha)|x\rangle=|x+\alpha\rangle$. For a state $|\psi\rangle$, relate the position-space and momentum-space wavefunctions for $U(\alpha)|\psi\rangle$ to $\psi(x)$ and $\tilde{\psi}(p)$ respectively.

  Now consider a harmonic oscillator with mass $m$, frequency $\omega$, and annihilation and creation operators

  $$a=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  Let $\psi_{n}(x)$ and $\tilde{\psi}_{n}(p)$ be the wavefunctions corresponding to the normalised energy eigenstates $|n\rangle$, where $n=0,1,2, \ldots$.

  (i) Express $\psi_{0}(x-\alpha)$ explicitly in terms of the wavefunctions $\psi_{n}(x)$.

  (ii) Given that $\tilde{\psi}_{n}(p)=f_{n}(u) \tilde{\psi}_{0}(p)$, where the $f_{n}$ are polynomials and $u=(2 / \hbar m \omega)^{1 / 2} p$, show that

  $$e^{-i \gamma u}=e^{-\gamma^{2} / 2} \sum_{n=0}^{\infty} \frac{\gamma^{n}}{\sqrt{n !}} f_{n}(u) \text { for any real } \gamma$$

  [You may quote standard results for a harmonic oscillator. You may also use, without proof, $e^{A+B}=e^{A} e^{B} e^{-\frac{1}{2}[A, B]}$ for operators $A$ and $B$ which each commute with $\left.[A, B] .\right]$

  comment

Principles of Statistics

• Paper 1, Section II, $\mathbf{2 7 J}$

  Principles of Statistics | Part II, 2016

  Derive the maximum likelihood estimator $\hat{\theta}_{n}$ based on independent observations $X_{1}, \ldots, X_{n}$ that are identically distributed as $N(\theta, 1)$, where the unknown parameter $\theta$ lies in the parameter space $\Theta=\mathbb{R}$. Find the limiting distribution of $\sqrt{n}\left(\widehat{\theta}_{n}-\theta\right)$ as $n \rightarrow \infty$.

  Now define

  $$\begin{array}{rll} \tilde{\theta}_{n} & =\widehat{\theta}_{n} & \text { whenever }\left|\widehat{\theta}_{n}\right|>n^{-1 / 4}, \\ & =0 & \text { otherwise, } \end{array}$$

  $$\begin{aligned} & =0 \text { otherwise, } \end{aligned}$$

  and find the limiting distribution of $\sqrt{n}\left(\tilde{\theta}_{n}-\theta\right)$ as $n \rightarrow \infty$.

  Calculate

  $$\lim _{n \rightarrow \infty} \sup _{\theta \in \Theta} n E_{\theta}\left(T_{n}-\theta\right)^{2}$$

  for the choices $T_{n}=\widehat{\theta}_{n}$ and $T_{n}=\widetilde{\theta}_{n}$. Based on the above findings, which estimator $T_{n}$ of $\theta$ would you prefer? Explain your answer.

  [Throughout, you may use standard facts of stochastic convergence, such as the central limit theorem, provided they are clearly stated.]

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2016

  Throughout this question $(E, \mathcal{E}, \mu)$ is a measure space and $\left(f_{n}\right), f$ are measurable functions.

  (a) Give the definitions of pointwise convergence, pointwise a.e. convergence, and convergence in measure.

  (b) If $f_{n} \rightarrow f$ pointwise a.e., does $f_{n} \rightarrow f$ in measure? Give a proof or a counterexample.

  (c) If $f_{n} \rightarrow f$ in measure, does $f_{n} \rightarrow f$ pointwise a.e.? Give a proof or a counterexample.

  (d) Now suppose that $(E, \mathcal{E})=([0,1], \mathcal{B}([0,1]))$ and that $\mu$ is Lebesgue measure on $[0,1]$. Suppose $\left(f_{n}\right)$ is a sequence of Borel measurable functions on $[0,1]$ which converges pointwise a.e. to $f$.

  (i) For each $n, k$ let $E_{n, k}=\bigcup_{m \geqslant n}\left\{x:\left|f_{m}(x)-f(x)\right|>1 / k\right\}$. Show that $\lim _{n \rightarrow \infty} \mu\left(E_{n, k}\right)=0$ for each $k \in \mathbb{N}$.

  (ii) Show that for every $\epsilon>0$ there exists a set $A$ with $\mu(A)<\epsilon$ so that $f_{n} \rightarrow f$ uniformly on $[0,1] \backslash A$.

  (iii) Does (ii) hold with $[0,1]$ replaced by $\mathbb{R}$ ? Give a proof or a counterexample.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2016

  Let $N$ be a normal subgroup of the finite group $G$. Explain how a (complex) representation of $G / N$ gives rise to an associated representation of $G$, and briefly describe which representations of $G$ arise this way.

  Let $G$ be the group of order 54 which is given by

  $$G=\left\langle a, b: a^{9}=b^{6}=1, b^{-1} a b=a^{2}\right\rangle$$

  Find the conjugacy classes of $G$. By observing that $N_{1}=\langle a\rangle$ and $N_{2}=\left\langle a^{3}, b^{2}\right\rangle$ are normal in $G$, or otherwise, construct the character table of $G$.

  comment

Riemann Surfaces

• Paper 1, Section II, H

  Riemann Surfaces | Part II, 2016

  (a) Let $f: R \rightarrow S$ be a non-constant holomorphic map between Riemann surfaces. Prove that $f$ takes open sets of $R$ to open sets of $S$.

  (b) Let $U$ be a simply connected domain strictly contained in $\mathbb{C}$. Is there a conformal equivalence between $U$ and $\mathbb{C}$ ? Justify your answer.

  (c) Let $R$ be a compact Riemann surface and $A \subset R$ a discrete subset. Given a non-constant holomorphic function $f: R \backslash A \rightarrow \mathbb{C}$, show that $f(R \backslash A)$ is dense in $\mathbb{C}$.

  comment

Statistical Modelling

• Paper 1, Section I, K

  Statistical Modelling | Part II, 2016

  The body mass index (BMI) of your closest friend is a good predictor of your own BMI. A scientist applies polynomial regression to understand the relationship between these two variables among 200 students in a sixth form college. The $R$ commands

  $>$ fit. $1<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI , 2, raw=T $))$

  $>$ fit. $2<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI, 3, raw $=\mathrm{T}))$

  fit the models $Y=\beta_{0}+\beta_{1} X+\beta_{2} X^{2}+\varepsilon$ and $Y=\beta_{0}+\beta_{1} X+\beta_{2} X^{2}+\beta_{3} X^{3}+\varepsilon$, respectively, with $\varepsilon \sim N\left(0, \sigma^{2}\right)$ in each case.

  Setting the parameters raw to FALSE:

  $>$ fit. $3<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI , 2, raw=F $)$ )

  $>$ fit. $4<-\operatorname{lm}(\mathrm{BMI} \sim$ poly $($ friendBMI, 3, raw $=\mathrm{F}))$

  fits the models $Y=\beta_{0}+\beta_{1} P_{1}(X)+\beta_{2} P_{2}(X)+\varepsilon$ and $Y=\beta_{0}+\beta_{1} P_{1}(X)+\beta_{2} P_{2}(X)+$ $\beta_{3} P_{3}(X)+\varepsilon$, with $\varepsilon \sim N\left(0, \sigma^{2}\right)$. The function $P_{i}$ is a polynomial of degree $i$. Furthermore, the design matrix output by the function poly with raw=F satisfies:

  $>t($ poly $($ friendBMI, 3, raw $=F)) \% * \%$ poly $(a, 3$, raw $=F)$

  $\begin{array}{rrrr}1 & 2 & 3 \\ 1 & 1.000000 e+00 & 1.288032 \mathrm{e}-16 & 3.187554 \mathrm{e}-17 \\ 2 & 1.288032 \mathrm{e}-16 & 1.000000 \mathrm{e}+00 & -6.201636 \mathrm{e}-17 \\ 3 & 3.187554 \mathrm{e}-17 & -6.201636 \mathrm{e}-17 & 1.000000 \mathrm{e}+00\end{array}$

  How does the variance of $\hat{\beta}$ differ in the models $f i t .2$ and $f i t .4$ ? What about the variance of the fitted values $\hat{Y}=X \hat{\beta}$ ? Finally, consider the output of the commands

  $>\operatorname{anova}$ (fit.1,fit.2)

  anova(fit.3,fit.4)

  Define the test statistic computed by this function and specify its distribution. Which command yields a higher statistic?

  comment

• Paper 1, Section II, K

  Statistical Modelling | Part II, 2016

  (a) Let $Y$ be an $n$-vector of responses from the linear model $Y=X \beta+\varepsilon$, with $\beta \in \mathbb{R}^{p}$. The internally studentized residual is defined by

  $$s_{i}=\frac{Y_{i}-x_{i}^{\top} \hat{\beta}}{\tilde{\sigma} \sqrt{1-p_{i}}},$$

  where $\hat{\beta}$ is the least squares estimate, $p_{i}$ is the leverage of sample $i$, and

  $$\tilde{\sigma}^{2}=\frac{\|Y-X \hat{\beta}\|_{2}^{2}}{(n-p)} .$$

  Prove that the joint distribution of $s=\left(s_{1}, \ldots, s_{n}\right)^{\top}$ is the same in the following two models: (i) $\varepsilon \sim N(0, \sigma I)$, and (ii) $\varepsilon \mid \sigma \sim N(0, \sigma I)$, with $1 / \sigma \sim \chi_{\nu}^{2}$ (in this model, $\varepsilon_{1}, \ldots, \varepsilon_{n}$ are identically $t_{\nu}$-distributed). [Hint: A random vector $Z$ is spherically symmetric if for any orthogonal matrix $H, H Z \stackrel{d}{=} Z$. If $Z$ is spherically symmetric and a.s. nonzero, then $Z /\|Z\|_{2}$ is a uniform point on the sphere; in addition, any orthogonal projection of $Z$ is also spherically symmetric. A standard normal vector is spherically symmetric.]

  (b) A social scientist regresses the income of 120 Cambridge graduates onto 20 answers from a questionnaire given to the participants in their first year. She notices one questionnaire with very unusual answers, which she suspects was due to miscoding. The sample has a leverage of $0.8$. To check whether this sample is an outlier, she computes its externally studentized residual,

  $$t_{i}=\frac{Y_{i}-x_{i}^{\top} \hat{\beta}}{\tilde{\sigma}_{(i)} \sqrt{1-p_{i}}}=4.57,$$

  where $\tilde{\sigma}_{(i)}$ is estimated from a fit of all samples except the one in question, $\left(x_{i}, Y_{i}\right)$. Is this a high leverage point? Can she conclude this sample is an outlier at a significance level of $5 \%$ ?

  (c) After examining the following plot of residuals against the response, the investigator calculates the externally studentized residual of the participant denoted by the black dot, which is $2.33$. Can she conclude this sample is an outlier with a significance level of $5 \%$ ?

  

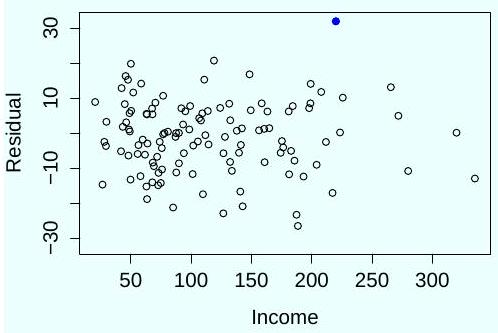
  Part II, $2016 \quad$ List of Questions

  comment

Statistical Physics

• Paper 1, Section II, C

  Statistical Physics | Part II, 2016

  Consider an ideal quantum gas with one-particle states $|i\rangle$ of energy $\epsilon_{i}$. Let $p_{i}^{\left(n_{i}\right)}$ denote the probability that state $|i\rangle$ is occupied by $n_{i}$ particles. Here, $n_{i}$ can take the values 0 or 1 for fermions and any non-negative integer for bosons. The entropy of the gas is given by

  $$S=-k_{B} \sum_{i} \sum_{n_{i}} p_{i}^{\left(n_{i}\right)} \ln p_{i}^{\left(n_{i}\right)}$$

  (a) Write down the constraints that must be satisfied by the probabilities if the average energy $\langle E\rangle$ and average particle number $\langle N\rangle$ are kept at fixed values.

  Show that if $S$ is maximised then

  $$p_{i}^{\left(n_{i}\right)}=\frac{1}{\mathcal{Z}_{i}} e^{-\left(\beta \epsilon_{i}+\gamma\right) n_{i}}$$

  where $\beta$ and $\gamma$ are Lagrange multipliers. What is $\mathcal{Z}_{i}$ ?

  (b) Insert these probabilities $p_{i}^{\left(n_{i}\right)}$ into the expression for $S$, and combine the result with the first law of thermodynamics to find the meaning of $\beta$ and $\gamma$.

  (c) Calculate the average occupation number $\left\langle n_{i}\right\rangle=\sum_{n_{i}} n_{i} p_{i}^{\left(n_{i}\right)}$ for a gas of fermions.

  comment

Stochastic Financial Models

• Paper 1, Section II, 28K

  Stochastic Financial Models | Part II, 2016

  (a) What is a Brownian motion?

  (b) State the Brownian reflection principle. State the Cameron-Martin theorem for Brownian motion with constant drift.

  (c) Let $\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion. Show that

  $$\mathbb{P}\left(\max _{0 \leqslant s \leqslant t}\left(W_{s}+a s\right) \leqslant b\right)=\Phi\left(\frac{b-a t}{\sqrt{t}}\right)-e^{2 a b} \Phi\left(\frac{-b-a t}{\sqrt{t}}\right)$$

  where $\Phi$ is the standard normal distribution function.

  (d) Find

  $$\mathbb{P}\left(\max _{u \geqslant t}\left(W_{u}+a u\right) \leqslant b\right)$$

  comment

Topics in Analysis

• Paper 1, Section I, H

  Topics in Analysis | Part II, 2016

  By considering the function $\mathbb{R}^{n+1} \rightarrow \mathbb{R}$ defined by

  $$R\left(a_{0}, \ldots, a_{n}\right)=\sup _{t \in[-1,1]}\left|\sum_{j=0}^{n} a_{j} t^{j}\right|$$

  or otherwise, show that there exist $K_{n}>0$ and $\delta_{n}>0$ such that

  $$K_{n} \sum_{j=0}^{n}\left|a_{j}\right| \geqslant \sup _{t \in[-1,1]}\left|\sum_{j=0}^{n} a_{j} t^{j}\right| \geqslant \delta_{n} \sum_{j=0}^{n}\left|a_{j}\right|$$

  for all $a_{j} \in \mathbb{R}, 0 \leqslant j \leqslant n$.

  Show, quoting carefully any theorems you use, that we must have $\delta_{n} \rightarrow 0$ as $n \rightarrow \infty$.

  comment

Waves

• Paper 1, Section II, D

  Waves | Part II, 2016

  Write down the linearised equations governing motion of an inviscid compressible fluid at uniform entropy. Assuming that the velocity is irrotational, show that it may be derived from a velocity potential $\phi(\mathbf{x}, t)$ satisfying the wave equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=c_{0}^{2} \nabla^{2} \phi$$

  and identify the wave speed $c_{0}$. Obtain from these linearised equations the energyconservation equation

  $$\frac{\partial E}{\partial t}+\nabla \cdot \mathbf{I}=0$$

  and give expressions for the acoustic-energy density $E$ and the acoustic-energy flux $\mathbf{I}$ in terms of $\phi$.

  Such a fluid occupies a semi-infinite waveguide $x>0$ of square cross-section $0<y<a$, $0<z<a$ bounded by rigid walls. An impenetrable membrane closing the end $x=0$ makes prescribed small displacements to

  $$x=X(y, z, t) \equiv \operatorname{Re}\left[e^{-i \omega t} A(y, z)\right]$$

  where $\omega>0$ and $|A| \ll a, c_{0} / \omega$. Show that the velocity potential is given by

  $$\phi=\operatorname{Re}\left[e^{-i \omega t} \sum_{m=0}^{\infty} \sum_{n=0}^{\infty} \cos \left(\frac{m \pi y}{a}\right) \cos \left(\frac{n \pi z}{a}\right) f_{m n}(x)\right]$$

  where the functions $f_{m n}(x)$, including their amplitudes, are to be determined, with the sign of any square roots specified clearly.

  If $0<\omega<\pi c_{0} / a$, what is the asymptotic behaviour of $\phi$ as $x \rightarrow+\infty$ ? Using this behaviour and the energy-conservation equation averaged over both time and the crosssection, or otherwise, determine the double-averaged energy flux along the waveguide,

  $$\left\langle\overline{I_{x}}\right\rangle(x) \equiv \frac{\omega}{2 \pi a^{2}} \int_{0}^{2 \pi / \omega} \int_{0}^{a} \int_{0}^{a} I_{x}(x, y, z, t) \mathrm{d} y \mathrm{~d} z \mathrm{~d} t$$

  explaining why this is independent of $x$.

  comment