Part II, 2014, Paper 4

Algebraic Geometry

• Paper 4, Section II, H

  Algebraic Geometry | Part II, 2014

  Let $X$ be a smooth projective curve of genus $g>0$ over an algebraically closed field of characteristic $\neq 2$, and suppose there is a degree 2 morphism $\pi: X \rightarrow \mathbf{P}^{1}$. How many ramification points of $\pi$ are there?

  Suppose $Q$ and $R$ are distinct ramification points of $\pi$. Show that $Q \nsim R$, but $2 Q \sim 2 R$.

  Now suppose $g=2$. Show that every divisor of degree 2 on $X$ is linearly equivalent to $P+P^{\prime}$ for some $P, P^{\prime} \in X$, and deduce that every divisor of degree 0 is linearly equivalent to $P_{1}-P_{2}$ for some $P_{1}, P_{2} \in X$.

  Show that the subgroup $\left\{[D] \in C l^{0}(X) \mid 2[D]=0\right\}$ of the divisor class group of $X$ has order $16 .$

  comment

Algebraic Topology

• Paper 4, Section II, F

  Algebraic Topology | Part II, 2014

  State the Lefschetz fixed point theorem.

  Let $X$ be an orientable surface of genus $g$ (which you may suppose has a triangulation), and let $f: X \rightarrow X$ be a continuous map such that

  1. $f^{3}=\operatorname{Id}_{X}$,

  2. $f$ has no fixed points.

  By considering the eigenvalues of the linear map $f_{*}: H_{1}(X ; \mathbb{Q}) \rightarrow H_{1}(X ; \mathbb{Q})$, and their multiplicities, show that $g$ must be congruent to 1 modulo 3 .

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, A

  Applications of Quantum Mechanics | Part II, 2014

  Let $\Lambda$ be a Bravais lattice in three dimensions. Define the reciprocal lattice $\Lambda^{*}$.

  State and prove Bloch's theorem for a particle moving in a potential $V(\mathbf{x})$ obeying

  $$V(\mathbf{x}+\ell)=V(\mathbf{x}) \quad \forall \ell \in \Lambda, \mathbf{x} \in \mathbb{R}^{3}$$

  Explain what is meant by a Brillouin zone for this potential and how it is related to the reciprocal lattice.

  A simple cubic lattice $\Lambda_{1}$ is given by the set of points

  $$\Lambda_{1}=\left\{\ell \in \mathbb{R}^{3}: \ell=n_{1} \hat{\mathbf{i}}+n_{2} \hat{\mathbf{j}}+n_{3} \hat{\mathbf{k}}, n_{1}, n_{2}, n_{3} \in \mathbb{Z}\right\}$$

  where $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are unit vectors parallel to the Cartesian coordinate axes in $\mathbb{R}^{3}$. A bodycentred cubic $\left(\mathrm{BCC}\right.$ ) lattice $\Lambda_{B C C}$ is obtained by adding to $\Lambda_{1}$ the points at the centre of each cube, i.e. all points of the form

  $$\ell+\frac{1}{2}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}), \quad \ell \in \Lambda_{1}$$

  Show that $\Lambda_{B C C}$ is Bravais with primitive vectors

  $$\begin{aligned} \mathbf{a}_{1} &=\frac{1}{2}(\hat{\mathbf{j}}+\hat{\mathbf{k}}-\hat{\mathbf{i}}) \\ \mathbf{a}_{2} &=\frac{1}{2}(\hat{\mathbf{k}}+\hat{\mathbf{i}}-\hat{\mathbf{j}}) \\ \mathbf{a}_{3} &=\frac{1}{2}(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}) \end{aligned}$$

  Find the reciprocal lattice $\Lambda_{B C C}^{*}$. Hence find a consistent choice for the first Brillouin zone of a potential $V(\mathbf{x})$ obeying

  $$\begin{aligned} & V(\mathbf{x}+\ell)=V(\mathbf{x}) \quad \forall \ell \in \Lambda_{B C C}, \mathbf{x} \in \mathbb{R}^{3} \\ & \text { [Hint: The matrix } \left.M=\frac{1}{2}\left(\begin{array}{rrr}-1 & 1 & 1 \\1 & -1 & 1 \\1 & 1 & -1\end{array}\right) \text { has inverse } M^{-1}=\left(\begin{array}{lll}0 & 1 & 1 \\1 & 0 & 1 \\1 & 1 & 0\end{array}\right) .\right] \end{aligned}$$

  comment

Applied Probability

• Paper 4, Section II, J

  Applied Probability | Part II, 2014

  (i) Define the $M / M / 1$ queue with arrival rate $\lambda$ and service rate $\mu$. Find conditions on the parameters $\lambda$ and $\mu$ for the queue to be transient, null recurrent, and positive recurrent, briefly justifying your answers. In the last case give with justification the invariant distribution explicitly. Answer the same questions for an $M / M / \infty$ queue.

  (ii) At a taxi station, customers arrive at a rate of 3 per minute, and taxis at a rate of 2 per minute. Suppose that a taxi will wait no matter how many other taxis are present. However, if a person arriving does not find a taxi waiting he or she leaves to find alternative transportation.

  Find the long-run proportion of arriving customers who get taxis, and find the average number of taxis waiting in the long run.

  An agent helps to assign customers to taxis, and so long as there are taxis waiting he is unable to have his coffee. Once a taxi arrives, how long will it take on average before he can have another sip of his coffee?

  comment

Asymptotic Methods

• Paper 4, Section II, C

  Asymptotic Methods | Part II, 2014

  Derive the leading-order Liouville Green (or WKBJ) solution for $\epsilon \ll 1$ to the ordinary differential equation

  $$\epsilon^{2} \frac{d^{2} f}{d y^{2}}+\Phi(y) f=0$$

  where $\Phi(y)>0$.

  The function $f(y ; \epsilon)$ satisfies the ordinary differential equation

  $$\epsilon^{2} \frac{d^{2} f}{d y^{2}}+\left(1+\frac{1}{y}-\frac{2 \epsilon^{2}}{y^{2}}\right) f=0$$

  subject to the boundary condition $f^{\prime \prime}(0)=2$. Show that the Liouville-Green solution of (1) for $\epsilon \ll 1$ takes the asymptotic forms

  where $\alpha_{1}, \alpha_{2}, B$ and $\theta_{2}$ are constants.

  $\left[\right.$ Hint: You may assume that $\left.\int_{0}^{y} \sqrt{1+u^{-1}} d u=\sqrt{y(1+y)}+\sinh ^{-1} \sqrt{y} \cdot\right]$

  Explain, showing the relevant change of variables, why the leading-order asymptotic behaviour for $0 \leqslant y \ll 1$ can be obtained from the reduced equation

  $$\frac{d^{2} f}{d x^{2}}+\left(\frac{1}{x}-\frac{2}{x^{2}}\right) f=0$$

  The unique solution to $(2)$ with $f^{\prime \prime}(0)=2$ is $f=x^{1 / 2} J_{3}\left(2 x^{1 / 2}\right)$, where the Bessel function $J_{3}(z)$ is known to have the asymptotic form

  $$J_{3}(z) \sim\left(\frac{2}{\pi z}\right)^{1 / 2} \cos \left(z-\frac{7 \pi}{4}\right) \text { as } z \rightarrow \infty .$$

  Hence find the values of $\alpha_{1}$ and $\alpha_{2}$.

  $$\begin{aligned} & f \sim \alpha_{1} y^{\frac{1}{4}} \exp (2 i \sqrt{y} / \epsilon)+\alpha_{2} y^{\frac{1}{4}} \exp (-2 i \sqrt{y} / \epsilon) \quad \text { for } \quad \epsilon^{2} \ll y \ll 1 \\ & \text { and } \quad f \sim B \cos \left[\theta_{2}+(y+\log \sqrt{y}) / \epsilon\right] \quad \text { for } \quad y \gg 1, \end{aligned}$$

  comment

Classical Dynamics

• Paper 4, Section I, A

  Classical Dynamics | Part II, 2014

  Consider a heavy symmetric top of mass $M$ with principal moments of inertia $I_{1}$, $I_{2}$ and $I_{3}$, where $I_{1}=I_{2} \neq I_{3}$. The top is pinned at point $P$, which is at a distance $l$ from the centre of mass, $C$, as shown in the figure.

  

  Its angular velocity in a body frame $\left(\mathbf{e}_{\mathbf{1}}, \mathbf{e}_{\mathbf{2}}, \mathbf{e}_{\mathbf{3}}\right)$ is given by

  $$\boldsymbol{\omega}=[\dot{\phi} \sin \theta \sin \psi+\dot{\theta} \cos \psi] \mathbf{e}_{1}+[\dot{\phi} \sin \theta \cos \psi-\dot{\theta} \sin \psi] \mathbf{e}_{2}+[\dot{\psi}+\dot{\phi} \cos \theta] \mathbf{e}_{3}$$

  where $\phi, \theta$ and $\psi$ are the Euler angles.

  (a) Assuming that $\left\{\mathbf{e}_{a}\right\}, a=1,2,3$, are chosen to be the principal axes, write down the Lagrangian of the top in terms of $\omega_{a}$ and the principal moments of inertia. Hence find the Lagrangian in terms of the Euler angles.

  (b) Find all conserved quantities. Show that $\omega_{3}$, the spin of the top, is constant.

  (c) By eliminating $\dot{\phi}$ and $\dot{\psi}$, derive a second-order differential equation for $\theta$.

  comment

• Paper 4, Section II, A

  Classical Dynamics | Part II, 2014

  (a) Consider a system with one degree of freedom, which undergoes periodic motion in the potential $V(q)$. The system's Hamiltonian is

  $$H(p, q)=\frac{p^{2}}{2 m}+V(q)$$

  (i) Explain what is meant by the angle and action variables, $\theta$ and $I$, of the system and write down the integral expression for the action variable $I$. Is $I$ conserved? Is $\theta$ conserved?

  (ii) Consider $V(q)=\lambda q^{6}$, where $\lambda$ is a positive constant. Find $I$ in terms of $\lambda$, the total energy $E$, the mass $M$, and a dimensionless constant factor (which you need not compute explicitly).

  (iii) Hence describe how $E$ changes with $\lambda$ if $\lambda$ varies slowly with time. Justify your answer.

  (b) Consider now a particle which moves in a plane subject to a central force-field $\mathbf{F}=-k r^{-2} \hat{\mathbf{r}}$.

  (i) Working in plane polar coordinates $(r, \phi)$, write down the Hamiltonian of the system. Hence deduce two conserved quantities. Prove that the system is integrable and state the number of action variables.

  (ii) For a particle which moves on an elliptic orbit find the action variables associated with radial and tangential motions. Can the relationship between the frequencies of the two motions be deduced from this result? Justify your answer.

  (iii) Describe how $E$ changes with $m$ and $k$ if one or both of them vary slowly with time.

  [You may use

  $$\int_{r_{1}}^{r_{2}}\left\{\left(1-\frac{r_{1}}{r}\right)\left(\frac{r_{2}}{r}-1\right)\right\}^{\frac{1}{2}} d r=\frac{\pi}{2}\left(r_{1}+r_{2}\right)-\pi \sqrt{r_{1} r_{2}}$$

  where $0<r_{1}<r_{2}$.]

  comment

Coding and Cryptography

• Paper 4, Section I, I

  Coding and Cryptography | Part II, 2014

  Explain what is meant by a Bose-Ray Chaudhuri-Hocquenghem (BCH) code with design distance $\delta$. Prove that, for such a code, the minimum distance between code words is at least $\delta$. How many errors will the code detect? How many errors will it correct?

  comment

Cosmology

• Paper 4, Section I, E

  Cosmology | Part II, 2014

  A homogeneous and isotropic universe, with cosmological constant $\Lambda$, has expansion scale factor $a(t)$ and Hubble expansion rate $H=\dot{a} / a$. The universe contains matter with density $\rho$ and pressure $P$ which satisfy the positive-energy condition $\rho+3 P / c^{2} \geqslant 0$. The acceleration equation is

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)+\frac{1}{3} \Lambda c^{2}$$

  If $\Lambda \leqslant 0$, show that

  $$\frac{d}{d t}\left(H^{-1}\right) \geqslant 1$$

  Deduce that $H \rightarrow \infty$ and $a \rightarrow 0$ at a finite time in the past or the future. What property of $H$ distinguishes the two cases?

  Give a simple counterexample with $\rho=P=0$ to show that this deduction fails to hold when $\Lambda>0$.

  comment

Differential Geometry

• Paper 4, Section II, G

  Differential Geometry | Part II, 2014

  Let $I=[0, l]$ be a closed interval, $k(s), \tau(s)$ smooth real valued functions on $I$ with $k$ strictly positive at all points, and $\mathbf{t}_{0}, \mathbf{n}_{0}, \mathbf{b}_{0}$ a positively oriented orthonormal triad of vectors in $\mathbf{R}^{3}$. An application of the fundamental theorem on the existence of solutions to ODEs implies that there exists a unique smooth family of triples of vectors $\mathbf{t}(s), \mathbf{n}(s), \mathbf{b}(s)$ for $s \in I$ satisfying the differential equations

  $$\mathbf{t}^{\prime}=k \mathbf{n}, \quad \mathbf{n}^{\prime}=-k \mathbf{t}-\tau \mathbf{b}, \quad \mathbf{b}^{\prime}=\tau \mathbf{n}$$

  with initial conditions $\mathbf{t}(0)=\mathbf{t}_{0}, \mathbf{n}(0)=\mathbf{n}_{0}$ and $\mathbf{b}(0)=\mathbf{b}_{0}$, and that $\{\mathbf{t}(s), \mathbf{n}(s), \mathbf{b}(s)\}$ forms a positively oriented orthonormal triad for all $s \in I$. Assuming this fact, consider $\alpha: I \rightarrow \mathbf{R}^{3}$ defined by $\alpha(s)=\int_{0}^{s} \mathbf{t}(t) d t$; show that $\alpha$ defines a smooth immersed curve parametrized by arc-length, which has curvature and torsion given by $k(s)$ and $\tau(s)$, and that $\alpha$ is uniquely determined by this property up to rigid motions of $\mathbf{R}^{3}$. Prove that $\alpha$ is a plane curve if and only if $\tau$ is identically zero.

  If $a>0$, calculate the curvature and torsion of the smooth curve given by

  $$\alpha(s)=(a \cos (s / c), a \sin (s / c), b s / c), \quad \text { where } c=\sqrt{a^{2}+b^{2}}$$

  Suppose now that $\alpha:[0,2 \pi] \rightarrow \mathbf{R}^{3}$ is a smooth simple closed curve parametrized by arc-length with curvature everywhere positive. If both $k$ and $\tau$ are constant, show that $k=1$ and $\tau=0$. If $k$ is constant and $\tau$ is not identically zero, show that $k>1$. Explain what it means for $\alpha$ to be knotted; if $\alpha$ is knotted and $\tau$ is constant, show that $k(s)>2$ for some $s \in[0,2 \pi]$. [You may use standard results from the course if you state them precisely.]

  comment

Dynamical Systems

• Paper 4, Section I, D

  Dynamical Systems | Part II, 2014

  Consider the map $x_{n+1}=\lambda x_{n}\left(1-x_{n}^{2}\right)$ for $-1 \leqslant x_{n} \leqslant 1$. What is the maximum value, $\lambda_{\max }$, for which the interval $[-1,1]$ is mapped into itself?

  Analyse the first two bifurcations that occur as $\lambda$ increases from 0 towards $\lambda_{\max }$, including an identification of the values of $\lambda$ at which the bifurcation occurs and the type of bifurcation.

  What type of bifurcation do you expect as the third bifurcation? Briefly give your reasoning.

  comment

• Paper 4, Section II, D

  Dynamical Systems | Part II, 2014

  A dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ has a fixed point at the origin. Define the terms Lyapunov stability, asymptotic stability and Lyapunov function with respect to this fixed point. State and prove Lyapunov's first theorem and state (without proof) La Salle's invariance principle.

  (a) Consider the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-y-x^{3}+x^{5} \end{aligned}$$

  Construct a Lyapunov function of the form $V=f(x)+g(y)$. Deduce that the origin is asymptotically stable, explaining your reasoning carefully. Find the greatest value of $y_{0}$ such that use of this Lyapunov function guarantees that the trajectory through $\left(0, y_{0}\right)$ approaches the origin as $t \rightarrow \infty$.

  (b) Consider the system

  $$\begin{aligned} &\dot{x}=x+4 y+x^{2}+2 y^{2}, \\ &\dot{y}=-3 x-3 y . \end{aligned}$$

  Show that the origin is asymptotically stable and that the basin of attraction of the origin includes the region $x^{2}+x y+y^{2}<\frac{1}{4}$.

  comment

Electrodynamics

• Paper 4, Section II, 35C

  Electrodynamics | Part II, 2014

  (i) The action $S$ for a point particle of rest mass $m$ and charge $q$ moving along a trajectory $x^{\mu}(\lambda)$ in the presence of an electromagnetic 4 -vector potential $A^{\mu}$ is

  $$S=-m c \int\left(-\eta_{\mu \nu} \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda}\right)^{1 / 2} d \lambda+q \int A_{\mu} \frac{d x^{\mu}}{d \lambda} d \lambda$$

  where $\lambda$ is an arbitrary parametrization of the path and $\eta_{\mu \nu}$ is the Minkowski metric. By varying the action with respect to $x^{\mu}(\lambda)$, derive the equation of motion $m \ddot{x}^{\mu}=q F^{\mu} \dot{x}^{\nu}$, where $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ and overdots denote differentiation with respect to proper time for the particle.

  (ii) The particle moves in constant electric and magnetic fields with non-zero Cartesian components $E_{z}=E$ and $B_{y}=B$, with $B>E / c>0$ in some inertial frame. Verify that a suitable 4-vector potential has components

  $$A^{\mu}=(0,0,0,-B x-E t)$$

  in that frame.

  Find the equations of motion for $x, y, z$ and $t$ in terms of proper time $\tau$. For the case of a particle that starts at rest at the spacetime origin at $\tau=0$, show that

  $$\ddot{z}+\frac{q^{2}}{m^{2}}\left(B^{2}-\frac{E^{2}}{c^{2}}\right) z=\frac{q E}{m} .$$

  Find the trajectory $x^{\mu}(\tau)$ and sketch its projection onto the $(x, z)$ plane.

  comment

Fluid Dynamics II

• Paper 4, Section II, B

  Fluid Dynamics II | Part II, 2014

  An incompressible fluid of density $\rho$ and kinematic viscosity $\nu$ is confined in a channel with rigid stationary walls at $y=\pm h$. A spatially uniform pressure gradient $-G \cos \omega t$ is applied in the $x$-direction. What is the physical significance of the dimensionless number $S=\omega h^{2} / \nu ?$

  Assuming that the flow is unidirectional and time-harmonic, obtain expressions for the velocity profile and the total flux. [You may leave your answers as the real parts of complex functions.]

  In each of the limits $S \rightarrow 0$ and $S \rightarrow \infty$, find and sketch the flow profiles, find leading-order asymptotic expressions for the total flux, and give a physical interpretation.

  Suppose now that $G=0$ and that the channel walls oscillate in their own plane with velocity $U \cos \omega t$ in the $x$-direction. Without explicit calculation of the solution, sketch the flow profile in each of the limits $S \rightarrow 0$ and $S \rightarrow \infty$.

  comment

Further Complex Methods

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2014

  Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a function such that

  $$f\left(z+\omega_{1}\right)=f(z), \quad f\left(z+\omega_{2}\right)=f(z)$$

  where $\omega_{1}, \omega_{2} \in \mathbb{C} \backslash\{0\}$ and $\omega_{1} / \omega_{2}$ is not real. Show that if $f$ is analytic on $\mathbb{C}$ then it is a constant. [Liouville's theorem may be used if stated.] Give an example of a non-constant meromorphic function which satisfies (1).

  comment

Galois Theory

• Paper 4, Section II, H

  Galois Theory | Part II, 2014

  (i) Let $G$ be a finite subgroup of the multiplicative group of a field. Show that $G$ is cyclic.

  (ii) Let $\Phi_{n}(X)$ be the $n$th cyclotomic polynomial. Let $p$ be a prime not dividing $n$, and let $L$ be a splitting field for $\Phi_{n}$ over $\mathbb{F}_{p}$. Show that $L$ has $p^{m}$ elements, where $m$ is the least positive integer such that $p^{m} \equiv 1(\bmod n)$.

  (iii) Find the degrees of the irreducible factors of $X^{35}-1$ over $\mathbb{F}_{2}$, and the number of factors of each degree.

  comment

General Relativity

• Paper 4, Section II, E

  General Relativity | Part II, 2014

  A plane-wave spacetime has line element

  $$d s^{2}=H d u^{2}+2 d u d v+d x^{2}+d y^{2}$$

  where $H=x^{2}-y^{2}$. Show that the line element is unchanged by the coordinate transformation

  $$u=\bar{u}, \quad v=\bar{v}+\bar{x} e^{\bar{u}}-\frac{1}{2} e^{2 \bar{u}}, \quad x=\bar{x}-e^{\bar{u}}, \quad y=\bar{y}$$

  Show more generally that the line element is unchanged by coordinate transformations of the form

  $$u=\bar{u}+a, \quad v=\bar{v}+b \bar{x}+c, \quad x=\bar{x}+p, \quad y=\bar{y}$$

  where $a, b, c$ and $p$ are functions of $\bar{u}$, which you should determine and which depend in total on four parameters (arbitrary constants of integration).

  Deduce (without further calculation) that the line element is unchanged by a 6parameter family of coordinate transformations, of which a 5 -parameter family leave invariant the surfaces $u=$ constant.

  For a general coordinate transformation $x^{a}=x^{a}\left(\bar{x}^{b}\right)$, give an expression for the transformed Ricci tensor $\bar{R}_{c d}$ in terms of the Ricci tensor $R_{a b}$ and the transformation matrices $\frac{\partial x^{a}}{\partial \bar{x}^{c}}$. Calculate $\bar{R}_{\bar{x} \bar{x}}$ when the transformation is given by $(*)$ and deduce that $R_{v v}=R_{v x}$

  comment

Geometry and Groups

• Paper 4, Section I, F

  Geometry and Groups | Part II, 2014

  Define the limit set $\Lambda(G)$ of a Kleinian group $G$. Assuming that $G$ has no finite orbit in $\mathbb{H}^{3} \cup S_{\infty}^{2}$, and that $\Lambda(G) \neq \emptyset$, prove that if $E \subset \mathbb{C} \cup\{\infty\}$ is any non-empty closed set which is invariant under $G$, then $\Lambda(G) \subset E$.

  comment

• Paper 4, Section II, F

  Geometry and Groups | Part II, 2014

  Define the $s$-dimensional Hausdorff measure $\mathcal{H}^{s}(F)$ of a set $F \subset \mathbb{R}^{N}$. Explain briefly how properties of this measure may be used to define the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of such a set.

  Prove that the limit sets of conjugate Kleinian groups have equal Hausdorff dimension. Hence, or otherwise, prove that there is no subgroup of $\mathbb{P} S L(2, \mathbb{R})$ which is conjugate in $\mathbb{P} S L(2, \mathbb{C})$ to $\mathbb{P} S L(2, \mathbb{Z} \oplus \mathbb{Z} i)$.

  comment

Graph Theory

• Paper 4, Section II, I

  Graph Theory | Part II, 2014

  Define the Ramsey number $R^{(r)}(s, t)$. What is the value of $R^{(1)}(s, t)$ ? Prove that $R^{(r)}(s, t) \leqslant 1+R^{(r-1)}\left(R^{(r)}(s-1, t), R^{(r)}(s, t-1)\right)$ holds for $r \geqslant 2$ and deduce that $R^{(r)}(s, t)$ exists.

  Show that $R^{(2)}(3,3)=6$ and that $R^{(2)}(3,4)=9$.

  Show that $7 \leqslant R^{(3)}(4,4) \leqslant 19$. [Hint: For the lower bound, choose a suitable subset $U$ and colour e red if $|U \cap e|$ is odd.]

  comment

Linear Analysis

• Paper 4, Section II, G

  Linear Analysis | Part II, 2014

  Define the spectrum $\sigma(T)$ and the approximate point spectrum $\sigma_{\mathrm{ap}}(T)$ of a bounded linear operator $T$ on a Banach space. Prove that $\sigma_{\mathrm{ap}}(T) \subset \sigma(T)$ and that $\sigma(T)$ is a closed and bounded subset of $\mathbb{C}$. [You may assume without proof that the set of invertible operators is open.]

  Let $T$ be a hermitian operator on a non-zero Hilbert space. Prove that $\sigma(T)$ is not empty

  Let $K$ be a non-empty, compact subset of $\mathbb{C}$. Show that there is a bounded linear operator $T: \ell_{2} \rightarrow \ell_{2}$ with $\sigma(T)=K .$ [You may assume without proof that a compact metric space is separable.]

  comment

Logic and Set Theory

• Paper 4, Section II, I

  Logic and Set Theory | Part II, 2014

  Explain what is meant by a chain-complete poset. State the Bourbaki-Witt fixedpoint theorem.

  We call a poset $(P, \leqslant)$ Bourbakian if every order-preserving map $f: P \rightarrow P$ has a least fixed point $\mu(f)$. Suppose $P$ is Bourbakian, and let $f, g: P \rightrightarrows P$ be order-preserving maps with $f(x) \leqslant g(x)$ for all $x \in P$; show that $\mu(f) \leqslant \mu(g)$. [Hint: Consider the function $h: P \rightarrow P$ defined by $h(x)=f(x)$ if $x \leqslant \mu(g), h(x)=\mu(g)$ otherwise.]

  Suppose $P$ is Bourbakian and $f: \alpha \rightarrow P$ is an order-preserving map from an ordinal to $P$. Show that there is an order-preserving map $g: P \rightarrow P$ whose fixed points are exactly the upper bounds of the set $\{f(\beta) \mid \beta<\alpha\}$, and deduce that this set has a least upper bound.

  Let $C$ be a chain with no greatest member. Using the Axiom of Choice and Hartogs' Lemma, show that there is an order-preserving map $f: \alpha \rightarrow C$, for some ordinal $\alpha$, whose image has no upper bound in $C$. Deduce that any Bourbakian poset is chain-complete.

  comment

Mathematical Biology

• Paper 4, Section I, B

  Mathematical Biology | Part II, 2014

  The concentration $c(x, t)$ of a chemical in one dimension obeys the equations

  $$\frac{\partial c}{\partial t}=\frac{\partial}{\partial x}\left(c^{2} \frac{\partial c}{\partial x}\right), \quad \int_{-\infty}^{\infty} c(x, t) d x=1$$

  State the physical interpretation of each equation.

  Seek a similarity solution of the form $c=t^{\alpha} f(\xi)$, where $\xi=t^{\beta} x$. Find equations involving $\alpha$ and $\beta$ from the differential equation and the integral. Show that these are satisfied by $\alpha=\beta=-1 / 4$.

  Find the solution for $f(\xi)$. Find and sketch the solution for $c(x, t)$.

  comment

Number Fields

• Paper 4, Section II, F

  Number Fields | Part II, 2014

  Explain what is meant by an integral basis for a number field. Splitting into the cases $d \equiv 1(\bmod 4)$ and $d \equiv 2,3(\bmod 4)$, find an integral basis for $K=\mathbb{Q}(\sqrt{d})$ where $d \neq 0,1$ is a square-free integer. Justify your answer.

  Find the fundamental unit in $\mathbb{Q}(\sqrt{13})$. Determine all integer solutions to the equation $x^{2}+x y-3 y^{2}=17$.

  comment

Number Theory

• Paper 4, Section I, F

  Number Theory | Part II, 2014

  State the Chinese Remainder Theorem.

  Find all solutions to the simultaneous congruences

  $$\begin{aligned} &x \equiv 2 \quad(\bmod 3) \\ &x \equiv 3(\bmod 5) \\ &x \equiv 5(\bmod 7) \end{aligned}$$

  A positive integer is said to be square-free if it is the product of distinct primes. Show that there are 100 consecutive numbers that are not square-free.

  comment

• Paper 4, Section II, F

  Number Theory | Part II, 2014

  Define the Legendre and Jacobi symbols.

  State the law of quadratic reciprocity for the Legendre symbol.

  State the law of quadratic reciprocity for the Jacobi symbol, and deduce it from the corresponding result for the Legendre symbol.

  Let $p$ be a prime with $p \equiv 1(\bmod 4)$. Prove that the sum of the quadratic residues in the set $\{1,2, \ldots, p-1\}$ is equal to the sum of the quadratic non-residues in this set.

  For which primes $p$ is 7 a quadratic residue?

  comment

Numerical Analysis

• Paper 4, Section II, D

  Numerical Analysis | Part II, 2014

  Let $A$ be a real symmetric $n \times n$ matrix with $n$ distinct real eigenvalues $\lambda_{1}<\lambda_{2}<$ $\cdots<\lambda_{n}$ and a corresponding orthogonal basis of normalized real eigenvectors $\left\{\mathbf{w}_{i}\right\}_{i=1}^{n}$.

  (i) Let $s \in \mathbb{R}$ satisfy $s<\lambda_{1}$. Given a unit vector $\mathbf{x}^{(0)} \in \mathbb{R}^{n}$, the iteration scheme

  $$\begin{gathered} (A-s I) \mathbf{y}=\mathbf{x}^{(k)} \\ \mathbf{x}^{(k+1)}=\mathbf{y} /\|\mathbf{y}\| \end{gathered}$$

  generates a sequence of vectors $\mathbf{x}^{(k+1)}$ for $k=0,1,2, \ldots$. Assuming that $\mathbf{x}^{(0)}=\sum c_{i} \mathbf{w}_{i}$ with $c_{1} \neq 0$, prove that $\mathbf{x}^{(k)}$ tends to $\pm \mathbf{w}_{1}$ as $k \rightarrow \infty$. What happens to $\mathbf{x}^{(k)}$ if $s>\lambda_{1}$ ? [Consider all cases.]

  (ii) Describe how to implement an inverse-iteration algorithm to compute the eigenvalues and eigenvectors of $A$, given some initial estimates for the eigenvalues.

  (iii) Let $n=2$. For iterates $\mathbf{x}^{(k)}$ of an inverse-iteration algorithm with a fixed value of $s \neq \lambda_{1}, \lambda_{2}$, show that if

  $$\mathbf{x}^{(k)}=\left(\mathbf{w}_{1}+\epsilon_{k} \mathbf{w}_{2}\right) /\left(1+\epsilon_{k}^{2}\right)^{1 / 2}$$

  where $\left|\epsilon_{k}\right|$ is small, then $\left|\epsilon_{k+1}\right|$ is of the same order of magnitude as $\left|\epsilon_{k}\right|$.

  (iv) Let $n=2$ still. Consider the iteration scheme

  $$s_{k}=\left(\mathbf{x}^{(k)}, A \mathbf{x}^{(k)}\right), \quad\left(A-s_{k} I\right) \mathbf{y}=\mathbf{x}^{(k)}, \quad \mathbf{x}^{(k+1)}=\mathbf{y} /\|\mathbf{y}\|$$

  for $k=0,1,2, \ldots$, where $(,$, denotes the inner product. Show that with this scheme $\left|\epsilon_{k+1}\right|=\left|\epsilon_{k}\right|^{3} .$

  comment

Optimization and Control

• Paper 4, Section II, J

  Optimization and Control | Part II, 2014

  A girl begins swimming from a point $(0,0)$ on the bank of a straight river. She swims at a constant speed $v$ relative to the water. The speed of the downstream current at a distance $y$ from the shore is $c(y)$. Hence her trajectory is described by

  $$\dot{x}=v \cos \theta+c(y), \quad \dot{y}=v \sin \theta$$

  where $\theta$ is the angle at which she swims relative to the direction of the current.

  She desires to reach a downstream point $(1,0)$ on the same bank as she starts, as quickly as possible. Construct the Hamiltonian for this problem, and describe how Pontryagin's maximum principle can be used to give necessary conditions that must hold on an optimal trajectory. Given that $c(y)$ is positive, increasing and differentiable in $y$, show that on an optimal trajectory

  $$\frac{d}{d t} \tan (\theta(t))=-c^{\prime}(y(t))$$

  comment

Partial Differential Equations

• Paper 4, Section II, D

  Partial Differential Equations | Part II, 2014

  (a) Derive the solution of the one-dimensional wave equation

  $$u_{t t}-u_{x x}=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x),$$

  with Cauchy data given by $C^{2}$ functions $u_{j}=u_{j}(x), j=0,1$, and where $x \in \mathbb{R}$ and $u_{t t}=\partial_{t}^{2} u$ etc. Explain what is meant by the property of finite propagation speed for the wave equation. Verify that the solution to (1) satisfies this property.

  (b) Consider the Cauchy problem

  $$u_{t t}-u_{x x}+x^{2} u=0, \quad u(0, x)=u_{0}(x), \quad u_{t}(0, x)=u_{1}(x)$$

  By considering the quantities

  $$e=\frac{1}{2}\left(u_{t}^{2}+u_{x}^{2}+x^{2} u^{2}\right) \quad \text { and } \quad p=-u_{t} u_{x}$$

  prove that solutions of (2) also satisfy the property of finite propagation speed.

  (c) Define what is meant by a strongly continuous one-parameter group of unitary operators on a Hilbert space. Consider the Cauchy problem for the Schrödinger equation for $\psi(x, t) \in \mathbb{C}$ :

  $$i \psi_{t}=-\psi_{x x}+x^{2} \psi, \quad \psi(x, 0)=\psi_{0}(x), \quad-\infty<x<\infty$$

  [In the following you may use without proof the fact that there is an orthonormal set of (real-valued) Schwartz functions $\left\{f_{j}(x)\right\}_{j=1}^{\infty}$ which are eigenfunctions of the differential operator $P=-\partial_{x}^{2}+x^{2}$ with eigenvalues $2 j+1$, i.e.

  $$P f_{j}=(2 j+1) f_{j}, \quad f_{j} \in \mathcal{S}(\mathbb{R}), \quad\left(f_{j}, f_{k}\right)_{L^{2}}=\int_{\mathbb{R}} f_{j}(x) f_{k}(x) d x=\delta_{j k},$$

  and which have the property that any function $u \in L^{2}$ can be written uniquely as a sum $u(x)=\sum_{j}\left(f_{j}, u\right)_{L^{2}} f_{j}(x)$ which converges in the metric defined by the $L^{2}$ norm.]

  Write down the solution to (3) in the case that $\psi_{0}$ is given by a finite sum $\psi_{0}=\sum_{j=1}^{N}\left(f_{j}, \psi_{0}\right)_{L^{2}} f_{j}$ and show that your formula extends to define a strongly continuous one-parameter group of unitary operators on the Hilbert space $L^{2}$ of square-integrable (complex-valued) functions, with inner product $(f, g)_{L^{2}}=\int_{\mathbb{R}} \overline{f(x)} g(x) d x$.

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, A

  Principles of Quantum Mechanics | Part II, 2014

  Define the interaction picture for a quantum mechanical system with Schrödinger picture Hamiltonian $H_{0}+V(t)$ and explain why the interaction and Schrödinger pictures give the same physical predictions for transition rates between eigenstates of $H_{0}$. Derive the equation of motion for the interaction picture states $|\overline{\psi(t)}\rangle$.

  A system consists of just two states $|1\rangle$ and $|2\rangle$, with respect to which

  $$H_{0}=\left(\begin{array}{cc} E_{1} & 0 \\ 0 & E_{2} \end{array}\right), \quad V(t)=\hbar \lambda\left(\begin{array}{cc} 0 & e^{i \omega t} \\ e^{-i \omega t} & 0 \end{array}\right)$$

  Writing the interaction picture state as $\overline{\langle(t)}\rangle=a_{1}(t)|1\rangle+a_{2}(t)|2\rangle$, show that the interaction picture equation of motion can be written as

  $$i \dot{a}_{1}(t)=\lambda e^{i \mu t} a_{2}(t), \quad i \dot{a}_{2}(t)=\lambda e^{-i \mu t} a_{1}(t)$$

  where $\mu=\omega-\omega_{21}$ and $\omega_{21}=\left(E_{2}-E_{1}\right) / \hbar$. Hence show that $a_{2}(t)$ satisfies

  $$\ddot{a}_{2}+i \mu \dot{a}_{2}+\lambda^{2} a_{2}=0 .$$

  Given that $a_{2}(0)=0$, show that the solution takes the form

  $$a_{2}(t)=\alpha e^{-i \mu t / 2} \sin \Omega t,$$

  where $\Omega$ is a frequency to be determined and $\alpha$ is a complex constant of integration.

  Substitute this solution for $a_{2}(t)$ into $(*)$ to determine $a_{1}(t)$ and, by imposing the normalization condition $\||\overline{\psi(t)}\rangle \|^{2}=1$ at $t=0$, show that $|\alpha|^{2}=\lambda^{2} / \Omega^{2}$.

  At time $t=0$ the system is in the state $|1\rangle$. Write down the probability of finding the system in the state $|2\rangle$ at time $t$.

  comment

Principles of Statistics

• Paper 4, Section II, J

  Principles of Statistics | Part II, 2014

  Suppose you have at hand a pseudo-random number generator that can simulate an i.i.d. sequence of uniform $U[0,1]$ distributed random variables $U_{1}^{*}, \ldots, U_{N}^{*}$ for any $N \in \mathbb{N}$. Construct an algorithm to simulate an i.i.d. sequence $X_{1}^{*}, \ldots, X_{N}^{*}$ of standard normal $N(0,1)$ random variables. [Should your algorithm depend on the inverse of any cumulative probability distribution function, you are required to provide an explicit expression for this inverse function.]

  Suppose as a matter of urgency you need to approximately evaluate the integral

  $$I=\frac{1}{\sqrt{2 \pi}} \int_{\mathbb{R}} \frac{1}{(\pi+|x|)^{1 / 4}} e^{-x^{2} / 2} d x$$

  Find an approximation $I_{N}$ of this integral that requires $N$ simulation steps from your pseudo-random number generator, and which has stochastic accuracy

  $$\operatorname{Pr}\left(\left|I_{N}-I\right|>N^{-1 / 4}\right) \leqslant N^{-1 / 2}$$

  where Pr denotes the joint law of the simulated random variables. Justify your answer.

  comment

Probability and Measure

• Paper 4, Section II, K

  Probability and Measure | Part II, 2014

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent identically distributed random variables. Set $S_{n}=X_{1}+\cdots+X_{n}$.

  (i) State the strong law of large numbers in terms of the random variables $X_{n}$.

  (ii) Assume now that the $X_{n}$ are non-negative and that their expectation is infinite. Let $R \in(0, \infty)$. What does the strong law of large numbers say about the limiting behaviour of $S_{n}^{R} / n$, where $S_{n}^{R}=\left(X_{1} \wedge R\right)+\cdots+\left(X_{n} \wedge R\right)$ ?

  Deduce that $S_{n} / n \rightarrow \infty$ almost surely.

  Show that

  $$\sum_{n=0}^{\infty} \mathbb{P}\left(X_{n} \geqslant n\right)=\infty$$

  Show that $X_{n} \geqslant R n$ infinitely often almost surely.

  (iii) Now drop the assumption that the $X_{n}$ are non-negative but continue to assume that $\mathbb{E}\left(\left|X_{1}\right|\right)=\infty$. Show that, almost surely,

  $$\limsup _{n \rightarrow \infty}\left|S_{n}\right| / n=\infty$$

  comment

Representation Theory

• Paper 4, Section II, H

  Representation Theory | Part II, 2014

  Let $G=\mathrm{SU}(2)$.

  (i) Sketch a proof that there is an isomorphism of topological groups $G /\{\pm I\} \cong$ $\mathrm{SO}(3)$

  (ii) Let $V_{2}$ be the irreducible complex representation of $G$ of dimension 3. Compute the character of the (symmetric power) representation $S^{n}\left(V_{2}\right)$ of $G$ for any $n \geqslant 0$. Show that the dimension of the space of invariants $\left(S^{n}\left(V_{2}\right)\right)^{G}$, meaning the subspace of $S^{n}\left(V_{2}\right)$ where $G$ acts trivially, is 1 for $n$ even and 0 for $n$ odd. [Hint: You may find it helpful to restrict to the unit circle subgroup $S^{1} \leqslant G$. The irreducible characters of $G$ may be quoted without proof.]

  Using the fact that $V_{2}$ yields the standard 3-dimensional representation of $\mathrm{SO}(3)$, show that $\bigoplus_{n \geqslant 0} S^{n} V_{2} \cong \mathbb{C}[x, y, z]$. Deduce that the ring of complex polynomials in three variables $x, y, z$ which are invariant under the action of $\mathrm{SO}(3)$ is a polynomial ring in one generator. Find a generator for this polynomial ring.

  comment

Statistical Modelling

• Paper 4, Section I, $5 K$

  Statistical Modelling | Part II, 2014

  Consider the normal linear model where the $n$-vector of responses $Y$ satisfies $Y=X \beta+\varepsilon$ with $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ and $X$ is an $n \times p$ design matrix with full column rank. Write down a $(1-\alpha)$-level confidence set for $\beta$.

  Define the Cook's distance for the observation $\left(Y_{i}, x_{i}\right)$ where $x_{i}^{T}$ is the $i$ th row of $X$, and give its interpretation in terms of confidence sets for $\beta$.

  In the model above with $n=100$ and $p=4$, you observe that one observation has Cook's distance 3.1. Would you be concerned about the influence of this observation? Justify your answer.

  [Hint: You may find some of the following facts useful:

  1. If $Z \sim \chi_{4}^{2}$, then $\mathbb{P}(Z \leqslant 1.06)=0.1, \mathbb{P}(Z \leqslant 7.78)=0.9$.

  2. If $Z \sim F_{4,96}$, then $\mathbb{P}(Z \leqslant 0.26)=0.1, \mathbb{P}(Z \leqslant 2.00)=0.9$.

  3. If $Z \sim F_{96,4}$, then $\left.\mathbb{P}(Z \leqslant 0.50)=0.1, \mathbb{P}(Z \leqslant 3.78)=0.9 .\right]$

  comment

• Paper 4, Section II, K

  Statistical Modelling | Part II, 2014

  In a study on infant respiratory disease, data are collected on a sample of 2074 infants. The information collected includes whether or not each infant developed a respiratory disease in the first year of their life; the gender of each infant; and details on how they were fed as one of three categories (breast-fed, bottle-fed and supplement). The data are tabulated in $\mathrm{R}$ as follows:

  $\begin{array}{rrrrr} & \text { disease } & \text { nondisease } & \text { gender } & \text { food } \\ 1 & 77 & 381 & \text { Boy } & \text { Bottle-fed } \\ 2 & 19 & 128 & \text { Boy } & \text { Supplement } \\ 3 & 47 & 447 & \text { Boy } & \text { Breast-fed } \\ 4 & 48 & 336 & \text { Girl } & \text { Bottle-fed } \\ 5 & 16 & 111 & \text { Girl } & \text { Supplement } \\ 6 & 31 & 433 & \text { Girl } & \text { Breast-fed }\end{array}$

  Write down the model being fit by the $R$ commands on the following page:

  

  The following (slightly abbreviated) output from $R$ is obtained.

  

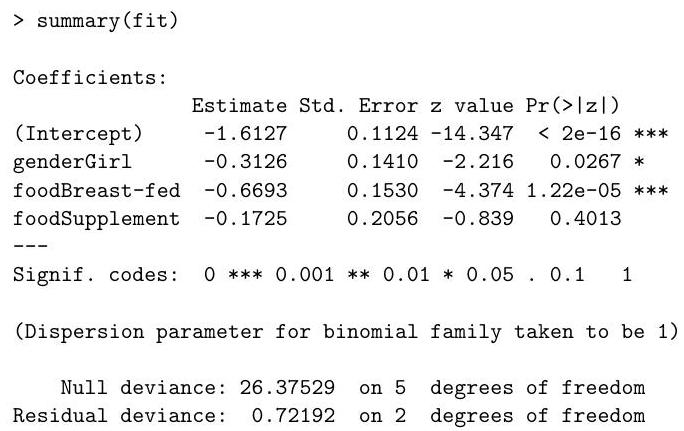
  Briefly explain the justification for the standard errors presented in the output above.

  Explain the relevance of the output of the following $R$ code to the data being studied, justifying your answer:

  $>\exp (c(-0.6693-1.96 * 0.153,-0.6693+1.96 * 0.153))$

  [1] $0.3793940 \quad 0.6911351$

  [Hint: It may help to recall that if $Z \sim N(0,1)$ then $\mathbb{P}(Z \geqslant 1.96)=0.025 .]$

  Let $D_{1}$ be the deviance of the model fitted by the following $\mathrm{R}$ command.

  $>$ fit $1<-$ glm (disease/total gender + food + gender:food,

  $+$ family = binomial, weights = total $)$

  What is the numerical value of $D_{1}$ ? Which of the two models that have been fitted should you prefer, and why?

  comment

Statistical Physics

• Paper 4, Section II, E

  Statistical Physics | Part II, 2014

  The Dieterici equation of state of a gas is

  $$P=\frac{k_{B} T}{v-b} \exp \left(-\frac{a}{k_{B} T v}\right)$$

  where $P$ is the pressure, $v=V / N$ is the volume divided by the number of particles, $T$ is the temperature, and $k_{B}$ is the Boltzmann constant. Provide a physical interpretation for the constants $a$ and $b$.

  Briefly explain how the Dieterici equation captures the liquid-gas phase transition. What is the maximum temperature at which such a phase transition can occur?

  The Gibbs free energy is given by

  $$G=E+P V-T S$$

  where $E$ is the energy and $S$ is the entropy. Explain why the Gibbs free energy is proportional to the number of particles in the system.

  On either side of a first-order phase transition the Gibbs free energies are equal. Use this fact to derive the Clausius-Clapeyron equation for a line along which there is a first-order liquid-gas phase transition,

  $$\frac{d P}{d T}=\frac{L}{T\left(V_{\text {gas }}-V_{\text {liquid }}\right)}$$

  where $L$ is the latent heat which you should define.

  Assume that the volume of liquid is negligible compared to the volume of gas and that the latent heat is constant. Further assume that the gas can be well approximated by the ideal gas law. Solve $(*)$ to obtain an equation for the phase-transition line in the $(P, T)$ plane.

  comment

Stochastic Financial Models

• Paper 4, Section II, K

  Stochastic Financial Models | Part II, 2014

  Write down the Black-Scholes partial differential equation (PDE), and explain briefly its relevance to option pricing.

  Show how a change of variables reduces the Black-Scholes PDE to the heat equation:

  $$\begin{aligned} &\frac{\partial f}{\partial t}+\frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}}=0 \text { for all }(t, x) \in[0, T) \times \mathbb{R}, \\ &f(T, x)=\varphi(x) \text { for all } x \in \mathbb{R} \end{aligned}$$

  where $\varphi$ is a given boundary function.

  Consider the following numerical scheme for solving the heat equation on the equally spaced grid $\left(t_{n}, x_{k}\right) \in[0, T] \times \mathbb{R}$ where $t_{n}=n \Delta t$ and $x_{k}=k \Delta x, n=0,1, \ldots, N$ and $k \in \mathbb{Z}$, and $\Delta t=T / N$. We approximate $f\left(t_{n}, x_{k}\right)$ by $f_{k}^{n}$ where

  $$0=\frac{f^{n+1}-f^{n}}{\Delta t}+\theta L f^{n+1}+(1-\theta) L f^{n}, \quad f_{k}^{N}=\varphi\left(x_{k}\right)$$

  and $\theta \in[0,1]$ is a constant and the operator $L$ is the matrix with non-zero entries $L_{k k}=-\frac{1}{(\Delta x)^{2}}$ and $L_{k, k+1}=L_{k, k-1}=\frac{1}{2(\Delta x)^{2}}$. By considering what happens when $\varphi(x)=\exp (i \omega x)$, show that the finite-difference scheme $(*)$ is stable if and only if

  $$1 \geqslant \lambda(2 \theta-1),$$

  where $\lambda \equiv \Delta t /(\Delta x)^{2}$. For what values of $\theta$ is the scheme $(*)$ unconditionally stable?

  comment

Topics in Analysis

• Paper 4, Section I, $2 G$

  Topics in Analysis | Part II, 2014

  State Liouville's theorem on approximation of algebraic numbers by rationals.

  Prove that the number $\sum_{n=0}^{\infty} \frac{1}{2^{n^{n}}}$ is transcendental.

  comment

Waves

• Paper 4, Section II, C

  Waves | Part II, 2014

  A one-dimensional shock wave propagates at a constant speed along a tube aligned with the $x$-axis and containing a perfect gas. In the reference frame where the shock is at rest at $x=0$, the gas has speed $U_{0}$, density $\rho_{0}$ and pressure $p_{0}$ in the region $x<0$ and speed $U_{1}$, density $\rho_{1}$ and pressure $p_{1}$ in the region $x>0$.

  Write down equations of conservation of mass, momentum and energy across the shock. Show that

  $$\frac{\gamma}{\gamma-1}\left(\frac{p_{1}}{\rho_{1}}-\frac{p_{0}}{\rho_{0}}\right)=\frac{p_{1}-p_{0}}{2}\left(\frac{1}{\rho_{1}}+\frac{1}{\rho_{0}}\right)$$

  where $\gamma$ is the ratio of specific heats.

  From now on, assume $\gamma=2$ and let $P=p_{1} / p_{0}$. Show that $\frac{1}{3}<\rho_{1} / \rho_{0}<3$.

  The increase in entropy from $x<0$ to $x>0$ is given by $\Delta S=C_{V} \log \left(p_{1} \rho_{0}^{2} / p_{0} \rho_{1}^{2}\right)$, where $C_{V}$ is a positive constant. Show that $\Delta S$ is a monotonic function of $P$.

  If $\Delta S>0$, deduce that $P>1, \rho_{1} / \rho_{0}>1,\left(U_{0} / c_{0}\right)^{2}>1$ and $\left(U_{1} / c_{1}\right)^{2}<1$, where $c_{0}$ and $c_{1}$ are the sound speeds in $x<0$ and $x>0$, respectively. Given that $\Delta S$ must have the same sign as $U_{0}$ and $U_{1}$, interpret these inequalities physically in terms of the properties of the flow upstream and downstream of the shock.

  comment