Part II, 2012, Paper 4

Algebraic Geometry

• Paper 4, Section II, I

  Algebraic Geometry | Part II, 2012

  Let $X$ be a smooth projective curve of genus 2, defined over the complex numbers. Show that there is a morphism $f: X \rightarrow \mathbf{P}^{1}$ which is a double cover, ramified at six points.

  Explain briefly why $X$ cannot be embedded into $\mathbf{P}^{2}$.

  For any positive integer $n$, show that there is a smooth affine plane curve which is a double cover of $\mathbf{A}^{1}$ ramified at $n$ points.

  [State clearly any theorems that you use.]

  comment

Algebraic Topology

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2012

  State and prove the Lefschetz fixed-point theorem. Hence show that the $n$-sphere $S^{n}$ does not admit a topological group structure for any even $n>0$. [The existence and basic properties of simplicial homology with rational coefficients may be assumed.]

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, $33 E$

  Applications of Quantum Mechanics | Part II, 2012

  Consider a one-dimensional crystal lattice of lattice spacing $a$ with the $n$-th atom having position $r_{n}=n a+x_{n}$ and momentum $p_{n}$, for $n=0,1, \ldots, N-1$. The atoms interact with their nearest neighbours with a harmonic force and the classical Hamiltonian is

  $$H=\sum_{n} \frac{p_{n}^{2}}{2 m}+\frac{1}{2} \lambda\left(x_{n}-x_{n-1}\right)^{2}$$

  where we impose periodic boundary conditions: $x_{N}=x_{0}$. Show that the normal mode frequencies for the classical harmonic vibrations of the system are given by

  $$\omega_{l}=2 \sqrt{\frac{\lambda}{m}}\left|\sin \left(\frac{k_{l} a}{2}\right)\right|,$$

  where $k_{l}=2 \pi l / N a$, with $l$ integer and (for $N$ even, which you may assume) $-N / 2<l \leqslant$ $N / 2$. What is the velocity of sound in this crystal?

  Show how the system may be quantized to give the quantum operator

  $$x_{n}(t)=X_{0}(t)+\sum_{l \neq 0} \sqrt{\frac{\hbar}{2 N m \omega_{l}}}\left[a_{l} e^{-i\left(\omega_{l} t-k_{l} n a\right)}+a_{l}^{\dagger} e^{i\left(\omega_{l} t-k_{l} n a\right)}\right],$$

  where $a_{l}^{\dagger}$ and $a_{l}$ are creation and annihilation operators, respectively, whose commutation relations should be stated. Briefly describe the spectrum of energy eigenstates for this system, stating the definition of the ground state $|0\rangle$ and giving the expression for the energy eigenvalue of any eigenstate.

  The Debye-Waller factor $e^{-W(Q)}$ associated with Bragg scattering from this crystal is defined by the matrix element

  $$e^{-W(Q)}=\left\langle 0\left|e^{i Q x_{0}(0)}\right| 0\right\rangle$$

  In the case where $\left\langle 0\left|X_{0}\right| 0\right\rangle=0$, calculate $W(Q)$.

  comment

Applied Probability

• Paper 4, Section II, $26 K$

  Applied Probability | Part II, 2012

  (a) Define the Moran model and Kingman's $n$-coalescent. State and prove a theorem which describes the relationship between them. [You may use without proof a construction of the Moran model for all $-\infty<t<\infty$.]

  (b) Let $\theta>0$. Suppose that a population of $N \geqslant 2$ individuals evolves according to the rules of the Moran model. Assume also that each individual in the population undergoes a mutation at constant rate $u=\theta /(N-1)$. Each time a mutation occurs, we assume that the allelic type of the corresponding individual changes to an entirely new type, never seen before in the population. Let $p(\theta)$ be the homozygosity probability, i.e., the probability that two individuals sampled without replacement from the population have the same genetic type. Give an expression for $p(\theta)$.

  (c) Let $q(\theta)$ denote the probability that a sample of size $n$ consists of one allelic type (monomorphic population). Show that $q(\theta)=\mathbb{E}\left(\exp \left\{-(\theta / 2) L_{n}\right\}\right)$, where $L_{n}$ denotes the sum of all the branch lengths in the genealogical tree of the sample - that is, $L_{n}=\sum_{i=2}^{n} i\left(\tau_{i}-\tau_{i-1}\right)$, where $\tau_{i}$ is the first time that the genealogical tree of the sample has $i$ lineages. Deduce that

  $$q(\theta)=\frac{(n-1) !}{\prod_{i=1}^{n-1}(\theta+i)}$$

  comment

Asymptotic Methods

• Paper 4, Section II, B

  Asymptotic Methods | Part II, 2012

  The stationary Schrödinger equation in one dimension has the form

  $$\epsilon^{2} \frac{d^{2} \psi}{d x^{2}}=-(E-V(x)) \psi$$

  where $\epsilon$ can be assumed to be small. Using the Liouville-Green method, show that two approximate solutions in a region where $V(x)<E$ are

  $$\psi(x) \sim \frac{1}{(E-V(x))^{1 / 4}} \exp \left\{\pm \frac{i}{\epsilon} \int_{c}^{x}\left(E-V\left(x^{\prime}\right)\right)^{1 / 2} d x^{\prime}\right\}$$

  where $c$ is suitably chosen.

  Without deriving connection formulae in detail, describe how one obtains the condition

  $$\frac{1}{\epsilon} \int_{a}^{b}\left(E-V\left(x^{\prime}\right)\right)^{1 / 2} d x^{\prime}=\left(n+\frac{1}{2}\right) \pi$$

  for the approximate energies $E$ of bound states in a smooth potential well. State the appropriate values of $a, b$ and $n$.

  Estimate the range of $n$ for which $(*)$ gives a good approximation to the true bound state energies in the cases

  (i) $V(x)=|x|$,

  (ii) $V(x)=x^{2}+\lambda x^{6}$ with $\lambda$ small and positive,

  (iii) $V(x)=x^{2}-\lambda x^{6}$ with $\lambda$ small and positive.

  comment

Classical Dynamics

• Paper 4, Section I, A

  Classical Dynamics | Part II, 2012

  Consider a one-dimensional dynamical system with generalized coordinate and momentum $(q, p)$.

  (a) Define the Poisson bracket $\{f, g\}$ of two functions $f(q, p, t)$ and $g(q, p, t)$.

  (b) Find the Poisson brackets $\{q, q\},\{p, p\}$ and $\{q, p\}$.

  (c) Assuming Hamilton's equations of motion prove that

  $$\frac{d f}{d t}=\{f, H\}+\frac{\partial f}{\partial t}$$

  (d) State the condition for a transformation $(q, p) \rightarrow(Q, P)$ to be canonical in terms of the Poisson brackets found in (b). Use this to determine whether or not the following transformations are canonical:

  (i) $Q=\sin q, P=\frac{p-a}{\cos q}$,

  (ii) $Q=\cos q, P=\frac{p-a}{\sin q}$,

  where $a$ is constant.

  comment

• Paper 4, Section II, A

  Classical Dynamics | Part II, 2012

  A homogenous thin rod of mass $M$ and length $l$ is constrained to rotate in a horizontal plane about its centre $O$. A bead of mass $m$ is set to slide along the rod without friction. The bead is attracted to $O$ by a force resulting in a potential $k x^{2} / 2$, where $x$ is the distance from $O$.

  (a) Identify suitable generalized coordinates and write down the Lagrangian of the system.

  (b) Identify all conserved quantities.

  (c) Derive the equations of motion and show that one of them can be written as

  $$m \ddot{x}=-\frac{\partial V_{\mathrm{eff}}(x)}{\partial x}$$

  where the form of the effective potential $V_{\text {eff }}(x)$ should be found explicitly.

  (d) Sketch the effective potential. Find and characterize all points of equilibrium.

  (e) Find the frequencies of small oscillations around the stable equilibria.

  comment

Coding and Cryptography

• Paper 4, Section I, G

  Coding and Cryptography | Part II, 2012

  Describe the BB84 protocol for quantum key exchange.

  Suppose we attempt to implement the BB84 protocol but cannot send single photons. Instead we send $K$ photons at a time all with the same polarization. An enemy can separate one of these photons from the other $K-1$. Explain briefly how the enemy can intercept the key exchange without our knowledge.

  Show that an enemy can find our common key if $K=3$. Can she do so when $K=2$ (with suitable equipment)?

  comment

Cosmology

• Paper 4, Section I, E

  Cosmology | Part II, 2012

  The number density of a species $\star$ of non-relativistic particles of mass $m$, in equilibrium at temperature $T$ and chemical potential $\mu$, is

  $$n_{\star}=g_{\star}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} e^{\left(\mu-m c^{2}\right) / k T},$$

  where $g_{\star}$ is the spin degeneracy. During primordial nucleosynthesis, deuterium, $D$, forms through the nuclear reaction

  $$p+n \leftrightarrow D,$$

  where $p$ and $n$ are non-relativistic protons and neutrons. Write down the relationship between the chemical potentials in equilibrium.

  Using the fact that $g_{D}=4$, and explaining the approximations you make, show that

  $$\frac{n_{D}}{n_{n} n_{p}} \approx\left(\frac{h^{2}}{\pi m_{p} k T}\right)^{3 / 2} \exp \left(\frac{B_{D}}{k T}\right)$$

  where $B_{D}$ is the deuterium binding energy, i.e. $B_{D}=\left(m_{n}+m_{p}-m_{D}\right) c^{2}$.

  Let $X_{\star}=n_{\star} / n_{B}$ where $n_{B}$ is the baryon number density of the universe. Using the fact that $n_{\gamma} \propto T^{3}$, show that

  $$\frac{X_{D}}{X_{n} X_{p}} \propto T^{3 / 2} \eta \exp \left(\frac{B_{D}}{k T}\right)$$

  where $\eta$ is the baryon asymmetry parameter

  $$\eta=\frac{n_{B}}{n_{\gamma}}$$

  Briefly explain why primordial deuterium does not form until temperatures well below $k T \sim B_{D}$.

  comment

Differential Geometry

• Paper 4, Section II, I

  Differential Geometry | Part II, 2012

  For manifolds $X, Y \subset \mathbb{R}^{n}$, define the terms tangent space to $X$ at a point $x \in X$ and derivative $d f_{x}$ of a smooth map $f: X \rightarrow Y$. State the Inverse Function Theorem for smooth maps between manifolds without boundary.

  Now let $X$ be a submanifold of $Y$ and $f: X \rightarrow Y$ the inclusion map. By considering the map $f^{-1}: f(X) \rightarrow X$, or otherwise, show that $d f_{x}$ is injective for each $x \in X$.

  Show further that there exist local coordinates around $x$ and around $y=f(x)$ such that $f$ is given in these coordinates by

  $$\left(x_{1}, \ldots, x_{l}\right) \in \mathbb{R}^{l} \mapsto\left(x_{1}, \ldots, x_{l}, 0, \ldots, 0\right) \in \mathbb{R}^{k},$$

  where $l=\operatorname{dim} X$ and $k=\operatorname{dim} Y$. [You may assume that any open ball in $\mathbb{R}^{l}$ is diffeomorphic to $\mathbb{R}^{l}$.]

  comment

Dynamical Systems

• Paper 4, Section I, D

  Dynamical Systems | Part II, 2012

  Describe the different types of bifurcation from steady states of a one-dimensional map of the form $x_{n+1}=f\left(x_{n}\right)$, and give examples of simple equations exhibiting each type.

  Consider the map $x_{n+1}=\alpha x_{n}^{2}\left(1-x_{n}\right), 0<x_{n}<1$. What is the maximum value of $\alpha$ for which the interval is mapped into itself?

  Show that as $\alpha$ increases from zero to its maximum value there is a saddle-node bifurcation and a period-doubling bifurcation, and determine the values of $\alpha$ for which they occur.

  comment

• Paper 4, Section II, D

  Dynamical Systems | Part II, 2012

  What is meant by the statement that a continuous map of an interval $I$ into itself has a horseshoe? State without proof the properties of such a map.

  Define the property of chaos of such a map according to Glendinning.

  A continuous map $f: I \rightarrow I$ has a periodic orbit of period 5 , in which the elements $x_{j}, j=1, \ldots, 5$ satisfy $x_{j}<x_{j+1}, j=1, \ldots, 4$ and the points are visited in the order $x_{1} \rightarrow x_{3} \rightarrow x_{4} \rightarrow x_{2} \rightarrow x_{5} \rightarrow x_{1}$. Show that the map is chaotic. [The Intermediate Value theorem can be used without proof.]

  comment

Electrodynamics

• Paper 4, Section II, B

  Electrodynamics | Part II, 2012

  The charge and current densities are given by $\rho(t, \mathbf{x}) \neq 0$ and $\mathbf{j}(t, \mathbf{x})$ respectively. The electromagnetic scalar and vector potentials are given by $\phi(t, \mathbf{x})$ and $\mathbf{A}(t, \mathbf{x})$ respectively. Explain how one can regard $j^{\mu}=(\rho, \mathbf{j})$ as a four-vector that obeys the current conservation rule $\partial_{\mu} j^{\mu}=0$.

  In the Lorenz gauge $\partial_{\mu} A^{\mu}=0$, derive the wave equation that relates $A^{\mu}=(\phi, \mathbf{A})$ to $j^{\mu}$ and hence show that it is consistent to treat $A^{\mu}$ as a four-vector.

  In the Lorenz gauge, with $j^{\mu}=0$, a plane wave solution for $A^{\mu}$ is given by

  $$A^{\mu}=\epsilon^{\mu} \exp \left(i k_{\nu} x^{\nu}\right)$$

  where $\epsilon^{\mu}, k^{\mu}$ and $x^{\mu}$ are four-vectors with

  $$\epsilon^{\mu}=\left(\epsilon^{0}, \boldsymbol{\epsilon}\right), \quad k^{\mu}=\left(k^{0}, \mathbf{k}\right), \quad x^{\mu}=(t, \mathbf{x}) .$$

  Show that $k_{\mu} k^{\mu}=k_{\mu} \epsilon^{\mu}=0$.

  Interpret the components of $k^{\mu}$ in terms of the frequency and wavelength of the wave.

  Find what residual gauge freedom there is and use it to show that it is possible to set $\epsilon^{0}=0$. What then is the physical meaning of the components of $\boldsymbol{\epsilon}$ ?

  An observer at rest in a frame $S$ measures the angular frequency of a plane wave travelling parallel to the $z$-axis to be $\omega$. A second observer travelling at velocity $v$ in $S$ parallel to the $z$-axis measures the radiation to have frequency $\omega^{\prime}$. Express $\omega^{\prime}$ in terms of $\omega$.

  comment

Fluid Dynamics II

• Paper 4, Section II, C

  Fluid Dynamics II | Part II, 2012

  A steady, two-dimensional flow in the region $y>0$ takes the form $(u, v)=$ $(E x,-E y)$ at large $y$, where $E$ is a positive constant. The boundary at $y=0$ is rigid and no-slip. Consider the velocity field $u=\partial \psi / \partial y, v=-\partial \psi / \partial x$ with stream function $\psi=\operatorname{Ex} \delta f(\eta)$, where $\eta=y / \delta$ and $\delta=(\nu / E)^{1 / 2}$ and $\nu$ is the kinematic viscosity. Show that this velocity field satisfies the Navier-Stokes equations provided that $f(\eta)$ satisfies

  $$f^{\prime \prime \prime}+f f^{\prime \prime}-\left(f^{\prime}\right)^{2}=-1$$

  What are the conditions on $f$ at $\eta=0$ and as $\eta \rightarrow \infty$ ?

  comment

Further Complex Methods

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2012

  Use the Laplace kernel method to write integral representations in the complex $t$-plane for two linearly independent solutions of the confluent hypergeometric equation

  $$z \frac{d^{2} w(z)}{d z^{2}}+(c-z) \frac{d w(z)}{d z}-a w(z)=0$$

  in the case that $\operatorname{Re}(z)>0, \operatorname{Re}(c)>\operatorname{Re}(a)>0, a$ and $c-a$ are not integers.

  comment

Galois Theory

• Paper 4, Section II, H

  Galois Theory | Part II, 2012

  Let $F=\mathbb{C}\left(X_{1}, \ldots, X_{n}\right)$ be a field of rational functions in $n$ variables over $\mathbb{C}$, and let $s_{1}, \ldots, s_{n}$ be the elementary symmetric polynomials:

  $$s_{j}:=\sum_{\left\{i_{1}, \ldots, i_{j}\right\} \subset\{1, \ldots, n\}} X_{i_{1}} \cdots X_{i_{j}} \in F \quad(1 \leqslant j \leqslant n),$$

  and let $K=\mathbb{C}\left(s_{1}, \ldots, s_{n}\right)$ be the subfield of $F$ generated by $s_{1}, \ldots, s_{n}$. Let $1 \leqslant m \leqslant n$, and $Y:=X_{1}+\cdots+X_{m} \in F$. Let $K(Y)$ be the subfield of $F$ generated by $Y$ over $K$. Find the degree $[K(Y): K]$.

  [Standard facts about the fields $F, K$ and Galois extensions can be quoted without proof, as long as they are clearly stated.]

  comment

General Relativity

• Paper 4, Section II, B

  General Relativity | Part II, 2012

  The metric for a homogenous isotropic universe, in comoving coordinates, can be written as

  $$d s^{2}=-d t^{2}+a^{2}\left\{d r^{2}+f^{2}\left[d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right]\right\}$$

  where $a=a(t)$ and $f=f(r)$ are some functions.

  Write down expressions for the Hubble parameter $H$ and the deceleration parameter $q$ in terms of $a(\eta)$ and $h \equiv d \log a / d \eta$, where $\eta$ is conformal time, defined by $d \eta=a^{-1} d t$.

  The universe is composed of a perfect fluid of density $\rho$ and pressure $p=(\gamma-1) \rho$, where $\gamma$ is a constant. Defining $\Omega=\rho / \rho_{c}$, where $\rho_{c}=3 H^{2} / 8 \pi G$, show that

  $$\frac{k}{h^{2}}=\Omega-1, \quad q=\alpha \Omega, \quad \frac{d \Omega}{d \eta}=2 q h(\Omega-1)$$

  where $k$ is the curvature parameter $(k=+1,0$ or $-1)$ and $\alpha \equiv \frac{1}{2}(3 \gamma-2)$. Hence deduce that

  $$\frac{d \Omega}{d a}=\frac{2 \alpha}{a} \Omega(\Omega-1)$$

  and

  $$\Omega=\frac{1}{1-A a^{2 \alpha}}$$

  where $A$ is a constant. Given that $A=\frac{k}{2 G M}$, sketch curves of $\Omega$ against $a$ in the case when $\gamma>2 / 3$.

  [You may assume an Einstein equation, for the given metric, in the form

  $$\frac{h^{2}}{a^{2}}+\frac{k}{a^{2}}=\frac{8}{3} \pi G \rho$$

  and the energy conservation equation

  $$\left.\frac{d \rho}{d t}+3 H(\rho+p)=0 .\right]$$

  comment

Geometry and Groups

• Paper 4, Section I, G

  Geometry and Groups | Part II, 2012

  Explain briefly how to extend a Möbius transformation

  $$T: z \mapsto \frac{a z+b}{c z+d} \quad \text { with } a d-b c=1$$

  from the boundary of the upper half-space $\mathbb{R}_{+}^{3}$ to give a hyperbolic isometry $\widetilde{T}$of the upper half-space. Write down explicitly the extension of the transformation $z \mapsto \lambda^{2} z$ for any constant $\lambda \in \mathbb{C} \backslash\{0\}$.

  Show that, if $\tilde{T}$ has an axis, which is a hyperbolic line that is mapped onto itself by $\tilde{T}$ with the orientation preserved, then $\widetilde{T}$moves each point of this axis by the same hyperbolic distance, $\ell$ say. Prove that

  $$\ell=2|\log | \frac{1}{2}\left(a+d+\sqrt{(a+d)^{2}-4}\right)||$$

  comment

• Paper 4, Section II, $12 \mathrm{G}$

  Geometry and Groups | Part II, 2012

  Define the Hausdorff dimension of a subset of the Euclidean plane.

  Let $\Delta$ be a closed disc of radius $r_{0}$ in the Euclidean plane. Define a sequence of sets $K_{n} \subseteq \Delta, n=1,2, \ldots$, as follows: $K_{1}=\Delta$ and for each $n \geqslant 1$ a subset $K_{n+1} \subset K_{n}$ is produced by replacing each component disc $\Gamma$ of $K_{n}$ by three disjoint, closed discs inside $\Gamma$ with radius at most $c_{n}$ times the radius of $\Gamma$. Let $K$ be the intersection of the sets $K_{n}$. Show that if the factors $c_{n}$ converge to a limit $c$ with $0<c<1$, then the Hausdorff dimension of $K$ is at most $\log \frac{1}{3} / \log c$.

  comment

Graph Theory

• Paper 4, Section II, F

  Graph Theory | Part II, 2012

  (a) Show that every finite tree of order at least 2 has a leaf. Hence, or otherwise, show that a tree of order $n \geqslant 1$ must have precisely $n-1$ edges.

  (b) Let $G$ be a graph. Explain briefly why $|G| / \alpha(G) \leqslant \chi(G) \leqslant \Delta(G)+1$.

  Let $k=\chi(G)$, and assume $k \geqslant 2$. By induction on $|G|$, or otherwise, show that $G$ has a subgraph $H$ with $\delta(H) \geqslant k-1$. Hence, or otherwise, show that if $T$ is a tree of order $k$ then $T \subseteq G$.

  (c) Let $s, t \geqslant 2$ be integers, let $n=(s-1)(t-1)+1$ and let $T$ be a tree of order $t$. Show that whenever the edges of the complete graph $K_{n}$ are coloured blue and yellow then it must contain either a blue $K_{s}$ or a yellow $T$.

  Does this remain true if $K_{n}$ is replaced by $K_{n-1}$ ? Justify your answer.

  [The independence number $\alpha(G)$ of a graph $G$ is the size of the largest set $W \subseteq V(G)$ of vertices such that no edge of $G$ joins two points of $W$. Recall that $\chi(G)$ is the chromatic number and $\delta(G), \Delta(G)$ are respectively the minimal/maximal degrees of vertices in $G$.]

  comment

Linear Analysis

• Paper 4, Section II, G

  Linear Analysis | Part II, 2012

  Let $X$ be a Banach space and suppose that $T: X \rightarrow X$ is a bounded linear operator. What is an eigenvalue of $T ?$ What is the spectrum $\sigma(T)$ of $T ?$

  Let $X=C[0,1]$ be the space of continuous real-valued functions $f:[0,1] \rightarrow \mathbb{R}$ endowed with the sup norm. Define an operator $T: X \rightarrow X$ by

  $$T f(x)=\int_{0}^{1} G(x, y) f(y) d y$$

  where

  $$G(x, y)= \begin{cases}y(x-1) & \text { if } y \leqslant x \\ x(y-1) & \text { if } x \leqslant y\end{cases}$$

  Prove the following facts about $T$ :

  (i) $T f(0)=T f(1)=0$ and the second derivative $(T f)^{\prime \prime}(x)$ is equal to $f(x)$ for $x \in(0,1)$;

  (ii) $T$ is compact;

  (iii) $T$ has infinitely many eigenvalues;

  (iv) 0 is not an eigenvalue of $T$;

  (v) $0 \in \sigma(T)$.

  [The Arzelà-Ascoli theorem may be assumed without proof.]

  comment

Logic and Set Theory

• Paper 4, Section II, H

  Logic and Set Theory | Part II, 2012

  State and prove Hartogs' lemma. [You may assume the result that any well-ordered set is isomorphic to a unique ordinal.]

  Let $a$ and $b$ be sets such that there is a bijection $a \sqcup b \rightarrow a \times b$. Show, without assuming the Axiom of Choice, that there is either a surjection $b \rightarrow a$ or an injection $b \rightarrow a$. By setting $b=\gamma(a)$ (the Hartogs ordinal of $a$ ) and considering $(a \sqcup b) \times(a \sqcup b)$, show that the assertion 'For all infinite cardinals $m$, we have $m^{2}=m^{\prime}$ implies the Axiom of Choice. [You may assume the Cantor-Bernstein theorem.]

  comment

Mathematical Biology

• Paper 4, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2012

  The master equation describing the evolution of the probability $P(n, t)$ that a population has $n$ members at time $t$ takes the form

  $$\frac{\partial P(n, t)}{\partial t}=b(n-1) P(n-1, t)-[b(n)+d(n)] P(n, t)+d(n+1) P(n+1, t)$$

  where the functions $b(n)$ and $d(n)$ are both positive for all $n$.

  From (1) derive the corresponding Fokker-Planck equation in the form

  $$\frac{\partial P(x, t)}{\partial t}=-\frac{\partial}{\partial x}\left\{a_{1}(x) P(x, t)\right\}+\frac{1}{2} \frac{\partial^{2}}{\partial x^{2}}\left\{a_{2}(x) P(x, t)\right\}$$

  making clear any assumptions that you make and giving explicit forms for $a_{1}(x)$ and $a_{2}(x)$.

  Assume that (2) has a steady state solution $P_{s}(x)$ and that $a_{1}(x)$ is a decreasing function of $x$ with a single zero at $x_{0}$. Under what circumstances may $P_{s}(x)$ be approximated by a Gaussian centred at $x_{0}$ and what is the corresponding estimate of the variance?

  comment

Number Fields

• Paper 4, Section II, F

  Number Fields | Part II, 2012

  Let $K=\mathbb{Q}(\sqrt{p}, \sqrt{q})$ where $p$ and $q$ are distinct primes with $p \equiv q \equiv 3(\bmod 4)$. By computing the relative traces $\operatorname{Tr}_{K / k}(\theta)$ where $k$ runs through the three quadratic subfields of $K$, show that the algebraic integers $\theta$ in $K$ have the form

  $$\theta=\frac{1}{2}(a+b \sqrt{p})+\frac{1}{2}(c+d \sqrt{p}) \sqrt{q}$$

  where $a, b, c, d$ are rational integers. Show further that if $c$ and $d$ are both even then $a$ and $b$ are both even. Hence prove that an integral basis for $K$ is

  $$1, \sqrt{p}, \frac{1+\sqrt{p q}}{2}, \frac{\sqrt{p}+\sqrt{q}}{2} .$$

  Calculate the discriminant of $K$.

  comment

Number Theory

• Paper 4, Section I, I

  Number Theory | Part II, 2012

  Define what it means for the composite natural number $N$ to be a pseudoprime to the base $b$.

  Find the number of bases (less than 21) to which 21 is a pseudoprime. [You may, if you wish, assume the Chinese Remainder Theorem.]

  comment

• Paper 4, Section II, I

  Number Theory | Part II, 2012

  Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, where $\mathbb{N}$ denotes the (positive) natural numbers.

  Define what it means for $f$ to be a multiplicative function.

  Prove that if $f$ is a multiplicative function, then the function $g: \mathbb{N} \rightarrow \mathbb{R}$ defined by

  $$g(n)=\sum_{d \mid n} f(d)$$

  is also multiplicative.

  Define the Möbius function $\mu$. Is $\mu$ multiplicative? Briefly justify your answer.

  Compute

  $$\sum_{d \mid n} \mu(d)$$

  for all positive integers $n$.

  Define the Riemann zeta function $\zeta$ for complex numbers $s$ with $\Re(s)>1$.

  Prove that if $s$ is a complex number with $\Re(s)>1$, then

  $$\frac{1}{\zeta(s)}=\sum_{n=1}^{\infty} \frac{\mu(n)}{n^{s}}$$

  comment

Numerical Analysis

• Paper 4, Section II, $39 \mathrm{D}$

  Numerical Analysis | Part II, 2012

  (i) Formulate the conjugate gradient method for the solution of a system $A \mathbf{x}=\mathbf{b}$ with $A \in \mathbb{R}^{n \times n}$ and $\mathbf{b} \in \mathbb{R}^{n}, n>0$.

  (ii) Prove that if the conjugate gradient method is applied in exact arithmetic then, for any $\mathbf{x}^{(0)} \in \mathbb{R}^{n}$, termination occurs after at most $n$ iterations.

  (iii) The polynomial $p(x)=x^{m}+\sum_{i=0}^{m-1} c_{i} x^{i}$ is the minimal polynomial of the $n \times n$ matrix $A$ if it is the polynomial of lowest degree that satisfies $p(A)=0 . \quad[$ Note that $m \leqslant n$.] Give an example of a $3 \times 3$ symmetric positive definite matrix with a quadratic minimal polynomial.

  Prove that (in exact arithmetic) the conjugate gradient method requires at most $m$ iterations to calculate the exact solution of $A \mathbf{x}=\mathbf{b}$, where $m$ is the degree of the minimal polynomial of $A$.

  comment

Optimization and Control

• Paper 4, Section II, J

  Optimization and Control | Part II, 2012

  A factory has a tank of capacity $3 \mathrm{~m}^{3}$ in which it stores chemical waste. Each week the factory produces, independently of other weeks, an amount of waste that is equally likely to be 0,1 , or $2 \mathrm{~m}^{3}$. If the amount of waste exceeds the remaining space in the tank then the excess must be specially handled at a cost of $£ C$ per $\mathrm{m}^{3}$. The tank may be emptied or not at the end of each week. Emptying costs $£ D$, plus a variable cost of $£ \alpha$ for each $\mathrm{m}^{3}$ of its content. It is always emptied when it ends the week full.

  It is desired to minimize the average cost per week. Write down equations from which one can determine when it is optimal to empty the tank.

  Find the average cost per week of a policy $\pi$, which empties the tank if and only if its content at the end of the week is 2 or $3 \mathrm{~m}^{3}$.

  Describe the policy improvement algorithm. Explain why, starting from $\pi$, this algorithm will find an optimal policy in at most three iterations.

  Prove that $\pi$ is optimal if and only if $C \geqslant \alpha+(4 / 3) D$.

  comment

Partial Differential Equations

• Paper 4, Section II, 30B

  Partial Differential Equations | Part II, 2012

  i) State the Lax-Milgram lemma.

  ii) Consider the boundary value problem

  $$\begin{aligned} \Delta^{2} u-\Delta u+u=f & \text { in } \Omega \\ u=\nabla u \cdot \gamma=0 & \text { on } \partial \Omega \end{aligned}$$

  where $\Omega$ is a bounded domain in $\mathbb{R}^{n}$ with a smooth boundary, $\gamma$ is the exterior unit normal vector to $\partial \Omega$, and $f \in L^{2}(\Omega)$. Show (using the Lax-Milgram lemma) that the boundary value problem has a unique weak solution in the space

  $$H_{0}^{2}(\Omega):=\{u: \Omega \rightarrow \mathbb{R} ; u=\nabla u \cdot \gamma=0 \text { on } \partial \Omega\}$$

  [Hint. Show that

  $$\|\Delta u\|_{L^{2}(\Omega)}^{2}=\sum_{i, j=1}^{n}\left\|\frac{\partial^{2} u}{\partial x_{i} \partial x_{j}}\right\|_{L^{2}(\Omega)}^{2} \quad \text { for all } u \in C_{0}^{\infty}(\Omega)$$

  and then use the fact that $C_{0}^{\infty}(\Omega)$ is dense in $\left.H_{0}^{2}(\Omega) .\right]$

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, A

  Principles of Quantum Mechanics | Part II, 2012

  Setting $\hbar=1$, the raising and lowering operators $J_{\pm}=J_{1} \pm i J_{2}$ for angular momentum satisfy

  $$\left[J_{3}, J_{\pm}\right]=\pm J_{\pm}, \quad J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle,$$

  where $J_{3}|j m\rangle=m|j m\rangle$. Find the matrix representation $S_{\pm}$for $J_{\pm}$in the basis

  

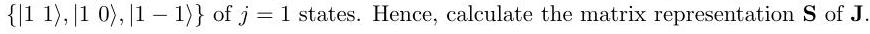
  Suppose that the angular momentum of the state $\mathbf{v}=|1 m\rangle$ is measured in the direction $\mathbf{n}=(0, \sin \theta, \cos \theta)$ to be $+1$. Find the components of $\mathbf{v}$, expressing each component by a single term consisting of products of powers of $\sin (\theta / 2)$ and $\cos (\theta / 2)$ multiplied by constants.

  Suppose that two measurements of a total angular momentum 1 system are made. The first is made in the third direction with value $+1$, and the second measurement is subsequently immediately made in direction $\mathbf{n}$. What is the probability that the second measurement is also $+1$ ?

  comment

Principles of Statistics

• Paper 4, Section II, K

  Principles of Statistics | Part II, 2012

  For $i=1, \ldots, n$, the pairs $\left(X_{i}, Y_{i}\right)$ have independent bivariate normal distributions, with $\mathbb{E}\left(X_{i}\right)=\mu_{X}, \mathbb{E}\left(Y_{i}\right)=\mu_{Y}, \operatorname{var}\left(X_{i}\right)=\operatorname{var}\left(Y_{i}\right)=\phi$, and $\operatorname{corr}\left(X_{i}, Y_{i}\right)=\rho$. The means $\mu_{X}, \mu_{Y}$ are known; the parameters $\phi>0$ and $\rho \in(-1,1)$ are unknown.

  Show that the joint distribution of all the variables belongs to an exponential family, and identify the natural sufficient statistic, natural parameter, and mean-value parameter. Hence or otherwise, find the maximum likelihood estimator $\hat{\rho}$ of $\rho$.

  Let $U_{i}:=X_{i}+Y_{i}, V_{i}:=X_{i}-Y_{i}$. What is the joint distribution of $\left(U_{i}, V_{i}\right) ?$

  Show that the distribution of

  $$\frac{(1+\hat{\rho}) /(1-\hat{\rho})}{(1+\rho) /(1-\rho)}$$

  is $F_{n}^{n}$. Hence describe a $(1-\alpha)$-level confidence interval for $\rho$. Briefly explain what would change if $\mu_{X}$ and $\mu_{Y}$ were also unknown.

  [Recall that the distribution $F_{\nu_{2}}^{\nu_{1}}$ is that of $\left(W_{1} / \nu_{1}\right) /\left(W_{2} / \nu_{2}\right)$, where, independently for $j=1$ and $j=2, W_{j}$ has the chi-squared distribution with $\nu_{j}$ degrees of freedom.]

  comment

Probability and Measure

• Paper 4, Section II, J

  Probability and Measure | Part II, 2012

  State and prove Fatou's lemma. [You may use the monotone convergence theorem.]

  For $(E, \mathcal{E}, \mu)$ a measure space, define $L^{1}:=L^{1}(E, \mathcal{E}, \mu)$ to be the vector space of $\mu$ integrable functions on $E$, where functions equal almost everywhere are identified. Prove that $L^{1}$ is complete for the norm $\|\cdot\|_{1}$,

  $$\|f\|_{1}:=\int_{E}|f| d \mu, \quad f \in L^{1} .$$

  [You may assume that $\|\cdot\|_{1}$ indeed defines a norm on $L^{1}$.] Give an example of a measure space $(E, \mathcal{E}, \mu)$ and of a sequence $f_{n} \in L^{1}$ that converges to $f$ almost everywhere such that $f \notin L^{1}$.

  Now let

  $$\mathcal{D}:=\left\{f \in L^{1}: f \geqslant 0 \text { almost everywhere }, \int_{E} f d \mu=1\right\} \text {. }$$

  If a sequence $f_{n} \in \mathcal{D}$ converges to $f$ in $L^{1}$, does it follow that $f \in \mathcal{D} ?$ If $f_{n} \in \mathcal{D}$ converges to $f$ almost everywhere, does it follow that $f \in \mathcal{D}$ ? Justify your answers.

  comment

Representation Theory

• Paper 4, Section II, H

  Representation Theory | Part II, 2012

  Write an essay on the finite-dimensional representations of $\mathrm{SU}(2)$, including a proof of their complete reducibility, and a description of the irreducible representations and the decomposition of their tensor products.

  comment

Statistical Modelling

• Paper 4, Section I, K

  Statistical Modelling | Part II, 2012

  Define the concepts of an exponential dispersion family and the corresponding variance function. Show that the family of Poisson distributions with parameter $\lambda>0$ is an exponential dispersion family. Find the corresponding variance function and deduce from it expressions for $E(Y)$ and $\operatorname{Var}(Y)$ when $Y \sim \operatorname{Pois}(\lambda)$. What is the canonical link function in this case?

  comment

• Paper 4, Section II, K

  Statistical Modelling | Part II, 2012

  Let $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)$ be jointly independent and identically distributed with $X_{i} \sim N(0,1)$ and conditional on $X_{i}=x, Y_{i} \sim N(x \theta, 1), i=1,2, \ldots, n$.

  (a) Write down the likelihood of the data $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)$, and find the maximum likelihood estimate $\hat{\theta}$ of $\theta$. [You may use properties of conditional probability/expectation without providing a proof.]

  (b) Find the Fisher information $I(\theta)$ for a single observation, $\left(X_{1}, Y_{1}\right)$.

  (c) Determine the limiting distribution of $\sqrt{n}(\hat{\theta}-\theta)$. [You may use the result on the asymptotic distribution of maximum likelihood estimators, without providing a proof.]

  (d) Give an asymptotic confidence interval for $\theta$ with coverage $(1-\alpha)$ using your answers to (b) and (c).

  (e) Define the observed Fisher information. Compare the confidence interval in part (d) with an asymptotic confidence interval with coverage $(1-\alpha)$ based on the observed Fisher information.

  (f) Determine the exact distribution of $\left(\sum_{i=1}^{n} X_{i}^{2}\right)^{1 / 2}(\hat{\theta}-\theta)$ and find the true coverage probability for the interval in part (e). [Hint. Condition on $X_{1}, X_{2}, \ldots, X_{n}$ and use the following property of conditional expectation: for $U, V$ random vectors, any suitable function $g$, and $x \in \mathbb{R}$,

  $$P\{g(U, V) \leqslant x\}=E[P\{g(U, V) \leqslant x \mid V\}] .]$$

  comment

Statistical Physics

• Paper 4, Section II, C

  Statistical Physics | Part II, 2012

  Non-relativistic electrons of mass $m$ are confined to move in a two-dimensional plane of area $A$. Each electron has two spin states. Compute the density of states $g(E)$ and show that it is constant.

  Write down expressions for the number of particles $N$ and the average energy $\langle E\rangle$ of a gas of fermions in terms of the temperature $T$ and chemical potential $\mu$. Find an expression for the Fermi Energy $E_{F}$ in terms of $N$.

  For $k_{B} T \ll E_{F}$, you may assume that the chemical potential does not change with temperature. Compute the low temperature heat capacity of a gas of fermions. [You may use the approximation that, for large $z$,

  $$\left.\int_{0}^{\infty} \frac{x^{n} d x}{z^{-1} e^{x}+1} \approx \frac{1}{n+1}(\log z)^{n+1}+\frac{\pi^{2} n}{6}(\log z)^{n-1} .\right]$$

  comment

Stochastic Financial Models

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2012

  In a one-period market, there are $n$ risky assets whose returns at time 1 are given by a column vector $R=\left(R^{1}, \ldots, R^{n}\right)^{\prime}$. The return vector $R$ has a multivariate Gaussian distribution with expectation $\mu$ and non-singular covariance matrix $V$. In addition, there is a bank account giving interest $r>0$, so that one unit of cash invested at time 0 in the bank account will be worth $R_{f}=1+r$ units of cash at time 1 .

  An agent with the initial wealth $w$ invests $x=\left(x_{1}, \ldots, x_{n}\right)^{\prime}$ in risky assets and keeps the remainder $x_{0}=w-x \cdot \mathbf{1}$ in the bank account. The return on the agent's portfolio is

  $$Z:=x \cdot R+(w-x \cdot \mathbf{1}) R_{f}$$

  The agent's utility function is $u(Z)=-\exp (-\gamma Z)$, where $\gamma>0$ is a parameter. His objective is to maximize $\mathbb{E}(u(Z))$.

  (i) Find the agent's optimal portfolio and its expected return.

  [Hint. Relate $\mathbb{E}(u(Z))$ to $\mathbb{E}(Z)$ and $\operatorname{Var}(Z) .]$

  (ii) Under which conditions does the optimal portfolio that you found in (i) require borrowing from the bank account?

  (iii) Find the optimal portfolio if it is required that all of the agent's wealth be invested in risky assets.

  comment

Topics in Analysis

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2012

  Let $A_{1}, A_{2}, \ldots, A_{n}$ be real numbers and suppose that $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ are distinct. Suppose that the formula

  $$\int_{-1}^{1} p(x) d x=\sum_{j=1}^{n} A_{j} p\left(x_{j}\right)$$

  is valid for every polynomial $p$ of degree $\leqslant 2 n-1$. Prove the following:

  (i) $A_{j}>0$ for each $j=1,2, \ldots, n$.

  (ii) $\sum_{j=1}^{n} A_{j}=2$.

  (iii) $x_{1}, x_{2}, \ldots, x_{n}$ are the roots of the Legendre polynomial of degree $n$.

  [You may assume standard orthogonality properties of the Legendre polynomials.]

  comment

Waves

• Paper 4, Section II, 38D

  Waves | Part II, 2012

  The shallow-water equations

  $$\frac{\partial h}{\partial t}+u \frac{\partial h}{\partial x}+h \frac{\partial u}{\partial x}=0, \quad \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+g \frac{\partial h}{\partial x}=0$$

  describe one-dimensional flow in a channel with depth $h(x, t)$ and velocity $u(x, t)$, where $g$ is the acceleration due to gravity.

  (i) Find the speed $c(h)$ of linearized waves on fluid at rest and of uniform depth.

  (ii) Show that the Riemann invariants $u \pm 2 c$ are constant on characteristic curves $C_{\pm}$of slope $u \pm c$ in the $(x, t)$-plane.

  (iii) Use the shallow-water equations to derive the equation of momentum conservation

  $$\frac{\partial(h u)}{\partial t}+\frac{\partial I}{\partial x}=0$$

  and identify the horizontal momentum flux $I$.

  (iv) A hydraulic jump propagates at constant speed along a straight constant-width channel. Ahead of the jump the fluid is at rest with uniform depth $h_{0}$. Behind the jump the fluid has uniform depth $h_{1}=h_{0}(1+\beta)$, with $\beta>0$. Determine both the speed $V$ of the jump and the fluid velocity $u_{1}$ behind the jump.

  Express $V / c\left(h_{0}\right)$ and $\left(V-u_{1}\right) / c\left(h_{1}\right)$ as functions of $\beta$. Hence sketch the pattern of characteristics in the frame of reference of the jump.

  comment