Part II, 2012, Paper 2

Algebraic Geometry

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2012

  Let $k$ be a field, $J$ an ideal of $k\left[x_{1}, \ldots, x_{n}\right]$, and let $R=k\left[x_{1}, \ldots, x_{n}\right] / J$. Define the radical $\sqrt{J}$ of $J$ and show that it is also an ideal.

  The Nullstellensatz says that if $J$ is a maximal ideal, then the inclusion $k \subseteq R$ is an algebraic extension of fields. Suppose from now on that $k$ is algebraically closed. Assuming the above statement of the Nullstellensatz, prove the following.

  (i) If $J$ is a maximal ideal, then $J=\left(x_{1}-a_{1}, \ldots, x_{n}-a_{n}\right)$, for some $\left(a_{1}, \ldots, a_{n}\right) \in k^{n}$.

  (ii) If $J \neq k\left[x_{1}, \ldots, x_{n}\right]$, then $Z(J) \neq \emptyset$, where

  $$Z(J)=\left\{a \in k^{n} \mid f(a)=0 \text { for all } f \in J\right\}$$

  (iii) For $V$ an affine subvariety of $k^{n}$, we set

  $$I(V)=\left\{f \in k\left[x_{1}, \ldots, x_{n}\right] \mid f(a)=0 \text { for all } a \in V\right\}$$

  Prove that $J=I(V)$ for some affine subvariety $V \subseteq k^{n}$, if and only if $J=\sqrt{J}$.

  [Hint. Given $f \in J$, you may wish to consider the ideal in $k\left[x_{1}, \ldots, x_{n}, y\right]$ generated $b y J$ and $y f-1$.]

  (iv) If $A$ is a finitely generated algebra over $k$, and $A$ does not contain nilpotent elements, then there is an affine variety $V \subseteq k^{n}$, for some $n$, with $A=k\left[x_{1}, \ldots, x_{n}\right] / I(V)$.

  Assuming $\operatorname{char}(k) \neq 2$, find $\sqrt{J}$ when $J$ is the ideal $\left(x(x-y)^{2}, y(x+y)^{2}\right)$ in $k[x, y]$.

  comment

Algebraic Topology

• Paper 2, Section II, G

  Algebraic Topology | Part II, 2012

  State the Seifert-Van Kampen Theorem. Deduce that if $f: S^{1} \rightarrow X$ is a continuous map, where $X$ is path-connected, and $Y=X \cup_{f} B^{2}$ is the space obtained by adjoining a disc to $X$ via $f$, then $\Pi_{1}(Y)$ is isomorphic to the quotient of $\Pi_{1}(X)$ by the smallest normal subgroup containing the image of $f_{*}: \Pi_{1}\left(S^{1}\right) \rightarrow \Pi_{1}(X)$.

  State the classification theorem for connected triangulable 2-manifolds. Use the result of the previous paragraph to obtain a presentation of $\Pi_{1}\left(M_{g}\right)$, where $M_{g}$ denotes the compact orientable 2 -manifold of genus $g>0$.

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, E

  Applications of Quantum Mechanics | Part II, 2012

  A solution of the $S$-wave Schrödinger equation at large distances for a particle of mass $m$ with momentum $\hbar k$ and energy $E=\hbar^{2} k^{2} / 2 m$, has the form

  $$\psi_{0}(\boldsymbol{r}) \sim \frac{A}{r}[\sin k r+g(k) \cos k r] .$$

  Define the phase shift $\delta_{0}$ and verify that $\tan \delta_{0}(k)=g(k)$.

  Write down a formula for the cross-section $\sigma$, for a particle of momentum $\hbar k$ scattering on a radially symmetric potential of finite range, as a function of the phase shifts $\delta_{l}$ for the partial waves with quantum number $l$.

  (i) Suppose that $g(k)=-k / K$ for $K>0$. Show that there is a bound state of energy $E_{B}=-\hbar^{2} K^{2} / 2 m$. Neglecting the contribution from partial waves with $l>0$ show that the cross section is

  $$\sigma=\frac{4 \pi}{K^{2}+k^{2}} .$$

  (ii) Suppose now that $g(k)=\gamma /\left(K_{0}-k\right)$ with $K_{0}>0, \gamma>0$ and $\gamma \ll K_{0}$. Neglecting the contribution from partial waves with $l>0$, derive an expression for the cross section $\sigma$, and show that it has a local maximum when $E \approx \hbar^{2} K_{0}^{2} / 2 \mathrm{~m}$. Discuss the interpretation of this phenomenon in terms of resonant behaviour and derive an expression for the decay width of the resonant state.

  comment

Applied Probability

• Paper 2, Section II, K

  Applied Probability | Part II, 2012

  (a) A colony of bacteria evolves as follows. Let $X$ be a random variable with values in the positive integers. Each bacterium splits into $X$ copies of itself after an exponentially distributed time of parameter $\lambda>0$. Each of the $X$ daughters then splits in the same way but independently of everything else. This process keeps going forever. Let $Z_{t}$ denote the number of bacteria at time $t$. Specify the $Q$-matrix of the Markov chain $Z=\left(Z_{t}, t \geqslant 0\right)$. [It will be helpful to introduce $p_{n}=\mathbb{P}(X=n)$, and you may assume for simplicity that $\left.p_{0}=p_{1}=0 .\right]$

  (b) Using the Kolmogorov forward equation, or otherwise, show that if $u(t)=$ $\mathbb{E}\left(Z_{t} \mid Z_{0}=1\right)$, then $u^{\prime}(t)=\alpha u(t)$ for some $\alpha$ to be explicitly determined in terms of $X$. Assuming that $\mathbb{E}(X)<\infty$, deduce the value of $u(t)$ for all $t \geqslant 0$, and show that $Z$ does not explode. [You may differentiate series term by term and exchange the order of summation without justification.]

  (c) We now assume that $X=2$ with probability 1 . Fix $0<q<1$ and let $\phi(t)=\mathbb{E}\left(q^{Z_{t}} \mid Z_{0}=1\right)$. Show that $\phi$ satisfies

  $$\phi(t)=q e^{-\lambda t}+\int_{0}^{t} \lambda e^{-\lambda s} \phi(t-s)^{2} d s$$

  By making the change of variables $u=t-s$, show that $d \phi / d t=\lambda \phi(\phi-1)$. Deduce that for all $n \geqslant 1, \mathbb{P}\left(Z_{t}=n \mid Z_{0}=1\right)=\beta^{n-1}(1-\beta)$ where $\beta=1-e^{-\lambda t}$.

  comment

Classical Dynamics

• Paper 2, Section I, A

  Classical Dynamics | Part II, 2012

  (a) The action for a system with a generalized coordinate $q$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

  State the Principle of Least Action and state the Euler-Lagrange equation.

  (b) Consider a light rigid circular wire of radius $a$ and centre $O$. The wire lies in a vertical plane, which rotates about the vertical axis through $O$. At time $t$ the plane containing the wire makes an angle $\phi(t)$ with a fixed vertical plane. A bead of mass $m$ is threaded onto the wire. The bead slides without friction along the wire, and its location is denoted by $A$. The angle between the line $O A$ and the downward vertical is $\theta(t)$.

  Show that the Lagrangian of this system is

  $$\frac{m a^{2}}{2} \dot{\theta}^{2}+\frac{m a^{2}}{2} \dot{\phi}^{2} \sin ^{2} \theta+m g a \cos \theta .$$

  Calculate two independent constants of the motion, and explain their physical significance.

  comment

• Paper 2, Section II, A

  Classical Dynamics | Part II, 2012

  Consider a rigid body with principal moments of inertia $I_{1}, I_{2}, I_{3}$.

  (a) Derive Euler's equations of torque-free motion

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}, \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} \end{aligned}$$

  with components of the angular velocity $\boldsymbol{\omega}=\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ given in the body frame.

  (b) Show that rotation about the second principal axis is unstable if $\left(I_{2}-I_{3}\right)\left(I_{1}-I_{2}\right)>0$.

  (c) The principal moments of inertia of a uniform cylinder of radius $R$, height $h$ and mass $M$ about its centre of mass are

  $$I_{1}=I_{2}=\frac{M R^{2}}{4}+\frac{M h^{2}}{12} \quad ; \quad I_{3}=\frac{M R^{2}}{2} .$$

  The cylinder has two identical cylindrical holes of radius $r$ drilled along its length. The axes of symmetry of the holes are at a distance $a$ from the axis of symmetry of the cylinder such that $r<R / 2$ and $r<a<R-r$. All three axes lie in a single plane. Compute the principal moments of inertia of the body.

  comment

Coding and Cryptography

• Paper 2, Section I, G

  Coding and Cryptography | Part II, 2012

  What is a (binary) linear code? What does it mean to say that a linear code has length $n$ and minimum weight $d$ ? When is a linear code perfect? Show that, if $n=2^{r}-1$, there exists a perfect linear code of length $n$ and minimum weight 3 .

  comment

• Paper 2, Section II, G

  Coding and Cryptography | Part II, 2012

  What does it mean to say that $f: \mathbb{F}_{2}^{d} \rightarrow \mathbb{F}_{2}^{d}$ is a linear feedback shift register? Let $\left(x_{n}\right)_{n \geqslant 0}$ be a stream produced by such a register. Show that there exist $N, M$ with $N+M \leqslant 2^{d}-1$ such that $x_{r+N}=x_{r}$ for all $r \geqslant M$.

  Describe and justify the Berlekamp-Massey method for 'breaking' a cipher stream arising from a linear feedback register of unknown length.

  Let $x_{n}, y_{n}, z_{n}$ be three streams produced by linear feedback registers. Set

  $$\begin{aligned} &k_{n}=x_{n} \quad \text { if } y_{n}=z_{n} \\ &k_{n}=y_{n} \quad \text { if } y_{n} \neq z_{n} \end{aligned}$$

  Show that $k_{n}$ is also a stream produced by a linear feedback register. Sketch proofs of any theorems you use.

  comment

Cosmology

• Paper 2, Section I, E

  Cosmology | Part II, 2012

  The Friedmann equation for the scale factor $a(t)$ of a homogeneous and isotropic universe of mass density $\rho$ is

  $$H^{2}=\frac{8 \pi G \rho}{3}-\frac{k c^{2}}{a^{2}}, \quad\left(H=\frac{\dot{a}}{a}\right)$$

  where $\dot{a}=d a / d t$ and $k$ is a constant. The mass conservation equation for a fluid of mass density $\rho$ and pressure $P$ is

  $$\dot{\rho}=-3\left(\rho+P / c^{2}\right) H$$

  Conformal time $\tau$ is defined by $d \tau=a^{-1} d t$. Show that

  $$\mathcal{H}=a H, \quad\left(\mathcal{H}=\frac{a^{\prime}}{a}\right)$$

  where $a^{\prime}=d a / d \tau$. Hence show that the acceleration equation can be written as

  $$\mathcal{H}^{\prime}=-\frac{4 \pi}{3} G\left(\rho+3 P / c^{2}\right) a^{2}$$

  Define the density parameter $\Omega_{m}$ and show that in a matter-dominated era, in which $P=0$, it satisfies the equation

  $$\Omega_{m}^{\prime}=\mathcal{H} \Omega_{m}\left(\Omega_{m}-1\right)$$

  Use this result to briefly explain the "flatness problem" of cosmology.

  comment

Differential Geometry

• Paper 2, Section II, I

  Differential Geometry | Part II, 2012

  Define the Gauss map $N$ for an oriented surface $S \subset \mathbb{R}^{3}$. Show that at each $p \in S$ the derivative of the Gauss map

  $$d N_{p}: T_{p} S \rightarrow T_{N(p)} S^{2}=T_{p} S$$

  is self-adjoint. Define the principal curvatures $k_{1}, k_{2}$ of $S$.

  Now suppose that $S$ is compact (and without boundary). By considering the square of the distance to the origin, or otherwise, prove that $S$ has a point $p$ with $k_{1}(p) k_{2}(p)>0$.

  [You may assume that the intersection of $S$ with a plane through the normal direction at $p \in S$ contains a regular curve through $p$.]

  comment

Dynamical Systems

• Paper 2, Section I, D

  Dynamical Systems | Part II, 2012

  Consider the dynamical system

  $$\dot{x}=\mu x+x^{3}-a x y, \quad \dot{y}=\mu-x^{2}-y,$$

  where $a$ is a constant.

  (a) Show that there is a bifurcation from the fixed point $(0, \mu)$ at $\mu=0$.

  (b) Find the extended centre manifold at leading non-trivial order in $x$. Hence find the type of bifurcation, paying particular attention to the special values $a=1$ and $a=-1$. [Hint. At leading order, the extended centre manifold is of the form $y=\mu+\alpha x^{2}+\beta \mu x^{2}+\gamma x^{4}$, where $\alpha, \beta, \gamma$ are constants to be determined.]

  comment

Fluid Dynamics II

• Paper 2, Section II, C

  Fluid Dynamics II | Part II, 2012

  An incompressible viscous liquid occupies the long thin region $0 \leqslant y \leqslant h(x)$ for $0 \leqslant x \leqslant \ell$, where $h(x)=d_{1}+\alpha x$ with $h(0)=d_{1}, h(\ell)=d_{2}<d_{1}$ and $d_{1} \ll \ell$. The top boundary at $y=h(x)$ is rigid and stationary. The bottom boundary at $y=0$ is rigid and moving at velocity $(U, 0,0)$. Fluid can move in and out of the ends $x=0$ and $x=\ell$, where the pressure is the same, namely $p_{0}$.

  Explaining the approximations of lubrication theory as you use them, find the velocity profile in the long thin region, and show that the volume flux $Q$ (per unit width in the $z$-direction) is

  $$Q=\frac{U d_{1} d_{2}}{d_{1}+d_{2}}$$

  Find also the value of $h(x)$ (i) where the pressure is maximum, (ii) where the tangential viscous stress on the bottom $y=0$ vanishes, and (iii) where the tangential viscous stress on the top $y=h(x)$ vanishes.

  comment

Further Complex Methods

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2012

  The hypergeometric function $F(a, b ; c ; z)$ is defined as the particular solution of the second order linear ODE characterised by the Papperitz symbol

  $$\mathrm{P}\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & a & z \\ 1-c & c-a-b & b \end{array}\right\}$$

  that is analytic at $z=0$ and satisfies $F(a, b ; c ; 0)=1$.

  Using the fact that a second solution $w(z)$ of the above ODE is of the form

  $$w(z)=z^{1-c} u(z)$$

  where $u(z)$ is analytic in the neighbourhood of the origin, express $w(z)$ in terms of $F$.

  comment

• Paper 2, Section II, $14 \mathrm{E}$

  Further Complex Methods | Part II, 2012

  Let the complex function $q(x, t)$ satisfy

  $$i \frac{\partial q(x, t)}{\partial t}+\frac{\partial^{2} q(x, t)}{\partial x^{2}}=0, \quad 0<x<\infty, 0<t<T$$

  where $T$ is a positive constant. The unified transform method implies that the solution of any well-posed problem for the above equation is given by

  $$\begin{aligned} q(x, t) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x-i k^{2} t} \hat{q}_{0}(k) d k \\ &-\frac{1}{2 \pi} \int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(i k^{2}, t\right)-i \tilde{g}_{1}\left(i k^{2}, t\right)\right] d k \end{aligned}$$

  where $L$ is the union of the rays $(i \infty, 0)$ and $(0, \infty), \hat{q}_{0}(k)$ denotes the Fourier transform of the initial condition $q_{0}(x)$, and $\tilde{g}_{0}, \tilde{g}_{1}$ denote the $t$-transforms of the boundary values $q(0, t), q_{x}(0, t)$ :

  $$\begin{gathered} \hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ =\int_{0}^{t} e^{k s} q(0, s) d s, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{k s} q_{x}(0, s) d s, \quad k \in \mathbb{C}, \quad 0<t<T . \end{gathered}$$

  Furthermore, $q_{0}(x), q(0, t)$ and $q_{x}(0, t)$ are related via the so-called global relation

  $$e^{i k^{2} t} \hat{q}(k, t)=\hat{q}_{0}(k)+k \tilde{g}_{0}\left(i k^{2}, t\right)-i \tilde{g}_{1}\left(i k^{2}, t\right), \quad \operatorname{Im} k \leqslant 0$$

  where $\hat{q}(k, t)$ denotes the Fourier transform of $q(x, t)$.

  (a) Assuming the validity of (1) and (2), use the global relation to eliminate $\tilde{g}_{1}$ from equation (1).

  (b) For the particular case that

  $$q_{0}(x)=e^{-a^{2} x}, \quad 0<x<\infty ; \quad q(0, t)=\cos b t, \quad 0<t<T,$$

  where $a$ and $b$ are real numbers, use the representation obtained in (a) to express the solution in terms of an integral along the real axis and an integral along $L$ (you should not attempt to evaluate these integrals). Show that it is possible to deform these two integrals to a single integral along a new contour $\tilde{L}$, which you should sketch.

  [You may assume the validity of Jordan's lemma.]

  comment

Galois Theory

• Paper 2, Section II, H

  Galois Theory | Part II, 2012

  Let $K, L$ be subfields of $\mathbb{C}$ with $K \subset L$.

  Suppose that $K$ is contained in $\mathbb{R}$ and $L / K$ is a finite Galois extension of odd degree. Prove that $L$ is also contained in $\mathbb{R}$.

  Give one concrete example of $K, L$ as above with $K \neq L$. Also give an example in which $K$ is contained in $\mathbb{R}$ and $L / K$ has odd degree, but is not Galois and $L$ is not contained in $\mathbb{R}$.

  [Standard facts on fields and their extensions can be quoted without proof, as long as they are clearly stated.]

  comment

General Relativity

• Paper 2, Section II, B

  General Relativity | Part II, 2012

  The metric of any two-dimensional rotationally-symmetric curved space can be written in terms of polar coordinates, $(r, \theta)$, with $0 \leqslant \theta<2 \pi, r \geqslant 0$, as

  $$d s^{2}=e^{2 \phi}\left(d r^{2}+r^{2} d \theta^{2}\right)$$

  where $\phi=\phi(r)$. Show that the Christoffel symbols $\Gamma_{r \theta}^{r}, \Gamma_{r r}^{\theta}$ and $\Gamma_{\theta \theta}^{\theta}$ are each zero, and compute $\Gamma_{r r}^{r}, \Gamma_{\theta \theta}^{r}$ and $\Gamma_{r \theta}^{\theta}=\Gamma_{\theta r}^{\theta}$.

  The Ricci tensor is defined by

  $$R_{a b}=\Gamma_{a b, c}^{c}-\Gamma_{a c, b}^{c}+\Gamma_{c d}^{c} \Gamma_{a b}^{d}-\Gamma_{a c}^{d} \Gamma_{b d}^{c}$$

  where a comma here denotes partial derivative. Prove that $R_{r \theta}=0$ and that

  $$R_{r r}=-\phi^{\prime \prime}-\frac{\phi^{\prime}}{r}, \quad R_{\theta \theta}=r^{2} R_{r r}$$

  Suppose now that, in this space, the Ricci scalar takes the constant value $-2$. Find a differential equation for $\phi(r)$.

  By a suitable coordinate transformation $r \rightarrow \chi(r), \theta$ unchanged, this space of constant Ricci scalar can be described by the metric

  $$d s^{2}=d \chi^{2}+\sinh ^{2} \chi d \theta^{2}$$

  From this coordinate transformation, find $\cosh \chi$ and $\sinh \chi$ in terms of $r$. Deduce that

  $$e^{\phi(r)}=\frac{2 A}{1-A^{2} r^{2}},$$

  where $0 \leqslant A r<1$, and $A$ is a positive constant.

  [You may use

  $$\left.\int \frac{d \chi}{\sinh \chi}=\frac{1}{2} \log (\cosh \chi-1)-\frac{1}{2} \log (\cosh \chi+1)+\text { constant } .\right]$$

  comment

Geometry and Groups

• Paper 2, Section I, G

  Geometry and Groups | Part II, 2012

  Define the modular group acting on the upper half-plane. Explain briefly why it acts discontinuously and describe a fundamental domain. You should prove that the region which you describe is a fundamental domain.

  comment

Graph Theory

• Paper 2, Section II, F

  Graph Theory | Part II, 2012

  Let $G$ be a $k$-connected graph $(k \geqslant 2)$. Let $v \in G$ and let $U \subset V(G) \backslash\{v\}$ with $|U| \geqslant k$. Show that $G$ contains $k$ paths from $v$ to $U$ with any two having only the vertex $v$ in common.

  [No form of Menger's theorem or of the Max-Flow-Min-Cut theorem may be assumed without proof.]

  Deduce that $G$ must contain a cycle of length at least $k$.

  Suppose further that $G$ has no independent set of vertices of size $>k$. Show that $G$ is Hamiltonian.

  [Hint. If not, let $C$ be a cycle of maximum length in $G$ and let $v \in V(G) \backslash V(C)$; consider the set of vertices on $C$ immediately preceding the endvertices of a collection of $k$ paths from $v$ to $C$ that have only the vertex $v$ in common.]

  comment

Integrable Systems

• Paper 2, Section II, D

  Integrable Systems | Part II, 2012

  Consider the $\mathrm{KdV}$ equation for the function $u(x, t)$

  $$u_{t}=6 u u_{x}-u_{x x x}$$

  (a) Write equation (1) in the Hamiltonian form

  $$u_{t}=\frac{\partial}{\partial x} \frac{\delta H[u]}{\delta u}$$

  where the functional $H[u]$ should be given. Use equation (1), together with the boundary conditions $u \rightarrow 0$ and $u_{x} \rightarrow 0$ as $|x| \rightarrow \infty$, to show that $\int_{\mathbb{R}} u^{2} d x$ is independent of $t$.

  (b) Use the Gelfand-Levitan-Marchenko equation

  $$K(x, y)+F(x+y)+\int_{x}^{\infty} K(x, z) F(z+y) d z=0$$

  to find the one soliton solution of the KdV equation, i.e.

  $$u(x, t)=-\frac{4 \beta \chi \exp (-2 \chi x)}{\left[1+\frac{\beta}{2 \chi} \exp (-2 \chi x)\right]^{2}}$$

  [Hint. Consider $F(x)=\beta \exp (-\chi x)$, with $\beta=\beta_{0} \exp \left(8 \chi^{3} t\right)$, where $\beta_{0}, \chi$ are constants, and $t$ should be regarded as a parameter in equation (2). You may use any facts about the Inverse Scattering Transform without proof.]

  comment

Linear Analysis

• Paper 2, Section II, G

  Linear Analysis | Part II, 2012

  What is meant by a normal topological space? State and prove Urysohn's lemma.

  Let $X$ be a normal topological space and let $S \subseteq X$ be closed. Show that there is a continuous function $f: X \rightarrow[0,1]$ with $f^{-1}(0)=S$ if, and only if, $S$ is a countable intersection of open sets.

  [Hint. If $S=\bigcap_{n=1}^{\infty} U_{n}$ then consider $\sum_{n=1}^{\infty} 2^{-n} f_{n}$, where the functions $f_{n}: X \rightarrow[0,1]$ are supplied by an appropriate application of Urysohn's lemma.]

  comment

Logic and Set Theory

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2012

  Explain what is meant by a substructure of a $\Sigma$-structure $A$, where $\Sigma$ is a first-order signature (possibly including both predicate symbols and function symbols). Show that if $B$ is a substructure of $A$, and $\phi$ is a first-order formula over $\Sigma$ with $n$ free variables, then $[\phi]_{B}=[\phi]_{A} \cap B^{n}$ if $\phi$ is quantifier-free. Show also that $[\phi]_{B} \subseteq[\phi]_{A} \cap B^{n}$ if $\phi$ is an existential formula (that is, one of the form $\left(\exists x_{1}, \ldots, x_{m}\right) \psi$ where $\psi$ is quantifier-free), and $[\phi]_{B} \supseteq[\phi]_{A} \cap B^{n}$ if $\phi$ is a universal formula. Give examples to show that the two latter inclusions can be strict.

  Show also that

  (a) if $T$ is a first-order theory whose axioms are all universal sentences, then any substructure of a $T$-model is a $T$-model;

  (b) if $T$ is a first-order theory such that every first-order formula $\phi$ is $T$-provably equivalent to a universal formula (that is, $T \vdash(\phi \Leftrightarrow \psi)$ for some universal $\psi$ ), and $B$ is a sub-T-model of a $T$-model $A$, then $[\phi]_{B}=[\phi]_{A} \cap B^{n}$ for every first-order formula $\phi$ with $n$ free variables.

  comment

Mathematical Biology

• Paper 2, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2012

  Consider a birth-death process in which the birth rate per individual is $\lambda$ and the death rate per individual in a population of size $n$ is $\beta n$.

  Let $P(n, t)$ be the probability that the population has size $n$ at time $t$. Write down the master equation for the system, giving an expression for $\partial P(n, t) / \partial t$.

  Show that

  $$\frac{d}{d t}\langle n\rangle=\lambda\langle n\rangle-\beta\left\langle n^{2}\right\rangle$$

  where $\langle.\rangle$ denotes the mean.

  Deduce that in a steady state $\langle n\rangle \leqslant \lambda / \beta$.

  comment

• Paper 2, Section II, C

  Mathematical Biology | Part II, 2012

  A population of blowflies is modelled by the equation

  $$\frac{d x}{d t}=R(x(t-T))-k x(t)$$

  where $k$ is a constant death rate and $R$ is a function of one variable such that $R(z)>0$ for $z>0$, with $R(z) \sim \beta z$ as $z \rightarrow 0$ and $R(z) \rightarrow 0$ as $z \rightarrow \infty$. The constants $T, k$ and $\beta$ are all positive, with $\beta>k$. Give a brief biological motivation for the term $R(x(t-T))$, in which you explain both the form of the function $R$ and the appearance of a delay time $T$.

  A suitable model for $R(z)$ is $\beta z \exp (-z / d)$, where $d$ is a positive constant. Show that in this case there is a single steady state of the system with non-zero population, i.e. with $x(t)=x_{s}>0$, with $x_{s}$ constant.

  Now consider the stability of this steady state. Show that if $x(t)=x_{s}+y(t)$, with $y(t)$ small, then $y(t)$ satisfies a delay differential equation of the form

  $$\frac{d y}{d t}=-k y(t)+B y(t-T),$$

  where $B$ is a constant to be determined. Show that $y(t)=e^{s t}$ is a solution of (2) if $s=-k+B e^{-s T}$. If $s=\sigma+i \omega$, where $\sigma$ and $\omega$ are both real, write down two equations relating $\sigma$ and $\omega$.

  Deduce that the steady state is stable if $|B|<k$. Show that, for this particular model for $R,|B|>k$ is possible only if $B<0$.

  By considering $B$ decreasing from small negative values, show that an instability will appear when $|B|>\left[k^{2}+\frac{g(k T)^{2}}{T^{2}}\right]^{1 / 2}$, where $\pi / 2<g(k T)<\pi$.

  Deduce that the steady state $x_{s}$ of (1) is unstable if

  $$\beta>k \exp \left[\left(1+\frac{\pi^{2}}{k^{2} T^{2}}\right)^{1 / 2}+1\right]$$

  comment

Number Fields

• Paper 2, Section II, F

  Number Fields | Part II, 2012

  Let $K=\mathbb{Q}(\alpha)$ where $\alpha$ is a root of $X^{2}-X+12=0$. Factor the elements 2,3 , $\alpha$ and $\alpha+2$ as products of prime ideals in $\mathcal{O}_{K}$. Hence compute the class group of $K$.

  Show that the equation $y^{2}+y=3\left(x^{5}-4\right)$ has no integer solutions.

  comment

Number Theory

• Paper 2, Section I, I

  Number Theory | Part II, 2012

  Define the Legendre symbol and the Jacobi symbol.

  State the law of quadratic reciprocity for the Jacobi symbol.

  Compute the value of the Jacobi symbol $\left(\frac{247}{321}\right)$, stating clearly any results you use.

  comment

Numerical Analysis

• Paper 2, Section II, D

  Numerical Analysis | Part II, 2012

  (i) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant x \leqslant 1, t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x), 0 \leqslant x \leqslant 1$, and with zero boundary conditions at $x=0$ and $x=1$, can be solved numerically by the method

  $$u_{m}^{n+1}=u_{m}^{n}+\mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right), \quad m=1,2, \ldots, M, n \geqslant 0$$

  where $\Delta x=1 /(M+1), \mu=\Delta t /(\Delta x)^{2}$, and $u_{m}^{n} \approx u(m \Delta x, n \Delta t)$. Prove that $\mu \leqslant 1 / 2$ implies convergence.

  (ii) By discretising the diffusion equation and employing the same notation as in (i) above, determine [without using Fourier analysis] conditions on $\mu$ and the constant $\alpha$ such that the method

  $$u_{m}^{n+1}-\frac{1}{2}(\mu-\alpha)\left(u_{m-1}^{n+1}-2 u_{m}^{n+1}+u_{m+1}^{n+1}\right)=u_{m}^{n}+\frac{1}{2}(\mu+\alpha)\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)$$

  is stable.

  comment

Optimization and Control

• Paper 2, Section II, J

  Optimization and Control | Part II, 2012

  Describe the elements of a generic stochastic dynamic programming equation for the problem of maximizing the expected sum of discounted rewards accrued at times $0,1, \ldots$ What is meant by the positive case? What is specially true in this case that is not true in general?

  An investor owns a single asset which he may sell once, on any of the days $t=0,1, \ldots$. On day $t$ he will be offered a price $X_{t}$. This value is unknown until day $t$, is independent of all other offers, and a priori it is uniformly distributed on $[0,1]$. Offers remain open, so that on day $t$ he may sell the asset for the best of the offers made on days $0, \ldots, t$. If he sells for $x$ on day $t$ then the reward is $x \beta^{t}$. Show from first principles that if $0<\beta<1$ then there exists $\bar{x}$ such that the expected reward is maximized by selling the first day the offer is at least $\bar{x}$.

  For $\beta=4 / 5$, find both $\bar{x}$ and the expected reward under the optimal policy.

  Explain what is special about the case $\beta=1$.

  comment

Partial Differential Equations

• Paper 2, Section II, B

  Partial Differential Equations | Part II, 2012

  Consider the elliptic Dirichlet problem on $\Omega \subset \mathbb{R}^{n}, \Omega$ bounded with a smooth boundary:

  $$\Delta u-e^{u}=f \text { in } \Omega, \quad u=u_{D} \text { on } \partial \Omega .$$

  Assume that $u_{D} \in L^{\infty}(\partial \Omega)$ and $f \in L^{\infty}(\Omega)$.

  (i) State the strong Minimum-Maximum Principle for uniformly elliptic operators.

  (ii) Prove that there exists at most one classical solution of the boundary value problem.

  (iii) Assuming further that $f \geqslant 0$ in $\Omega$, use the maximum principle to obtain an upper bound on the solution (assuming that it exists).

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, A

  Principles of Quantum Mechanics | Part II, 2012

  (a) Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture. Explain how the two pictures provide equivalent descriptions of physical results.

  (b) Derive the equation of motion for an operator in the Heisenberg picture.

  For a particle of mass $m$ moving in one dimension, the Hamiltonian is

  $$\hat{H}=\frac{\hat{p}^{2}}{2 m}+V(\hat{x})$$

  where $\hat{x}$ and $\hat{p}$ are the position and momentum operators, and the state vector is $|\Psi\rangle$. The eigenstates of $\hat{x}$ and $\hat{p}$ satisfy

  $$\langle x \mid p\rangle=\frac{1}{\sqrt{2 \pi \hbar}} e^{i p x / \hbar}, \quad\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right) .$$

  Use standard methods in the Dirac formalism to show that

  $$\begin{gathered} \left\langle x|\hat{p}| x^{\prime}\right\rangle=-i \hbar \frac{\partial}{\partial x} \delta\left(x-x^{\prime}\right) \\ \left\langle p|\hat{x}| p^{\prime}\right\rangle=i \hbar \frac{\partial}{\partial p} \delta\left(p-p^{\prime}\right) \end{gathered}$$

  Calculate $\left\langle x|\hat{H}| x^{\prime}\right\rangle$ and express $\langle x|\hat{p}| \Psi\rangle,\langle x|\hat{H}| \Psi\rangle$ in terms of the position space wavefunction $\Psi(x)$.

  Write down the momentum space Hamiltonian for the potential

  $$V(\hat{x})=m \omega^{2} \hat{x}^{4} / 2$$

  comment

Principles of Statistics

• Paper 2, Section II, $28 \mathrm{~K}$

  Principles of Statistics | Part II, 2012

  Carefully defining all italicised terms, show that, if a sufficiently general method of inference respects both the Weak Sufficiency Principle and the Conditionality Principle, then it respects the Likelihood Principle.

  The position $X_{t}$ of a particle at time $t>0$ has the Normal distribution $\mathcal{N}(0, \phi t)$, where $\phi$ is the value of an unknown parameter $\Phi$; and the time, $T_{x}$, at which the particle first reaches position $x \neq 0$ has probability density function

  $$p_{x}(t)=\frac{|x|}{\sqrt{2 \pi \phi t^{3}}} \exp \left(-\frac{x^{2}}{2 \phi t}\right) \quad(t>0) .$$

  Experimenter $E_{1}$ observes $X_{\tau}$, and experimenter $E_{2}$ observes $T_{\xi}$, where $\tau>0, \xi \neq 0$ are fixed in advance. It turns out that $T_{\xi}=\tau$. What does the Likelihood Principle say about the inferences about $\Phi$ to be made by the two experimenters?

  $E_{1}$ bases his inference about $\Phi$ on the distribution and observed value of $X_{\tau}^{2} / \tau$, while $E_{2}$ bases her inference on the distribution and observed value of $\xi^{2} / T_{\xi}$. Show that these choices respect the Likelihood Principle.

  comment

Probability and Measure

• Paper 2, Section II, J

  Probability and Measure | Part II, 2012

  The Fourier transform of a Lebesgue integrable function $f \in L^{1}(\mathbb{R})$ is given by

  $$\hat{f}(u)=\int_{\mathbb{R}} f(x) e^{i x u} d \mu(x)$$

  where $\mu$ is Lebesgue measure on the real line. For $f(x)=e^{-a x^{2}}, x \in \mathbb{R}, a>0$, prove that

  $$\hat{f}(u)=\sqrt{\frac{\pi}{a}} e^{-\frac{u^{2}}{4 a}}$$

  [You may use properties of derivatives of Fourier transforms without proof provided they are clearly stated, as well as the fact that $\phi(x)=(2 \pi)^{-1 / 2} e^{-x^{2} / 2}$ is a probability density function.]

  State and prove the almost everywhere Fourier inversion theorem for Lebesgue integrable functions on the real line. [You may use standard results from the course, such as the dominated convergence and Fubini's theorem. You may also use that $g_{t} * f(x):=\int_{\mathbb{R}} g_{t}(x-y) f(y) d y$ where $g_{t}(z)=t^{-1} \phi(z / t), t>0$, converges to $f$ in $L^{1}(\mathbb{R})$ as $t \rightarrow 0$ whenever $\left.f \in L^{1}(\mathbb{R}) .\right]$

  The probability density function of a Gamma distribution with scalar parameters $\lambda>0, \alpha>0$ is given by

  $$f_{\alpha, \lambda}(x)=\lambda e^{-\lambda x}(\lambda x)^{\alpha-1} 1_{[0, \infty)}(x)$$

  Let $0<\alpha<1, \lambda>0$. Is $\widehat{f_{\alpha, \lambda}}$ integrable?

  comment

Representation Theory

• Paper 2, Section II, H

  Representation Theory | Part II, 2012

  Suppose that $G$ is a finite group. Define the inner product of two complex-valued class functions on $G$. Prove that the characters of the irreducible representations of $G$ form an orthonormal basis for the space of complex-valued class functions.

  Suppose that $p$ is a prime and $\mathbb{F}_{p}$ is the field of $p$ elements. Let $G=\mathrm{GL}_{2}\left(\mathbb{F}_{p}\right)$. List the conjugacy classes of $G$.

  Let $G$ act naturally on the set of lines in the space $\mathbb{F}_{p}^{2}$. Compute the corresponding permutation character and show that it is reducible. Decompose this character as a sum of two irreducible characters.

  comment

Riemann Surfaces

• Paper 2, Section II, I

  Riemann Surfaces | Part II, 2012

  Let $X$ be the algebraic curve in $\mathbb{C}^{2}$ defined by the polynomial $p(z, w)=z^{d}+w^{d}+1$ where $d$ is a natural number. Using the implicit function theorem, or otherwise, show that there is a natural complex structure on $X$. Let $f: X \rightarrow \mathbb{C}$ be the function defined by $f(a, b)=b$. Show that $f$ is holomorphic. Find the ramification points and the corresponding branching orders of $f$.

  Assume that $f$ extends to a holomorphic map $g: Y \rightarrow \mathbb{C} \cup\{\infty\}$ from a compact Riemann surface $Y$ to the Riemann sphere so that $g^{-1}(\infty)=Y \backslash X$ and that $g$ has no ramification points in $g^{-1}(\infty)$. State the Riemann-Hurwitz formula and apply it to $g$ to calculate the Euler characteristic and the genus of $Y$.

  comment

Statistical Modelling

• Paper 2, Section I, K

  Statistical Modelling | Part II, 2012

  The purpose of the following study is to investigate differences among certain treatments on the lifespan of male fruit flies, after allowing for the effect of the variable 'thorax length' (thorax) which is known to be positively correlated with lifespan. Data was collected on the following variables:

  longevity lifespan in days

  thorax (body) length in $\mathrm{mm}$

  treat a five level factor representing the treatment groups. The levels were labelled as follows: "00", "10", "80", "11", "81".

  No interactions were found between thorax length and the treatment factor. A linear model with thorax as the covariate, treat as a factor (having the above 5 levels) and longevity as the response was fitted and the following output was obtained. There were 25 males in each of the five groups, which were treated identically in the provision of fresh food.

  Coefficients :

  $\begin{array}{lrrrr} & \text{Estimate} & \text{Std. Error} & \text{t value} & \operatorname{Pr}(>|t|) \\ \text { (Intercept) } & -49.98 & 10.61 & -4.71 & 6.7 e-06 \\ \text { treat10 } & 2.65 & 2.98 & 0.89 & 0.37 \\ \text { treat11 } & -7.02 & 2.97 & -2.36 & 0.02 \\ \text { treat80 } & 3.93 & 3.00 & 1.31 & 0.19 \\ \text { treat81 } & -19.95 & 3.01 & -6.64 & 1.0 e-09 \\ \text { thorax } & 135.82 & 12.44 & 10.92 & <2 \mathrm{e}-16\end{array}$

  Residual standard error: $10.5$ on 119 degrees of freedom

  Multiple R-Squared: $0.656$, Adjusted R-squared: $0.642$

  F-statistics: $45.5$ on 5 and 119 degrees of freedom, p-value: 0

  (a) Assuming the same treatment, how much longer would you expect a fly with a thorax length $0.1 \mathrm{~mm}$ greater than another to live?

  (b) What is the predicted difference in longevity between a male fly receiving treatment treat 10 and treat81 assuming they have the same thorax length?

  (c) Because the flies were randomly assigned to the five groups, the distribution of thorax lengths in the five groups are essentially equal. What disadvantage would the investigators have incurred by ignoring the thorax length in their analysis (i.e., had they done a one-way ANOVA instead)?

  (d) The residual-fitted plot is shown in the left panel of Figure 1 overleaf. Is it possible to determine if the regular residuals or the studentized residuals have been used to construct this plot? Explain.

  (e) The Box-Cox procedure was used to determine a good transformation for this data. The plot of the log-likelihood for $\lambda$ is shown in the right panel of Figure 1 . What transformation should be used to improve the fit and yet retain some interpretability?

  

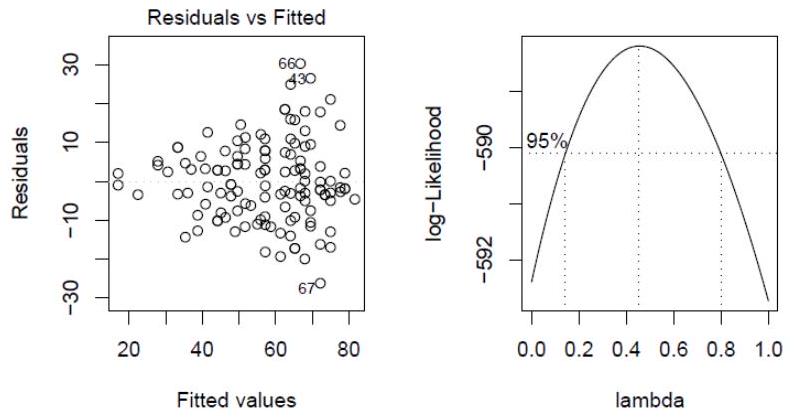
  Figure 1: Residual-Fitted plot on the left and Box-Cox plot on the right

  comment

Statistical Physics

• Paper 2, Section II, C

  Statistical Physics | Part II, 2012

  Explain what is meant by an isothermal expansion and an adiabatic expansion of a gas.

  By first establishing a suitable Maxwell relation, show that

  $$\left.\frac{\partial E}{\partial V}\right|_{T}=\left.T \frac{\partial p}{\partial T}\right|_{V}-p$$

  and

  $$\left.\frac{\partial C_{V}}{\partial V}\right|_{T}=\left.T \frac{\partial^{2} p}{\partial T^{2}}\right|_{V}$$

  The energy in a gas of blackbody radiation is given by $E=a V T^{4}$, where $a$ is a constant. Derive an expression for the pressure $p(V, T)$.

  Show that if the radiation expands adiabatically, $V T^{3}$ is constant.

  comment

Stochastic Financial Models

• Paper 2, Section II, J

  Stochastic Financial Models | Part II, 2012

  (i) Give the definition of Brownian motion.

  (ii) The price $S_{t}$ of an asset evolving in continuous time is represented as

  $$S_{t}=S_{0} \exp \left(\sigma W_{t}+\mu t\right)$$

  where $\left(W_{t}\right)_{t \geqslant 0}$ is a standard Brownian motion and $\sigma$ and $\mu$ are constants. If riskless investment in a bank account returns a continuously compounded rate of interest $r$, derive the Black-Scholes formula for the time-0 price of a European call option on asset $S$ with strike price $K$ and expiry $T$. [Standard results from the course may be used without proof but must be stated clearly.]

  (iii) In the same financial market, a certain contingent claim $C$ pays $\left(S_{T}\right)^{n}$ at time $T$, where $n \geqslant 1$. Find the closed-form expression for the time- 0 value of this contingent claim.

  Show that for every $s>0$ and $n \geqslant 1$,

  $$s^{n}=n(n-1) \int_{0}^{s} k^{n-2}(s-k) d k .$$

  Using this identity, how would you replicate (at least approximately) the contingent claim $C$ with a portfolio consisting only of European calls?

  comment

Topics in Analysis

• Paper 2, Section I, $2 F$

  Topics in Analysis | Part II, 2012

  (a) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map such that $\gamma(0)=\gamma(1)$. Define the winding number $w(\gamma ; 0)$ of $\gamma$ about the origin. State precisely a theorem about homotopy invariance of the winding number.

  (b) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a continuous map such that $z^{-10} f(z)$ is bounded as $|z| \rightarrow \infty$. Prove that there exists a complex number $z_{0}$ such that

  $$f\left(z_{0}\right)=z_{0}^{11}$$

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2012

  (a) State Runge's theorem about uniform approximability of analytic functions by complex polynomials.

  (b) Let $K$ be a compact subset of the complex plane.

  (i) Let $\Sigma$ be an unbounded, connected subset of $\mathbb{C} \backslash K$. Prove that for each $\zeta \in \Sigma$, the function $f(z)=(z-\zeta)^{-1}$ is uniformly approximable on $K$ by a sequence of complex polynomials.

  [You may not use Runge's theorem without proof.]

  (ii) Let $\Gamma$ be a bounded, connected component of $\mathbb{C} \backslash K$. Prove that there is no point $\zeta \in \Gamma$ such that the function $f(z)=(z-\zeta)^{-1}$ is uniformly approximable on $K$ by a sequence of complex polynomials.

  comment

Waves

• Paper 2, Section II, 38D

  Waves | Part II, 2012

  Derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  for wave propagation through a slowly-varying medium with local dispersion relation $\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$. The meaning of the notation $d / d t$ should be carefully explained.

  A non-dispersive slowly varying medium has a local wave speed $c$ that depends only on the $z$ coordinate. State and prove Snell's Law relating the angle $\psi$ between a ray and the $z$-axis to $c$.

  Consider the case of a medium with wavespeed $c=A \cosh \beta z$, where $A$ and $\beta$ are positive constants. Find the equation of the ray that passes through the origin with wavevector $\left(k_{0}, 0, m_{0}\right)$, and show that it remains in the region $\beta|z| \leqslant \sinh ^{-1}\left(m_{0} / k_{0}\right)$. Sketch several rays passing through the origin.

  comment