Part II, 2011, Paper 1

Algebraic Geometry

• Paper 1, Section II, H

  Algebraic Geometry | Part II, 2011

  (i) Let $X$ be an affine variety over an algebraically closed field. Define what it means for $X$ to be irreducible, and show that if $U$ is a non-empty open subset of an irreducible $X$, then $U$ is dense in $X$.

  (ii) Show that $n \times n$ matrices with distinct eigenvalues form an affine variety, and are a Zariski open subvariety of affine space $\mathbb{A}^{n^{2}}$ over an algebraically closed field.

  (iii) Let $\operatorname{char}_{A}(x)=\operatorname{det}(x I-A)$ be the characteristic polynomial of $A$. Show that the $n \times n$ matrices $A$ such that $\operatorname{char}_{A}(A)=0$ form a Zariski closed subvariety of $\mathbb{A}^{n^{2}}$. Hence conclude that this subvariety is all of $\mathbb{A}^{n^{2}}$.

  comment

Algebraic Topology

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2011

  Are the following statements true or false? Justify your answers.

  (i) If $x$ and $y$ lie in the same path-component of $X$, then $\Pi_{1}(X, x) \cong \Pi_{1}(X, y)$.

  (ii) If $x$ and $y$ are two points of the Klein bottle $K$, and $u$ and $v$ are two paths from $x$ to $y$, then $u$ and $v$ induce the same isomorphism from $\Pi_{1}(K, x)$ to $\Pi_{1}(K, y)$.

  (iii) $\Pi_{1}(X \times Y,(x, y))$ is isomorphic to $\Pi_{1}(X, x) \times \Pi_{1}(Y, y)$ for any two spaces $X$ and $Y$.

  (iv) If $X$ and $Y$ are connected polyhedra and $H_{1}(X) \cong H_{1}(Y)$, then $\Pi_{1}(X) \cong \Pi_{1}(Y)$.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  In one dimension a particle of mass $m$ and momentum $\hbar k, k>0$, is scattered by a potential $V(x)$ where $V(x) \rightarrow 0$ as $|x| \rightarrow \infty$. Incoming and outgoing plane waves of positive $(+)$ and negative $(-)$ parity are given, respectively, by

  $$\begin{array}{ll} I_{+}(k, x)=e^{-i k|x|}, & I_{-}(k, x)=\operatorname{sgn}(x) e^{-i k|x|} \\ O_{+}(k, x)=e^{i k|x|}, & O_{-}(k, x)=-\operatorname{sgn}(x) e^{i k|x|} \end{array}$$

  The scattering solutions to the time-independent Schrödinger equation with positive and negative parity incoming waves are $\psi_{+}(x)$ and $\psi_{-}(x)$, respectively. State how the asymptotic behaviour of $\psi_{+}$and $\psi_{-}$can be expressed in terms of $I_{+}, I_{-}, O_{+}, O_{-}$and the S-matrix denoted by

  $$\boldsymbol{S}=\left(\begin{array}{cc} S_{++} & S_{+-} \\ S_{-+} & S_{--} \end{array}\right)$$

  In the case where $V(x)=V(-x)$ explain briefly why you expect $S_{+-}=S_{-+}=0$.

  The potential $V(x)$ is given by

  $$V(x)=V_{0}[\delta(x-a)+\delta(x+a)]$$

  where $V_{0}$ is a constant. In this case, show that

  $$S_{--}(k)=e^{-2 i k a}\left[\frac{\left(2 k-i U_{0}\right) e^{i k a}+i U_{0} e^{-i k a}}{\left(2 k+i U_{0}\right) e^{-i k a}-i U_{0} e^{i k a}}\right]$$

  where $U_{0}=2 m V_{0} / \hbar^{2}$. Verify that $\left|S_{--}\right|^{2}=1$ and explain briefly the physical meaning of this result.

  For $V_{0}<0$, by considering the poles or zeros of $S_{--}(k)$ show that there exists one bound state of negative parity in this potential if $U_{0} a<-1$.

  For $V_{0}>0$ and $U_{0} a \gg 1$, show that $S_{--}(k)$ has a pole at

  $$k a=\pi+\alpha-i \gamma$$

  where, to leading order in $1 /\left(U_{0} a\right)$,

  $$\alpha=-\frac{\pi}{U_{0} a}, \quad \gamma=\left(\frac{\pi}{U_{0} a}\right)^{2}$$

  Explain briefy the physical meaning of this result, and why you expect that $\gamma>0$.

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2011

  (i) Let $X$ be a Markov chain with finitely many states. Define a stopping time and state the strong Markov property.

  (ii) Let $X$ be a Markov chain with state-space $\{-1,0,1\}$ and Q-matrix

  $$Q=\left(\begin{array}{ccc} -(q+\lambda) & \lambda & q \\ 0 & 0 & 0 \\ q & \lambda & -(q+\lambda) \end{array}\right), \text { where } q, \lambda>0$$

  Consider the integral $\int_{0}^{t} X(s) \mathrm{d} s$, the signed difference between the times spent by the chain at states $+1$ and $-1$ by time $t$, and let

  $$\begin{aligned} Y &=\sup \left[\int_{0}^{t} X(s) \mathrm{d} s: t>0\right] \\ \psi_{\pm}(c) &=\mathbb{P}\left(Y>c \mid X_{0}=\pm 1\right), \quad c>0 \end{aligned}$$

  Derive the equation

  $$\psi_{-}(c)=\int_{0}^{\infty} q e^{-(\lambda+q) u_{+}} \psi_{+}(c+u) \mathrm{d} u$$

  (iii) Obtain another equation relating $\psi_{+}$to $\psi_{-}$.

  (iv) Assuming that $\psi_{+}(c)=e^{-c A}, c>0$, where $A$ is a non-negative constant, calculate $A$.

  (v) Give an intuitive explanation why the function $\psi_{+}$must have the exponential form $\psi_{+}(c)=e^{-c A}$ for some $A$.

  comment

Asymptotic Methods

• Paper 1, Section II, A

  Asymptotic Methods | Part II, 2011

  A function $f(n)$, defined for positive integer $n$, has an asymptotic expansion for large $n$ of the following form:

  $$f(n) \sim \sum_{k=0}^{\infty} a_{k} \frac{1}{n^{2 k}}, \quad n \rightarrow \infty$$

  What precisely does this mean?

  Show that the integral

  $$I(n)=\int_{0}^{2 \pi} \frac{\cos n t}{1+t^{2}} d t$$

  has an asymptotic expansion of the form $(*)$. [The Riemann-Lebesgue lemma may be used without proof.] Evaluate the coefficients $a_{0}, a_{1}$ and $a_{2}$.

  comment

Classical Dynamics

• Paper 1, Section I, C

  Classical Dynamics | Part II, 2011

  (i) A particle of mass $m$ and charge $q$, at position $\mathbf{x}$, moves in an electromagnetic field with scalar potential $\phi(\mathbf{x}, t)$ and vector potential $\mathbf{A}(\mathbf{x}, t)$. Verify that the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-q(\phi-\dot{\mathbf{x}} \cdot \mathbf{A})$$

  gives the correct equations of motion.

  [Note that $\mathbf{E}=-\nabla \phi-\dot{\mathbf{A}}$ and $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$.]

  (ii) Consider the case of a constant uniform magnetic field, with $\mathbf{E}=\mathbf{0}$, given by $\phi=0$, $\mathbf{A}=(0, x B, 0)$, where $(x, y, z)$ are Cartesian coordinates and $B$ is a constant. Find the motion of the particle, and describe it carefully.

  comment

Coding and Cryptography

• Paper 1, Section I, G

  Coding and Cryptography | Part II, 2011

  I think of an integer $n$ with $1 \leqslant n \leqslant 10^{6}$. Explain how to find $n$ using twenty questions (or less) of the form 'Is it true that $n \geqslant m$ ?' to which I answer yes or no.

  I have watched a horse race with 15 horses. Is it possible to discover the order in which the horses finished by asking me twenty questions to which I answer yes or no?

  Roughly how many questions of the yes/no type are required to discover the order in which $n$ horses finished if $n$ is large?

  [You may assume that I answer honestly.]

  comment

• Paper 1, Section II, $12 G$

  Coding and Cryptography | Part II, 2011

  Describe the Rabin-Williams coding scheme. Show that any method for breaking it will enable us to factorise the product of two primes.

  Explain how the Rabin-Williams scheme can be used for bit sharing (that is to say 'tossing coins by phone').

  comment

Cosmology

• Paper 1, Section I, E

  Cosmology | Part II, 2011

  Light of wavelength $\lambda_{e}$ emitted by a distant object is observed by us to have wavelength $\lambda_{0}$. The redshift $z$ of the object is defined by

  $$1+z=\frac{\lambda_{0}}{\lambda_{e}}$$

  Assuming that the object is at a fixed comoving distance from us in a homogeneous and isotropic universe with scale factor $a(t)$, show that

  $$1+z=\frac{a\left(t_{0}\right)}{a\left(t_{e}\right)}$$

  where $t_{e}$ is the time of emission and $t_{0}$ the time of observation (i.e. today).

  [You may assume the non-relativistic Doppler shift formula $\Delta \lambda / \lambda=(v / c) \cos \theta$ for the shift $\Delta \lambda$ in the wavelength of light emitted by a nearby object travelling with velocity $v$ at angle $\theta$ to the line of sight.]

  Given that the object radiates energy $L$ per unit time, explain why the rate at which energy passes through a sphere centred on the object and intersecting the Earth is $L /(1+z)^{2}$.

  comment

• Paper 1, Section II, E

  Cosmology | Part II, 2011

  A homogeneous and isotropic universe, with scale factor $a$, curvature parameter $k$, energy density $\rho$ and pressure $P$, satisfies the Friedmann and energy conservation equations

  $$\begin{aligned} &H^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho \\ &\dot{\rho}+3 H\left(\rho+P / c^{2}\right)=0 \end{aligned}$$

  where $H=\dot{a} / a$, and the dot indicates a derivative with respect to cosmological time $t$.

  (i) Derive the acceleration equation

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  Given that the strong energy condition $\rho c^{2}+3 P \geqslant 0$ is satisfied, show that $(a H)^{2}$ is a decreasing function of $t$ in an expanding universe. Show also that the density parameter $\Omega=8 \pi G \rho /\left(3 H^{2}\right)$ satisfies

  $$\Omega-1=\frac{k c^{2}}{a^{2} H^{2}}$$

  Hence explain, briefly, the flatness problem of standard big bang cosmology.

  (ii) A flat $(k=0)$ homogeneous and isotropic universe is filled with a radiation fluid $\left(w_{R}=1 / 3\right)$ and a dark energy fluid $\left(w_{\Lambda}=-1\right)$, each with an equation of state of the form $P_{i}=w_{i} \rho_{i} c^{2}$ and density parameters today equal to $\Omega_{R 0}$ and $\Omega_{\Lambda 0}$ respectively. Given that each fluid independently obeys the energy conservation equation, show that the total energy density $\left(\rho_{R}+\rho_{\Lambda}\right) c^{2}$ equals $\rho c^{2}$, where

  $$\rho(t)=\frac{3 H_{0}^{2}}{8 \pi G} \frac{\Omega_{R 0}}{a^{4}}\left(1+\frac{1-\Omega_{R 0}}{\Omega_{R 0}} a^{4}\right)$$

  with $H_{0}$ being the value of the Hubble parameter today. Hence solve the Friedmann equation to get

  $$a(t)=\alpha(\sinh \beta t)^{1 / 2}$$

  where $\alpha$ and $\beta$ should be expressed in terms $\Omega_{R 0}$ and $\Omega_{\Lambda 0}$. Show that this result agrees with the expected asymptotic solutions at both early $(t \rightarrow 0)$ and late $(t \rightarrow \infty)$ times.

  [Hint: $\int d x / \sqrt{x^{2}+1}=\operatorname{arcsinh} x$.]

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2011

  Let $X$ and $Y$ be manifolds and $f: X \rightarrow Y$ a smooth map. Define the notions critical point, critical value, regular value of $f$. Prove that if $y$ is a regular value of $f$, then $f^{-1}(y)$ (if non-empty) is a smooth manifold of $\operatorname{dimension} \operatorname{dim} X-\operatorname{dim} Y$.

  [The Inverse Function Theorem may be assumed without proof if accurately stated.]

  Let $M_{n}(\mathbb{R})$ be the set of all real $n \times n$ matrices and $\operatorname{SO}(n) \subset M_{n}(\mathbb{R})$ the group of all orthogonal matrices with determinant 1 . Show that $\mathrm{SO}(n)$ is a smooth manifold and find its dimension.

  Show further that $\mathrm{SO}(n)$ is compact and that its tangent space at $A \in \operatorname{SO}(n)$ is given by all matrices $H$ such that $A H^{t}+H A^{t}=0$.

  comment

Dynamical Systems

• Paper 1, Section I, C

  Dynamical Systems | Part II, 2011

  Find the fixed points of the dynamical system (with $\mu \neq 0$ )

  $$\begin{aligned} &\dot{x}=\mu^{2} x-x y \\ &\dot{y}=-y+x^{2} \end{aligned}$$

  and determine their type as a function of $\mu$.

  Find the stable and unstable manifolds of the origin correct to order $4 .$

  comment

Electrodynamics

• Paper 1, Section II, C

  Electrodynamics | Part II, 2011

  In the Landau-Ginzburg model of superconductivity, the energy of the system is given, for constants $\alpha$ and $\beta$, by

  $$E=\int\left\{\frac{1}{2 \mu_{0}} \mathbf{B}^{2}+\frac{1}{2 m}\left[(i \hbar \nabla-q \mathbf{A}) \psi^{*} \cdot(-i \hbar \nabla-q \mathbf{A}) \psi\right]+\alpha \psi^{*} \psi+\beta\left(\psi^{*} \psi\right)^{2}\right\} d^{3} \mathbf{x},$$

  where $\mathbf{B}$ is the time-independent magnetic field derived from the vector potential $\mathbf{A}$, and $\psi$ is the wavefunction of the charge carriers, which have mass $m$ and charge $q$.

  Describe the physical meaning of each of the terms in the integral.

  Explain why in a superconductor one must choose $\alpha<0$ and $\beta>0$. Find an expression for the number density $n$ of the charge carriers in terms of $\alpha$ and $\beta$.

  Show that the energy is invariant under the gauge transformations

  $$\mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda, \quad \psi \rightarrow \psi e^{i q \Lambda / \hbar}$$

  Assuming that the number density $n$ is uniform, show that, if $E$ is a minimum under variations of $\mathbf{A}$, then

  $$\operatorname{curl} \mathbf{B}=-\frac{\mu_{0} q^{2} n}{m}\left(\mathbf{A}-\frac{\hbar}{q} \nabla \phi\right)$$

  where $\phi=\arg \psi$.

  Find a formula for $\nabla^{2} \mathbf{B}$ and use it to explain why there cannot be a magnetic field inside the bulk of a superconductor.

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2011

  The steady two-dimensional boundary-layer equations for flow primarily in the $x$ direction are

  $$\begin{gathered} \rho\left(u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}\right)=-\frac{d P}{d x}+\mu \frac{\partial^{2} u}{\partial y^{2}} \\ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{gathered}$$

  A thin, steady, two-dimensional jet emerges from a point at the origin and flows along the $x$-axis in a fluid at rest far from the $x$-axis. Show that the momentum flux

  $$F=\int_{-\infty}^{\infty} \rho u^{2} d y$$

  is independent of position $x$ along the jet. Deduce that the thickness $\delta(x)$ of the jet increases along the jet as $x^{2 / 3}$, while the centre-line velocity $U(x)$ decreases as $x^{-1 / 3}$.

  A similarity solution for the jet is sought with a streamfunction $\psi$ of the form

  $$\psi(x, y)=U(x) \delta(x) f(\eta) \quad \text { with } \quad \eta=y / \delta(x) .$$

  Derive the nonlinear third-order non-dimensional differential equation governing $f$, and write down the boundary and normalisation conditions which must be applied.

  comment

Further Complex Methods

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2011

  Show that the following integral is well defined:

  $$I(a, b)=\int_{0}^{\infty}\left(\frac{e^{-b x}}{e^{i a} e^{x}-1}-\frac{e^{b x}}{e^{-i a} e^{x}-1}\right) d x, \quad 0<a<\infty, a \neq 2 n \pi, n \in \mathbb{Z}, 0<b<1$$

  Express $I(a, b)$ in terms of a combination of hypergeometric functions.

  [You may assume without proof that the hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

  $$F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  for appropriate restrictions on $c, b, z$. Furthermore,

  $$\Gamma(z+1)=z \Gamma(z) \cdot]$$

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2011

  (i) By assuming the validity of the Fourier transform pair, prove the validity of the following transform pair:

  $$\begin{gathered} \hat{q}(k)=\int_{0}^{\infty} e^{-i k x} q(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ q(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x} \hat{q}(k) d k+\frac{c}{2 \pi} \int_{L} e^{i k x} \hat{q}(-k) d k, \quad 0<x<\infty, \end{gathered}$$

  where $c$ is an arbitrary complex constant and $L$ is the union of the two rays arg $k=\frac{\pi}{2}$ and $\arg k=0$ with the orientation shown in the figure below:

  

  The contour $L$.

  (ii) Verify that the partial differential equation

  $$i q_{t}+q_{x x}=0, \quad 0<x<\infty, t>0,$$

  can be rewritten in the following form:

  $$\left(e^{-i k x+i k^{2} t} q\right)_{t}-\left[e^{-i k x+i k^{2} t}\left(-k q+i q_{x}\right)\right]_{x}=0, \quad k \in \mathbb{C} .$$

  Consider equation (2) supplemented with the conditions

  $$\begin{aligned} &q(x, 0)=q_{0}(x), \quad 0<x<\infty \\ &q(x, t) \text { vanishes sufficiently fast for all } t \text { as } x \rightarrow \infty \end{aligned}$$

  By using equations (1a) and (3), show that

  $$\hat{q}(k, t)=e^{-i k^{2} t} \hat{q}_{0}(k)+e^{-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)-i \tilde{g}_{1}\left(k^{2}, t\right)\right], \operatorname{Im} k \leqslant 0$$

  where

  $$\hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0$$

  Part II, $2011 \quad$ List of Questions

  [TURN OVER

  $$\tilde{g}_{0}(k, t)=\int_{0}^{t} e^{i k \tau} q(0, \tau) d \tau, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{i k \tau} q_{x}(0, \tau) d \tau, k \in \mathbb{C}, t>0 .$$

  Use (1b) to invert equation (5) and furthermore show that

  $$\int_{-\infty}^{\infty} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k=\int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k, t>0, x>0$$

  Hence determine the constant $c$ so that the solution of equation (2), with the conditions (4) and with the condition that either $q(0, t)$ or $q_{x}(0, t)$ is given, can be expressed in terms of an integral involving $\hat{q}_{0}(k)$ and either $\tilde{g}_{0}$ or $\tilde{g}_{1}$.

  comment

Galois Theory

• Paper 1, Section II, 18H

  Galois Theory | Part II, 2011

  Let $K$ be a field.

  (i) Let $F$ and $F^{\prime}$ be two finite extensions of $K$. When the degrees of these two extensions are equal, show that every $K$-homomorphism $F \rightarrow F^{\prime}$ is an isomorphism. Give an example, with justification, of two finite extensions $F$ and $F^{\prime}$ of $K$, which have the same degrees but are not isomorphic over $K$.

  (ii) Let $L$ be a finite extension of $K$. Let $F$ and $F^{\prime}$ be two finite extensions of $L$. Show that if $F$ and $F^{\prime}$ are isomorphic as extensions of $L$ then they are isomorphic as extensions of $K$. Prove or disprove the converse.

  comment

General Relativity

• Paper 1, Section II, 37D

  General Relativity | Part II, 2011

  Consider a metric of the form

  $$d s^{2}=-2 d u d v+d x^{2}+d y^{2}-2 H(u, x, y) d u^{2} .$$

  Let $x^{a}(\lambda)$ describe an affinely-parametrised geodesic, where $x^{a} \equiv\left(x^{1}, x^{2}, x^{3}, x^{4}\right)=$ $(u, v, x, y)$. Write down explicitly the Lagrangian

  $$L=g_{a b} \dot{x}^{a} \dot{x}^{b},$$

  with $\dot{x}^{a}=d x^{a} / d \lambda$, using the given metric. Hence derive the four geodesic equations. In particular, show that

  $$\ddot{v}+2\left(\frac{\partial H}{\partial x} \dot{x}+\frac{\partial H}{\partial y} \dot{y}\right) \dot{u}+\frac{\partial H}{\partial u} \dot{u}^{2}=0$$

  By comparing these equations with the standard form of the geodesic equation, show that $\Gamma_{13}^{2}=\partial H / \partial x$ and derive the other Christoffel symbols.

  The Ricci tensor, $R_{a b}$, is defined by

  $$R_{a b}=\Gamma_{a b, d}^{d}-\Gamma_{a d, b}^{d}+\Gamma_{d f}^{d} \Gamma_{b a}^{f}-\Gamma_{b f}^{d} \Gamma_{d a}^{f}$$

  By considering the case $a=1, b=1$, show that the vacuum Einstein field equations imply

  $$\frac{\partial^{2} H}{\partial x^{2}}+\frac{\partial^{2} H}{\partial y^{2}}=0$$

  comment

Geometry and Groups

• Paper 1, Section I, G

  Geometry and Groups | Part II, 2011

  Let $G$ be a finite subgroup of $\mathrm{SO}(3)$ and let $\Omega$ be the set of unit vectors that are fixed by some non-identity element of $G$. Show that the group $G$ permutes the unit vectors in $\Omega$ and that $\Omega$ has at most three orbits. Describe these orbits when $G$ is the group of orientation-preserving symmetries of a regular dodecahedron.

  comment

• Paper 1, Section II, G

  Geometry and Groups | Part II, 2011

  Prove that a group of Möbius transformations is discrete if, and only if, it acts discontinuously on hyperbolic 3 -space.

  Let $G$ be the set of Möbius transformations $z \mapsto \frac{a z+b}{c z+d}$ with

  $$a, b, c, d \in \mathbb{Z}[i]=\{u+i v: u, v \in \mathbb{Z}\} \quad \text { and } \quad a d-b c=1$$

  Show that $G$ is a group and that it acts discontinuously on hyperbolic 3-space. Show that $G$ contains transformations that are elliptic, parabolic, hyperbolic and loxodromic.

  comment

Graph Theory

• Paper 1, Section II, F

  Graph Theory | Part II, 2011

  Let $G$ be a bipartite graph with vertex classes $X$ and $Y$. What is a matching from $X$ to $Y$ ?

  Show that if $|\Gamma(A)| \geqslant|A|$ for all $A \subset X$ then $G$ contains a matching from $X$ to $Y$.

  Let $d$ be a positive integer. Show that if $|\Gamma(A)| \geqslant|A|-d$ for all $A \subset X$ then $G$ contains a set of $|X|-d$ independent edges.

  Show that if 0 is not an eigenvalue of $G$ then $G$ contains a matching from $X$ to $Y$.

  Suppose now that $|X|=|Y| \geqslant 1$ and that $G$ does contain a matching from $X$ to $Y$. Must it be the case that 0 is not an eigenvalue of $G$ ? Justify your answer.

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2011

  Define a finite-dimensional integrable system and state the Arnold-Liouville theorem.

  Consider a four-dimensional phase space with coordinates $\left(q_{1}, q_{2}, p_{1}, p_{2}\right)$, where $q_{2}>0$ and $q_{1}$ is periodic with period $2 \pi$. Let the Hamiltonian be

  $$H=\frac{\left(p_{1}\right)^{2}}{2\left(q_{2}\right)^{2}}+\frac{\left(p_{2}\right)^{2}}{2}-\frac{k}{q_{2}}, \quad \text { where } k>0$$

  Show that the corresponding Hamilton equations form an integrable system.

  Determine the sign of the constant $E$ so that the motion is periodic on the surface $H=E$. Demonstrate that in this case, the action variables are given by

  $$I_{1}=p_{1}, \quad I_{2}=\gamma \int_{\alpha}^{\beta} \frac{\sqrt{\left(q_{2}-\alpha\right)\left(\beta-q_{2}\right)}}{q_{2}} d q_{2},$$

  where $\alpha, \beta, \gamma$ are positive constants which you should determine.

  comment

Linear Analysis

• Paper 1, Section II, G

  Linear Analysis | Part II, 2011

  State a version of the Stone-Weierstrass Theorem for real-valued functions on a compact metric space.

  Suppose that $K:[0,1]^{2} \rightarrow \mathbb{R}$ is a continuous function. Show that $K(x, y)$ may be uniformly approximated by functions of the form $\sum_{i=1}^{n} f_{i}(x) g_{i}(y)$ with $f_{i}, g_{i}:[0,1] \rightarrow \mathbb{R}$ continuous.

  Let $X, Y$ be Banach spaces and suppose that $T: X \rightarrow Y$ is a bounded linear operator. What does it mean to say that $T$ is finite-rank? What does it mean to say that $T$ is compact? Give an example of a bounded linear operator from $C[0,1]$ to itself which is not compact.

  Suppose that $\left(T_{n}\right)_{n=1}^{\infty}$ is a sequence of finite-rank operators and that $T_{n} \rightarrow T$ in the operator norm. Briefly explain why the $T_{n}$ are compact. Show that $T$ is compact.

  Hence, show that the integral operator $T: C[0,1] \rightarrow C[0,1]$ defined by

  $$T f(x)=\int_{0}^{1} f(y) K(x, y) d y$$

  is compact.

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2011

  Give the inductive and synthetic definitions of ordinal addition, and prove that they are equivalent.

  Which of the following assertions about ordinals $\alpha, \beta$ and $\gamma$ are always true, and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha \beta=\beta \alpha$.

  (ii) $\alpha(\beta+\gamma)=\alpha \beta+\alpha \gamma$.

  (iii) If $\alpha \geqslant \omega^{2}$ then $\alpha+\omega^{2}=\omega^{2}+\alpha$.

  (iv) If $\alpha \geqslant \omega_{1}$ then $\alpha \omega_{1}=\omega_{1} \alpha$.

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2011

  A proposed model of insect dispersal is given by the equation

  $$\frac{\partial n}{\partial t}=D \frac{\partial}{\partial x}\left[\left(\frac{n_{0}}{n}\right) \frac{\partial n}{\partial x}\right]$$

  where $n(x, t)$ is the density of insects and $D$ and $n_{0}$ are constants.

  Interpret the term on the right-hand side.

  Explain why a solution of the form

  $$n(x, t)=n_{0}(D t)^{-\beta} g\left(x /(D t)^{\beta}\right),$$

  where $\beta$ is a positive constant, can potentially represent the dispersal of a fixed number $n_{0}$ of insects initially localised at the origin.

  Show that the equation (1) can be satisfied by a solution of the form (2) if $\beta=1$ and find the corresponding function $g$.

  comment

Number Fields

• Paper 1, Section II, F

  Number Fields | Part II, 2011

  Calculate the class group for the field $K=\mathbb{Q}(\sqrt{-17})$.

  [You may use any general theorem, provided that you state it accurately.]

  Find all solutions in $\mathbb{Z}$ of the equation $y^{2}=x^{5}-17$.

  comment

Number Theory

• Paper 1, Section I, I

  Number Theory | Part II, 2011

  Prove that, under the action of $\mathrm{SL}_{2}(\mathbb{Z})$, every positive definite binary quadratic form of discriminant $-163$, with integer coefficients, is equivalent to

  $$x^{2}+x y+41 y^{2} .$$

  comment

Numerical Analysis

• Paper 1, Section II, A

  Numerical Analysis | Part II, 2011

  The nine-point method for the Poisson equation $\nabla^{2} u=f$ (with zero Dirichlet boundary conditions) in a square, reads

  $$\begin{array}{r} \frac{2}{3}\left(u_{i-1, j}+u_{i+1, j}+u_{i, j-1}+u_{i, j+1}\right)+\frac{1}{6}\left(u_{i-1, j-1}+u_{i-1, j+1}+u_{i+1, j-1}+u_{i+1, j+1}\right) \\ -\frac{10}{3} u_{i, j}=h^{2} f_{i, j}, \quad i, j=1, \ldots, m, \end{array}$$

  where $u_{0, j}=u_{m+1, j}=u_{i, 0}=u_{i, m+1}=0$, for all $i, j=0, \ldots, m+1$.

  (i) By arranging the two-dimensional arrays $\left\{u_{i, j}\right\}_{i, j=1, \ldots, m}$ and $\left\{f_{i, j}\right\}_{i, j=1, \ldots, m}$ into column vectors $u \in \mathbb{R}^{m^{2}}$ and $b \in \mathbb{R}^{m^{2}}$ respectively, the linear system above takes the matrix form $A u=b$. Prove that, regardless of the ordering of the points on the grid, the matrix $A$ is symmetric and negative definite.

  (ii) Formulate the Jacobi method with relaxation for solving the above linear system.

  (iii) Prove that the iteration converges if the relaxation parameter $\omega$ is equal to $1 .$

  [You may quote without proof any relevant result about convergence of iterative methods.]

  comment

Partial Differential Equations

• Paper 1, Section II, A

  Partial Differential Equations | Part II, 2011

  Let $H=H(x, v), x, v \in \mathbb{R}^{n}$, be a smooth real-valued function which maps $\mathbb{R}^{2 n}$ into $\mathbb{R}$. Consider the initial value problem for the equation

  $$\begin{aligned} &f_{t}+\nabla_{v} H \cdot \nabla_{x} f-\nabla_{x} H \cdot \nabla_{v} f=0, \quad x, v \in \mathbb{R}^{n}, t>0 \\ &f(x, v, t=0)=f_{I}(x, v), \quad x, v \in \mathbb{R}^{n} \end{aligned}$$

  for the unknown function $f=f(x, v, t)$.

  (i) Use the method of characteristics to solve the initial value problem, locally in time.

  (ii) Let $f_{I} \geqslant 0$ on $\mathbb{R}^{2 n}$. Use the method of characteristics to prove that $f$ remains non-negative (as long as it exists).

  (iii) Let $F: \mathbb{R} \rightarrow \mathbb{R}$ be smooth. Prove that

  $$\int_{\mathbb{R}^{2 n}} F(f(x, v, t)) d x d v=\int_{\mathbb{R}^{2 n}} F\left(f_{I}(x, v)\right) d x d v$$

  as long as the solution exists.

  (iv) Let $H$ be independent of $x$, namely $H(x, v)=a(v)$, where $a$ is smooth and realvalued. Give the explicit solution of the initial value problem.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  Two individual angular momentum states $\left|j_{1}, m_{1}\right\rangle,\left|j_{2}, m_{2}\right\rangle$, acted on by $\mathbf{J}^{(1)}$ and $\mathbf{J}^{(2)}$ respectively, can be combined to form a combined state $|J, M\rangle$. What is the combined angular momentum operator $\mathbf{J}$ in terms of $\mathbf{J}^{(1)}$ and $\mathbf{J}^{(2)}$ ? [Units in which $\hbar=1$ are to be used throughout.]

  Defining raising and lowering operators $J_{\pm}^{(i)}$, where $i \in\{1,2\}$, find an expression for $\mathbf{J}^{2}$ in terms of $\mathbf{J}^{(i)^{2}}, J_{\pm}^{(i)}$ and $J_{3}^{(i)}$. Show that this implies

  $$\left[\mathbf{J}^{2}, J_{3}\right]=0$$

  Write down the state with $J=j_{1}+j_{2}$ and with $J_{3}$ eigenvalue $M=-j_{1}-j_{2}$ in terms of the individual angular momentum states. From this starting point, calculate the combined state with eigenvalues $J=j_{1}+j_{2}-1$ and $M=-j_{1}-j_{2}+1$ in terms of the individual angular momentum states.

  If $j_{1}=3$ and $j_{2}=1$ and the combined system is in the state $|3,-3\rangle$, what is the probability of measuring the $J_{3}^{(i)}$ eigenvalues of individual angular momentum states to be $-3$ and 0 , respectively?

  [You may assume without proof that standard angular momentum states $|j, m\rangle$ are joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, obeying

  $$J_{\pm}|j, m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j, m+1\rangle,$$

  and that

  $$\left.\left[J_{\pm}, J_{3}\right]=\pm J_{\pm} \cdot\right]$$

  comment

Principles of Statistics

• Paper 1, Section II, K

  Principles of Statistics | Part II, 2011

  Define admissible, Bayes, minimax decision rules.

  A random vector $X=\left(X_{1}, X_{2}, X_{3}\right)^{\mathrm{T}}$ has independent components, where $X_{i}$ has the normal distribution $\mathcal{N}\left(\theta_{i}, 1\right)$ when the parameter vector $\Theta$ takes the value $\theta=\left(\theta_{1}, \theta_{2}, \theta_{3}\right)^{\mathrm{T}}$. It is required to estimate $\Theta$ by a point $a \in \mathbb{R}^{3}$, with loss function $L(\theta, a)=\|a-\theta\|^{2}$. What is the risk function of the maximum-likelihood estimator $\widehat{\Theta}:=X ?$ Show that $\widehat{\Theta}$is dominated by the estimator $\widetilde{\Theta}:=\left(1-\|X\|^{-2}\right) X$.

  comment

Probability and Measure

• Paper 1, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2011

  (i) Let $(E, \mathcal{E}, \mu)$ be a measure space and let $1 \leqslant p<\infty$. For a measurable function $f$, let $\|f\|_{p}=\left(\int|f|^{p} d \mu\right)^{1 / p}$. Give the definition of the space $L^{p}$. Prove that $\left(L^{p},\|\cdot\|_{p}\right)$ forms a Banach space.

  [You may assume that $L^{p}$ is a normed vector space. You may also use in your proof any other result from the course provided that it is clearly stated.]

  (ii) Show that convergence in probability implies convergence in distribution.

  [Hint: Show the pointwise convergence of the characteristic function, using without proof the inequality $\left|e^{i y}-e^{i x}\right| \leqslant|x-y|$ for $x, y \in \mathbb{R}$.]

  (iii) Let $\left(\alpha_{j}\right)_{j \geqslant 1}$ be a given real-valued sequence such that $\sum_{j=1}^{\infty} \alpha_{j}^{2}=\sigma^{2}<\infty$. Let $\left(X_{j}\right)_{j \geqslant 1}$ be a sequence of independent standard Gaussian random variables defined on some probability space $(\Omega, \mathcal{F}, \mathbb{P})$. Let

  $$Y_{n}=\sum_{j=1}^{n} \alpha_{j} X_{j}$$

  Prove that there exists a random variable $Y$ such that $Y_{n} \rightarrow Y$ in $L^{2}$.

  (iv) Specify the distribution of the random variable $Y$ defined in part (iii), justifying carefully your answer.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2011

  Let $G$ be a finite group and $Z$ its centre. Suppose that $G$ has order $n$ and $Z$ has order $m$. Suppose that $\rho: G \rightarrow \mathrm{GL}(V)$ is a complex irreducible representation of degree $d .$

  (i) For $g \in Z$, show that $\rho(g)$ is a scalar multiple of the identity.

  (ii) Deduce that $d^{2} \leqslant n / m$.

  (iii) Show that, if $\rho$ is faithful, then $Z$ is cyclic.

  [Standard results may be quoted without proof, provided they are stated clearly.]

  Now let $G$ be a group of order 18 containing an elementary abelian subgroup $P$ of order 9 and an element $t$ of order 2 with $t x t^{-1}=x^{-1}$ for each $x \in P$. By considering the action of $P$ on an irreducible $\mathbb{C} G$-module prove that $G$ has no faithful irreducible complex representation.

  comment

Riemann Surfaces

• Paper 1, Section II, 23G

  Riemann Surfaces | Part II, 2011

  Suppose that $R_{1}$ and $R_{2}$ are Riemann surfaces, and $A$ is a discrete subset of $R_{1}$. For any continuous map $\alpha: R_{1} \rightarrow R_{2}$ which restricts to an analytic map of Riemann surfaces $R_{1} \backslash A \rightarrow R_{2}$, show that $\alpha$ is an analytic map.

  Suppose that $f$ is a non-constant analytic function on a Riemann surface $R$. Show that there is a discrete subset $A \subset R$ such that, for $P \in R \backslash A, f$ defines a local chart on some neighbourhood of $P$.

  Deduce that, if $\alpha: R_{1} \rightarrow R_{2}$ is a homeomorphism of Riemann surfaces and $f$ is a non-constant analytic function on $R_{2}$ for which the composite $f \circ \alpha$ is analytic on $R_{1}$, then $\alpha$ is a conformal equivalence. Give an example of a pair of Riemann surfaces which are homeomorphic but not conformally equivalent.

  [You may assume standard results for analytic functions on domains in the complex plane.]

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2011

  Let $Y_{1}, \ldots, Y_{n}$ be independent identically distributed random variables with model function $f(y, \theta), y \in \mathcal{Y}, \theta \in \Theta \subseteq \mathbb{R}$, and denote by $E_{\theta}$ and $\operatorname{Var}_{\theta}$ expectation and variance under $f(y, \theta)$, respectively. Define $U_{n}(\theta)=\sum_{i=1}^{n} \frac{\partial}{\partial \theta} \log f\left(Y_{i}, \theta\right)$. Prove that $E_{\theta} U_{n}(\theta)=0$. Show moreover that if $T=T\left(Y_{1}, \ldots, Y_{n}\right)$ is any unbiased estimator of $\theta$, then its variance satisfies $\operatorname{Var}_{\theta}(T) \geqslant\left(n \operatorname{Var}_{\theta}\left(U_{1}(\theta)\right)^{-1}\right.$. [You may use the Cauchy-Schwarz inequality without proof, and you may interchange differentiation and integration without justification if necessary.]

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2011

  The data consist of the record times in 1984 for 35 Scottish hill races. The columns list the record time in minutes, the distance in miles, and the total height gained during the route. The data are displayed in $R$ as follows (abbreviated):

  $\begin{array}{lrrr}\text { > hills } & & & \\ \text { Greenmantle } & 2.5 & 650 & 16.083 \\ \text { Carnethy } & 6.0 & 2500 & 48.350 \\ \text { Craig Dunain } & 6.0 & 900 & 33.650 \\ \text { Ben Rha } & 7.5 & 800 & 45.600 \\ \text { Ben Lomond } & 8.0 & 3070 & 62.267 \\ \text { [...] } & & & \\ \text { Cockleroi } & 4.5 & 850 & 28.100 \\ \text { Moffat Chase } & 20.0 & 5000 & 159.833\end{array}$

  Consider a simple linear regression of time on dist and climb. Write down this model mathematically, and explain any assumptions that you make. How would you instruct $R$ to fit this model and assign it to a variable hills. $\operatorname{lm} 1$ ?

  First, we test the hypothesis of no linear relationship to the variables dist and climb against the full model. $\mathrm{R}$ provides the following ANOVA summary:

  

  Using the information in this table, explain carefully how you would test this hypothesis. What do you conclude?

  The $\mathrm{R}$ command

  summary (hills. Im1)

  provides the following (slightly abbreviated) summary:

  

  Carefully explain the information that appears in each column of the table. What are your conclusions? In particular, how would you test for the significance of the variable climb in this model?

  

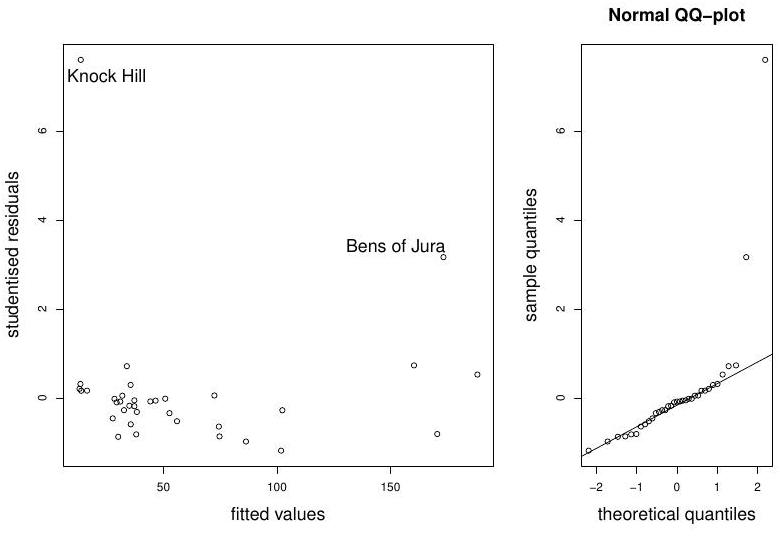
  Figure 1: Hills data: diagnostic plots

  Finally, we perform model diagnostics on the full model, by looking at studentised residuals versus fitted values, and the normal QQ-plot. The plots are displayed in Figure $1 .$ Comment on possible sources of model misspecification. Is it possible that the problem lies with the data? If so, what do you suggest?

  comment

Statistical Physics

• Paper 1, Section II, D

  Statistical Physics | Part II, 2011

  Describe the physical relevance of the microcanonical, canonical and grand canonical ensembles. Explain briefly the circumstances under which all ensembles are equivalent.

  The Gibbs entropy for a probability distribution $p(n)$ over states is

  $$S=-k_{B} \sum_{n} p(n) \log p(n) .$$

  By imposing suitable constraints on $p(n)$, show how maximising the entropy gives rise to the probability distributions for the microcanonical and canonical ensembles.

  A system consists of $N$ non-interacting particles fixed at points in a lattice. Each particle has three states with energies $E=-\epsilon, 0,+\epsilon$. If the system is at a fixed temperature $T$, determine the average energy $E$ and the heat capacity $C$. Evaluate each in the limits $T \rightarrow \infty$ and $T \rightarrow 0$.

  Describe a configuration of the system that would have negative temperature. Does this system obey the third law of thermodynamics?

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2011

  In a one-period market, there are $n$ assets whose prices at time $t$ are given by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$. The prices $S_{1}$ of the assets at time 1 have a $N(\mu, V)$ distribution, with non-singular covariance $V$, and the prices $S_{0}$ at time 0 are known constants. In addition, there is a bank account giving interest $r$, so that one unit of cash invested at time 0 will be worth $(1+r)$ units of cash at time 1 .

  An agent with initial wealth $w_{0}$ chooses a portfolio $\theta=\left(\theta^{1}, \ldots, \theta^{n}\right)$ of the assets to hold, leaving him with $x=w_{0}-\theta \cdot S_{0}$ in the bank account. His objective is to maximize his expected utility

  $$E\left(-\exp \left[-\gamma\left\{x(1+r)+\theta \cdot S_{1}\right\}\right]\right) \quad(\gamma>0)$$

  Find his optimal portfolio in each of the following three situations:

  (i) $\theta$ is unrestricted;

  (ii) no investment in the bank account is allowed: $x=0$;

  (iii) the initial holdings $x$ of cash must be non-negative.

  For the third problem, show that the optimal initial holdings of cash will be zero if and only if

  $$\frac{S_{0} \cdot(\gamma V)^{-1} \mu-w_{0}}{S_{0} \cdot(\gamma V)^{-1} S_{0}} \geqslant 1+r$$

  comment

Topics in Analysis

• Paper 1, Section I, F

  Topics in Analysis | Part II, 2011

  (i) State the Baire Category Theorem for metric spaces in its closed sets version.

  (ii) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a complex analytic function which is not a polynomial. Prove that there exists a point $z_{0} \in \mathbb{C}$ such that each coefficient of the Taylor series of $f$ at $z_{0}$ is non-zero.

  comment

Waves

• Paper 1, Section II, 39B

  Waves | Part II, 2011

  An inviscid fluid with sound speed $c_{0}$ occupies the region $0<y<\pi \alpha, 0<z<\pi \beta$ enclosed by the rigid boundaries of a rectangular waveguide. Starting with the acoustic wave equation, find the dispersion relation $\omega(k)$ for the propagation of sound waves in the $x$-direction.

  Hence find the phase speed $c(k)$ and the group velocity $c_{g}(k)$ of both the dispersive modes and the nondispersive mode, and sketch the form of the results for $k, \omega>0$.

  Define the time and cross-sectional average appropriate for a mode with frequency $\omega$. For each dispersive mode, show that the average kinetic energy is equal to the average compressive energy.

  A general multimode acoustic disturbance is created within the waveguide at $t=0$ in a region around $x=0$. Explain briefly how the amplitude of the disturbance varies with time as $t \rightarrow \infty$ at the moving position $x=V t$ for each of the cases $0<V<c_{0}$, $V=c_{0}$ and $V>c_{0}$. [You may quote without proof any generic results from the method of stationary phase.]

  comment