(i) By assuming the validity of the Fourier transform pair, prove the validity of the following transform pair:

$$\begin{gathered} \hat{q}(k)=\int_{0}^{\infty} e^{-i k x} q(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ q(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x} \hat{q}(k) d k+\frac{c}{2 \pi} \int_{L} e^{i k x} \hat{q}(-k) d k, \quad 0<x<\infty, \end{gathered}$$

where $c$ is an arbitrary complex constant and $L$ is the union of the two rays arg $k=\frac{\pi}{2}$ and $\arg k=0$ with the orientation shown in the figure below:

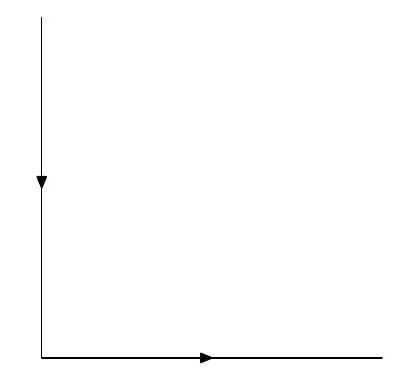
The contour $L$.

(ii) Verify that the partial differential equation

$$i q_{t}+q_{x x}=0, \quad 0<x<\infty, t>0,$$

can be rewritten in the following form:

$$\left(e^{-i k x+i k^{2} t} q\right)_{t}-\left[e^{-i k x+i k^{2} t}\left(-k q+i q_{x}\right)\right]_{x}=0, \quad k \in \mathbb{C} .$$

Consider equation (2) supplemented with the conditions

$$\begin{aligned} &q(x, 0)=q_{0}(x), \quad 0<x<\infty \\ &q(x, t) \text { vanishes sufficiently fast for all } t \text { as } x \rightarrow \infty \end{aligned}$$

By using equations (1a) and (3), show that

$$\hat{q}(k, t)=e^{-i k^{2} t} \hat{q}_{0}(k)+e^{-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)-i \tilde{g}_{1}\left(k^{2}, t\right)\right], \operatorname{Im} k \leqslant 0$$

where

$$\hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0$$

Part II, $2011 \quad$ List of Questions

[TURN OVER

$$\tilde{g}_{0}(k, t)=\int_{0}^{t} e^{i k \tau} q(0, \tau) d \tau, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{i k \tau} q_{x}(0, \tau) d \tau, k \in \mathbb{C}, t>0 .$$

Use (1b) to invert equation (5) and furthermore show that

$$\int_{-\infty}^{\infty} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k=\int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k, t>0, x>0$$

Hence determine the constant $c$ so that the solution of equation (2), with the conditions (4) and with the condition that either $q(0, t)$ or $q_{x}(0, t)$ is given, can be expressed in terms of an integral involving $\hat{q}_{0}(k)$ and either $\tilde{g}_{0}$ or $\tilde{g}_{1}$.