Part II, 2010, Paper 4

Algebraic Geometry

• Paper 4, Section II, G

  Algebraic Geometry | Part II, 2010

  Let $E \subseteq \mathbf{P}^{2}$ be the projective curve obtained from the affine curve $y^{2}=\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)\left(x-\lambda_{3}\right)$, where the $\lambda_{i}$ are distinct and $\lambda_{1} \lambda_{2} \lambda_{3} \neq 0$.

  (i) Show there is a unique point at infinity, $P_{\infty}$.

  (ii) Compute $\operatorname{div}(x), \operatorname{div}(y)$.

  (iii) Show $\mathcal{L}\left(P_{\infty}\right)=k$.

  (iv) Compute $l\left(n P_{\infty}\right)$ for all $n$.

  [You may not use the Riemann-Roch theorem.]

  comment

Algebraic Topology

• Paper 4, Section II, $\mathbf{2 1 H}$

  Algebraic Topology | Part II, 2010

  State the Snake Lemma. Explain how to define the boundary map which appears in it, and check that it is well-defined. Derive the Mayer-Vietoris sequence from the Snake Lemma.

  Given a chain complex $C$, let $A \subset C$ be the span of all elements in $C$ with grading greater than or equal to $n$, and let $B \subset C$ be the span of all elements in $C$ with grading less than $n$. Give a short exact sequence of chain complexes relating $A, B$, and $C$. What is the boundary map in the corresponding long exact sequence?

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, B

  Applications of Quantum Mechanics | Part II, 2010

  The scattering amplitude for electrons of momentum $\hbar \mathbf{k}$ incident on an atom located at the origin is $f(\hat{\mathbf{r}})$ where $\hat{\mathbf{r}}=\mathbf{r} / r$. Explain why, if the atom is displaced by a position vector a, the asymptotic form of the scattering wave function becomes

  $$\psi_{\mathbf{k}}(\mathbf{r}) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+e^{i \mathbf{k} \cdot \mathbf{a}} \frac{e^{i k r^{\prime}}}{r^{\prime}} f\left(\hat{\mathbf{r}}^{\prime}\right) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+e^{i\left(\mathbf{k}-\mathbf{k}^{\prime}\right) \cdot \mathbf{a}} \frac{e^{i k r}}{r} f(\hat{\mathbf{r}}),$$

  where $\mathbf{r}^{\prime}=\mathbf{r}-\mathbf{a}, r^{\prime}=\left|\mathbf{r}^{\prime}\right|, \hat{\mathbf{r}}^{\prime}=\mathbf{r}^{\prime} / r^{\prime}$ and $k=|\mathbf{k}|, \mathbf{k}^{\prime}=k \hat{\mathbf{r}}$. For electrons incident on $N$ atoms in a regular Bravais crystal lattice show that the differential cross-section for scattering in the direction $\hat{\mathbf{r}}$ is

  $$\frac{d \sigma}{d \Omega}=N|f(\hat{\mathbf{r}})|^{2} \Delta\left(\mathbf{k}-\mathbf{k}^{\prime}\right) .$$

  Derive an explicit form for $\Delta(\mathbf{Q})$ and show that it is strongly peaked when $\mathbf{Q} \approx \mathbf{b}$ for $\mathbf{b}$ a reciprocal lattice vector.

  State the Born approximation for $f(\hat{\mathbf{r}})$ when the scattering is due to a potential $V(\mathbf{r})$. Calculate the Born approximation for the case $V(\mathbf{r})=-a \delta(\mathbf{r}) .$

  Electrons with de Broglie wavelength $\lambda$ are incident on a target composed of many randomly oriented small crystals. They are found to be scattered strongly through an angle of $60^{\circ}$. What is the likely distance between planes of atoms in the crystal responsible for the scattering?

  comment

Applied Probability

• Paper 4, Section II, I

  Applied Probability | Part II, 2010

  (a) Let $\left(X_{t}\right)$ be an irreducible continuous-time Markov chain on a finite or countable state space. What does it mean to say that the chain is (i) transient, (ii) recurrent, (iii) positive recurrent, (iv) null recurrent? What is the relation between equilibrium distributions and properties (iii) and (iv)?

  A population of microorganisms develops in continuous time; the size of the population is a Markov chain $\left(X_{t}\right)$ with states $0,1,2, \ldots$ Suppose $X_{t}=n$. It is known that after a short time $s$, the probability that $X_{t}$ increased by one is $\lambda(n+1) s+o(s)$ and (if $n \geqslant 1$ ) the probability that the population was exterminated between times $t$ and $t+s$ and never revived by time $t+s$ is $\mu s+o(s)$. Here $\lambda$ and $\mu$ are given positive constants. All other changes in the value of $X_{t}$ have a combined probability $o(s)$.

  (b) Write down the Q-matrix of Markov chain $\left(X_{t}\right)$ and determine if $\left(X_{t}\right)$ is irreducible. Show that $\left(X_{t}\right)$ is non-explosive. Determine the jump chain.

  (c) Now assume that

  $$\mu=\lambda$$

  Determine whether the chain is transient or recurrent, and in the latter case whether it is positive or null recurrent. Answer the same questions for the jump chain. Justify your answers.

  comment

Asymptotic Methods

• Paper 4, Section II, C

  Asymptotic Methods | Part II, 2010

  (a) Consider for $\lambda>0$ the Laplace type integral

  $$I(\lambda)=\int_{a}^{b} f(t) \mathrm{e}^{-\lambda \phi(t)} d t$$

  for some finite $a, b \in \mathbb{R}$ and smooth, real-valued functions $f(t), \phi(t)$. Assume that the function $\phi(t)$ has a single minimum at $t=c$ with $a<c<b$. Give an account of Laplace's method for finding the leading order asymptotic behaviour of $I(\lambda)$ as $\lambda \rightarrow \infty$ and briefly discuss the difference if instead $c=a$ or $c=b$, i.e. when the minimum is attained at the boundary.

  (b) Determine the leading order asymptotic behaviour of

  $$I(\lambda)=\int_{-2}^{1} \cos t \mathrm{e}^{-\lambda t^{2}} d t$$

  as $\lambda \rightarrow \infty$

  (c) Determine also the leading order asymptotic behaviour when cos $t$ is replaced by $\sin t$ in $(*)$.

  comment

Classical Dynamics

• Paper 4, Section I, D

  Classical Dynamics | Part II, 2010

  A system with one degree of freedom has Lagrangian $L(q, \dot{q})$. Define the canonical momentum $p$ and the energy $E$. Show that $E$ is constant along any classical path.

  Consider a classical path $q_{c}(t)$ with the boundary-value data

  $$q_{c}(0)=q_{I}, \quad q_{c}(T)=q_{F}, \quad T>0$$

  Define the action $S_{c}\left(q_{I}, q_{F}, T\right)$ of the path. Show that the total derivative $d S_{c} / d T$ along the classical path obeys

  $$\frac{d S_{c}}{d T}=L$$

  Using Lagrange's equations, or otherwise, deduce that

  $$\frac{\partial S_{c}}{\partial q_{F}}=p_{F}, \quad \frac{\partial S_{c}}{\partial T}=-E,$$

  where $p_{F}$ is the final momentum.

  comment

• Paper 4, Section II, D

  Classical Dynamics | Part II, 2010

  A system is described by the Hamiltonian $H(q, p)$. Define the Poisson bracket $\{f, g\}$ of two functions $f(q, p, t), g(q, p, t)$, and show from Hamilton's equations that

  $$\frac{d f}{d t}=\{f, H\}+\frac{\partial f}{\partial t}$$

  Consider the Hamiltonian

  $$H=\frac{1}{2}\left(p^{2}+\omega^{2} q^{2}\right)$$

  and define

  $$a=(p-i \omega q) /(2 \omega)^{1 / 2}, \quad a^{*}=(p+i \omega q) /(2 \omega)^{1 / 2},$$

  where $i=\sqrt{-1}$. Evaluate $\{a, a\}$ and $\left\{a, a^{*}\right\}$, and show that $\{a, H\}=-i \omega a$ and $\left\{a^{*}, H\right\}=i \omega a^{*}$. Show further that, when $f(q, p, t)$ is regarded as a function of the independent complex variables $a, a^{*}$ and of $t$, one has

  $$\frac{d f}{d t}=i \omega\left(a^{*} \frac{\partial f}{\partial a^{*}}-a \frac{\partial f}{\partial a}\right)+\frac{\partial f}{\partial t}$$

  Deduce that both $\log a^{*}-i \omega t$ and $\log a+i \omega t$ are constant during the motion.

  comment

Coding and Cryptography

• Paper 4, Section I, H

  Coding and Cryptography | Part II, 2010

  What is the discrete logarithm problem?

  Describe the Diffie-Hellman key exchange system for two people. What is the connection with the discrete logarithm problem? Why might one use this scheme rather than just a public key system or a classical (pre-1960) coding system?

  Extend the Diffie-Hellman system to $n$ people using $n(n-1)$ transmitted numbers.

  comment

Cosmology

• Paper 4, Section I, D

  Cosmology | Part II, 2010

  The linearised equation for the growth of density perturbations, $\delta_{\mathbf{k}}$, in an isotropic and homogenous universe is

  $$\ddot{\delta}_{\mathbf{k}}+2 \frac{\dot{a}}{a} \dot{\delta}_{\mathbf{k}}+\left(\frac{c_{s}^{2} \mathbf{k}^{2}}{a^{2}}-4 \pi G \rho\right) \delta_{\mathbf{k}}=0$$

  where $\rho$ is the density of matter, $c_{s}$ the sound speed, $c_{s}^{2}=d P / d \rho$, and $\mathbf{k}$ is the comoving wavevector and $a(t)$ is the scale factor of the universe.

  What is the Jean's length? Discuss its significance for the growth of perturbations.

  Consider a universe filled with pressure-free matter with $a(t)=\left(t / t_{0}\right)^{2 / 3}$. Compute the resulting equation for the growth of density perturbations. Show that your equation has growing and decaying modes and comment briefly on the significance of this fact.

  comment

Differential Geometry

• Paper 4, Section II, H

  Differential Geometry | Part II, 2010

  (i) Let $S \subset \mathbb{R}^{3}$ be a regular surface. Define the notions exponential map, geodesic polar coordinates, geodesic circles.

  (ii) State and prove Gauss' lemma.

  (iii) Let $S$ be a regular surface. For fixed $r>0$, and points $p, q$ in $S$, let $S_{r}(p)$, $S_{r}(q)$ denote the geodesic circles around $p, q$, respectively, of radius $r$. Show the following statement: for each $p \in S$, there exists an $r=r(p)>0$ and a neighborhood $\mathcal{U}_{p}$ containing $p$ such that for all $q \in \mathcal{U}_{p}$, the sets $S_{r}(p)$ and $S_{r}(q)$ are smooth 1-dimensional manifolds which intersect transversally. What is the cardinality $\bmod 2$ of $S_{r}(p) \cap S_{r}(q)$ ?

  comment

Dynamical Systems

• Paper 4, Section I, D

  Dynamical Systems | Part II, 2010

  Consider the 2-dimensional flow

  $$\dot{x}=y+\frac{1}{4} x\left(1-2 x^{2}-2 y^{2}\right), \quad \dot{y}=-x+\frac{1}{2} y\left(1-x^{2}-y^{2}\right)$$

  Use the Poincaré-Bendixson theorem, which should be stated carefully, to obtain a domain $\mathcal{D}$ in the $x y$-plane, within which there is at least one periodic orbit.

  comment

• Paper 4, Section II, D

  Dynamical Systems | Part II, 2010

  Let $I=[0,1]$ and consider continuous maps $F: I \rightarrow I$. Give an informal outline description of the two different bifurcations of fixed points of $F$ that can occur.

  Illustrate your discussion by considering in detail the logistic map

  $$F(x)=\mu x(1-x),$$

  for $\mu \in(0,1+\sqrt{6}]$.

  Describe qualitatively what happens for $\mu \in(1+\sqrt{6}, 4]$.

  [You may assume without proof that

  $$x-F^{2}(x)=x(\mu x-\mu+1)\left(\mu^{2} x^{2}-\mu(\mu+1) x+\mu+1\right)$$

  comment

Electrodynamics

• Paper 4, Section II, B

  Electrodynamics | Part II, 2010

  In a superconductor the number density of charge carriers of charge $q$ is $n_{s}$. Suppose that there is a time-independent magnetic field described by the three-vector potential $\mathbf{A} .$

  Derive an expression for the superconducting current.

  Explain how your answer is gauge invariant.

  Suppose that for $z<0$ there is a constant magnetic field $\mathbf{B}_{0}$ in a vacuum and, for $z>0$, there is a uniform superconductor. Derive the magnetic field for $z>0$.

  comment

Fluid Dynamics II

• Paper 4, Section II, A

  Fluid Dynamics II | Part II, 2010

  An axisymmetric incompressible Stokes flow has the Stokes stream function $\Psi(R, \theta)$ in spherical polar coordinates $(R, \theta, \phi)$. Give expressions for the components $u_{R}, u_{\theta}$ of the flow field in terms of $\Psi$. Show that the equation satisfied by $\Psi$ is

  $$\mathcal{D}^{2}\left(\mathcal{D}^{2} \Psi\right)=0, \quad \text { where } \quad \mathcal{D}^{2}=\frac{\partial^{2}}{\partial R^{2}}+\frac{\sin \theta}{R^{2}} \frac{\partial}{\partial \theta}\left(\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\right)$$

  Fluid is contained between the two spheres $R=a, R=b$, with $b \gg a$. The fluid velocity vanishes on the outer sphere, while on the inner sphere $u_{R}=U \cos \theta, u_{\theta}=0$. It is assumed that Stokes flow applies.

  (i) Show that the Stokes stream function,

  $$\Psi(R, \theta)=a^{2} U \sin ^{2} \theta\left(A\left(\frac{a}{R}\right)+B\left(\frac{R}{a}\right)+C\left(\frac{R}{a}\right)^{2}+D\left(\frac{R}{a}\right)^{4}\right)$$

  is the general solution of $(*)$ proportional to $\sin ^{2} \theta$ and write down the conditions on $A, B, C, D$ that allow all the boundary conditions to be satisfied.

  (ii) Now let $b \rightarrow \infty$, with $|\mathbf{u}| \rightarrow 0$ as $R \rightarrow \infty$. Show that $A=B=1 / 4$ with $C=D=0$.

  (iii) Show that when $b / a$ is very large but finite, then the coefficients have the approximate form

  $$C \approx-\frac{3}{8} \frac{a}{b}, \quad D \approx \frac{1}{8} \frac{a^{3}}{b^{3}}, \quad A \approx \frac{1}{4}-\frac{3}{16} \frac{a}{b}, \quad B \approx \frac{1}{4}+\frac{9}{16} \frac{a}{b}$$

  comment

Further Complex Methods

• Paper 4, Section $I$, E

  Further Complex Methods | Part II, 2010

  The hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

  $$F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  for appropriate restrictions on $c, b, z$.

  Express the following integral in terms of a combination of hypergeometric functions

  $$I(u, A)=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{e^{i t(u+1)}}{e^{i t}+i A} d t, \quad|A|>1$$

  [You may use without proof that $\Gamma(z+1)=z \Gamma(z) .$ ]

  comment

Galois Theory

• Paper 4, Section II, H

  Galois Theory | Part II, 2010

  Let $K$ be a field of characteristic $\neq 2,3$, and assume that $K$ contains a primitive cubic root of unity $\zeta$. Let $P \in K[X]$ be an irreducible cubic polynomial, and let $\alpha, \beta, \gamma$ be its roots in the splitting field $F$ of $P$ over $K$. Recall that the Lagrange resolvent $x$ of $P$ is defined as $x=\alpha+\zeta \beta+\zeta^{2} \gamma$.

  (i) List the possibilities for the group $\operatorname{Gal}(F / K)$, and write out the set $\{\sigma(x) \mid \sigma \in \operatorname{Gal}(F / K)\}$ in each case.

  (ii) Let $y=\alpha+\zeta \gamma+\zeta^{2} \beta$. Explain why $x^{3}, y^{3}$ must be roots of a quadratic polynomial in $K[X]$. Compute this polynomial for $P=X^{3}+b X+c$, and deduce the criterion to identify $\operatorname{Gal}(F / K)$ through the element $-4 b^{3}-27 c^{2}$ of $K$.

  comment

General Relativity

• Paper 4, Section II, B

  General Relativity | Part II, 2010

  The Schwarzschild line element is given by

  $$d s^{2}=-F d t^{2}+F^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where $F=1-r_{s} / r$ and $r_{s}$ is the Schwarzschild radius. Obtain the equation of geodesic motion of photons moving in the equatorial plane, $\theta=\pi / 2$, in the form

  $$\left(\frac{d r}{d \tau}\right)^{2}=E^{2}-\frac{h^{2} F}{r^{2}}$$

  where $\tau$ is proper time, and $E$ and $h$ are constants whose physical significance should be indicated briefly.

  Defining $u=1 / r$ show that light rays are determined by

  $$\left(\frac{d u}{d \phi}\right)^{2}=\left(\frac{1}{b}\right)^{2}-u^{2}+r_{s} u^{3}$$

  where $b=h / E$ and $r_{s}$ may be taken to be small. Show that, to zeroth order in $r_{s}$, a light ray is a straight line passing at distance $b$ from the origin. Show that, to first order in $r_{s}$, the light ray is deflected through an angle $2 r_{s} / b$. Comment briefly on some observational evidence for the result.

  comment

Geometry of Group Actions

• Paper 4, Section I, F

  Geometry of Group Actions | Part II, 2010

  Define loxodromic transformations and explain how to determine when a Möbius transformation

  $$T: z \mapsto \frac{a z+b}{c z+d} \quad \text { with } \quad a d-b c=1$$

  is loxodromic.

  Show that any Möbius transformation that maps a disc $\Delta$ onto itself cannot be loxodromic.

  comment

• Paper 4, Section II, F

  Geometry of Group Actions | Part II, 2010

  Explain briefly how Möbius transformations of the Riemann sphere are extended to give isometries of the unit ball $B^{3} \subset \mathbb{R}^{3}$ for the hyperbolic metric.

  Which Möbius transformations have extensions that fix the origin in $B^{3}$ ?

  For which Möbius transformations $T$ can we find a hyperbolic line in $B^{3}$ that $T$ maps onto itself? For which of these Möbius transformations is there only one such hyperbolic line?

  comment

Graph Theory

• Paper 4, Section II, F

  Graph Theory | Part II, 2010

  State Euler's formula relating the number of vertices, edges and faces in a drawing of a connected planar graph. Deduce that every planar graph has chromatic number at most $5 .$

  Show also that any triangle-free planar graph has chromatic number at most 4 .

  Suppose $G$ is a planar graph which is minimal 5 -chromatic; that is to say, $\chi(G)=5$ but if $H$ is a subgraph of $G$ with $H \neq G$ then $\chi(H)<5$. Prove that $\delta(G) \geqslant 5$. Does this remain true if we drop the assumption that $G$ is planar? Justify your answer.

  [The Four Colour Theorem may not be assumed.]

  comment

Linear Analysis

• Paper 4, Section II, H

  Linear Analysis | Part II, 2010

  Let $X$ be a Banach space.

  a) What does it mean for a bounded linear map $T: X \rightarrow X$ to be compact?

  b) Let $\mathcal{B}(X)$ be the Banach space of all bounded linear maps $S: X \rightarrow X$. Let $\mathcal{B}_{0}(X)$ be the subset of $\mathcal{B}(X)$ consisting of all compact operators. Show that $\mathcal{B}_{0}(X)$ is a closed subspace of $\mathcal{B}(X)$. Show that, if $S \in \mathcal{B}(X)$ and $T \in \mathcal{B}_{0}(X)$, then $S T, T S \in \mathcal{B}_{0}(X)$.

  c) Let

  $$X=\ell^{2}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{j} \in \mathbb{C} \quad \text { and } \quad\|x\|_{2}^{2}=\sum_{j=1}^{\infty}\left|x_{j}\right|^{2}<\infty\right\}$$

  and $T: X \rightarrow X$ be defined by

  $$(T x)_{k}=\frac{x_{k+1}}{k+1} .$$

  Is $T$ compact? What is the spectrum of $T ?$ Explain your answers.

  comment

Logic and Set Theory

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2010

  State and prove the Completeness Theorem for Propositional Logic.

  [You do not need to give definitions of the various terms involved. You may assume that the set of primitive propositions is countable. You may also assume the Deduction Theorem.]

  Explain briefly how your proof should be modified if the set of primitive propositions is allowed to be uncountable.

  comment

Mathematical Biology

• Paper 4, Section I, A

  Mathematical Biology | Part II, 2010

  A concentration $u(x, t)$ obeys the differential equation

  $$\frac{\partial u}{\partial t}=D u_{x x}+f(u)$$

  in the domain $0 \leqslant x \leqslant L$, with boundary conditions $u(0, t)=u(L, t)=0$ and initial condition $u(x, 0)=u_{0}(x)$, and where $D$ is a positive constant. Assume $f(0)=0$ and $f^{\prime}(0)>0$. Linearising the dynamics around $u=0$, and representing $u(x, t)$ as a suitable Fourier expansion, show that the condition for the linear stability of $u=0$ can be expressed as the following condition on the domain length

  $$L<\pi\left[\frac{D}{f^{\prime}(0)}\right]^{1 / 2}$$

  comment

Number Fields

• Paper 4, Section II, G

  Number Fields | Part II, 2010

  Suppose that $\alpha$ is a zero of $x^{3}-x+3$ and that $K=\mathbb{Q}(\alpha)$. Show that $[K: \mathbb{Q}]=3$. Show that $O_{K}$, the ring of integers in $K$, is $O_{K}=\mathbb{Z}[\alpha]$.

  [You may quote any general theorem that you wish, provided that you state it clearly. Note that the discriminant of $x^{3}+p x+q$ is $-4 p^{3}-27 q^{2}$.]

  comment

Number Theory

• Paper 4, Section I, G

  Number Theory | Part II, 2010

  Let $p$ be a prime number, and put

  $$a_{k}=k p, \quad N_{k}=a_{k}^{p}-1 \quad(k=1,2, \ldots)$$

  Prove that $a_{k}$ has exact order $p$ modulo $N_{k}$ for all $k \geqslant 1$, and deduce that $N_{k}$ must be divisible by a prime $q$ with $q \equiv 1 \quad(\bmod p)$. By making a suitable choice of $k$, prove that there are infinitely many primes $q$ with $q \equiv 1 \quad(\bmod p)$.

  comment

• Paper 4, Section II, G

  Number Theory | Part II, 2010

  Let $\mathcal{S}$ be the set of all positive definite binary quadratic forms with integer coefficients. Define the action of the group $S L_{2}(\mathbb{Z})$ on $\mathcal{S}$, and prove that equivalent forms under this action have the same discriminant.

  Find necessary and sufficient conditions for an odd positive integer $n$, prime to 35 , to be properly represented by at least one of the two forms

  $$x^{2}+x y+9 y^{2}, \quad 3 x^{2}+x y+3 y^{2}$$

  comment

Numerical Analysis

• Paper 4, Section II, A

  Numerical Analysis | Part II, 2010

  An $s$-stage explicit Runge-Kutta method of order $p$, with constant step size $h>0$, is applied to the differential equation $y^{\prime}=\lambda y, t \geqslant 0$.

  (a) Prove that

  $$y_{n+1}=P_{s}(\lambda h) y_{n}$$

  where $P_{s}$ is a polynomial of degree $s$.

  (b) Prove that the order $p$ of any $s$-stage explicit Runge-Kutta method satisfies the inequality $p \leqslant s$ and, for $p=s$, write down an explicit expression for $P_{s}$.

  (c) Prove that no explicit Runge-Kutta method can be A-stable.

  comment

Optimization and Control

• Paper 4, Section II, J

  Optimization and Control | Part II, 2010

  Dr Seuss' wealth $x_{t}$ at time $t$ evolves as

  $$\frac{d x}{d t}=r x_{t}+\ell_{t}-c_{t}$$

  where $r>0$ is the rate of interest earned, $\ell_{t}$ is his intensity of working $(0 \leqslant \ell \leqslant 1)$, and $c_{t}$ is his rate of consumption. His initial wealth $x_{0}>0$ is given, and his objective is to maximize

  $$\int_{0}^{T} U\left(c_{t}, \ell_{t}\right) d t$$

  where $U(c, \ell)=c^{\alpha}(1-\ell)^{\beta}$, and $T$ is the (fixed) time his contract expires. The constants $\alpha$ and $\beta$ satisfy the inequalities $0<\alpha<1,0<\beta<1$, and $\alpha+\beta>1$. At all times, $c_{t}$ must be non-negative, and his final wealth $x_{T}$ must be non-negative. Establish the following properties of the optimal solution $\left(x^{*}, c^{*}, \ell^{*}\right)$ :

  (i) $\beta c_{t}^{*}=\alpha\left(1-\ell_{t}^{*}\right)$;

  (ii) $c_{t}^{*} \propto e^{-\gamma r t}$, where $\gamma \equiv(\beta-1+\alpha)^{-1}$;

  (iii) $x_{t}^{*}=A e^{r t}+B e^{-\gamma r t}-r^{-1}$ for some constants $A$ and $B$.

  Hence deduce that the optimal wealth is

  $$x_{t}^{*}=\frac{\left(1-e^{-\gamma r T}\left(1+r x_{0}\right)\right) e^{r t}+\left(\left(1+r x_{0}\right) e^{r T}-1\right) e^{-\gamma r t}}{r\left(e^{r T}-e^{-\gamma r T}\right)}-\frac{1}{r}$$

  comment

Partial Differential Equations

• Paper 4, Section II, 30E

  Partial Differential Equations | Part II, 2010

  a) Solve the Dirichlet problem for the Laplace equation in a disc in $\mathbb{R}^{2}$

  $$\begin{aligned} \Delta u &=0 \quad \text { in } \quad G=\left\{x^{2}+y^{2}<R^{2}\right\} \subseteq \mathbb{R}^{2}, R>0 \\ u &=u_{D} \quad \text { on } \quad \partial G \end{aligned}$$

  using polar coordinates $(r, \varphi)$ and separation of variables, $u(x, y)=R(r) \Theta(\varphi)$. Then use the ansatz $R(r)=r^{\alpha}$ for the radial function.

  b) Solve the Dirichlet problem for the Laplace equation in a square in $\mathbb{R}^{2}$

  $$\begin{aligned} &\Delta u=0 \quad \text { in } \quad G=[0, a] \times[0, a] \\ &u(x, 0)=f_{1}(x), \quad u(x, a)=f_{2}(x), \quad u(0, y)=f_{3}(y), \quad u(a, y)=f_{4}(y) \end{aligned}$$

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, C

  Principles of Quantum Mechanics | Part II, 2010

  The Hamiltonian for a quantum system in the Schrödinger picture is

  $$H_{0}+V(t)$$

  where $H_{0}$ is independent of time. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Let $|a\rangle$ and $|b\rangle$ be orthonormal eigenstates of $H_{0}$ with eigenvalues $E_{a}$ and $E_{b}$ respectively. Assume $V(t)=0$ for $t \leqslant 0$. Show that if the system is initially, at $t=0$, in the state $|a\rangle$ then the probability of measuring it to be the state $|b\rangle$ after a time $t$ is

  $$\frac{1}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle b\left|V\left(t^{\prime}\right)\right| a\right\rangle e^{i\left(E_{b}-E_{a}\right) t^{\prime} / \hbar}\right|^{2}$$

  to order $V(t)^{2}$.

  Suppose a system has a basis of just two orthonormal states $|1\rangle$ and $|2\rangle$, with respect to which

  $$H_{0}=E I, \quad V(t)=v t \sigma_{1}, \quad t \geqslant 0,$$

  where

  $$I=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right), \quad \sigma_{1}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)$$

  Use $(*)$ to calculate the probability of a transition from state $|1\rangle$ to state $|2\rangle$ after a time $t$ to order $v^{2}$.

  Show that the time dependent Schrödinger equation has a solution

  $$|\psi(t)\rangle=\exp \left(-\frac{i}{\hbar}\left(E t I+\frac{1}{2} v t^{2} \sigma_{1}\right)\right)|\psi(0)\rangle$$

  Calculate the transition probability exactly. Hence find the condition for the order $v^{2}$ approximation to be valid.

  comment

Principles of Statistics

• Paper 4, Section II, $\mathbf{2 7 J}$

  Principles of Statistics | Part II, 2010

  Define completeness and bounded completeness of a statistic $T$ in a statistical experiment.

  Random variables $X_{1}, X_{2}, X_{3}$ are generated as $X_{i}=\Theta^{1 / 2} Z+(1-\Theta)^{1 / 2} Y_{i}$, where $Z, Y_{1}, Y_{2}, Y_{3}$ are independently standard normal $\mathcal{N}(0,1)$, and the parameter $\Theta$ takes values in $(0,1)$. What is the joint distribution of $\left(X_{1}, X_{2}, X_{3}\right)$ when $\Theta=\theta$ ? Write down its density function, and show that a minimal sufficient statistic for $\Theta$ based on $\left(X_{1}, X_{2}, X_{3}\right)$ is $T=\left(T_{1}, T_{2}\right):=\left(\sum_{i=1}^{3} X_{i}^{2},\left(\sum_{i=1}^{3} X_{i}\right)^{2}\right)$.

  [Hint: You may use that if $I$ is the $n \times n$ identity matrix and $J$ is the $n \times n$ matrix all of whose entries are 1 , then $a I+b J$ has determinant $a^{n-1}(a+n b)$, and inverse $c I+d J$ with $c=1 / a, d=-b /(a(a+n b))$.]

  What is $\mathbb{E}_{\theta}\left(T_{1}\right) ?$ Is $T$ complete for $\Theta ?$

  Let $S:=\operatorname{Prob}\left(X_{1}^{2} \leqslant 1 \mid T\right)$. Show that $\mathbb{E}_{\theta}(S)$ is a positive constant $c$ which does not depend on $\theta$, but that $S$ is not identically equal to $c$. Is $T$ boundedly complete for $\Theta$ ?

  comment

Probability and Measure

• Paper 4, Section II, I

  Probability and Measure | Part II, 2010

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent normal random variables having mean 0 and variance 1 . Set $S_{n}=X_{1}+\ldots+X_{n}$ and $U_{n}=S_{n}-\left\lfloor S_{n}\right\rfloor$. Thus $U_{n}$ is the fractional part of $S_{n}$. Show that $U_{n}$ converges to $U$ in distribution, as $n \rightarrow \infty$ where $U$ is uniformly distributed on $[0,1]$.

  comment

Representation Theory

• Paper 4, Section II, F

  Representation Theory | Part II, 2010

  Define the circle group $U(1)$. Give a complete list of the irreducible representations of $U(1)$

  Define the spin group $G=S U(2)$, and explain briefly why it is homeomorphic to the unit 3-sphere in $\mathbb{R}^{4}$. Identify the conjugacy classes of $G$ and describe the classification of the irreducible representations of $G$. Identify the characters afforded by the irreducible representations. You need not give detailed proofs but you should define all the terms you use.

  Let $G$ act on the space $\mathrm{M}_{3}(\mathbb{C})$ of $3 \times 3$ complex matrices by conjugation, where $A \in S U(2)$ acts by

  $$A: M \mapsto A_{1} M A_{1}^{-1}$$

  in which $A_{1}$ denotes the $3 \times 3$ block diagonal matrix $\left(\begin{array}{cc}A & 0 \\ 0 & 1\end{array}\right)$. Show that this gives a representation of $G$ and decompose it into irreducibles.

  comment

Statistical Modelling

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2010

  Below is a simplified 1993 dataset of US cars. The columns list index, make, model, price (in $\$ 1000)$, miles per gallon, number of passengers, length and width in inches, and weight (in pounds). The data are displayed in $R$ as follows (abbreviated):

  

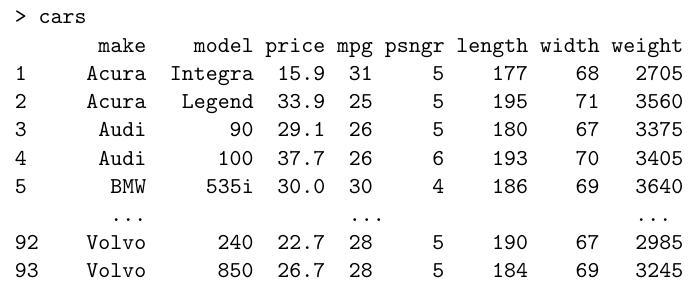
  It is reasonable to assume that prices for different makes of car are independent. We model the logarithm of the price as a linear combination of the other quantitative properties of the cars and an error term. Write down this model mathematically. How would you instruct $R$ to fit this model and assign it to a variable "fit"?

  $R$ provides the following (slightly abbreviated) summary:

  

  Briefly explain the information that is being provided in each column of the table. What are your conclusions and how would you try to improve the model?

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2010

  Every day, Barney the darts player comes to our laboratory. We record his facial expression, which can be either "mad", "weird" or "relaxed", as well as how many units of beer he has drunk that day. Each day he tries a hundred times to hit the bull's-eye, and we write down how often he succeeds. The data look like this:

  \begin{tabular}{rrrr} \multicolumn{1}{l}{} & & & \ Day & Beer & Expression & BullsEye \ 1 & 3 & Mad & 30 \ 2 & 3 & Mad & 32 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 60 & 2 & Mad & 37 \ 61 & 4 & Weird & 30 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 110 & 4 & Weird & 28 \ 111 & 2 & Relaxed & 35 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 150 & 3 & Relaxed & 31 \end{tabular}

  Write down a reasonable model for $Y_{1}, \ldots, Y_{n}$, where $n=150$ and where $Y_{i}$ is the number of times Barney has hit bull's-eye on the $i$ th day. Explain briefly why we may wish initially to include interactions between the variables. Write the $\mathrm{R}$ code to fit your model.

  The scientist of the above story fitted her own generalized linear model, and subsequently obtained the following summary (abbreviated):

  

  Why are ExpressionMad and Beer:ExpressionMad not listed? Suppose on a particular day, Barney's facial expression is weird, and he drank three units of beer. Give the linear predictor in the scientist's model for this day.

  Based on the summary, how could you improve your model? How could one fit this new model in $R$ (without modifying the data file)?

  comment

Statistical Physics

• Paper 4, Section II, C

  Statistical Physics | Part II, 2010

  (i) Let $\rho_{i}$ be the probability that a system is in a state labelled by $i$ with $N_{i}$ particles and energy $E_{i}$. Define

  $$s\left(\rho_{i}\right)=-k \sum_{i} \rho_{i} \log \rho_{i} .$$

  $s\left(\rho_{i}\right)$ has a maximum, consistent with a fixed mean total number of particles $N$, mean total energy $E$ and $\sum_{i} \rho_{i}=1$, when $\rho_{i}=\bar{\rho}_{i}$. Let $S(E, N)=s\left(\bar{\rho}_{i}\right)$ and show that

  $$\frac{\partial S}{\partial E}=\frac{1}{T}, \quad \frac{\partial S}{\partial N}=-\frac{\mu}{T},$$

  where $T$ may be identified with the temperature and $\mu$ with the chemical potential.

  (ii) For two weakly coupled systems 1,2 then $\rho_{i, j}=\rho_{1, i} \rho_{2, j}$ and $E_{i, j}=E_{1, i}+E_{2, j}$, $N_{i, j}=N_{1, i}+N_{2, j}$. Show that $S(E, N)=S_{1}\left(E_{1}, N_{1}\right)+S_{2}\left(E_{2}, N_{2}\right)$ where, if $S(E, N)$ is stationary under variations in $E_{1}, E_{2}$ and $N_{1}, N_{2}$ for $E=E_{1}+E_{2}, N=N_{1}+N_{2}$ fixed, we must have $T_{1}=T_{2}, \mu_{1}=\mu_{2}$.

  (iii) Define the grand partition function $\mathcal{Z}(T, \mu)$ for the system in (i) and show that

  $$k \log \mathcal{Z}=S-\frac{1}{T} E+\frac{\mu}{T} N, \quad S=\frac{\partial}{\partial T}(k T \log \mathcal{Z})$$

  (iv) For a system with single particle energy levels $\epsilon_{r}$ the possible states are labelled by $i=\left\{n_{r}: n_{r}=0,1\right\}$, where $N_{i}=\sum_{r} n_{r}, E_{i}=\sum_{r} n_{r} \epsilon_{r}$ and $\sum_{i}=\prod_{r} \sum_{n_{r}=0,1}$. Show that

  $$\bar{\rho}_{i}=\prod_{r} \frac{e^{-n_{r}\left(\epsilon_{r}-\mu\right) / k T}}{1+e^{-\left(\epsilon_{r}-\mu\right) / k T}} .$$

  Calculate $\bar{n}_{r}$. How is this related to a free fermion gas?

  comment

Stochastic Financial Models

• Paper 4, Section II, I

  Stochastic Financial Models | Part II, 2010

  Consider a market with no riskless asset and $d$ risky stocks where the price of stock $i \in\{1, \ldots, d\}$ at time $t \in\{0,1\}$ is denoted $S_{t}^{i}$. We assume the vector $S_{0} \in \mathbb{R}^{d}$ is not random, and we let $\mu=\mathbb{E} S_{1}$ and $V=\mathbb{E}\left[\left(S_{1}-\mu\right)\left(S_{1}-\mu\right)^{T}\right]$. Assume $V$ is not singular.

  Suppose an investor has initial wealth $X_{0}=x$, which he invests in the $d$ stocks so that his wealth at time 1 is $X_{1}=\pi^{T} S_{1}$ for some $\pi \in \mathbb{R}^{d}$. He seeks to minimize the $\operatorname{var}\left(X_{1}\right)$ subject to his budget constraint and the condition that $\mathbb{E} X_{1}=m$ for a given constant $m \in \mathbb{R}$.

  Illustrate this investor's problem by drawing a diagram of the mean-variance efficient frontier. Write down the Lagrangian for the problem. Show that there are two vectors $\pi_{A}$ and $\pi_{B}$ (which do not depend on the constants $x$ and $m$ ) such that the investor's optimal portfolio is a linear combination of $\pi_{A}$ and $\pi_{B}$.

  Another investor with initial wealth $Y_{0}=y$ seeks to maximize $\mathbb{E} U\left(Y_{1}\right)$ his expected utility of time 1 wealth, subject to his budget constraint. Assuming that $S_{1}$ is Gaussian and $U(w)=-e^{-\gamma w}$ for a constant $\gamma>0$, show that the optimal portfolio in this case is also a linear combination of $\pi_{A}$ and $\pi_{B}$.

  [You may use the moment generating function of the Gaussian distribution without derivation.]

  Continue to assume $S_{1}$ is Gaussian, but now assume that $U$ is increasing, concave, and twice differentiable, and that $U, U^{\prime}$ and $U^{\prime \prime}$ are of exponential growth but not necessarily of the form $U(w)=-e^{-\gamma w}$. (Recall that a function $f$ is of exponential growth if $|f(w)| \leqslant a e^{b|w|}$ for some constants positive constants $a, b$.) Prove that the utility maximizing investor still holds a linear combination of $\pi_{A}$ and $\pi_{B}$.

  [You may use the Gaussian integration by parts formula

  $$\mathbb{E}[\nabla f(Z)]=\mathbb{E}[Z f(Z)]$$

  where $Z=\left(Z_{1}, \ldots, Z_{d}\right)^{T}$ is a vector of independent standard normal random variables, and $f$ is differentiable and of exponential growth. You may also interchange integration and differentiation without justification.]

  comment

Topics in Analysis

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2010

  Find explicitly a polynomial $p$ of degree $\leqslant 3$ such that

  $$\sup _{x \in[-1,1]}\left|x^{4}-p(x)\right| \leqslant \sup _{x \in[-1,1]}\left|x^{4}-q(x)\right|$$

  for every polynomial $q$ of degree $\leqslant 3$. Justify your answer.

  comment

Waves

• Paper 4, Section II, A

  Waves | Part II, 2010

  Starting from the equations for one-dimensional unsteady flow of an inviscid compressible fluid, show that it is possible to find Riemann invariants $u \pm Q$ that are constant on characteristics $C_{\pm}$given by

  $$\frac{d x}{d t}=u \pm c$$

  where $u(x, t)$ is the velocity of the fluid and $c(x, t)$ is the local speed of sound. Show that $Q=2\left(c-c_{0}\right) /(\gamma-1)$ for the case of a perfect gas with adiabatic equation of state $p=p_{0}\left(\rho / \rho_{0}\right)^{\gamma}$, where $p_{0}, \rho_{0}$ and $\gamma$ are constants, $\gamma>1$ and $c=c_{0}$ when $\rho=\rho_{0}$.

  Such a gas initially occupies the region $x>0$ to the right of a piston in an infinitely long tube. The gas is initially uniform and at rest with density $\rho_{0}$. At $t=0$ the piston starts moving to the left at a constant speed $V$. Assuming that the gas keeps up with the piston, find $u(x, t)$ and $c(x, t)$ in each of the three distinct regions that are defined by families of $C_{+}$characteristics.

  Now assume that the gas does not keep up with the piston. Show that the gas particle at $x=x_{0}$ when $t=0$ follows a trajectory given, for $t>x_{0} / c_{0}$, by

  $$x(t)=\frac{\gamma+1}{\gamma-1}\left(\frac{c_{0} t}{x_{0}}\right)^{2 /(\gamma+1)} x_{0}-\frac{2 c_{0} t}{\gamma-1}$$

  Deduce that the velocity of any given particle tends to $-2 c_{0} /(\gamma-1)$ as $t \rightarrow \infty$.

  comment