Cars looking for a parking space are directed to one of three unlimited parking lots A, B and C. First, immediately after the entrance, the road forks: one direction is to lot A, the other to B and C. Shortly afterwards, the latter forks again, between B and C. See the diagram below.

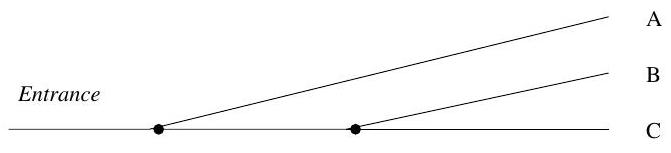
The policeman at the first road fork directs an entering car with probability $1 / 3$ to A and with probability $2 / 3$ to the second fork. The policeman at the second fork sends the passing cars to $\mathrm{B}$ or $\mathrm{C}$ alternately: cars $1,3,5, \ldots$ approaching the second fork go to $\mathrm{B}$ and cars $2,4,6, \ldots$ to $\mathrm{C}$.

Assuming that the total arrival process $(N(t))$ of cars is Poisson of rate $\lambda$, consider the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right), t \geqslant 0$, where $X^{i}(t)$ is the number of cars directed to lot $i$ by time $t$, for $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$. The times for a car to travel from the first to the second fork, or from a fork to the parking lot, are all negligible.

(a) Characterise each of the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right)$, by specifying if it is (i) Poisson, (ii) renewal or (iii) delayed renewal. Correspondingly, specify the rate, the holding-time distribution and the distribution of the delay.

(b) In the case of a renewal process, determine the equilibrium delay distribution.

(c) Given $s, t>0$, write down explicit expressions for the probability $\mathbb{P}\left(X^{i}(s)=X^{i}(s+t)\right)$ that the interval $(s, t+s)$ is free of points in the corresponding process, $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$.