Part II, 2009, Paper 4

Algebraic Geometry

• Paper 4, Section II, G

  Algebraic Geometry | Part II, 2009

  State the Riemann-Roch theorem for a smooth projective curve $V$, and use it to outline a proof of the Riemann-Hurwitz formula for a non-constant morphism between projective nonsingular curves in characteristic zero.

  Let $V \subset \mathbb{P}^{2}$ be a smooth projective plane cubic over an algebraically closed field $k$ of characteristic zero, written in normal form $X_{0} X_{2}^{2}=F\left(X_{0}, X_{1}\right)$ for a homogeneous cubic polynomial $F$, and let $P_{0}=(0: 0: 1)$ be the point at infinity. Taking the group law on $V$ for which $P_{0}$ is the identity element, let $P \in V$ be a point of order 3 . Show that there exists a linear form $H \in k\left[X_{0}, X_{1}, X_{2}\right]$ such that $V \cap V(H)=\{P\}$.

  Let $H_{1}, H_{2} \in k\left[X_{0}, X_{1}, X_{2}\right]$ be nonzero linear forms. Suppose the lines $\left\{H_{i}=0\right\}$ are distinct, do not meet at a point of $V$, and are nowhere tangent to $V$. Let $W \subset \mathbb{P}^{3}$ be given by the vanishing of the polynomials

  $$X_{0} X_{2}^{2}-F\left(X_{0}, X_{1}\right), \quad X_{3}^{2}-H_{1}\left(X_{0}, X_{1}, X_{2}\right) H_{2}\left(X_{0}, X_{1}, X_{2}\right)$$

  Show that $W$ has genus 4 . [You may assume without proof that $W$ is an irreducible smooth curve.]

  comment

Algebraic Topology

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the subset of $\mathbb{R}^{4}$ given by $X=A \cup B \cup C \subset \mathbb{R}^{4}$, where $A, B$ and $C$ are defined as follows:

  $$\begin{aligned} &A=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=1\right\} \\ &B=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}=x_{2}=0, x_{3}^{2}+x_{4}^{2} \leqslant 1\right\} \\ &C=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{3}=x_{4}=0, x_{1}^{2}+x_{2}^{2} \leqslant 1\right\} \end{aligned}$$

  Compute $H_{*}(X)$

  comment

Applications of Quantum Mechanics

• Paper 4, Section II, D

  Applications of Quantum Mechanics | Part II, 2009

  What are meant by Bloch states and the Brillouin zone for a quantum mechanical particle moving in a one-dimensional periodic potential?

  Derive an approximate value for the lowest-lying energy gap for the Schrödinger equation

  $$-\frac{d^{2} \psi}{d x^{2}}-V_{0}(\cos x+\cos 2 x) \psi=E \psi$$

  when $V_{0}$ is small and positive.

  Estimate the width of this gap in the case that $V_{0}$ is large and positive.

  comment

Applied Probability

• Paper 4, Section II, J

  Applied Probability | Part II, 2009

  A flea jumps on the vertices of a triangle $A B C$; its position is described by a continuous time Markov chain with a $Q$-matrix

  $$Q=\left(\begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & -1 \end{array}\right) \quad \begin{aligned} &A \\ &B \\ &C \end{aligned}$$

  (a) Draw a diagram representing the possible transitions of the flea together with the rates of each of these transitions. Find the eigenvalues of $Q$ and express the transition probabilities $p_{x y}(t), x, y=A, B, C$, in terms of these eigenvalues.

  [Hint: $\operatorname{det}(Q-\mu \mathbf{I})=(-1-\mu)^{3}+1$. Specifying the equilibrium distribution may help.]

  Hence specify the probabilities $\mathbb{P}\left(N_{t}=i \bmod 3\right)$ where $\left(N_{t}, t \geqslant 0\right)$ is a Poisson process of rate $1 .$

  (b) A second flea jumps on the vertices of the triangle $A B C$ as a Markov chain with Q-matrix

  $$Q^{\prime}=\left(\begin{array}{ccc} -\rho & 0 & \rho \\ \rho & -\rho & 0 \\ 0 & \rho & -\rho \end{array}\right) \quad \begin{aligned} &A \\ &B \\ &C \end{aligned}$$

  where $\rho>0$ is a given real number. Let the position of the second flea at time $t$ be denoted by $Y_{t}$. We assume that $\left(Y_{t}, t \geqslant 0\right)$ is independent of $\left(X_{t}, t \geqslant 0\right)$. Let $p(t)=\mathbb{P}\left(X_{t}=Y_{t}\right)$. Show that $\lim _{t \rightarrow \infty} p(t)$ exists and is independent of the starting points of $X$ and $Y$. Compute this limit.

  comment

Asymptotic Methods

• Paper 4, Section II, A

  Asymptotic Methods | Part II, 2009

  The differential equation

  $$f^{\prime \prime}=Q(x) f$$

  has a singular point at $x=\infty$. Assuming that $Q(x)>0$, write down the Liouville Green lowest approximations $f_{\pm}(x)$ for $x \rightarrow \infty$, with $f_{-}(x) \rightarrow 0$.

  The Airy function $\operatorname{Ai}(x)$ satisfies $(*)$ with

  $$Q(x)=x$$

  and $\operatorname{Ai}(x) \rightarrow 0$ as $x \rightarrow \infty$. Writing

  $$\operatorname{Ai}(x)=w(x) f_{-}(x)$$

  show that $w(x)$ obeys

  $$x^{2} w^{\prime \prime}-\left(2 x^{5 / 2}+\frac{1}{2} x\right) w^{\prime}+\frac{5}{16} w=0$$

  Derive the expansion

  $$w \sim c\left(1-\frac{5}{48} x^{-3 / 2}\right) \quad \text { as } \quad x \rightarrow \infty$$

  where $c$ is a constant.

  comment

Classical Dynamics

• Paper 4, Section I, E

  Classical Dynamics | Part II, 2009

  (a) A Hamiltonian system with $n$ degrees of freedom has the Hamiltonian $H(\mathbf{p}, \mathbf{q})$, where $\mathbf{q}=\left(q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right)$ are the coordinates and $\mathbf{p}=\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}\right)$ are the momenta.

  A second Hamiltonian system has the Hamiltonian $G=G(\mathbf{p}, \mathbf{q})$. Neither $H$ nor $G$ contains the time explicitly. Show that the condition for $H(\mathbf{p}, \mathbf{q})$ to be invariant under the evolution of the coordinates and momenta generated by the Hamiltonian $G(\mathbf{p}, \mathbf{q})$ is that the Poisson bracket $[H, G]$ vanishes. Deduce that $G$ is a constant of the motion for evolution under $H$.

  Show that, when $G=\alpha \sum_{k=1}^{n} p_{k}$, where $\alpha$ is constant, the motion it generates is a translation of each $q_{k}$ by an amount $\alpha t$, while the corresponding $p_{k}$ remains fixed. What do you infer is conserved when $H$ is invariant under this transformation?

  (b) When $n=3$ and $H$ is a function of $p_{1}^{2}+p_{2}^{2}+p_{3}^{2}$ and $q_{1}^{2}+q_{2}^{2}+q_{3}^{2}$ only, find $\left[H, L_{i}\right]$ when

  $$L_{i}=\epsilon_{i j k} q_{j} p_{k}$$

  comment

• Paper 4, Section II, E

  Classical Dynamics | Part II, 2009

  The Hamiltonian for a particle of mass $m$, charge $e$ and position vector $\mathbf{q}=(x, y, z)$, moving in an electromagnetic field, is given by

  $$H(\mathbf{p}, \mathbf{q}, t)=\frac{1}{2 m}\left(\mathbf{p}-\frac{e \mathbf{A}}{c}\right)^{2}$$

  where $\mathbf{A}(\mathbf{q}, t)$ is the vector potential. Write down Hamilton's equations and use them to derive the equations of motion for the charged particle.

  Show that, when $\mathbf{A}=\left(-y B_{0}(z, t), 0,0\right)$, there are solutions for which $p_{x}=0$ and for which the particle motion is such that

  $$\frac{d^{2} y}{d t^{2}}=-\Omega^{2} y$$

  where $\Omega=e B_{0} /(m c)$. Show in addition that the Hamiltonian may be written as

  $$H=\frac{m}{2}\left(\frac{d z}{d t}\right)^{2}+E^{\prime}$$

  where

  $$E^{\prime}=\frac{m}{2}\left(\left(\frac{d y}{d t}\right)^{2}+\Omega^{2} y^{2}\right)$$

  Assuming that $B_{0}$ is constant, find the action

  $$I\left(E^{\prime}, B_{0}\right)=\frac{1}{2 \pi} \oint m\left(\frac{d y}{d t}\right) d y$$

  associated with the $y$ motion.

  It is now supposed that $B_{0}$ varies on a time-scale much longer than $\Omega^{-1}$ and thus is slowly varying. Show by applying the theory of adiabatic invariance that the motion in the $z$ direction takes place under an effective potential and give an expression for it.

  comment

Coding and Cryptography

• Paper 4, Section I, H

  Coding and Cryptography | Part II, 2009

  What is a general feedback register? What is a linear feedback register? Give an example of a general feedback register which is not a linear feedback register and prove that it has the stated property.

  By giving proofs or counterexamples, establish which, if any, of the following statements are true and which, if any, are false.

  (i) Given two linear feedback registers, there always exist non-zero initial fills for which the outputs are identical.

  (ii) If two linear feedback registers have different lengths, there do not exist non-zero initial fills for which the outputs are identical.

  (iii) If two linear feedback registers have different lengths, there exist non-zero initial fills for which the outputs are not identical.

  (iv) There exist two linear feedback registers of different lengths and non-zero initial fills for which the outputs are identical.

  comment

Cosmology

• Paper 4, Section I, D

  Cosmology | Part II, 2009

  (a) Consider the motion of three galaxies $O, A, B$ at positions $\mathbf{r}_{O}, \mathbf{r}_{A}, \mathbf{r}_{B}$ in an isotropic and homogeneous universe. Assuming non-relativistic velocities $\mathbf{v}(\mathbf{r})$, show that spatial homogeneity implies

  $$\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{A}\right)=\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{O}\right)-\mathbf{v}\left(\mathbf{r}_{A}-\mathbf{r}_{O}\right)$$

  that is, that the velocity field $\mathbf{v}$ is linearly related to $\mathbf{r}$ by

  $$v_{i}=\sum_{j} H_{i j} r_{j},$$

  where the matrix coefficients $H_{i j}$ are independent of $\mathbf{r}$. Further show that isotropy implies Hubble's law,

  $$\mathbf{v}=H \mathbf{r} \text {, }$$

  where the Hubble parameter $H$ is independent of $\mathbf{r}$. Presuming $H$ to be a function of time $t$, show that Hubble's law can be integrated to obtain the solution

  $$\mathbf{r}(t)=a(t) \mathbf{x}$$

  where $\mathbf{x}$ is a constant (comoving) position and the scalefactor $a(t)$ satisfies $H=\dot{a} / a$.

  (b) Define the cosmological horizon $d_{H}(t)$. For models with $a(t)=t^{\alpha}$ where $0<\alpha<1$, show that the cosmological horizon $d_{H}(t)=c t /(1-\alpha)$ is finite. Briefly explain the horizon problem.

  comment

Differential Geometry

• Paper 4, Section II, H

  Differential Geometry | Part II, 2009

  (a) Let $X$ be a compact surface (without boundary) in $\mathbb{R}^{3}$. State the global GaussBonnet formula for $X$, identifying all terms in the formula.

  (b) Let $X \subset \mathbb{R}^{3}$ be a surface. Define what it means for a curve $\gamma: I \rightarrow X$ to be a geodesic. State a theorem concerning the existence of geodesics and define the exponential map.

  (c) Let $\psi: X \rightarrow Y$ be an isometry and let $\gamma$ be a geodesic. Show that $\psi \circ \gamma$ is a geodesic. If $K_{X}$ denotes the Gaussian curvature of $X$, and $K_{Y}$ denotes the Gaussian curvature of $Y$, show that $K_{Y} \circ \psi=K_{X}$.

  Now suppose $\psi: X \rightarrow Y$ is a smooth map such that $\psi \circ \gamma$ is a geodesic for all $\gamma$ a geodesic. Is $\psi$ necessarily an isometry? Give a proof or counterexample.

  Similarly, suppose $\psi: X \rightarrow Y$ is a smooth map such that $K_{Y} \circ \psi=K_{X}$. Is $\psi$ necessarily an isometry? Give a proof or counterexample.

  comment

Dynamical Systems

• Paper 4, Section I, $7 \mathbf{E}$

  Dynamical Systems | Part II, 2009

  Consider the two-dimensional dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ given in polar coordinates by

  $$\begin{aligned} &\dot{r}=\left(r-r^{2}\right)(r-g(\theta)), \\ &\dot{\theta}=r, \end{aligned}$$

  $$\begin{aligned} & \dot{\theta}=r, \end{aligned}$$

  where $g(\theta)$ is continuously differentiable and $2 \pi$-periodic. Find a periodic orbit $\gamma$ for $(*)$ and, using the hint or otherwise, compute the Floquet multipliers of $\gamma$ in terms of $g(\theta)$. Explain why one of the Floquet multipliers is independent of $g(\theta)$. Give a sufficient condition for $\gamma$ to be asymptotically stable.

  Investigate the stability of $\gamma$ and the dynamics of $(*)$ in the case $g(\theta)=2 \sin \theta$.

  [Hint: The determinant of the fundamental matrix $\Phi(t)$ satisfies

  $$\frac{d}{d t} \operatorname{det} \Phi=(\nabla \cdot \mathbf{f}) \operatorname{det} \Phi$$

  comment

• Paper 4, Section II, E

  Dynamical Systems | Part II, 2009

  Let $I, J$ be closed bounded intervals in $\mathbb{R}$, and let $F: \mathbb{R} \rightarrow \mathbb{R}$ be a continuous map.

  Explain what is meant by the statement that ' $I F$-covers $J$ ' (written $I \rightarrow J)$. For a collection of intervals $I_{0}, \ldots, I_{k}$ define the associated directed graph $\Gamma$ and transition matrix $A$. Derive an expression for the number of (not necessarily least) period- $n$ points of $F$ in terms of $A$.

  Let $F$ have a 5 -cycle

  $$x_{0}<x_{1}<x_{2}<x_{3}<x_{4}$$

  such that $x_{i+1}=F\left(x_{i}\right)$ for $i=0, \ldots, 4$ where indices are taken modulo 5 . Write down the directed graph $\Gamma$ and transition matrix $A$ for the $F$-covering relations between the intervals $\left[x_{i}, x_{i+1}\right]$. Compute the number of $n$-cycles which are guaranteed to exist for $F$, for each integer $1 \leqslant n \leqslant 4$, and the intervals the points move between.

  Explain carefully whether or not $F$ is guaranteed to have a horseshoe. Must $F$ be chaotic? Could $F$ be a unimodal map? Justify your answers.

  Similarly, a continuous map $G: \mathbb{R} \rightarrow \mathbb{R}$ has a 5 -cycle

  $$x_{3}<x_{1}<x_{0}<x_{2}<x_{4}$$

  For what integer values of $n, 1 \leqslant n \leqslant 4$, is $G$ guaranteed to have an $n$-cycle?

  Is $G$ guaranteed to have a horseshoe? Must $G$ be chaotic? Justify your answers.

  comment

Electrodynamics

• Paper 4, Section II, C

  Electrodynamics | Part II, 2009

  In a superconductor, the charge carriers have a charge $q$, mass $m$ and number density $n$. Describe how to construct the superconducting current in terms of the vector potential A and the wavefunction of the charge carriers.

  Show that the current is gauge invariant.

  Derive the Helmholtz equation

  $$\nabla^{2} \mathbf{B}=\mathbf{B} / \ell^{2}$$

  for a time-independent magnetic field and evaluate the length scale $\ell$ in terms of $n, q$ and $m$.

  Why does this imply that magnetic flux cannot exist in a superconductor?

  comment

Fluid Dynamics II

• Paper 4 , Section II, E

  Fluid Dynamics II | Part II, 2009

  Two regions of inviscid fluid with the same density are separated by a thin membrane at $y=0$. The fluid in $y>0$ has the uniform velocity $(U, 0,0)$ in Cartesian coordinates, while the fluid in $y<0$ is at rest.

  The membrane is now slightly perturbed to $y=\eta(x, t)$. The dynamical effect of the membrane is to induce a pressure difference across it equal to $\beta \partial^{4} \eta / \partial x^{4}$, where $\beta$ is a constant and the sign is such that the pressure is higher below the interface when $\partial^{4} \eta / \partial x^{4}>0$.

  On the assumption that the flow remains irrotational and all perturbations are small, derive the relation between $\sigma$ and $k$ for disturbances of the form $\eta(x, t)=\operatorname{Re}\left(C e^{i k x+\sigma t}\right)$, where $k$ is real but $\sigma$ may be complex. Show that there is instability only for $|k|<k_{\max }$, where $k_{\max }$ is to be determined. Find the maximum growth rate and the value of $|k|$ for which this is obtained.

  comment

Further Complex Methods

• Paper 4, Section I, D

  Further Complex Methods | Part II, 2009

  Show that

  $$\Gamma(\alpha) \Gamma(\beta)=\Gamma(\alpha+\beta) \int_{0}^{1} t^{\alpha-1}(1-t)^{\beta-1} d t, \quad \operatorname{Re} \alpha>0, \quad \operatorname{Re} \beta>0$$

  where $\Gamma(z)$ denotes the Gamma function

  $$\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0$$

  comment

Galois Theory

• Paper 4, Section II, H

  Galois Theory | Part II, 2009

  (a) Let $K$ be a field. State what it means for $\xi_{n} \in K$ to be a primitive $n$th root of unity.

  Show that if $\xi_{n}$ is a primitive $n$th root of unity, then the characteristic of $K$ does not divide $n$. Prove any theorems you use.

  (b) Determine the minimum polynomial of a primitive 10 th root of unity $\xi_{10}$ over $\mathbb{Q}$.

  Show that $\sqrt{5} \in \mathbb{Q}\left(\xi_{10}\right)$.

  (c) Determine $\mathbb{F}_{3}\left(\xi_{10}\right), \mathbb{F}_{11}\left(\xi_{10}\right), \mathbb{F}_{19}\left(\xi_{10}\right)$.

  [Hint: Write a necessary and sufficient condition on $q$ for a finite field $\mathbb{F}_{q}$ to contain a primitive 10 th root of unity.]

  comment

General Relativity

• Paper 4, Section II, D

  General Relativity | Part II, 2009

  The Schwarzschild metric is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where $M$ is the mass in gravitational units. By using the radial component of the geodesic equations, or otherwise, show for a particle moving on a geodesic in the equatorial plane $\theta=\pi / 2$ with $r$ constant that

  $$\left(\frac{d \phi}{d t}\right)^{2}=\frac{M}{r^{3}}$$

  Show that such an orbit is stable for $r>6 M$.

  An astronaut circles the Earth freely for a long time on a circular orbit of radius $R$, while the astronaut's twin remains motionless on Earth, which is assumed to be spherical, with radius $R_{0}$, and non-rotating. Show that, on returning to Earth, the astronaut will be younger than the twin only if $2 R<3 R_{0}$.

  comment

Geometry of Group Actions

• Paper 4, Section I, F

  Geometry of Group Actions | Part II, 2009

  For every $k \in \mathbb{R}$, show that there is a closed bounded totally disconnected subset $X$ of some Euclidean space, such that $X$ has Hausdorff dimension at least $k$. [Standard properties of Hausdorff dimension may be quoted without proof if carefully stated.]

  comment

• Paper 4, Section II, F

  Geometry of Group Actions | Part II, 2009

  Define three-dimensional hyperbolic space, the translation length of an isometry of hyperbolic 3 -space, and the axis of a hyperbolic isometry. Briefly explain how and why the latter two concepts are related.

  Find the translation length of the isometries defined by (i) $z \mapsto k z, k \in \mathbb{C} \backslash\{0\}$ and (ii) $z \mapsto \frac{3 z+2}{7 z+5}$.

  comment

Graph Theory

• Paper 4, Section II, F

  Graph Theory | Part II, 2009

  Let $X$ denote the number of triangles in a random graph $G$ chosen from $G(n, p)$. Find the mean and variance of $X$. Hence show that $p=n^{-1}$ is a threshold for the existence of a triangle, in the sense that if $p n \rightarrow 0$ then almost surely $G$ does not contain a triangle, while if $p n \rightarrow \infty$ then almost surely $G$ does contain a triangle.

  Now let $p=n^{-1 / 2}$, and let $Y$ denote the number of edges of $G$ (chosen as before from $G(n, p))$. By considering the mean of $Y-X$, show that for each $n \geqslant 3$ there exists a graph on $n$ vertices with at least $\frac{1}{6} n^{3 / 2}$ edges that is triangle-free. Is this within a constant factor of the best-possible answer (meaning the greatest number of edges that a triangle-free graph on $n$ vertices can have)?

  comment

Linear Analysis

• Paper 4, Section II, H

  Linear Analysis | Part II, 2009

  Let $X$ be a Banach space and let $T: X \rightarrow X$ be a bounded linear map.

  (a) Define the spectrum $\sigma(T)$, the resolvent set $\rho(T)$ and the point spectrum $\sigma_{p}(T)$ of $T$.

  (b) What does it mean for $T$ to be a compact operator?

  (c) Show that if $T$ is a compact operator on $X$ and $a>0$, then $T$ has at most finitely many linearly independent eigenvectors with eigenvalues having modulus larger than $a$.

  [You may use without proof the fact that for any finite dimensional proper subspace $Y$ of a Banach space $Z$, there exists $x \in Z$ with $\|x\|=1$ and $\operatorname{dist}(x, Y)=\inf _{y \in Y}\|x-y\|=1$.]

  (d) For a sequence $\left(\lambda_{n}\right)_{n \geqslant 1}$ of complex numbers, let $T: \ell^{2} \rightarrow \ell^{2}$ be defined by

  $$T\left(x_{1}, x_{2}, \ldots\right)=\left(\lambda_{1} x_{1}, \lambda_{2} x_{2}, \ldots\right) .$$

  Give necessary and sufficient conditions on the sequence $\left(\lambda_{n}\right)_{n} \geqslant 1$ for $T$ to be compact, and prove your assertion.

  comment

Logic and Set Theory

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2009

  What is a transitive class? What is the significance of this notion for models of set theory?

  Prove that for any set $x$ there is a least transitive set $\mathrm{TC}(x)$, the transitive closure of $x$, with $x \subseteq \mathrm{TC}(x)$. Show that for any set $x$, one has $\mathrm{TC}(x)=x \cup \mathrm{TC}(\bigcup x)$, and deduce that $\mathrm{TC}(\{x\})=\{x\} \cup \operatorname{TC}(x)$.

  A set $x$ is hereditarily countable when every member of $\mathrm{TC}(\{x\})$ is countable. Let $(\mathrm{HC}, \in)$ be the collection of hereditarily countable sets with the usual membership relation. Is HC transitive? Show that $(\mathrm{HC}, \in)$ satisfies the axiom of unions. Show that $(\mathrm{HC}, \in)$ satisfies the axiom of separation. What other axioms of ZF set theory are satisfied in $(\mathrm{HC}, \in) ?$

  comment

Mathematical Biology

• Paper 4, Section I, A

  Mathematical Biology | Part II, 2009

  The diffusion equation for a chemical concentration $C(r, t)$ in three dimensions which depends only on the radial coordinate $r$ is

  $$C_{t}=D \frac{1}{r^{2}}\left(r^{2} C_{r}\right)_{r}$$

  The general similarity solution of this equation takes the form

  $$C(r, t)=t^{\alpha} F(\xi), \quad \xi=\frac{r}{t^{\beta}},$$

  where $\alpha$ and $\beta$ are to be determined. By direct substitution into $(*)$ and the requirement of a valid similarity solution, find one relation involving the exponents. Use the conservation of the total number of molecules to determine a second relation. Comment on the relationship between these exponents and the ones appropriate to the similarity solution of the one-dimensional diffusion equation. Show that $F$ obeys

  $$D\left(F^{\prime \prime}+\frac{2}{\xi} F^{\prime}\right)+\frac{1}{2} \xi F^{\prime}+\frac{3}{2} F=0$$

  and that the relevant solution describing the spreading of a delta-function initial condition is $F(\xi)=A \exp \left(-\xi^{2} / 4 D\right)$, where $A$ is a suitable normalisation that need not be found.

  comment

Number Fields

• Paper 4, Section II, H

  Number Fields | Part II, 2009

  Suppose that $K$ is a number field of degree $n=r+2 s$, where $K$ has exactly real embeddings.

  Show that the group of units in $\mathcal{O}_{K}$ is a finitely generated abelian group of rank at most $r+s-1$. Identify the torsion subgroup in terms of roots of unity.

  [General results about discrete subgroups of a Euclidean real vector space may be used without proof, provided that they are stated clearly.]

  Find all the roots of unity in $\mathbb{Q}(\sqrt{11})$.

  comment

Number Theory

• Paper 4, Section I, G

  Number Theory | Part II, 2009

  Let $W$ denote the set of all positive definite binary quadratic forms, with integer coefficients, and having discriminant $-67$. Let $S L_{2}(\mathbb{Z})$ be the group of all $2 \times 2$ matrices with integer entries and determinant 1. Prove that $W$ is infinite, but that all elements of $W$ are equivalent under the action of the group $S L_{2}(\mathbb{Z})$

  comment

• Paper 4, Section II, G

  Number Theory | Part II, 2009

  Let $s=\sigma+i t$, where $\sigma$ and $t$ are real, and for $\sigma>1$ let

  $$\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}}$$

  Prove that $\zeta(s)$ has no zeros in the half plane $\sigma>1$. Show also that for $\sigma>1$,

  $$\frac{1}{\zeta(s)}=\sum_{n=1}^{\infty} \frac{\mu(n)}{n^{s}}$$

  where $\mu$ denotes the Möbius function. Assuming that $\zeta(s)-\frac{1}{s-1}$ has an analytic continuation to the half plane $\sigma>0$, show that if $s=1+i t$, with $t \neq 0$, and $\zeta(s)=0$ then $s$ is at most a simple zero of $\zeta$.

  comment

Numerical Analysis

• Paper 4, Section II, B

  Numerical Analysis | Part II, 2009

  (a) For the $s$-step $s$-order Backward Differentiation Formula (BDF) for ordinary differential equations,

  $$\sum_{m=0}^{s} a_{m} y_{n+m}=h f_{n+s}$$

  express the polynomial $\rho(w)=\sum_{m=0}^{s} a_{m} w^{m}$ in a convenient explicit form.

  (b) Prove that the interval $(-\infty, 0)$ belongs to the linear stability domain of the 2-step BDF method.

  comment

Optimization and Control

• Paper 4, Section II, I

  Optimization and Control | Part II, 2009

  Explain how transversality conditions can be helpful when employing Pontryagin's Maximum Principle to solve an optimal control problem.

  A particle in $\mathbb{R}^{2}$ starts at $(0,0.5)$ and follows the dynamics

  $$\dot{x}=u \sqrt{|y|}, \quad \dot{y}=v \sqrt{|y|}, \quad t \in[0, T],$$

  where controls $u(t)$ and $v(t)$ are to be chosen subject to $u^{2}(t)+v^{2}(t)=1$.

  Using Pontryagin's maximum principle do the following:

  (a) Find controls that minimize $-y(1)$;

  (b) Suppose we wish to choose $T$ and the controls $u, v$ to minimize $-y(T)+T$ under a constraint $(x(T), y(T))=(1,1)$. By expressing both $d y / d x$ and $d^{2} y / d x^{2}$ in terms of the adjoint variables, show that on an optimal trajectory,

  $$1+\left(\frac{d y}{d x}\right)^{2}+2 y \frac{d^{2} y}{d x^{2}}=0$$

  comment

Partial Differential Equations

• Paper 4, Section II, B

  Partial Differential Equations | Part II, 2009

  Consider the two-dimensional domain

  $$G=\left\{(x, y) \mid R_{1}^{2}<x^{2}+y^{2}<R_{2}^{2}\right\}$$

  where $0<R_{1}<R_{2}<\infty$. Solve the Dirichlet boundary value problem for the Laplace equation

  $$\begin{gathered} \Delta u=0 \text { in } G, \\ u=u_{1}(\varphi), r=R_{1}, \\ u=u_{2}(\varphi), r=R_{2}, \end{gathered}$$

  where $(r, \varphi)$ are polar coordinates. Assume that $u_{1}, u_{2}$ are $2 \pi$-periodic functions on the real line and $u_{1}, u_{2} \in L_{l o c}^{2}(\mathbb{R})$.

  [Hint: Use separation of variables in polar coordinates, $u=R(r) \Phi(\varphi)$, with periodic boundary conditions for the function $\Phi$ of the angle variable. Use an ansatz of the form $R(r)=r^{\alpha}$ for the radial function.]

  comment

Principles of Quantum Mechanics

• Paper 4, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  For any given operators $A$ and $B$, show that $F(\lambda)=e^{\lambda A} B e^{-\lambda A}$ has derivative $F^{\prime}(\lambda)=e^{\lambda A}[A, B] e^{-\lambda A}$ and deduce an analogous formula for the $n$th derivative. Hence, by considering $F(\lambda)$ as a power series in $\lambda$, show that

  $$e^{A} B e^{-A}=B+[A, B]+\frac{1}{2 !}[A,[A, B]]+\ldots+\frac{1}{n !}[A,[A, \ldots[A, B] \ldots]]+\ldots$$

  A particle of unit mass in one dimension has position $\hat{x}$ and momentum $\hat{p}$ in the Schrödinger picture, and Hamiltonian

  $$H=\frac{1}{2} \hat{p}^{2}-\alpha \hat{x},$$

  where $\alpha$ is a constant. Apply $(*)$ to find the Heisenberg picture operators $\hat{x}(t)$ and $\hat{p}(t)$ in terms of $\hat{x}$ and $\hat{p}$, and check explicitly that $H(\hat{x}(t), \hat{p}(t))=H(\hat{x}, \hat{p})$.

  A particle of unit mass in two dimensions has position $\hat{x}_{i}$ and momentum $\hat{p}_{i}$ in the Schrödinger picture, and Hamiltonian

  $$H=\frac{1}{2}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}\right)-\beta\left(\hat{x}_{1} \hat{p}_{2}-\hat{x}_{2} \hat{p}_{1}\right)$$

  where $\beta$ is a constant. Calculate the Heisenberg picture momentum components $\hat{p}_{i}(t)$ in terms of $\hat{p}_{i}$ and verify that $\hat{p}_{1}(t)^{2}+\hat{p}_{2}(t)^{2}$ is independent of time. Now consider the interaction picture corresponding to $H=H_{0}+V$ : show that if $H_{0}=\frac{1}{2}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}\right)$ then the interaction picture position operators are $\hat{x}_{i}+t \hat{p}_{i}$, and use this to find the Heisenberg picture position operators $\hat{x}_{i}(t)$ in terms of $\hat{x}_{i}$ and $\hat{p}_{i}$.

  [Hint: If $\left[H_{0}, V\right]=0$ and $\bar{Q}(t)$ is an operator in the interaction picture, then the corresponding operator in the Heisenberg picture is $\left.Q(t)=e^{i t V / \hbar} \bar{Q}(t) e^{-i t V / \hbar} \cdot\right]$

  comment

Principles of Statistics

• Paper 4, Section II, I

  Principles of Statistics | Part II, 2009

  Consider the double dichotomy, where the loss is 0 for a correct decision and 1 for an incorrect decision. Describe the form of a Bayes decision rule. Assuming the equivalence of normal and extensive form analyses, deduce the Neyman-Pearson lemma.

  For a problem with random variable $X$ and real parameter $\theta$, define monotone likelihood ratio (MLR) and monotone test.

  Suppose the problem has MLR in a real statistic $T=t(X)$. Let $\phi$ be a monotone test, with power function $\gamma(\cdot)$, and let $\phi^{\prime}$ be any other test, with power function $\gamma^{\prime}(\cdot)$. Show that if $\theta_{1}>\theta_{0}$ and $\gamma\left(\theta_{0}\right)>\gamma^{\prime}\left(\theta_{0}\right)$, then $\gamma\left(\theta_{1}\right)>\gamma^{\prime}\left(\theta_{1}\right)$. Deduce that there exists $\theta^{*} \in[-\infty, \infty]$ such that $\gamma(\theta) \leqslant \gamma^{\prime}(\theta)$ for $\theta<\theta^{*}$, and $\gamma(\theta) \geqslant \gamma^{\prime}(\theta)$ for $\theta>\theta^{*}$.

  For an arbitrary prior distribution $\Pi$ with density $\pi(\cdot)$, and an arbitrary value $\theta^{*}$, show that the posterior odds

  $$\frac{\Pi\left(\theta>\theta^{*} \mid X=x\right)}{\Pi\left(\theta \leqslant \theta^{*} \mid X=x\right)}$$

  is a non-decreasing function of $t(x)$.

  comment

Probability and Measure

• Paper 4, Section II, J

  Probability and Measure | Part II, 2009

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\mathcal{G}$ be a sub- $\sigma$-algebra of $\mathcal{F}$. Show that, for any random variable $X \in L^{2}(\mathbb{P})$, there exists a $\mathcal{G}$-measurable random variable $Y \in L^{2}(\mathbb{P})$ such that $\mathbb{E}((X-Y) Z)=0$ for all $\mathcal{G}$-measurable random variables $Z \in L^{2}(\mathbb{P})$.

  [You may assume without proof the completeness of $L^{2}(\mathbb{P}) .$ ]

  Let $(G, X)$ be a Gaussian random variable in $\mathbb{R}^{2}$, with mean $(\mu, \nu)$ and covariance $\operatorname{matrix}\left(\begin{array}{cc}u & v \\ v & w\end{array}\right)$. Assume that $\mathcal{F}=\sigma(G, X)$ and $\mathcal{G}=\sigma(G)$. Find the random variable $Y$ explicitly in this case.

  comment

Representation Theory

• Paper 4, Section II, F

  Representation Theory | Part II, 2009

  Let $H \leqslant G$ be finite groups.

  (a) Let $\rho$ be a representation of $G$ affording the character $\chi$. Define the restriction, $\operatorname{Res}_{H}^{G} \rho$ of $\rho$ to $H$.

  Suppose $\chi$ is irreducible and suppose $\operatorname{Res}_{H}^{G} \rho$ affords the character $\chi_{H}$. Let $\psi_{1}, \ldots, \psi_{r}$ be the irreducible characters of $H$. Prove that $\chi_{H}=d_{1} \psi_{1}+\cdots+d_{r} \psi_{r}$, where the nonnegative integers $d_{1}, \ldots, d_{r}$ satisfy the inequality

  $$\sum_{i=1}^{r} d_{i}^{2} \leqslant|G: H|$$

  Prove that there is equality in (1) if and only if $\chi(g)=0$ for all elements $g$ of $G$ which lie outside $H$.

  (b) Let $\psi$ be a class function of $H$. Define the induced class function, $\operatorname{Ind}_{H}^{G} \psi$.

  State the Frobenius reciprocity theorem for class functions and deduce that if $\psi$ is a character of $H$ then $\operatorname{Ind}_{H}^{G} \psi$ is a character of $G$.

  Assuming $\psi$ is a character, identify a $G$-space affording the character $\operatorname{Ind}_{H}^{G} \psi$. Briefly justify your answer.

  (c) Let $\chi_{1}, \ldots, \chi_{k}$ be the irreducible characters of $G$ and let $\psi$ be an irreducible character of $H$. Show that the integers $e_{1}, \ldots, e_{k}$, which are given by $\operatorname{Ind}_{H}^{G}(\psi)=$ $e_{1} \chi_{1}+\cdots+e_{k} \chi_{k}$, satisfy

  $$\sum_{i=1}^{k} e_{i}^{2} \leqslant|G: H|$$

  comment

Statistical Modelling

• Paper 4, Section I, $5 I$

  Statistical Modelling | Part II, 2009

  Sulphur dioxide is one of the major air pollutants. A dataset by Sokal and Rohlf (1981) was collected on 41 US cities/regions in 1969-1971. The annual measurements obtained for each region include (average) sulphur dioxide content, temperature, number of manufacturing enterprises employing more than 20 workers, population size in thousands, wind speed, precipitation, and the number of days with precipitation. The data are displayed in $R$ as follows (abbreviated):

  

  Describe the model being fitted by the following $R$ commands.

  $>$ fit $<-\operatorname{lm}(\log (\mathrm{so} 2) \sim$ temp $+$ manuf $+$ pop $+$ wind $+$ precip $+$ days $)$

  Explain the (slightly abbreviated) output below, describing in particular how the hypothesis tests are performed and your conclusions based on their results:

  

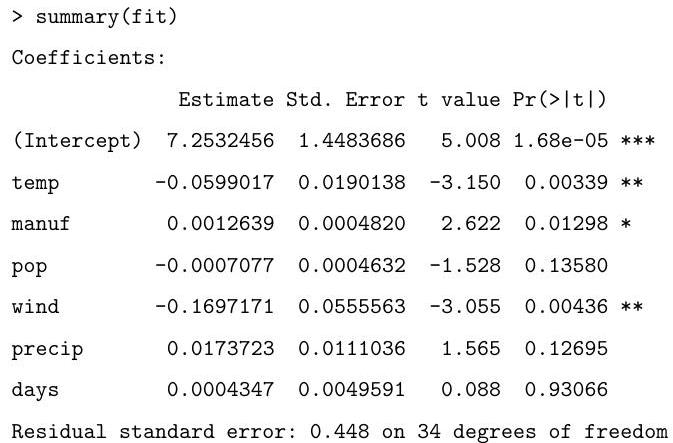
  Based on the summary above, suggest an alternative model.

  Finally, what is the value obtained by the following command?

  $>\operatorname{sqrt}\left(\operatorname{sum}\left(\operatorname{resid}(f i t)^{\sim} 2\right) / \mathrm{fit} \$ \mathrm{df}\right)$

  comment

• Paper 4, Section II, I

  Statistical Modelling | Part II, 2009

  Consider the linear model $Y=X \beta+\varepsilon$, where $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ and $X$ is an $n \times p$ matrix of full rank $p<n$. Find the form of the maximum likelihood estimator $\hat{\beta}$ of $\beta$, and derive its distribution assuming that $\sigma^{2}$ is known.

  Assuming the prior $\pi\left(\beta, \sigma^{2}\right) \propto \sigma^{-2}$ find the joint posterior of $\left(\beta, \sigma^{2}\right)$ up to a normalising constant. Derive the posterior conditional distribution $\pi\left(\beta \mid \sigma^{2}, X, Y\right)$.

  Comment on the distribution of $\hat{\beta}$ found above and the posterior conditional $\pi\left(\beta \mid \sigma^{2}, X, Y\right)$. Comment further on the predictive distribution of $y^{*}$ at input $x^{*}$ under both the maximum likelihood and Bayesian approaches.

  comment

Statistical Physics

• Paper 4, Section II, D

  Statistical Physics | Part II, 2009

  Briefly state the ergodic hypothesis and explain its importance.

  Consider an ideal, classical, monatomic gas in the presence of a uniform gravitational field in the negative $z$-direction. For convenience, assume the gas is in an arbitrarily large cubic box.

  (i) Compute the internal energy $E$ of the gas.

  (ii) Explain your result for $E$ in relation to the equipartition theorem.

  (iii) What is the probability that an atom is located at a height between $z$ and $z+d z ?$

  (iv) What is the most probable speed of an atom of this gas?

  comment

Stochastic Financial Models

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2009

  An agent with utility $U(x)=-\exp (-\gamma x)$, where $\gamma>0$ is a constant, may select at time 0 a portfolio of $n$ assets, which he then holds to time 1 . The values $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ of the assets at time 1 have a multivariate normal distribution with mean $\mu$ and nonsingular covariance matrix $V$. Prove that the agent will prefer portfolio $\psi \in \mathbb{R}^{n}$ to portfolio $\theta \in \mathbb{R}^{n}$ if and only if $q(\psi)>q(\theta)$, where

  $$q(x)=x \cdot \mu-\frac{\gamma}{2} x \cdot V x$$

  Determine his optimal portfolio.

  The agent initially holds portfolio $\theta$, which he may change to portfolio $\theta+z$ at cost $\varepsilon \sum_{i=1}^{n}\left|z_{i}\right|$, where $\varepsilon$ is some positive transaction cost. By considering the function $t \mapsto q(\theta+t z)$ for $0 \leqslant t \leqslant 1$, or otherwise, prove that the agent will have no reason to change his initial portfolio $\theta$ if and only if, for every $i=1, \ldots, n$,

  $$\left|\mu_{i}-\gamma(V \theta)_{i}\right| \leqslant \varepsilon$$

  comment

Topics in Analysis

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  State Liouville's theorem on approximation of algebraic numbers by rationals, and use it to prove that the number

  $$\sum_{n=0}^{\infty} \frac{1}{10^{n !}}$$

  is transcendental.

  comment

Waves

• Paper 4, Section II, A

  Waves | Part II, 2009

  A perfect gas occupies a tube that lies parallel to the $x$-axis. The gas is initially at rest, with density $\rho_{1}$, pressure $p_{1}$ and specific heat ratio $\gamma$, and occupies the region $x>0$. For times $t>0$ a piston, initially at $x=0$, is pushed into the gas at a constant speed $V$. A shock wave propagates at constant speed $U$ into the undisturbed gas ahead of the piston. Show that the pressure in the gas next to the piston, $p_{2}$, is given by the expression

  $$V^{2}=\frac{\left(p_{2}-p_{1}\right)^{2}}{\rho_{1}\left(\frac{\gamma+1}{2} p_{2}+\frac{\gamma-1}{2} p_{1}\right)} .$$

  [You may assume that the internal energy per unit mass of perfect gas is given by

  $$E=\frac{1}{\gamma-1} \frac{p}{\rho}$$

  comment