Part II, 2009, Paper 1

Algebraic Geometry

• Paper 1, Section II, G

  Algebraic Geometry | Part II, 2009

  Define what is meant by a rational map from a projective variety $V \subset \mathbb{P}^{n}$ to $\mathbb{P}^{m}$. What is a regular point of a rational map?

  Consider the rational map $\phi: \mathbb{P}^{2}-\rightarrow \mathbb{P}^{2}$ given by

  $$\left(X_{0}: X_{1}: X_{2}\right) \mapsto\left(X_{1} X_{2}: X_{0} X_{2}: X_{0} X_{1}\right)$$

  Show that $\phi$ is not regular at the points $(1: 0: 0),(0: 1: 0),(0: 0: 1)$ and that it is regular elsewhere, and that it is a birational map from $\mathbb{P}^{2}$ to itself.

  Let $V \subset \mathbb{P}^{2}$ be the plane curve given by the vanishing of the polynomial $X_{0}^{2} X_{1}^{3}+X_{1}^{2} X_{2}^{3}+X_{2}^{2} X_{0}^{3}$ over a field of characteristic zero. Show that $V$ is irreducible, and that $\phi$ determines a birational equivalence between $V$ and a nonsingular plane quartic.

  comment

Algebraic Topology

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the space obtained by identifying two copies of the Möbius strip along their boundary. Use the Seifert-Van Kampen theorem to find a presentation of the fundamental group $\pi_{1}(X)$. Show that $\pi_{1}(X)$ is an infinite non-abelian group.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, $34 \mathrm{D}$

  Applications of Quantum Mechanics | Part II, 2009

  Consider the scaled one-dimensional Schrödinger equation with a potential $V(x)$ such that there is a complete set of real, normalized bound states $\psi_{n}(x), n=0,1,2, \ldots$, with discrete energies $E_{0}<E_{1}<E_{2}<\ldots$, satisfying

  $$-\frac{d^{2} \psi_{n}}{d x^{2}}+V(x) \psi_{n}=E_{n} \psi_{n}$$

  Show that the quantity

  $$\langle E\rangle=\int_{-\infty}^{\infty}\left(\left(\frac{d \psi}{d x}\right)^{2}+V(x) \psi^{2}\right) d x$$

  where $\psi(x)$ is a real, normalized trial function depending on one or more parameters $\alpha$, can be used to estimate $E_{0}$, and show that $\langle E\rangle \geqslant E_{0}$.

  Let the potential be $V(x)=|x|$. Using a suitable one-parameter family of either Gaussian or piecewise polynomial trial functions, find a good estimate for $E_{0}$ in this case.

  How could you obtain a good estimate for $E_{1}$ ? [ You should suggest suitable trial functions, but DO NOT carry out any further integration.]

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2009

  (a) Let $\left(X_{t}, t \geqslant 0\right)$ be a continuous-time Markov chain on a countable state space I. Explain what is meant by a stopping time for the chain $\left(X_{t}, t \geqslant 0\right)$. State the strong Markov property. What does it mean to say that $X$ is irreducible?

  (b) Let $\left(X_{t}, t \geqslant 0\right)$ be a Markov chain on $I=\{0,1, \ldots\}$ with $Q$-matrix given by $Q=\left(q_{i, j}\right)_{i, j \in I}$ such that:

  (1) $q_{i, 0}>0$ for all $i \geqslant 1$, but $q_{0, j}=0$ for all $j \in I$, and

  (2) $q_{i, i+1}>0$ for all $i \geqslant 1$, but $q_{i, j}=0$ if $j>i+1$.

  Is $\left(X_{t}, t \geqslant 0\right)$ irreducible? Fix $M \geqslant 1$, and assume that $X_{0}=i$, where $1 \leqslant i \leqslant M$. Show that if $J_{1}=\inf \left\{t \geqslant 0: X_{t} \neq X_{0}\right\}$ is the first jump time, then there exists $\delta>0$ such that $\mathbb{P}_{i}\left(X_{J_{1}}=0\right) \geqslant \delta$, uniformly over $1 \leqslant i \leqslant M$. Let $T_{0}=0$ and define recursively for $m \geqslant 0$,

  $$T_{m+1}=\inf \left\{t \geqslant T_{m}: X_{t} \neq X_{T_{m}} \text { and } 1 \leqslant X_{t} \leqslant M\right\}$$

  Let $A_{m}$ be the event $A_{m}=\left\{T_{m}<\infty\right\}$. Show that $\mathbb{P}_{i}\left(A_{m}\right) \leqslant(1-\delta)^{m}$, for $1 \leqslant i \leqslant M$.

  (c) Let $\left(X_{t}, t \geqslant 0\right)$ be the Markov chain from (b). Define two events $E$ and $F$ by

  $$E=\left\{X_{t}=0 \text { for all } t \text { large enough }\right\}, \quad F=\left\{\lim _{t \rightarrow \infty} X_{t}=+\infty\right\}$$

  Show that $\mathbb{P}_{i}(E \cup F)=1$ for all $i \in I$.

  comment

Asymptotic Methods

• Paper 1, Section II, A

  Asymptotic Methods | Part II, 2009

  Consider the integral

  $$I(\lambda)=\int_{0}^{A} \mathrm{e}^{-\lambda t} f(t) d t, \quad A>0$$

  in the limit $\lambda \rightarrow \infty$, given that $f(t)$ has the asymptotic expansion

  $$f(t) \sim \sum_{n=0}^{\infty} a_{n} t^{n \beta}$$

  as $t \rightarrow 0_{+}$, where $\beta>0$. State Watson's lemma.

  Now consider the integral

  $$J(\lambda)=\int_{a}^{b} \mathrm{e}^{\lambda \phi(t)} F(t) d t$$

  where $\lambda \gg 1$ and the real function $\phi(t)$ has a unique maximum in the interval $[a, b]$ at $c$, with $a<c<b$, such that

  $$\phi^{\prime}(c)=0, \phi^{\prime \prime}(c)<0$$

  By making a monotonic change of variable from $t$ to a suitable variable $\zeta$ (Laplace's method), or otherwise, deduce the existence of an asymptotic expansion for $J(\lambda)$ as $\lambda \rightarrow \infty$. Derive the leading term

  $$J(\lambda) \sim \mathrm{e}^{\lambda \phi(c)} F(c)\left(\frac{2 \pi}{\lambda\left|\phi^{\prime \prime}(c)\right|}\right)^{\frac{1}{2}}$$

  The gamma function is defined for $x>0$ by

  $$\Gamma(x+1)=\int_{0}^{\infty} \exp (x \log t-t) d t$$

  By means of the substitution $t=x s$, or otherwise, deduce Stirling's formula

  $$\Gamma(x+1) \sim x^{\left(x+\frac{1}{2}\right)} \mathrm{e}^{-x} \sqrt{2 \pi}\left(1+\frac{1}{12 x}+\cdots\right)$$

  as $x \rightarrow \infty$

  comment

Classical Dynamics

• Paper 1, Section I, E

  Classical Dynamics | Part II, 2009

  Lagrange's equations for a system with generalized coordinates $q_{i}(t)$ are given by

  $$\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{i}}\right)-\frac{\partial L}{\partial q_{i}}=0$$

  where $L$ is the Lagrangian. The Hamiltonian is given by

  $$H=\sum_{j} p_{j} \dot{q}_{j}-L,$$

  where the momentum conjugate to $q_{j}$ is

  $$p_{j}=\frac{\partial L}{\partial \dot{q}_{j}}$$

  Derive Hamilton's equations in the form

  $$\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}, \quad \dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}$$

  Explain what is meant by the statement that $q_{k}$ is an ignorable coordinate and give an associated constant of the motion in this case.

  The Hamiltonian for a particle of mass $m$ moving on the surface of a sphere of radius $a$ under a potential $V(\theta)$ is given by

  $$H=\frac{1}{2 m a^{2}}\left(p_{\theta}^{2}+\frac{p_{\phi}^{2}}{\sin ^{2} \theta}\right)+V(\theta)$$

  where the generalized coordinates are the spherical polar angles $(\theta, \phi)$. Write down two constants of the motion and show that it is possible for the particle to move with constant $\theta$ provided that

  $$p_{\phi}^{2}=\left(\frac{m a^{2} \sin ^{3} \theta}{\cos \theta}\right) \frac{d V}{d \theta} .$$

  comment

Coding and Cryptography

• Paper 1, Section I, H

  Coding and Cryptography | Part II, 2009

  I am putting up my Christmas lights. If I plug in a set of bulbs and one is defective, none will light up. A badly written note left over from the previous year tells me that exactly one of my 10 bulbs is defective and that the probability that the $k$ th bulb is defective is $k / 55$.

  (i) Find an explicit procedure for identifying the defective bulb in the least expected number of steps.

  [You should explain your method but no proof is required.]

  (ii) Is there a different procedure from the one you gave in (i) with the same expected number of steps? Either write down another procedure and explain briefly why it gives the same expected number or explain briefly why no such procedure exists.

  (iii) Because I make such a fuss about each test, my wife wishes me to tell her the maximum number $N$ of trials that might be required. Will the procedure in (i) give the minimum $N$ ? Either write down another procedure and explain briefly why it gives a smaller $N$ or explain briefly why no such procedure exists.

  comment

• Paper 1, Section II, H

  Coding and Cryptography | Part II, 2009

  (i) State and prove Gibbs' inequality.

  (ii) A casino offers me the following game: I choose strictly positive numbers $a_{1}, \ldots, a_{n}$ with $\sum_{j=1}^{n} a_{j}=1$. I give the casino my entire fortune $f$ and roll an $n$-sided die. With probability $p_{j}$ the casino returns $u_{j}^{-1} a_{j} f$ for $j=1,2, \ldots, n$. If I intend to play the game many times (staking my entire fortune each time) explain carefully why I should choose $a_{1}, \ldots, a_{n}$ to maximise $\sum_{j=1}^{n} p_{j} \log \left(u_{j}^{-1} a_{j}\right)$.

  [You should assume $n \geqslant 2$ and $u_{j}, p_{j}>0$ for each $j .$ ]

  (iii) Determine the appropriate $a_{1}, \ldots, a_{n}$. Let $\sum_{i=1}^{n} u_{i}=U$. Show that, if $U<1$, then, in the long run with high probability, my fortune increases. Show that, if $U>1$, the casino can choose $u_{1}, \ldots, u_{n}$ in such a way that, in the long run with high probability, my fortune decreases. Is it true that, if $U>1$, any choice of $u_{1}, \ldots, u_{n}$ will ensure that, in the long run with high probability, my fortune decreases? Why?

  comment

Cosmology

• Paper 1, Section I, D

  Cosmology | Part II, 2009

  Prior to a time $t \sim 100,000$ years, the Universe was filled with a gas of photons and non-relativistic free electrons and protons maintained in equilibrium by Thomson scattering. At around $t \sim 400,000$ years, the protons and electrons began combining to form neutral hydrogen,

  $$p+e^{-} \leftrightarrow H+\gamma$$

  [You may assume that the equilibrium number density of a non-relativistic species $\left(k T \ll m c^{2}\right)$ is given by

  $$n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left(\left(\mu-m c^{2}\right) / k T\right)$$

  while the photon number density is

  $$n_{\gamma}=16 \pi \zeta(3)\left(\frac{k T}{h c}\right)^{3}, \quad(\zeta(3) \approx 1.20 \ldots)$$

  Deduce Saha's equation for the recombination process $(*)$ stating clearly your assumptions and the steps made in the calculation,

  $$\frac{n_{e}^{2}}{n_{H}}=\left(\frac{2 \pi m_{e} k T}{h^{2}}\right)^{3 / 2} \exp (-I / k T)$$

  where $I$ is the ionization energy of hydrogen.

  Consider now the fractional ionization $X_{e}=n_{e} / n_{B}$ where $n_{B}=n_{p}+n_{H}=\eta n_{\gamma}$ is the baryon number of the Universe and $\eta$ is the baryon to photon ratio. Find an expression for the ratio

  $$\left(1-X_{e}\right) / X_{e}^{2}$$

  in terms only of $k T$ and constants such as $\eta$ and $I$.

  Suggest a reason why neutral hydrogen forms at a temperature $k T \approx 0.3 \mathrm{eV}$ which is much lower than the hydrogen ionization temperature $k T=I \approx 13 \mathrm{eV}$.

  comment

• Paper 1, Section II, D

  Cosmology | Part II, 2009

  (i) In a homogeneous and isotropic universe, the scalefactor $a(t)$ obeys the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho,$$

  where $\rho(t)$ is the matter density which, together with the pressure $P(t)$, satisfies

  $$\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+P / c^{2}\right)$$

  Use these two equations to derive the Raychaudhuri equation,

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  (ii) Conformal time $\tau$ is defined by taking $d t / d \tau=a$, so that $\dot{a}=a^{\prime} / a \equiv \mathcal{H}$ where primes denote derivatives with respect to $\tau$. For matter obeying the equation of state $P=w \rho c^{2}$, show that the Friedmann and energy conservation equations imply

  $$\mathcal{H}^{2}+k c^{2}=\frac{8 \pi G}{3} \rho_{0} a^{-(1+3 w)}$$

  where $\rho_{0}=\rho\left(t_{0}\right)$ and we take $a\left(t_{0}\right)=1$ today. Use the Raychaudhuri equation to derive the expression

  $$\mathcal{H}^{\prime}+\frac{1}{2}(1+3 w)\left[\mathcal{H}^{2}+k c^{2}\right]=0$$

  For a $k c^{2}=1$ closed universe, by solving first for $\mathcal{H}$ (or otherwise), show that the scale factor satisfies

  $$a=\alpha(\sin \beta \tau)^{2 /(1+3 w)}$$

  where $\alpha, \beta$ are constants. [Hint: You may assume that $\int d x /\left(1+x^{2}\right)=-\cot ^{-1} x+$ const.]

  For a closed universe dominated by pressure-free matter $(P=0)$, find the complete parametric solution

  $$a=\frac{1}{2} \alpha(1-\cos 2 \beta \tau), \quad t=\frac{\alpha}{4 \beta}(2 \beta \tau-\sin 2 \beta \tau)$$

  comment

Differential Geometry

• Paper 1, Section II, H

  Differential Geometry | Part II, 2009

  (i) Define manifold and manifold with boundary for subsets $X \subset \mathbb{R}^{N}$.

  (ii) Let $X$ and $Y$ be manifolds and $f: X \rightarrow Y$ a smooth map. Define what it means for $y \in Y$ to be a regular value of $f$.

  (iii) Let $n \geqslant 0$ and let $\mathbb{S}^{n}$ denote the set $\left\{\left(x^{1}, \ldots, x^{n+1}\right) \in \mathbb{R}^{n+1}: \sum_{i=1}^{n+1}\left(x^{i}\right)^{2}=1\right\}$. Let $B^{n+1}$ denote the set $\left\{\left(x^{1}, \ldots, x^{n+1}\right) \in \mathbb{R}^{n+1}: \sum_{i=1}^{n+1}\left(x^{i}\right)^{2} \leqslant 1\right\}$. Show that $\mathbb{S}^{n}$ is an $n$-dimensional manifold and $B^{n+1}$ is an $(n+1)$-dimensional manifold with boundary, with $\partial B^{n+1}=\mathbb{S}^{n}$.

  [You may use standard theorems involving regular values of smooth functions provided that you state them clearly.]

  (iv) For $n \geqslant 0$, consider the map $h: \mathbb{S}^{n} \rightarrow \mathbb{S}^{n}$ taking $\mathbf{x}$ to $-\mathbf{x}$. Show that $h$ is smooth. Now let $f$ be a smooth map $f: \mathbb{S}^{n} \rightarrow \mathbb{S}^{n}$ such that $f \circ h=f$. Show that $f$ is not smoothly homotopic to the identity map.

  comment

Dynamical Systems

• Paper 1, Section I, E

  Dynamical Systems | Part II, 2009

  Let $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ be a two-dimensional dynamical system with a fixed point at $\mathbf{x}=\mathbf{0}$. Define a Lyapunov function $V(\mathbf{x})$ and explain what it means for $\mathbf{x}=\mathbf{0}$ to be Lyapunov stable.

  Determine the values of $\beta$ for which $V=x^{2}+\beta y^{2}$ is a Lyapunov function in a sufficiently small neighbourhood of the origin for the system

  $$\begin{aligned} &\dot{x}=-x+2 y+2 x y-x^{2}-4 y^{2}, \\ &\dot{y}=-y+x y . \end{aligned}$$

  What can be deduced about the basin of attraction of the origin using $V$ when $\beta=2 ?$

  comment

Electrodynamics

• Paper 1, Section II, C

  Electrodynamics | Part II, 2009

  The action for a modified version of electrodynamics is given by

  $$I=\int d^{4} x\left(-\frac{1}{4} F_{a b} F^{a b}-\frac{1}{2} m^{2} A_{a} A^{a}+\mu_{0} J^{a} A_{a}\right)$$

  where $m$ is an arbitrary constant, $F_{a b}=\partial_{a} A_{b}-\partial_{b} A_{a}$ and $J^{a}$ is a conserved current.

  (i) By varying $A_{a}$, derive the field equations analogous to Maxwell's equations by demanding that $\delta I=0$ for an arbitrary variation $\delta A_{a}$.

  (ii) Show that $\partial_{a} A^{a}=0$.

  (iii) Suppose that the current $J^{a}(x)$ is a function of position only. Show that

  $$A^{a}(\mathbf{x})=\frac{\mu_{0}}{4 \pi} \int d^{3} x^{\prime} \frac{J^{a}\left(\mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} e^{-m\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}$$

  comment

Fluid Dynamics II

• Paper 1, Section II, E

  Fluid Dynamics II | Part II, 2009

  Explain the assumptions of lubrication theory and its use in determining the flow in thin films.

  A cylindrical roller of radius a rotates at angular velocity $\Omega$ below the free surface at $y=0$ of a fluid of density $\rho$ and dynamic viscosity $\mu$. The gravitational acceleration is $g$, and the pressure above the free surface is $p_{0}$. The minimum distance of the roller below the fluid surface is $b$, where $b \ll a$. The depth of the roller $d(x)$ below the free surface may be approximated by $d(x) \approx b+x^{2} / 2 a$, where $x$ is the horizontal distance.

  (i) State the conditions for lubrication theory to be applicable to this problem. On the further assumption that the free surface may be taken to be flat, find the flow above the roller and calculate the horizontal volume flux $Q$ (per unit length in the third dimension) and the horizontal pressure gradient.

  (ii) Use the pressure gradient you have found to estimate the order of magnitude of the departure $h(x)$ of the free surface from $y=0$, and give conditions on the parameters that ensure that $|h| \ll b$, as required for part (i).

  [Hint: Integrals of the form

  $$I_{n}=\int_{-\infty}^{\infty}\left(1+t^{2}\right)^{-n} d t$$

  satisfy $I_{1}=\pi$ and

  $$I_{n+1}=\left(\frac{2 n-1}{2 n}\right) I_{n}$$

  for $n \geqslant 1 .]$

  comment

Further Complex Methods

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2009

  Find all second order linear ordinary homogenous differential equations which have a regular singular point at $z=0$, a regular singular point at $z=\infty$, and for which every other point in the complex $z$-plane is an analytic point.

  [You may use without proof Liouville's theorem.]

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2009

  Let $F(z)$ be defined by

  $$F(z)=\int_{0}^{\infty} \frac{e^{-2 z t}}{1+t^{3}} d t, \quad|\arg z|<\frac{\pi}{2}$$

  Let $\tilde{F}(z)$ be defined by

  $$\tilde{F}(z)=\int_{0}^{-i \infty} \frac{e^{-2 z \zeta}}{1+\zeta^{3}} d \zeta, \quad \alpha<\arg z<\beta$$

  where the above integral is along the negative imaginary axis of the complex $\zeta$-plane and the real constants $\alpha$ and $\beta$ are to be determined.

  Using Cauchy's theorem, or otherwise, compute $F(z)-\tilde{F}(z)$ and hence find a formula for the analytic continuation of $F(z)$ for $\frac{\pi}{2} \leqslant \arg z<\pi$.

  comment

Galois Theory

• Paper 1, Section II, H

  Galois Theory | Part II, 2009

  Define a $K$-isomorphism, $\varphi: L \rightarrow L^{\prime}$, where $L, L^{\prime}$ are fields containing a field $K$, and define $\operatorname{Aut}_{K}(L)$.

  Suppose $\alpha$ and $\beta$ are algebraic over $K$. Show that $K(\alpha)$ and $K(\beta)$ are $K$-isomorphic via an isomorphism mapping $\alpha$ to $\beta$ if and only if $\alpha$ and $\beta$ have the same minimal polynomial.

  Show that $\operatorname{Aut}_{K} K(\alpha)$ is finite, and a subgroup of the symmetric group $S_{d}$, where $d$ is the degree of $\alpha$.

  Give an example of a field $K$ of characteristic $p>0$ and $\alpha$ and $\beta$ of the same degree, such that $K(\alpha)$ is not isomorphic to $K(\beta)$. Does such an example exist if $K$ is finite? Justify your answer.

  comment

General Relativity

• Paper 1, Section II, D

  General Relativity | Part II, 2009

  Write down the differential equations governing geodesic curves $x^{a}(\lambda)$ both when $\lambda$ is an affine parameter and when it is a general one.

  A conformal transformation of a spacetime is given by

  $$g_{a b} \rightarrow \tilde{g}_{a b}=\Omega^{2}(x) g_{a b}$$

  Obtain a formula for the new Christoffel symbols $\tilde{\Gamma}_{b c}^{a}$ in terms of the old ones and the derivatives of $\Omega$. Hence show that null geodesics in the metric $g_{a b}$ are also geodesic in the metric $\tilde{g}_{a b}$.

  Show that the Riemann tensor has only one independent component in two dimensions, and hence derive

  $$R=2 \operatorname{det}\left(g^{a b}\right) R_{0101}$$

  where $R$ is the Ricci scalar.

  It is given that in a 2-dimensional spacetime $M, R$ transforms as

  $$R \rightarrow \tilde{R}=\Omega^{-2}(R-2 \square \log \Omega)$$

  where $\square \phi=g^{a b} \nabla_{a} \nabla_{b} \phi$. Assuming that the equation $\square \phi=\rho(x)$ can always be solved, show that $\Omega$ can be chosen to set $\tilde{g}$ to be the metric of 2-dimensional Minkowski spacetime. Hence show that all null curves in $M$ are geodesic.

  Discuss the null geodesics if the line element of $M$ is

  $$d s^{2}=-t^{-1} d t^{2}+t d \theta^{2}$$

  where $t \in(-\infty, 0)$ or $(0, \infty)$ and $\theta \in[0,2 \pi]$.

  comment

Geometry of Group Actions

• Paper 1, Section I, F

  Geometry of Group Actions | Part II, 2009

  Explain what is meant by stereographic projection from the 2-dimensional sphere to the complex plane.

  Prove that $u$ and $v$ are the images under stereographic projection of antipodal points on the sphere if and only if $u \bar{v}=-1$.

  comment

• Paper 1, Section II, F

  Geometry of Group Actions | Part II, 2009

  Define frieze group and crystallographic group and give three examples of each, identifying them as abstract groups as well as geometrically.

  Let $G$ be a discrete group of isometries of the Euclidean plane which contains a translation. Prove that $G$ contains no element of order 5 .

  comment

Graph Theory

• Paper 1, Section II, $17 \mathrm{~F}$

  Graph Theory | Part II, 2009

  (i) State and prove Hall's theorem concerning matchings in bipartite graphs.

  (ii) The matching number of a graph $G$ is the maximum size of a family of independent edges (edges without shared vertices) in $G$. Deduce from Hall's theorem that if $G$ is a $k$-regular bipartite graph on $n$ vertices (some $k>0$ ) then $G$ has matching number $n / 2$.

  (iii) Now suppose that $G$ is an arbitrary $k$-regular graph on $n$ vertices (some $k>0)$. Show that $G$ has a matching number at least $\frac{k}{4 k-2} n$. [Hint: Let $S$ be the set of vertices in a maximal set of independent edges. Consider the edges of $G$ with exactly one endpoint in $S$.]

  For $k=2$, show that there are infinitely many graphs $G$ for which equality holds.

  comment

Integrable Systems

• Paper 1, Section II, B

  Integrable Systems | Part II, 2009

  Let $H$ be a smooth function on a $2 n$-dimensional phase space with local coordinates $\left(p_{j}, q_{j}\right)$. Write down the Hamilton equations with the Hamiltonian given by $H$ and state the Arnold-Liouville theorem.

  By establishing the existence of sufficiently many first integrals demonstrate that the system of $n$ coupled harmonic oscillators with the Hamiltonian

  $$H=\frac{1}{2} \sum_{k=1}^{n}\left(p_{k}^{2}+\omega_{k}^{2} q_{k}^{2}\right)$$

  where $\omega_{1}, \ldots, \omega_{n}$ are constants, is completely integrable. Find the action variables for this system.

  comment

Linear Analysis

• Paper 1, Section II, H

  Linear Analysis | Part II, 2009

  (a) State and prove the Baire category theorem.

  (b) Let $X$ be a normed space. Show that every proper linear subspace $V \subset X$ has empty interior.

  (c) Let $\mathcal{P}$ be the vector space of all real polynomials in one variable. Using the Baire category theorem and the result from (b), prove that for any norm $\|\cdot\|$ on $\mathcal{P}$, the normed space $(\mathcal{P},\|\cdot\|)$ is not a Banach space.

  comment

Logic and Set Theory

• Paper 1, Section II, G

  Logic and Set Theory | Part II, 2009

  Prove that if $G:$ On $\times V \rightarrow V$ is a definable function, then there is a definable function $F:$ On $\rightarrow V$ satisfying

  $$F(\alpha)=G(\alpha,\{F(\beta): \beta<\alpha\})$$

  Define the notion of an initial ordinal, and explain its significance for cardinal arithmetic. State Hartogs' lemma. Using the recursion theorem define, giving justification, a function $\omega:$ On $\rightarrow$ On which enumerates the infinite initial ordinals.

  Is there an ordinal $\alpha$ with $\alpha=\omega_{\alpha} ?$ Justify your answer.

  comment

Mathematical Biology

• Paper 1, Section I, A

  Mathematical Biology | Part II, 2009

  A discrete model for a population $N_{t}$ consists of

  $$N_{t+1}=\frac{r N_{t}}{\left(1+b N_{t}\right)^{2}},$$

  where $t$ is discrete time and $r, b>0$. What do $r$ and $b$ represent in this model? Show that for $r>1$ there is a stable fixed point.

  Suppose the initial condition is $N_{1}=1 / b$, and that $r>4$. Show, with the help of a cobweb, that the population $N_{t}$ is bounded by

  $$\frac{4 r^{2}}{(4+r)^{2} b} \leqslant N_{t} \leqslant \frac{r}{4 b}$$

  and attains those bounds.

  comment

Number Fields

• Paper 1, Section II, H

  Number Fields | Part II, 2009

  Suppose that $K$ is a number field with ring of integers $\mathcal{O}_{K}$.

  (i) Suppose that $M$ is a sub- $\mathbb{Z}$-module of $\mathcal{O}_{K}$ of finite index $r$ and that $M$ is closed under multiplication. Define the discriminant of $M$ and of $\mathcal{O}_{K}$, and show that $\operatorname{disc}(M)=r^{2} \operatorname{disc}\left(\mathcal{O}_{K}\right) .$

  (ii) Describe $\mathcal{O}_{K}$ when $K=\mathbb{Q}[X] /\left(X^{3}+2 X+1\right)$.

  [You may assume that the polynomial $X^{3}+p X+q$ has discriminant $-4 p^{3}-27 q^{2}$.]

  (iii) Suppose that $f, g \in \mathbb{Z}[X]$ are monic quadratic polynomials with equal discriminant $d$, and that $d \notin\{0,1\}$ is square-free. Show that $\mathbb{Z}[X] /(f)$ is isomorphic to $\mathbb{Z}[X] /(g)$.

  [Hint: Classify quadratic fields in terms of discriminants.]

  comment

Number Theory

• Paper 1, Section I, G

  Number Theory | Part II, 2009

  State the Chinese Remainder Theorem.

  Determine all integers $x$ satisfying the congruences $x \equiv 2 \bmod 3, x \equiv 2 \bmod 5$, $x \equiv 6 \bmod 7 .$

  comment

Numerical Analysis

• Paper 1, Section II, B

  Numerical Analysis | Part II, 2009

  (i) Define the Jacobi method with relaxation for solving the linear system $A \boldsymbol{x}=\boldsymbol{b}$.

  (ii) For $\boldsymbol{x}^{*}$ and $\boldsymbol{x}^{(\nu)}$ being the exact and the iterated solution, respectively, let $e^{(\nu)}:=\boldsymbol{x}^{(\nu)}-\boldsymbol{x}^{*}$ be the error and $H_{\omega}$ the iteration matrix, so that

  $$e^{(\nu+1)}=H_{\omega} e^{(\nu)}$$

  Express $H_{\omega}$ in terms of the matrix $A$, its diagonal part $D$ and the relaxation parameter $\omega$, and find the eigenvectors $\boldsymbol{v}_{k}$ and the eigenvalues $\lambda_{k}(\omega)$ of $H_{\omega}$ for the $n \times n$ tridiagonal matrix

  $$A=\left[\begin{array}{rrrrr} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 2 & -1 \\ & & & -1 & 2 \end{array}\right]$$

  [Hint: The eigenvectors and eigenvalues of $A$ are

  $$\left.\left(\boldsymbol{u}_{k}\right)_{i}=\sin \frac{k i \pi}{n+1}, \quad i=1, \ldots, n, \quad \lambda_{k}(A)=4 \sin ^{2} \frac{k \pi}{2(n+1)}, \quad k=1, \ldots, n .\right]$$

  (iii) For $A$ as above, let

  $$\boldsymbol{e}^{(\nu)}=\sum_{k=1}^{n} a_{k}^{(\nu)} \boldsymbol{v}_{k}$$

  be the expansion of the error with respect to the eigenvectors $\left(\boldsymbol{v}_{k}\right)$ of $H_{\omega}$.

  Find the range of parameter $\omega$ which provides convergence of the method for any $n$, and prove that, for any such $\omega$, the rate of convergence $e^{(\nu)} \rightarrow 0$ is not faster than $\left(1-c / n^{2}\right)^{\nu}$.

  (iv) Show that, for some $\omega$, the high frequency components $\left(\frac{n+1}{2} \leqslant k \leqslant n\right)$ of the error $e^{(\nu)}$ tend to zero much faster. Determine the optimal parameter $\omega_{*}$ which provides the largest suppression of the high frequency components per iteration, and find the corresponding attenuation factor $\mu_{*}$ (i.e. the least $\mu_{\omega}$ such that $\left|a_{k}^{(\nu+1)}\right| \leqslant \mu_{\omega}\left|a_{k}^{(\nu)}\right|$ for $\left.\frac{n+1}{2} \leqslant k \leqslant n\right)$.

  comment

Partial Differential Equations

• Paper 1, Section II, B

  Partial Differential Equations | Part II, 2009

  Consider the initial value problem for the so-called Liouville equation

  $$\begin{gathered} f_{t}+v \cdot \nabla_{x} f-\nabla V(x) \cdot \nabla_{v} f=0,(x, v) \in \mathbb{R}^{2 d}, t \in \mathbb{R} \\ f(x, v, t=0)=f_{I}(x, v) \end{gathered}$$

  for the function $f=f(x, v, t)$ on $\mathbb{R}^{2 d} \times \mathbb{R}$. Assume that $V=V(x)$ is a given function with $V, \nabla_{x} V$ Lipschitz continuous on $\mathbb{R}^{d}$.

  (i) Let $f_{I}(x, v)=\delta\left(x-x_{0}, v-v_{0}\right)$, for $x_{0}, v_{0} \in \mathbb{R}^{d}$ given. Show that a solution $f$ is given by

  $$f(x, v, t)=\delta\left(x-\hat{x}\left(t, x_{0}, v_{0}\right), v-\hat{v}\left(t, x_{0}, v_{0}\right)\right)$$

  where $(\hat{x}, \hat{v})$ solve the Newtonian system

  $$\begin{array}{ll} \dot{\hat{x}}=\hat{v}, & \hat{x}(t=0)=x_{0} \\ \dot{\hat{v}}=-\nabla V(\hat{x}), & \hat{v}(t=0)=v_{0} \end{array}$$

  (ii) Let $f_{I} \in L_{l o c}^{1}\left(\mathbb{R}^{2 d}\right), f_{I} \geqslant 0$. Prove (by using characteristics) that $f$ remains nonnegative (as long as it exists).

  (iii) Let $f_{I} \in L^{p}\left(\mathbb{R}^{2 d}\right), f_{I} \geqslant 0$ on $\mathbb{R}^{2 d}$. Show (by a formal argument) that

  $$\|f(\cdot, \cdot, t)\|_{L^{p}\left(\mathbb{R}^{2 d}\right)}=\left\|f_{I}\right\|_{L^{p}\left(\mathbb{R}^{2 d}\right)}$$

  for all $t \in \mathbb{R}, 1 \leqslant p<\infty$.

  (iv) Let $V(x)=\frac{1}{2}|x|^{2}$. Use the method of characteristics to solve the initial value problem for general initial data.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  The position and momentum for a harmonic oscillator can be written

  $$\hat{x}=\left(\frac{\hbar}{2 m \omega}\right)^{1 / 2}\left(a+a^{\dagger}\right), \quad \hat{p}=\left(\frac{\hbar m \omega}{2}\right)^{1 / 2} i\left(a^{\dagger}-a\right)$$

  where $m$ is the mass, $\omega$ is the frequency, and the Hamiltonian is

  $$H=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2}=\hbar \omega\left(a^{\dagger} a+\frac{1}{2}\right)$$

  Starting from the commutation relations for $a$ and $a^{\dagger}$, determine the energy levels of the oscillator. Assuming a unique ground state, explain how all other energy eigenstates can be constructed from it.

  Consider a modified Hamiltonian

  $$H^{\prime}=H+\lambda \hbar \omega\left(a^{2}+a^{\dagger 2}\right)$$

  where $\lambda$ is a dimensionless parameter. Calculate the modified energy levels to second order in $\lambda$, quoting any standard formulas which you require. Show that the modified Hamiltonian can be written as

  $$H^{\prime}=\frac{1}{2 m} \alpha \hat{p}^{2}+\frac{1}{2} m \omega^{2} \beta \hat{x}^{2}$$

  where $\alpha$ and $\beta$ depend on $\lambda$. Hence find the modified energies exactly, assuming $|\lambda|<\frac{1}{2}$, and show that the results are compatible with those obtained from perturbation theory.

  comment

Principles of Statistics

• Paper 1, Section II, I

  Principles of Statistics | Part II, 2009

  (i) Let $X_{1}, \ldots, X_{n}$ be independent and identically distributed random variables, having the exponential distribution $\mathcal{E}(\lambda)$ with density $p(x \mid \lambda)=\lambda \exp (-\lambda x)$ for $x, \lambda>0$. Show that $T_{n}=\sum_{i=1}^{n} X_{i}$ is minimal sufficient and complete for $\lambda$.

  [You may assume uniqueness of Laplace transforms.]

  (ii) For given $x>0$, it is desired to estimate the quantity $\phi=\operatorname{Prob}\left(X_{1}>x \mid \lambda\right)$. Compute the Fisher information for $\phi$.

  (iii) State the Lehmann-Scheffé theorem. Show that the estimator $\tilde{\phi}_{n}$ of $\phi$ defined by

  $$\tilde{\phi}_{n}= \begin{cases}0, & \text { if } T_{n}<x, \\ \left(1-\frac{x}{T_{n}}\right)^{n-1}, & \text { if } T_{n} \geqslant x\end{cases}$$

  is the minimum variance unbiased estimator of $\phi$ based on $\left(X_{1}, \ldots, X_{n}\right)$. Without doing any computations, state whether or not the variance of $\tilde{\phi}_{n}$ achieves the Cramér-Rao lower bound, justifying your answer briefly.

  Let $k \leqslant n$. Show that $\mathbb{E}\left(\tilde{\phi}_{k} \mid T_{n}, \lambda\right)=\tilde{\phi}_{n}$.

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2009

  Let $(E, \mathcal{E}, \mu)$ be a measure space. Explain what is meant by a simple function on $(E, \mathcal{E}, \mu)$ and state the definition of the integral of a simple function with respect to $\mu$.

  Explain what is meant by an integrable function on $(E, \mathcal{E}, \mu)$ and explain how the integral of such a function is defined.

  State the monotone convergence theorem.

  Show that the following map is linear

  $$f \mapsto \mu(f): L^{1}(E, \mathcal{E}, \mu) \rightarrow \mathbb{R}$$

  where $\mu(f)$ denotes the integral of $f$ with respect to $\mu$.

  [You may assume without proof any fact concerning simple functions and their integrals. You are not expected to prove the monotone convergence theorem.]

  comment

Representation Theory

• Paper 1, Section II, F

  Representation Theory | Part II, 2009

  Let $G$ be a finite group, and suppose $G$ acts on the finite sets $X_{1}, X_{2}$. Define the permutation representation $\rho_{X_{1}}$ corresponding to the action of $G$ on $X_{1}$, and compute its character $\pi_{X_{1}}$. State and prove "Burnside's Lemma".

  Let $G$ act on $X_{1} \times X_{2}$ via the usual diagonal action. Prove that the character inner product $\left\langle\pi_{X_{1}}, \pi_{X_{2}}\right\rangle$ is equal to the number of $G$-orbits on $X_{1} \times X_{2}$.

  Hence, or otherwise, show that the general linear group $\mathrm{GL}_{2}(q)$ of invertible $2 \times 2$ matrices over the finite field of $q$ elements has an irreducible complex representation of dimension equal to $q$.

  Let $S_{n}$ be the symmetric group acting on the set $X=\{1,2, \ldots, n\}$. Denote by $Z$ the set of all 2-element subsets $\{i, j\}(i \neq j)$ of elements of $X$, with the natural action of $S_{n}$. If $n \geqslant 4$, decompose $\pi_{Z}$ into irreducible complex representations, and determine the dimension of each irreducible constituent. What can you say when $n=3$ ?

  comment

Riemann Surfaces

• Paper 1, Section II, G

  Riemann Surfaces | Part II, 2009

  (a) Let $X=\mathbb{C} \cup\{\infty\}$ be the Riemann sphere. Define the notion of a rational function $r$ and describe the function $f: X \rightarrow X$ determined by $r$. Assuming that $f$ is holomorphic and non-constant, define the degree of $r$ as a rational function and the degree of $f$ as a holomorphic map, and prove that the two degrees coincide. [You are not required to prove that the degree of $f$ is well-defined.]

  Let $A=\left\{a_{1}, a_{2}, a_{3}\right\}$ and $B=\left\{b_{1}, b_{2}, b_{3}\right\}$ be two subsets of $X$ each containing three distinct elements. Prove that $X \backslash A$ is biholomorphic to $X \backslash B$.

  (b) Let $Z \subset \mathbb{C}^{2}$ be the algebraic curve defined by the vanishing of the polynomial $p(z, w)=w^{2}-z^{3}+z^{2}+z$. Prove that $Z$ is smooth at every point. State the implicit function theorem and define a complex structure on $Z$, so that the maps $g, h: Z \rightarrow \mathbb{C}$ given by $g(z, w)=w, h(z, w)=z$ are holomorphic.

  Define what is meant by a ramification point of a holomorphic map between Riemann surfaces. Give an example of a ramification point of $g$ and calculate the branching order of $g$ at that point.

  comment

Statistical Modelling

• Paper 1, Section I, I

  Statistical Modelling | Part II, 2009

  Consider a binomial generalised linear model for data $y_{1}, \ldots, y_{n}$, modelled as realisations of independent $Y_{i} \sim \operatorname{Bin}\left(1, \mu_{i}\right)$ and $\operatorname{logit} \operatorname{link}$, i.e. $\log \frac{\mu_{i}}{1-\mu_{i}}=\beta x_{i}$, for some known constants $x_{1}, \ldots, x_{n}$, and an unknown parameter $\beta$. Find the log-likelihood for $\beta$, and the likelihood equations that must be solved to find the maximum likelihood estimator $\hat{\beta}$ of $\beta$.

  Compute the first and second derivatives of the log-likelihood for $\beta$, and explain the algorithm you would use to find $\hat{\beta}$.

  comment

• Paper 1, Section II, I

  Statistical Modelling | Part II, 2009

  A three-year study was conducted on the survival status of patients suffering from cancer. The age of the patients at the start of the study was recorded, as well as whether or not the initial tumour was malignant. The data are tabulated in $\mathrm{R}$ as follows:

  $$\begin{array}{rrrrr} > & \text { cancer } & & & \\ & & \text { age malignant } & \text { survive } & \text { die } \\ 1 & <50 & \text { no } & 77 & 10 \\ 2 & <50 & \text { yes } & 51 & 13 \\ 3 & 50-69 & \text { no } & 51 & 11 \\ 4 & 50-69 & \text { yes } & 38 & 20 \\ 5 & 70+ & \text { no } & 7 & 3 \\ 6 & 70+ & \text { yes } & 6 & 3 \end{array}$$

  Describe the model that is being fitted by the following $\mathrm{R}$ commands:

  

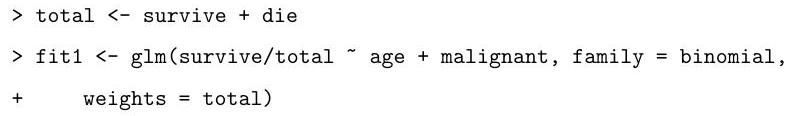
  Explain the (slightly abbreviated) output from the code below, describing how the hypothesis tests are performed and your conclusions based on their results.

  

  Based on the summary above, motivate and describe the following alternative model:

  

  Based on the output of the code that follows, which of the two models do you prefer? Why?

  

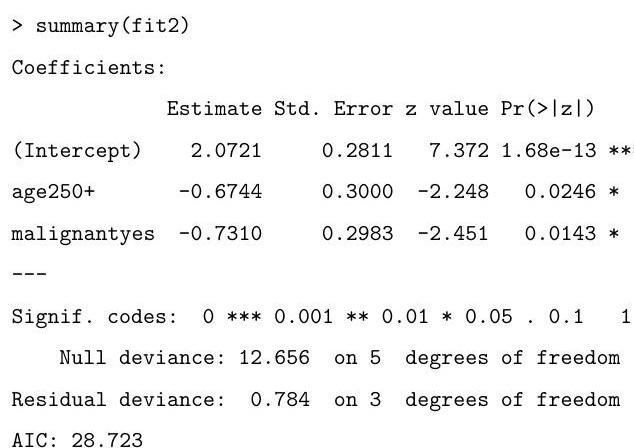
  What is the final value obtained by the following commands?

  

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2009

  An investor must decide how to invest his initial wealth $w_{0}$ in $n$ assets for the coming year. At the end of the year, one unit of asset $i$ will be worth $X_{i}, i=1, \ldots, n$, where $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ has a multivariate normal distribution with mean $\mu$ and non-singular covariance matrix $V$. At the beginning of the year, one unit of asset $i$ costs $p_{i}$. In addition, he may invest in a riskless bank account; an initial investment of 1 in the bank account will have grown to $1+r>1$ at the end of the year.

  (a) The investor chooses to hold $\theta_{i}$ units of asset $i$, with the remaining $\varphi=w_{0}-\theta \cdot p$ in the bank account. His objective is to minimise the variance of his wealth $w_{1}=\varphi(1+r)+\theta \cdot X$ at the end of the year, subject to a required mean value $m$ for $w_{1}$. Derive the optimal portfolio $\theta^{*}$, and the minimised variance.

  (b) Describe the set $A \subseteq \mathbb{R}^{2}$ of achievable pairs $\left(\mathbb{E}\left[w_{1}\right], \operatorname{var}\left(w_{1}\right)\right)$ of mean and variance of the terminal wealth. Explain what is meant by the mean-variance efficient frontier as you do so.

  (c) Suppose that the investor requires expected mean wealth at time 1 to be $m$. He wishes to minimise the expected shortfall $\mathbb{E}\left[\left(w_{1}-(1+r) w_{0}\right)^{-}\right]$subject to this requirement. Show that he will choose a portfolio corresponding to a point on the mean-variance efficient frontier.

  comment

Topics in Analysis

• Paper 1, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  (i) Let $n \geqslant 1$ and let $x_{1}, \ldots, x_{n}$ be distinct points in $[-1,1]$. Show that there exist numbers $A_{1}, \ldots, A_{n}$ such that

  $$\int_{-1}^{1} P(x) d x=\sum_{j=1}^{n} A_{j} P\left(x_{j}\right)$$

  for every polynomial $P$ of degree $\leqslant n-1$.

  (ii) Explain, without proof, how one can choose the points $x_{1}, \ldots, x_{n}$ and the numbers $A_{1}, \ldots, A_{n}$ such that $(*)$ holds for all polynomials $P$ of degree $\leqslant 2 n-1$.

  comment

Waves

• Paper 1, Section II, 38A

  Waves | Part II, 2009

  The wave equation with spherical symmetry may be written

  $$\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \tilde{p})-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} \tilde{p}=0$$

  Find the solution for the pressure disturbance $\tilde{p}$ in an outgoing wave, driven by a timevarying source with mass outflow rate $q(t)$ at the origin, in an infinite fluid.

  A semi-infinite fluid of density $\rho$ and sound speed $c$ occupies the half space $x>0$. The plane $x=0$ is occupied by a rigid wall, apart from a small square element of side $h$ that is centred on the point $\left(0, y^{\prime}, z^{\prime}\right)$ and oscillates in and out with displacement $f_{0} e^{i \omega t}$. By modelling this element as a point source, show that the pressure field in $x>0$ is given by

  $$\tilde{p}(t, x, y, z)=-\frac{2 \rho \omega^{2} f_{0} h^{2}}{4 \pi R} e^{i \omega\left(t-\frac{R}{c}\right)}$$

  where $R=\left[x^{2}+\left(y-y^{\prime}\right)^{2}+\left(z-z^{\prime}\right)^{2}\right]^{1 / 2}$, on the assumption that $R \gg c / \omega \gg f_{0}, h$. Explain the factor 2 in the above formula.

  Now suppose that the plane $x=0$ is occupied by a loudspeaker whose displacement is given by

  $$x=f(y, z) e^{i \omega t},$$

  where $f(y, z)=0$ for $|y|,|z|>L$. Write down an integral expression for the pressure in $x>0$. In the far field where $r=\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2} \gg L, \omega L^{2} / c, c / \omega$, show that

  $$\tilde{p}(t, x, y, z) \approx-\frac{\rho \omega^{2}}{2 \pi r} e^{i \omega(t-r / c)} \hat{f}(m, n)$$

  where $m=-\frac{\omega y}{r c}, n=-\frac{\omega z}{r c}$ and

  $$\hat{f}(m, n)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f\left(y^{\prime}, z^{\prime}\right) e^{-i\left(m y^{\prime}+n z^{\prime}\right)} d y^{\prime} d z^{\prime}$$

  Evaluate this integral when $f$ is given by

  $$f(y, z)= \begin{cases}1, & -a<y<a,-b<z<b \\ 0, & \text { otherwise }\end{cases}$$

  and discuss the result in the case $\omega b / c$ is small but $\omega a / c$ is of order unity.

  comment