Part II, 2008, Paper 3

Algebraic Topology

• 3.II.20F

  Algebraic Topology | Part II, 2008

  Let $X$ be the quotient space obtained by identifying one pair of antipodal points on $S^{2}$. Using the Mayer-Vietoris exact sequence, calculate the homology groups and the Betti numbers of $X$.

  comment

Applications of Quantum Mechanics

• 3.II.33E

  Applications of Quantum Mechanics | Part II, 2008

  Consider the body-centred cuboidal lattice $L$ with lattice points $\left(n_{1} a, n_{2} a, n_{3} b\right)$ and $\left(\left(n_{1}+\frac{1}{2}\right) a,\left(n_{2}+\frac{1}{2}\right) a,\left(n_{3}+\frac{1}{2}\right) b\right)$, where $a$ and $b$ are positive and $n_{1}, n_{2}$ and $n_{3}$ take all possible integer values. Find the reciprocal lattice $\widetilde{L}$and describe its geometrical form. Calculate the volumes of the unit cells of the lattices $L$ and $\widetilde{L}$.

  Find the reciprocal lattice vector associated with the lattice planes parallel to the plane containing the points $(0,0, b),(0, a, b),\left(\frac{1}{2} a, \frac{1}{2} a, \frac{1}{2} b\right),(a, 0,0)$ and $(a, a, 0)$. Deduce the allowed Bragg scattering angles of X-rays off these planes, assuming that $b=\frac{4}{3} a$ and that the X-rays have wavelength $\lambda=\frac{1}{2} a$.

  comment

Applied Probability

• 3.II.25I

  Applied Probability | Part II, 2008

  Let $\left(X_{t}\right)$ be an irreducible continuous-time Markov chain with countably many states. What does it mean to say the chain is (i) positive recurrent, (ii) null recurrent? Consider the chain $\left(X_{t}\right)$ with the arrow diagram below.

  

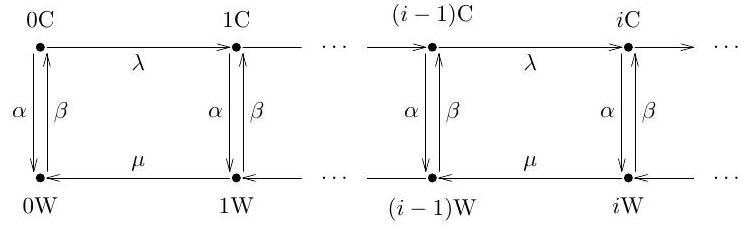
  In this question we analyse the existence of equilibrium probabilities $\pi_{i \mathrm{C}}$ and $\pi_{i \mathrm{~W}}$ of the chain $\left(X_{t}\right)$ being in state $i \mathrm{C}$ or $i \mathrm{~W}, i=0,1, \ldots$, and the impact of this fact on positive and null recurrence of the chain.

  (a) Write down the invariance equations $\pi Q=0$ and check that they have the form

  $$\begin{aligned} \pi_{0 C} &=\frac{\beta}{\lambda+\alpha} \pi_{0 \mathrm{~W}}, \\ \left(\pi_{1 \mathrm{C}}, \pi_{1 \mathrm{~W}}\right) &=\frac{\beta \pi_{0 \mathrm{~W}}}{\lambda+\alpha}\left(\frac{\lambda(\mu+\beta)}{\mu(\lambda+\alpha)}, \frac{\lambda}{\mu}\right) \\ \left(\pi_{(i+1) \mathrm{C}}, \pi_{(i+1) \mathrm{W}}\right) &=\left(\pi_{i \mathrm{C}}, \pi_{i \mathrm{~W}}\right) B, \quad i=1,2, \ldots, \end{aligned}$$

  where $B$ is a $2 \times 2$ recursion matrix:

  $$B=\left(\begin{array}{cc} \frac{\lambda \mu-\beta \alpha}{\mu(\lambda+\alpha)} & -\frac{\alpha}{\mu} \\ \frac{\beta(\beta+\mu)}{\mu(\lambda+\alpha)} & \frac{\beta+\mu}{\mu} \end{array}\right)$$

  (b) Verify that the row vector $\left(\pi_{1 \mathrm{C}}, \pi_{1 \mathrm{~W}}\right)$ is an eigenvector of $B$ with the eigenvalue $\theta$ where

  $$\theta=\frac{\lambda(\mu+\beta)}{\mu(\lambda+\alpha)}$$

  Hence, specify the form of equilibrium probabilities $\pi_{i \mathrm{C}}$ and $\pi_{i \mathrm{~W}}$ and conclude that the chain $\left(X_{t}\right)$ is positive recurrent if and only if $\mu \alpha>\lambda \beta$.

  comment

Asymptotic Methods

• 3.II $. 30 \mathrm{~A}$

  Asymptotic Methods | Part II, 2008

  Describe how the leading-order approximation may be found by the method of stationary phase of

  $$I(\lambda)=\int_{a}^{b} f(t) \exp (i \lambda g(t)) d t$$

  for $\lambda \gg 1$, where $\lambda, f$ and $g$ are real. You should consider the cases for which: (a) $g^{\prime}(t)$ has one simple zero at $t=t_{0}$, where $a<t_{0}<b$; (b) $g^{\prime}(t)$ has more than one simple zero in the region $a<t<b$; and (c) $g^{\prime}(t)$ has only a simple zero at $t=b$.

  What is the order of magnitude of $I(\lambda)$ if $g^{\prime}(t)$ is non zero for $a \leqslant t \leqslant b$ ?

  Use the method of stationary phase to find the leading-order approximation for $\lambda \gg 1$ to

  $$J(\lambda)=\int_{0}^{1} \sin \left(\lambda\left(t^{3}-t\right)\right) d t$$

  [Hint:

  $$\left.\int_{-\infty}^{\infty} \exp \left(i u^{2}\right) d u=\sqrt{\pi} e^{i \pi / 4} .\right]$$

  comment

Classical Dynamics

• 3.I.9E

  Classical Dynamics | Part II, 2008

  Writing $\mathbf{x}=\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}, q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right)$, Hamilton's equations may be written in the form

  $$\dot{\mathbf{x}}=\mathbf{J} \frac{\partial H}{\partial \mathbf{x}} \text {, }$$

  where the $2 n \times 2 n$ matrix

  $$\mathbf{J}=\left(\begin{array}{rr} 0 & -I \\ I & 0 \end{array}\right)$$

  and $I$ and 0 denote the $n \times n$ unit and zero matrices respectively.

  Explain what is meant by the statement that the transformation $\mathbf{x} \rightarrow \mathbf{y}$,

  $$\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}, q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right) \rightarrow\left(P_{1}, P_{2}, P_{3}, \ldots, P_{n}, Q_{1}, Q_{2}, Q_{3}, \ldots, Q_{n}\right)$$

  is canonical, and show that the condition for this is that

  $$\mathbf{J}=\mathcal{J} \mathbf{J} \mathcal{J}^{T}$$

  where $\mathcal{J}$ is the Jacobian matrix with elements

  $$\mathcal{J}_{i j}=\frac{\partial y_{i}}{\partial x_{j}}$$

  Use this condition to show that for a system with $n=1$ the transformation given by

  $$P=p+2 q, \quad Q=\frac{1}{2} q-\frac{1}{4} p$$

  is canonical.

  comment

Coding and Cryptography

• 3.I.4G

  Coding and Cryptography | Part II, 2008

  Define the Hamming code $h: \mathbb{F}_{2}^{4} \rightarrow \mathbb{F}_{2}^{7}$ and prove that the minimum distance between two distinct code words is 3. Explain how the Hamming code allows one error to be corrected.

  A new code $c: \mathbb{F}_{2}^{4} \rightarrow \mathbb{F}_{2}^{8}$ is obtained by using the Hamming code for the first 7 bits and taking the last bit as a check digit on the previous 7 . Find the minimum distance between two distinct code words for this code. How many errors can this code detect? How many errors can it correct?

  comment

Differential Geometry

• 3.II.23H

  Differential Geometry | Part II, 2008

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define the Gauss Map, principal curvatures $k_{i}$, Gaussian curvature $K$ and mean curvature $H$. State the Theorema Egregium.

  (b) Define what is meant for $S$ to be minimal. Prove that if $S$ is minimal, then $K \leqslant 0$. Give an example of a minimal surface whose Gaussian curvature is not identically 0 , justifying your answer.

  (c) Does there exist a compact minimal surface $S \subset \mathbb{R}^{3}$ ? Justify your answer.

  comment

Dynamical Systems

• 3.I.7A

  Dynamical Systems | Part II, 2008

  State the normal-form equations for (i) a saddle-node bifurcation, (ii) a transcritical bifurcation and (iii) a pitchfork bifurcation, for a one-dimensional map $x_{n+1}=F\left(x_{n} ; \mu\right)$.

  Consider a period-doubling bifurcation of the form

  $$x_{n+1}=-x_{n}+\alpha+\beta x_{n}+\gamma x_{n}^{2}+\delta x_{n}^{3}+O\left(x_{n}^{4}\right),$$

  where $x_{n}=O\left(\mu^{1 / 2}\right), \alpha, \beta=O(\mu)$, and $\gamma, \delta=O(1)$ as $\mu \rightarrow 0$. Show that

  $$X_{n+2}=X_{n}+\hat{\mu} X_{n}-A X_{n}^{3}+O\left(X_{n}^{4}\right),$$

  where $X_{n}=x_{n}-\frac{1}{2} \alpha$, and the parameters $\hat{\mu}$ and $A$ are to be identified in terms of $\alpha, \beta$, $\gamma$ and $\delta$. Deduce the condition for the bifurcation to be supercritical.

  comment

• 3.II.14A

  Dynamical Systems | Part II, 2008

  Define the Poincaré index of a simple closed curve, not necessarily a trajectory, and the Poincaré index of an isolated fixed point $\mathbf{x}_{0}$ for a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$. State the Poincaré index of a periodic orbit.

  Consider the system

  $$\begin{aligned} &\dot{x}=y+a x-b x^{3} \\ &\dot{y}=x^{3}-x \end{aligned}$$

  where $a$ and $b$ are constants and $a \neq 0$.

  (a) Find and classify the fixed points, and state their Poincaré indices.

  (b) By considering a suitable function $H(x, y)$, show that any periodic orbit $\Gamma$ satisfies

  $$\oint_{\Gamma}\left(x-x^{3}\right)\left(a x-b x^{3}\right) d t=0$$

  where $x(t)$ is evaluated along the orbit.

  (c) Deduce that if $b / a<1$ then the second-order differential equation

  $$\ddot{x}-\left(a-3 b x^{2}\right) \dot{x}+x-x^{3}=0$$

  has no periodic solutions.

  comment

Fluid Dynamics II

• 3.II.36A

  Fluid Dynamics II | Part II, 2008

  Show that, in cylindrical polar co-ordinates, the streamfunction $\psi(r, \phi)$ for the velocity $\mathbf{u}=\left(u_{r}(r, \phi), u_{\phi}(r, \phi), 0\right)$ and vorticity $(0,0, \omega(r, \phi))$ of two-dimensional Stokes flow of incompressible fluid satisfies the equations

  $$\mathbf{u}=\left(\frac{1}{r} \frac{\partial \psi}{\partial \phi},-\frac{\partial \psi}{\partial r}, 0\right), \quad \nabla^{2} \omega=-\nabla^{4} \psi=0$$

  Show also that the pressure $p(r, \phi)$ satisfies $\nabla^{2} p=0$.

  A stationary rigid circular cylinder of radius $a$ occupies the region $r \leqslant a$. The flow around the cylinder tends at large distances to a simple shear flow, with velocity given in cartesian coordinates $(x, y, z)$ by $\mathbf{u}=(\Gamma y, 0,0)$. Inertial forces may be neglected.

  By solving the equation for $\psi$ in cylindrical polars, determine the flow field everywhere. Determine the torque on the cylinder per unit length in $z$.

  [Hint: in cylindrical polars

  $$\nabla^{2} V=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} V}{\partial \phi^{2}}$$

  The off-diagonal component of the rate-of-strain tensor is given by

  $$\left.e_{r \phi}=\frac{1}{2}\left(\frac{1}{r} \frac{\partial u_{r}}{\partial \phi}+r \frac{\partial}{\partial r}\left(\frac{u_{\phi}}{r}\right)\right) .\right]$$

  comment

Further Complex Methods

• 3.I.8C

  Further Complex Methods | Part II, 2008

  What is the effect of the Möbius transformation $z \rightarrow \frac{z}{z-1}$ on the points $z=0$, $z=\infty$ and $z=1$ ?

  By considering

  $$(z-1)^{-a} P\left\{\begin{array}{cccc} 0 & \infty & 1 & \\ 0 & a & 0 & z(z-1)^{-1} \\ 1-c & c-b & b-a & \end{array}\right\}$$

  or otherwise, show that $(z-1)^{-a} F\left(a, c-b ; c ; z(z-1)^{-1}\right)$ is a branch of the $P$-function

  

  Give a linearly independent branch.

  comment

Galois Theory

• 3.II.18H

  Galois Theory | Part II, 2008

  Let $L / K$ be a field extension.

  (a) State what it means for $\alpha \in L$ to be algebraic over $K$, and define its degree $\operatorname{deg}_{K}(\alpha)$. Show that if $\operatorname{deg}_{K}(\alpha)$ is odd, then $K(\alpha)=K\left(\alpha^{2}\right)$.

  [You may assume any standard results.]

  Show directly from the definitions that if $\alpha, \beta \in L$ are algebraic over $K$, then so too is $\alpha+\beta$.

  (b) State what it means for $\alpha \in L$ to be separable over $K$, and for the extension $L / K$ to be separable.

  Give an example of an inseparable extension $L / K$.

  Show that an extension $L / K$ is separable if $L$ is a finite field.

  comment

Geometry of Group Actions

• 3.I.3G

  Geometry of Group Actions | Part II, 2008

  Let $\operatorname{dim}_{H}$ denote the Hausdorff dimension of a set in $\mathbb{R}^{n}$. Prove that if $\operatorname{dim}_{H}(F)<1$ then $F$ is totally disconnected.

  [You may assume that if $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is a Lipschitz map then

  $$\left.\operatorname{dim}_{H}(f(F)) \leqslant \operatorname{dim}_{H}(F) .\right]$$

  comment

Graph Theory

• 3.II $. 17 \mathrm{~F} \quad$

  Graph Theory | Part II, 2008

  Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that if $G$ has $n$ vertices and $m$ edges then

  $$p_{G}(t)=a_{n} t^{n}-a_{n-1} t^{n-1}+a_{n-2} t^{n-2}-\ldots+(-1)^{n} a_{0}$$

  where $a_{n}=1$ and $a_{n-1}=m$ and $a_{i} \geqslant 0$ for all $0 \leqslant i \leqslant n$. [You may assume the deletion-contraction relation, provided it is clearly stated.]

  Show that if $G$ is a tree on $n$ vertices then $p_{G}(t)=t(t-1)^{n-1}$. Does the converse hold?

  [Hint: if $G$ is disconnected, how is the chromatic polynomial of $G$ related to the chromatic polynomials of its components?]

  Show that if $G$ is a graph on $n$ vertices with the same chromatic polynomial as $T_{r}(n)$ (the Turán graph on $n$ vertices with $r$ vertex classes) then $G$ must be isomorphic to $T_{r}(n)$.

  comment

Integrable Systems

• 3.II.31C

  Integrable Systems | Part II, 2008

  Let $U(\lambda)$ and $V(\lambda)$ be matrix-valued functions of $(x, y)$ depending on the auxiliary parameter $\lambda$. Consider a system of linear PDEs

  $$\frac{\partial}{\partial x} \Phi=U(\lambda) \Phi, \quad \frac{\partial}{\partial y} \Phi=V(\lambda) \Phi$$

  where $\Phi$ is a column vector whose components depend on $(x, y, \lambda)$. Derive the zero curvature representation as the compatibility conditions for this system.

  Assume that

  $$U(\lambda)=-\left(\begin{array}{ccc} u_{x} & 0 & \lambda \\ 1 & -u_{x} & 0 \\ 0 & 1 & 0 \end{array}\right), \quad V(\lambda)=-\left(\begin{array}{ccc} 0 & e^{-2 u} & 0 \\ 0 & 0 & e^{u} \\ \lambda^{-1} e^{u} & 0 & 0 \end{array}\right)$$

  and show that (1) is compatible if the function $u=u(x, y)$ satisfies the PDE

  $$\frac{\partial^{2} u}{\partial x \partial y}=F(u)$$

  for some $F(u)$ which should be determined.

  Show that the transformation

  $$(x, y) \longrightarrow\left(c x, c^{-1} y\right), \quad c \in \mathbb{R} \backslash\{0\}$$

  forms a symmetry group of the PDE (2) and find the vector field generating this group.

  Find the ODE characterising the group-invariant solutions of (2).

  comment

Linear Analysis

• 3.II.21F

  Linear Analysis | Part II, 2008

  State and prove the Stone-Weierstrass theorem for real-valued functions. You may assume that the function $x \mapsto|x|$ can be uniformly approximated by polynomials on any interval $[-k, k]$.

  Suppose that $0<a<b<1$. Let $\mathcal{F}$ be the set of functions which can be uniformly approximated on $[a, b]$ by polynomials with integer coefficients. By making appropriate use of the identity

  $$\frac{1}{2}=\frac{x}{1-(1-2 x)}=\sum_{n=0}^{\infty} x(1-2 x)^{n}$$

  or otherwise, show that $\mathcal{F}=\mathcal{C}([a, b])$.

  Is it true that every continuous function on $[0, b]$ can be uniformly approximated by polynomials with integer coefficients?

  comment

Logic and Set Theory

• 3.II.16G

  Logic and Set Theory | Part II, 2008

  What is a transitive set? Show that if $x$ is transitive then so are the union $\bigcup x$ and the power set $P x$ of $x$. If $\bigcup x$ is transitive, is $x$ transitive? If $P x$ is transitive, is $x$ transitive? Justify your answers.

  What is the transitive closure of a set? Show that any set $x$ has a transitive closure $T C(x)$.

  Suppose that $x$ has rank $\alpha$. What is the rank of $P x$ ? What is the rank of $T C(x)$ ?

  [You may use standard properties of rank.]

  comment

Mathematical Biology

• 3.I.6B

  Mathematical Biology | Part II, 2008

  An allosteric enzyme $E$ reacts with a substrate $S$ to produce a product $P$ according to the mechanism

  $$\begin{gathered} S+E \underset{k_{-1}}{\stackrel{k_{1}}{\rightleftharpoons}} C_{1} \stackrel{k_{2}}{\longrightarrow} E+P \\ S+C_{1} \underset{k_{-3}}{\stackrel{k_{3}}{\rightleftharpoons}} C_{2} \stackrel{k_{4}}{\rightarrow} C_{1}+P \end{gathered}$$

  where $C_{1}$ and $C_{2}$ are enzyme-substrate complexes. With lowercase letters denoting concentrations, write down a system of differential equations based on the Law of Mass Action which model this reaction mechanism.

  The initial conditions are $s=s_{0}, e=e_{0}, c_{1}=c_{2}=p=0 .$ Using $u=s / s_{0}$, $v_{i}=c_{i} / e_{0}, \tau=k_{1} e_{0} t$ and $\epsilon=e_{0} / s_{0}$, show that the nondimensional reaction mechanism reduces to

  $$\frac{d u}{d \tau}=f\left(u, v_{1}, v_{2}\right) \quad \text { and } \quad \epsilon \frac{d v_{i}}{d \tau}=g_{i}\left(u, v_{1}, v_{2}\right) \quad \text { for } \quad i=1,2$$

  finding expressions for $f, g_{1}$ and $g_{2}$.

  comment

• 3.II.13B

  Mathematical Biology | Part II, 2008

  Consider the activator-inhibitor system in the fast-inhibitor limit

  $$\begin{gathered} u_{t}=D u_{x x}-u(u-r)(u-1)-\rho(v-u) \\ 0=v_{x x}-(v-u) \end{gathered}$$

  where $D$ is small, $0<r<1$ and $0<\rho<1$.

  Examine the linear stability of the state $u=v=0$ using perturbations of the form $\exp (i k x+\sigma t)$. Sketch the growth-rate $\sigma$ as a function of the wavenumber $k$. Find the growth-rate of the most unstable wave, and so determine the boundary in the $r$ - $\rho$ parameter plane which separates stable and unstable modes.

  Show that the system is unchanged under the transformation $u \rightarrow 1-u, v \rightarrow 1-v$ and $r \rightarrow 1-r$. Hence write down the equation for the boundary between stable and unstable modes of the state $u=v=1$.

  comment

Number Theory

• 3.I.1H

  Number Theory | Part II, 2008

  Prove that, for all $x \geqslant 2$, we have

  $$\sum_{p \leqslant x} \frac{1}{p}>\log \log x-\frac{1}{2}$$

  [You may assume that, for $0<u<1$,

  $$-\log (1-u)-u<\frac{u^{2}}{2(1-u)} .$$

  comment

• 3.II.11H

  Number Theory | Part II, 2008

  State the reciprocity law for the Jacobi symbol.

  Let $a$ be an odd integer $>1$, which is not a square. Prove that there exists a positive integer $n$ such that $n \equiv 1 \bmod 4$ and

  $$\left(\frac{n}{a}\right)=-1$$

  Prove further that there exist infinitely many prime numbers $p$ such that

  $$\left(\frac{a}{p}\right)=-1$$

  comment

Numerical Analysis

• 3.II.38C

  Numerical Analysis | Part II, 2008

  (a) A numerical method for solving the ordinary differential equation

  $$y^{\prime}(t)=f(t, y), \quad t \in[0, T], \quad y(0)=y_{0},$$

  generates for every $h>0$ a sequence $\left\{y_{n}\right\}$, where $y_{n}$ is an approximation to $y\left(t_{n}\right)$ and $t_{n}=n h$. Explain what is meant by the convergence of the method.

  (b) Prove from first principles that if the function $f$ is sufficiently smooth and satisfies the Lipschitz condition

  $$|f(t, x)-f(t, y)| \leqslant \lambda|x-y|, \quad x, y \in \mathbb{R}, \quad t \in[0, T],$$

  for some $\lambda>0$, then the trapezoidal rule

  $$y_{n+1}=y_{n}+\frac{1}{2} h\left[f\left(t_{n}, y_{n}\right)+f\left(t_{n+1}, y_{n+1}\right)\right]$$

  converges.

  comment

Optimization and Control

• 3.II.28I

  Optimization and Control | Part II, 2008

  Let $Q$ be a positive-definite symmetric $m \times m$ matrix. Show that a non-negative quadratic form on $\mathbb{R}^{d} \times \mathbb{R}^{m}$ of the form

  $$c(x, a)=x^{T} R x+x^{T} S^{T} a+a^{T} S x+a^{T} Q a, \quad x \in \mathbb{R}^{d}, \quad a \in \mathbb{R}^{m}$$

  is minimized over $a$, for each $x$, with value $x^{T}\left(R-S^{T} Q^{-1} S\right) x$, by taking $a=K x$, where $K=-Q^{-1} S$.

  Consider for $k \leqslant n$ the controllable stochastic linear system in $\mathbb{R}^{d}$

  $$X_{j+1}=A X_{j}+B U_{j}+\varepsilon_{j+1}, \quad j=k, k+1, \ldots, n-1,$$

  starting from $X_{k}=x$ at time $k$, where the control variables $U_{j}$ take values in $\mathbb{R}^{m}$, and where $\varepsilon_{k+1}, \ldots, \varepsilon_{n}$ are independent, zero-mean random variables, with $\operatorname{var}\left(\varepsilon_{j}\right)=N_{j}$. Here, $A, B$ and $N_{j}$ are, respectively, $d \times d, d \times m$ and $d \times d$ matrices. Assume that a cost $c\left(X_{j}, U_{j}\right)$ is incurred at each time $j=k, \ldots, n-1$ and that a final cost $C\left(X_{n}\right)=X_{n}^{T} \Pi_{0} X_{n}$ is incurred at time $n$. Here, $\Pi_{0}$ is a given non-negative-definite symmetric matrix. It is desired to minimize, over the set of all controls $u$, the total expected cost $V^{u}(k, x)$. Write down the optimality equation for the infimal cost function $V(k, x)$.

  Hence, show that $V(k, x)$ has the form

  $$V(k, x)=x^{T} \Pi_{n-k} x+\gamma_{k}$$

  for some non-negative-definite symmetric matrix $\Pi_{n-k}$ and some real constant $\gamma_{k}$. Show how to compute the matrix $\Pi_{n-k}$ and constant $\gamma_{k}$ and how to determine an optimal control.

  comment

Partial Differential Equations

• 3.II.29C

  Partial Differential Equations | Part II, 2008

  Let $C_{p e r}^{\infty}=\left\{u \in C^{\infty}(\mathbb{R}): u(x+2 \pi)=u(x)\right\}$ be the space of smooth $2 \pi$-periodic functions of one variable.

  (i) For $f \in C_{p e r}^{\infty}$ show that there exists a unique $u_{f} \in C_{p e r}^{\infty}$ such that

  $$-\frac{d^{2} u_{f}}{d x^{2}}+u_{f}=f$$

  (ii) Show that $I_{f}\left[u_{f}+\phi\right]>I_{f}\left[u_{f}\right]$ for every $\phi \in C_{p e r}^{\infty}$ which is not identically zero, where $I_{f}: C_{p e r}^{\infty} \rightarrow \mathbb{R}$ is defined by

  $$I_{f}[u]=\frac{1}{2} \int_{-\pi}^{+\pi}\left[\left(\frac{\partial u}{\partial x}\right)^{2}+u^{2}-2 f(x) u\right] d x$$

  (iii) Show that the equation

  $$\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{\partial x^{2}}+u=f(x)$$

  with initial data $u(0, x)=u_{0}(x) \in C_{\text {per }}^{\infty}$ has, for $t>0$, a smooth solution $u(t, x)$ such that $u(t, \cdot) \in C_{p e r}^{\infty}$ for each fixed $t>0$. Give a representation of this solution as a Fourier series in $x$. Calculate $\lim _{t \rightarrow+\infty} u(t, x)$ and comment on your answer in relation to (i).

  (iv) Show that $I_{f}[u(t, \cdot)] \leqslant I_{f}[u(s, \cdot)]$ for $t>s>0$, and that $I_{f}[u(t, \cdot)] \rightarrow I_{f}\left[u_{f}\right]$ as $t \rightarrow+\infty$.

  comment

Principles of Quantum Mechanics

• 3.II $32 \mathrm{D}$

  Principles of Quantum Mechanics | Part II, 2008

  Explain, in a few lines, how the Pauli matrices $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ with

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  are used to represent angular momentum operators with respect to basis states $|\uparrow\rangle$ and $|\downarrow\rangle$ corresponding to spin up and spin down along the 3 -axis. You should state clearly which properties of the matrices correspond to general features of angular momentum and which are specific to spin half.

  Consider two spin-half particles labelled A and B, each with its spin operators and spin eigenstates. Find the matrix representation of

  $$\boldsymbol{\sigma}^{(\mathrm{A})} \cdot \boldsymbol{\sigma}^{(\mathrm{B})}=\sigma_{1}^{(\mathrm{A})} \sigma_{1}^{(\mathrm{B})}+\sigma_{2}^{(\mathrm{A})} \sigma_{2}^{(\mathrm{B})}+\sigma_{3}^{(\mathrm{A})} \sigma_{3}^{(\mathrm{B})}$$

  with respect to a basis of two-particle states $|\uparrow\rangle_{\mathrm{A}}|\uparrow\rangle_{\mathrm{B}},|\downarrow\rangle_{\mathrm{A}}|\uparrow\rangle_{\mathrm{B}},|\uparrow\rangle_{\mathrm{A}}|\downarrow\rangle_{\mathrm{B}},|\downarrow\rangle_{\mathrm{A}}|\downarrow\rangle_{\mathrm{B}}$. Show that the eigenvalues of the matrix are $1,1,1,-3$ and find the eigenvectors.

  What is the behaviour of each eigenvector under interchange of $\mathrm{A}$ and $\mathrm{B}$ ? If the particles are identical, and there are no other relevant degrees of freedom, which of the two-particle states are allowed?

  By relating $\left(\boldsymbol{\sigma}^{(\mathrm{A})}+\boldsymbol{\sigma}^{(\mathrm{B})}\right)^{2}$ to the operator discussed above, show that your findings are consistent with standard results for addition of angular momentum.

  comment

Principles of Statistics

• 3.II.26I

  Principles of Statistics | Part II, 2008

  Define the notion of exponential family $(E F)$, and show that, for data arising as a random sample of size $n$ from an exponential family, there exists a sufficient statistic whose dimension stays bounded as $n \rightarrow \infty$.

  The log-density of a normal distribution $\mathcal{N}(\mu, v)$ can be expressed in the form

  $$\log p(x \mid \boldsymbol{\phi})=\phi_{1} x+\phi_{2} x^{2}-k(\boldsymbol{\phi})$$

  where $\phi=\left(\phi_{1}, \phi_{2}\right)$ is the value of an unknown parameter $\Phi=\left(\Phi_{1}, \Phi_{2}\right)$. Determine the function $k$, and the natural parameter-space $\mathbb{F}$. What is the mean-value parameter $\mathrm{H}=\left(\mathrm{H}_{1}, \mathrm{H}_{2}\right)$ in terms of $\Phi ?$

  Determine the maximum likelihood estimator $\widehat{\Phi}_{1}$ of $\Phi_{1}$ based on a random sample $\left(X_{1}, \ldots, X_{n}\right)$, and give its asymptotic distribution for $n \rightarrow \infty$.

  How would these answers be affected if the variance of $X$ were known to have value $v_{0}$ ?

  comment

Representation Theory

• 3.II.19G

  Representation Theory | Part II, 2008

  Let $V_{2}$ denote the irreducible representation $\operatorname{Sym}^{2}\left(\mathbb{C}^{2}\right)$ of $S U(2)$; thus $V_{2}$ has dimension 3. Compute the character of the representation $\operatorname{Sym}^{n}\left(V_{2}\right)$ of $S U(2)$ for any $n \geqslant 0$. Compute the dimension of the invariants $\operatorname{Sym}^{n}\left(V_{2}\right)^{S U(2)}$, meaning the subspace of $\operatorname{Sym}^{n}\left(V_{2}\right)$ where $S U(2)$ acts trivially.

  Hence, or otherwise, show that the ring of complex polynomials in three variables $x, y, z$ which are invariant under the action of $S O(3)$ is a polynomial ring. Find a generator for this polynomial ring.

  comment

Riemann Surfaces

• 3.II $. 22$

  Riemann Surfaces | Part II, 2008

  Define the degree of a non-constant holomorphic map between compact connected Riemann surfaces and state the Riemann-Hurwitz formula.

  Show that there exists a compact connected Riemann surface of any genus $g \geqslant 0$.

  [You may use without proof any foundational results about holomorphic maps and complex algebraic curves from the course, provided that these are accurately stated. You may also assume that if $h(s)$ is a non-constant complex polynomial without repeated roots then the algebraic curve $C=\left\{(s, t) \in \mathbb{C}^{2}: t^{2}-h(s)=0\right\}$ is path connected.]

  comment

Statistical Modelling

• 3.I.5J

  Statistical Modelling | Part II, 2008

  Consider the linear model $Y=X \beta+\varepsilon$. Here, $Y$ is an $n$-dimensional vector of observations, $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p$-dimensional parameter, and $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$, with $\sigma^{2}$ unknown. Assume that $X$ has full rank and that $p \ll n$. Suppose that we are interested in checking the assumption $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Let $\hat{Y}=X \hat{\beta}$, where $\hat{\beta}$ is the maximum likelihood estimate of $\beta$. Write in terms of $X$ an expression for the projection matrix $P=\left(p_{i j}: 1 \leqslant i, j \leqslant n\right)$ which appears in the maximum likelihood equation $\hat{Y}=X \hat{\beta}=P Y$.

  Find the distribution of $\hat{\varepsilon}=Y-\hat{Y}$, and show that, in general, the components of $\hat{\varepsilon}$ are not independent.

  A standard procedure used to check our assumption on $\varepsilon$ is to check whether the studentized fitted residuals

  $$\hat{\eta}_{i}=\frac{\hat{\varepsilon}_{i}}{\tilde{\sigma} \sqrt{1-p_{i i}}}, \quad i=1, \ldots, n$$

  look like a random sample from an $N(0,1)$ distribution. Here,

  $$\tilde{\sigma}^{2}=\frac{1}{n-p}\|Y-X \hat{\beta}\|^{2} .$$

  Say, briefly, how you might do this in R.

  This procedure appears to ignore the dependence between the components of $\hat{\varepsilon}$ noted above. What feature of the given set-up makes this reasonable?

  comment

Statistical Physics

• 3.II.34E

  Statistical Physics | Part II, 2008

  Derive the following two relations:

  $$T d S=C_{p} d T-\left.T \frac{\partial V}{\partial T}\right|_{p} d p$$

  and

  $$T d S=C_{V} d T+\left.T \frac{\partial p}{\partial T}\right|_{V} d V$$

  [You may use any standard Maxwell relation without proving it.]

  Experimentalists very seldom measure $C_{V}$ directly; they measure $C_{p}$ and use thermodynamics to extract $C_{V}$. Use your results from the first part of this question to find a formula for $C_{p}-C_{V}$ in terms of the easily measured quantities

  $$\alpha=\left.\frac{1}{V} \frac{\partial V}{\partial T}\right|_{p}$$

  (the volume coefficient of expansion) and

  $$\kappa=-\left.\frac{1}{V} \frac{\partial V}{\partial p}\right|_{T}$$

  (the isothermal compressibility).

  comment

Stochastic Financial Models

• 3.II.27J

  Stochastic Financial Models | Part II, 2008

  Consider a vector of asset prices evolving over time $\bar{S}=\left(S_{t}^{0}, S_{t}^{1}, \ldots, S_{t}^{d}\right)_{t \in\{0,1, \ldots, T\}}$. The asset price $S^{0}$ is assumed constant over time. In this context, explain what is an arbitrage and prove that the existence of an equivalent martingale measure implies noarbitrage.

  Suppose that over two periods a stock price moves on a binomial tree

  

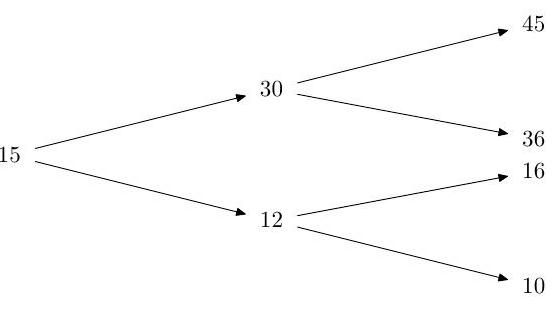
  Assume riskless rate $r=1 / 4$. Determine the equivalent martingale measure. [No proof is required.]

  Sell an American put with strike 15 and expiry 2 at its no-arbitrage price, which you should determine.

  Verify that the buyer of the option should use his early exercise right if the first period is bad.

  Assume that the first period is bad, and that the buyer forgets to exercise. How much risk-free profit can you lock in?

  comment

Waves

• 3.II $. 37 \mathrm{~B} \quad$

  Waves | Part II, 2008

  The real function $\phi(x, t)$ satisfies the Klein-Gordon equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=\frac{\partial^{2} \phi}{\partial x^{2}}-\phi, \quad-\infty<x<\infty, t \geqslant 0$$

  Find the dispersion relation for disturbances of wavenumber $k$ and deduce their phase and group velocities.

  Suppose that at $t=0$

  $$\phi(x, 0)=0 \quad \text { and } \quad \frac{\partial \phi}{\partial t}(x, 0)=e^{-|x|}$$

  Use Fourier transforms to find an integral expression for $\phi(x, t)$ when $t>0$.

  Use the method of stationary phase to find $\phi(V t, t)$ for $t \rightarrow \infty$ for fixed $0<V<1$. What can be said if $V>1$ ?

  [Hint: you may assume that

  $$\left.\int_{-\infty}^{\infty} e^{-a x^{2}} d x=\sqrt{\frac{\pi}{a}}, \quad \operatorname{Re}(a)>0 .\right]$$

  comment