3.I.8C
What is the effect of the Möbius transformation on the points , and ?
By considering
or otherwise, show that is a branch of the -function
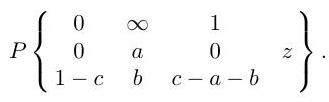
Give a linearly independent branch.
Typos? Please submit corrections to this page on GitHub.
3.I.8C
What is the effect of the Möbius transformation on the points , and ?
By considering
or otherwise, show that is a branch of the -function
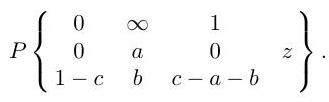
Give a linearly independent branch.