Part II, 2007, Paper 3

Applications of Quantum Mechanics

• 3.II.33A

  Applications of Quantum Mechanics | Part II, 2007

  Consider the Hamiltonian

  $$H=\mathbf{B}(t) \cdot \mathbf{S}$$

  for a particle of spin $\frac{1}{2}$ fixed in space, in a rotating magnetic field, where

  $$S_{1}=\frac{\hbar}{2}\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad S_{2}=\frac{\hbar}{2}\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad S_{3}=\frac{\hbar}{2}\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  and

  $$\mathbf{B}(t)=B(\sin \alpha \cos \omega t, \sin \alpha \sin \omega t, \cos \alpha)$$

  with $B, \alpha$ and $\omega$ constant, and $B>0, \omega>0$.

  There is an exact solution of the time-dependent Schrödinger equation for this Hamiltonian,

  $$\chi(t)=\left(\cos \left(\frac{1}{2} \lambda t\right)-i \frac{B-\omega \cos \alpha}{\lambda} \sin \left(\frac{1}{2} \lambda t\right)\right) e^{-i \omega t / 2} \chi_{+}+i\left(\frac{\omega}{\lambda} \sin \alpha \sin \left(\frac{1}{2} \lambda t\right)\right) e^{i \omega t / 2} \chi_{-}$$

  where $\lambda \equiv\left(\omega^{2}-2 \omega B \cos \alpha+B^{2}\right)^{1 / 2}$ and

  $$\chi_{+}=\left(\begin{array}{c} \cos \frac{\alpha}{2} \\ e^{i \omega t} \sin \frac{\alpha}{2} \end{array}\right), \quad \chi_{-}=\left(\begin{array}{c} e^{-i \omega t} \sin \frac{\alpha}{2} \\ -\cos \frac{\alpha}{2} \end{array}\right)$$

  Show that, for $\omega \ll B$, this exact solution simplifies to a form consistent with the adiabatic approximation. Find the dynamic phase and the geometric phase in the adiabatic regime. What is the Berry phase for one complete cycle of $\mathbf{B}$ ?

  The Berry phase can be calculated as an integral of the form

  $$\Gamma=i \oint\left\langle\psi \mid \nabla_{\mathbf{R}} \psi\right\rangle \cdot d \mathbf{R}$$

  Evaluate $\Gamma$ for the adiabatic evolution described above.

  comment

Applied Probability

• 3.II.25J

  Applied Probability | Part II, 2007

  For a discrete-time Markov chain, if the probability of transition $i \rightarrow j$ does not depend on $i$ then the chain is reduced to a sequence of independent random variables (states). In this case, the chain forgets about its initial state and enters equilibrium after a single transition. In the continuous-time case, a Markov chain whose rates $q_{i j}$ of transition $i \rightarrow j$ depend on $j$ but not on $i \neq j$ still 'remembers' its initial state and reaches equilibrium only in the limit as the time grows indefinitely. This question is an illustration of this property.

  A protean sea sponge may change its colour among $s$ varieties $1, \ldots, s$, under the influence of the environment. The rate of transition from colour $i$ to $j$ equals $r_{j} \geqslant 0$ and does not depend on $i, i \neq j$. Consider a Q-matrix $Q=\left(q_{i j}\right)$ with entries

  $$q_{i j}= \begin{cases}r_{j}, & i \neq j \\ -R+r_{i}, & i=j\end{cases}$$

  where $R=r_{1}+\ldots+r_{s}$. Assume that $R>0$ and let $\left(X_{t}\right)$ be the continuous-time Markov chain with generator $Q$. Given $t \geqslant 0$, let $P(t)=\left(p_{i j}(t)\right)$ be the matrix of transition probabilities in time $t$ in chain $\left(X_{t}\right)$.

  (a) State the exponential relation between the matrices $Q$ and $P(t)$.

  (b) Set $\pi_{j}=r_{j} / R, j=1, \ldots, s$. Check that $\pi_{1}, \ldots, \pi_{s}$ are equilibrium probabilities for the chain $\left(X_{t}\right)$. Is this a unique equilibrium distribution? What property of the vector with entries $\pi_{j}$ relative to the matrix $Q$ is involved here?

  (c) Let $\mathbf{x}$ be a vector with components $x_{1}, \ldots, x_{s}$ such that $x_{1}+\ldots+x_{s}=0$. Show that $\mathbf{x}^{\mathrm{T}} Q=-R \mathbf{x}^{\mathrm{T}}$. Compute $\mathbf{x}^{\mathrm{T}} P(t)$

  (d) Now let $\delta_{i}$ denote the (column) vector whose entries are 0 except for the $i$ th one which equals 1. Observe that the $i$ th row of $P(t)$ is $\delta_{i}^{\mathrm{T}} P(t)$. Prove that $\delta_{i}^{\mathrm{T}} P(t)=\pi^{\mathrm{T}}+e^{-t R}\left(\delta_{i}^{\mathrm{T}}-\pi^{\mathrm{T}}\right) .$

  (e) Deduce the expression for transition probabilities $p_{i j}(t)$ in terms of rates $r_{j}$ and their sum $R$.

  comment

Asymptotic Methods

• 3.II.30B

  Asymptotic Methods | Part II, 2007

  Explain the method of stationary phase for determining the behaviour of the integral

  $$I(x)=\int_{a}^{b} d u e^{i x f(u)}$$

  for large $x$. Here, the function $f(u)$ is real and differentiable, and $a, b$ and $x$ are all real.

  Apply this method to show that the first term in the asymptotic behaviour of the function

  $$\Gamma(m+1)=\int_{0}^{\infty} d u u^{m} e^{-u}$$

  where $m=i n$ with $n>0$ and real, is

  $$\Gamma(i n+1) \sim \sqrt{2 \pi} e^{-i n} \exp \left[\left(i n+\frac{1}{2}\right)\left(\frac{i \pi}{2}+\log n\right)\right]$$

  as $n \rightarrow \infty$

  comment

Classical Dynamics

• 3.I.9C

  Classical Dynamics | Part II, 2007

  A particle of mass $m_{1}$ is constrained to move in the horizontal $(x, y)$ plane, around a circle of fixed radius $r_{1}$ whose centre is at the origin of a Cartesian coordinate system $(x, y, z)$. A second particle of mass $m_{2}$ is constrained to move around a circle of fixed radius $r_{2}$ that also lies in a horizontal plane, but whose centre is at $(0,0, a)$. It is given that the Lagrangian $L$ of the system can be written as

  $$L=\frac{m_{1}}{2} r_{1}^{2} \dot{\phi}_{1}^{2}+\frac{m_{2}}{2} r_{2}^{2} \dot{\phi}_{2}^{2}+\omega^{2} r_{1} r_{2} \cos \left(\phi_{2}-\phi_{1}\right)$$

  using the particles' cylindrical polar angles $\phi_{1}$ and $\phi_{2}$ as generalized coordinates. Deduce the equations of motion and use them to show that $m_{1} r_{1}^{2} \dot{\phi}_{1}+m_{2} r_{2}^{2} \dot{\phi}_{2}$ is constant, and that $\psi=\phi_{2}-\phi_{1}$ obeys an equation of the form

  $$\ddot{\psi}=-k^{2} \sin \psi$$

  where $k$ is a constant to be determined.

  Find two values of $\psi$ corresponding to equilibria, and show that one of the two equilibria is stable. Find the period of small oscillations about the stable equilibrium.

  comment

Cosmology

• 3.I.10A

  Cosmology | Part II, 2007

  The number density of a non-relativistic species in thermal equilibrium is given by

  $$n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left[\left(\mu-m c^{2}\right) / k T\right]$$

  Suppose that thermal and chemical equilibrium is maintained between protons p (mass $m_{\mathrm{p}}$, degeneracy $g_{s}=2$ ), neutrons $\mathrm{n}$ (mass $m_{\mathrm{n}} \approx m_{\mathrm{p}}$, degeneracy $g_{s}=2$ ) and helium-4 nuclei ${ }^{4} \mathrm{He}\left(\right.$ mass $m_{\mathrm{He}} \approx 4 m_{\mathrm{p}}$, degeneracy $g_{s}=1$ ) via the interaction

  $$2 \mathrm{p}+2 \mathrm{n} \leftrightarrow{ }^{4} \mathrm{He}+\gamma$$

  where you may assume the photons $\gamma$ have zero chemical potential $\mu_{\gamma}=0$. Given that the binding energy of helium-4 obeys $B_{\mathrm{He}} / c^{2} \equiv 2 m_{\mathrm{p}}+2 n_{\mathrm{n}}-m_{\mathrm{He}} \ll m_{\mathrm{He}}$, show that the ratio of the number densities can be written as

  $$\frac{n_{\mathrm{p}}^{2} n_{\mathrm{n}}^{2}}{n_{\mathrm{He}}}=2\left(\frac{2 \pi m_{\mathrm{p}} k T}{h^{2}}\right)^{9 / 2} \exp \left(-B_{\mathrm{He}} / k T\right)$$

  Explain briefly why the baryon-to-photon ratio $\eta \equiv n_{B} / n_{\gamma}$ remains constant during the expansion of the universe, where $n_{B} \approx n_{\mathrm{p}}+n_{\mathrm{n}}+4 n_{\mathrm{He}}$ and $n_{\gamma} \approx\left(16 \pi /(h c)^{3}\right)(k T)^{3}$.

  By considering the fractional densities $X_{i} \equiv n_{i} / n_{B}$ of the species $i$, re-express the ratio ( $\uparrow$ ) in the form

  $$\frac{X_{\mathrm{p}}^{2} X_{\mathrm{n}}^{2}}{X_{\mathrm{He}}}=\eta^{-3} \frac{1}{32}\left(\frac{\pi}{2}\right)^{3 / 2}\left(\frac{m_{\mathrm{p}} c^{2}}{k T}\right)^{9 / 2} \exp \left(-B_{\mathrm{He}} / k T\right)$$

  Given that $B_{\mathrm{He}} \approx 30 \mathrm{MeV}$, verify (very approximately) that this ratio approaches unity when $k T \approx 0.3 \mathrm{MeV}$. In reality, helium-4 is not formed until after deuterium production at a considerably lower temperature. Explain briefly the reason for this delay.

  comment

• 3.II.15A

  Cosmology | Part II, 2007

  A spherically symmetric star with outer radius $R$ has mass density $\rho(r)$ and pressure $P(r)$, where $r$ is the distance from the centre of the star. Show that hydrostatic equilibrium implies the pressure support equation,

  $$\tag{†} \frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $m(r)$ is the mass inside radius $r$. State without proof any results you may need.

  Write down an integral expression for the total gravitational potential energy $E_{\text {grav }}$ of the star. Hence use $(†))$ to deduce the virial theorem

  $$\tag{*} E_{\mathrm{grav}}=-3\langle P\rangle V,$$

  where $\langle P\rangle$ is the average pressure and $V$ is the volume of the star.

  Given that a non-relativistic ideal gas obeys $P=2 E_{\mathrm{kin}} / 3 \mathrm{~V}$ and that an ultrarelativistic gas obeys $P=E_{\text {kin }} / 3 V$, where $E_{\text {kin }}$ is the kinetic energy, discuss briefly the gravitational stability of a star in these two limits.

  At zero temperature, the number density of particles obeying the Pauli exclusion principle is given by

  $$n=\frac{4 \pi g_{s}}{h^{3}} \int_{0}^{p_{\mathrm{F}}} p^{2} d p=\frac{4 \pi g_{s}}{3}\left(\frac{p_{\mathrm{F}}}{h}\right)^{3}$$

  where $p_{\mathrm{F}}$ is the Fermi momentum, $g_{s}$ is the degeneracy and $h$ is Planck's constant. Deduce that the non-relativistic internal energy $E_{\text {kin }}$ of these particles is

  $$E_{\mathrm{kin}}=\frac{4 \pi g_{s} V h^{2}}{10 m_{p}}\left(\frac{p_{\mathrm{F}}}{h}\right)^{5}$$

  where $m_{p}$ is the mass of a particle. Hence show that the non-relativistic Fermi degeneracy pressure satisfies

  $$P \sim \frac{h^{2}}{m_{p}} n^{5 / 3} .$$

  Use the virial theorem $(*)$ to estimate that the radius $R$ of a star supported by Fermi degeneracy pressure is approximately

  $$R \sim \frac{h^{2} M^{-1 / 3}}{G m_{p}^{8 / 3}},$$

  where $M$ is the total mass of the star.

  [Hint: Assume $\rho(r)=m_{p} n(r) \sim m_{p}\langle n\rangle$ and note that $\left.M \approx\left(4 \pi R^{3} / 3\right) m_{p}\langle n\rangle .\right]$

  comment

Differential Geometry

• 3.II.23H

  Differential Geometry | Part II, 2007

  (i) Let $f: X \rightarrow Y$ be a smooth map between manifolds without boundary. Define critical point, critical value and regular value. State Sard's theorem.

  (ii) Explain how to define the degree modulo 2 of a smooth map $f$, indicating clearly the hypotheses on $X$ and $Y$. Show that a smooth map with non-zero degree modulo 2 must be surjective.

  (iii) Let $S$ be the torus of revolution obtained by rotating the circle $(y-2)^{2}+z^{2}=1$ in the $y z$-plane around the $z$-axis. Describe the critical points and the critical values of the Gauss map $N$ of $S$. Find the degree modulo 2 of $N$. Justify your answer by means of a sketch or otherwise.

  comment

Dynamical Systems

• 3.I.7E

  Dynamical Systems | Part II, 2007

  State the Poincaré-Bendixson Theorem for a system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$.

  Prove that if $k^{2}<4$ then the system

  $$\begin{aligned} &\dot{x}=x-y-x^{3}-x y^{2}-k^{2} x y^{2} \\ &\dot{y}=y+x-x^{2} y-y^{3}-k^{2} x^{2} y \end{aligned}$$

  has a periodic orbit in the region $2 /\left(2+k^{2}\right) \leqslant x^{2}+y^{2} \leqslant 1$.

  comment

• 3.II.14E

  Dynamical Systems | Part II, 2007

  The Lorenz equations are

  $$\begin{aligned} &\dot{x}=\sigma(y-x) \\ &\dot{y}=r x-y-x z \\ &\dot{z}=x y-b z \end{aligned}$$

  where $r, \sigma$ and $b$ are positive constants and $(x, y, z) \in \mathbb{R}^{3}$.

  (i) Show that the origin is globally asymptotically stable for $0<r<1$ by considering a function $V(x, y, z)=\frac{1}{2}\left(x^{2}+A y^{2}+B z^{2}\right)$ with a suitable choice of constants $A$ and $B$

  (ii) State, without proof, the Centre Manifold Theorem.

  Show that the fixed point at the origin is nonhyperbolic at $r=1$. What are the dimensions of the linear stable and (non-extended) centre subspaces at this point?

  (iii) Let $\sigma=1$ from now on. Make the substitutions $u=x+y, v=x-y$ and $\mu=r-1$ and derive the resulting equations for $\dot{u}, \dot{v}$ and $\dot{z}$.

  The extended centre manifold is given by

  $$v=V(u, \mu), \quad z=Z(u, \mu)$$

  where $V$ and $Z$ can be expanded as power series about $u=\mu=0$. What is known about $V$ and $Z$ from the Centre Manifold Theorem? Assuming that $\mu=O\left(u^{2}\right)$, determine $Z$ correct to $O\left(u^{2}\right)$ and $V$ to $O\left(u^{3}\right)$. Hence obtain the evolution equation on the extended centre manifold correct to $O\left(u^{3}\right)$, and identify the type of bifurcation.

  comment

Electrodynamics

• 3.II $. 35 \mathrm{E} \quad$

  Electrodynamics | Part II, 2007

  Consider a particle of charge $q$ moving with 3 -velocity $\mathbf{v}$. If the particle is moving slowly then Larmor's formula asserts that the instantaneous radiated power is

  $$\mathcal{P}=\frac{\mu_{0}}{6 \pi} q^{2}\left|\frac{d \mathbf{v}}{d t}\right|^{2}$$

  Suppose, however, that the particle is moving relativistically. Give reasons why one should conclude that $\mathcal{P}$ is a Lorentz invariant. Writing the 4-velocity as $U^{a}=(\gamma, \gamma \mathbf{v})$ where $\gamma=1 / \sqrt{1-|\mathbf{v}|^{2}}$ and $c=1$, show that

  $$\dot{U}^{a}=\left(\gamma^{3} \alpha, \gamma^{3} \alpha \mathbf{v}+\gamma \dot{\mathbf{v}}\right)$$

  where $\alpha=\mathbf{v} \cdot \dot{\mathbf{v}}$ and $\dot{f}=d f / d s$ where $s$ is the particle's proper time. Show also that

  $$\dot{U}^{a} \dot{U}_{a}=-\gamma^{4} \alpha^{2}-\gamma^{2}|\dot{\mathbf{v}}|^{2} .$$

  Deduce the relativistic version of Larmor's formula.

  Suppose the particle moves in a circular orbit perpendicular to a uniform magnetic field $\mathbf{B}$. Show that

  $$\mathcal{P}=\frac{\mu_{0}}{6 \pi} \frac{q^{4}}{m^{2}}\left(\gamma^{2}-1\right)|\mathbf{B}|^{2}$$

  where $m$ is the mass of the particle, and comment briefly on the slow motion limit.

  comment

Fluid Dynamics II

• 3.II $. 36$ B

  Fluid Dynamics II | Part II, 2007

  

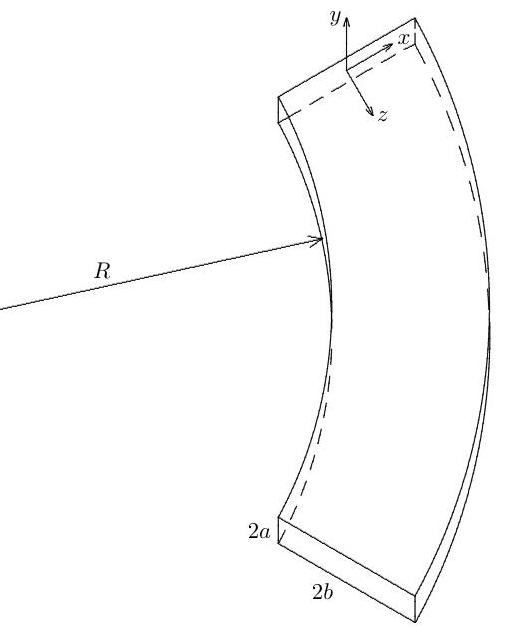
  Viscous fluid of kinematic viscosity $\nu$ and density $\rho$ flows in a curved pipe of constant rectangular cross section and constant curvature. The cross-section has height $2 a$ and width $2 b$ (in the radial direction) with $b \gg a$, and the radius of curvature of the inner wall is $R$, with $R \gg b$. A uniform pressure gradient $-G$ is applied along the pipe.

  (i) Assume to a first approximation that the pipe is straight, and ignore variation in the $x$-direction, where $(x, y, z)$ are Cartesian coordinates referred to an origin at the centre of the section, with $x$ increasing radially and $z$ measured along the pipe. Find the flow field along the pipe in the form $\mathbf{u}=(0,0, w(y))$.

  (ii) It is given that the largest component of the inertial acceleration $\mathbf{u} \cdot \nabla \mathbf{u}$ due to the curvature of the pipe is $-w^{2} / R$ in the $x$ direction. Consider the secondary flow $\mathbf{u}_{s}$ induced in the $x, y$ plane, again ignoring variations in $x$ and any end effects (except for the requirement that there be zero total mass flux in the $x$ direction). Show that $\mathbf{u}_{s}$ takes the form $\mathbf{u}_{s}=(u(y), 0,0)$, where

  $$u(y)=\frac{G^{2}}{120 \rho^{2} \nu^{3} R}\left(5 a^{2} y^{4}-y^{6}\right)+\frac{C}{2} y^{2}+D$$

  and write down two equations determining the constants $C$ and $D$. [It is not necessary to solve these equations.]

  Give conditions on the parameters that ensure that $|u| \ll|w|$.

  comment

Further Complex Methods

• 3.I.8B

  Further Complex Methods | Part II, 2007

  Let $w_{1}(z)$ and $w_{2}(z)$ be any two linearly independent branches of the $P$-function

  $$\left\{\begin{array}{cccc} 0 & \infty & 1 & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  where $\alpha+\alpha^{\prime}+\beta+\beta^{\prime}+\gamma+\gamma^{\prime}=1$, and let $W(z)$ be the Wronskian of $w_{1}(z)$ and $w_{2}(z)$.

  (i) How is $W(z)$ related to the Wronskian of the principal branches of the $P$-function at $z=0$ ?

  (ii) Show that $z^{-\alpha-\alpha^{\prime}+1}(1-z)^{-\gamma-\gamma^{\prime}+1} W(z)$ is an entire function.

  (iii) Given that $z^{\beta+\beta^{\prime}+1} W(z)$ is bounded as $z \rightarrow \infty$, show that

  $$W(z)=A z^{\alpha+\alpha^{\prime}-1}(1-z)^{\gamma+\gamma^{\prime}-1}$$

  where $A$ is a non-zero constant.

  comment

Galois Theory

• 3.II.18F

  Galois Theory | Part II, 2007

  (i) Let $K$ be the splitting field of the polynomial $x^{4}-3$ over $\mathbb{Q}$. Describe the field $K$, the Galois group $G=\operatorname{Aut}(K / \mathbb{Q})$, and the action of $G$ on $K$.

  (ii) Let $K$ be the splitting field of the polynomial $x^{4}+4 x^{2}+2$ over $\mathbb{Q}$. Describe the field $K$ and determine $\operatorname{Aut}(K / \mathbb{Q})$.

  comment

Geometry of Group Actions

• 3.I.3G

  Geometry of Group Actions | Part II, 2007

  Let $G$ be a 2-dimensional Euclidean crystallographic group. Define the lattice and point group corresponding to $G$.

  Prove that any non-trivial rotation in the point group of $G$ must have order $2,3,4$ or $6 .$

  comment

Graph Theory

• 3.II.17H

  Graph Theory | Part II, 2007

  Let $G$ be a bipartite graph with vertex classes $X$ and $Y$, each of size $n$. State and prove Hall's theorem giving a necessary and sufficient condition for $G$ to contain a perfect matching.

  A vertex $x \in X$ is flexible if every edge from $x$ is contained in a perfect matching. Show that if $|\Gamma(A)|>|A|$ for every subset $A$ of $X$ with $\emptyset \neq A \neq X$, then every $x \in X$ is flexible.

  Show that whenever $G$ contains a perfect matching, there is at least one flexible $x \in X$.

  Give an example of such a $G$ where no $x \in X$ of minimal degree is flexible.

  comment

Integrable Systems

• 3.II.31E

  Integrable Systems | Part II, 2007

  Find a Lax pair formulation for the linearised NLS equation

  $$i q_{t}+q_{x x}=0$$

  Use this Lax pair formulation to show that the initial value problem on the infinite line of the linearised NLS equation is associated with the following Riemann-Hilbert problem

  $$\begin{array}{ccc} M^{+}(x, t, k) & =M^{-}(x, t, k)\left(\begin{array}{cc} 1 & e^{i k x-i k^{2} t} \hat{q}_{0}(k) \\ 0 & 1 \end{array}\right), & k \in \mathbb{R} \\ M & =\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right)+O\left(\frac{1}{k}\right), & k \rightarrow \infty \end{array}$$

  By deforming the above problem obtain the Riemann-Hilbert problem and hence the linear integral equation associated with the following system of nonlinear evolution PDEs

  $$\begin{aligned} i q_{t}+q_{x x}-2 \vartheta q^{2} &=0 \\ -i \vartheta_{t}+\vartheta_{x x}-2 \vartheta^{2} q &=0 \end{aligned}$$

  comment

Linear Analysis

• 3.II.21G

  Linear Analysis | Part II, 2007

  State and prove the Arzela-Ascoli theorem.

  Let $N$ be a positive integer. Consider the subset $\mathcal{S}_{N} \subset C([0,1])$ consisting of all thrice differentiable solutions to the differential equation

  $f^{\prime \prime}=f+\left(f^{\prime}\right)^{2} \quad$ with $\quad|f(0)| \leqslant N, \quad|f(1)| \leqslant N, \quad\left|f^{\prime}(0)\right| \leqslant N, \quad\left|f^{\prime}(1)\right| \leqslant N .$

  Show that this set is totally bounded as a subset of $C([0,1])$.

  [It may be helpful to consider interior maxima.]

  comment

Mathematical Biology

• 3.I.6B

  Mathematical Biology | Part II, 2007

  Consider a birth and death process in which births always give rise to two offspring, with rate $\lambda$, while the death rate per individual is $\beta$.

  Write down the master equation (or probability balance equation) for this system.

  Show that the population mean is given by

  $$\langle n\rangle=\frac{2 \lambda}{\beta}\left(1-e^{-\beta t}\right)+n_{0} e^{-\beta t}$$

  where $n_{0}$ is the initial population mean, and that the population variance satisfies

  $$\sigma^{2} \rightarrow 3 \lambda / \beta \quad \text { as } \quad t \rightarrow \infty$$

  comment

• 3.II.13B

  Mathematical Biology | Part II, 2007

  The number density of a population of cells is $n(\mathbf{x}, t)$. The cells produce a chemical whose concentration is $C(\mathbf{x}, t)$ and respond to it chemotactically. The equations governing $n$ and $C$ are

  $$\begin{aligned} \frac{\partial n}{\partial t} &=\gamma n\left(n_{0}-n\right)+D_{n} \nabla^{2} n-\chi \nabla \cdot(n \nabla C) \\ \frac{\partial C}{\partial t} &=\alpha n-\beta C+D_{c} \nabla^{2} C \end{aligned}$$

  (i) Give a biological interpretation of each term in these equations, where you may assume that $\alpha, \beta, \gamma, n_{0}, D_{n}, D_{c}$ and $\chi$ are all positive.

  (ii) Show that there is a steady-state solution that is stable to spatially invariant disturbances.

  (iii) Analyse small, spatially-varying perturbations to the steady state that satisfy $\nabla^{2} \phi=-k^{2} \phi$ for any variable $\phi$, and show that a chemotactic instability is possible if

  $$\chi \alpha n_{0}>\beta D_{n}+\gamma n_{0} D_{c}+\left(4 \beta \gamma n_{0} D_{n} D_{c}\right)^{1 / 2}$$

  (iv) Find the critical value of $k$ at which the instability first appears as $\chi$ is increased.

  comment

Number Theory

• 3.II.11F

  Number Theory | Part II, 2007

  State the Chinese remainder theorem. Let $n$ be an odd positive integer. If $n$ is divisible by the square of a prime number $p$, prove that there exists an integer $z$ such that $z^{p} \equiv 1(\bmod n)$ but $z \not \equiv 1(\bmod n)$.

  Define the Jacobi symbol

  $$\left(\frac{a}{n}\right)$$

  for any non-zero integer $a$. Give a numerical example to show that

  $$\left(\frac{a}{n}\right)=+1$$

  does not imply in general that $a$ is a square modulo $n$. State and prove the law of quadratic reciprocity for the Jacobi symbol.

  [You may assume the law of quadratic reciprocity for the Legendre symbol.]

  Assume now that $n$ is divisible by the square of a prime number. Prove that there exists an integer $a$ with $(a, n)=1$ such that the congruence

  $$a^{\frac{n-1}{2}} \equiv\left(\frac{a}{n}\right) \quad(\bmod n)$$

  does not hold. Show further that this congruence fails to hold for at least half of all relatively prime residue classes modulo $n$.

  comment

Numerical Analysis

• 3.II.38C

  Numerical Analysis | Part II, 2007

  (a) Prove that all Toeplitz symmetric tridiagonal $M \times M$ matrices

  $$A=\left[\begin{array}{ccccc} a & b & 0 & \cdots & 0 \\ b & a & b & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & \ddots & b & a & b \\ 0 & \cdots & 0 & b & a \end{array}\right]$$

  share the same eigenvectors $\left(v^{(k)}\right)_{k=1}^{M}$ with components $v_{i}^{(k)}=\sin \frac{k i \pi}{M+1}$, $i=1, \ldots, M$, and eigenvalues to be determined.

  (b) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant x \leqslant 1, \quad 0 \leqslant t \leqslant T$$

  is approximated by the Crank-Nicolson scheme

  $$\begin{aligned} u_{m}^{n+1}-\frac{1}{2} \mu\left(u_{m-1}^{n+1}-2 u_{m}^{n+1}+u_{m+1}^{n+1}\right) &=u_{m}^{n}+\frac{1}{2} \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right), \\ \text { for } \quad m &=1, \ldots, M, \end{aligned}$$

  where $\mu=\Delta t /(\Delta x)^{2}, \quad \Delta x=1 /(M+1)$, and $u_{m}^{n}$ is an approximation to $u(m \Delta x, n \Delta t)$. Assuming that $u(0, t)=u(1, t)=0, \forall t, \quad$ show that the above scheme can be written in the form

  $$B u^{n+1}=C u^{n}, \quad 0 \leqslant n \leqslant(T / \Delta t)-1$$

  where $u^{n}=\left[u_{1}^{n}, \ldots, u_{M}^{n}\right]^{\top}$ and the real matrices $B$ and $C$ should be found. Using matrix analysis, find the range of $\mu$ for which the scheme is stable. [Do not use Fourier analysis.]

  comment

Optimization and Control

• 3.II.28I

  Optimization and Control | Part II, 2007

  Let $P$ be a discrete-time controllable dynamical system (or Markov decision process) with countable state-space $S$ and action-space $A$. Consider the $n$-horizon dynamic optimization problem with instantaneous costs $c(k, x, a)$, on choosing action $a$ in state $x$ at time $k \leqslant n-1$, with terminal cost $C(x)$, in state $x$ at time $n$. Explain what is meant by a Markov control and how the choice of a control gives rise to a time-inhomogeneous Markov chain.

  Suppose we can find a bounded function $V$ and a Markov control $u^{*}$ such that

  $$V(k, x) \leqslant(c+P V)(k, x, a), \quad 0 \leqslant k \leqslant n-1, \quad x \in S, \quad a \in A$$

  with equality when $a=u^{*}(k, x)$, and such that $V(n, x)=C(x)$ for all $x$. Here $P V(k, x, a)$ denotes the expected value of $V\left(k+1, X_{k+1}\right)$, given that we choose action $a$ in state $x$ at time $k$. Show that $u^{*}$ is an optimal Markov control.

  A well-shuffled pack of cards is placed face-down on the table. The cards are turned over one by one until none are left. Exactly once you may place a bet of $£ 1000$ on the event that the next two cards will be red. How should you choose the moment to bet? Justify your answer.

  comment

Partial Differential Equations

• 3.II.29A

  Partial Differential Equations | Part II, 2007

  Write down the formula for the solution $u=u(t, x)$ for $t>0$ of the initial value problem for the heat equation in one space dimension

  $$\begin{aligned} &\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{\partial x^{2}}=0 \\ &u(0, x)=g(x) \end{aligned}$$

  for $g: \mathbb{R} \rightarrow \mathbb{C}$ a given smooth bounded function.

  Define the distributional derivative of a tempered distribution $T \in \mathcal{S}^{\prime}(\mathbb{R})$. Define a fundamental solution of a constant-coefficient linear differential operator $P$, and show that the distribution defined by the function $\frac{1}{2} e^{-|x|}$ is a fundamental solution for the operator $P=-\frac{d^{2}}{d x^{2}}+1$.

  For the equation

  $$\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{\partial x^{2}}=e^{t} \phi(x)$$

  where $\phi \in \mathcal{S}(\mathbb{R})$, prove that there is a unique solution of the form $e^{t} v(x)$ with $v \in \mathcal{S}(\mathbb{R})$. Hence write down the solution of $(*)$ with general initial data $u(0, x)=f(x)$ and describe the large time behaviour.

  comment

Principles of Quantum Mechanics

• 3.II.32D

  Principles of Quantum Mechanics | Part II, 2007

  Let

  $$\hat{x}=\left(\frac{\hbar}{2 m \omega}\right)^{1 / 2}\left(a+a^{\dagger}\right), \quad \hat{p}=\left(\frac{\hbar m \omega}{2}\right)^{1 / 2} i\left(a^{\dagger}-a\right)$$

  be the position and momentum operators for a one-dimensional harmonic oscillator of mass $m$ and frequency $\omega$. Write down the commutation relations obeyed by $a$ and $a^{\dagger}$ and give an expression for the oscillator Hamiltonian $H(\hat{x}, \hat{p})$ in terms of them. Prove that the only energies allowed are $E_{n}=\hbar \omega\left(n+\frac{1}{2}\right)$ with $n=0,1,2, \ldots$ and give, without proof, a formula for a general normalised eigenstate $|n\rangle$ in terms of $|0\rangle$.

  A three-dimensional oscillator with charge is subjected to a weak electric field so that its total Hamiltonian is

  $$H_{1}+H_{2}+H_{3}+\lambda m \omega^{2}\left(\hat{x}_{1} \hat{x}_{2}+\hat{x}_{2} \hat{x}_{3}+\hat{x}_{3} \hat{x}_{1}\right)$$

  where $H_{i}=H\left(\hat{x}_{i}, \hat{p}_{i}\right)$ for $i=1,2,3$ and $\lambda$ is a small, dimensionless parameter. Express the general eigenstate for the Hamiltonian with $\lambda=0$ in terms of one-dimensional oscillator states, and give the corresponding energy eigenvalue. Use perturbation theory to compute the changes in energies of states in the lowest two levels when $\lambda \neq 0$, working to the leading order at which non-vanishing corrections occur.

  comment

Principles of Statistics

• 3.II.26I

  Principles of Statistics | Part II, 2007

  (i) In the context of decision theory, what is a Bayes rule with respect to a given loss function and prior? What is an extended Bayes rule?

  Characterise the Bayes rule with respect to a given prior in terms of the posterior distribution for the parameter given the observation. When $\Theta=\mathcal{A}=\mathbb{R}^{d}$ for some $d$, and the loss function is $L(\theta, a)=\|\theta-a\|^{2}$, what is the Bayes rule?

  (ii) Suppose that $\mathcal{A}=\Theta=\mathbb{R}$, with loss function $L(\theta, a)=(\theta-a)^{2}$ and suppose further that under $P_{\theta}, X \sim N(\theta, 1)$.

  Supposing that a $N\left(0, \tau^{-1}\right)$ prior is taken over $\theta$, compute the Bayes risk of the decision rule $d_{\lambda}(X)=\lambda X$. Find the posterior distribution of $\theta$ given $X$, and confirm that its mean is of the form $d_{\lambda}(X)$ for some value of $\lambda$ which you should identify. Hence show that the decision rule $d_{1}$ is an extended Bayes rule.

  comment

Probability and Measure

• 3.II.24J

  Probability and Measure | Part II, 2007

  Let $(E, \mathcal{E}, \mu)$ be a finite measure space, i.e. $\mu(E)<\infty$, and let $1 \leqslant p \leqslant \infty$.

  (a) Define the $L^{p}$-norm $\|f\|_{p}$ of a measurable function $f: E \rightarrow \overline{\mathbb{R}}$, define the space $L^{p}(E, \mathcal{E}, \mu)$ and define convergence in $L^{p} .$

  In the following you may use inequalities from the lectures without proof, provided they are clearly stated.

  (b) Let $f, f_{1}, f_{2}, \ldots \in L^{p}(E, \mathcal{E}, \mu)$. Show that $f_{n} \rightarrow f$ in $L^{p}$ implies $\left\|f_{n}\right\|_{p} \rightarrow\|f\|_{p}$.

  (c) Let $f: E \rightarrow \mathbb{R}$ be a bounded measurable function with $\|f\|_{\infty}>0$. Let

  $$M_{n}=\int_{E}|f|^{n} d \mu$$

  Show that $M_{n} \in(0, \infty)$ and $M_{n+1} M_{n-1} \geqslant M_{n}^{2}$.

  By using Jensen's inequality, or otherwise, show that

  $$\mu(E)^{-1 / n}\|f\|_{n} \leqslant M_{n+1} / M_{n} \leqslant\|f\|_{\infty}$$

  Prove that $\lim _{n \rightarrow \infty} M_{n+1} / M_{n}=\|f\|_{\infty} .$

  $\left[\right.$ Observe that $\left.|f| \geqslant 1_{\left\{|f|>\|f\|_{\infty}-\epsilon\right\}}\left(\|f\|_{\infty}-\epsilon\right) .\right]$

  comment

Representation Theory

• 3.II.19H

  Representation Theory | Part II, 2007

  Let $G$ be a finite group with a permutation action on the set $X$. Describe the corresponding permutation character $\pi_{X}$. Show that the multiplicity in $\pi_{X}$ of the principal character $1_{G}$ equals the number of orbits of $G$ on $X$.

  Assume that $G$ is transitive on $X$, with $|X|>1$. Show that $G$ contains an element $g$ which is fixed-point-free on $X$, that is, $g \alpha \neq \alpha$ for all $\alpha$ in $X$.

  Assume that $\pi_{X}=1_{G}+m \chi$, with $\chi$ an irreducible character of $G$, for some natural number $m$. Show that $m=1$.

  [You may use without proof any facts about algebraic integers, provided you state them correctly.]

  Explain how the action of $G$ on $X$ induces an action of $G$ on $X^{2}$. Assume that $G$ has $r$ orbits on $X^{2}$. If now

  $$\pi_{X}=1_{G}+m_{2} \chi_{2}+\ldots+m_{k} \chi_{k}$$

  with $1_{G}, \chi_{2}, \ldots, \chi_{k}$ distinct irreducible characters of $G$, and $m_{2}, \ldots, m_{k}$ natural numbers, show that $r=1+m_{2}^{2}+\ldots+m_{k}^{2}$. Deduce that, if $r \leqslant 5$, then $k=r$ and $m_{2}=\ldots=m_{k}=1$.

  comment

Riemann Surfaces

• 3.II.22F

  Riemann Surfaces | Part II, 2007

  (i) Let $R$ and $S$ be compact connected Riemann surfaces and $f: R \rightarrow S$ a non-constant holomorphic map. Define the branching order $v_{f}(p)$ at $p \in R$ showing that it is well defined. Prove that the set of ramification points $\left\{p \in R: v_{f}(p)>1\right\}$ is finite. State the Riemann-Hurwitz formula.

  Now suppose that $R$ and $S$ have the same genus $g$. Prove that, if $g>1$, then $f$ is biholomorphic. In the case when $g=1$, write down an example where $f$ is not biholomorphic.

  [The inverse mapping theorem for holomorphic functions on domains in $\mathbb{C}$ may be assumed without proof if accurately stated.]

  (ii) Let $Y$ be a non-singular algebraic curve in $\mathbb{C}^{2}$. Describe, without detailed proofs, a family of charts for $Y$, so that the restrictions to $Y$ of the first and second projections $\mathbb{C}^{2} \rightarrow \mathbb{C}$ are holomorphic maps. Show that the algebraic curve

  $$Y=\left\{(s, t) \in \mathbb{C}^{2}: t^{4}=\left(s^{2}-1\right)(s-4)\right\}$$

  is non-singular. Find all the ramification points of the $\operatorname{map} f: Y \rightarrow \mathbb{C} ;(s, t) \mapsto s$.

  comment

Set Theory and Logic

• 3.II.16G

  Set Theory and Logic | Part II, 2007

  Write down the recursive definitions of ordinal addition, multiplication and exponentiation. Prove carefully that $\omega^{\alpha} \geqslant \alpha$ for all $\alpha$, and hence show that for each non-zero ordinal $\alpha$ there exists a unique $\alpha_{0} \leqslant \alpha$ such that

  $$\omega^{\alpha_{0}} \leqslant \alpha<\omega^{\alpha_{0}+1} .$$

  Deduce that any non-zero ordinal $\alpha$ has a unique representation of the form

  $$\omega^{\alpha_{0}} \cdot a_{0}+\omega^{\alpha_{1}} \cdot \alpha_{1}+\cdots+\omega^{\alpha_{n}} \cdot a_{n}$$

  where $\alpha \geqslant \alpha_{0}>\alpha_{1}>\cdots>\alpha_{n}$ and $a_{0}, a_{1}, \ldots, a_{n}$ are non-zero natural numbers.

  Two ordinals $\beta, \gamma$ are said to be commensurable if we have neither $\beta+\gamma=\gamma$ nor $\gamma+\beta=\beta$. Show that $\beta$ and $\gamma$ are commensurable if and only if there exists $\alpha$ such that both $\beta$ and $\gamma$ lie in the set

  $$\left\{\delta \mid \omega^{\alpha} \leqslant \delta<\omega^{\alpha+1}\right\}$$

  comment

Statistical Modelling

• 3.I.5I

  Statistical Modelling | Part II, 2007

  Consider two possible experiments giving rise to observed data $y_{i j}$ where $i=1, \ldots, I, j=1, \ldots, J .$

  1. The data are realizations of independent Poisson random variables, i.e.,

  $$Y_{i j} \sim f_{1}\left(y_{i j} ; \mu_{i j}\right)=\frac{\mu_{i j}^{y_{i j}}}{y_{i j} !} \exp \left\{-\mu_{i j}\right\}$$

  where $\mu_{i j}=\mu_{i j}(\beta)$, with $\beta$ an unknown (possibly vector) parameter. Write $\hat{\beta}$ for the maximum likelihood estimator (m.l.e.) of $\beta$ and $\hat{y}_{i j}=\mu_{i j}(\hat{\beta})$ for the $(i, j)$ th fitted value under this model.

  2. The data are components of a realization of a multinomial random 'vector'

  $$Y \sim f_{2}\left(\left(y_{i j}\right) ; n,\left(p_{i j}\right)\right)=n ! \prod_{i=1}^{I} \prod_{j=1}^{J} \frac{p_{i j}^{y_{i j}}}{y_{i j} !}$$

  where the $y_{i j}$ are non-negative integers with

  $$\sum_{i=1}^{I} \sum_{j=1}^{J} y_{i j}=n \quad \text { and } \quad p_{i j}(\beta)=\frac{\mu_{i j}(\beta)}{n}$$

  Write $\beta^{*}$ for the m.l.e. of $\beta$ and $y_{i j}^{*}=n p_{i j}\left(\beta^{*}\right)$ for the $(i, j)$ th fitted value under this model.

  Show that, if

  $$\sum_{i=1}^{I} \sum_{j=1}^{J} \hat{y}_{i j}=n$$

  then $\hat{\beta}=\beta^{*}$ and $\hat{y}_{i j}=y_{i j}^{*}$ for all $i, j$. Explain the relevance of this result in the context of fitting multinomial models within a generalized linear model framework.

  comment

Statistical Physics

• 3.II.34D

  Statistical Physics | Part II, 2007

  For a 2-dimensional gas of $N$ nonrelativistic, non-interacting, spinless bosons, find the density of states $g(\varepsilon)$ in the neighbourhood of energy $\varepsilon$. [Hint: consider the gas in a box of size $L \times L$ which has periodic boundary conditions. Work in the thermodynamic limit $N \rightarrow \infty, L \rightarrow \infty$, with $N / L^{2}$ held finite.]

  Calculate the number of particles per unit area at a given temperature and chemical potential.

  Explain why Bose-Einstein condensation does not occur in this gas at any temperature.

  [Recall that

  $$\left.\frac{1}{\Gamma(n)} \int_{0}^{\infty} \frac{x^{n-1} d x}{z^{-1} e^{x}-1}=\sum_{\ell=1}^{\infty} \frac{z^{\ell}}{\ell^{n}}\right]$$

  comment

Stochastic Financial Models

• 3.II.27J

  Stochastic Financial Models | Part II, 2007

  Suppose that over two periods a stock price moves on a binomial tree

  

  (i) Determine for what values of the riskless rate $r$ there is no arbitrage. From here on, fix $r=1 / 4$ and determine the equivalent martingale measure.

  (ii) Find the time-zero price and replicating portfolio for a European put option with strike 15 and expiry $2 .$

  (iii) Find the time-zero price and optimal exercise policy for an American put option with the same strike and expiry.

  (iv) Deduce the corresponding (European and American) call option prices for the same strike and expiry.

  comment

Topics in Analysis

• 3.II.12F

  Topics in Analysis | Part II, 2007

  (i) State and prove Liouville's theorem on approximation of algebraic numbers by rationals.

  (ii) Consider the continued fraction

  $$x=\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\frac{1}{a_{4}+\ldots}}}}$$

  where the $a_{j}$ are strictly positive integers. You may assume the following algebraic facts about the $n$th convergent $p_{n} / q_{n}$.

  $$p_{n} q_{n-1}-p_{n-1} q_{n}=(-1)^{n}, \quad q_{n}=a_{n} q_{n-1}+q_{n-2} .$$

  Show that

  $$\left|\frac{p_{n}}{q_{n}}-x\right| \leqslant \frac{1}{q_{n} q_{n+1}}$$

  Give explicit values for $a_{n}$ so that $x$ is transcendental and prove that you have done SO.

  comment

Waves

• 3.II.37C

  Waves | Part II, 2007

  Waves propagating in a slowly-varying medium satisfy the local dispersion relation

  $$\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$$

  in the standard notation. Give a brief derivation of the ray-tracing equations for such waves; a formal justification is not required.

  An ocean occupies the region $x>0, \quad-\infty<y<\infty$. Water waves are incident on a beach near $x=0$. The undisturbed water depth is

  $$h(x)=\alpha x^{p}$$

  with $\alpha$ a small positive constant and $p$ positive. The local dispersion relation is

  $$\Omega^{2}=g \kappa \tanh (\kappa h) \quad \text { where } \quad \kappa^{2}=k_{1}^{2}+k_{2}^{2}$$

  and where $k_{1}, k_{2}$ are the wavenumber components in the $x, y$ directions. Far from the beach, the waves are planar with frequency $\omega_{\infty}$ and crests making an acute angle $\theta_{\infty}$ with the shoreline $x=0$. Obtain a differential equation (in implicit form) for a ray $y=y(x)$, and show that near the shore the ray satisfies

  $$y-y_{0} \sim A x^{q}$$

  where $A$ and $q$ should be found. Sketch the appearance of the wavecrests near the shoreline.

  comment