Over two periods a stock price $\left\{S_{t}: t=0,1,2\right\}$ moves on a binomial tree.

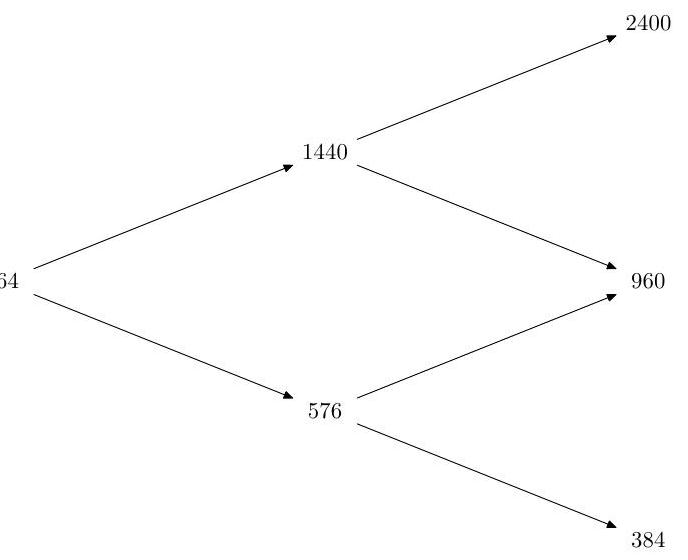
Assuming that the riskless rate is constant at $r=1 / 3$, verify that all risk-neutral up-probabilities are given by one value $p \in(0,1)$. Find the time- 0 value of the following three put options all struck at $K=S_{0}=864=2^{5} \times 3^{3}$, with expiry 2 :

(a) a European put;

(b) an American put;

(c) a European put modified by raising the strike to $K=992$ at time 1 if the stock went down in the first period.