Part II, 2005

Algebraic Topology

• 1.II.21H

  Algebraic Topology | Part II, 2005

  (i) Show that if $E \rightarrow T$ is a covering map for the torus $T=S^{1} \times S^{1}$, then $E$ is homeomorphic to one of the following: the plane $\mathbb{R}^{2}$, the cylinder $\mathbb{R} \times S^{1}$, or the torus $T$.

  (ii) Show that any continuous map from a sphere $S^{n}(n \geqslant 2)$ to the torus $T$ is homotopic to a constant map.

  [General theorems from the course may be used without proof, provided that they are clearly stated.]

  comment

• 2.II.21H

  Algebraic Topology | Part II, 2005

  State the Van Kampen Theorem. Use this theorem and the fact that $\pi_{1} S^{1}=\mathbb{Z}$ to compute the fundamental groups of the torus $T=S^{1} \times S^{1}$, the punctured torus $T \backslash\{p\}$, for some point $p \in T$, and the connected sum $T \# T$ of two copies of $T$.

  comment

• 3.II.20H

  Algebraic Topology | Part II, 2005

  Let $X$ be a space that is triangulable as a simplicial complex with no $n$-simplices. Show that any continuous map from $X$ to $S^{n}$ is homotopic to a constant map.

  [General theorems from the course may be used without proof, provided they are clearly stated.]

  comment

• 4.II.21H

  Algebraic Topology | Part II, 2005

  Let $X$ be a simplicial complex. Suppose $X=B \cup C$ for subcomplexes $B$ and $C$, and let $A=B \cap C$. Show that the inclusion of $A$ in $B$ induces an isomorphism $H_{*} A \rightarrow H_{*} B$ if and only if the inclusion of $C$ in $X$ induces an isomorphism $H_{*} C \rightarrow H_{*} X$.

  comment

Applications of Quantum Mechanics

• 1.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  A beam of particles is incident on a central potential $V(r)(r=|\mathbf{x}|)$ that vanishes for $r>R$. Define the differential cross-section $d \sigma / d \Omega$.

  Given that each incoming particle has momentum $\hbar \mathbf{k}$, explain the relevance of solutions to the time-independent Schrödinger equation with the asymptotic form

  $$\psi(\mathbf{x}) \sim e^{i \mathbf{k} \cdot \mathbf{x}}+f(\hat{\mathbf{x}}) \frac{e^{i k r}}{r}$$

  as $r \rightarrow \infty$, where $k=|\mathbf{k}|$ and $\hat{\mathbf{x}}=\mathbf{x} / r$. Write down a formula that determines $d \sigma / d \Omega$ in this case.

  Write down the time-independent Schrödinger equation for a particle of mass $m$ and energy $E=\frac{\hbar^{2} k^{2}}{2 m}$ in a central potential $V(r)$, and show that it allows a solution of the form

  $$\psi(\mathbf{x})=e^{i \mathbf{k} \cdot \mathbf{x}}-\frac{m}{2 \pi \hbar^{2}} \int d^{3} x^{\prime} \frac{e^{i k\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} V\left(r^{\prime}\right) \psi\left(\mathbf{x}^{\prime}\right) .$$

  Show that this is consistent with $(*)$ and deduce an expression for $f(\hat{\mathbf{x}})$. Obtain the Born approximation for $f(\hat{\mathbf{x}})$, and show that $f(\hat{\mathbf{x}})=F(k \hat{\mathbf{x}}-\mathbf{k})$, where

  $$F(\mathbf{q})=-\frac{m}{2 \pi \hbar^{2}} \int d^{3} x e^{-i \mathbf{q} \cdot \mathbf{x}} V(r)$$

  Under what conditions is the Born approximation valid?

  Obtain a formula for $f(\hat{\mathbf{x}})$ in terms of the scattering angle $\theta$ in the case that

  $$V(r)=K \frac{e^{-\mu r}}{r},$$

  for constants $K$ and $\mu$. Hence show that $f(\hat{\mathbf{x}})$ is independent of $\hbar$ in the limit $\mu \rightarrow 0$, when expressed in terms of $\theta$ and the energy $E$.

  [You may assume that $\left.\left(\nabla^{2}+k^{2}\right)\left(\frac{e^{i k r}}{r}\right)=-4 \pi \delta^{3}(\mathbf{x}) .\right]$

  comment

• 2.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  Describe briefly the variational approach to the determination of an approximate ground state energy $E_{0}$ of a Hamiltonian $H$.

  Let $\left|\psi_{1}\right\rangle$ and $\left|\psi_{2}\right\rangle$ be two states, and consider the trial state

  $$|\psi\rangle=a_{1}\left|\psi_{1}\right\rangle+a_{2}\left|\psi_{2}\right\rangle$$

  for real constants $a_{1}$ and $a_{2}$. Given that

  $$\begin{aligned} \left\langle\psi_{1} \mid \psi_{1}\right\rangle &=\left\langle\psi_{2} \mid \psi_{2}\right\rangle=1, &\left\langle\psi_{2} \mid \psi_{1}\right\rangle=\left\langle\psi_{1} \mid \psi_{2}\right\rangle=s, \\ \left\langle\psi_{1}|H| \psi_{1}\right\rangle &=\left\langle\psi_{2}|H| \psi_{2}\right\rangle=\mathcal{E}, &\left\langle\psi_{2}|H| \psi_{1}\right\rangle=\left\langle\psi_{1}|H| \psi_{2}\right\rangle=\epsilon, \end{aligned}$$

  and that $\epsilon<s \mathcal{E}$, obtain an upper bound on $E_{0}$ in terms of $\mathcal{E}, \epsilon$ and $s$.

  The normalized ground-state wavefunction of the Hamiltonian

  $$H_{1}=\frac{p^{2}}{2 m}-K \delta(x), \quad K>0,$$

  $$\psi_{1}(x)=\sqrt{\lambda} e^{-\lambda|x|}, \quad \lambda=\frac{m K}{\hbar^{2}} .$$

  Verify that the ground state energy of $H_{1}$ is

  $$E_{B} \equiv\left\langle\psi_{1}|H| \psi_{1}\right\rangle=-\frac{1}{2} K \lambda .$$

  Now consider the Hamiltonian

  $$H=\frac{p^{2}}{2 m}-K \delta(x)-K \delta(x-R)$$

  and let $E_{0}(R)$ be its ground-state energy as a function of $R$. Assuming that

  $$\psi_{2}(x)=\sqrt{\lambda} e^{-\lambda|x-R|},$$

  use $(*)$ to compute $s, \mathcal{E}$ and $\epsilon$ for $\psi_{1}$ and $\psi_{2}$ as given. Hence show that

  $$E_{0}(R) \leqslant E_{B}\left[1+2 \frac{e^{-\lambda R}\left(1+e^{-\lambda R}\right)}{1+(1+\lambda R) e^{-\lambda R}}\right]$$

  Why should you expect this inequality to become an approximate equality for sufficiently large $R$ ? Describe briefly how this is relevant to molecular binding.

  comment

• 3.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  Let $\{\mathbf{l}\}$ be the set of lattice vectors of some lattice. Define the reciprocal lattice. What is meant by a Bravais lattice?

  Let $\mathbf{i}, \mathbf{j}, \mathbf{k}$ be mutually orthogonal unit vectors. A crystal has identical atoms at positions given by the vectors

  $$\begin{array}{ll} a\left[n_{1} \mathbf{i}+n_{2} \mathbf{j}+n_{3} \mathbf{k}\right], & a\left[\left(n_{1}+\frac{1}{2}\right) \mathbf{i}+\left(n_{2}+\frac{1}{2}\right) \mathbf{j}+n_{3} \mathbf{k}\right] \\ a\left[\left(n_{1}+\frac{1}{2}\right) \mathbf{i}+\mathbf{j}+\left(n_{3}+\frac{1}{2}\right) \mathbf{k}\right], & a\left[n_{1} \mathbf{i}+\left(n_{2}+\frac{1}{2}\right) \mathbf{j}+\left(n_{3}+\frac{1}{2}\right) \mathbf{k}\right] \end{array}$$

  where $\left(n_{1}, n_{2}, n_{3}\right)$ are arbitrary integers and $a$ is a constant. Show that these vectors define a Bravais lattice with basis vectors

  $$\mathbf{a}_{1}=a \frac{1}{2}(\mathbf{j}+\mathbf{k}), \quad \mathbf{a}_{2}=a \frac{1}{2}(\mathbf{i}+\mathbf{k}), \quad \mathbf{a}_{3}=a \frac{1}{2}(\mathbf{i}+\mathbf{j})$$

  Verify that a basis for the reciprocal lattice is

  $$\mathbf{b}_{1}=\frac{2 \pi}{a}(\mathbf{j}+\mathbf{k}-\mathbf{i}), \quad \mathbf{b}_{2}=\frac{2 \pi}{a}(\mathbf{i}+\mathbf{k}-\mathbf{j}), \quad \mathbf{b}_{3}=\frac{2 \pi}{a}(\mathbf{i}+\mathbf{j}-\mathbf{k})$$

  In Bragg scattering, an incoming plane wave of wave-vector $\mathbf{k}$ is scattered to an outgoing wave of wave-vector $\mathbf{k}^{\prime}$. Explain why $\mathbf{k}^{\prime}=\mathbf{k}+\mathbf{g}$ for some reciprocal lattice vector g. Given that $\theta$ is the scattering angle, show that

  $$\sin \frac{1}{2} \theta=\frac{|\mathbf{g}|}{2|\mathbf{k}|} .$$

  For the above lattice, explain why you would expect scattering through angles $\theta_{1}$ and $\theta_{2}$ such that

  $$\frac{\sin \frac{1}{2} \theta_{1}}{\sin \frac{1}{2} \theta_{2}}=\frac{\sqrt{3}}{2}$$

  comment

• 4.II.33B

  Applications of Quantum Mechanics | Part II, 2005

  A semiconductor has a valence energy band with energies $E \leqslant 0$ and density of states $g_{v}(E)$, and a conduction energy band with energies $E \geqslant E_{g}$ and density of states $g_{c}(E)$. Assume that $g_{v}(E) \sim A_{v}(-E)^{\frac{1}{2}}$ as $E \rightarrow 0$, and that $g_{c}(E) \sim A_{c}\left(E-E_{g}\right)^{\frac{1}{2}}$ as $E \rightarrow E_{g}$. At zero temperature all states in the valence band are occupied and the conduction band is empty. Let $p$ be the number of holes in the valence band and $n$ the number of electrons in the conduction band at temperature $T$. Under suitable approximations derive the result

  $$p n=N_{v} N_{c} e^{-E_{g} / k T}$$

  where

  $$N_{v}=\frac{1}{2} \sqrt{\pi} A_{v}(k T)^{\frac{3}{2}}, \quad N_{c}=\frac{1}{2} \sqrt{\pi} A_{c}(k T)^{\frac{3}{2}} .$$

  Briefly describe how a semiconductor may conduct electricity but with a conductivity that is strongly temperature dependent.

  Describe how doping of the semiconductor leads to $p \neq n$. A $p n$ junction is formed between an $n$-type semiconductor, with $N_{d}$ donor atoms, and a $p$-type semiconductor, with $N_{a}$ acceptor atoms. Show that there is a potential difference $V_{n p}=\Delta E /|e|$ across the junction, where $e$ is the electron charge, and

  $$\Delta E=E_{g}-k T \ln \frac{N_{v} N_{c}}{N_{d} N_{a}} .$$

  Two semiconductors, one $p$-type and one $n$-type, are joined to make a closed circuit with two $p n$ junctions. Explain why a current will flow around the circuit if the junctions are at different temperatures.

  [The Fermi-Dirac distribution function at temperature $T$ and chemical potential $\mu$ is $\frac{g(E)}{e^{(E-\mu) / k T}+1}$, where $g(E)$ is the number of states with energy $E$.

  Note that $\int_{0}^{\infty} x^{\frac{1}{2}} e^{-x} d x=\frac{1}{2} \sqrt{\pi}$.]

  comment

Applied Probability

• 1.II.26I

  Applied Probability | Part II, 2005

  A cell has been placed in a biological solution at time $t=0$. After an exponential time of rate $\mu$, it is divided, producing $k$ cells with probability $p_{k}, k=0,1, \ldots$, with the mean value $\rho=\sum_{k=1}^{\infty} k p_{k}(k=0$ means that the cell dies $)$. The same mechanism is applied to each of the living cells, independently.

  (a) Let $M_{t}$ be the number of living cells in the solution by time $t>0$. Prove that $\mathbb{E} M_{t}=\exp [t \mu(\rho-1)]$. [You may use without proof, if you wish, the fact that, if a positive function $a(t)$ satisfies $a(t+s)=a(t) a(s)$ for $t, s \geqslant 0$ and is differentiable at zero, then $a(t)=e^{\alpha t}, t \geqslant 0$, for some $\left.\alpha .\right]$

  Let $\phi_{t}(s)=\mathbb{E} s^{M_{t}}$ be the probability generating function of $M_{t}$. Prove that it satisfies the following differential equation

  $$\frac{\mathrm{d}}{\mathrm{d} t} \phi_{t}(s)=\mu\left(-\phi_{t}(s)+\sum_{k=0}^{\infty} p_{k}\left[\phi_{t}(s)\right]^{k}\right), \quad \text { with } \quad \phi_{0}(s)=s$$

  (b) Now consider the case where each cell is divided in two cells $\left(p_{2}=1\right)$. Let $N_{t}=M_{t}-1$ be the number of cells produced in the solution by time $t$.

  Calculate the distribution of $N_{t}$. Is $\left(N_{t}\right)$ an inhomogeneous Poisson process? If so, what is its rate $\lambda(t)$ ? Justify your answer.

  comment

• 2.II.26I

  Applied Probability | Part II, 2005

  What does it mean to say that $\left(X_{t}\right)$ is a renewal process?

  Let $\left(X_{t}\right)$ be a renewal process with holding times $S_{1}, S_{2}, \ldots$ and let $s>0$. For $n \geqslant 1$, set $T_{n}=S_{X_{s}+n}$. Show that

  $$\mathbb{P}\left(T_{n}>t\right) \geqslant \mathbb{P}\left(S_{n}>t\right), \quad t \geqslant 0,$$

  for all $n$, with equality if $n \geqslant 2$.

  Consider now the case where $S_{1}, S_{2}, \ldots$ are exponential random variables. Show that

  $$\mathbb{P}\left(T_{1}>t\right)>\mathbb{P}\left(S_{1}>t\right), \quad t>0$$

  and that, as $s \rightarrow \infty$,

  $$\mathbb{P}\left(T_{1}>t\right) \rightarrow \mathbb{P}\left(S_{1}+S_{2}>t\right), \quad t \geqslant 0$$

  comment

• 3.II.25I

  Applied Probability | Part II, 2005

  Consider an $\mathrm{M} / \mathrm{G} / r / 0$ loss system with arrival rate $\lambda$ and service-time distribution $F$. Thus, arrivals form a Poisson process of rate $\lambda$, service times are independent with common distribution $F$, there are $r$ servers and there is no space for waiting. Use Little's Lemma to obtain a relation between the long-run average occupancy $L$ and the stationary probability $\pi$ that the system is full.

  Cafe-Bar Duo has 23 serving tables. Each table can be occupied either by one person or two. Customers arrive either singly or in a pair; if a table is empty they are seated and served immediately, otherwise, they leave. The times between arrivals are independent exponential random variables of mean $20 / 3$. Each arrival is twice as likely to be a single person as a pair. A single customer stays for an exponential time of mean 20 , whereas a pair stays for an exponential time of mean 30 ; all these times are independent of each other and of the process of arrivals. The value of orders taken at each table is a constant multiple $2 / 5$ of the time that it is occupied.

  Express the long-run rate of revenue of the cafe as a function of the probability $\pi$ that an arriving customer or pair of customers finds the cafe full.

  By imagining a cafe with infinitely many tables, show that $\pi \leqslant \mathbb{P}(N \geqslant 23)$ where $N$ is a Poisson random variable of parameter $7 / 2$. Deduce that $\pi$ is very small. [Credit will be given for any useful numerical estimate, an upper bound of $10^{-3}$ being sufficient for full credit.]

  comment

• 4.II.26I

  Applied Probability | Part II, 2005

  A particle performs a continuous-time nearest neighbour random walk on a regular triangular lattice inside an angle $\pi / 3$, starting from the corner. See the diagram below. The jump rates are $1 / 3$ from the corner and $1 / 6$ in each of the six directions if the particle is inside the angle. However, if the particle is on the edge of the angle, the rate is $1 / 3$ along the edge away from the corner and $1 / 6$ to each of three other neighbouring sites in the angle. See the diagram below, where a typical trajectory is also shown.

  

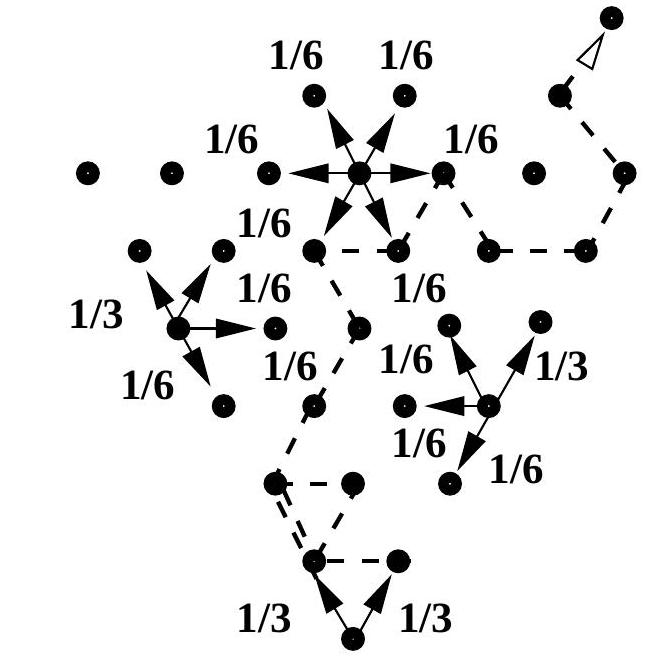
  The particle position at time $t \geqslant 0$ is determined by its vertical level $V_{t}$ and its horizontal position $G_{t}$. For $k \geqslant 0$, if $V_{t}=k$ then $G_{t}=0, \ldots, k$. Here $1, \ldots, k-1$ are positions inside, and 0 and $k$ positions on the edge of the angle, at vertical level $k$.

  Let $J_{1}^{V}, J_{2}^{V}, \ldots$ be the times of subsequent jumps of process $\left(V_{t}\right)$ and consider the embedded discrete-time Markov chains

  $$Y_{n}^{\text {in }}=\left(\widehat{G}_{n}^{\text {in }}, \widehat{V}_{n}\right) \text { and } Y_{n}^{\text {out }}=\left(\widehat{G}_{n}^{\text {out }}, \widehat{V}_{n}\right)$$

  where $\widehat{V}_{n}$ is the vertical level immediately after time $J_{n}^{V}, \widehat{G}_{n}^{\text {in }}$ is the horizontal position immediately after time $J_{n}^{V}$, and $\widehat{G}_{n}^{\text {out }}$ is the horizontal position immediately before time $J_{n+1}^{V}$. (a) Assume that $\left(\widehat{V}_{n}\right)$ is a Markov chain with transition probabilities

  $$\mathbb{P}\left(\widehat{V}_{n}=k+1 \mid \widehat{V}_{n-1}=k\right)=\frac{k+2}{2(k+1)}, \mathbb{P}\left(\widehat{V}_{n}=k-1 \mid \widehat{V}_{n-1}=k\right)=\frac{k}{2(k+1)},$$

  and that $\left(V_{t}\right)$ is a continuous-time Markov chain with rates

  $$q_{k k-1}=\frac{k}{3(k+1)}, \quad q_{k k}=-\frac{2}{3}, \quad q_{k k+1}=\frac{k+2}{3(k+1)}$$

  [You will be asked to justify these assumptions in part (b) of the question.] Determine whether the chains $\left(\widehat{V}_{n}\right)$ and $\left(V_{t}\right)$ are transient, positive recurrent or null recurrent.

  (b) Now assume that, conditional on $\widehat{V}_{n}=k$ and previously passed vertical levels, the horizontal positions $\widehat{G}_{n}^{\text {in }}$ and $\widehat{G}_{n}^{\text {out }}$ are uniformly distributed on $\{0, \ldots, k\}$. In other words, for all attainable values $k, k_{n-1}, \ldots, k_{1}$ and for all $i=0, \ldots, k$,

  $$\begin{aligned} &\mathbb{P}\left(\widehat{G}_{n}^{\text {in }}=i \mid \widehat{V}_{n}=k, \widehat{V}_{n-1}=k_{n-1}, \ldots, \widehat{V}_{1}=k_{1}, \widehat{V}_{0}=0\right) \\ &\quad=\mathbb{P}\left(\widehat{G}_{n}^{\text {out }}=i \mid \widehat{V}_{n}=k, \widehat{V}_{n-1}=k_{n-1}, \ldots, \widehat{V}_{1}=k_{1}, \widehat{V}_{0}=0\right)=\frac{1}{k+1} \end{aligned}$$

  Deduce that $\left(\widehat{V}_{n}\right)$ and $\left(V_{t}\right)$ are indeed Markov chains with transition probabilities and rates as in (a).

  (c) Finally, prove property $(*)$.

  comment

Asymptotic Methods

• 1.II $. 30 \mathrm{~A}$

  Asymptotic Methods | Part II, 2005

  Explain what is meant by an asymptotic power series about $x=a$ for a real function $f(x)$ of a real variable. Show that a convergent power series is also asymptotic.

  Show further that an asymptotic power series is unique (assuming that it exists).

  Let the function $f(t)$ be defined for $t \geqslant 0$ by

  $$f(t)=\frac{1}{\pi^{1 / 2}} \int_{0}^{\infty} \frac{e^{-x}}{x^{1 / 2}(1+2 x t)} d x$$

  By suitably expanding the denominator of the integrand, or otherwise, show that, as $t \rightarrow 0_{+}$,

  $$f(t) \sim \sum_{k=0}^{\infty}(-1)^{k} 1.3 \ldots(2 k-1) t^{k}$$

  and that the error, when the series is stopped after $n$ terms, does not exceed the absolute value of the $(n+1)$ th term of the series.

  comment

• 3.II $. 30$

  Asymptotic Methods | Part II, 2005

  Explain, without proof, how to obtain an asymptotic expansion, as $x \rightarrow \infty$, of

  $$I(x)=\int_{0}^{\infty} e^{-x t} f(t) d t$$

  if it is known that $f(t)$ possesses an asymptotic power series as $t \rightarrow 0$.

  Indicate the modification required to obtain an asymptotic expansion, under suitable conditions, of

  $$\int_{-\infty}^{\infty} e^{-x t^{2}} f(t) d t$$

  Find an asymptotic expansion as $z \rightarrow \infty$ of the function defined by

  $$I(z)=\int_{-\infty}^{\infty} \frac{e^{-t^{2}}}{(z-t)} d t \quad(\operatorname{Im}(z)<0)$$

  and its analytic continuation to $\operatorname{Im}(z) \geqslant 0$. Where are the Stokes lines, that is, the critical lines separating the Stokes regions?

  comment

• 4.II $. 31 \mathrm{~A}$

  Asymptotic Methods | Part II, 2005

  Consider the differential equation

  $$\frac{d^{2} w}{d x^{2}}=q(x) w$$

  where $q(x) \geqslant 0$ in an interval $(a, \infty)$. Given a solution $w(x)$ and a further smooth function $\xi(x)$, define

  $$W(x)=\left[\xi^{\prime}(x)\right]^{1 / 2} w(x) .$$

  Show that, when $\xi$ is regarded as the independent variable, the function $W(\xi)$ obeys the differential equation

  $$\frac{d^{2} W}{d \xi^{2}}=\left\{\dot{x}^{2} q(x)+\dot{x}^{1 / 2} \frac{d^{2}}{d \xi^{2}}\left[\dot{x}^{-1 / 2}\right]\right\} W$$

  where $\dot{x}$ denotes $d x / d \xi$.

  Taking the choice

  $$\xi(x)=\int q^{1 / 2}(x) d x$$

  show that equation $(*)$ becomes

  $$\frac{d^{2} W}{d \xi^{2}}=(1+\phi) W$$

  where

  $$\phi=-\frac{1}{q^{3 / 4}} \frac{d^{2}}{d x^{2}}\left(\frac{1}{q^{1 / 4}}\right)$$

  In the case that $\phi$ is negligible, deduce the Liouville-Green approximate solutions

  $$w_{\pm}=q^{-1 / 4} \exp \left(\pm \int q^{1 / 2} d x\right)$$

  Consider the Whittaker equation

  $$\frac{d^{2} w}{d x^{2}}=\left[\frac{1}{4}+\frac{s(s-1)}{x^{2}}\right] w$$

  where $s$ is a real constant. Show that the Liouville-Green approximation suggests the existence of solutions $w_{A, B}(x)$ with asymptotic behaviour of the form

  $$w_{A} \sim \exp (x / 2)\left(1+\sum_{n=1}^{\infty} a_{n} x^{-n}\right), \quad w_{B} \sim \exp (-x / 2)\left(1+\sum_{n=1}^{\infty} b_{n} x^{-n}\right)$$

  as $x \rightarrow \infty$.

  Given that these asymptotic series may be differentiated term-by-term, show that

  $$a_{n}=\frac{(-1)^{n}}{n !}(s-n)(s-n+1) \ldots(s+n-1) \text {. }$$

  comment

Classical Dynamics

• 1.I.9C

  Classical Dynamics | Part II, 2005

  A particle of mass $m_{1}$ is constrained to move on a circle of radius $r_{1}$, centre $x=y=0$ in a horizontal plane $z=0$. A second particle of mass $m_{2}$ moves on a circle of radius $r_{2}$, centre $x=y=0$ in a horizontal plane $z=c$. The two particles are connected by a spring whose potential energy is

  $$V=\frac{1}{2} \omega^{2} d^{2}$$

  where $d$ is the distance between the particles. How many degrees of freedom are there? Identify suitable generalized coordinates and write down the Lagrangian of the system in terms of them.

  comment

• 1.II.15C

  Classical Dynamics | Part II, 2005

  (i) The action for a system with generalized coordinates $\left(q_{a}\right)$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L\left(q_{a}, \dot{q}_{b}\right) d t$$

  Derive Lagrange's equations from the principle of least action by considering all paths with fixed endpoints, $\delta q_{a}\left(t_{1}\right)=\delta q_{a}\left(t_{2}\right)=0$.

  (ii) A pendulum consists of a point mass $m$ at the end of a light rod of length $l$. The pivot of the pendulum is attached to a mass $M$ which is free to slide without friction along a horizontal rail. Choose as generalized coordinates the position $x$ of the pivot and the angle $\theta$ that the pendulum makes with the vertical.

  Write down the Lagrangian and derive the equations of motion.

  Find the frequency of small oscillations around the stable equilibrium.

  Now suppose that a force acts on the pivot causing it to travel with constant acceleration in the $x$-direction. Find the equilibrium angle $\theta$ of the pendulum.

  comment

• 2.I.9C

  Classical Dynamics | Part II, 2005

  A rigid body has principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$ and is moving under the action of no forces with angular velocity components $\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$. Its motion is described by Euler's equations

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}-\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}=0 \\ &I_{2} \dot{\omega}_{2}-\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1}=0 \\ &I_{3} \dot{\omega}_{3}-\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}=0 \end{aligned}$$

  Are the components of the angular momentum to be evaluated in the body frame or the space frame?

  Now suppose that an asymmetric body is moving with constant angular velocity $(\Omega, 0,0)$. Show that this motion is stable if and only if $I_{1}$ is the largest or smallest principal moment.

  comment

• 3.I.9C

  Classical Dynamics | Part II, 2005

  Define the Poisson bracket $\{f, g\}$ between two functions $f\left(q_{a}, p_{a}\right)$ and $g\left(q_{a}, p_{a}\right)$ on phase space. If $f\left(q_{a}, p_{a}\right)$ has no explicit time dependence, and there is a Hamiltonian $H$, show that Hamilton's equations imply

  $$\frac{d f}{d t}=\{f, H\} .$$

  A particle with position vector $\mathbf{x}$ and momentum $\mathbf{p}$ has angular momentum $\mathbf{L}=\mathbf{x} \times \mathbf{p}$. Compute $\left\{p_{a}, L_{b}\right\}$ and $\left\{L_{a}, L_{b}\right\}$.

  comment

• 3.II.15C

  Classical Dynamics | Part II, 2005

  (i) A point mass $m$ with position $q$ and momentum $p$ undergoes one-dimensional periodic motion. Define the action variable $I$ in terms of $q$ and $p$. Prove that an orbit of energy $E$ has period

  $$T=2 \pi \frac{d I}{d E} .$$

  (ii) Such a system has Hamiltonian

  $$H(q, p)=\frac{p^{2}+q^{2}}{\mu^{2}-q^{2}}$$

  where $\mu$ is a positive constant and $|q|<\mu$ during the motion. Sketch the orbits in phase space both for energies $E \gg 1$ and $E \ll 1$. Show that the action variable $I$ is given in terms of the energy $E$ by

  $$I=\frac{\mu^{2}}{2} \frac{E}{\sqrt{E+1}} .$$

  Hence show that for $E \gg 1$ the period of the orbit is $T \approx \frac{1}{2} \pi \mu^{3} / p_{0}$, where $p_{0}$ is the greatest value of the momentum during the orbit.

  comment

• 4.I.9C

  Classical Dynamics | Part II, 2005

  Define a canonical transformation for a one-dimensional system with coordinates $(q, p) \rightarrow(Q, P)$. Show that if the transformation is canonical then $\{Q, P\}=1$.

  Find the values of constants $\alpha$ and $\beta$ such that the following transformations are canonical: (i) $Q=p q^{\beta}, P=\alpha q^{-1}$. (ii) $Q=q^{\alpha} \cos (\beta p), P=q^{\alpha} \sin (\beta p)$.

  comment

Coding and Cryptography

• 1.I.4J

  Coding and Cryptography | Part II, 2005

  Briefly describe the methods of Shannon-Fano and Huffman for economical coding. Illustrate both methods by finding decipherable binary codings in the case where messages $\mu_{1}, \ldots, \mu_{5}$ are emitted with probabilities $0.45,0.25,0.2,0.05,0.05$. Compute the expected word length in each case.

  comment

• 2.I.4J

  Coding and Cryptography | Part II, 2005

  What is a linear binary code? What is the weight $w(C)$ of a linear binary code $C ?$ Define the bar product $C_{1} \mid C_{2}$ of two binary linear codes $C_{1}$ and $C_{2}$, stating the conditions that $C_{1}$ and $C_{2}$ must satisfy. Under these conditions show that

  $$w\left(C_{1} \mid C_{2}\right) \geqslant \min \left(2 w\left(C_{1}\right), w\left(C_{2}\right)\right)$$

  comment

• 2.II.12J

  Coding and Cryptography | Part II, 2005

  What does it means to say that $f: \mathbb{F}_{2}^{d} \rightarrow \mathbb{F}_{2}^{d}$ is a linear feedback shift register? Let $\left(x_{n}\right)_{n \geqslant 0}$ be a stream produced by such a register. Show that there exist $N, M$ with $N+M \leqslant 2^{d}-1$ such that $x_{r+N}=x_{r}$ for all $r \geqslant M$.

  Explain and justify the Berlekamp-Massey method for 'breaking' a cipher stream arising from a linear feedback register of unknown length.

  Let $x_{n}, y_{n}, z_{n}$ be three streams produced by linear feedback registers. Set

  $$\begin{aligned} &k_{n}=x_{n} \text { if } y_{n}=z_{n} \\ &k_{n}=y_{n} \text { if } y_{n} \neq z_{n} \end{aligned}$$

  Show that $k_{n}$ is also a stream produced by a linear feedback register. Sketch proofs of any theorems that you use.

  comment

• 3.I.4J

  Coding and Cryptography | Part II, 2005

  Briefly explain how and why a signature scheme is used. Describe the el Gamal scheme.

  comment

• 3.II.12J

  Coding and Cryptography | Part II, 2005

  Define a cyclic code. Define the generator and check polynomials of a cyclic code and show that they exist.

  Show that Hamming's original code is a cyclic code with check polynomial $X^{4}+X^{2}+X+1$. What is its generator polynomial? Does Hamming's original code contain a subcode equivalent to its dual?

  comment

• 4.I.4J

  Coding and Cryptography | Part II, 2005

  What does it mean to transmit reliably at rate $r$ through a binary symmetric channel (BSC) with error probability $p$ ? Assuming Shannon's second coding theorem, compute the supremum of all possible reliable transmission rates of a BSC. What happens if (i) $p$ is very small, (ii) $p=1 / 2$, or (iii) $p>1 / 2$ ?

  comment

Cosmology

• 1.I.10D

  Cosmology | Part II, 2005

  (a) Around $t \approx 1 \mathrm{~s}$ after the big bang $(k T \approx 1 \mathrm{MeV})$, neutrons and protons are kept in equilibrium by weak interactions such as

  $$\tag{*} n+\nu_{e} \leftrightarrow p+e^{-}$$

  Show that, in equilibrium, the neutron-to-proton ratio is given by

  $$\frac{n_{n}}{n_{p}} \approx e^{-Q / k T}$$

  where $Q=\left(m_{n}-m_{p}\right) c^{2}=1.29 \mathrm{MeV}$ corresponds to the mass difference between the neutron and the proton. Explain briefly why we can neglect the difference $\mu_{n}-\mu_{p}$ in the chemical potentials.

  (b) The ratio of the weak interaction rate $\Gamma_{W} \propto T^{5}$ which maintains (*) to the Hubble expansion rate $H \propto T^{2}$ is given by

  $$\tag{†} \frac{\Gamma_{W}}{H} \approx\left(\frac{k T}{0.8 \mathrm{MeV}}\right)^{3}$$

  Explain why the neutron-to-proton ratio effectively "freezes out" once $k T<0.8 \mathrm{MeV}$, except for some slow neutron decay. Also explain why almost all neutrons are subsequently captured in ${ }^{4} \mathrm{He}$; estimate the value of the relative mass density $Y_{^{4} \mathrm{He}}=\rho_{^{4}\mathrm{He}} / \rho_{\mathrm{B}}$ (with $\rho_{\mathrm{B}}=\rho_{n}+\rho_{p}$ ) given a final ratio $n_{n} / n_{p} \approx 1 / 8$.

  (c) Suppose instead that the weak interaction rate were very much weaker than that described by equation $(†)$. Describe the effect on the relative helium density $Y_{^{4} \mathrm{He}}$. Briefly discuss the wider implications of this primordial helium-to-hydrogen ratio on stellar lifetimes and life on earth.

  comment

• 2.I.10D

  Cosmology | Part II, 2005

  (a) A spherically symmetric star obeys the pressure-support equation

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $P(r)$ is the pressure at a distance $r$ from the centre, $\rho(r)$ is the density, and the mass $m(r)$ is defined through the relation $d m / d r=4 \pi r^{2} \rho(r)$. Multiply $(*)$ by $4 \pi r^{3}$ and integrate over the total volume $V$ of the star to derive the virial theorem

  $$\langle P\rangle V=-\frac{1}{3} E_{\text {grav }}$$

  where $\langle P\rangle$ is the average pressure and $E_{\text {grav }}$ is the total gravitational potential energy.

  (b) Consider a white dwarf supported by electron Fermi degeneracy pressure $P \approx h^{2} n^{5 / 3} / m_{\mathrm{e}}$, where $m_{\mathrm{e}}$ is the electron mass and $n$ is the number density. Assume a uniform density $\rho(r)=m_{\mathrm{p}} n(r) \approx m_{\mathrm{p}}\langle n\rangle$, so the total mass of the star is given by $M=(4 \pi / 3)\langle n\rangle m_{\mathrm{p}} R^{3}$ where $R$ is the star radius and $m_{\mathrm{p}}$ is the proton mass. Show that the total energy of the white dwarf can be written in the form

  $$E_{\mathrm{total}}=E_{\mathrm{kin}}+E_{\mathrm{grav}}=\frac{\alpha}{R^{2}}-\frac{\beta}{R}$$

  where $\alpha, \beta$ are positive constants which you should determine. [You may assume that for an ideal gas $E_{\mathrm{kin}}=\frac{3}{2}\langle P\rangle V$.] Use this expression to explain briefly why a white dwarf is stable.

  comment

• 2.II.15D

  Cosmology | Part II, 2005

  (a) Consider a homogeneous and isotropic universe with scale factor $a(t)$ and filled with mass density $\rho(t)$. Show how the conservation of kinetic energy plus gravitational potential energy for a test particle on the edge of a spherical region in this universe can be used to derive the Friedmann equation

  $$\tag{*} \left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho$$

  where $k$ is a constant. State clearly any assumptions you have made.

  (b) Now suppose that the universe was filled throughout its history with radiation with equation of state $P=\rho c^{2} / 3$. Using the fluid conservation equation and the definition of the relative density $\Omega$, show that the density of this radiation can be expressed as

  $$\rho=\frac{3 H_{0}^{2}}{8 \pi G} \frac{\Omega_{0}}{a^{4}},$$

  where $H_{0}$ is the Hubble parameter today and $\Omega_{0}$ is the relative density today $\left(t=t_{0}\right)$ and $a_{0} \equiv a\left(t_{0}\right)=1$ is assumed. Show also that $k c^{2}=H_{0}^{2}\left(\Omega_{0}-1\right)$ and hence rewrite the Friedmann equation $(*)$ as

  $$\tag{†} \left(\frac{\dot{a}}{a}\right)^{2}=H_{0}^{2} \Omega_{0}\left(\frac{1}{a^{4}}-\frac{\beta}{a^{2}}\right)$$

  where $\beta \equiv\left(\Omega_{0}-1\right) / \Omega_{0}$.

  (c) Now consider a closed model with $k>0$ (or $\Omega>1)$. Rewrite ( $\dagger$ ) using the new time variable $\tau$ defined by

  $$\frac{d t}{d \tau}=a$$

  Hence, or otherwise, solve $(†)$ to find the parametric solution

  $$a(\tau)=\frac{1}{\sqrt{\beta}}(\sin \alpha \tau), \quad t(\tau)=\frac{1}{\alpha \sqrt{\beta}}(1-\cos \alpha \tau),$$

  where $\alpha \equiv H_{0} \sqrt{\left(\Omega_{0}-1\right)} . \quad$ Recall that $\left.\int d x / \sqrt{1-x^{2}}=\sin ^{-1} x .\right]$

  Using the solution for $a(\tau)$, find the value of the new time variable $\tau=\tau_{0}$ today and hence deduce that the age of the universe in this model is

  $$t_{0}=H_{0}^{-1} \frac{\sqrt{\Omega_{0}}-1}{\Omega_{0}-1}$$

  comment

• 3.I.10D

  Cosmology | Part II, 2005

  (a) Define and discuss the concept of the cosmological horizon and the Hubble radius for a homogeneous isotropic universe. Illustrate your discussion with the specific examples of the Einstein-de Sitter universe $\left(a \propto t^{2 / 3}\right.$ for $\left.t>0\right)$ and a de Sitter universe $\left(a \propto e^{H t}\right.$ with $H$ constant, $t>-\infty)$.

  (b) Explain the horizon problem for a decelerating universe in which $a(t) \propto t^{\alpha}$ with $\alpha<1$. How can inflation cure the horizon problem?

  (c) Consider a Tolman (radiation-filled) universe $\left(a(t) \propto t^{1 / 2}\right.$ ) beginning at $t_{\mathrm{r}} \sim$ $10^{-35} \mathrm{~s}$ and lasting until today at $t_{0} \approx 10^{17} \mathrm{~s}$. Estimate the horizon size today $d_{H}\left(t_{0}\right)$ and project this lengthscale backwards in time to show that it had a physical size of about 1 metre at $t \approx t_{\mathrm{r}}$.

  Prior to $t \approx t_{\mathrm{r}}$, assume an inflationary (de Sitter) epoch with constant Hubble parameter $H$ given by its value at $t \approx t_{\mathrm{r}}$ for the Tolman universe. How much expansion during inflation is required for the observable universe today to have begun inside one Hubble radius?

  comment

• 4.I.10D

  Cosmology | Part II, 2005

  The linearised equation for the growth of a density fluctuation $\delta_{k}$ in a homogeneous and isotropic universe is

  $$\frac{d^{2} \delta_{k}}{d t^{2}}+2 \frac{\dot{a}}{a} \frac{d \delta_{k}}{d t}-\left(4 \pi G \rho_{\mathrm{m}}-\frac{v_{s}^{2} k^{2}}{a^{2}}\right) \delta_{k}=0,$$

  where $\rho_{\mathrm{m}}$ is the non-relativistic matter density, $k$ is the comoving wavenumber and $v_{s}$ is the sound speed $\left(v_{s}^{2} \equiv d P / d \rho\right)$.

  (a) Define the Jeans length $\lambda_{\mathrm{J}}$ and discuss its significance for perturbation growth.

  (b) Consider an Einstein-de Sitter universe with $a(t)=\left(t / t_{0}\right)^{2 / 3}$ filled with pressure-free matter $(P=0)$. Show that the perturbation equation $(*)$ can be re-expressed as

  $$\ddot{\delta}_{k}+\frac{4}{3 t} \dot{\delta}_{k}-\frac{2}{3 t^{2}} \delta_{k}=0 .$$

  By seeking power law solutions, find the growing and decaying modes of this equation.

  (c) Qualitatively describe the evolution of non-relativistic matter perturbations $(k>a H)$ in the radiation era, $a(t) \propto t^{1 / 2}$, when $\rho_{\mathrm{r}} \gg \rho_{\mathrm{m}}$. What feature in the power spectrum is associated with the matter-radiation transition?

  comment

• 4.II.15D

  Cosmology | Part II, 2005

  For an ideal gas of bosons, the average occupation number can be expressed as

  $$\bar{n}_{k}=\frac{g_{k}}{e^{\left(E_{k}-\mu\right) / k T}-1},$$

  where $g_{k}$ has been included to account for the degeneracy of the energy level $E_{k}$. In the approximation in which a discrete set of energies $E_{k}$ is replaced with a continuous set with momentum $p$, the density of one-particle states with momentum in the range $p$ to $p+d p$ is $g(p) d p$. Explain briefly why

  $$g(p) \propto p^{2} V,$$

  where $V$ is the volume of the gas. Using this formula with equation $(*)$, obtain an expression for the total energy density $\epsilon=E / V$ of an ultra-relativistic gas of bosons at zero chemical potential as an integral over $p$. Hence show that

  $$\epsilon \propto T^{\alpha}$$

  where $\alpha$ is a number you should find. Why does this formula apply to photons?

  Prior to a time $t \sim 100,000$ years, the universe was filled with a gas of photons and non-relativistic free electrons and protons. Subsequently, at around $t \sim 400,000$ years, the protons and electrons began combining to form neutral hydrogen,

  $$p+e^{-} \leftrightarrow H+\gamma$$

  Deduce Saha's equation for this recombination process stating clearly the steps required:

  $$\frac{n_{\mathrm{e}}^{2}}{n_{\mathrm{H}}}=\left(\frac{2 \pi m_{\mathrm{e}} k T}{h^{2}}\right)^{3 / 2} \exp (-I / k T)$$

  where $I$ is the ionization energy of hydrogen. [Note that the equilibrium number density of a non-relativistic species $\left(k T \ll m c^{2}\right)$ is given by $n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left[\left(\mu-m c^{2}\right) / k T\right]$, while the photon number density is $n_{\gamma}=16 \pi \zeta(3)\left(\frac{k T}{h c}\right)^{3}$, where $\left.\zeta(3) \approx 1.20 \ldots\right]$

  Consider now the fractional ionization $X_{\mathrm{e}}=n_{\mathrm{e}} / n_{\mathrm{B}}$, where $n_{B}=n_{\mathrm{p}}+n_{\mathrm{H}}=\eta n_{\gamma}$ is the baryon number of the universe and $\eta$ is the baryon-to-photon ratio. Find an expression for the ratio

  $$\left(1-X_{\mathrm{e}}\right) / X_{\mathrm{e}}^{2}$$

  in terms only of $k T$ and constants such as $\eta$ and $I$. One might expect neutral hydrogen to form at a temperature given by $k T \approx I \approx 13 \mathrm{eV}$, but instead in our universe it forms at the much lower temperature $k T \approx 0.3 \mathrm{eV}$. Briefly explain why.

  comment

Differential Geometry

• 1.II.24H

  Differential Geometry | Part II, 2005

  Let $f: X \rightarrow Y$ be a smooth map between manifolds without boundary.

  (i) Define what is meant by a critical point, critical value and regular value of $f$.

  (ii) Show that if $y$ is a regular value of $f$ and $\operatorname{dim} X \geqslant \operatorname{dim} Y$, then the set $f^{-1}(y)$ is a submanifold of $X$ with $\operatorname{dim} f^{-1}(y)=\operatorname{dim} X-\operatorname{dim} Y$.

  [You may assume the inverse function theorem.]

  (iii) Let $S L(n, \mathbb{R})$ be the group of all $n \times n$ real matrices with determinant 1. Prove that $S L(n, \mathbb{R})$ is a submanifold of the set of all $n \times n$ real matrices. Find the tangent space to $S L(n, \mathbb{R})$ at the identity matrix.

  comment

• 2.II.24H

  Differential Geometry | Part II, 2005

  State the isoperimetric inequality in the plane.

  Let $S \subset \mathbb{R}^{3}$ be a surface. Let $p \in S$ and let $S_{r}(p)$ be a geodesic circle of centre $p$ and radius $r$ ( $r$ small). Let $L$ be the length of $S_{r}(p)$ and $A$ be the area of the region bounded by $S_{r}(p)$. Prove that

  $$4 \pi A-L^{2}=\pi^{2} r^{4} K(p)+\varepsilon(r),$$

  where $K(p)$ is the Gaussian curvature of $S$ at $p$ and

  $$\lim _{r \rightarrow 0} \frac{\varepsilon(r)}{r^{4}}=0 .$$

  When $K(p)>0$ and $r$ is small, compare this briefly with the isoperimetric inequality in the plane.

  comment

• 3.II.23H

  Differential Geometry | Part II, 2005

  (i) Define geodesic curvature and state the Gauss-Bonnet theorem.

  (ii) Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a closed regular curve parametrized by arc-length, and assume that $\alpha$ has non-zero curvature everywhere. Let $n: I \rightarrow S^{2} \subset \mathbb{R}^{3}$ be the curve given by the normal vector $n(s)$ to $\alpha(s)$. Let $\bar{s}$ be the arc-length of the curve $n$ on $S^{2}$. Show that the geodesic curvature $k_{g}$ of $n$ is given by

  $$k_{g}=-\frac{d}{d s} \tan ^{-1}(\tau / k) \frac{d s}{d \bar{s}},$$

  where $k$ and $\tau$ are the curvature and torsion of $\alpha$.

  (iii) Suppose now that $n(s)$ is a simple curve (i.e. it has no self-intersections). Show that $n(I)$ divides $S^{2}$ into two regions of equal area.

  comment

• 4.II.24H

  Differential Geometry | Part II, 2005

  (i) Define what is meant by an isothermal parametrization. Let $\phi: U \rightarrow \mathbb{R}^{3}$ be an isothermal parametrization. Prove that

  $$\phi_{u u}+\phi_{v v}=2 \lambda^{2} \mathbf{H}$$

  where $\mathbf{H}$ is the mean curvature vector and $\lambda^{2}=\left\langle\phi_{u}, \phi_{u}\right\rangle$.

  Define what it means for $\phi$ to be minimal, and deduce that $\phi$ is minimal if and only if $\Delta \phi=0$.

  [You may assume that the mean curvature $H$ can be written as

  $$\left.H=\frac{e G-2 f F+g E}{2\left(E G-F^{2}\right)} .\right]$$

  (ii) Write $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$. Consider the complex valued functions

  $$\varphi_{1}=x_{u}-i x_{v}, \quad \varphi_{2}=y_{u}-i y_{v}, \quad \varphi_{3}=z_{u}-i z_{v}$$

  Show that $\phi$ is isothermal if and only if $\varphi_{1}^{2}+\varphi_{2}^{2}+\varphi_{3}^{2} \equiv 0$.

  Suppose now that $\phi$ is isothermal. Prove that $\phi$ is minimal if and only if $\varphi_{1}, \varphi_{2}$ and $\varphi_{3}$ are holomorphic functions.

  (iii) Consider the immersion $\phi: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}$ given by

  $$\phi(u, v)=\left(u-u^{3} / 3+u v^{2},-v+v^{3} / 3-u^{2} v, u^{2}-v^{2}\right)$$

  Find $\varphi_{1}, \varphi_{2}$ and $\varphi_{3}$. Show that $\phi$ is an isothermal parametrization of a minimal surface.

  comment

Dynamical Systems

• 1.I.7B

  Dynamical Systems | Part II, 2005

  State Dulac's Criterion and the Poincaré-Bendixson Theorem regarding the existence of periodic solutions to the dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$. Hence show that

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-x+y\left(\mu-2 x^{2}-y^{2}\right) \end{aligned}$$

  has no periodic solutions if $\mu<0$ and at least one periodic solution if $\mu>0$.

  comment

• 1.II.14B

  Dynamical Systems | Part II, 2005

  Consider the equations

  $$\begin{aligned} &\dot{x}=\left(a-x^{2}\right)\left(a^{2}-y\right) \\ &\dot{y}=x-y \end{aligned}$$

  as a function of the parameter $a$. Find the fixed points and plot their location in the $(a, x)$ plane. Hence, or otherwise, deduce that there are bifurcations at $a=0$ and $a=1$.

  Investigate the bifurcation at $a=1$ by making the substitutions $u=x-1, v=y-x$ and $\mu=a-1$. Find the equation of the extended centre manifold to second order. Find the evolution equation on the centre manifold to second order, and determine the stability of its fixed points.

  Show which branches of fixed points in the $(a, x)$ plane are stable and which are unstable, and state, without calculation, the type of bifurcation at $a=0$. Hence sketch the structure of the $(x, y)$ phase plane very near the origin for $|a| \ll 1$ in the cases (i) $a<0$ and (ii) $a>0$.

  The system is perturbed to $\dot{x}=\left(a-x^{2}\right)\left(a^{2}-y\right)+\epsilon$, where $0<\epsilon \ll 1$, with $\dot{y}=x-y$ still. Sketch the possible changes to the bifurcation diagram near $a=0$ and $a=1$. [Calculation is not required.]

  comment

• 2.I.7B

  Dynamical Systems | Part II, 2005

  Define Lyapunov stability and quasi-asymptotic stability of a fixed point $\mathbf{x}_{0}$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$.

  By considering a Lyapunov function of the form $V=g(x)+y^{2}$, show that the origin is an asymptotically stable fixed point of

  $$\begin{aligned} &\dot{x}=-y-x^{3} \\ &\dot{y}=x^{5} \end{aligned}$$

  [Lyapunov's Second Theorem may be used without proof, provided you show that its conditions apply.]

  comment

• 2.II.14B

  Dynamical Systems | Part II, 2005

  Prove that if a continuous map $F$ of an interval into itself has a periodic orbit of period three then it also has periodic orbits of least period $n$ for all positive integers $n$.

  Explain briefly why there must be at least two periodic orbits of least period $5 .$

  [You may assume without proof:

  (i) If $U$ and $V$ are non-empty closed bounded intervals such that $V \subseteq F(U)$ then there is a closed bounded interval $K \subseteq U$ such that $F(K)=V$.

  (ii) The Intermediate Value Theorem.]

  comment

• 3.I.7B

  Dynamical Systems | Part II, 2005

  Define the stable and unstable invariant subspaces of the linearisation of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ at a saddle point located at the origin in $\mathbb{R}^{n}$. How, according to the Stable Manifold Theorem, are the stable and unstable manifolds related to the invariant subspaces?

  Calculate the stable and unstable manifolds, correct to cubic order, for the system

  $$\begin{aligned} &\dot{x}=x+x^{2}+2 x y+3 y^{2} \\ &\dot{y}=-y+3 x^{2} \end{aligned}$$

  comment

• 4.I.7B

  Dynamical Systems | Part II, 2005

  Find and classify the fixed points of the system

  $$\begin{aligned} &\dot{x}=x(1-y) \\ &\dot{y}=-y+x^{2} . \end{aligned}$$

  Sketch the phase plane.

  What is the $\omega$-limit for the point $(2,-1)$ ? Which points have $(0,0)$ as their $\omega$-limit?

  comment

Electrodynamics

• 1.II $. 34 \mathrm{~B} \quad$

  Electrodynamics | Part II, 2005

  In a frame $\mathcal{F}$ the electromagnetic fields $(\mathbf{E}, \mathbf{B})$ are encoded into the Maxwell field 4-tensor $F^{a b}$ and its dual ${ }^{*} F^{a b}$, where

  $$F^{a b}=\left(\begin{array}{cccc} 0 & -E_{x} & -E_{y} & -E_{z} \\ E_{x} & 0 & -B_{z} & B_{y} \\ E_{y} & B_{z} & 0 & -B_{x} \\ E_{z} & -B_{y} & B_{x} & 0 \end{array}\right)$$

  and

  $${ }^{*} F^{a b}=\left(\begin{array}{cccc} 0 & -B_{x} & -B_{y} & -B_{z} \\ B_{x} & 0 & E_{z} & -E_{y} \\ B_{y} & -E_{z} & 0 & E_{x} \\ B_{z} & E_{y} & -E_{x} & 0 \end{array}\right)$$

  [Here the signature is $(+---)$ and units are chosen so that $c=1$.] Obtain two independent Lorentz scalars of the electromagnetic field in terms of $\mathbf{E}$ and $\mathbf{B}$.

  Suppose that $\mathbf{E} \cdot \mathbf{B}>0$ in the frame $\mathcal{F}$. Given that there exists a frame $\mathcal{F}^{\prime}$ in which $\mathbf{E}^{\prime} \times \mathbf{B}^{\prime}=\mathbf{0}$, show that

  $$E^{\prime}=\left[(\mathbf{E} \cdot \mathbf{B})\left(K+\sqrt{1+K^{2}}\right)\right]^{1 / 2}, \quad B^{\prime}=\left[\frac{\mathbf{E} \cdot \mathbf{B}}{K+\sqrt{1+K^{2}}}\right]^{1 / 2},$$

  where $\left(E^{\prime}, B^{\prime}\right)$ are the magnitudes of $\left(\mathbf{E}^{\prime}, \mathbf{B}^{\prime}\right)$, and

  $$K=\frac{1}{2}\left(|\mathbf{E}|^{2}-|\mathbf{B}|^{2}\right) /(\mathbf{E} \cdot \mathbf{B})$$

  [Hint: there is no need to consider the Lorentz transformations for $\mathbf{E}^{\prime}$ and $\mathbf{B}^{\prime}$.]

  comment

• 3.II $. 35 \mathrm{~B} \quad$

  Electrodynamics | Part II, 2005

  A non-relativistic particle of rest mass $m$ and charge $q$ is moving slowly with velocity $\mathbf{v}(t)$. The power $d P / d \Omega$ radiated per unit solid angle in the direction of a unit vector $\mathbf{n}$ is

  $$\frac{d P}{d \Omega}=\frac{\mu_{0}}{16 \pi^{2}}|\mathbf{n} \times q \dot{\mathbf{v}}|^{2} .$$

  Obtain Larmor's formula

  $$P=\frac{\mu_{0} q^{2}}{6 \pi}|\dot{\mathbf{v}}|^{2} .$$

  The particle has energy $\mathcal{E}$ and, starting from afar, makes a head-on collision with a fixed central force described by a potential $V(r)$, where $V(r)>\mathcal{E}$ for $r<r_{0}$ and $V(r)<\mathcal{E}$ for $r>r_{0}$. Let $W$ be the total energy radiated by the particle. Given that $W \ll \mathcal{E}$, show that

  $$W \approx \frac{\mu_{0} q^{2}}{3 \pi m^{2}} \sqrt{\frac{m}{2}} \int_{r_{0}}^{\infty}\left(\frac{d V}{d r}\right)^{2} \frac{d r}{\sqrt{V\left(r_{0}\right)-V(r)}}$$

  comment

• 4.II $. 35 \mathrm{~B} \quad$

  Electrodynamics | Part II, 2005

  In Ginzburg-Landau theory, superconductivity is due to "supercarriers" of mass $m_{s}$ and charge $q_{s}$, which are described by a macroscopic wavefunction $\psi$ with "Mexican hat" potential

  $$V=\alpha(T)|\psi|^{2}+\frac{1}{2} \beta|\psi|^{4}$$

  Here, $\beta>0$ is constant and $\alpha(T)$ is a function of temperature $T$ such that $\alpha(T)>0$ for $T>T_{c}$ but $\alpha(T)<0$ for $T<T_{c}$, where $T_{c}$ is a critical temperature. In the presence of a magnetic field $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$, the total energy of the superconducting system is

  $$E\left[\psi, \psi^{*}, \mathbf{A}\right]=\int d^{3} x\left[\frac{1}{2 \mu_{0}} A_{k, j}\left(A_{k, j}-A_{j, k}\right)+\frac{\hbar^{2}}{2 m_{s}}\left|\psi_{, k}+i \frac{q_{s}}{\hbar} A_{k} \psi\right|^{2}+V\right]$$

  Use this to derive the equations

  $$-\frac{\hbar^{2}}{2 m_{s}}\left(\nabla-i \frac{q_{s}}{\hbar} \mathbf{A}\right)^{2} \psi+\left(\alpha+\beta|\psi|^{2}\right) \psi=0$$

  and

  $$\boldsymbol{\nabla} \times \mathbf{B} \equiv \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{A})-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{j}$$

  where

  $$\begin{aligned} \mathbf{j} &=-\frac{i q_{s} \hbar}{2 m_{s}}\left(\psi^{*} \boldsymbol{\nabla} \psi-\psi \boldsymbol{\nabla} \psi^{*}\right)-\frac{q_{s}^{2}}{m_{s}}|\psi|^{2} \mathbf{A} \\ &=\frac{q_{s}}{2 m_{s}}\left[\psi^{*}\left(-i \hbar \boldsymbol{\nabla}-q_{s} \mathbf{A}\right) \psi+\psi\left(i \hbar \boldsymbol{\nabla}-q_{s} \mathbf{A}\right) \psi^{*}\right] \end{aligned}$$

  Suppose that we write the wavefunction as

  $$\psi=\sqrt{n_{s}} e^{i \theta}$$

  where $n_{s}$ is the (real positive) supercarrier density and $\theta$ is a real phase function. Given that

  $$\left(\boldsymbol{\nabla}-\frac{i q_{s}}{\hbar} \mathbf{A}\right) \psi=0$$

  show that $n_{s}$ is constant and that $\hbar \boldsymbol{\nabla} \theta=q_{s} \mathbf{A}$. Given also that $T<T_{c}$, deduce that (*) allows such solutions for a certain choice of $n_{s}$, which should be determined. Verify that your results imply $\mathbf{j}=\mathbf{0}$. Show also that $\mathbf{B}=\mathbf{0}$ and hence that ( $\dagger$ ) is solved.

  Let $\mathcal{S}$ be a surface within the superconductor with closed boundary $\mathcal{C}$. Show that the magnetic flux through $\mathcal{S}$ is

  $$\Phi \equiv \int_{\mathcal{S}} \mathbf{B} \cdot \mathbf{d} \mathbf{S}=\frac{\hbar}{q_{s}}[\theta]_{\mathcal{C}}$$

  Discuss, briefly, flux quantization.

  comment

Fluid Dynamics II

• $3 . \mathrm{II} . 36 \mathrm{E} \quad$

  Fluid Dynamics II | Part II, 2005

  Write down the Navier-Stokes equations for an incompressible fluid.

  Explain the concepts of the Euler and Prandtl limits applied to the Navier-Stokes equations near a rigid boundary.

  A steady two-dimensional flow given by $(U, 0)$ far upstream flows past a semi-infinite flat plate, held at $y=0, x>0$. Derive the boundary layer equation

  $$\frac{\partial \psi}{\partial y} \frac{\partial^{2} \psi}{\partial x \partial y}-\frac{\partial \psi}{\partial x} \frac{\partial^{2} \psi}{\partial y^{2}}=\nu \frac{\partial^{3} \psi}{\partial y^{3}}$$

  for the stream-function $\psi(x, y)$ near the plate, explaining any approximations made.

  Show that the appropriate solution must be of the form

  $$\psi(x, y)=(\nu U x)^{1 / 2} f(\eta),$$

  and determine the dimensionless variable $\eta$.

  Derive the equation and boundary conditions satisfied by $f(\eta)$. [You need not solve them.]

  Suppose now that the plate has a finite length $L$ in the direction of the flow. Show that the force $F$ on the plate (per unit width perpendicular to the flow) is given by

  $$F=\frac{4 \rho U^{2} L}{(U L / \nu)^{1 / 2}} \frac{f^{\prime \prime}(0)}{\left[f^{\prime}(\infty)\right]^{2}} .$$

  comment

• 1.II.36E

  Fluid Dynamics II | Part II, 2005

  Consider a unidirectional flow with dynamic viscosity $\mu$ along a straight rigid-walled channel of uniform cross-sectional shape $\mathcal{D}$ driven by a uniform applied pressure gradient $G$. Write down the differential equation and boundary conditions governing the velocity $w$ along the channel.

  Consider the situation when the boundary includes a sharp corner of angle $2 \alpha$. Explain why one might expect that, sufficiently close to the corner, the solution should be of the form

  $$w=(G / \mu) r^{2} f(\theta)$$

  where $r$ and $\theta$ are polar co-ordinates with origin at the vertex and $\theta=\pm \alpha$ describing the two planes emanating from the corner. Determine $f(\theta)$.

  If $\mathcal{D}$ is the sector bounded by the lines $\theta=\pm \alpha$ and the circular arc $r=a$, show that the flow is given by

  $$w=(G / \mu) r^{2} f(\theta)+\sum_{n=0}^{\infty} A_{n} r^{\lambda_{n}} \cos \lambda_{n} \theta$$

  where $\lambda_{n}$ and $A_{n}$ are to be determined.

  [Note that $\int \cos (a x) \cos (b x) d x=\{a \sin (a x) \cos (b x)-b \sin (b x) \cos (a x)\} /\left(a^{2}-b^{2}\right)$.]

  Considering the values of $\lambda_{0}$ and $\lambda_{1}$, comment briefly on the cases: (i) $2 \alpha<\frac{1}{2} \pi$;

  (ii) $\frac{1}{2} \pi<2 \alpha<\frac{3}{2} \pi$; and (iii) $\frac{3}{2} \pi<2 \alpha<2 \pi$.

  comment

• 2.II.36E

  Fluid Dynamics II | Part II, 2005

  A volume $V$ of very viscous fluid of density $\rho$ and dynamic viscosity $\mu$ is released at the origin on a rigid horizontal boundary at time $t=0$. Using lubrication theory, determine the velocity profile in the gravity current once it has spread sufficiently that the axisymmetric thickness $h(r, t)$ of the current is much less than the radius $R(t)$ of the front.

  Derive the differential equation

  $$\frac{\partial h}{\partial t}=\frac{\beta}{r} \frac{\partial}{\partial r}\left(r h^{3} \frac{\partial h}{\partial r}\right)$$

  where $\beta$ is to be determined.

  Write down the other equations that are needed to determine the appropriate similarity solution for this problem.

  Determine the similarity solution and calculate $R(t)$.

  comment

• 4.II.37E

  Fluid Dynamics II | Part II, 2005

  Consider flow of an incompressible fluid of uniform density $\rho$ and dynamic viscosity $\mu$. Show that the rate of viscous dissipation per unit volume is given by

  $$\Phi=2 \mu e_{i j} e_{i j},$$

  where $e_{i j}$ is the strain rate.

  Determine expressions for $e_{i j}$ and $\Phi$ when the flow is irrotational with velocity potential $\phi$. Hence determine the rate of viscous dissipation, averaged over a wave period $2 \pi / \omega$, for an irrotational two-dimensional surface wave of wavenumber $k$ and small amplitude $a \ll k^{-1}$ in a fluid of very small viscosity $\mu \ll \rho \omega / k^{2}$ and great depth $H \gg 1 / k$.

  [You may use without derivation that in deep water a linearised wave with surface displacement $\eta=a \cos (k x-w t)$ has velocity potential $\phi=-(\omega a / k) e^{-k z} \sin (k x-\omega t)$.]

  Calculate the depth-integrated time-averaged kinetic energy per wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order like $e^{-\gamma t}$, where

  $$\gamma=4 \mu k^{2} / \rho$$

  comment

Further Complex Methods

• 1.I.8A

  Further Complex Methods | Part II, 2005

  Explain what is meant by the Papperitz symbol

  $$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  The hypergeometric function $F(a, b ; c ; z)$ is defined as the solution of the equation determined by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & \infty & 1 \\ 0 & a & 0 \\ 1-c & b & c-a-b \end{array}\right\}$$

  that is analytic at $z=0$ and satisfies $F(a, b ; c ; 0)=1$.

  Show, explaining each step, that

  $$F(a, b ; c ; z)=(1-z)^{c-a-b} F(c-a, c-b ; c ; z)$$

  comment

• 2.I.8A

  Further Complex Methods | Part II, 2005

  The Hankel representation of the gamma function is

  $$\Gamma(z)=\frac{1}{2 i \sin (\pi z)} \int_{-\infty}^{\left(0^{+}\right)} t^{z-1} e^{t} d t$$

  where the path of integration is the Hankel contour.

  Use this representation to find the residue of $\Gamma(z)$ at $z=-n$, where $n$ is a nonnegative integer.

  Is there a pole at $z=n$, where $n$ is a positive integer? Justify your answer carefully, working only from the above representation of $\Gamma(z)$.

  comment

• 3.I.8A

  Further Complex Methods | Part II, 2005

  The functions $f$ and $g$ have Laplace transforms $\widehat{f}$ and $\widehat{g}$, and satisfy $f(t)=0=g(t)$ for $t<0$. The convolution $h$ of $f$ and $g$ is defined by

  $$h(u)=\int_{0}^{u} f(u-v) g(v) d v$$

  and has Laplace transform $\widehat{h}$. Prove (the convolution theorem) that $\widehat{h}(p)=\widehat{f}(p) \widehat{g}(p)$.

  Given that $\int_{0}^{t}(t-s)^{-1 / 2} s^{-1 / 2} d s=\pi \quad(t>0)$, deduce the Laplace transform of the function $f(t)$, where

  $$f(t)=\left\{\begin{array}{l} t^{-1 / 2}, \quad t>0 \\ 0, \quad t \leqslant 0 \end{array}\right.$$

  comment

• 3.II.14A

  Further Complex Methods | Part II, 2005

  Show that the equation

  $$z w^{\prime \prime}+2 k w^{\prime}+z w=0,$$

  where $k$ is constant, has solutions of the form

  $$w(z)=\int_{\gamma}\left(t^{2}+1\right)^{k-1} e^{z t} d t$$

  provided that the path $\gamma$ is chosen so that $\left[\left(t^{2}+1\right)^{k} e^{z t}\right]_{\gamma}=0$.

  (i) In the case Re $k>0$, show that there is a choice of $\gamma$ for which $w(0)=i B\left(k, \frac{1}{2}\right)$.

  (ii) In the case $k=n / 2$, where $n$ is any integer, show that $\gamma$ can be a finite contour and that the corresponding solution satisfies $w(0)=0$ if $n \leqslant-1$.

  comment

• 4.I.8A

  Further Complex Methods | Part II, 2005

  Write down necessary and sufficient conditions on the functions $p(z)$ and $q(z)$ for the point $z=0$ to be (i) an ordinary point and (ii) a regular singular point of the equation

  $$w^{\prime \prime}+p(z) w^{\prime}+q(z) w=0 .$$

  Show that the point $z=\infty$ is an ordinary point if and only if

  $$p(z)=2 z^{-1}+z^{-2} P\left(z^{-1}\right), \quad q(z)=z^{-4} Q\left(z^{-1}\right),$$

  where $P$ and $Q$ are analytic in a neighbourhood of the origin.

  Find the most general equation of the form $(*)$ that has a regular singular point at $z=0$ but no other singular points.

  comment

• 4.II.14A

  Further Complex Methods | Part II, 2005

  Two representations of the zeta function are

  $$\zeta(z)=\frac{\Gamma(1-z)}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \frac{t^{z-1}}{e^{-t}-1} d t \quad \text { and } \quad \zeta(z)=\sum_{1}^{\infty} n^{-z}$$

  where, in the integral representation, the path is the Hankel contour and the principal branch of $t^{z-1}$, for which $|\arg z|<\pi$, is to be used. State the range of $z$ for which each representation is valid.

  Evaluate the integral

  $$\int_{\gamma} \frac{t^{z-1}}{e^{-t}-1} d t$$

  where $\gamma$ is a closed path consisting of the straight line $z=\pi i+x$, with $|x|<2 N \pi$, and the semicircle $|z-\pi i|=2 N \pi$, with $\operatorname{Im} z>\pi$, where $N$ is a positive integer.

  Making use of this result and assuming, when necessary, that the integral along the curved part of $\gamma$ is negligible when $N$ is large, derive the functional equation

  $$\zeta(z)=2^{z} \pi^{z-1} \sin (\pi z / 2) \Gamma(1-z) \zeta(1-z)$$

  for $z \neq 1$.

  comment

Galois Theory

• 1.II.18G

  Galois Theory | Part II, 2005

  Let $L / K$ be a field extension. State what it means for an element $x \in L$ to be algebraic over $K$. Show that $x$ is algebraic over $K$ if and only if the field $K(x)$ is finite dimensional as a vector space over $K$.

  State what it means for a field extension $L / K$ to be algebraic. Show that, if $M / L$ is algebraic and $L / K$ is algebraic, then $M / K$ is algebraic.

  comment

• 2.II.18G

  Galois Theory | Part II, 2005

  Let $K$ be a field of characteristic 0 containing all roots of unity.

  (i) Let $L$ be the splitting field of the polynomial $X^{n}-a$ where $a \in K$. Show that the Galois group of $L / K$ is cyclic.

  (ii) Suppose that $M / K$ is a cyclic extension of degree $m$ over $K$. Let $g$ be a generator of the Galois group and $\zeta \in K$ a primitive $m$-th root of 1 . By considering the resolvent

  $$R(w)=\sum_{i=0}^{m-1} \frac{g^{i}(w)}{\zeta^{i}}$$

  of elements $w \in M$, show that $M$ is the splitting field of a polynomial $X^{m}-a$ for some $a \in K$.

  comment

• 3.II.18G

  Galois Theory | Part II, 2005

  Find the Galois group of the polynomial

  $$x^{4}+x+1$$

  over $\mathbb{F}_{2}$ and $\mathbb{F}_{3}$. Hence or otherwise determine the Galois group over $\mathbb{Q}$.

  [Standard general results from Galois theory may be assumed.]

  comment

• 4.II.18G

  Galois Theory | Part II, 2005

  (i) Let $K$ be the splitting field of the polynomial

  $$x^{4}-4 x^{2}-1$$

  over $\mathbb{Q}$. Show that $[K: \mathbb{Q}]=8$, and hence show that the Galois group of $K / \mathbb{Q}$ is the dihedral group of order 8 .

  (ii) Let $L$ be the splitting field of the polynomial

  $$x^{4}-4 x^{2}+1$$

  over $\mathbb{Q}$. Show that $[L: \mathbb{Q}]=4$. Show that the Galois group of $L / \mathbb{Q}$ is $C_{2} \times C_{2}$.

  comment

General Relativity

• 1.II.35C

  General Relativity | Part II, 2005

  Suppose $(x(\tau), t(\tau))$ is a timelike geodesic of the metric

  $$d s^{2}=\frac{d x^{2}}{1+x^{2}}-\left(1+x^{2}\right) d t^{2}$$

  where $\tau$ is proper time along the world line. Show that $d t / d \tau=E /\left(1+x^{2}\right)$, where $E>1$ is a constant whose physical significance should be stated. Setting $a^{2}=E^{2}-1$, show that

  $$d \tau=\frac{d x}{\sqrt{a^{2}-x^{2}}}, \quad d t=\frac{E d x}{\left(1+x^{2}\right) \sqrt{a^{2}-x^{2}}} .$$

  Deduce that $x$ is a periodic function of proper time $\tau$ with period $2 \pi$. Sketch $d x / d \tau$ as a function of $x$ and superpose on this a sketch of $d x / d t$ as a function of $x$. Given the identity

  $$\int_{-a}^{a} \frac{E d x}{\left(1+x^{2}\right) \sqrt{a^{2}-x^{2}}}=\pi$$

  deduce that $x$ is also a periodic function of $t$ with period $2 \pi$.

  Next consider the family of metrics

  $$d s^{2}=\frac{[1+f(x)]^{2} d x^{2}}{1+x^{2}}-\left(1+x^{2}\right) d t^{2},$$

  where $f$ is an odd function of $x, f(-x)=-f(x)$, and $|f(x)|<1$ for all $x$. Derive expressions analogous to $(*)$ above. Deduce that $x$ is a periodic function of $\tau$ and also that $x$ is a periodic function of $t$. What are the periods?

  comment

• 2.II.35C

  General Relativity | Part II, 2005

  State without proof the properties of local inertial coordinates $x^{a}$ centred on an arbitrary spacetime event $p$. Explain their physical significance.

  Obtain an expression for $\partial_{a} \Gamma_{b}{ }^{c}$ at $p$ in inertial coordinates. Use it to derive the formula

  $$R_{a b c d}=\frac{1}{2}\left(\partial_{b} \partial_{c} g_{a d}+\partial_{a} \partial_{d} g_{b c}-\partial_{b} \partial_{d} g_{a c}-\partial_{a} \partial_{c} g_{b d}\right)$$

  for the components of the Riemann tensor at $p$ in local inertial coordinates. Hence deduce that at any point in any chart $R_{a b c d}=R_{c d a b}$.

  Consider the metric

  $$d s^{2}=\frac{\eta_{a b} d x^{a} d x^{b}}{\left(1+L^{-2} \eta_{a b} x^{a} x^{b}\right)^{2}}$$

  where $\eta_{a b}=\operatorname{diag}(1,1,1,-1)$ is the Minkowski metric tensor and $L$ is a constant. Compute the Ricci scalar $R=R_{a b}^{a b}$ at the origin $x^{a}=0$.

  comment

• 4.II.36C

  General Relativity | Part II, 2005

  State clearly, but do not prove, Birkhoff's Theorem about spherically symmetric spacetimes. Let $(r, \theta, \phi)$ be standard spherical polar coordinates and define $F(r)=$ $1-2 M / r$, where $M$ is a constant. Consider the metric

  $$d s^{2}=\frac{d r^{2}}{F(r)}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-F(r) d t^{2}$$

  Explain carefully why this is appropriate for the region outside a spherically symmetric star that is collapsing to form a black hole.

  By considering radially infalling timelike geodesics $x^{a}=(r(\tau), 0,0, t(\tau))$, where $\tau$ is proper time along the curve, show that a freely falling observer will reach the event horizon after a finite proper time. Show also that a distant observer would see the horizon crossing only after an infinite time.

  comment

Geometry of Group Actions

• 1.I.3G

  Geometry of Group Actions | Part II, 2005

  Let $G$ be a subgroup of the group of isometries $\operatorname{Isom}\left(\mathbb{R}^{2}\right)$ of the Euclidean plane. What does it mean to say that $G$ is discrete?

  Supposing that $G$ is discrete, show that the subgroup $G_{T}$ of $G$ consisting of all translations in $G$ is generated by translations in at most two linearly independent vectors in $\mathbb{R}^{2}$. Show that there is a homomorphism $G \rightarrow O(2)$ with kernel $G_{T}$.

  Draw, and briefly explain, pictures which illustrate two different possibilities for $G$ when $G_{T}$ is isomorphic to the additive group $\mathbb{Z}$.

  comment

• 1.II.12G

  Geometry of Group Actions | Part II, 2005

  What is the limit set of a subgroup $G$ of Möbius transformations?

  Suppose that $G$ is complicated and has no finite orbit in $\mathbb{C} \cup\{\infty\}$. Prove that the limit set of $G$ is infinite. Can the limit set be countable?

  State Jørgensen's inequality, and deduce that not every two-generator subgroup $G=\langle A, B\rangle$ of Möbius transformations is discrete. Briefly describe two examples of discrete two-generator subgroups, one for which the limit set is connected and one for which it is disconnected.

  comment

• 2.I.3G

  Geometry of Group Actions | Part II, 2005

  Describe the geodesics in the disc model of the hyperbolic plane $\mathbb{H}^{2}$.

  Define the area of a region in $\mathbb{H}^{2}$. Compute the area $A(r)$ of a hyperbolic circle of radius $r$ from the definition just given. Compute the circumference $C(r)$ of a hyperbolic circle of radius $r$, and check explicitly that $d A(r) / d r=C(r)$.

  How could you define $\pi$ geometrically if you lived in $\mathbb{H}^{2}$ ? Briefly justify your answer.

  comment

• 3.I.3G

  Geometry of Group Actions | Part II, 2005

  By considering fixed points in $\mathbb{C} \cup\{\infty\}$, prove that any complex Möbius transformation is conjugate either to a map of the form $z \mapsto k z$ for some $k \in \mathbb{C}$ or to $z \mapsto z+1$. Deduce that two Möbius transformations $g, h$ (neither the identity) are conjugate if and only if $\operatorname{tr}^{2}(g)=\operatorname{tr}^{2}(h)$.

  Does every Möbius transformation $g$ also have a fixed point in $\mathbb{H}^{3}$ ? Briefly justify your answer.

  comment

• 4.I.3G

  Geometry of Group Actions | Part II, 2005

  Show that a set $F \subset \mathbb{R}^{n}$ with Hausdorff dimension strictly less than one is totally disconnected.

  What does it mean for a Möbius transformation to pair two discs? By considering a pair of disjoint discs and a pair of tangent discs, or otherwise, explain in words why there is a 2-generator Schottky group with limit set $\Lambda \subset \mathbb{S}^{2}$ which has Hausdorff dimension at least 1 but which is not homeomorphic to a circle.

  comment

• 4.II.12G

  Geometry of Group Actions | Part II, 2005

  For real $s \geqslant 0$ and $F \subset \mathbb{R}^{n}$, give a careful definition of the $s$-dimensional Hausdorff measure of $F$ and of the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of $F$.

  For $1 \leqslant i \leqslant k$, suppose $S_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is a similarity with contraction factor $c_{i} \in(0,1)$. Prove there is a unique non-empty compact invariant set $I$ for the $\left\{S_{i}\right\}$. State a formula for the Hausdorff dimension of $I$, under an assumption on the $S_{i}$ you should state.

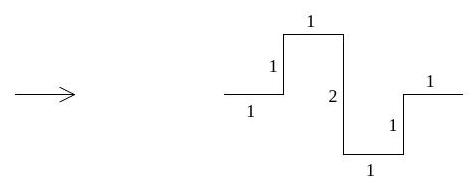
  Hence show the Hausdorff dimension of the fractal $F$ given by iterating the scheme below (at each stage replacing each edge by a new copy of the generating template) is $\operatorname{dim}_{H}(F)=3 / 2$.

  

  [Numbers denote lengths]

  comment

Graph Theory

• 1.II .17F

  Graph Theory | Part II, 2005

  Show that an acyclic graph has a vertex of degree at most one. Prove that a tree (that is, a connected acyclic graph) of order $n$ has size $n-1$, and deduce that every connected graph of order $n$ and size $n-1$ is a tree.

  Let $T$ be a tree of order $t$. Show that if $G$ is a graph with $\delta(G) \geqslant t-1$ then $T$ is a subgraph of $G$, but that this need not happen if $\delta(G) \geqslant t-2$.

  comment

• 2.II.17F

  Graph Theory | Part II, 2005

  Brooks' Theorem states that if $G$ is a connected graph then $\chi(G) \leqslant \Delta(G)$ unless $G$ is complete or is an odd cycle. Prove the theorem for 3-connected graphs $G$.

  Let $G$ be a graph, and let $d_{1}+d_{2}=\Delta(G)-1$. By considering a partition $V_{1}, V_{2}$ of $V(G)$ that minimizes the quantity $d_{2} e\left(G\left[V_{1}\right]\right)+d_{1} e\left(G\left[V_{2}\right]\right)$, show that there is a partition with $\Delta\left(G\left[V_{i}\right]\right) \leqslant d_{i}, i=1,2$.

  By taking $d_{1}=3$, show that if a graph $G$ contains no $K_{4}$ then $\chi(G) \leqslant \frac{3}{4} \Delta(G)+\frac{3}{2}$.

  comment

• 3.II.17F

  Graph Theory | Part II, 2005

  Let $X$ and $Y$ be disjoint sets of $n \geqslant 6$ vertices each. Let $G$ be a bipartite graph formed by adding edges between $X$ and $Y$ randomly and independently with probability $p=1 / 100$. Let $e(U, V)$ be the number of edges of $G$ between the subsets $U \subset X$ and $V \subset Y$. Let $k=\left\lceil n^{1 / 2}\right\rceil$. Consider three events $\mathcal{A}, \mathcal{B}$ and $\mathcal{C}$, as follows.

  $$\begin{array}{ll} \mathcal{A}: & \text { there exist } U \subset X, V \subset Y \text { with }|U|=|V|=k \text { and } e(U, V)=0 \\ \mathcal{B}: & \text { there exist } x \in X, W \subset Y \text { with }|W|=n-k \text { and } e(\{x\}, W)=0 \\ \mathcal{C}: & \text { there exist } Z \subset X, y \in Y \text { with }|Z|=n-k \text { and } e(Z,\{y\})=0 \end{array}$$

  Show that $\operatorname{Pr}(\mathcal{A}) \leqslant n^{2 k}(1-p)^{k^{2}}$ and $\operatorname{Pr}(\mathcal{B} \cup \mathcal{C}) \leqslant 2 n^{k+1}(1-p)^{n-k}$. Hence show that $\operatorname{Pr}(\mathcal{A} \cup \mathcal{B} \cup \mathcal{C})<3 n^{2 k}(1-p)^{n / 2}$ and so show that, almost surely, none of $\mathcal{A}, \mathcal{B}$ or $\mathcal{C}$ occur. Deduce that, almost surely, $G$ has a matching from $X$ to $Y$.

  comment

• 4.II.17F

  Graph Theory | Part II, 2005

  Write an essay on extremal graph theory. Your essay should include the proof of at least one extremal theorem. You should state the Erdős-Stone theorem, as well as describing its proof and showing how it can be applied.

  comment

Integrable Systems

• 1.II.31D

  Integrable Systems | Part II, 2005

  Let $\phi(t)$ satisfy the linear singular integral equation

  $$\left(t^{2}+t-1\right) \phi(t)-\frac{t^{2}-t-1}{\pi i} \oint_{L} \frac{\phi(\tau) d \tau}{\tau-t}-\frac{1}{\pi i} \int_{L}\left(\tau+\frac{1}{\tau}\right) \phi(\tau) d \tau=t-1, \quad t \in L,$$

  where $\oint$ denotes the principal value integral and $L$ denotes a counterclockwise smooth closed contour, enclosing the origin but not the points $\pm 1$.

  (a) Formulate the associated Riemann-Hilbert problem.

  (b) For this Riemann-Hilbert problem, find the index, the homogeneous canonical solution and the solvability condition.

  (c) Find $\phi(t)$.

  comment

• 2.II.31C

  Integrable Systems | Part II, 2005

  Suppose $q(x, t)$ satisfies the $m K d V$ equation

  $$q_{t}+q_{x x x}+6 q^{2} q_{x}=0$$

  where $q_{t}=\partial q / \partial t$ etc.

  (a) Find the 1-soliton solution.

  [You may use, without proof, the indefinite integral $\int \frac{d x}{x \sqrt{1-x^{2}}}=-\operatorname{arcsech} x$.]

  (b) Express the self-similar solution of the $\mathrm{KKdV}$ equation in terms of a solution, denoted by $v(z)$, of the Painlevé II equation.

  (c) Using the Ansatz

  $$\frac{d v}{d z}+i v^{2}-\frac{i}{6} z=0$$

  find a particular solution of the mKdV equation in terms of a solution of the Airy equation

  $$\frac{d^{2} \Psi}{d z^{2}}+\frac{z}{6} \Psi=0$$

  comment

• 3.II.31A

  Integrable Systems | Part II, 2005

  Let $Q(x, t)$ be an off-diagonal $2 \times 2$ matrix. The matrix NLS equation

  $$i Q_{t}-Q_{x x} \sigma_{3}+2 Q^{3} \sigma_{3}=0, \quad \sigma_{3}=\operatorname{diag}(1,-1),$$

  admits the Lax pair

  $$\begin{aligned} &\mu_{x}+i k\left[\sigma_{3}, \mu\right]=Q \mu \\ &\mu_{t}+2 i k^{2}\left[\sigma_{3}, \mu\right]=\left(2 k Q-i Q^{2} \sigma_{3}-i Q_{x} \sigma_{3}\right) \mu \end{aligned}$$

  where $k \in \mathbb{C}, \mu(x, t, k)$ is a $2 \times 2$ matrix and $\left[\sigma_{3}, \mu\right]$ denotes the matrix commutator.

  Let $S(k)$ be a $2 \times 2$ matrix-valued function decaying as $|k| \rightarrow \infty$. Let $\mu(x, t, k)$ satisfy the $2 \times 2$-matrix Riemann-Hilbert problem

  $$\begin{gathered} \mu^{+}(x, t, k)=\mu^{-}(x, t, k) e^{-i\left(k x+2 k^{2} t\right) \sigma_{3}} S(k) e^{i\left(k x+2 k^{2} t\right) \sigma_{3}}, \quad k \in \mathbb{R} \\ \mu=\operatorname{diag}(1,1)+\mathrm{O}\left(\frac{1}{k}\right), \quad k \rightarrow \infty \end{gathered}$$

  (a) Find expressions for $Q(x, t), A(x, t)$ and $B(x, t)$, in terms of the coefficients in the large $k$ expansion of $\mu$, so that $\mu$ solves

  $$\mu_{x}+i k\left[\sigma_{3}, \mu\right]-Q \mu=0$$

  and

  $$\mu_{t}+2 i k^{2}\left[\sigma_{3}, \mu\right]-(k A+B) \mu=0$$

  (b) Use the result of (a) to establish that

  $$A=2 Q, \quad B=-i\left(Q^{2}+Q_{x}\right) \sigma_{3}$$

  (c) Show that the above results provide a linearization of the matrix NLS equation. What is the disadvantage of this approach in comparison with the inverse scattering method?

  comment

Linear Analysis

• 1.II.22F

  Linear Analysis | Part II, 2005

  Let $K$ be a compact Hausdorff space, and let $C(K)$ denote the Banach space of continuous, complex-valued functions on $K$, with the supremum norm. Define what it means for a set $S \subset C(K)$ to be totally bounded, uniformly bounded, and equicontinuous.

  Show that $S$ is totally bounded if and only if it is both uniformly bounded and equicontinuous.

  Give, with justification, an example of a Banach space $X$ and a subset $S \subset X$ such that $S$ is bounded but not totally bounded.

  comment

• 2.II.22F

  Linear Analysis | Part II, 2005

  Let $X$ and $Y$ be Banach spaces. Define what it means for a linear operator $T: X \rightarrow Y$ to be compact. For a linear operator $T: X \rightarrow X$, define the spectrum, point spectrum, and resolvent set of $T$.

  Now let $H$ be a complex Hilbert space. Define what it means for a linear operator $T: H \rightarrow H$ to be self-adjoint. Suppose $e_{1}, e_{2}, \ldots$ is an orthonormal basis for $H$. Define a linear operator $T: H \rightarrow H$ by setting $T e_{i}=\frac{1}{i} e_{i}$. Is $T$ compact? Is $T$ self-adjoint? Justify your answers. Describe, with proof, the spectrum, point spectrum, and resolvent set of $T$.

  comment

• 3.II.21F

  Linear Analysis | Part II, 2005

  Let $X$ be a normed vector space. Define the dual $X^{*}$ of $X$. Define the normed vector spaces $l^{s}=l^{s}(\mathbb{C})$ for all $1 \leqslant s \leqslant \infty$. [You are not required to prove that the norms you have given are indeed norms.]

  Now let $1<p, q<\infty$ be such that $p^{-1}+q^{-1}=1$. Show that $\left(l^{q}\right)^{*}$ is isometrically isomorphic to $l^{p}$ as a normed vector space. [You may assume any standard inequalities.]

  Show by a similar argument that $\left(l^{1}\right)^{*}$ is isomorphic to $l^{\infty}$. Does your argument also show that $\left(l^{\infty}\right)^{*}$ is isomorphic to $l^{1}$ ? If not, where does it fail?

  comment

• 4.II.22F

  Linear Analysis | Part II, 2005

  Let $X$ and $Y$ be normed vector spaces. Show that a linear map $T: X \rightarrow Y$ is continuous if and only if it is bounded.

  Now let $X, Y, Z$ be Banach spaces. We say that a map $F: X \times Y \rightarrow Z$ is bilinear

  $$\begin{aligned} &F(\alpha x+\beta y, z)=\alpha F(x, z)+\beta F(y, z), \text { for all scalars } \alpha, \beta \text { and } x, y \in X, z \in Y \\ &F(x, \alpha y+\beta z)=\alpha F(x, y)+\beta F(x, z), \text { for all scalars } \alpha, \beta \text { and } x \in X, y, z \in Y . \end{aligned}$$

  Suppose that $F$ is bilinear and is continuous in each variable separately. Show that there exists a constant $M \geqslant 0$ such that

  $$\|F(x, y)\| \leqslant M\|x\|\|y\|$$

  for all $x \in X, y \in Y$.

  [Hint: For each fixed $x \in X$, consider the map $y \mapsto F(x, y)$ from $Y$ to $Z$.]

  comment

Logic and Set Theory

• 1.II.16F

  Logic and Set Theory | Part II, 2005

  State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Where in your argument have you made use of the Axiom of Choice?

  Show that $\mathbb{R}$, considered as a rational vector space, has a basis.

  Prove that $\mathbb{R}$ and $\mathbb{R}^{2}$ are isomorphic as rational vector spaces.

  comment

• 2.II.16F

  Logic and Set Theory | Part II, 2005

  Give the inductive and the synthetic definitions of ordinal addition, and prove that they are equivalent. Give an example to show that ordinal addition is not commutative.

  Which of the following assertions about ordinals $\alpha, \beta$ and $\gamma$ are always true, and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha+(\beta+\gamma)=(\alpha+\beta)+\gamma$.

  (ii) If $\alpha$ and $\beta$ are limit ordinals then $\alpha+\beta=\beta+\alpha$.

  (iii) If $\alpha+\beta=\omega_{1}$ then $\alpha=0$ or $\alpha=\omega_{1}$.

  (iv) If $\alpha+\beta=\omega_{1}$ then $\beta=0$ or $\beta=\omega_{1}$.

  comment

• 3.II.16F

  Logic and Set Theory | Part II, 2005

  State the Axiom of Foundation and the Principle of $\in$-Induction, and show that they are equivalent (in the presence of the other axioms of ZF). [You may assume the existence of transitive closures.]

  Explain briefly how the Principle of $\in$-Induction implies that every set is a member of some $V_{\alpha}$.

  For each natural number $n$, find the cardinality of $V_{n}$. For which ordinals $\alpha$ is the cardinality of $V_{\alpha}$ equal to that of the reals?

  comment

• 4.II.16F

  Logic and Set Theory | Part II, 2005

  State and prove the Completeness Theorem for Propositional Logic. [You do not need to give definitions of the various terms involved. You may assume that the set of primitive propositions is countable. You may also assume the Deduction Theorem, provided that you state it clearly.]

  Where in your argument have you used the third axiom, namely $(\neg \neg p) \Rightarrow p ?$

  State the Compactness Theorem, and deduce it from the Completeness Theorem.

  comment

Mathematical Biology

• $3 . \mathrm{I} . 6 \mathrm{E} \quad$

  Mathematical Biology | Part II, 2005

  Let $x$ be the concentration of a binary master sequence of length $L$ and let $y$ be the total concentration of all mutant sequences. Master sequences try to self-replicate at a total rate $a x$, but each independent digit is only copied correctly with probability $q$. Mutant sequences self-replicate at a total rate $b y$, where $a>b$, and the probability of mutation back to the master sequence is negligible.

  (a) The evolution of $x$ is given by

  $$\frac{d x}{d t}=a q^{L} x$$

  Write down the corresponding equation for $y$ and derive a differential equation for the master-to-mutant ratio $z=x / y$.

  (b) What is the maximum length $L_{\max }$ for which there is a positive steady-state value of $z$ ? Is the positive steady state stable when it exists?

  (c) Obtain a first-order approximation to $L_{\max }$ assuming that both $1-q \ll 1$ and $s \ll 1$, where the selection coefficient $s$ is defined by $b=a(1-s)$.

  comment

• 1.I.6E

  Mathematical Biology | Part II, 2005

  Consider a biological system in which concentrations $x(t)$ and $y(t)$ satisfy

  $$\frac{d x}{d t}=f(y)-x \quad \text { and } \quad \frac{d y}{d t}=g(x)-y$$

  where $f$ and $g$ are positive and monotonically decreasing functions of their arguments, so that $x$ represses the synthesis of $y$ and vice versa.

  (a) Suppose the functions $f$ and $g$ are bounded. Sketch the phase plane and explain why there is always at least one steady state. Show that if there is a steady state with

  $$\frac{\partial \ln f}{\partial \ln y} \frac{\partial \ln g}{\partial \ln x}>1$$

  then the system is multistable.

  (b) If $f=\lambda /\left(1+y^{m}\right)$ and $g=\lambda /\left(1+x^{n}\right)$, where $\lambda, m$ and $n$ are positive constants, what values of $m$ and $n$ allow the system to display multistability for some value of $\lambda$ ?

  Can $f=\lambda / y^{m}$ and $g=\lambda / x^{n}$ generate multistability? Explain your answer carefully.

  comment

• 2.I.6E

  Mathematical Biology | Part II, 2005

  Consider a system with stochastic reaction events

  $$x \stackrel{\lambda}{\longrightarrow} x+1 \quad \text { and } \quad x \stackrel{\beta x^{2}}{\longrightarrow} x-2,$$

  where $\lambda$ and $\beta$ are rate constants.

  (a) State or derive the exact differential equation satisfied by the average number of molecules $<x>$. Assuming that fluctuations are negligible, approximate the differential equation to obtain the steady-state value of $\langle x\rangle$.

  (b) Using this approximation, calculate the elasticity $H$, the average lifetime $\tau$, and the average chemical event size $<r>$ (averaged over fluxes).

  (c) State the stationary Fluctuation Dissipation Theorem for the normalised variance $\eta$. Hence show that

  $$\eta=\frac{3}{4<x>} .$$

  comment

• 2.II.13E

  Mathematical Biology | Part II, 2005

  Consider the reaction-diffusion system

  $$\begin{aligned} &\frac{\partial u}{\partial \tau}=\beta_{u}\left(\frac{u^{2}}{v}-u\right)+D_{u} \frac{\partial^{2} u}{\partial x^{2}} \\ &\frac{\partial v}{\partial \tau}=\beta_{v}\left(u^{2}-v\right)+D_{v} \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  for an activator $u$ and inhibitor $v$, where $\beta_{u}$ and $\beta_{v}$ are degradation rate constants and $D_{u}$ and $D_{v}$ are diffusion rate constants.

  (a) Find a suitably scaled time $t$ and length $s$ such that

  $$\begin{aligned} \frac{\partial u}{\partial t} &=\frac{u^{2}}{v}-u+\frac{\partial^{2} u}{\partial s^{2}} \\ \frac{1}{Q} \frac{\partial v}{\partial t} &=u^{2}-v+P \frac{\partial^{2} v}{\partial s^{2}} \end{aligned}$$

  and find expressions for $P$ and $Q$.

  (b) Show that the Jacobian matrix for small spatially homogenous deviations from a nonzero steady state of $(*)$ is

  $$J=\left(\begin{array}{cc} 1 & -1 \\ 2 Q & -Q \end{array}\right)$$

  and find the values of $Q$ for which the steady state is stable.

  [Hint: The eigenvalues of a $2 \times 2$ real matrix both have positive real parts iff the matrix has a positive trace and determinant.]

  (c) Derive linearised ordinary differential equations for the amplitudes $\hat{u}(t)$ and $\hat{v}(t)$ of small spatially inhomogeneous deviations from a steady state of $(*)$ that are proportional to $\cos (s / L)$, where $L$ is a constant.

  (d) Assuming that the system is stable to homogeneous perturbations, derive the condition for inhomogeneous instability. Interpret this condition in terms of how far activator and inhibitor molecules diffuse on average before they are degraded.

  (e) Calculate the lengthscale $L_{\text {crit }}$ of disturbances that are expected to be observed when the condition for inhomogeneous instability is just satisfied. What are the dominant mechanisms for stabilising disturbances on lengthscales (i) much less than and (ii) much greater than $L_{\text {crit }}$ ?

  comment

• 3.II.13E

  Mathematical Biology | Part II, 2005

  Protein synthesis by RNA can be represented by the stochastic system

  $$\begin{array}{lll} x_{1} \stackrel{\lambda_{1}}{\longrightarrow} x_{1}+1 & \text { and } & x_{1} \stackrel{\beta_{1} x_{1}}{\longrightarrow} x_{1}-1 \\ x_{2} \stackrel{\lambda_{2} x_{1}}{\longrightarrow} x_{2}+1 & \text { and } & x_{2} \stackrel{\beta_{2} x_{2}}{\longrightarrow} x_{2}-1 \end{array}$$

  in which $x_{1}$ is an environmental variable corresponding to the number of RNA molecules per cell and $x_{2}$ is a system variable, with birth rate proportional to $x_{1}$, corresponding to the number of protein molecules.

  (a) Use the normalized stationary Fluctuation-Dissipation Theorem (FDT) to calculate the (exact) normalized stationary variances $\eta_{11}=\sigma_{1}^{2} /<x_{1}>^{2}$ and $\eta_{22}=$ $\sigma_{2}^{2} /<x_{2}>^{2}$ in terms of the averages $<x_{1}>$ and $<x_{2}>$.

  (b) Separate $\eta_{22}$ into an intrinsic and an extrinsic term by considering the limits when $x_{1}$ does not fluctuate (intrinsic), and when $x_{2}$ responds deterministically to changes in $x_{1}$ (extrinsic). Explain how the extrinsic term represents the magnitude of environmental fluctuations and time-averaging.

  (c) Assume now that the birth rate of $x_{2}$ is changed from the "constitutive" mechanism $\lambda_{2} x_{1}$ in (1) to a "negative feedback" mechanism $\lambda_{2} x_{1} f\left(x_{2}\right)$, where $f$ is a monotonically decreasing function of $x_{2}$. Use the stationary FDT to approximate $\eta_{22}$ in terms of $h=\left|\partial \ln f / \partial \ln x_{2}\right|$. Apply your answer to the case $f\left(x_{2}\right)=k / x_{2}$.

  [Hint: To reduce the algebra introduce the elasticity $H_{22}=\partial \ln \left(R_{2}^{-} / R_{2}^{+}\right) / \partial \ln x_{2}$, where $R_{2}^{-}$and $R_{2}^{+}$are the death and birth rates of $x_{2}$ respectively.]

  (d) Explain the extrinsic term for the negative feedback system in terms of environmental fluctuations, time-averaging, and static susceptibility.

  (e) Explain why the FDT is exact for the constitutive system but approximate for the feedback system. When, generally speaking, does the FDT approximation work well?

  (f) Consider the following three experimental observations: (i) Large changes in $\lambda_{2}$ have no effect on $\eta_{22}$; (ii) When $x_{2}$ is perturbed by $1 \%$ from its stationary average, perturbations are corrected more rapidly in the feedback system than in the constitutive system; (iii) The feedback system displays lower values $\eta_{22}$ than the constitutive system.

  What does (i) imply about the relative importance of the noise terms? Can (ii) be directly explained by (iii), i.e., does rapid adjustment reduce noise? Justify your answers.

  comment

• 4.I.6E

  Mathematical Biology | Part II, 2005

  The output of a linear perceptron is given by $y=\mathbf{w} \cdot \mathbf{x}$, where $\mathbf{w}$ is a vector of weights connecting a fluctuating input vector $x$ to an output unit. The weights are given random initial values and are then updated according to a learning rule that has a time-constant $\tau$ much greater than the fluctuation timescale of the inputs.

  (a) Find the behaviour of $|\mathbf{w}|$ for each of the following two rules (i) $\tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}$ (ii) $\tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}-\alpha y^{2} \mathbf{w}|\mathbf{w}|^{2}$, where $\alpha$ is a positive constant.

  (b) Consider a third learning rule

  $$\text { (iii) } \tau \frac{d \mathbf{w}}{d t}=y \mathbf{x}-\mathbf{w}|\mathbf{w}|^{2} \text {. }$$

  Show that in a steady state the vector of weights satisfies the eigenvalue equation

  $$\mathbf{C w}=\lambda \mathbf{w}$$

  where the matrix $\mathbf{C}$ and eigenvalue $\lambda$ should be identified.

  (c) Comment briefly on the biological implications of the three rules.

  comment

Number Fields

• 1.II.20G

  Number Fields | Part II, 2005

  Let $K=\mathbb{Q}(\sqrt{2}, \sqrt{p})$ where $p$ is a prime with $p \equiv 3 \operatorname{(\operatorname {mod}4)\text {.Bycomputingthe}}$ relative traces $\operatorname{Tr}_{K / k}(\theta)$ where $k$ runs through the three quadratic subfields of $K$, show that the algebraic integers $\theta$ in $K$ have the form

  $$\theta=\frac{1}{2}(a+b \sqrt{p})+\frac{1}{2}(c+d \sqrt{p}) \sqrt{2}$$

  where $a, b, c, d$ are rational integers. By further computing the relative norm $\mathrm{N}_{K / k}(\theta)$ where $k=\mathbb{Q}(\sqrt{2})$, show that 4 divides

  $$a^{2}+p b^{2}-2\left(c^{2}+p d^{2}\right) \quad \text { and } \quad 2(a b-2 c d)$$

  Deduce that $a$ and $b$ are even and $c \equiv d(\bmod 2)$. Hence verify that an integral basis for $K$ is

  $$1, \quad \sqrt{2}, \quad \sqrt{p}, \quad \frac{1}{2}(1+\sqrt{p}) \sqrt{2} .$$

  comment

• 2.II.20G

  Number Fields | Part II, 2005

  Show that $\varepsilon=(3+\sqrt{7}) /(3-\sqrt{7})$ is a unit in $k=\mathbb{Q}(\sqrt{7})$. Show further that 2 is the square of the principal ideal in $k$ generated by $3+\sqrt{7}$.

  Assuming that the Minkowski constant for $k$ is $\frac{1}{2}$, deduce that $k$ has class number 1 .

  Assuming further that $\varepsilon$ is the fundamental unit in $k$, show that the complete solution in integers $x, y$ of the equation $x^{2}-7 y^{2}=2$ is given by

  $$x+\sqrt{7} y=\pm \varepsilon^{n}(3+\sqrt{7}) \quad(n=0, \pm 1, \pm 2, \ldots) .$$

  Calculate the particular solution in positive integers $x, y$ when $n=1$

  comment

• 4.II.20G

  Number Fields | Part II, 2005

  State Dedekind's theorem on the factorisation of rational primes into prime ideals.

  A rational prime is said to ramify totally in a field with degree $n$ if it is the $n$-th power of a prime ideal in the field. Show that, in the quadratic field $\mathbb{Q}(\sqrt{d})$ with $d$ a squarefree integer, a rational prime ramifies totally if and only if it divides the discriminant of the field.

  Verify that the same holds in the cyclotomic field $\mathbb{Q}(\zeta)$, where $\zeta=e^{2 \pi i / q}$ with $q$ an odd prime, and also in the cubic field $\mathbb{Q}(\sqrt[3]{2})$.

  $[$ The cases $d \equiv 2,3(\bmod 4)$ and $d \equiv 1(\bmod 4)$ for the quadratic field should be carefully distinguished. It can be assumed that $\mathbb{Q}(\zeta)$ has a basis $1, \zeta, \ldots, \zeta^{q-2}$ and discriminant $(-1)^{(q-1) / 2} q^{q-1}$, and that $\mathbb{Q}(\sqrt[3]{2})$ has a basis $1, \sqrt[3]{2},(\sqrt[3]{2})^{2}$ and discriminant $\left.-108 .\right]$

  comment

Number Theory

• 1.I.1H

  Number Theory | Part II, 2005

  Define the Legendre symbol $\left(\frac{a}{p}\right)$. Prove that, if $p$ is an odd prime, then

  $$\left(\frac{2}{p}\right)=(-1)^{\frac{p^{2}-1}{8}} .$$

  Use the law of quadratic reciprocity to calculate $\left(\frac{91}{167}\right)$.

  [You may use the Gauss Lemma without proof.]

  comment

• 2.I.1H

  Number Theory | Part II, 2005

  Recall that, if $p$ is an odd prime, a primitive root modulo $p$ is a generator of the cyclic (multiplicative) group $(\mathbb{Z} / p \mathbb{Z})^{\times}$. Let $p$ be an odd prime of the form $2^{2^{n}}+1$; show that $a$ is a primitive root $\bmod p$ if and only if $a$ is not a quadratic residue mod $p$. Use this result to prove that 7 is a primitive root modulo every such prime.

  comment

• 3.I.1H

  Number Theory | Part II, 2005

  Let $\pi(x)$ be the number of primes $p \leqslant x$. State the Legendre formula, and prove that

  $$\lim _{x \rightarrow \infty} \frac{\pi(x)}{x}=0 .$$

  [You may use the formula

  $$\prod_{p \leqslant x}(1-1 / p)^{-1} \geqslant \log x$$

  without proof.]

  comment

• 3.II.11H

  Number Theory | Part II, 2005

  Show that there are exactly two reduced positive definite integer binary quadratic forms with discriminant $-20$; write these forms down.

  State a criterion for an odd integer $n$ to be properly represented by a positive definite integer binary quadratic form of given discriminant $d$.

  Describe, in terms of congruences modulo 20, which primes other than 2,5 are properly represented by the form $x^{2}+5 y^{2}$, and justify your answer.

  comment

• 4.I.1H

  Number Theory | Part II, 2005

  If $n$ is an odd integer and $b$ is an integer prime with $n$, state what it means for $n$ to be a pseudoprime to the base $b$. What is a Carmichael number? State a criterion for $n$ to be a Carmichael number and use the criterion to show that:

  (i) Every Carmichael number is the product of at least three distinct primes.

  (ii) 561 is a Carmichael number.

  comment

• 4.II.11H

  Number Theory | Part II, 2005

  (a) Let $N$ be a non-square integer. Describe the integer solutions of the Pell equation $x^{2}-N y^{2}=1$ in terms of the convergents to $\sqrt{N}$. Show that the set of integer solutions forms an abelian group. Denote the addition law in this group by $\circ$; given solutions $\left(x_{0}, y_{0}\right)$ and $\left(x_{1}, y_{1}\right)$, write down an explicit formula for $\left(x_{0}, y_{0}\right) \circ\left(x_{1}, y_{1}\right)$. If $(x, y)$ is a solution, write down an explicit formula for $(x, y) \circ(x, y) \circ(x, y)$ in the group law.

  (b) Find the continued fraction expansion of $\sqrt{11}$. Find the smallest solution in integers $x, y>0$ of the Pell equation $x^{2}-11 y^{2}=1$. Use the formula in Part (a) to compute $(x, y) \circ(x, y) \circ(x, y)$.

  comment

Numerical Analysis

• 1.II.38A

  Numerical Analysis | Part II, 2005

  Let

  $$\frac{\mu}{4} u_{m-1}^{n+1}+u_{m}^{n+1}-\frac{\mu}{4} u_{m+1}^{n+1}=-\frac{\mu}{4} u_{m-1}^{n}+u_{m}^{n}+\frac{\mu}{4} u_{m+1}^{n},$$

  where $n$ is a positive integer and $m$ ranges over all integers, be a finite-difference method for the advection equation

  $$\frac{\partial u}{\partial t}=\frac{\partial u}{\partial x}, \quad-\infty<x<\infty, \quad t \geqslant 0$$

  Here $\mu=\frac{\Delta t}{\Delta x}$ is the Courant number.

  (a) Show that the local error of the method is $O\left((\Delta x)^{3}\right)$.

  (b) Determine the range of $\mu>0$ for which the method is stable.

  comment

• 2.II.38A

  Numerical Analysis | Part II, 2005

  Define a Krylov subspace $\mathcal{K}_{n}(A, v)$.

  Let $d_{n}$ be the dimension of $\mathcal{K}_{n}(A, v)$. Prove that the sequence $\left\{d_{m}\right\}_{m=1,2, . .}$ increases monotonically. Show that, moreover, there exists an integer $k$ with the following property: $d_{m}=m$ for $m=1,2, \ldots, k$, while $d_{m}=k$ for $m \geqslant k$. Assuming that $A$ has a full set of eigenvectors, show that $k$ is equal to the number of eigenvectors of $A$ required to represent the vector $v$.

  comment

• 3.II.38A

  Numerical Analysis | Part II, 2005

  Consider the Runge-Kutta method

  $$\begin{aligned} k_{1} &=f\left(y_{n}\right) \\ k_{2} &=f\left(y_{n}+(1-a) h k_{1}+a h k_{2}\right), \\ y_{n+1} &=y_{n}+\frac{h}{2}\left(k_{1}+k_{2}\right) \end{aligned}$$

  for the solution of the scalar ordinary differential equation $y^{\prime}=f(y)$. Here $a$ is a real parameter.

  (a) Determine the order of the method.

  (b) Find the range of values of $a$ for which the method is A-stable.

  comment

• 4.II.39A

  Numerical Analysis | Part II, 2005

  An $n \times n$ skew-symmetric matrix $A$ is converted into an upper-Hessenberg form $B$, say, by Householder reflections.

  (a) Describe each step of the procedure and observe that $B$ is tridiagonal. Your algorithm should take advantage of the special form of $A$ to reduce the number of computations.

  (b) Compare the cost (counting only products and looking only at the leading term) of converting a skew-symmetric and a symmetric matrix to an upper-Hessenberg form using Householder reflections.

  comment

Optimization and Control

• 2.II.29I

  Optimization and Control | Part II, 2005

  Explain what is meant by a time-homogeneous discrete time Markov decision problem.

  What is the positive programming case?

  A discrete time Markov decision problem has state space $\{0,1, \ldots, N\}$. In state $i, i \neq 0, N$, two actions are possible. We may either stop and obtain a terminal reward $r(i) \geqslant 0$, or may continue, in which case the subsequent state is equally likely to be $i-1$ or $i+1$. In states 0 and $N$ stopping is automatic (with terminal rewards $r(0)$ and $r(N)$ respectively). Starting in state $i$, denote by $V_{n}(i)$ and $V(i)$ the maximal expected terminal reward that can be obtained over the first $n$ steps and over the infinite horizon, respectively. Prove that $\lim _{n \rightarrow \infty} V_{n}=V$.

  Prove that $V$ is the smallest concave function such that $V(i) \geqslant r(i)$ for all $i$.

  Describe an optimal policy.

  Suppose $r(0), \ldots, r(N)$ are distinct numbers. Show that the optimal policy is unique, or give a counter-example.

  comment

• 3.II.28I

  Optimization and Control | Part II, 2005

  Consider the problem

  $$\operatorname{minimize} E\left[x(T)^{2}+\int_{0}^{T} u(t)^{2} d t\right]$$

  where for $0 \leqslant t \leqslant T$,

  $$\dot{x}(t)=y(t) \text { and } \quad \dot{y}(t)=u(t)+\epsilon(t),$$

  $u(t)$ is the control variable, and $\epsilon(t)$ is Gaussian white noise. Show that the problem can be rewritten as one of controlling the scalar variable $z(t)$, where

  $$z(t)=x(t)+(T-t) y(t) .$$

  By guessing the form of the optimal value function and ensuring it satisfies an appropriate optimality equation, show that the optimal control is

  $$u(t)=-\frac{(T-t) z(t)}{1+\frac{1}{3}(T-t)^{3}} .$$

  Is this certainty equivalence control?

  comment

• 4.II.29I

  Optimization and Control | Part II, 2005

  A continuous-time control problem is defined in terms of state variable $x(t) \in \mathbb{R}^{n}$ and control $u(t) \in \mathbb{R}^{m}, 0 \leqslant t \leqslant T$. We desire to minimize $\int_{0}^{T} c(x, t) d t+K(x(T))$, where $T$ is fixed and $x(T)$ is unconstrained. Given $x(0)$ and $\dot{x}=a(x, u)$, describe further boundary conditions that can be used in conjunction with Pontryagin's maximum principle to find $x, u$ and the adjoint variables $\lambda_{1}, \ldots, \lambda_{n}$.

  Company 1 wishes to steal customers from Company 2 and maximize the profit it obtains over an interval $[0, T]$. Denoting by $x_{i}(t)$ the number of customers of Company $i$, and by $u(t)$ the advertising effort of Company 1 , this leads to a problem

  $$\operatorname{minimize} \int_{0}^{T}\left[x_{2}(t)+3 u(t)\right] d t$$

  where $\dot{x}_{1}=u x_{2}, \dot{x}_{2}=-u x_{2}$, and $u(t)$ is constrained to the interval $[0,1]$. Assuming $x_{2}(0)>3 / T$, use Pontryagin's maximum principle to show that the optimal advertising policy is bang-bang, and that there is just one change in advertising effort, at a time $t^{*}$, where

  $$3 e^{t^{*}}=x_{2}(0)\left(T-t^{*}\right) .$$

  comment

Partial Differential Equations

• 1.II.29C

  Partial Differential Equations | Part II, 2005

  Consider the equation

  $$x_{2} \frac{\partial u}{\partial x_{1}}-x_{1} \frac{\partial u}{\partial x_{2}}+a \frac{\partial u}{\partial x_{3}}=u,$$

  where $a \in \mathbb{R}$, to be solved for $u=u\left(x_{1}, x_{2}, x_{3}\right)$. State clearly what it means for a hypersurface

  $$S_{\phi}=\left\{\left(x_{1}, x_{2}, x_{3}\right): \phi\left(x_{1}, x_{2}, x_{3}\right)=0\right\},$$

  defined by a $C^{1}$ function $\phi$, to be non-characteristic for $(*)$. Does the non-characteristic condition hold when $\phi\left(x_{1}, x_{2}, x_{3}\right)=x_{3}$ ?

  Solve $(*)$ for $a>0$ with initial condition $u\left(x_{1}, x_{2}, 0\right)=f\left(x_{1}, x_{2}\right)$ where $f \in C^{1}\left(\mathbb{R}^{2}\right)$. For the case $f\left(x_{1}, x_{2}\right)=x_{1}^{2}+x_{2}^{2}$ discuss the limiting behaviour as $a \rightarrow 0_{+}$.

  comment

• 2.II.30C

  Partial Differential Equations | Part II, 2005

  Define a fundamental solution of a linear partial differential operator $P$. Prove that the function

  $$G(x)=\frac{1}{2} e^{-|x|}$$

  defines a distribution which is a fundamental solution of the operator $P$ given by

  $$P u=-\frac{d^{2} u}{d x^{2}}+u .$$

  Hence find a solution $u_{0}$ to the equation

  $$-\frac{d^{2} u_{0}}{d x^{2}}+u_{0}=V(x),$$

  where $V(x)=0$ for $|x|>1$ and $V(x)=1$ for $|x| \leqslant 1$.

  Consider the functional

  $$I[u]=\int_{\mathbb{R}}\left\{\frac{1}{2}\left[\left(\frac{d u}{d x}\right)^{2}+u^{2}\right]-V u\right\} d x .$$

  Show that $I\left[u_{0}+\phi\right]>I\left[u_{0}\right]$ for all Schwartz functions $\phi$ that are not identically zero.

  comment

• 3.II.29C

  Partial Differential Equations | Part II, 2005

  Write down a formula for the solution $u=u(t, x)$ of the $n$-dimensional heat equation

  $$w_{t}(t, x)-\Delta w=0, \quad w(0, x)=g(x),$$

  for $g: \mathbb{R}^{n} \rightarrow \mathbb{C}$ a given Schwartz function; here $w_{t}=\partial_{t} w$ and $\Delta$ is taken in the variables $x \in \mathbb{R}^{n}$. Show that

  $$w(t, x) \leqslant \frac{\int|g(x)| d x}{(4 \pi t)^{n / 2}}$$

  Consider the equation

  $$u_{t}-\Delta u=e^{i t} f(x),$$

  where $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$ is a given Schwartz function. Show that $(*)$ has a solution of the form

  $$u(t, x)=e^{i t} v(x),$$

  where $v$ is a Schwartz function.

  Prove that the solution $u(t, x)$ of the initial value problem for $(*)$ with initial data $u(0, x)=g(x)$ satisfies

  $$\lim _{t \rightarrow+\infty}\left|u(t, x)-e^{i t} v(x)\right|=0 .$$

  comment

• 4.II.30C

  Partial Differential Equations | Part II, 2005

  Write down the solution of the three-dimensional wave equation

  $$u_{t t}-\Delta u=0, \quad u(0, x)=0, \quad u_{t}(0, x)=g(x),$$

  for a Schwartz function $g$. Here $\Delta$ is taken in the variables $x \in \mathbb{R}^{3}$ and $u_{t}=\partial u / \partial t$ etc. State the "strong" form of Huygens principle for this solution. Using the method of descent, obtain the solution of the corresponding problem in two dimensions. State the "weak" form of Huygens principle for this solution.

  Let $u \in C^{2}\left([0, T] \times \mathbb{R}^{3}\right)$ be a solution of

  $$u_{t t}-\Delta u+|x|^{2} u=0, \quad u(0, x)=0, \quad u_{t}(0, x)=0$$

  Show that

  $$\partial_{t} e+\nabla \cdot \mathbf{p}=0$$

  where

  $$e=\frac{1}{2}\left(u_{t}^{2}+|\nabla u|^{2}+|x|^{2} u^{2}\right), \quad \text { and } \quad \mathbf{p}=-u_{t} \nabla u .$$

  Hence deduce, by integration of $(* *)$ over the region

  $$K=\left\{(t, x): 0 \leqslant t \leqslant t_{0}-a \leqslant t_{0},\left|x-x_{0}\right| \leqslant t_{0}-t\right\}$$

  or otherwise, that $(*)$ satisfies the weak Huygens principle.

  comment

Principles of Quantum Mechanics

• 1.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  A one-dimensional harmonic oscillator has Hamiltonian

  $$H=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2}=\hbar \omega\left(a^{\dagger} a+\frac{1}{2}\right),$$

  where

  $$a=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right) \quad \text { obey } \quad\left[a, a^{\dagger}\right]=1$$

  Assuming the existence of a normalised state $|0\rangle$ with $a|0\rangle=0$, verify that

  $$|n\rangle=\frac{1}{\sqrt{n !}} a^{\dagger n}|0\rangle, \quad n=0,1,2, \ldots$$

  are eigenstates of $H$ with energies $E_{n}$, to be determined, and that these states all have unit norm.

  The Hamiltonian is now modified by a term

  $$\lambda V=\lambda \hbar \omega\left(a^{r}+a^{\dagger r}\right)$$

  where $r$ is a positive integer. Use perturbation theory to find the change in the lowest energy level to order $\lambda^{2}$ for any $r$. [You may quote any standard formula you need.]

  Compute by perturbation theory, again to order $\lambda^{2}$, the change in the first excited energy level when $r=1$. Show that in this special case, $r=1$, the exact change in all energy levels as a result of the perturbation is $-\lambda^{2} \hbar \omega$.

  comment

• 2.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  The components of $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ are $2 \times 2$ hermitian matrices obeying

  $$\left[\sigma_{i}, \sigma_{j}\right]=2 i \varepsilon_{i j k} \sigma_{k} \quad \text { and } \quad(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=1$$

  for any unit vector $\mathbf{n}$. Show that these properties imply

  $$(\mathbf{a} \cdot \boldsymbol{\sigma})(\mathbf{b} \cdot \boldsymbol{\sigma})=\mathbf{a} \cdot \mathbf{b}+i(\mathbf{a} \times \mathbf{b}) \cdot \boldsymbol{\sigma}$$

  for any constant vectors a and $\mathbf{b}$. Assuming that $\theta$ is real, explain why the matrix $U=\exp (-i \mathbf{n} \cdot \boldsymbol{\sigma} \theta / 2)$ is unitary, and show that

  $$U=\cos (\theta / 2)-i \mathbf{n} \cdot \boldsymbol{\sigma} \sin (\theta / 2)$$

  Hence deduce that

  $$U \mathbf{m} \cdot \boldsymbol{\sigma} U^{-1}=\mathbf{m} \cdot \boldsymbol{\sigma} \cos \theta+(\mathbf{n} \times \mathbf{m}) \cdot \boldsymbol{\sigma} \sin \theta$$

  where $\mathbf{m}$ is any unit vector orthogonal to $\mathbf{n}$.

  Write down an equation relating the matrices $\sigma$ and the angular momentum operator $\mathbf{S}$ for a particle of spin one half, and explain briefly the significance of the conditions $(*)$. Show that if $|\chi\rangle$ is a state with spin 'up' measured along the direction $(0,0,1)$ then, for a certain choice of $\mathbf{n}, U|\chi\rangle$ is a state with spin 'up' measured along the direction $(\sin \theta, 0, \cos \theta)$.

  comment

• 3.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  The angular momentum operators $\mathbf{J}^{(1)}$ and $\mathbf{J}^{(2)}$ refer to independent systems, each with total angular momentum one. The combination of these systems has a basis of states which are of product form $\left|m_{1} ; m_{2}\right\rangle=\left|1 m_{1}\right\rangle\left|1 m_{2}\right\rangle$ where $m_{1}$ and $m_{2}$ are the eigenvalues of $J_{3}^{(1)}$ and $J_{3}^{(2)}$ respectively. Let $|J M\rangle$ denote the alternative basis states which are simultaneous eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, where $\mathbf{J}=\mathbf{J}^{(1)}+\mathbf{J}^{(2)}$ is the combined angular momentum. What are the possible values of $J$ and $M$ ? Find expressions for all states with $J=1$ in terms of product states. How do these states behave when the constituent systems are interchanged?

  Two spin-one particles $A$ and $B$ have no mutual interaction but they each move in a potential $V(\mathbf{r})$ which is independent of spin. The single-particle energy levels $E_{i}$ and the corresponding wavefunctions $\psi_{i}(\mathbf{r})(i=1,2, \ldots)$ are the same for either $A$ or $B$. Given that $E_{1}<E_{2}<\ldots$, explain how to construct the two-particle states of lowest energy and combined total spin $J=1$ for the cases that (i) $A$ and $B$ are identical, and (ii) $A$ and $B$ are not identical.

  [You may assume $\hbar=1$ and use the result $\left.J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .\right]$

  comment

• 4.II.32D

  Principles of Quantum Mechanics | Part II, 2005

  The Hamiltonian for a quantum system in the Schrödinger picture is

  $$H_{0}+\lambda V(t),$$

  where $H_{0}$ is independent of time and the parameter $\lambda$ is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Let $|a\rangle$ and $|b\rangle$ be eigenstates of $H_{0}$ with distinct eigenvalues $E_{a}$ and $E_{b}$ respectively. Show that if the system is initially in state $|a\rangle$ then the probability of measuring it to be in state $|b\rangle$ after a time $t$ is

  $$\frac{\lambda^{2}}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle b\left|V\left(t^{\prime}\right)\right| a\right\rangle e^{i\left(E_{b}-E_{a}\right) t^{\prime} / \hbar}\right|^{2}+O\left(\lambda^{3}\right)$$

  Deduce that if $V(t)=e^{-\mu t / \hbar} W$, where $W$ is a time-independent operator and $\mu$ is a positive constant, then the probability for such a transition to have occurred after a very long time is approximately

  $$\frac{\lambda^{2}}{\mu^{2}+\left(E_{b}-E_{a}\right)^{2}}|\langle b|W| a\rangle|^{2}$$

  comment

Principles of Statistics

• 1.II.27I

  Principles of Statistics | Part II, 2005

  State Wilks' Theorem on the asymptotic distribution of likelihood-ratio test statistics.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent with common $N\left(\mu, \sigma^{2}\right)$ distribution, where the parameters $\mu$ and $\sigma$ are both unknown. Find the likelihood-ratio test statistic for testing $H_{0}: \mu=0$ against $H_{1}: \mu$ unrestricted, and state its (approximate) distribution.

  What is the form of the $t$-test of $H_{0}$ against $H_{1}$ ? Explain why for large $n$ the likelihood-ratio test and the $t$-test are nearly the same.

  comment

• 2.II.27I

  Principles of Statistics | Part II, 2005

  (i) Suppose that $X$ is a multivariate normal vector with mean $\mu \in \mathbb{R}^{d}$ and covariance matrix $\sigma^{2} I$, where $\mu$ and $\sigma^{2}$ are both unknown, and $I$ denotes the $d \times d$ identity matrix. Suppose that $\Theta_{0} \subset \Theta_{1}$ are linear subspaces of $\mathbb{R}^{d}$ of dimensions $d_{0}$ and $d_{1}$, where $d_{0}<d_{1}<d$. Let $P_{i}$ denote orthogonal projection onto $\Theta_{i}(i=0,1)$. Carefully derive the joint distribution of $\left(\left|X-P_{1} X\right|^{2},\left|P_{1} X-P_{0} X\right|^{2}\right)$ under the hypothesis $H_{0}: \mu \in \Theta_{0}$. How could you use this to make a test of $H_{0}$ against $H_{1}: \mu \in \Theta_{1}$ ?

  (ii) Suppose that $I$ students take $J$ exams, and that the mark $X_{i j}$ of student $i$ in exam $j$ is modelled as

  $$X_{i j}=m+\alpha_{i}+\beta_{j}+\varepsilon_{i j}$$

  where $\sum_{i} \alpha_{i}=0=\sum_{j} \beta_{j}$, the $\varepsilon_{i j}$ are independent $N\left(0, \sigma^{2}\right)$, and the parameters $m, \alpha, \beta$ and $\sigma$ are unknown. Construct a test of $H_{0}: \beta_{j}=0$ for all $j$ against $H_{1}: \sum_{j} \beta_{j}=0$.

  comment

• 3.II.26I

  Principles of Statistics | Part II, 2005

  In the context of decision theory, explain the meaning of the following italicized terms: loss function, decision rule, the risk of a decision rule, a Bayes rule with respect to prior $\pi$, and an admissible rule. Explain how a Bayes rule with respect to a prior $\pi$ can be constructed.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent with common $N(0, v)$ distribution, where $v>0$ is supposed to have a prior density $f_{0}$. In a decision-theoretic approach to estimating $v$, we take a quadratic loss: $L(v, a)=(v-a)^{2}$. Write $X=\left(X_{1}, \ldots, X_{n}\right)$ and $|X|=\left(X_{1}^{2}+\ldots+X_{n}^{2}\right)^{1 / 2}$.

  By considering decision rules (estimators) of the form $\hat{v}(X)=\alpha|X|^{2}$, prove that if $\alpha \neq 1 /(n+2)$ then the estimator $\hat{v}(X)=\alpha|X|^{2}$ is not Bayes, for any choice of prior $f_{0}$.

  By considering decision rules of the form $\hat{v}(X)=\alpha|X|^{2}+\beta$, prove that if $\alpha \neq 1 / n$ then the estimator $\hat{v}(X)=\alpha|X|^{2}$ is not Bayes, for any choice of prior $f_{0}$.

  [You may use without proof the fact that, if $Z$ has a $N(0,1)$ distribution, then $E Z^{4}=3$.]

  comment

• 4.II.27I

  Principles of Statistics | Part II, 2005

  A group of $n$ hospitals is to be 'appraised'; the 'performance' $\theta_{i}$ of hospital $i$ has a $N(0,1 / \tau)$ prior distribution, different hospitals being independent. The 'performance' cannot be measured directly, so an expensive firm of management consultants has been hired to arrive at each hospital's Standardised Index of Quality [SIQ], this being a number $X_{i}$ for hospital $i$ related to $\theta_{i}$ by the commercially-sensitive formula

  $$X_{i}=\theta_{i}+\varepsilon_{i}$$

  where the $\varepsilon_{i}$ are independent with common $N\left(0,1 / \tau_{\varepsilon}\right)$ distribution.

  (i) Assume that $\tau$ and $\tau_{\varepsilon}$ are known. What is the posterior distribution of $\theta$ given $X$ ? Suppose that hospital $j$ was the hospital with the lowest SIQ, with a value $X_{j}=x$; conditional on $X$, what is the distribution of $\theta_{j}$ ?

  (ii) Now, instead of assuming $\tau$ and $\tau_{\varepsilon}$ known, suppose that $\tau$ has a Gamma prior with parameters $(\alpha, \beta)$, density

  $$f(t)=(\beta t)^{\alpha-1} \beta e^{-\beta t} / \Gamma(\alpha)$$

  for known $\alpha$ and $\beta$, and that $\tau_{\varepsilon}=\kappa \tau$, where $\kappa$ is a known constant. Find the posterior distribution of $(\theta, \tau)$ given $X$. Comment briefly on the form of the distribution.

  comment

Probability and Measure

• $3 . \mathrm{II} . 24 \mathrm{~J} \quad$

  Probability and Measure | Part II, 2005

  Let $(\Omega, \mathcal{F}, \mu)$ be a measure space. For a measurable function $f: \Omega \rightarrow \mathbb{R}$, and $p \in[1, \infty)$, let $\|f\|_{p}=\left[\mu\left(|f|^{p}\right)\right]^{1 / p}$. Let $L^{p}$ be the space of all such $f$ with $\|f\|_{p}<\infty$. Explain what is meant by each of the following statements:

  (a) A sequence of functions $\left(f_{n}: n \geqslant 1\right)$ is Cauchy in $L^{p}$.

  (b) $L^{p}$ is complete.

  Show that $L^{p}$ is complete for $p \in[1, \infty)$.

  Take $\Omega=(1, \infty), \mathcal{F}$ the Borel $\sigma$-field of $\Omega$, and $\mu$ the Lebesgue measure on $(\Omega, \mathcal{F})$. For $p=1,2$, determine which if any of the following sequences of functions are Cauchy in $L^{p}$

  (i) $f_{n}(x)=x^{-1} 1_{(1, n)}(x)$,

  (ii) $g_{n}(x)=x^{-2} 1_{(1, n)}(x)$,

  where $1_{A}$ denotes the indicator function of the set $A$.

  comment

• 1.II $. 25 \mathrm{~J} \quad$

  Probability and Measure | Part II, 2005

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space. For $\mathcal{G} \subseteq \mathcal{F}$, what is meant by saying that $\mathcal{G}$ is a $\pi$-system? State the 'uniqueness of extension' theorem for measures on $\sigma(\mathcal{G})$ having given values on $\mathcal{G}$.

  For $\mathcal{G}, \mathcal{H} \subseteq \mathcal{F}$, we call $\mathcal{G}, \mathcal{H}$ independent if

  $$\mathbb{P}(G \cap H)=\mathbb{P}(G) \mathbb{P}(H) \quad \text { for all } \quad G \in \mathcal{G}, H \in \mathcal{H}$$

  If $\mathcal{G}$ and $\mathcal{H}$ are independent $\pi$-systems, show that $\sigma(\mathcal{G})$ and $\sigma(\mathcal{H})$ are independent.

  Let $Y_{1}, Y_{2}, \ldots, Y_{m}, Z_{1}, Z_{2}, \ldots, Z_{n}$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$. Show that the $\sigma$-fields $\sigma(Y)=\sigma\left(Y_{1}, Y_{2}, \ldots, Y_{m}\right)$ and $\sigma(Z)=\sigma\left(Z_{1}, Z_{2}, \ldots, Z_{n}\right)$ are independent.

  comment

• 2.II.25J

  Probability and Measure | Part II, 2005

  Let $\mathcal{R}$ be a family of random variables on the common probability space $(\Omega, \mathcal{F}, \mathbb{P})$. What is meant by saying that $\mathcal{R}$ is uniformly integrable? Explain the use of uniform integrability in the study of convergence in probability and in $L^{1}$. [Clear definitions should be given of any terms used, but proofs may be omitted.]

  Let $\mathcal{R}_{1}$ and $\mathcal{R}_{2}$ be uniformly integrable families of random variables on $(\Omega, \mathcal{F}, \mathbb{P})$. Show that the family $\mathcal{R}$ given by

  $$\mathcal{R}=\left\{X+Y: X \in \mathcal{R}_{1}, Y \in \mathcal{R}_{2}\right\}$$

  is uniformly integrable.

  comment

• 4.II.25J

  Probability and Measure | Part II, 2005

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be Borel-measurable. State Fubini's theorem for the double integral

  $$\int_{y \in \mathbb{R}} \int_{x \in \mathbb{R}} f(x, y) d x d y$$

  Let $0<a<b$. Show that the function

  $$f(x, y)= \begin{cases}e^{-x y} & \text { if } x \in(0, \infty), y \in[a, b] \\ 0 & \text { otherwise }\end{cases}$$

  is measurable and integrable on $\mathbb{R}^{2}$.

  Evaluate

  $$\int_{0}^{\infty} \frac{e^{-a x}-e^{-b x}}{x} d x$$

  by Fubini's theorem or otherwise.

  comment

Representation Theory

• 1.II.19G

  Representation Theory | Part II, 2005

  Let the finite group $G$ act on finite sets $X$ and $Y$, and denote by $\mathbb{C}[X], \mathbb{C}[Y]$ the associated permutation representations on the spaces of complex functions on $X$ and $Y$. Call their characters $\chi_{X}$ and $\chi_{Y}$.

  (i) Show that the inner product $\left\langle\chi_{X} \mid \chi_{Y}\right\rangle$ is the number of orbits for the diagonal action of $G$ on $X \times Y$.

  (ii) Assume that $|X|>1$, and let $S \subset \mathbb{C}[X]$ be the subspace of those functions whose values sum to zero. By considering $\left\|\chi_{X}\right\|^{2}$, show that $S$ is irreducible if and only if the $G$-action on $X$ is doubly transitive: this means that for any two pairs $\left(x_{1}, x_{2}\right)$ and $\left(x_{1}^{\prime}, x_{2}^{\prime}\right)$ of points in $X$ with $x_{1} \neq x_{2}$ and $x_{1}^{\prime} \neq x_{2}^{\prime}$, there exists some $g \in G$ with $g x_{1}=x_{1}^{\prime}$ and $g x_{2}=x_{2}^{\prime}$.

  (iii) Let now $G=S_{n}$ acting on the set $X=\{1,2, \ldots, n\}$. Call $Y$ the set of 2element subsets of $X$, with the natural action of $S_{n}$. If $n \geqslant 4$, show that $\mathbb{C}[Y]$ decomposes under $S_{n}$ into three irreducible representations, one of which is the trivial representation and another of which is $S$. What happens when $n=3$ ?

  [Hint: Consider $\left\langle 1 \mid \chi_{Y}\right\rangle,\left\langle\chi_{X} \mid \chi_{Y}\right\rangle$ and $\left\|\chi_{Y}\right\|^{2}$.]

  comment

• 2.II.19G

  Representation Theory | Part II, 2005

  Let $G$ be a finite group and $\left\{\chi_{i}\right\}$ the set of its irreducible characters. Also choose representatives $g_{j}$ for the conjugacy classes, and denote by $Z\left(g_{j}\right)$ their centralisers.

  (i) State the orthogonality and completeness relations for the $\chi_{k}$.

  (ii) Using Part (i), or otherwise, show that

  $$\sum_{i} \overline{\chi_{i}\left(g_{j}\right)} \cdot \chi_{i}\left(g_{k}\right)=\delta_{j k} \cdot\left|Z\left(g_{j}\right)\right|$$

  (iii) Let $A$ be the matrix with $A_{i j}=\chi_{i}\left(g_{j}\right)$. Prove that

  $$|\operatorname{det} A|^{2}=\prod_{j}\left|Z\left(g_{j}\right)\right|$$

  (iv) Show that $\operatorname{det} A$ is either real or purely imaginary, explaining when each situation occurs.

  [Hint for (iv): Consider the effect of complex conjugation on the rows of the matrix A.]

  comment

• 3.II.19G

  Representation Theory | Part II, 2005

  Let $G$ be the group with 21 elements generated by $a$ and $b$, subject to the relations $a^{7}=b^{3}=1$ and $b a=a^{2} b .$

  (i) Find the conjugacy classes of $G$.

  (ii) Find three non-isomorphic one-dimensional representations of $G$.

  (iii) For a subgroup $H$ of a finite group $K$, write down (without proof) the formula for the character of the $K$-representation induced from a representation of $H$.

  (iv) By applying Part (iii) to the case when $H$ is the subgroup $\langle a\rangle$ of $K=G$, find the remaining irreducible characters of $G$.

  comment

• 4.II.19G

  Representation Theory | Part II, 2005

  (i) State and prove the Weyl integration formula for $S U(2)$.

  (ii) Determine the characters of the symmetric powers of the standard 2-dimensional representation of $S U(2)$ and prove that they are irreducible.

  [Any general theorems from the course may be used.]

  comment

Riemann Surfaces

• 1.II.23H

  Riemann Surfaces | Part II, 2005

  Let $\Lambda$ be a lattice in $\mathbb{C}$ generated by 1 and $\tau$, where $\tau$ is a fixed complex number with $\operatorname{Im} \tau>0$. The Weierstrass $\wp$-function is defined as a $\Lambda$-periodic meromorphic function such that

  (1) the only poles of $\wp$ are at points of $\Lambda$, and

  (2) there exist positive constants $\varepsilon$ and $M$ such that for all $|z|<\varepsilon$, we have

  $$\left|\wp(z)-1 / z^{2}\right|<M|z|$$

  Show that $\wp$ is uniquely determined by the above properties and that $\wp(-z)=\wp(z)$. By considering the valency of $\wp$ at $z=1 / 2$, show that $\wp^{\prime \prime}(1 / 2) \neq 0$.

  Show that $\wp$ satisfies the differential equation

  $$\wp^{\prime \prime}(z)=6 \wp^{2}(z)+A,$$

  for some complex constant $A$.

  [Standard theorems about doubly-periodic meromorphic functions may be used without proof provided they are accurately stated, but any properties of the $\wp$-function that you use must be deduced from first principles.]

  comment

• 2.II.23H

  Riemann Surfaces | Part II, 2005

  Define the terms function element and complete analytic function.

  Let $(f, D)$ be a function element such that $f(z)^{n}=p(z)$, for some integer $n \geqslant 2$, where $p(z)$ is a complex polynomial with no multiple roots. Let $F$ be the complete analytic function containing $(f, D)$. Show that every function element $(\tilde{f}, \tilde{D})$ in $F$ satisfies $\tilde{f}(z)^{n}=p(z) .$

  Describe how the non-singular complex algebraic curve

  $$C=\left\{(z, w) \in \mathbb{C}^{2} \mid w^{n}-p(z)=0\right\}$$

  can be made into a Riemann surface such that the first and second projections $\mathbb{C}^{2} \rightarrow \mathbb{C}$ define, by restriction, holomorphic maps $f_{1}, f_{2}: C \rightarrow \mathbb{C}$.

  Explain briefly the relation between $C$ and the Riemann surface $S(F)$ for the complete analytic function $F$ given earlier.

  [You do not need to prove the Inverse Function Theorem, provided that you state it accurately.]

  comment

• 3.II.22H

  Riemann Surfaces | Part II, 2005

  Explain what is meant by a meromorphic differential on a compact connected Riemann surface $S$. Show that if $f$ is a meromorphic function on $S$ then $d f$ defines a meromorphic differential on $S$. Show also that if $\eta$ and $\omega$ are two meromorphic differentials on $S$ which are not identically zero then $\eta=h \omega$ for some meromorphic function $h$. Show that zeros and poles of a meromorphic differential are well-defined and explain, without proof, how to obtain the genus of $S$ by counting zeros and poles of $\omega$.

  Let $V_{0} \subset \mathbb{C}^{2}$ be the affine curve with equation $u^{2}=v^{2}+1$ and let $V \subset \mathbb{P}^{2}$ be the corresponding projective curve. Show that $V$ is non-singular with two points at infinity, and that $d v$ extends to a meromorphic differential on $V$.

  [You may assume without proof that that the map

  $$(u, v)=\left(\frac{t^{2}+1}{t^{2}-1}, \frac{2 t}{t^{2}-1}\right), \quad t \in \mathbb{C} \backslash\{-1,1\},$$

  is onto $V_{0} \backslash\{(1,0)\}$ and extends to a biholomorphic map from $\mathbb{P}^{1}$ onto $V$.]

  comment

• 4.II.23H

  Riemann Surfaces | Part II, 2005

  Define what is meant by the degree of a non-constant holomorphic map between compact connected Riemann surfaces, and state the Riemann-Hurwitz formula.

  Let $E_{\Lambda}=\mathbb{C} / \Lambda$ be an elliptic curve defined by some lattice $\Lambda$. Show that the map

  $$\psi: z+\Lambda \in E_{\Lambda} \rightarrow-z+\Lambda \in E_{\Lambda}$$

  is biholomorphic, and that there are four points in $E_{\Lambda}$ fixed by $\psi$.

  Let $S=E_{\Lambda} / \sim$ be the quotient surface (the topological surface obtained by identifying $z+\Lambda$ and $\psi(z+\Lambda)$, for each $z)$ and let $\pi: E_{\Lambda} \rightarrow S$ be the corresponding projection map. Denote by $E_{\Lambda}^{0} \subset E_{\Lambda}$ the complement of the four points fixed by $\psi$, and let $S^{0}=\pi\left(E_{\Lambda}^{0}\right)$. Describe briefly a family of charts making $S^{0}$ into a Riemann surface, so that $\pi: E_{\Lambda}^{0} \rightarrow S^{0}$ is a holomorphic map.

  Now assume that the complex structure of $S^{0}$ extends to $S$, so that $S$ is a Riemann surface, and that the map $\pi$ is in fact holomorphic on all of $E_{\Lambda}$. Calculate the genus of $S$.

  comment

Statistical Modelling

• 1.I.5I

  Statistical Modelling | Part II, 2005

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\frac{\left(y_{i} \theta_{i}-b\left(\theta_{i}\right)\right)}{\phi}+c\left(y_{i}, \phi\right)\right]$$

  Assume that $\mathbb{E}\left(Y_{i}\right)=\mu_{i}$ and that there is a known link function $g(.)$ such that

  $$g\left(\mu_{i}\right)=\beta^{T} x_{i}$$

  where $x_{1}, \ldots, x_{n}$ are known $p$-dimensional vectors and $\beta$ is an unknown $p$-dimensional parameter. Show that $\mathbb{E}\left(Y_{i}\right)=b^{\prime}\left(\theta_{i}\right)$ and that, if $\ell(\beta, \phi)$ is the log-likelihood function from the observations $\left(y_{1}, \ldots, y_{n}\right)$, then

  $$\frac{\partial \ell(\beta, \phi)}{\partial \beta}=\sum_{1}^{n} \frac{\left(y_{i}-\mu_{i}\right) x_{i}}{g^{\prime}\left(\mu_{i}\right) V_{i}}$$

  where $V_{i}$ is to be defined.

  comment

• 1.II.13I

  Statistical Modelling | Part II, 2005

  The Independent, June 1999 , under the headline 'Tourists get hidden costs warnings' gave the following table of prices in pounds, called 'How the resorts compared'.

  $\begin{array}{lrrrrrr}\text { Algarve } & 8.00 & 0.50 & 3.50 & 3.00 & 4.00 & 100.00 \\ \text { CostaDelSol } & 6.95 & 1.30 & 4.10 & 12.30 & 4.10 & 130.85 \\ \text { Majorca } & 10.25 & 1.45 & 5.35 & 6.15 & 3.30 & 122.20 \\ \text { Tenerife } & 12.30 & 1.25 & 4.90 & 3.70 & 2.90 & 130.85 \\ \text { Florida } & 15.60 & 1.90 & 5.05 & 5.00 & 2.50 & 114.00 \\ \text { Tunisia } & 10.90 & 1.40 & 5.45 & 1.90 & 2.75 & 218.10 \\ \text { Cyprus } & 11.60 & 1.20 & 5.95 & 3.00 & 3.60 & 149.45 \\ \text { Turkey } & 6.50 & 1.05 & 6.50 & 4.90 & 2.85 & 263.00 \\ \text { Corfu } & 5.20 & 1.05 & 3.75 & 4.20 & 2.50 & 137.60 \\ \text { Sorrento } & 7.70 & 1.40 & 6.30 & 8.75 & 4.75 & 215.40 \\ \text { Malta } & 11.20 & 0.70 & 4.55 & 8.00 & 4.80 & 87.85 \\ \text { Rhodes } & 6.30 & 1.05 & 5.20 & 3.15 & 2.70 & 261.30 \\ \text { Sicily } & 13.25 & 1.75 & 4.20 & 7.00 & 3.85 & 174.40 \\ \text { Madeira } & 10.25 & 0.70 & 5.10 & 6.85 & 6.85 & 153.70\end{array}$

  Here the column headings are, respectively: Three-course meal, Bottle of Beer, Suntan Lotion, Taxi (5km), Film (24 exp), Car Hire (per week). Interpret the $R$ commands, and explain how to interpret the corresponding (slightly abbreviated) $R$ output given below. Your solution should include a careful statement of the underlying statistical model, but you may quote without proof any distributional results required.

  

  Residual standard error: $0.3425$ on 65 degrees of freedom

  Multiple R-Squared: $0.962$

  comment

• 2.I.5I

  Statistical Modelling | Part II, 2005

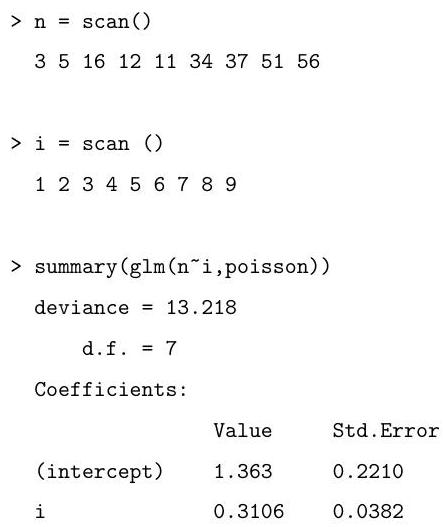
  You see below three $R$ commands, and the corresponding output (which is slightly abbreviated). Explain the effects of the commands. How is the deviance defined, and why do we have d.f. $=7$ in this case? Interpret the numerical values found in the output.

  

  comment

• 3.I.5I

  Statistical Modelling | Part II, 2005

  Consider the model $Y=X \beta+\epsilon$, where $Y$ is an $n$-dimensional observation vector, $X$ is an $n \times p$ matrix of rank $p, \epsilon$ is an $n$-dimensional vector with components $\epsilon_{1}, \ldots, \epsilon_{n}$, and $\epsilon_{1}, \ldots, \epsilon_{n}$ are independently and normally distributed, each with mean 0 and variance $\sigma^{2}$

  (a) Let $\hat{\beta}$ be the least-squares estimator of $\beta$. Show that

  $$\left(X^{T} X\right) \hat{\beta}=X^{T} Y$$

  and find the distribution of $\hat{\beta}$.

  (b) Define $\hat{Y}=X \hat{\beta}$. Show that $\hat{Y}$ has distribution $N\left(X \beta, \sigma^{2} H\right)$, where $H$ is a matrix that you should define.

  [You may quote without proof any results you require about the multivariate normal distribution.]

  comment

• 4.I.5I

  Statistical Modelling | Part II, 2005

  You see below five $R$ commands, and the corresponding output (which is slightly abbreviated). Without giving any mathematical proofs, explain the purpose of these commands, and interpret the output.

  

  Residual deviance: $1.9369$ on 2 degrees of freedom

  Number of Fisher Scoring iterations: 4

  comment

• 4.II.13I

  Statistical Modelling | Part II, 2005

  (i) Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \beta, \nu\right)=\left(\frac{\nu y_{i}}{\mu_{i}}\right)^{\nu} e^{-y_{i} \nu / \mu_{i}} \frac{1}{\Gamma(\nu)} \frac{1}{y_{i}} \text { for } y_{i}>0$$

  where

  $$1 / \mu_{i}=\beta^{T} x_{i}, \text { for } \quad 1 \leqslant i \leqslant n,$$

  and $x_{1}, \ldots, x_{n}$ are given $p$-dimensional vectors, and $\nu$ is known.

  Show that $\mathbb{E}\left(Y_{i}\right)=\mu_{i}$ and that $\operatorname{var}\left(Y_{i}\right)=\mu_{i}^{2} / \nu$.

  (ii) Find the equation for $\hat{\beta}$, the maximum likelihood estimator of $\beta$, and suggest an iterative scheme for its solution.

  (iii) If $p=2$, and $x_{i}=\left(\begin{array}{c}1 \\ z_{i}\end{array}\right)$, find the large-sample distribution of $\hat{\beta}_{2}$. Write your answer in terms of $a, b, c$ and $\nu$, where $a, b, c$ are defined by

  $$a=\sum \mu_{i}^{2}, \quad b=\sum z_{i} \mu_{i}^{2}, \quad c=\sum z_{i}^{2} \mu_{i}^{2} .$$

  comment

Statistical Physics

• 2.II.34D

  Statistical Physics | Part II, 2005

  Write down the first law of thermodynamics in differential form applied to an infinitesimal reversible change.

  Explain what is meant by an adiabatic change.

  Starting with the first law in differential form, derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  Hence show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=T\left(\frac{\partial P}{\partial T}\right)_{V}-P$$

  For radiation in thermal equilibrium at temperature $T$ in volume $V$, it is given that $E=V e(T)$ and $P=e(T) / 3$. Hence deduce Stefan's Law,

  $$E=a V T^{4}$$

  where $a$ is a constant.

  The radiation is allowed to expand adiabatically. Show that $V T^{3}$ is constant during the expansion.

  comment

• 3.II.34D

  Statistical Physics | Part II, 2005

  A free spinless particle moving in two dimensions is confined to a square box of side $L$. By imposing periodic boundary conditions show that the number of states in the energy range $\epsilon \rightarrow \epsilon+d \epsilon$ is $g(\epsilon) d \epsilon$, where

  $$g(\epsilon)=\frac{m L^{2}}{2 \pi \hbar^{2}}$$

  If, instead, the particle is an electron with magnetic moment $\mu$ moving in a constant external magnetic field $H$, show that

  $$g(\epsilon)= \begin{cases}\frac{m L^{2}}{2 \pi \hbar^{2}}, & -\mu H<\epsilon<\mu H \\ \frac{m L^{2}}{\pi \hbar^{2}}, & \mu H<\epsilon\end{cases}$$

  Let there be $N$ electrons in the box. Explain briefly how to construct the ground state of the system. Let $\epsilon$ be the Fermi energy. Show that when $\epsilon>\mu H$

  $$N=\frac{m L^{2}}{\pi \hbar^{2}} \epsilon .$$

  Show also that the magnetic moment $M$ of the system in its ground state is given by

  $$M=\frac{\mu^{2} m L^{2}}{\pi \hbar^{2}} H$$

  and that the ground state energy is

  $$\frac{1}{2} \frac{\pi \hbar^{2}}{m L^{2}} N^{2}-\frac{1}{2} M H$$

  comment

• 4.II.34D

  Statistical Physics | Part II, 2005

  Write down an expression for the partition function of a classical particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical particles is placed in the potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. The gas is in equilibrium at temperature $T$. Using a suitable rescaling of variables, show that the free energy $F$ is given by

  $$\frac{F}{N}=-k T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k T+\log I_{n}\right)$$

  where

  $$I_{n}=\left(\frac{2 m \pi}{h^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} e^{-u^{2 n}} d u$$

  Regarding $V$ as an external parameter, find the thermodynamic force $P$, conjugate to $V$, exerted by this system. Find the equation of state and compare with that of an ideal gas confined in a volume $V$.

  Derive expressions for the entropy $S$, the internal energy $E$ and the total heat capacity $C_{V}$ at constant $V$.

  Show that for all $n$ the total heat capacity at constant $P$ is given by

  $$C_{P}=C_{V}+N k$$

  [Note that $\left.\int_{0}^{\infty} u^{2} e^{-u^{2} / 2} d u=\sqrt{\frac{\pi}{2}} .\right]$

  comment

Stochastic Financial Models

• 1.II.28J

  Stochastic Financial Models | Part II, 2005

  Let $X \equiv\left(X_{0}, X_{1}, \ldots, X_{J}\right)^{T}$ be a zero-mean Gaussian vector, with covariance matrix $V=\left(v_{j k}\right)$. In a simple single-period economy with $J$ agents, agent $i$ will receive $X_{i}$ at time $1(i=1, \ldots, J)$. If $Y$ is a contingent claim to be paid at time 1 , define agent $i$ 's reservation bid price for $Y$, assuming his preferences are given by $E\left[U_{i}\left(X_{i}+Z\right)\right]$ for any contingent claim $Z$.

  Assuming that $U_{i}(x) \equiv-\exp \left(-\gamma_{i} x\right)$ for each $i$, where $\gamma_{i}>0$, show that agent $i$ 's reservation bid price for $\lambda$ units of $X_{0}$ is

  $$p_{i}(\lambda)=-\frac{1}{2} \gamma_{i}\left(\lambda^{2} v_{00}+2 \lambda v_{0 i}\right)$$

  As $\lambda \rightarrow 0$, find the limit of agent $i$ 's per-unit reservation bid price for $X_{0}$, and comment on the expression you obtain.

  The agents bargain, and reach an equilibrium. Assuming that the contingent claim $X_{0}$ is in zero net supply, show that the equilibrium price of $X_{0}$ will be

  $$p=-\Gamma v_{0 \bullet}$$

  where $\Gamma^{-1}=\sum_{i=1}^{J} \gamma_{i}^{-1}$ and $v_{0 \bullet}=\sum_{i=1}^{J} v_{0 i}$. Show that at that price agent $i$ will choose to buy

  $$\theta_{i}=\left(\Gamma v_{0 \bullet}-\gamma_{i} v_{0 i}\right) /\left(\gamma_{i} v_{00}\right)$$

  units of $X_{0}$.

  By computing the improvement in agent $i$ 's expected utility, show that the value to agent $i$ of access to this market is equal to a fixed payment of

  $$\frac{\left(\gamma_{i} v_{0 i}-\Gamma v_{0 \bullet}\right)^{2}}{2 \gamma_{i} v_{00}}$$

  comment

• 2.II.28J

  Stochastic Financial Models | Part II, 2005

  (i) At the beginning of year $n$, an investor makes decisions about his investment and consumption for the coming year. He first takes out an amount $c_{n}$ from his current wealth $w_{n}$, and sets this aside for consumption. He splits his remaining wealth between a bank account (unit wealth invested at the start of the year will have grown to a sure amount $r>1$ by the end of the year), and the stock market. Unit wealth invested in the stock market will have become the random amount $X_{n+1}>0$ by the end of the year.

  The investor's objective is to invest and consume so as to maximise the expected value of $\sum_{n=1}^{N} U\left(c_{n}\right)$, where $U$ is strictly increasing and strictly convex. Consider the dynamic programming equation (Bellman equation) for his problem,

  $$\begin{aligned} V_{n}(w) &=\sup _{c, \theta}\left\{U(c)+E_{n}\left[V_{n+1}\left(\theta(w-c) X_{n+1}+(1-\theta)(w-c) r\right)\right]\right\} \quad(0 \leqslant n<N), \\ V_{N}(w) &=U(w) . \end{aligned}$$

  Explain all undefined notation, and explain briefly why the equation holds.

  (ii) Supposing that the $X_{i}$ are independent and identically distributed, and that $U(x)=x^{1-R} /(1-R)$, where $R>0$ is different from 1 , find as explicitly as you can the form of the agent's optimal policy.

  (iii) Return to the general problem of (i). Assuming that the sample space $\Omega$ is finite, and that all suprema are attained, show that

  $$\begin{aligned} E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\left(X_{n+1}-r\right)\right] &=0 \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=U^{\prime}\left(c_{n}^{*}\right) \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=V_{n}^{\prime}\left(w_{n}^{*}\right) \end{aligned}$$

  where $\left(c_{n}^{*}, w_{n}^{*}\right)_{0 \leqslant n \leqslant N}$ denotes the optimal consumption and wealth process for the problem. Explain the significance of each of these equalities.

  comment

• 3.II.27J

  Stochastic Financial Models | Part II, 2005

  Suppose that over two periods a stock price moves on a binomial tree:

  

  (a) Find an arbitrage opportunity when the riskless rate equals $1 / 10$. Give precise details of when and how much you buy, borrow and sell.

  (b) From here on, assume instead that the riskless rate equals $1 / 4$. Determine the equivalent martingale measure. [No proof is required.]

  (c) Determine the time-zero price of an American put with strike 15 and expiry 2 . Assume you sell it at this price. Which hedge do you put on at time zero? Consider the scenario of two bad periods. How does your hedge work?

  (d) The buyer of the American put turns out to be an unsophisticated investor who fails to use his early exercise right when he should. Assume the first period was bad. How much profit can you make out of this? You should detail your exact strategy.

  comment

• 4.II.28J

  Stochastic Financial Models | Part II, 2005

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be spot price, $K$ be strike price, $T$ be time to maturity, and assume constant interest rate $r$, volatility $\sigma$ and absence of dividends. Write down explicitly the prices of a European call and put,

  $$E C\left(S_{0}, K, \sigma, r, T\right) \text { and } E P\left(S_{0}, K, \sigma, r, T\right)$$

  Use $\Phi$ for the normal distribution function. [No proof is required.]

  (b) From here on assume $r=0$. Keeping $T, \sigma$ fixed, we shorten the notation to $E C\left(S_{0}, K\right)$ and similarly for $E P$. Show that put-call symmetry holds:

  $$E C\left(S_{0}, K\right)=E P\left(K, S_{0}\right)$$

  Check homogeneity: for every real $\alpha>0$

  $$E C\left(\alpha S_{0}, \alpha K\right)=\alpha E C\left(S_{0}, K\right)$$

  (c) Show that the price of a down-and-out European call with strike $K<S_{0}$ and barrier $B \leqslant K$ is given by

  $$E C\left(S_{0}, K\right)-\frac{S_{0}}{B} E C\left(\frac{B^{2}}{S_{0}}, K\right)$$

  (d)

  (i) Specialize the last expression to $B=K$ and simplify.

  (ii) Answer a popular interview question in investment banks: What is the fair value of a down-and-out call given that $S_{0}=100, B=K=80, \sigma=20 \%, r=0, T=1$ ? Identify the corresponding hedge. [It may be helpful to compute Delta first.]

  (iii) Does this hedge work beyond the Black-Scholes model? When does it fail?

  comment

Topics in Analysis

• $2 . \mathrm{I} . 2 \mathrm{~F}$

  Topics in Analysis | Part II, 2005

  (i) Let $\alpha$ be an algebraic number and let $p$ and $q$ be integers with $q \neq 0$. What does Liouville's theorem say about $\alpha$ and $p / q$ ?

  (ii) Let $p$ and $q$ be integers with $q \neq 0$. Prove that

  $$\left|\sqrt{2}-\frac{p}{q}\right| \geqslant \frac{1}{4 q^{2}} .$$

  [In (ii), you may not use Liouville's theorem unless you prove it.]

  comment

• $3 . \mathrm{I} . 2 \mathrm{~F} \quad$

  Topics in Analysis | Part II, 2005

  Let $-1 \leqslant x_{1}<x_{2}<\ldots<x_{n} \leqslant 1$ and let $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers such that

  $$\int_{-1}^{1} p(t) d t=\sum_{i=1}^{n} a_{i} p\left(x_{i}\right)$$

  for every polynomial $p$ of degree less than $2 n$. Prove the following three facts.

  (i) $a_{i}>0$ for every $i$.

  (ii) $\sum_{i=1}^{n} a_{i}=2$.

  (iii) The numbers $x_{1}, x_{2}, \ldots, x_{n}$ are the roots of the Legendre polynomial of degree $n$.

  [You may assume standard orthogonality properties of the Legendre polynomials.]

  comment

• 1.I.2F

  Topics in Analysis | Part II, 2005

  Prove that $\cosh (1 / 2)$ is irrational.

  comment

• 1.II.11F

  Topics in Analysis | Part II, 2005

  State and prove a discrete form of Brouwer's theorem, concerning colourings of points in triangular grids. Use it to deduce that there is no continuous retraction from a disc to its boundary.

  comment

• 2.II.11F

  Topics in Analysis | Part II, 2005

  (i) State the Baire category theorem. Deduce from it a statement about nowhere dense sets.

  (ii) Let $X$ be the set of all real numbers with decimal expansions consisting of the digits 4 and 5 only. Prove that there is a real number $t$ that cannot be written in the form $x+y$ with $x \in X$ and $y$ rational.

  comment

• 4.I.2F

  Topics in Analysis | Part II, 2005

  (i) Let $D \subset \mathbb{C}$ be a domain, let $f: D \rightarrow \mathbb{C}$ be an analytic function and let $z_{0} \in D$. What does Taylor's theorem say about $z_{0}, f$ and $D$ ?

  (ii) Let $K$ be the square consisting of all complex numbers $z$ such that

  $$-1 \leqslant \operatorname{Re}(z) \leqslant 1 \text { and }-1 \leqslant \operatorname{Im}(z) \leqslant 1,$$

  and let $w$ be a complex number not belonging to $K$. Prove that the function $f(z)=$ $(z-w)^{-1}$ can be uniformly approximated on $K$ by polynomials.

  comment

Waves

• 1.II $37 \mathrm{E} \quad$

  Waves | Part II, 2005

  An elastic solid with density $\rho$ has Lamé moduli $\lambda$ and $\mu$. Write down equations satisfied by the dilational and shear potentials $\phi$ and $\boldsymbol{\psi}$.

  For a two-dimensional disturbance give expressions for the displacement field $\mathbf{u}=\left(u_{x}, u_{y}, 0\right)$ in terms of $\phi(x, y ; t)$ and $\psi=(0,0, \psi(x, y ; t))$.

  Suppose the solid occupies the region $y<0$ and that the surface $y=0$ is free of traction. Find a combination of solutions for $\phi$ and $\psi$ that represent a propagating surface wave (a Rayleigh wave) near $y=0$. Show that the wave is non-dispersive and obtain an equation for the speed $c$. [You may assume without proof that this equation has a unique positive root.]

  comment

• 2.II.37E

  Waves | Part II, 2005

  Show that, in the standard notation for a one-dimensional flow of a perfect gas at constant entropy, the quantity $u+2\left(c-c_{0}\right) /(\gamma-1)$ remains constant along characteristics $d x / d t=u+c$.

  A perfect gas is initially at rest and occupies a tube in $x>0$. A piston is pushed into the gas so that its position at time $t$ is $x(t)=\frac{1}{2} f t^{2}$, where $f>0$ is a constant. Find the time and position at which a shock first forms in the gas.

  comment

• 3.II.37E

  Waves | Part II, 2005

  The real function $\phi(x, t)$ satisfies the equation

  $$\frac{\partial \phi}{\partial t}+U \frac{\partial \phi}{\partial x}=\frac{\partial^{3} \phi}{\partial x^{3}},$$

  where $U>0$ is a constant. Find the dispersion relation for waves of wavenumber $k$ and deduce whether wave crests move faster or slower than a wave packet.

  Suppose that $\phi(x, 0)$ is given by a Fourier transform as

  $$\phi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  Use the method of stationary phase to find $\phi(V t, t)$ as $t \rightarrow \infty$ for fixed $V>U$.

  [You may use the result that $\int_{-\infty}^{\infty} e^{-a \xi^{2}} d \xi=(\pi / a)^{1 / 2}$ if $\left.\operatorname{Re}(a) \geqslant 0 .\right]$

  What can be said if $V<U$ ? [Detailed calculation is not required in this case.]

  comment

• 4.II $. 38 \mathrm{E} \quad$

  Waves | Part II, 2005

  Starting from the equations of conservation of mass and momentum for an inviscid compressible fluid, show that for small perturbations about a state of rest and uniform density the velocity is irrotational and the velocity potential satisfies the wave equation. Identify the sound speed $c_{0}$.

  Define the acoustic energy density and acoustic energy flux, and derive the equation for conservation of acoustic energy.

  Show that in any (not necessarily harmonic) acoustic plane wave of wavenumber $\mathbf{k}$ the kinetic and potential energy densities are equal and that the acoustic energy is transported with velocity $c_{0} \widehat{\mathbf{k}}$.

  Calculate the kinetic and potential energy densities for a spherically symmetric outgoing wave. Are they equal?

  comment