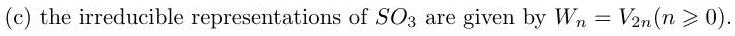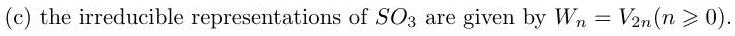Let $V_{n}$ be the space of homogeneous polynomials of degree $n$ in two variables $z_{1}$ and $z_{2}$. Define a left action of $G=S U_{2}$ on the space of polynomials by setting

$$(g P) z=P(z g),$$

where $P \in \mathbb{C}\left[z_{1}, z_{2}\right], \quad g=\left(\begin{array}{cc}a & b \\ c & d\end{array}\right), \quad z=\left(z_{1}, z_{2}\right) \quad$ and $\quad z g=\left(a z_{1}+c z_{2}, b z_{1}+d z_{2}\right)$.

Show that

(a) the representations $V_{n}$ are irreducible,

(b) the representations $V_{n}$ exhaust the irreducible representations of $S U_{2}$, and