Part II, 2002, Paper 3

Algebraic Curves

• B3.10

  Algebraic Curves | Part II, 2002

  Let $f=f(x, y)$ be an irreducible polynomial of degree $n \geq 2$ (over an algebraically closed field of characteristic zero) and $V_{0}=\{f=0\} \subset \mathbb{A}^{2}$ the corresponding affine plane curve. Assume that $V_{0}$ is smooth (non-singular) and that the projectivization $V \subset \mathbb{P}^{2}$ of $V_{0}$ intersects the line at infinity $\mathbb{P}^{2}-\mathbb{A}^{2}$ in $n$ distinct points. Show that $V$ is smooth and determine the divisor of the rational differential $\omega=\frac{d x}{f_{y}^{\prime}}$ on $V$. Deduce a formula for the genus of $V$.

  comment

Algebraic Topology

• B3.7

  Algebraic Topology | Part II, 2002

  For a finite simplicial complex $X$, let $b_{i}(X)$ denote the rank of the finitely generated abelian group $H_{i} X$. Define the Euler characteristic $\chi(X)$ by the formula

  $$\chi(X)=\sum_{i}(-1)^{i} b_{i}(X) .$$

  Let $a_{i}$ denote the number of $i$-simplices in $X$, for each $i \geqslant 0$. Show that

  $$\chi(X)=\sum_{i}(-1)^{i} a_{i}$$

  comment

Algorithms and Networks

• A3.10

  Algorithms and Networks | Part II, 2002

  (i) Consider the unconstrained geometric programme GP

  $$\text { minimise } g(t)=\sum_{i=1}^{n} c_{i} \prod_{j=1}^{m} t_{j}^{a_{i j}}$$

  subject to $t_{j}>0 \quad j=1, \ldots, m$.

  State the dual problem to GP. Give a careful statement of the AM-GM inequality, and use it to prove the primal-dual inequality for GP.

  (ii) Define min-path and max-tension problems. State and outline the proof of the max-tension min-path theorem.

  A company has branches in five cities $A, B, C, D$ and $E$. The fares for direct flights between these cities are as follows:

  \begin{tabular}{l|lllll} & $\mathrm{A}$ & $\mathrm{B}$ & $\mathrm{C}$ & $\mathrm{D}$ & $\mathrm{E}$ \ \hline $\mathrm{A}$ & $-$ & 50 & 40 & 25 & 10 \ $\mathrm{~B}$ & 50 & $-$ & 20 & 90 & 25 \ $\mathrm{C}$ & 40 & 20 & $-$ & 10 & 25 \ $\mathrm{D}$ & 25 & 90 & 10 & $-$ & 55 \ $\mathrm{E}$ & 10 & 25 & 25 & 55 & $-$ \end{tabular}

  Formulate this as a min-path problem. Illustrate the max-tension min-path algorithm by finding the cost of travelling by the cheapest routes between $D$ and each of the other cities.

  comment

Applications of Quantum Mechanics

• B3.23

  Applications of Quantum Mechanics | Part II, 2002

  A periodic potential is expressed as $V(\mathbf{x})=\sum_{\mathbf{g}} a_{\mathbf{g}} e^{i \mathbf{g} \cdot \mathbf{x}}$, where $\{\mathbf{g}\}$ are reciprocal lattice vectors and $a_{\mathbf{g}}{ }^{*}=a_{-\mathbf{g}}, a_{\mathbf{0}}=0$. In the nearly free electron model explain why it is appropriate, near the boundaries of energy bands, to consider a Bloch wave state

  $$\left|\psi_{\mathbf{k}}\right\rangle=\sum_{r} \alpha_{r}\left|\mathbf{k}_{r}\right\rangle, \quad \mathbf{k}_{r}=\mathbf{k}+\mathbf{g}_{r},$$

  where $|\mathbf{k}\rangle$ is a free electron state for wave vector $\mathbf{k},\left\langle\mathbf{k}^{\prime} \mid \mathbf{k}\right\rangle=\delta_{\mathbf{k}^{\prime} \mathbf{k}}$, and the sum is restricted to reciprocal lattice vectors $\mathbf{g}_{r}$ such that $\left|\mathbf{k}_{r}\right| \approx|\mathbf{k}|$. Obtain a determinantal formula for the possible energies $E(\mathbf{k})$ corresponding to Bloch wave states of this form.

  [You may take $\mathbf{g}_{1}=\mathbf{0}$ and assume $e^{i \mathbf{b} \cdot \mathbf{x}}|\mathbf{k}\rangle=|\mathbf{k}+\mathbf{b}\rangle$ for any $\mathbf{b}$.]

  Suppose the sum is restricted to just $\mathbf{k}$ and $\mathbf{k}+\mathbf{g}$. Show that there is a gap $2\left|a_{\mathbf{g}}\right|$ between energy bands. Setting $\mathbf{k}=-\frac{1}{2} \mathbf{g}+\mathbf{q}$, show that there are two Bloch wave states with energies near the boundaries of the energy bands

  $$E_{\pm}(\mathbf{k}) \approx \frac{\hbar^{2}|\mathbf{g}|^{2}}{8 m} \pm\left|a_{\mathbf{g}}\right|+\frac{\hbar^{2}|\mathbf{q}|^{2}}{2 m} \pm \frac{\hbar^{4}}{8 m^{2}\left|a_{\mathbf{g}}\right|}(\mathbf{q} \cdot \mathbf{g})^{2}$$

  What is meant by effective mass? Determine the value of the effective mass at the top and the bottom of the adjacent energy bands if $\mathbf{q}$ is parallel to $\mathrm{g}$.

  comment

Applied Probability

• B3.13

  Applied Probability | Part II, 2002

  (a) Define a renewal process and a discrete renewal process.

  (b) State and prove the Discrete Renewal Theorem.

  (c) The sequence $\mathbf{u}=\left\{u_{n}: n \geqslant 0\right\}$ satisfies

  $$u_{0}=1, \quad u_{n}=\sum_{i=1}^{n} f_{i} u_{n-i}, \quad \text { for } n \geqslant 1$$

  for some collection of non-negative numbers $\left(f_{i}: i \in \mathbb{N}\right)$ summing to 1 . Let $U(s)=$ $\sum_{n=1}^{\infty} u_{n} s^{n}, F(s)=\sum_{n=1}^{\infty} f_{n} s^{n}$. Show that

  $$F(s)=\frac{U(s)}{1+U(s)} .$$

  Give a probabilistic interpretation of the numbers $u_{n}, f_{n}$ and $m_{n}=\sum_{i=1}^{n} u_{i}$.

  (d) Let the sequence $u_{n}$ be given by

  $$u_{2 n}=\left(\begin{array}{c} 2 n \\ n \end{array}\right)\left(\frac{1}{2}\right)^{2 n}, \quad u_{2 n+1}=0, \quad n \geqslant 1 .$$

  How is this related to the simple symmetric random walk on the integers $\mathbb{Z}$ starting from the origin, and its subsequent returns to the origin? Determine $F(s)$ in this case, either by calculating $U(s)$ or by showing that $F$ satisfies the quadratic equation

  $$F^{2}-2 F+s^{2}=0, \quad \text { for } \quad 0 \leqslant s<1 .$$

  comment

Dynamical Systems

• B3.17

  Dynamical Systems | Part II, 2002

  Let $\mathcal{A}$ be a finite alphabet of letters and $\Sigma$ either the semi-infinite space or the doubly infinite space of sequences whose elements are drawn from $\mathcal{A}$. Define the natural topology on $\Sigma$. If $W$ is a set of words, denote by $\Sigma_{W}$ the subspace of $\Sigma$ consisting of those sequences none of whose subsequences is in $W$. Prove that $\Sigma_{W}$ is a closed subspace of $\Sigma$; and state and prove a necessary and sufficient condition for a closed subspace of $\Sigma$ to have the form $\Sigma_{W}$ for some $W$.

  $$\begin{aligned} &\text { If } \mathcal{A}=\{0,1\} \text { and } \quad W=\{000,111,010,101\} \end{aligned}$$

  what is the space $\Sigma_{W}$ ?

  comment

Dynamics of Differential Equations

• A3.6 B3.4

  Dynamics of Differential Equations | Part II, 2002

  (i) Define the Floquet multiplier and Liapunov exponent for a periodic orbit $\hat{\mathbf{x}}(t)$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$. Show that one multiplier is always unity, and that the other is given by

  $$\exp \left(\int_{0}^{T} \nabla \cdot \mathbf{f}(\hat{\mathbf{x}}(t)) d t\right)$$

  where $T$ is the period of the orbit.

  The Van der Pol oscillator $\ddot{x}+\epsilon \dot{x}\left(x^{2}-1\right)+x=0,0<\epsilon \ll 1$ has a limit cycle $\hat{x}(t) \approx 2 \sin t$. Show using $(*)$ that this orbit is stable.

  (ii) Show, by considering the normal form for a Hopf bifurcation from a fixed point $\mathbf{x}_{0}(\mu)$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}, \mu)$, that in some neighbourhood of the bifurcation the periodic orbit is stable when it exists in the range of $\mu$ for which $\mathbf{x}_{0}$ is unstable, and unstable in the opposite case.

  Now consider the system

  $$\left.\begin{array}{l} \dot{x}=x(1-y)+\mu x \\ \dot{y}=y(x-1)-\mu x \end{array}\right\} \quad x>0$$

  Show that the fixed point $(1+\mu, 1+\mu)$ has a Hopf bifurcation when $\mu=0$, and is unstable (stable) when $\mu>0(\mu<0)$.

  Suppose that a periodic orbit exists in $\mu>0$. Show without solving for the orbit that the result of part (i) shows that such an orbit is unstable. Define a similar result for $\mu<0$.

  What do you conclude about the existence of periodic orbits when $\mu \neq 0$ ? Check your answer by applying Dulac's criterion to the system, using the weighting $\rho=e^{-(x+y)}$.

  comment

Electromagnetism

• A3.5 B3.3

  Electromagnetism | Part II, 2002

  (i) A plane electromagnetic wave in a vacuum has an electric field

  $$\mathbf{E}=\left(E_{1}, E_{2}, 0\right) \cos (k z-\omega t),$$

  referred to cartesian axes $(x, y, z)$. Show that this wave is plane polarized and find the orientation of the plane of polarization. Obtain the corresponding plane polarized magnetic field and calculate the rate at which energy is transported by the wave.

  (ii) Suppose instead that

  $$\mathbf{E}=\left(E_{1} \cos (k z-\omega t), E_{2} \cos (k z-\omega t+\phi), 0\right),$$

  with $\phi$ a constant, $0<\phi<\pi$. Show that, if the axes are now rotated through an angle $\psi$ so as to obtain an elliptically polarized wave with an electric field

  $$\mathbf{E}^{\prime}=\left(F_{1} \cos (k z-\omega t+\chi), F_{2} \sin (k z-\omega t+\chi), 0\right),$$

  then

  $$\tan 2 \psi=\frac{2 E_{1} E_{2} \cos \phi}{E_{1}^{2}-E_{2}^{2}} .$$

  Show also that if $E_{1}=E_{2}=E$ there is an elliptically polarized wave with

  $$\mathbf{E}^{\prime}=\sqrt{2} E\left(\cos \left(k z-\omega t+\frac{1}{2} \phi\right) \cos \frac{1}{2} \phi, \sin \left(k z-\omega t+\frac{1}{2} \phi\right) \sin \frac{1}{2} \phi, 0\right) .$$

  comment

Fluid Dynamics II

• B3.24

  Fluid Dynamics II | Part II, 2002

  (i) Suppose that, with spherical polar coordinates, the Stokes streamfunction

  $$\Psi_{\lambda}(r, \theta)=r^{\lambda} \sin ^{2} \theta \cos \theta$$

  represents a Stokes flow and thus satisfies the equation $D^{2}\left(D^{2} \Psi_{\lambda}\right)=0$, where

  $$D^{2}=\frac{\partial^{2}}{\partial r^{2}}+\frac{\sin \theta}{r^{2}} \frac{\partial}{\partial \theta} \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} .$$

  Show that the possible values of $\lambda$ are $5,3,0$ and $-2$. For which of these values is the corresponding flow irrotational? Sketch the streamlines of the flow for the case $\lambda=3$.

  (ii) A spherical drop of liquid of viscosity $\mu_{1}$, radius $a$ and centre at $r=0$, is suspended in another liquid of viscosity $\mu_{2}$ which flows with streamfunction

  $$\Psi \sim \Psi_{\infty}(r, \theta)=\alpha r^{3} \sin ^{2} \theta \cos \theta$$

  far from the drop. The two liquids are of equal densities, surface tension is sufficiently strong to keep the drop spherical, and inertia is negligible. Show that

  $$\Psi= \begin{cases}\left(A r^{5}+B r^{3}\right) \sin ^{2} \theta \cos \theta & (r<a), \\ \left(\alpha r^{3}+C+D / r^{2}\right) \sin ^{2} \theta \cos \theta & (r>a)\end{cases}$$

  and obtain four equations determining the constants $A, B, C$ and $D$. (You need not solve these equations.)

  [You may assume, with standard notation, that

  $$\left.u_{r}=\frac{1}{r^{2} \sin \theta} \frac{\partial \Psi}{\partial \theta} \quad, \quad u_{\theta}=-\frac{1}{r \sin \theta} \frac{\partial \Psi}{\partial r} \quad, \quad e_{r \theta}=\frac{1}{2}\left\{r \frac{\partial}{\partial r}\left(\frac{u_{\theta}}{r}\right)+\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right\} .\right]$$

  comment

Foundations of Quantum Mechanics

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2002

  (i) Two particles with angular momenta $j_{1}, j_{2}$ and basis states $\left|j_{1} m_{1}\right\rangle,\left|j_{2} m_{2}\right\rangle$ are combined to give total angular momentum $j$ and basis states $|j m\rangle$. State the possible values of $j, m$ and show how a state with $j=m=j_{1}+j_{2}$ can be constructed. Briefly describe, for a general allowed value of $j$, what the Clebsch-Gordan coefficients are.

  (ii) If the angular momenta $j_{1}$ and $j_{2}$ are both 1 show that the combined state $|20\rangle$ is

  

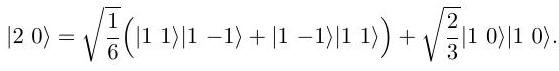
  Determine the corresponding expressions for the combined states $\left|\begin{array}{lll}1 & 0\rangle\end{array}\right\rangle$ and $|0 \quad 0\rangle$, assuming that they are respectively antisymmetric and symmetric under interchange of the two particles.

  If the combined system is in state $|0 \quad 0\rangle$ what is the probability that measurements of the $z$-component of angular momentum for either constituent particle will give the value of 1 ?

  $\left[\right.$ Hint: $\left.\quad J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .\right]$

  comment

Functional Analysis

• A3.3 B3.2

  Functional Analysis | Part II, 2002

  (i) Suppose that $\left(f_{n}\right)$ is a decreasing sequence of continuous real-valued functions on a compact metric space $(X, d)$ which converges pointwise to 0 . By considering sets of the form $B_{n}=\left\{x: f_{n}(x)<\epsilon\right\}$, for $\epsilon>0$, or otherwise, show that $f_{n}$ converges uniformly to 0 .

  Can the condition that $\left(f_{n}\right)$ is decreasing be dropped? Can the condition that $(X, d)$ is compact be dropped? Justify your answers.

  (ii) Suppose that $k$ is a positive integer. Define polynomials $p_{n}$ recursively by

  $$p_{0}=0, \quad p_{n+1}(t)=p_{n}(t)+\left(t-p_{n}^{k}(t)\right) / k$$

  Show that $0 \leqslant p_{n}(t) \leqslant p_{n+1}(t) \leqslant t^{1 / k}$, for $t \in[0,1]$, and show that $p_{n}(t)$ converges to $t^{1 / k}$ uniformly on $[0,1]$.

  [You may wish to use the identity $a^{k}-b^{k}=(a-b)\left(a^{k-1}+a^{k-2} b+\ldots+b^{k-1}\right)$.]

  Suppose that $A$ is a closed subalgebra of the algebra $C(X)$ of continuous real-valued functions on a compact metric space $(X, d)$, equipped with the uniform norm, and suppose that $A$ has the property that for each $x \in X$ there exists $a \in A$ with $a(x) \neq 0$. Show that there exists $h \in A$ such that $0<h(x) \leqslant 1$ for all $x \in X$.

  Show that $h^{1 / k} \in A$ for each positive integer $k$, and show that $A$ contains the constant functions.

  comment

Galois Theory

• B3.6

  Galois Theory | Part II, 2002

  Show that the polynomial $f(X)=X^{5}+27 X+16$ has no rational roots. Show that the splitting field of $f$ over the finite field $\mathbb{F}_{3}$ is an extension of degree 4 . Hence deduce that $f$ is irreducible over the rationals. Prove that $f$ has precisely two (non-multiple) roots over the finite field $\mathbb{F}_{7}$. Find the Galois group of $f$ over the rationals.

  [You may assume any general results you need including the fact that $A_{5}$ is the only index 2 subgroup of $S_{5}$.]

  comment

Geometry of Surfaces

• A3.7

  Geometry of Surfaces | Part II, 2002

  (i) State what it means for surfaces $f: U \rightarrow \mathbb{R}^{3}$ and $g: V \rightarrow \mathbb{R}^{3}$ to be isometric.

  Let $f: U \rightarrow \mathbb{R}^{3}$ be a surface, $\phi: V \rightarrow U$ a diffeomorphism, and let $g=f \circ \phi: V \rightarrow$ $\mathbb{R}^{3} .$

  State a formula comparing the first fundamental forms of $f$ and $g$.

  (ii) Give a proof of the formula referred to at the end of part (i). Deduce that "isometry" is an equivalence relation.

  The catenoid and the helicoid are the surfaces defined by

  $$(u, v) \rightarrow(u \cos v, u \sin v, v)$$

  and

  $$(\vartheta, z) \rightarrow(\cosh z \cos \vartheta, \cosh z \sin \vartheta, z)$$

  Show that the catenoid and the helicoid are isometric.

  comment

Groups, Rings and Fields

• A3.4

  Groups, Rings and Fields | Part II, 2002

  (i) What does it mean for a ring to be Noetherian? State Hilbert's Basis Theorem. Give an example of a Noetherian ring which is not a principal ideal domain.

  (ii) Prove Hilbert's Basis Theorem.

  Is it true that if the ring $R[X]$ is Noetherian, then so is $R ?$

  comment

Hilbert Spaces

• B3.8

  Hilbert Spaces | Part II, 2002

  Let $H$ be an infinite-dimensional, separable Hilbert space. Let $T$ be a compact linear operator on $H$, and let $\lambda$ be a non-zero, approximate eigenvalue of $T$. Prove that $\lambda$ is an eigenvalue, and that the corresponding eigenspace $E_{\lambda}(T)=\{x \in H: T x=\lambda x\}$ is finite-dimensional.

  Let $S$ be a compact, self-adjoint operator on $H$. Prove that there is an orthonormal basis $\left(e_{n}\right)_{n \geqslant 0}$ of $H$, and a sequence $\left(\lambda_{n}\right)_{n \geqslant 0}$ in $\mathbb{C}$, such that (i) $S e_{n}=\lambda_{n} e_{n}(n \geqslant 0)$ and (ii) $\lambda_{n} \rightarrow 0$ as $n \rightarrow \infty$.

  Now let $S$ be compact, self-adjoint and injective. Let $R$ be a bounded self-adjoint operator on $H$ such that $R S=S R$. Prove that $H$ has an orthonormal basis $\left(e_{n}\right)_{n \geqslant 1}$, where, for every $n, e_{n}$ is an eigenvector, both of $S$ and of $R$.

  [You may assume, without proof, results about self-adjoint operators on finite-dimensional spaces.]

  comment

Logic, Computation and Set Theory

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2002

  (i) Explain briefly what is meant by the terms register machine and computable function.

  Let $u$ be the universal computable function $u(m, n)=f_{m}(n)$ and $s$ a total computable function with $f_{s(m, n)}(k)=f_{m}(n, k)$. Here $f_{m}(n)$ and $f_{m}(n, k)$ are the unary and binary functions computed by the $m$-th register machine program $P_{m}$. Suppose $h: \mathbb{N} \rightarrow \mathbb{N}$ is a total computable function. By considering the function

  $$g(m, n)=u(h(s(m, m)), n)$$

  show that there is a number $a$ such that $f_{a}=f_{h(a)}$.

  (ii) Let $P$ be the set of all partial functions $\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$. Consider the mapping $\Phi: P \rightarrow P$ defined by

  $$\Phi(g)(m, n)= \begin{cases}n+1 & \text { if } m=0, \\ g(m-1,1) & \text { if } m>0, n=0 \text { and } g(m-1,1) \text { defined } \\ g(m-1, g(m, n-1)) & \text { if } m n>0 \text { and } g(m-1, g(m, n-1)) \text { defined }, \\ \text { undefined } & \text { otherwise. }\end{cases}$$

  (a) Show that any fixed point of $\Phi$ is a total function $\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$. Deduce that $\Phi$ has a unique fixed point.

  [The Bourbaki- Witt Theorem may be assumed if stated precisely.]

  (b) It follows from standard closure properties of the computable functions that there is a computable function $\psi$ such that

  $$\psi(p, m, n)=\Phi\left(f_{p}\right)(m, n) .$$

  Assuming this, show that there is a total computable function $h$ such that

  $$\Phi\left(f_{p}\right)=f_{h(p)} \text { for all } p .$$

  Deduce that the fixed point of $\Phi$ is computable.

  comment

Markov Chains

• A3.1 B3.1

  Markov Chains | Part II, 2002

  (i) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ on $\{1,2,3,4,5,6,7\}$ with generator matrix

  $$Q=\left(\begin{array}{rrrrrrr} -6 & 2 & 0 & 0 & 0 & 4 & 0 \\ 2 & -3 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & -5 & 1 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 2 & 0 & -6 & 0 & 2 \\ 1 & 2 & 0 & 0 & 0 & -3 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & -2 \end{array}\right)$$

  Compute the probability, starting from state 3 , that $X_{t}$ hits state 2 eventually.

  Deduce that

  $$\lim _{t \rightarrow \infty} \mathbb{P}\left(X_{t}=2 \mid X_{0}=3\right)=\frac{4}{15}$$

  [Justification of standard arguments is not expected.]

  (ii) A colony of cells contains immature and mature cells. Each immature cell, after an exponential time of parameter 2, becomes a mature cell. Each mature cell, after an exponential time of parameter 3, divides into two immature cells. Suppose we begin with one immature cell and let $n(t)$ denote the expected number of immature cells at time $t$. Show that

  $$n(t)=\left(4 e^{t}+3 e^{-6 t}\right) / 7$$

  comment

Mathematical Methods

• A3.17

  Mathematical Methods | Part II, 2002

  (i) State the Fredholm alternative for Fredholm integral equations of the second kind.

  Show that the integral equation

  $$\phi(x)-\lambda \int_{0}^{1}(x+t) \phi(t) d t=f(x), \quad 0 \leqslant x \leqslant 1$$

  where $f$ is a continuous function, has a unique solution for $\phi$ if $\lambda \neq-6 \pm 4 \sqrt{3}$. Derive this solution.

  (ii) Describe the WKB method for finding approximate solutions $f(x)$ of the equation

  $$\frac{d^{2} f(x)}{d x^{2}}+q(\epsilon x) f(x)=0$$

  where $q$ is an arbitrary non-zero, differentiable function and $\epsilon$ is a small parameter. Obtain these solutions in terms of an exponential with slowly varying exponent and slowly varying amplitude.

  Hence, by means of a suitable change of independent variable, find approximate solutions $w(t)$ of the equation

  $$\frac{d^{2} w}{d t^{2}}+\lambda^{2} t w=0$$

  in $t>0$, where $\lambda$ is a large parameter.

  comment

Methods of Mathematical Physics

• B3.19

  Methods of Mathematical Physics | Part II, 2002

  Show that the equation

  $$z w^{\prime \prime}+w^{\prime}+(\lambda-z) w=0$$

  has solutions of the form

  $$w(z)=\int_{\gamma}(t-1)^{(\lambda-1) / 2}(t+1)^{-(\lambda+1) / 2} e^{z t} d t$$

  Give examples of possible choices of $\gamma$ to provide two independent solutions, assuming $\operatorname{Re}(z)>0$. Distinguish between the cases $\operatorname{Re} \lambda>-1$ and $\operatorname{Re} \lambda<1$. Comment on the case $-1<\operatorname{Re} \lambda<1$ and on the case that $\lambda$ is an odd integer.

  Show that, if $\operatorname{Re} \lambda<1$, there is a solution $w_{1}(z)$ that is bounded as $z \rightarrow+\infty$, and that, in this limit,

  $$w_{1}(z) \sim A e^{-z} z^{(\lambda-1) / 2}\left(1-\frac{(1-\lambda)^{2}}{8 z}\right),$$

  where $A$ is a constant.

  comment

Nonlinear Waves

• A3.18

  Nonlinear Waves | Part II, 2002

  (i) Show that the equation

  $$\frac{\partial \phi}{\partial t}-\frac{\partial^{2} \phi}{\partial x^{2}}+1-\phi^{2}=0$$

  has two solutions which are independent of both $x$ and $t$. Show that one of these is linearly stable. Show that the other solution is linearly unstable, and find the range of wavenumbers that exhibit the instability.

  Sketch the nonlinear evolution of the unstable solution after it receives a small, smooth, localized perturbation in the direction towards the stable solution.

  (ii) Show that the equations

  $$\begin{array}{r} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial x}=e^{-u+v} \\ -\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}=e^{-u-v} \end{array}$$

  are a Bäcklund pair for the equations

  $$\frac{\partial^{2} u}{\partial x \partial y}=e^{-2 u}, \quad \frac{\partial^{2} v}{\partial x \partial y}=0$$

  By choosing $v$ to be a suitable constant, and using the Bäcklund pair, find a solution of the equation

  $$\frac{\partial^{2} u}{\partial x \partial y}=e^{-2 u}$$

  which is non-singular in the region $y<4 x$ of the $(x, y)$ plane and has the value $u=0$ at $x=\frac{1}{2}, y=0$.

  comment

Number Theory

• A3.9

  Number Theory | Part II, 2002

  (i) Let $\pi(x)$ denote the number of primes $\leqslant x$, where $x$ is a positive real number. State and prove Legendre's formula relating $\pi(x)$ to $\pi(\sqrt{x})$. Use this formula to compute $\pi(100)-\pi(10) .$

  (ii) Let $\zeta(s)=\sum_{n=1}^{\infty} n^{-s}$, where $s$ is a real number greater than 1 . Prove the following two assertions rigorously, assuming always that $s>1$. (a) $\zeta(s)=\prod_{p}\left(1-p^{-s}\right)^{-1}$, where the product is taken over all primes $p$; (b) $\zeta(s)=\frac{1}{1-2^{1-s}} \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{s}}$.

  Explain why (b) enables us to define $\zeta(s)$ for $0<s<1$. Deduce from (b) that $\lim _{s \rightarrow 1}(s-1) \zeta(s)=1$.

  comment

Numerical Analysis

• A3.19 B3.20

  Numerical Analysis | Part II, 2002

  (i) Determine the order of the multistep method

  $$\mathbf{y}_{n+2}-(1+\alpha) \mathbf{y}_{n+1}+\alpha \mathbf{y}_{n}=h\left[\frac{1}{12}(5+\alpha) \mathbf{f}_{n+2}+\frac{2}{3}(1-\alpha) \mathbf{f}_{n+1}-\frac{1}{12}(1+5 \alpha) \mathbf{f}_{n}\right]$$

  for the solution of ordinary differential equations for different choices of $\alpha$ in the range $-1 \leqslant \alpha \leqslant 1$.

  (ii) Prove that no such choice of $\alpha$ results in a method whose linear stability domain includes the interval $(-\infty, 0)$.

  comment

Optimization and Control

• B3.14

  Optimization and Control | Part II, 2002

  Consider a scalar system with $x_{t+1}=\left(x_{t}+u_{t}\right) \xi_{t}$, where $\xi_{0}, \xi_{1}, \ldots$ is a sequence of independent random variables, uniform on the interval $[-a, a]$, with $a \leqslant 1$. We wish to choose $u_{0}, \ldots, u_{h-1}$ to minimize the expected value of

  $$\sum_{t=0}^{h-1}\left(c+x_{t}^{2}+u_{t}^{2}\right)+3 x_{h}^{2},$$

  where $u_{t}$ is chosen knowing $x_{t}$ but not $\xi_{t}$. Prove that the minimal expected cost can be written $V_{h}\left(x_{0}\right)=h c+x_{0}^{2} \Pi_{h}$ and derive a recurrence for calculating $\Pi_{1}, \ldots, \Pi_{h}$.

  How does your answer change if $u_{t}$ is constrained to lie in the set $\mathcal{U}\left(x_{t}\right)=\{u:$ $\left.\left|u+x_{t}\right|<\left|x_{t}\right|\right\} ?$

  Consider a stopping problem for which there are two options in state $x_{t}, t \geqslant 0$ :

  (1) stop: paying a terminal cost $3 x_{t}^{2}$; no further costs are incurred;

  (2) continue: choosing $u_{t} \in \mathcal{U}\left(x_{t}\right)$, paying $c+u_{t}^{2}+x_{t}^{2}$, and moving to state $x_{t+1}=\left(x_{t}+u_{t}\right) \xi_{t} .$

  Consider the problem of minimizing total expected cost subject to the constraint that no more than $h$ continuation steps are allowed. Suppose $a=1$. Show that an optimal policy stops if and only if either $h$ continuation steps have already been taken or $x^{2} \leqslant 2 c / 3$.

  [Hint: Use induction on $h$ to show that a one-step-look-ahead rule is optimal. You should not need to find the optimal $u_{t}$ for the continuation steps.]

  comment

Partial Differential Equations

• B3.18

  Partial Differential Equations | Part II, 2002

  Define the Schwartz space $\mathcal{S}\left(\mathbb{R}^{n}\right)$ and the space of tempered distributions $\mathcal{S}^{\prime}\left(\mathbb{R}^{n}\right)$. State the Fourier inversion theorem for the Fourier transform of a Schwartz function.

  Consider the initial value problem:

  $$\begin{gathered} \frac{\partial^{2} u}{\partial t^{2}}-\Delta u+u=0, x \in \mathbb{R}^{n}, 0<t<\infty \\ u(0, x)=f(x), \quad \frac{\partial u}{\partial t}(0, x)=0 \end{gathered}$$

  for $f$ in the Schwartz space $\mathcal{S}\left(\mathbb{R}^{n}\right)$.

  Show that the solution can be written as

  $$u(t, x)=(2 \pi)^{-n / 2} \int_{\mathbb{R}^{n}} e^{i x \cdot \xi} \hat{u}(t, \xi) d \xi,$$

  where

  $$\hat{u}(t, \xi)=\cos \left(t \sqrt{1+|\xi|^{2}}\right) \hat{f}(\xi)$$

  and

  $$\hat{f}(\xi)=(2 \pi)^{-n / 2} \int_{\mathbb{R}^{n}} e^{-i x \cdot \xi} f(x) d x .$$

  State the Plancherel-Parseval theorem and hence deduce that

  $$\int_{\mathbb{R}^{n}}|u(t, x)|^{2} d x \leq \int_{\mathbb{R}^{n}}|f(x)|^{2} d x .$$

  comment

Principles of Dynamics

• A3.2

  Principles of Dynamics | Part II, 2002

  (i) Show that Hamilton's equations follow from the variational principle

  $$\delta \int_{t_{1}}^{t_{2}}[p \dot{q}-H(q, p, t)] d t=0$$

  under the restrictions $\delta q\left(t_{1}\right)=\delta q\left(t_{2}\right)=\delta p\left(t_{1}\right)=\delta p\left(t_{2}\right)=0$. Comment on the difference from the variational principle for Lagrange's equations.

  (ii) Suppose we transform from $p$ and $q$ to $p^{\prime}=p^{\prime}(q, p, t)$ and $q^{\prime}=q^{\prime}(q, p, t)$, with

  $$p^{\prime} \dot{q}^{\prime}-H^{\prime}=p \dot{q}-H+\frac{\mathrm{d}}{\mathrm{d} t} F\left(q, p, q^{\prime}, p^{\prime}, t\right)$$

  where $H^{\prime}$ is the new Hamiltonian. Show that $p^{\prime}$ and $q^{\prime}$ obey Hamilton's equations with Hamiltonian $H^{\prime}$.

  Show that the time independent generating function $F=F_{1}\left(q, q^{\prime}\right)=q^{\prime} / q$ takes the Hamiltonian

  $$H=\frac{1}{2 q^{2}}+\frac{1}{2} p^{2} q^{4}$$

  to harmonic oscillator form. Show that $q^{\prime}$ and $p^{\prime}$ obey the Poisson bracket relation

  $$\left\{q^{\prime}, p^{\prime}\right\}=1$$

  comment

Principles of Statistics

• A3.12 B3.15

  Principles of Statistics | Part II, 2002

  (i) Describe in detail how to perform the Wald, score and likelihood ratio tests of a simple null hypothesis $H_{0}: \theta=\theta_{0}$ given a random sample $X_{1}, \ldots, X_{n}$ from a regular oneparameter density $f(x ; \theta)$. In each case you should specify the asymptotic null distribution of the test statistic.

  (ii) Let $X_{1}, \ldots, X_{n}$ be an independent, identically distributed sample from a distribution $F$, and let $\hat{\theta}\left(X_{1}, \ldots, X_{n}\right)$ be an estimator of a parameter $\theta$ of $F$.

  Explain what is meant by: (a) the empirical distribution function of the sample; (b) the bootstrap estimator of the bias of $\hat{\theta}$, based on the empirical distribution function. Explain how a bootstrap estimator of the distribution function of $\hat{\theta}-\theta$ may be used to construct an approximate $1-\alpha$ confidence interval for $\theta$.

  Suppose the parameter of interest is $\theta=\mu^{2}$, where $\mu$ is the mean of $F$, and the estimator is $\hat{\theta}=\bar{X}^{2}$, where $\bar{X}=n^{-1} \sum_{i=1}^{n} X_{i}$ is the sample mean.

  Derive an explicit expression for the bootstrap estimator of the bias of $\hat{\theta}$ and show that it is biased as an estimator of the true bias of $\hat{\theta}$.

  Let $\hat{\theta}_{i}$ be the value of the estimator $\hat{\theta}\left(X_{1}, \ldots, X_{i-1}, X_{i+1}, \ldots, X_{n}\right)$ computed from the sample of size $n-1$ obtained by deleting $X_{i}$ and let $\hat{\theta} . n^{-1} \sum_{i=1}^{n} \hat{\theta}_{i}$. The jackknife estimator of the bias of $\hat{\theta}$ is

  $$b_{J}=(n-1)(\hat{\theta} .-\hat{\theta}) .$$

  Derive the jackknife estimator $b_{J}$ for the case $\hat{\theta}=\bar{X}^{2}$, and show that, as an estimator of the true bias of $\hat{\theta}$, it is unbiased.

  comment

Probability and Measure

• B3.12

  Probability and Measure | Part II, 2002

  Derive the characteristic function of a real-valued random variable which is normally distributed with mean $\mu$ and variance $\sigma^{2}$. What does it mean to say that an $\mathbb{R}^{n}$-valued random variable has a multivariate Gaussian distribution? Prove that the distribution of such a random variable is determined by its $\left(\mathbb{R}^{n}\right.$-valued) mean and its covariance matrix.

  Let $X$ and $Y$ be random variables defined on the same probability space such that $(X, Y)$ has a Gaussian distribution. Show that $X$ and $Y$ are independent if and only if $\operatorname{cov}(X, Y)=0$. Show that, even if they are not independent, one may always write $X=a Y+Z$ for some constant $a$ and some random variable $Z$ independent of $Y$.

  [The inversion theorem for characteristic functions and standard results about independence may be assumed.]

  comment

Representation Theory

• B3.5

  Representation Theory | Part II, 2002

  Let $G$ be a finite group acting on a finite set $X$. Define the permutation representation $(\rho, \mathbb{C}[X])$ of $G$ and compute its character $\pi_{X}$. Prove that $\left\langle\pi_{X}, 1_{G}\right\rangle_{G}$ equals the number of orbits of $G$ on $X$. If $G$ acts also on the finite set $Y$, with character $\pi_{Y}$, show that $\left\langle\pi_{X}, \pi_{Y}\right\rangle_{G}$ equals the number of orbits of $G$ on $X \times Y$.

  Now let $G$ be the symmetric group $S_{n}$ acting naturally on the set $X=\{1, \ldots, n\}$, and let $X_{r}$ be the set of all $r$-element subsets of $X$. Let $\pi_{r}$ be the permutation character of $G$ on $X_{r}$. Prove that

  $$\left\langle\pi_{k}, \pi_{\ell}\right\rangle_{G}=\ell+1 \text { for } 0 \leqslant \ell \leqslant k \leqslant n / 2$$

  Deduce that the class functions

  $$\chi_{r}=\pi_{r}-\pi_{r-1}$$

  are irreducible characters of $S_{n}$, for $1 \leqslant r \leqslant n / 2$.

  comment

Riemann Surfaces

• B3.9

  Riemann Surfaces | Part II, 2002

  Let $\alpha_{1}, \alpha_{2}$ be two non-zero complex numbers with $\alpha_{1} / \alpha_{2} \notin \mathbb{R}$. Let $L$ be the lattice $\mathbb{Z} \alpha_{1} \oplus \mathbb{Z} \alpha_{2} \subset \mathbb{C}$. A meromorphic function $f$ on $\mathbb{C}$ is elliptic if $f(z+\lambda)=f(z)$, for all $z \in \mathbb{C}$ and $\lambda \in L$. The Weierstrass functions $\wp(z), \zeta(z), \sigma(z)$ are defined by the following properties:

  • $\wp(z)$ is elliptic, has double poles at the points of $L$ and no other poles, and $\wp(z)=$ $1 / z^{2}+O\left(z^{2}\right)$ near 0

  • $\zeta^{\prime}(z)=-\wp(z)$, and $\zeta(z)=1 / z+O\left(z^{3}\right)$ near 0 ;

  • $\sigma(z)$ is odd, and $\sigma^{\prime}(z) / \sigma(z)=\zeta(z)$, and $\sigma(z) / z \rightarrow 1$ as $z \rightarrow 0$.

  Prove the following

  (a) $\wp$, and hence $\zeta$ and $\sigma$, are uniquely determined by these properties. You are not expected to prove the existence of $\wp, \zeta, \sigma$, and you may use Liouville's theorem without proof.

  (b) $\zeta\left(z+\alpha_{i}\right)=\zeta(z)+2 \eta_{i}$, and $\sigma\left(z+\alpha_{i}\right)=k_{i} e^{2 \eta_{i} z} \sigma(z)$, for some constants $\eta_{i}, k_{i}(i=1,2)$.

  (c) $\sigma$ is holomorphic, has simple zeroes at the points of $L$, and has no other zeroes.

  (d) Given $a_{1}, \ldots, a_{n}$ and $b_{1}, \ldots, b_{n}$ in $\mathbb{C}$ with $a_{1}+\ldots+a_{n}=b_{1}+\ldots+b_{n}$, the function

  $$\frac{\sigma\left(z-a_{1}\right) \cdots \sigma\left(z-a_{n}\right)}{\sigma\left(z-b_{1}\right) \cdots \sigma\left(z-b_{n}\right)}$$

  is elliptic.

  (e) $\wp(u)-\wp(v)=-\frac{\sigma(u+v) \sigma(u-v)}{\sigma^{2}(u) \sigma^{2}(v)}$.

  (f) Deduce from (e), or otherwise, that $\frac{1}{2} \frac{\wp^{\prime}(u)-\wp^{\prime}(v)}{\wp(u)-\wp(v)}=\zeta(u+v)-\zeta(u)-\zeta(v)$.

  comment

Statistical Physics

• B3.22

  Statistical Physics | Part II, 2002

  A system consisting of non-interacting bosons has single-particle levels uniquely labelled by $r$ with energies $\epsilon_{r}, \epsilon_{r} \geq 0$. Show that the free energy in the grand canonical ensemble is

  $$F=k T \sum_{r} \log \left(1-e^{-\beta\left(\epsilon_{r}-\mu\right)}\right) .$$

  What is the maximum value for $\mu$ ?

  A system of $N$ bosons in a large volume $V$ has one energy level of energy zero and a large number $M \gg 1$ of energy levels of the same energy $\epsilon$, where $M$ takes the form $M=A V$ with $A$ a positive constant. What are the dimensions of $A ?$

  Show that the free energy is

  $$F=k T\left(\log \left(1-e^{\beta \mu}\right)+A V \log \left(1-e^{-\beta(\epsilon-\mu)}\right)\right)$$

  The numbers of particles with energies $0, \epsilon$ are respectively $N_{0}, N_{\epsilon}$. Write down expressions for $N_{0}, N_{\epsilon}$ in terms of $\mu$.

  At temperature $T$ what is the maximum number of bosons $N_{\epsilon}^{\max }$ in the normal phase (the state with energy $\epsilon$ )? Explain what happens when $N>N_{\epsilon}^{\max }$.

  Given $N$ and $T$ calculate the transition temperature $T_{B}$ at which Bose condensation occurs.

  For $T>T_{B}$ show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. What is the value of $\mu$ for $T<T_{B}$ ?

  Calculate the mean energy $E$ for (a) $T>T_{B}$ (b) $T<T_{B}$, and show that the heat capacity of the system at constant volume is

  $$C_{V}=\left\{\begin{array}{cl} \frac{1}{k T^{2}} \frac{A V \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B} \end{array}\right.$$

  comment

Statistical Physics and Cosmology

• A3.14

  Statistical Physics and Cosmology | Part II, 2002

  (i) Write down the first law of thermodynamics for the change $d U$ in the internal energy $U(N, V, S)$ of a gas of $N$ particles in a volume $V$ with entropy $S$.

  Given that

  $$P V=(\gamma-1) U,$$

  where $P$ is the pressure, use the first law to show that $P V^{\gamma}$ is constant at constant $N$ and

  Write down the Boyle-Charles law for a non-relativistic ideal gas and hence deduce that the temperature $T$ is proportional to $V^{1-\gamma}$ at constant $N$ and $S$.

  State the principle of equipartition of energy and use it to deduce that

  $$U=\frac{3}{2} N k T$$

  Hence deduce the value of $\gamma$. Show that this value of $\gamma$ is such that the ratio $E_{i} / k T$ is unchanged by a change of volume at constant $N$ and $S$, where $E_{i}$ is the energy of the $i$-th one particle eigenstate of a non-relativistic ideal gas.

  (ii) A classical gas of non-relativistic particles of mass $m$ at absolute temperature $T$ and number density $n$ has a chemical potential

  $$\mu=m c^{2}-k T \ln \left(\frac{g_{s}}{n}\left(\frac{m k T}{2 \pi \hbar^{2}}\right)^{\frac{3}{2}}\right)$$

  where $g_{s}$ is the particle's spin degeneracy factor. What condition on $n$ is needed for the validity of this formula and why?

  Thermal and chemical equilibrium between two species of non-relativistic particles $a$ and $b$ is maintained by the reaction

  $$a+\alpha \leftrightarrow b+\beta$$

  where $\alpha$ and $\beta$ are massless particles with zero chemical potential. Given that particles $a$ and $b$ have masses $m_{a}$ and $m_{b}$ respectively, but equal spin degeneracy factors, find the number density ratio $n_{a} / n_{b}$ as a function of $m_{a}, m_{b}$ and $T$. Given that $m_{a}>m_{b}$ but $m_{a}-m_{b} \ll m_{b}$ show that

  $$\frac{n_{a}}{n_{b}} \approx f\left(\frac{\left(m_{a}-m_{b}\right) c^{2}}{k T}\right)$$

  for some function $f$ which you should determine.

  Explain how a reaction of the above type is relevant to a determination of the neutron to proton ratio in the early universe and why this ratio does not fall rapidly to zero as the universe cools. Explain briefly the process of primordial nucleosynthesis by which neutrons are converted into stable helium nuclei. Let

  $$Y_{H e}=\frac{\rho_{H e}}{\rho}$$

  be the fraction of the universe that ends up in helium. Compute $Y_{H e}$ as a function of the ratio $r=n_{a} / n_{b}$ at the time of nucleosynthesis.

  comment

Stochastic Financial Models

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2002

  (i) Explain briefly what it means to say that a stochastic process $\left\{W_{t}, t \geqslant 0\right\}$ is a standard Brownian motion.

  Let $\left\{W_{t}, t \geqslant 0\right\}$ be a standard Brownian motion and let $a, b$ be real numbers. What condition must $a$ and $b$ satisfy to ensure that the process $e^{a W_{t}+b t}$ is a martingale? Justify your answer carefully.

  (ii) At the beginning of each of the years $r=0,1, \ldots, n-1$ an investor has income $X_{r}$, of which he invests a proportion $\rho_{r}, 0 \leqslant \rho_{r} \leqslant 1$, and consumes the rest during the year. His income at the beginning of the next year is

  $$X_{r+1}=X_{r}+\rho_{r} X_{r} W_{r}$$

  where $W_{0}, \ldots, W_{n-1}$ are independent positive random variables with finite means and $X_{0} \geqslant 0$ is a constant. He decides on $\rho_{r}$ after he has observed both $X_{r}$ and $W_{r}$ at the beginning of year $r$, but at that time he does not have any knowledge of the value of $W_{s}$, for any $s>r$. The investor retires in year $n$ and consumes his entire income during that year. He wishes to determine the investment policy that maximizes his expected total consumption

  $$\mathbb{E}\left[\sum_{r=0}^{n-1}\left(1-\rho_{r}\right) X_{r}+X_{n}\right]$$

  Prove that the optimal policy may be expressed in terms of the numbers $b_{0}, b_{1}, \ldots$, $b_{n}$ where $b_{n}=1, b_{r}=b_{r+1}+\mathbb{E} \max \left(b_{r+1} W_{r}, 1\right)$, for $r<n$, and determine the optimal expected total consumption.

  comment

Symmetries and Groups in Physics

• A3.15

  Symmetries and Groups in Physics | Part II, 2002

  (i) Let $D_{6}$ denote the symmetry group of rotations and reflections of a regular hexagon. The elements of $D_{6}$ are given by $\left\{e, c, c^{2}, c^{3}, c^{4}, c^{5}, b, b c, b c^{2}, b c^{3}, b c^{4}, b c^{5}\right\}$ with $c^{6}=b^{2}=e$ and $c b=b c^{5}$. The conjugacy classes of $D_{6}$ are $\{e\},\left\{c, c^{5}\right\},\left\{c^{2}, c^{4}\right\},\left\{c^{3}\right\},\left\{b, b c^{2}, b c^{4}\right\}$ and $\left\{b c, b c^{3}, b c^{5}\right\}$.

  Show that the character table of $D_{6}$ is

  \begin{tabular}{l|rrrrrr} $D_{6}$ & $e$ & $\left\{c, c^{5}\right\}$ & $\left\{c^{2}, c^{4}\right\}$ & $\left\{c^{3}\right\}$ & $\left\{b, b c^{2}, b c^{4}\right\}$ & $\left\{b c, b c^{3}, b c^{5}\right\}$ \ \hline$\chi_{1}$ & 1 & 1 & 1 & 1 & 1 & 1 \ $\chi_{2}$ & 1 & 1 & 1 & 1 & $-1$ & $-1$ \ $\chi_{3}$ & 1 & $-1$ & 1 & $-1$ & 1 & $-1$ \ $\chi_{4}$ & 1 & $-1$ & 1 & $-1$ & $-1$ & 1 \ $\chi_{5}$ & 2 & 1 & $-1$ & $-2$ & 0 & 0 \ $\chi_{6}$ & 2 & $-1$ & $-1$ & 2 & 0 & 0 \end{tabular}

  (ii) Show that the character of an $S O(3)$ rotation with angle $\theta$ in the $2 l+1$ dimensional irreducible representation of $S O(3)$ is given by

  $$\chi_{l}(\theta)=1+2 \cos \theta+2 \cos (2 \theta)+\ldots+2 \cos ((l-1) \theta)+2 \cos (l \theta)$$

  For a hexagonal crystal of atoms find how the degeneracy of the D-wave orbital states $(l=2)$ in the atomic central potential is split by the crystal potential with $D_{6}$ symmetry and give the new degeneracies.

  By using the fact that $D_{3}$ is isomorphic to $D_{6} /\left\{e, c^{3}\right\}$, or otherwise, find the degeneracies of eigenstates if the hexagonal symmetry is broken to the subgroup $D_{3}$ by a deformation. The introduction of a magnetic field further reduces the symmetry to $C_{3}$. What will the degeneracies of the energy eigenstates be now?

  comment

Transport Processes

• A3.16

  Transport Processes | Part II, 2002

  (i) A layer of fluid of depth $h(x, t)$, density $\rho$ and viscosity $\mu$ sits on top of a rigid horizontal plane at $y=0$. Gravity $g$ acts vertically and surface tension is negligible.

  Assuming that the horizontal velocity component $u$ and pressure $p$ satisfy the lubrication equations

  $$\begin{aligned} &0=-p_{x}+\mu u_{y y} \\ &0=-p_{y}-\rho g, \end{aligned}$$

  together with appropriate boundary conditions at $y=0$ and $y=h$ (which should be stated), show that $h$ satisfies the partial differential equation

  $$h_{t}=\frac{g}{3 \nu}\left(h^{3} h_{x}\right)_{x},$$

  where $\nu=\mu / \rho$.

  (ii) A two-dimensional blob of the above fluid has fixed area $A$ and time-varying width $2 X(t)$, such that

  $$A=\int_{-X(t)}^{X(t)} h(x, t) d x$$

  The blob spreads under gravity.

  Use scaling arguments to show that, after an initial transient, $X(t)$ is proportional to $t^{1 / 5}$ and $h(0, t)$ is proportional to $t^{-1 / 5}$. Hence show that equation $(*)$ of Part (i) has a similarity solution of the form

  $$h(x, t)=\left(\frac{A^{2} \nu}{g t}\right)^{1 / 5} H(\xi), \quad \text { where } \quad \xi=\frac{x}{\left(A^{3} g t / \nu\right)^{1 / 5}}$$

  and find the differential equation satisfied by $H(\xi)$.

  Deduce that

  $$H= \begin{cases}{\left[\frac{9}{10}\left(\xi_{0}^{2}-\xi^{2}\right)\right]^{1 / 3}} & \text { in }-\xi_{0}<\xi<\xi_{0} \\ 0 & \text { in }|\xi|>\xi_{0}\end{cases}$$

  where

  $$X(t)=\xi_{0}\left(\frac{A^{3} g t}{\nu}\right)^{1 / 5}$$

  Express $\xi_{0}$ in terms of the integral

  $$I=\int_{-1}^{1}\left(1-u^{2}\right)^{1 / 3} d u$$

  comment

Waves in Fluid and Solid Media

• B3.25

  Waves in Fluid and Solid Media | Part II, 2002

  Consider the equation

  $$\frac{\partial \phi}{\partial t}+\frac{\partial \phi}{\partial x}-\frac{\partial^{3} \phi}{\partial x^{3}}=0$$

  Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$. Do the wave crests move faster or slower than a packet of waves?

  Write down the solution with initial value

  $$\phi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  where $A(k)$ is real and $A(-k)=A(k)$.

  Use the method of stationary phase to obtain an approximation to $\phi(x, t)$ for large $t$, with $x / t$ having the constant value $V$. Explain, using the notion of group velocity, the constraint that must be placed on $V$.

  comment