(i) Two particles with angular momenta $j_{1}, j_{2}$ and basis states $\left|j_{1} m_{1}\right\rangle,\left|j_{2} m_{2}\right\rangle$ are combined to give total angular momentum $j$ and basis states $|j m\rangle$. State the possible values of $j, m$ and show how a state with $j=m=j_{1}+j_{2}$ can be constructed. Briefly describe, for a general allowed value of $j$, what the Clebsch-Gordan coefficients are.

(ii) If the angular momenta $j_{1}$ and $j_{2}$ are both 1 show that the combined state $|20\rangle$ is

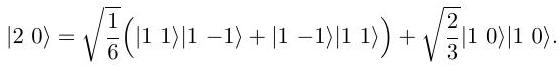
Determine the corresponding expressions for the combined states $\left|\begin{array}{lll}1 & 0\rangle\end{array}\right\rangle$ and $|0 \quad 0\rangle$, assuming that they are respectively antisymmetric and symmetric under interchange of the two particles.

If the combined system is in state $|0 \quad 0\rangle$ what is the probability that measurements of the $z$-component of angular momentum for either constituent particle will give the value of 1 ?

$\left[\right.$ Hint: $\left.\quad J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .\right]$