Part IB, 2019, Paper 4

Analysis II

• Paper 4, Section I, E

  Analysis II | Part IB, 2019

  Let $A \subset \mathbb{R}$. What does it mean to say that a sequence of real-valued functions on $A$ is uniformly convergent?

  (i) If a sequence $\left(f_{n}\right)$ of real-valued functions on $A$ converges uniformly to $f$, and each $f_{n}$ is continuous, must $f$ also be continuous?

  (ii) Let $f_{n}(x)=e^{-n x}$. Does the sequence $\left(f_{n}\right)$ converge uniformly on $[0,1]$ ?

  (iii) If a sequence $\left(f_{n}\right)$ of real-valued functions on $[-1,1]$ converges uniformly to $f$, and each $f_{n}$ is differentiable, must $f$ also be differentiable?

  Give a proof or counterexample in each case.

  comment

• Paper 4, Section II, E

  Analysis II | Part IB, 2019

  (a) (i) Show that a compact metric space must be complete.

  (ii) If a metric space is complete and bounded, must it be compact? Give a proof or counterexample.

  (b) A metric space $(X, d)$ is said to be totally bounded if for all $\epsilon>0$, there exists $N \in \mathbb{N}$ and $\left\{x_{1}, \ldots, x_{N}\right\} \subset X$ such that $X=\bigcup_{i=1}^{N} B_{\epsilon}\left(x_{i}\right) .$

  (i) Show that a compact metric space is totally bounded.

  (ii) Show that a complete, totally bounded metric space is compact.

  [Hint: If $\left(x_{n}\right)$ is Cauchy, then there is a subsequence $\left(x_{n_{j}}\right)$ such that

  $$\left.\sum_{j} d\left(x_{n_{j+1}}, x_{n_{j}}\right)<\infty .\right]$$

  (iii) Consider the space $C[0,1]$ of continuous functions $f:[0,1] \rightarrow \mathbb{R}$, with the metric

  $$d(f, g)=\min \left\{\int_{0}^{1}|f(t)-g(t)| d t, 1\right\} .$$

  Is this space compact? Justify your answer.

  comment

Complex Analysis

• Paper 4, Section I, $4 \mathbf{F}$

  Complex Analysis | Part IB, 2019

  State the Cauchy Integral Formula for a disc. If $f: D\left(z_{0} ; r\right) \rightarrow \mathbb{C}$ is a holomorphic function such that $|f(z)| \leqslant\left|f\left(z_{0}\right)\right|$ for all $z \in D\left(z_{0} ; r\right)$, show using the Cauchy Integral Formula that $f$ is constant.

  comment

Complex Methods

• Paper 4, Section II, D

  Complex Methods | Part IB, 2019

  (a) Using the Bromwich contour integral, find the inverse Laplace transform of $1 / s^{2}$.

  The temperature $u(r, t)$ of mercury in a spherical thermometer bulb $r \leqslant a$ obeys the radial heat equation

  $$\frac{\partial u}{\partial t}=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r u)$$

  with unit diffusion constant. At $t=0$ the mercury is at a uniform temperature $u_{0}$ equal to that of the surrounding air. For $t>0$ the surrounding air temperature lowers such that at the edge of the thermometer bulb

  $$\left.\frac{1}{k} \frac{\partial u}{\partial r}\right|_{r=a}=u_{0}-u(a, t)-t$$

  where $k$ is a constant.

  (b) Find an explicit expression for $U(r, s)=\int_{0}^{\infty} e^{-s t} u(r, t) d t$.

  (c) Show that the temperature of the mercury at the centre of the thermometer bulb at late times is

  $$u(0, t) \approx u_{0}-t+\frac{a}{3 k}+\frac{a^{2}}{6}$$

  [You may assume that the late time behaviour of $u(r, t)$ is determined by the singular part of $U(r, s)$ at $s=0 .]$

  comment

Electromagnetism

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2019

  Write down Maxwell's Equations for electric and magnetic fields $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$ in the absence of charges and currents. Show that there are solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}, \quad \mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}$$

  if $\mathbf{E}_{0}$ and $\mathbf{k}$ satisfy a constraint and if $\mathbf{B}_{0}$ and $\omega$ are then chosen appropriately.

  Find the solution with $\mathbf{E}_{0}=E(1, i, 0)$, where $E$ is real, and $\mathbf{k}=k(0,0,1)$. Compute the Poynting vector and state its physical significance.

  comment

Fluid Dynamics

• Paper 4, Section II, C

  Fluid Dynamics | Part IB, 2019

  The linear shallow-water equations governing the motion of a fluid layer in the neighbourhood of a point on the Earth's surface in the northern hemisphere are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-g \frac{\partial \eta}{\partial y} \\ \frac{\partial \eta}{\partial t} &=-h\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) \end{aligned}$$

  where $u(x, y, t)$ and $v(x, y, t)$ are the horizontal velocity components and $\eta(x, y, t)$ is the perturbation of the height of the free surface.

  (a) Explain the meaning of the three positive constants $f, g$ and $h$ appearing in the equations above and outline the assumptions made in deriving these equations.

  (b) Show that $\zeta$, the $z$-component of vorticity, satisfies

  $$\frac{\partial \zeta}{\partial t}=-f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)$$

  and deduce that the potential vorticity

  $$q=\zeta-\frac{f}{h} \eta$$

  satisfies

  $$\frac{\partial q}{\partial t}=0$$

  (c) Consider a steady geostrophic flow that is uniform in the latitudinal $(y)$ direction. Show that

  $$\frac{d^{2} \eta}{d x^{2}}-\frac{f^{2}}{g h} \eta=\frac{f}{g} q .$$

  Given that the potential vorticity has the piecewise constant profile

  $$q= \begin{cases}q_{1}, & x<0 \\ q_{2}, & x>0\end{cases}$$

  where $q_{1}$ and $q_{2}$ are constants, and that $v \rightarrow 0$ as $x \rightarrow \pm \infty$, solve for $\eta(x)$ and $v(x)$ in terms of the Rossby radius $R=\sqrt{g h} / f$. Sketch the functions $\eta(x)$ and $v(x)$ in the case $q_{1}>q_{2}$.

  comment

Geometry

• Paper 4, Section II, E

  Geometry | Part IB, 2019

  Let $H=\{x+i y \mid x, y \in \mathbb{R}, y>0\}$ be the upper-half plane with hyperbolic metric $\frac{d x^{2}+d y^{2}}{y^{2}}$. Define the group $P S L(2, \mathbb{R})$, and show that it acts by isometries on $H$. [If you use a generation statement you must carefully state it.]

  (a) Prove that $P S L(2, \mathbb{R})$ acts transitively on the collection of pairs $(l, P)$, where $l$ is a hyperbolic line in $H$ and $P \in l$.

  (b) Let $l^{+} \subset H$ be the imaginary half-axis. Find the isometries of $H$ which fix $l^{+}$ pointwise. Hence or otherwise find all isometries of $H$.

  (c) Describe without proof the collection of all hyperbolic lines which meet $l^{+}$with (signed) angle $\alpha, 0<\alpha<\pi$. Explain why there exists a hyperbolic triangle with angles $\alpha, \beta$ and $\gamma$ whenever $\alpha+\beta+\gamma<\pi$.

  (d) Is this triangle unique up to isometry? Justify your answer. [You may use without proof the fact that Möbius maps preserve angles.]

  comment

Groups, Rings and Modules

• Paper 4, Section I, G

  Groups, Rings and Modules | Part IB, 2019

  Let $G$ be a group and $P$ a subgroup.

  (a) Define the normaliser $N_{G}(P)$.

  (b) Suppose that $K \triangleleft G$ and $P$ is a Sylow $p$-subgroup of $K$. Using Sylow's second theorem, prove that $G=N_{G}(P) K$.

  comment

• Paper 4, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  (a) Define the Smith Normal Form of a matrix. When is it guaranteed to exist?

  (b) Deduce the classification of finitely generated abelian groups.

  (c) How many conjugacy classes of matrices are there in $G L_{10}(\mathbb{Q})$ with minimal polynomial $X^{7}-4 X^{3} ?$

  comment

Linear Algebra

• Paper 4, Section I, F

  Linear Algebra | Part IB, 2019

  What is an eigenvalue of a matrix $A$ ? What is the eigenspace corresponding to an eigenvalue $\lambda$ of $A$ ?

  Consider the matrix

  $$A=\left(\begin{array}{cccc} a a & a b & a c & a d \\ b a & b b & b c & b d \\ c a & c b & c c & c d \\ d a & d b & d c & d d \end{array}\right)$$

  for $(a, b, c, d) \in \mathbb{R}^{4}$ a non-zero vector. Show that $A$ has rank 1 . Find the eigenvalues of $A$ and describe the corresponding eigenspaces. Is $A$ diagonalisable?

  comment

• Paper 4, Section II, F

  Linear Algebra | Part IB, 2019

  If $U$ is a finite-dimensional real vector space with inner product $\langle\cdot, \cdot\rangle$, prove that the linear map $\phi: U \rightarrow U^{*}$ given by $\phi(u)\left(u^{\prime}\right)=\left\langle u, u^{\prime}\right\rangle$ is an isomorphism. [You do not need to show that it is linear.]

  If $V$ and $W$ are inner product spaces and $\alpha: V \rightarrow W$ is a linear map, what is meant by the adjoint $\alpha^{*}$ of $\alpha$ ? If $\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}$ is an orthonormal basis for $V,\left\{f_{1}, f_{2}, \ldots, f_{m}\right\}$ is an orthonormal basis for $W$, and $A$ is the matrix representing $\alpha$ in these bases, derive a formula for the matrix representing $\alpha^{*}$ in these bases.

  Prove that $\operatorname{Im}(\alpha)=\operatorname{Ker}\left(\alpha^{*}\right)^{\perp}$.

  If $w_{0} \notin \operatorname{Im}(\alpha)$ then the linear equation $\alpha(v)=w_{0}$ has no solution, but we may instead search for a $v_{0} \in V$ minimising $\left\|\alpha(v)-w_{0}\right\|^{2}$, known as a least-squares solution. Show that $v_{0}$ is such a least-squares solution if and only if it satisfies $\alpha^{*} \alpha\left(v_{0}\right)=\alpha^{*}\left(w_{0}\right)$. Hence find a least-squares solution to the linear equation

  $$\left(\begin{array}{ll} 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right)=\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right)$$

  comment

Markov Chains

• Paper 4, Section I, H

  Markov Chains | Part IB, 2019

  For a Markov chain $X$ on a state space $S$ with $u, v \in S$, we let $p_{u v}(n)$ for $n \in\{0,1, \ldots\}$ be the probability that $X_{n}=v$ when $X_{0}=u$.

  (a) Let $X$ be a Markov chain. Prove that if $X$ is recurrent at a state $v$, then $\sum_{n=0}^{\infty} p_{v v}(n)=\infty$. [You may use without proof that the number of returns of a Markov chain to a state $v$ when starting from $v$ has the geometric distribution.]

  (b) Let $X$ and $Y$ be independent simple symmetric random walks on $\mathbb{Z}^{2}$ starting from the origin 0 . Let $Z=\sum_{n=0}^{\infty} \mathbf{1}_{\left\{X_{n}=Y_{n}\right\}}$. Prove that $\mathbb{E}[Z]=\sum_{n=0}^{\infty} p_{00}(2 n)$ and deduce that $\mathbb{E}[Z]=\infty$. [You may use without proof that $p_{x y}(n)=p_{y x}(n)$ for all $x, y \in \mathbb{Z}^{2}$ and $n \in \mathbb{N}$, and that $X$ is recurrent at 0.]

  comment

Methods

• Paper 4, Section I, D

  Methods | Part IB, 2019

  Let

  $$g_{\epsilon}(x)=\frac{-2 \epsilon x}{\pi\left(\epsilon^{2}+x^{2}\right)^{2}} .$$

  By considering the integral $\int_{-\infty}^{\infty} \phi(x) g_{\epsilon}(x) d x$, where $\phi$ is a smooth, bounded function that vanishes sufficiently rapidly as $|x| \rightarrow \infty$, identify $\lim _{\epsilon \rightarrow 0} g_{\epsilon}(x)$ in terms of a generalized function.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2019

  (a) Show that the operator

  $$\frac{d^{4}}{d x^{4}}+p \frac{d^{2}}{d x^{2}}+q \frac{d}{d x}+r$$

  where $p(x), q(x)$ and $r(x)$ are real functions, is self-adjoint (for suitable boundary conditions which you need not state) if and only if

  $$q=\frac{d p}{d x}$$

  (b) Consider the eigenvalue problem

  $$\frac{d^{4} y}{d x^{4}}+p \frac{d^{2} y}{d x^{2}}+\frac{d p}{d x} \frac{d y}{d x}=\lambda y$$

  on the interval $[a, b]$ with boundary conditions

  $$y(a)=\frac{d y}{d x}(a)=y(b)=\frac{d y}{d x}(b)=0$$

  Assuming that $p(x)$ is everywhere negative, show that all eigenvalues $\lambda$ are positive.

  (c) Assume now that $p \equiv 0$ and that the eigenvalue problem (*) is on the interval $[-c, c]$ with $c>0$. Show that $\lambda=1$ is an eigenvalue provided that

  $$\cos c \sinh c \pm \sin c \cosh c=0$$

  and show graphically that this condition has just one solution in the range $0<c<\pi$.

  [You may assume that all eigenfunctions are either symmetric or antisymmetric about $x=0 .]$

  comment

Metric and Topological Spaces

• Paper 4, Section II, G

  Metric and Topological Spaces | Part IB, 2019

  (a) Define the subspace, quotient and product topologies.

  (b) Let $X$ be a compact topological space and $Y$ a Hausdorff topological space. Prove that a continuous bijection $f: X \rightarrow Y$ is a homeomorphism.

  (c) Let $S=[0,1] \times[0,1]$, equipped with the product topology. Let $\sim$ be the smallest equivalence relation on $S$ such that $(s, 0) \sim(s, 1)$ and $(0, t) \sim(1, t)$, for all $s, t \in[0,1]$. Let

  $$T=\left\{(x, y, z) \in \mathbb{R}^{3} \mid\left(\sqrt{x^{2}+y^{2}}-2\right)^{2}+z^{2}=1\right\}$$

  equipped with the subspace topology from $\mathbb{R}^{3}$. Prove that $S / \sim$ and $T$ are homeomorphic.

  [You may assume without proof that $S$ is compact.]

  comment

Numerical Analysis

• Paper 4, Section I, C

  Numerical Analysis | Part IB, 2019

  Calculate the $L U$ factorization of the matrix

  $$A=\left(\begin{array}{rrrr} 3 & 2 & -3 & -3 \\ 6 & 3 & -7 & -8 \\ 3 & 1 & -6 & -4 \\ -6 & -3 & 9 & 6 \end{array}\right)$$

  Use this to evaluate $\operatorname{det}(A)$ and to solve the equation

  $$A \mathbf{x}=\mathbf{b}$$

  with

  $$\mathbf{b}=\left(\begin{array}{r} 3 \\ 3 \\ -1 \\ -3 \end{array}\right)$$

  comment

Optimization

• Paper 4, Section II, H

  Optimization | Part IB, 2019

  (a) State and prove the max-flow min-cut theorem.

  (b) (i) Apply the Ford-Fulkerson algorithm to find the maximum flow of the network illustrated below, where $S$ is the source and $T$ is the sink.

  

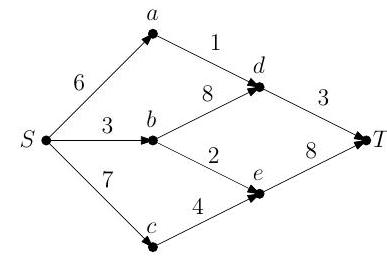
  (ii) Verify the optimality of your solution using the max-flow min-cut theorem.

  (iii) Is there a unique flow which attains the maximum? Explain your answer.

  (c) Prove that the Ford-Fulkerson algorithm always terminates when the network is finite, the capacities are integers, and the algorithm is initialised where the initial flow is 0 across all edges. Prove also in this case that the flow across each edge is an integer.

  comment

Quantum Mechanics

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2019

  (a) Define the probability density $\rho$ and probability current $j$ for the wavefunction $\Psi(x, t)$ of a particle of mass $m$. Show that

  $$\frac{\partial \rho}{\partial t}+\frac{\partial j}{\partial x}=0$$

  and deduce that $j=0$ for a normalizable, stationary state wavefunction. Give an example of a non-normalizable, stationary state wavefunction for which $j$ is non-zero, and calculate the value of $j$.

  (b) A particle has the instantaneous, normalized wavefunction

  $$\Psi(x, 0)=\left(\frac{2 \alpha}{\pi}\right)^{1 / 4} e^{-\alpha x^{2}+i k x}$$

  where $\alpha$ is positive and $k$ is real. Calculate the expectation value of the momentum for this wavefunction.

  comment

Statistics

• Paper 4, Section II, 19H

  Statistics | Part IB, 2019

  Consider the linear model

  $$Y_{i}=\beta x_{i}+\epsilon_{i} \quad \text { for } \quad i=1, \ldots, n$$

  where $x_{1}, \ldots, x_{n}$ are known and $\epsilon_{1}, \ldots, \epsilon_{n}$ are i.i.d. $N\left(0, \sigma^{2}\right)$. We assume that the parameters $\beta$ and $\sigma^{2}$ are unknown.

  (a) Find the MLE $\widehat{\beta}$ of $\beta$. Explain why $\widehat{\beta}$ is the same as the least squares estimator of $\beta$.

  (b) State and prove the Gauss-Markov theorem for this model.

  (c) For each value of $\theta \in \mathbb{R}$ with $\theta \neq 0$, determine the unbiased linear estimator $\tilde{\beta}$ of $\beta$ which minimizes

  $$\mathbb{E}_{\beta, \sigma^{2}}[\exp (\theta(\tilde{\beta}-\beta))]$$

  comment

Variational Principles

• Paper 4, Section II, A

  Variational Principles | Part IB, 2019

  Consider the functional

  $$I[y]=\int_{-\infty}^{\infty}\left(\frac{1}{2} y^{\prime 2}+\frac{1}{2} U(y)^{2}\right) d x$$

  where $y(x)$ is subject to boundary conditions $y(x) \rightarrow a_{\pm}$as $x \rightarrow \pm \infty$ with $U\left(a_{\pm}\right)=0$. [You may assume the integral converges.]

  (a) Find expressions for the first-order and second-order variations $\delta I$ and $\delta^{2} I$ resulting from a variation $\delta y$ that respects the boundary conditions.

  (b) If $a_{\pm}=a$, show that $I[y]=0$ if and only if $y(x)=a$ for all $x$. Explain briefly how this is consistent with your results for $\delta I$ and $\delta^{2} I$ in part (a).

  (c) Now suppose that $U(y)=c^{2}-y^{2}$ with $a_{\pm}=\pm c(c>0)$. By considering an integral of $U(y) y^{\prime}$, show that

  $$I[y] \geqslant \frac{4 c^{3}}{3},$$

  with equality if and only if $y$ satisfies a first-order differential equation. Deduce that global minima of $I[y]$ with the specified boundary conditions occur precisely for

  $$y(x)=c \tanh \left\{c\left(x-x_{0}\right)\right\}$$

  where $x_{0}$ is a constant. How is the first-order differential equation that appears in this case related to your general result for $\delta I$ in part (a)?

  comment