Part IB, 2019, Paper 2

Analysis II

• Paper 2, Section I, E

  Analysis II | Part IB, 2019

  Consider the map $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by

  $$f(x, y)=\left(x^{1 / 3}+y^{2}, y^{5}\right)$$

  where $x^{1 / 3}$ denotes the unique real cube root of $x \in \mathbb{R}$.

  (a) At what points is $f$ continuously differentiable? Calculate its derivative there.

  (b) Show that $f$ has a local differentiable inverse near any $(x, y)$ with $x y \neq 0$.

  You should justify your answers, stating accurately any results that you require.

  comment

• Paper 2, Section II, 12E

  Analysis II | Part IB, 2019

  (a) (i) Define what it means for two norms on a vector space to be Lipschitz equivalent.

  (ii) Show that any two norms on a finite-dimensional vector space are Lipschitz equivalent.

  (iii) Show that if two norms $\|\cdot\|,\|\cdot\|^{\prime}$ on a vector space $V$ are Lipschitz equivalent then the following holds: for any sequence $\left(v_{n}\right)$ in $V,\left(v_{n}\right)$ is Cauchy with respect to $\|\cdot\|$ if and only if it is Cauchy with respect to $\|\cdot\|^{\prime}$.

  (b) Let $V$ be the vector space of real sequences $x=\left(x_{i}\right)$ such that $\sum\left|x_{i}\right|<\infty$. Let

  $$\|x\|_{\infty}=\sup \left\{\left|x_{i}\right|: i \in \mathbb{N}\right\},$$

  and for $1 \leqslant p<\infty$, let

  $$\|x\|_{p}=\left(\sum\left|x_{i}\right|^{p}\right)^{1 / p}$$

  You may assume that $\|\cdot\|_{\infty}$ and $\|\cdot\|_{p}$ are well-defined norms on $V$.

  (i) Show that $\|\cdot\|_{p}$ is not Lipschitz equivalent to $\|\cdot\|_{\infty}$ for any $1 \leqslant p<\infty$.

  (ii) Are there any $p, q$ with $1 \leqslant p<q<\infty$ such that $\|\cdot\|_{p}$ and $\|\cdot\|_{q}$ are Lipschitz equivalent? Justify your answer.

  comment

Complex Analysis or Complex Methods

• Paper 2, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2019

  Let $C_{1}$ and $C_{2}$ be smooth curves in the complex plane, intersecting at some point $p$. Show that if the map $f: \mathbb{C} \rightarrow \mathbb{C}$ is complex differentiable, then it preserves the angle between $C_{1}$ and $C_{2}$ at $p$, provided $f^{\prime}(p) \neq 0$. Give an example that illustrates why the condition $f^{\prime}(p) \neq 0$ is important.

  Show that $f(z)=z+1 / z$ is a one-to-one conformal map on each of the two regions $|z|>1$ and $0<|z|<1$, and find the image of each region.

  Hence construct a one-to-one conformal map from the unit disc to the complex plane with the intervals $(-\infty,-1 / 2]$ and $[1 / 2, \infty)$ removed.

  comment

Electromagnetism

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2019

  Write down the solution for the scalar potential $\varphi(\mathbf{x})$ that satisfies

  $$\nabla^{2} \varphi=-\frac{1}{\varepsilon_{0}} \rho,$$

  with $\varphi(\mathbf{x}) \rightarrow 0$ as $r=|\mathbf{x}| \rightarrow \infty$. You may assume that the charge distribution $\rho(\mathbf{x})$ vanishes for $r>R$, for some constant $R$. In an expansion of $\varphi(\mathbf{x})$ for $r \gg R$, show that the terms of order $1 / r$ and $1 / r^{2}$ can be expressed in terms of the total charge $Q$ and the electric dipole moment $\mathbf{p}$, which you should define.

  Write down the analogous solution for the vector potential $\mathbf{A}(\mathbf{x})$ that satisfies

  $$\nabla^{2} \mathbf{A}=-\mu_{0} \mathbf{J}$$

  with $\mathbf{A}(\mathbf{x}) \rightarrow \mathbf{0}$ as $r \rightarrow \infty$. You may assume that the current $\mathbf{J}(\mathbf{x})$ vanishes for $r>R$ and that it obeys $\nabla \cdot \mathbf{J}=0$ everywhere. In an expansion of $\mathbf{A}(\mathbf{x})$ for $r \gg R$, show that the term of order $1 / r$ vanishes.

  $\left[\right.$ Hint: $\left.\frac{\partial}{\partial x_{j}}\left(x_{i} J_{j}\right)=J_{i}+x_{i} \frac{\partial J_{j}}{\partial x_{j}} .\right]$

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2019

  Consider a conductor in the shape of a closed curve $C$ moving in the presence of a magnetic field B. State Faraday's Law of Induction, defining any quantities that you introduce.

  Suppose $C$ is a square horizontal loop that is allowed to move only vertically. The location of the loop is specified by a coordinate $z$, measured vertically upwards, and the edges of the loop are defined by $x=\pm a,-a \leqslant y \leqslant a$ and $y=\pm a,-a \leqslant x \leqslant a$. If the magnetic field is

  $$\mathbf{B}=b(x, y,-2 z),$$

  where $b$ is a constant, find the induced current $I$, given that the total resistance of the loop is $R$.

  Calculate the resulting electromagnetic force on the edge of the loop $x=a$, and show that this force acts at an angle $\tan ^{-1}(2 z / a)$ to the vertical. Find the total electromagnetic force on the loop and comment on its direction.

  Now suppose that the loop has mass $m$ and that gravity is the only other force acting on it. Show that it is possible for the loop to fall with a constant downward velocity $R m g /\left(8 b a^{2}\right)^{2}$.

  comment

Fluid Dynamics

• Paper 2, Section I, C

  Fluid Dynamics | Part IB, 2019

  Consider the steady flow

  $$u_{x}=\sin x \cos y, \quad u_{y}=-\cos x \sin y, \quad u_{z}=0$$

  where $(x, y, z)$ are Cartesian coordinates. Show that $\boldsymbol{\nabla} \cdot \mathbf{u}=0$ and determine the streamfunction. Calculate the vorticity and verify that the vorticity equation is satisfied in the absence of viscosity. Sketch the streamlines in the region $0<x<2 \pi, 0<y<2 \pi$.

  comment

Geometry

• Paper 2, Section II, E

  Geometry | Part IB, 2019

  Define a smooth embedded surface in $\mathbb{R}^{3}$. Sketch the surface $C$ given by

  $$\left(\sqrt{2 x^{2}+2 y^{2}}-4\right)^{2}+2 z^{2}=2$$

  and find a smooth parametrisation for it. Use this to calculate the Gaussian curvature of $C$ at every point.

  Hence or otherwise, determine which points of the embedded surface

  $$\left(\sqrt{x^{2}+2 x z+z^{2}+2 y^{2}}-4\right)^{2}+(z-x)^{2}=2$$

  have Gaussian curvature zero. [Hint: consider a transformation of $\mathbb{R}^{3}$.]

  [You should carefully state any result that you use.]

  comment

Groups, Rings and Modules

• Paper 2, Section I, G

  Groups, Rings and Modules | Part IB, 2019

  Let $R$ be an integral domain. A module $M$ over $R$ is torsion-free if, for any $r \in R$ and $m \in M, r m=0$ only if $r=0$ or $m=0$.

  Let $M$ be a module over $R$. Prove that there is a quotient

  $$q: M \rightarrow M_{0}$$

  with $M_{0}$ torsion-free and with the following property: whenever $N$ is a torsion-free module and $f: M \rightarrow N$ is a homomorphism of modules, there is a homomorphism $f_{0}: M_{0} \rightarrow N$ such that $f=f_{0} \circ q$.

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  (a) Let $k$ be a field and let $f(X)$ be an irreducible polynomial of degree $d>0$ over $k$. Prove that there exists a field $F$ containing $k$ as a subfield such that

  $$f(X)=(X-\alpha) g(X)$$

  where $\alpha \in F$ and $g(X) \in F[X]$. State carefully any results that you use.

  (b) Let $k$ be a field and let $f(X)$ be a monic polynomial of degree $d>0$ over $k$, which is not necessarily irreducible. Prove that there exists a field $F$ containing $k$ as a subfield such that

  $$f(X)=\prod_{i=1}^{d}\left(X-\alpha_{i}\right)$$

  where $\alpha_{i} \in F$.

  (c) Let $k=\mathbb{Z} /(p)$ for $p$ a prime, and let $f(X)=X^{p^{n}}-X$ for $n \geqslant 1$ an integer. For $F$ as in part (b), let $K$ be the set of roots of $f(X)$ in $F$. Prove that $K$ is a field.

  comment

Linear Algebra

• Paper 2, Section I, F

  Linear Algebra | Part IB, 2019

  If $U$ and $W$ are finite-dimensional subspaces of a vector space $V$, prove that

  $$\operatorname{dim}(U+W)=\operatorname{dim}(U)+\operatorname{dim}(W)-\operatorname{dim}(U \cap W)$$

  Let

  $$\begin{aligned} U &=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid x_{1}=7 x_{3}+8 x_{4}, x_{2}+5 x_{3}+6 x_{4}=0\right\} \\ W &=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid x_{1}+2 x_{2}+3 x_{3}=0, x_{4}=0\right\} . \end{aligned}$$

  Show that $U+W$ is 3 -dimensional and find a linear map $\ell: \mathbb{R}^{4} \rightarrow \mathbb{R}$ such that

  $$U+W=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid \ell(\mathbf{x})=0\right\}$$

  comment

• Paper 2, Section II, F

  Linear Algebra | Part IB, 2019

  Let $A$ and $B$ be $n \times n$ matrices over $\mathbb{C}$.

  (a) Assuming that $A$ is invertible, show that $A B$ and $B A$ have the same characteristic polynomial.

  (b) By considering the matrices $A-s I$, show that $A B$ and $B A$ have the same characteristic polynomial even when $A$ is singular.

  (c) Give an example to show that the minimal polynomials $m_{A B}(t)$ and $m_{B A}(t)$ of $A B$ and $B A$ may be different.

  (d) Show that $m_{A B}(t)$ and $m_{B A}(t)$ differ at most by a factor of $t$. Stating carefully any results which you use, deduce that if $A B$ is diagonalisable then so is $(B A)^{2}$.

  comment

Markov Chains

• Paper 2, Section II, H

  Markov Chains | Part IB, 2019

  Fix $n \geqslant 1$ and let $G$ be the graph consisting of a copy of $\{0, \ldots, n\}$ joining vertices $A$ and $B$, a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $C$, and a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $D$. Let $E$ be the vertex adjacent to $B$ on the segment from $B$ to $C$. Shown below is an illustration of $G$ in the case $n=5$. The vertices are solid squares and edges are indicated by straight lines.

  

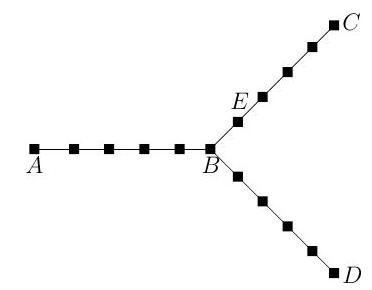
  Let $\left(X_{k}\right)$ be a simple random walk on $G$. In other words, in each time step, $X$ moves to one of its neighbours with equal probability. Assume that $X_{0}=A$.

  (a) Compute the expected amount of time for $X$ to hit $B$.

  (b) Compute the expected amount of time for $X$ to hit $E$. [Hint: first show that the expected amount of time $x$ for $X$ to go from $B$ to $E$ satisfies $x=\frac{1}{3}+\frac{2}{3}(L+x)$ where $L$ is the expected return time of $X$ to $B$ when starting from $B$.]

  (c) Compute the expected amount of time for $X$ to hit $C$. [Hint: for each $i$, let $v_{i}$ be the vertex which is $i$ places to the right of $B$ on the segment from $B$ to $C$. Derive an equation for the expected amount of time $x_{i}$ for $X$ to go from $v_{i}$ to $v_{i+1}$.]

  Justify all of your answers.

  comment

Methods

• Paper 2, Section I, B

  Methods | Part IB, 2019

  Let $r, \theta, \phi$ be spherical polar coordinates, and let $P_{n}$ denote the $n$th Legendre polynomial. Write down the most general solution for $r>0$ of Laplace's equation $\nabla^{2} \Phi=0$ that takes the form $\Phi(r, \theta, \phi)=f(r) P_{n}(\cos \theta)$.

  Solve Laplace's equation in the spherical shell $1 \leqslant r \leqslant 2$ subject to the boundary conditions

  $$\begin{aligned} &\Phi=3 \cos 2 \theta \text { at } r=1 \\ &\Phi=0 \quad \text { at } r=2 \end{aligned}$$

  [The first three Legendre polynomials are

  $$\left.P_{0}(x)=1, \quad P_{1}(x)=x \quad \text { and } \quad P_{2}(x)=\frac{3}{2} x^{2}-\frac{1}{2} .\right]$$

  comment

• Paper 2, Section II, D

  Methods | Part IB, 2019

  For $n=0,1,2, \ldots$, the degree $n$ polynomial $C_{n}^{\alpha}(x)$ satisfies the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-(2 \alpha+1) x y^{\prime}+n(n+2 \alpha) y=0$$

  where $\alpha$ is a real, positive parameter. Show that, when $m \neq n$,

  $$\int_{a}^{b} C_{m}^{\alpha}(x) C_{n}^{\alpha}(x) w(x) d x=0$$

  for a weight function $w(x)$ and values $a<b$ that you should determine.

  Suppose that the roots of $C_{n}^{\alpha}(x)$ that lie inside the domain $(a, b)$ are $\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$, with $k \leqslant n$. By considering the integral

  $$\int_{a}^{b} C_{n}^{\alpha}(x) \prod_{i=1}^{k}\left(x-x_{i}\right) w(x) d x$$

  show that in fact all $n$ roots of $C_{n}^{\alpha}(x)$ lie in $(a, b)$.

  comment

Metric and Topological Spaces

• Paper 2, Section I, G

  Metric and Topological Spaces | Part IB, 2019

  (a) Let $f: X \rightarrow Y$ be a continuous surjection of topological spaces. Prove that, if $X$ is connected, then $Y$ is also connected.

  (b) Let $g:[0,1] \rightarrow[0,1]$ be a continuous map. Deduce from part (a) that, for every $y$ between $g(0)$ and $g(1)$, there is $x \in[0,1]$ such that $g(x)=y$. [You may not assume the Intermediate Value Theorem, but you may use the fact that suprema exist in $\mathbb{R}$.]

  comment

Numerical Analysis

• Paper 2, Section II, C

  Numerical Analysis | Part IB, 2019

  Define the linear least squares problem for the equation

  $$A \mathbf{x}=\mathbf{b}$$

  where $A$ is a given $m \times n$ matrix with $m>n, \mathbf{b} \in \mathbb{R}^{m}$ is a given vector and $\mathbf{x} \in \mathbb{R}^{n}$ is an unknown vector.

  Explain how the linear least squares problem can be solved by obtaining a $Q R$ factorization of the matrix $A$, where $Q$ is an orthogonal $m \times m$ matrix and $R$ is an uppertriangular $m \times n$ matrix in standard form.

  Use the Gram-Schmidt method to obtain a $Q R$ factorization of the matrix

  $$A=\left(\begin{array}{lll} 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 0 \end{array}\right)$$

  and use it to solve the linear least squares problem in the case

  $$\mathbf{b}=\left(\begin{array}{l} 1 \\ 2 \\ 3 \\ 6 \end{array}\right)$$

  comment

Optimization

• Paper 2, Section I, H

  Optimization | Part IB, 2019

  State the Lagrange sufficiency theorem.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2}=1$$

  using Lagrange multipliers. Carefully justify why your solution is in fact the maximum.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2} \leqslant 1$$

  comment

Quantum Mechanics

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2019

  Let $x, y, z$ be Cartesian coordinates in $\mathbb{R}^{3}$. The angular momentum operators satisfy the commutation relation

  $$\left[L_{x}, L_{y}\right]=i \hbar L_{z}$$

  and its cyclic permutations. Define the total angular momentum operator $\mathbf{L}^{2}$ and show that $\left[L_{z}, \mathbf{L}^{2}\right]=0$. Write down the explicit form of $L_{z}$.

  Show that a function of the form $(x+i y)^{m} z^{n} f(r)$, where $r^{2}=x^{2}+y^{2}+z^{2}$, is an eigenfunction of $L_{z}$ and find the eigenvalue. State the analogous result for $(x-i y)^{m} z^{n} f(r)$.

  There is an energy level for a particle in a certain spherically symmetric potential well that is 6-fold degenerate. A basis for the (unnormalized) energy eigenstates is of the form

  $$\left(x^{2}-1\right) f(r),\left(y^{2}-1\right) f(r),\left(z^{2}-1\right) f(r), x y f(r), x z f(r), y z f(r) \text {. }$$

  Find a new basis that consists of simultaneous eigenstates of $L_{z}$ and $\mathbf{L}^{2}$ and identify their eigenvalues.

  [You may quote the range of $L_{z}$ eigenvalues associated with a particular eigenvalue of $\mathbf{L}^{2}$.]

  comment

Statistics

• Paper 2, Section I, H

  Statistics | Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. coin tosses with probability $\theta$ of obtaining a head.

  (a) Compute the posterior distribution of $\theta$ given the observations $X_{1}, \ldots, X_{n}$ in the case of a uniform prior on $[0,1]$.

  (b) Give the definition of the quadratic error loss function.

  (c) Determine the value $\widehat{\theta}$of $\theta$ which minimizes the quadratic error loss function. Justify your answer. Calculate $\mathbb{E}[\hat{\theta}]$.

  [You may use that the $\beta(a, b), a, b>0$, distribution has density function on $[0,1]$ given by

  $$c_{a, b} x^{a-1}(1-x)^{b-1}$$

  where $c_{a, b}$ is a normalizing constant. You may also use without proof that the mean of a $\beta(a, b)$ random variable is $a /(a+b) .]$

  comment

Variational Principles

• Paper 2, Section II, A

  Variational Principles | Part IB, 2019

  Write down the Euler-Lagrange (EL) equations for a functional

  $$\int_{a}^{b} f\left(u, w, u^{\prime}, w^{\prime}, x\right) d x$$

  where $u(x)$ and $w(x)$ each take specified values at $x=a$ and $x=b$. Show that the EL equations imply that

  $$\kappa=f-u^{\prime} \frac{\partial f}{\partial u^{\prime}}-w^{\prime} \frac{\partial f}{\partial w^{\prime}}$$

  is independent of $x$ provided $f$ satisfies a certain condition, to be specified. State conditions under which there exist additional first integrals of the $\mathrm{EL}$ equations.

  Consider

  $$f=\left(1-\frac{m}{u}\right) w^{\prime 2}-\left(1-\frac{m}{u}\right)^{-1} u^{\prime 2}$$

  where $m$ is a positive constant. Show that solutions of the EL equations satisfy

  $$u^{\prime 2}=\lambda^{2}+\kappa\left(1-\frac{m}{u}\right)$$

  for some constant $\lambda$. Assuming that $\kappa=-\lambda^{2}$, find $d w / d u$ and hence determine the most general solution for $w$ as a function of $u$ subject to the conditions $u>m$ and $w \rightarrow-\infty$ as $u \rightarrow \infty$. Show that, for any such solution, $w \rightarrow \infty$ as $u \rightarrow m$.

  [Hint:

  $$\left.\frac{d}{d z}\left\{\log \left(\frac{z^{1 / 2}-1}{z^{1 / 2}+1}\right)\right\}=\frac{1}{z^{1 / 2}(z-1)} . \quad\right]$$

  comment