Part IB, 2015, Paper 1

Analysis II

• Paper 1, Section II, G

  Analysis II | Part IB, 2015

  Define what it means for a sequence of functions $f_{n}:[0,1] \rightarrow \mathbb{R}$ to converge uniformly on $[0,1]$ to a function $f$.

  Let $f_{n}(x)=n^{p} x e^{-n^{q} x}$, where $p, q$ are positive constants. Determine all the values of $(p, q)$ for which $f_{n}(x)$ converges pointwise on $[0,1]$. Determine all the values of $(p, q)$ for which $f_{n}(x)$ converges uniformly on $[0,1]$.

  Let now $f_{n}(x)=e^{-n x^{2}}$. Determine whether or not $f_{n}$ converges uniformly on $[0,1]$.

  Let $f:[0,1] \rightarrow \mathbb{R}$ be a continuous function. Show that the sequence $x^{n} f(x)$ is uniformly convergent on $[0,1]$ if and only if $f(1)=0$.

  [If you use any theorems about uniform convergence, you should prove these.]

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, B

  Complex Analysis or Complex Methods | Part IB, 2015

  Consider the analytic (holomorphic) functions $f$ and $g$ on a nonempty domain $\Omega$ where $g$ is nowhere zero. Prove that if $|f(z)|=|g(z)|$ for all $z$ in $\Omega$ then there exists a real constant $\alpha$ such that $f(z)=e^{i \alpha} g(z)$ for all $z$ in $\Omega$.

  comment

• Paper 1, Section II, B

  Complex Analysis or Complex Methods | Part IB, 2015

  (i) Show that transformations of the complex plane of the form

  $$\zeta=\frac{a z+b}{c z+d}$$

  always map circles and lines to circles and lines, where $a, b, c$ and $d$ are complex numbers such that $a d-b c \neq 0$.

  (ii) Show that the transformation

  $$\zeta=\frac{z-\alpha}{\bar{\alpha} z-1}, \quad|\alpha|<1$$

  maps the unit disk centered at $z=0$ onto itself.

  (iii) Deduce a conformal transformation that maps the non-concentric annular domain $\Omega=\{|z|<1,|z-c|>c\}, 0<c<1 / 2$, to a concentric annular domain.

  comment

Electromagnetism

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2015

  (i) Write down the Lorentz force law for $d \mathbf{p} / d t$ due to an electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ acting on a particle of charge $q$ moving with velocity $\dot{\mathbf{x}}$.

  (ii) Write down Maxwell's equations in terms of $c$ (the speed of light in a vacuum), in the absence of charges and currents.

  (iii) Show that they can be manipulated into a wave equation for each component of $\mathbf{E}$.

  (iv) Show that Maxwell's equations admit solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left(\mathbf{E}_{0} e^{i(\omega t-\mathbf{k} \cdot \mathbf{x})}\right)$$

  where $\mathbf{E}_{\mathbf{0}}$ and $\mathbf{k}$ are constant vectors and $\omega$ is a constant (all real). Derive a condition on $\mathbf{k} \cdot \mathbf{E}_{\mathbf{0}}$ and relate $\omega$ and $\mathbf{k}$.

  (v) Suppose that a perfect conductor occupies the region $z<0$ and that a plane wave with $\mathbf{k}=(0,0,-k), \mathbf{E}_{0}=\left(E_{0}, 0,0\right)$ is incident from the vacuum region $z>0$. Write down boundary conditions for the $\mathbf{E}$ and $\mathbf{B}$ fields. Show that they can be satisfied if a suitable reflected wave is present, and determine the total $\mathbf{E}$ and $\mathbf{B}$ fields in real form.

  (vi) At time $t=\pi /(4 \omega)$, a particle of charge $q$ and mass $m$ is at $(0,0, \pi /(4 k))$ moving with velocity $(c / 2,0,0)$. You may assume that the particle is far enough away from the conductor so that we can ignore its effect upon the conductor and that $q E_{0}>0$. Give a unit vector for the direction of the Lorentz force on the particle at time $t=\pi /(4 \omega)$.

  (vii) Ignoring relativistic effects, find the magnitude of the particle's rate of change of velocity in terms of $E_{0}, q$ and $m$ at time $t=\pi /(4 \omega)$. Why is this answer inaccurate?

  comment

Fluid Dynamics

• Paper 1, Section I, B

  Fluid Dynamics | Part IB, 2015

  Consider a spherical bubble of radius $a$ in an inviscid fluid in the absence of gravity. The flow at infinity is at rest and the bubble undergoes translation with velocity $\mathbf{U}=U(t) \hat{\mathbf{x}}$. We assume that the flow is irrotational and derives from a potential given in spherical coordinates by

  $$\phi(r, \theta)=U(t) \frac{a^{3}}{2 r^{2}} \cos \theta,$$

  where $\theta$ is measured with respect to $\hat{\mathbf{x}}$. Compute the force, $\mathbf{F}$, acting on the bubble. Show that the formula for $\mathbf{F}$ can be interpreted as the acceleration force of a fraction $\alpha<1$ of the fluid displaced by the bubble, and determine the value of $\alpha$.

  comment

• Paper 1, Section II, B

  Fluid Dynamics | Part IB, 2015

  A fluid layer of depth $h_{1}$ and dynamic viscosity $\mu_{1}$ is located underneath a fluid layer of depth $h_{2}$ and dynamic viscosity $\mu_{2}$. The total fluid system of depth $h=h_{1}+h_{2}$ is positioned between a stationary rigid plate at $y=0$ and a rigid plate at $y=h$ moving with speed $\mathbf{U}=U \hat{\mathbf{x}}$, where $U$ is constant. Ignore the effects of gravity.

  (i) Using dimensional analysis only, and the fact that the stress should be linear in $U$, derive the expected form of the shear stress acted by the fluid on the plate at $y=0$ as a function of $U, h_{1}, h_{2}, \mu_{1}$ and $\mu_{2}$.

  (ii) Solve for the unidirectional velocity profile between the two plates. State clearly all boundary conditions you are using to solve this problem.

  (iii) Compute the exact value of the shear stress acted by the fluid on the plate at $y=0$. Compare with the results in (i).

  (iv) What is the condition on the viscosity of the bottom layer, $\mu_{1}$, for the stress in (iii) to be smaller than it would be if the fluid had constant viscosity $\mu_{2}$ in both layers?

  (v) Show that the stress acting on the plate at $y=h$ is equal and opposite to the stress on the plate at $y=0$ and justify this result physically.

  comment

Geometry

• Paper 1, Section I, F

  Geometry | Part IB, 2015

  (i) Give a model for the hyperbolic plane. In this choice of model, describe hyperbolic lines.

  Show that if $\ell_{1}, \ell_{2}$ are two hyperbolic lines and $p_{1} \in \ell_{1}, p_{2} \in \ell_{2}$ are points, then there exists an isometry $g$ of the hyperbolic plane such that $g\left(\ell_{1}\right)=\ell_{2}$ and $g\left(p_{1}\right)=p_{2}$.

  (ii) Let $T$ be a triangle in the hyperbolic plane with angles $30^{\circ}, 30^{\circ}$ and $45^{\circ}$. What is the area of $T$ ?

  comment

Groups, Rings and Modules

• Paper 1, Section II, F

  Groups, Rings and Modules | Part IB, 2015

  (i) Give the definition of a $p$-Sylow subgroup of a group.

  (ii) Let $G$ be a group of order $2835=3^{4} \cdot 5 \cdot 7$. Show that there are at most two possibilities for the number of 3-Sylow subgroups, and give the possible numbers of 3-Sylow subgroups.

  (iii) Continuing with a group $G$ of order 2835 , show that $G$ is not simple.

  comment

Linear Algebra

• Paper 1, Section I, E

  Linear Algebra | Part IB, 2015

  Let $U$ and $V$ be finite dimensional vector spaces and $\alpha: U \rightarrow V$ a linear map. Suppose $W$ is a subspace of $U$. Prove that

  $$r(\alpha) \geqslant r\left(\left.\alpha\right|_{W}\right) \geqslant r(\alpha)-\operatorname{dim}(U)+\operatorname{dim}(W)$$

  where $r(\alpha)$ denotes the rank of $\alpha$ and $\left.\alpha\right|_{W}$ denotes the restriction of $\alpha$ to $W$. Give examples showing that each inequality can be both a strict inequality and an equality.

  comment

• Paper 1, Section II, E

  Linear Algebra | Part IB, 2015

  Determine the characteristic polynomial of the matrix

  $$M=\left(\begin{array}{cccc} x & 1 & 1 & 0 \\ 1-x & 0 & -1 & 0 \\ 2 & 2 x & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  For which values of $x \in \mathbb{C}$ is $M$ invertible? When $M$ is not invertible determine (i) the Jordan normal form $J$ of $M$, (ii) the minimal polynomial of $M$.

  Find a basis of $\mathbb{C}^{4}$ such that $J$ is the matrix representing the endomorphism $M: \mathbb{C}^{4} \rightarrow \mathbb{C}^{4}$ in this basis. Give a change of basis matrix $P$ such that $P^{-1} M P=J$.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2015

  Consider a particle moving between the vertices of the graph below, taking steps along the edges. Let $X_{n}$ be the position of the particle at time $n$. At time $n+1$ the particle moves to one of the vertices adjoining $X_{n}$, with each of the adjoining vertices being equally likely, independently of previous moves. Explain briefly why $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain on the vertices. Is this chain irreducible? Find an invariant distribution for this chain.

  

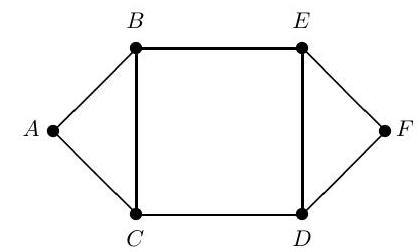
  Suppose that the particle starts at $B$. By adapting the transition matrix, or otherwise, find the probability that the particle hits vertex $A$ before vertex $F$.

  Find the expected first passage time from $B$ to $F$ given no intermediate visit to $A$.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

Methods

• Paper 1, Section II, C

  Methods | Part IB, 2015

  (i) Briefly describe the Sturm-Liouville form of an eigenfunction equation for real valued functions with a linear, second-order ordinary differential operator. Briefly summarize the properties of the solutions.

  (ii) Derive the condition for self-adjointness of the differential operator in (i) in terms of the boundary conditions of solutions $y_{1}, y_{2}$ to the Sturm-Liouville equation. Give at least three types of boundary conditions for which the condition for self-adjointness is satisfied.

  (iii) Consider the inhomogeneous Sturm-Liouville equation with weighted linear term

  $$\frac{1}{w(x)} \frac{d}{d x}\left(p(x) \frac{d y}{d x}\right)-\frac{q(x)}{w(x)} y-\lambda y=f(x),$$

  on the interval $a \leqslant x \leqslant b$, where $p$ and $q$ are real functions on $[a, b]$ and $w$ is the weighting function. Let $G(x, \xi)$ be a Green's function satisfying

  $$\frac{d}{d x}\left(p(x) \frac{d G}{d x}\right)-q(x) G(x, \xi)=\delta(x-\xi)$$

  Let solutions $y$ and the Green's function $G$ satisfy the same boundary conditions of the form $\alpha y^{\prime}+\beta y=0$ at $x=a, \mu y^{\prime}+\nu y=0$ at $x=b(\alpha, \beta$ are not both zero and $\mu, \nu$ are not both zero) and likewise for $G$ for the same constants $\alpha, \beta, \mu$ and $\nu$. Show that the Sturm-Liouville equation can be written as a so-called Fredholm integral equation of the form

  $$\psi(\xi)=U(\xi)+\lambda \int_{a}^{b} K(x, \xi) \psi(x) d x$$

  where $K(x, \xi)=\sqrt{w(\xi) w(x)} G(x, \xi), \psi=\sqrt{w} y$ and $U$ depends on $K, w$ and the forcing term $f$. Write down $U$ in terms of an integral involving $f, K$ and $w$.

  (iv) Derive the Fredholm integral equation for the Sturm-Liouville equation on the interval $[0,1]$

  $$\frac{d^{2} y}{d x^{2}}-\lambda y=0,$$

  with $y(0)=y(1)=0$.

  comment

Metric and Topological Spaces

• Paper 1, Section II, E

  Metric and Topological Spaces | Part IB, 2015

  Give the definition of a metric on a set $X$ and explain how this defines a topology on $X$.

  Suppose $(X, d)$ is a metric space and $U$ is an open set in $X$. Let $x, y \in X$ and $\epsilon>0$ such that the open ball $B_{\epsilon}(y) \subseteq U$ and $x \in B_{\epsilon / 2}(y)$. Prove that $y \in B_{\epsilon / 2}(x) \subseteq U$.

  Explain what it means (i) for a set $S$ to be dense in $X$, (ii) to say $\mathcal{B}$ is a base for a topology $\mathcal{T}$.

  Prove that any metric space which contains a countable dense set has a countable basis.

  comment

Numerical Analysis

• Paper 1, Section I, 6D

  Numerical Analysis | Part IB, 2015

  Let

  $$A=\left[\begin{array}{rrrr} 1 & 4 & 3 & 2 \\ 4 & 17 & 13 & 11 \\ 3 & 13 & 13 & 12 \\ 2 & 11 & 12 & \lambda \end{array}\right], \quad b=\left[\begin{array}{l} 1 \\ 1 \\ 3 \\ 2 \end{array}\right]$$

  where $\lambda$ is a real parameter. Find the $L U$ factorization of the matrix $A$. Give the constraint on $\lambda$ for A to be positive definite.

  For $\lambda=18$, use this factorization to solve the system $A x=b$ via forward and backward substitution.

  comment

• Paper 1, Section II, 18D

  Numerical Analysis | Part IB, 2015

  Determine the real coefficients $b_{1}, b_{2}, b_{3}$ such that

  $$\int_{-2}^{2} f(x) d x=b_{1} f(-1)+b_{2} f(0)+b_{3} f(1)$$

  is exact when $f(x)$ is any real polynomial of degree 2 . Check explicitly that the quadrature is exact for $f(x)=x^{2}$ with these coefficients.

  State the Peano kernel theorem and define the Peano kernel $K(\theta)$. Use this theorem to show that if $f \in C^{3}[-2,2]$, and $b_{1}, b_{2}, b_{3}$ are chosen as above, then

  $$\left|\int_{-2}^{2} f(x) d x-b_{1} f(-1)-b_{2} f(0)-b_{3} f(1)\right| \leqslant \frac{4}{9} \max _{\xi \in[-2,2]}\left|f^{(3)}(\xi)\right|$$

  comment

Optimization

• Paper 1, Section I, H

  Optimization | Part IB, 2015

  (a) Consider a network with vertices in $V=\{1, \ldots, n\}$ and directed edges $(i, j)$ in $E \subseteq V \times V$. Suppose that 1 is the source and $n$ is the sink. Let $C_{i j}, 0<C_{i j}<\infty$, be the capacity of the edge from vertex $i$ to vertex $j$ for $(i, j) \in E$. Let a cut be a partition of $V=\{1, \ldots, n\}$ into $S$ and $V \backslash S$ with $1 \in S$ and $n \in V \backslash S$. Define the capacity of the cut $S$. Write down the maximum flow problem. Prove that the maximum flow is bounded above by the minimum cut capacity.

  (b) Find the maximum flow from the source to the sink in the network below, where the directions and capacities of the edges are shown. Explain your reasoning.

  

  comment

Quantum Mechanics

• Paper 1, Section II, D

  Quantum Mechanics | Part IB, 2015

  Write down expressions for the probability density $\rho(x, t)$ and the probability current $j(x, t)$ for a particle in one dimension with wavefunction $\Psi(x, t)$. If $\Psi(x, t)$ obeys the timedependent Schrödinger equation with a real potential, show that

  $$\frac{\partial j}{\partial x}+\frac{\partial \rho}{\partial t}=0$$

  Consider a stationary state, $\Psi(x, t)=\psi(x) e^{-i E t / \hbar}$, with

  $$\psi(x) \sim \begin{cases}e^{i k_{1} x}+R e^{-i k_{1} x} & x \rightarrow-\infty \\ T e^{i k_{2} x} & x \rightarrow+\infty\end{cases}$$

  where $E, k_{1}, k_{2}$ are real. Evaluate $j(x, t)$ for this state in the regimes $x \rightarrow+\infty$ and $x \rightarrow-\infty$.

  Consider a real potential,

  $$V(x)=-\alpha \delta(x)+U(x), \quad U(x)= \begin{cases}0 & x<0 \\ V_{0} & x>0\end{cases}$$

  where $\delta(x)$ is the Dirac delta function, $V_{0}>0$ and $\alpha>0$. Assuming that $\psi(x)$ is continuous at $x=0$, derive an expression for

  $$\lim _{\epsilon \rightarrow 0}\left[\psi^{\prime}(\epsilon)-\psi^{\prime}(-\epsilon)\right]$$

  Hence calculate the reflection and transmission probabilities for a particle incident from $x=-\infty$ with energy $E>V_{0} .$

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2015

  Suppose that $X_{1}, \ldots, X_{n}$ are independent normally distributed random variables, each with mean $\mu$ and variance 1 , and consider testing $H_{0}: \mu=0$ against $H_{1}: \mu=1$. Explain what is meant by the critical region, the size and the power of a test.

  For $0<\alpha<1$, derive the test that is most powerful among all tests of size at most $\alpha$. Obtain an expression for the power of your test in terms of the standard normal distribution function $\Phi(\cdot)$.

  [Results from the course may be used without proof provided they are clearly stated.]

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2015

  Suppose $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables each with probability mass function $\mathbb{P}\left(X_{i}=x_{i}\right)=p\left(x_{i} ; \theta\right)$, where $\theta$ is an unknown parameter. State what is meant by a sufficient statistic for $\theta$. State the factorisation criterion for a sufficient statistic. State and prove the Rao-Blackwell theorem.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables with

  $$\mathbb{P}\left(X_{i}=x_{i}\right)=\left(\begin{array}{c} m \\ x_{i} \end{array}\right) \theta^{x_{i}}(1-\theta)^{m-x_{i}}, \quad x_{i}=0, \ldots, m$$

  where $m$ is a known positive integer and $\theta$ is unknown. Show that $\tilde{\theta}=X_{1} / m$ is unbiased for $\theta$.

  Show that $T=\sum_{i=1}^{n} X_{i}$ is sufficient for $\theta$ and use the Rao-Blackwell theorem to find another unbiased estimator $\hat{\theta}$ for $\theta$, giving details of your derivation. Calculate the variance of $\hat{\theta}$ and compare it to the variance of $\tilde{\theta}$.

  A statistician cannot remember the exact statement of the Rao-Blackwell theorem and calculates $\mathbb{E}\left(T \mid X_{1}\right)$ in an attempt to find an estimator of $\theta$. Comment on the suitability or otherwise of this approach, giving your reasons.

  [Hint: If $a$ and $b$ are positive integers then, for $r=0,1, \ldots, a+b,\left(\begin{array}{c}a+b \\ r\end{array}\right)=$ $\left.\sum_{j=0}^{r}\left(\begin{array}{c}a \\ j\end{array}\right)\left(\begin{array}{c}b \\ r-j\end{array}\right) .\right]$

  comment

Variational Principles

• Paper 1, Section I, A

  Variational Principles | Part IB, 2015

  Consider a frictionless bead on a stationary wire. The bead moves under the action of gravity acting in the negative $y$-direction and the wire traces out a path $y(x)$, connecting points $(x, y)=(0,0)$ and $(1,0)$. Using a first integral of the Euler-Lagrange equations, find the choice of $y(x)$ which gives the shortest travel time, starting from rest. You may give your solution for $y$ and $x$ separately, in parametric form.

  comment