Let $\left(X_{n}\right)_{n \geqslant 0}$ be the symmetric random walk on vertices of a connected graph. At each step this walk jumps from the current vertex to a neighbouring vertex, choosing uniformly amongst them. Let $T_{i}=\inf \left\{n \geqslant 1: X_{n}=i\right\}$. For each $i \neq j$ let $q_{i j}=P\left(T_{j}<T_{i} \mid X_{0}=i\right)$ and $m_{i j}=E\left(T_{j} \mid X_{0}=i\right)$. Stating any theorems that you use:

(i) Prove that the invariant distribution $\pi$ satisfies detailed balance.

(ii) Use reversibility to explain why $\pi_{i} q_{i j}=\pi_{j} q_{j i}$ for all $i, j$.

Consider a symmetric random walk on the graph shown below.

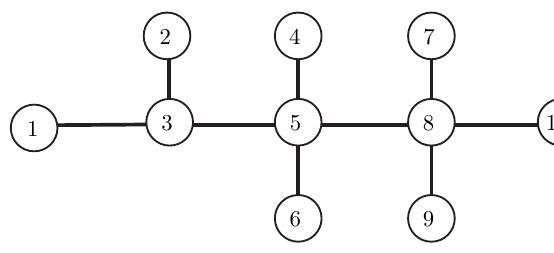
(iii) Find $m_{33}$.

(iv) The removal of any edge $(i, j)$ leaves two disjoint components, one which includes $i$ and one which includes $j$. Prove that $m_{i j}=1+2 e_{i j}(i)$, where $e_{i j}(i)$ is the number of edges in the component that contains $i$.

(v) Show that $m_{i j}+m_{j i} \in\{18,36,54,72\}$ for all $i \neq j$.