Part IB, 2009, Paper 2

Analysis II

• Paper 2, Section I, E

  Analysis II | Part IB, 2009

  State and prove the contraction mapping theorem. Let $f(x)=e^{-x}$. By considering $f(f(x))$ and using the contraction mapping theorem, show that there is a unique real number $x$ such that $x=e^{-x}$.

  comment

• Paper 2, Section II, E

  Analysis II | Part IB, 2009

  Let $U \subseteq \mathbb{R}^{n}$ be a set. What does it mean to say that $U$ is open? Show that if $U$ is open and if $f: U \rightarrow\{0,1\}$ is a continuous function then $f$ is also differentiable, and that its derivative is zero.

  Suppose that $g: U \rightarrow \mathbb{R}$ is differentiable and that $\left\|\left.(D g)\right|_{x}\right\| \leqslant M$ for all $x$, where $\left.(D g)\right|_{x}$ denotes the derivative of $g$ at $x$ and $\|\cdot\|$ is the operator norm. Suppose that $\mathbf{a}, \mathbf{b} \in \mathbb{R}^{n}$ and that the line segment $[\mathbf{a}, \mathbf{b}]=\{\lambda \mathbf{a}+(1-\lambda) \mathbf{b}: \lambda \in[0,1]\}$ lies wholly in $U$. Prove that $|g(\mathbf{a})-g(\mathbf{b})| \leqslant M\|\mathbf{a}-\mathbf{b}\|$.

  Let $\ell_{1}, \ldots, \ell_{k}$ be (infinite) lines in $\mathbb{R}^{3}$, and write $V=\mathbb{R}^{3} \backslash\left(\ell_{1} \cup \cdots \cup \ell_{k}\right)$. If $\mathbf{a}, \mathbf{b} \in V$, show that there is some $\mathbf{c} \in V$ such that the line segments $[\mathbf{a}, \mathbf{c}]$ and $[\mathbf{c}, \mathbf{b}]$ both lie inside V. [You may assume without proof that $\mathbb{R}^{3}$ may not be written as the union of finitely many planes.]

  Show that if $V \rightarrow\{0,1\}$ is a continuous function then $f$ is constant on $V$.

  comment

Complex Analysis or Complex Methods

• Paper 2, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Show that both the following transformations from the $z$-plane to the $\zeta$-plane are conformal, except at certain critical points which should be identified in both planes, and in each case find a domain in the $z$-plane that is mapped onto the upper half $\zeta$-plane:

  $$\begin{aligned} &\text { (i) } \zeta=z+\frac{b^{2}}{z} \\ &\text { (ii) } \zeta=\cosh \frac{\pi z}{b} \end{aligned}$$

  where $b$ is real and positive.

  comment

Electromagnetism

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2009

  For a volume $V$ with surface $S$, state Gauss's Law relating the flux of $\mathbf{E}$ across $S$ to the total charge within $V$.

  A uniformly charged sphere of radius $R$ has total charge $Q$.

  (a) Find the electric field inside the sphere.

  (b) Using the differential relation $d \mathbf{F}=\mathbf{E} d q$ between the force $d \mathbf{F}$ on a small charge $d q$ in an electric field $\mathbf{E}$, find the force on the top half of the sphere due to its bottom half. Express your answer in terms of $R$ and $Q$.

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2009

  Starting from Maxwell's equations in vacuo, show that the cartesian components of $\mathbf{E}$ and $\mathbf{B}$ each satisfy

  $$\nabla^{2} f=\frac{1}{c^{2}} \frac{\partial^{2} f}{\partial t^{2}}$$

  Consider now a rectangular waveguide with its axis along $z$, width $a$ along $x$ and $b$ along $y$, with $a \geqslant b$. State and explain the boundary conditions on the fields $\mathbf{E}$ and $\mathbf{B}$ at the interior waveguide surfaces.

  One particular type of propagating wave has

  $$\mathbf{B}(x, y, z, t)=B_{0}(x, y) \hat{\mathbf{z}} e^{i(k z-\omega t)}$$

  Show that

  $$B_{x}=\frac{i}{(\omega / c)^{2}-k^{2}}\left(k \frac{\partial B_{z}}{\partial x}-\frac{\omega}{c^{2}} \frac{\partial E_{z}}{\partial y}\right)$$

  and derive an equivalent expression for $B_{y}$.

  Assume now that $E_{z}=0$. Write down the equation satisfied by $B_{z}$, find separable solutions, and show that the above implies Neumann boundary conditions on $B_{z}$. Find the "cutoff frequency" below which travelling waves do not propagate. For higher frequencies, find the wave velocity and the group velocity and explain the significance of your results.

  comment

Fluid Dynamics

• Paper 2, Section I, D

  Fluid Dynamics | Part IB, 2009

  A fireman's hose full of water has cross-sectional area $A_{0}$, apart from a smooth contraction to the outlet nozzle which has cross-sectional area $A_{1}<A_{0}$. The volume flow rate of water through the hose is $Q$.

  Use Bernoulli's equation to calculate the pressure in the main part of the tube (relative to atmospheric pressure). Then use the integral momentum equation in the direction of the flow to show that the force $F$ that the fireman has to exert on the nozzle to keep it still is given by

  $$F=\frac{\rho Q^{2}}{2 A_{0}}\left(\frac{A_{0}}{A_{1}}-1\right)^{2}$$

  where $\rho$ is the density of water.

  comment

Geometry

• Paper 2, Section II, G

  Geometry | Part IB, 2009

  What is meant by stereographic projection from the unit sphere in $\mathbb{R}^{3}$ to the complex plane? Briefly explain why a spherical triangle cannot map to a Euclidean triangle under stereographic projection.

  Derive an explicit formula for stereographic projection. Hence, or otherwise, prove that if a Möbius map corresponds via stereographic projection to a rotation of the sphere, it has two fixed points $p$ and $q$ which satisfy $p \bar{q}=-1$. Give, with justification:

  (i) a Möbius transformation which fixes a pair of points $p, q \in \mathbb{C}$ satisfying $p \bar{q}=-1$ but which does not arise from a rotation of the sphere;

  (ii) an isometry of the sphere (for the spherical metric) which does not correspond to any Möbius transformation under stereographic projection.

  comment

Groups, Rings and Modules

• Paper 2, Section $\mathbf{I}$, $2 F$

  Groups, Rings and Modules | Part IB, 2009

  State Sylow's theorems. Use them to show that a group of order 56 must have either a normal subgroup of order 7 or a normal subgroup of order 8 .

  comment

• Paper 2, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Define the centre of a group, and prove that a group of prime-power order has a nontrivial centre. Show also that if the quotient group $G / Z(G)$ is cyclic, where $Z(G)$ is the centre of $G$, then it is trivial. Deduce that a non-abelian group of order $p^{3}$, where $p$ is prime, has centre of order $p$.

  Let $F$ be the field of $p$ elements, and let $G$ be the group of $3 \times 3$ matrices over $F$ of the form

  $$\left(\begin{array}{lll} 1 & a & b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{array}\right)$$

  Identify the centre of $G$.

  comment

Linear Algebra

• Paper 2, Section I, $1 \mathbf{G}$

  Linear Algebra | Part IB, 2009

  Let $V$ denote the vector space of polynomials $f(x, y)$ in two variables of total degree at most $n$. Find the dimension of $V$.

  If $S: V \rightarrow V$ is defined by

  $$(S f)(x, y)=x^{2} \frac{\partial^{2} f}{\partial x^{2}}+y^{2} \frac{\partial^{2} f}{\partial y^{2}}$$

  find the kernel of $S$ and the image of $S$. Compute the trace of $S$ for each $n$ with $1 \leqslant n \leqslant 4$.

  comment

• Paper 2, Section II, G

  Linear Algebra | Part IB, 2009

  Let $V$ be a finite-dimensional vector space and let $T: V \rightarrow V$ be an endomorphism of $V$. Show that there is a positive integer $l$ such that $V=\operatorname{ker}\left(T^{l}\right) \oplus \operatorname{im}\left(T^{l}\right)$. Hence, or otherwise, show that if $T$ has zero determinant there is some non-zero endomorphism $S$ with $T S=0=S T$.

  Suppose $T_{1}$ and $T_{2}$ are endomorphisms of $V$ for which $T_{i}^{2}=T_{i}, i=1,2$. Show that $T_{1}$ is similar to $T_{2}$ if and only if they have the same rank.

  comment

Markov Chains

• Paper 2, Section II, H

  Markov Chains | Part IB, 2009

  Suppose that $B$ is a non-empty subset of the statespace $I$ of a Markov chain $X$ with transition matrix $P$, and let $\tau \equiv \inf \left\{n \geqslant 0: X_{n} \in B\right\}$, with the convention that inf $\emptyset=\infty$. If $h_{i}=P\left(\tau<\infty \mid X_{0}=i\right)$, show that the equations

  (a)

  $$g_{i} \geqslant(P g)_{i} \equiv \sum_{j \in I} p_{i j} g_{j} \geqslant 0 \quad \forall i$$

  $$g_{i}=1 \quad \forall i \in B$$

  are satisfied by $g=h$.

  If $g$ satisfies (a), prove that $g$ also satisfies

  $(c)$

  $$g_{i} \geqslant(\tilde{P} g)_{i} \quad \forall i,$$

  where

  $$\tilde{p}_{i j}=\left\{\begin{array}{cl} p_{i j} & (i \notin B), \\ \delta_{i j} & (i \in B) \end{array}\right.$$

  By interpreting the transition matrix $\tilde{P}$, prove that $h$ is the minimal solution to the equations (a), (b).

  Now suppose that $P$ is irreducible. Prove that $P$ is recurrent if and only if the only solutions to (a) are constant functions.

  comment

Methods

• Paper 2, Section I, B

  Methods | Part IB, 2009

  Expand $f(x)=x, 0<x<\pi$, as a half-range sine series.

  By integrating the series show that a Fourier cosine series for $x^{2}, 0<x<\pi$, can be written as

  $$x^{2}=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  where $a_{n}, n=1,2, \ldots$, should be determined and

  $$a_{0}=8 \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}$$

  By evaluating $a_{0}$ another way show that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 2, Section II, B

  Methods | Part IB, 2009

  A string of uniform density $\rho$ is stretched under tension along the $x$-axis and undergoes small transverse oscillations in the $(x, y)$ plane with amplitude $y(x, t)$. Given that waves in the string travel at velocity $c$, write down the equation of motion satisfied by $y(x, t)$.

  The string is now fixed at $x=0$ and $x=L$. Derive the general separable solution for the amplitude $y(x, t)$.

  For $t<0$ the string is at rest. At time $t=0$ the string is struck by a hammer in the interval $[l-a / 2, l+a / 2]$, distance being measured from one end. The effect of the hammer is to impart a constant velocity $v$ to the string inside the interval and zero velocity outside it. Calculate the proportion of the total energy given to the string in each mode.

  If $l=L / 3$ and $a=L / 10$, find all the modes of the string which are not excited in the motion.

  comment

Metric and Topological Spaces

• Paper 2, Section I, $4 F$

  Metric and Topological Spaces | Part IB, 2009

  Explain what is meant by a Hausdorff (topological) space, and prove that every compact subset of a Hausdorff space is closed.

  Let $X$ be an uncountable set, and consider the topology $\mathcal{T}$ on $X$ defined by

  $$U \in \mathcal{T} \Leftrightarrow \text { either } U=\emptyset \text { or } X \backslash U \text { is countable. }$$

  Is $(X, \mathcal{T})$ Hausdorff? Is every compact subset of $X$ closed? Justify your answers.

  comment

Numerical Analysis

• Paper 2, Section II, C

  Numerical Analysis | Part IB, 2009

  The real orthogonal matrix $\Omega^{[p, q]} \in \mathbb{R}^{m \times m}$ with $1 \leqslant p<q \leqslant m$ is a Givens rotation with rotation angle $\theta$. Write down the form of $\Omega^{[p, q]}$.

  Show that for any matrix $A \in \mathbb{R}^{m \times m}$ it is possible to choose $\theta$ such that the matrix $\Omega^{[p, q]} A$ satisfies $\left(\Omega^{[p, q]} A\right)_{q, j}=0$ for any $j$, where $1 \leqslant j \leqslant m$.

  Let

  $$A=\left[\begin{array}{ccc} 1 & 3 & 2 \\ 1 & 4 & 4 \\ \sqrt{2} & 7 / \sqrt{2} & 4 \sqrt{2} \end{array}\right]$$

  By applying a sequence of Givens rotations of the form $\Omega^{[1,3]} \Omega^{[1,2]}$, chosen to reduce the elements in the first column below the main diagonal to zero, find a factorisation of the matrix $A \in \mathbb{R}^{3 \times 3}$ of the form $A=Q R$, where $Q \in \mathbb{R}^{3 \times 3}$ is an orthogonal matrix and $R \in \mathbb{R}^{3 \times 3}$ is an upper-triangular matrix for which the leading non-zero element in each row is positive.

  comment

Optimization

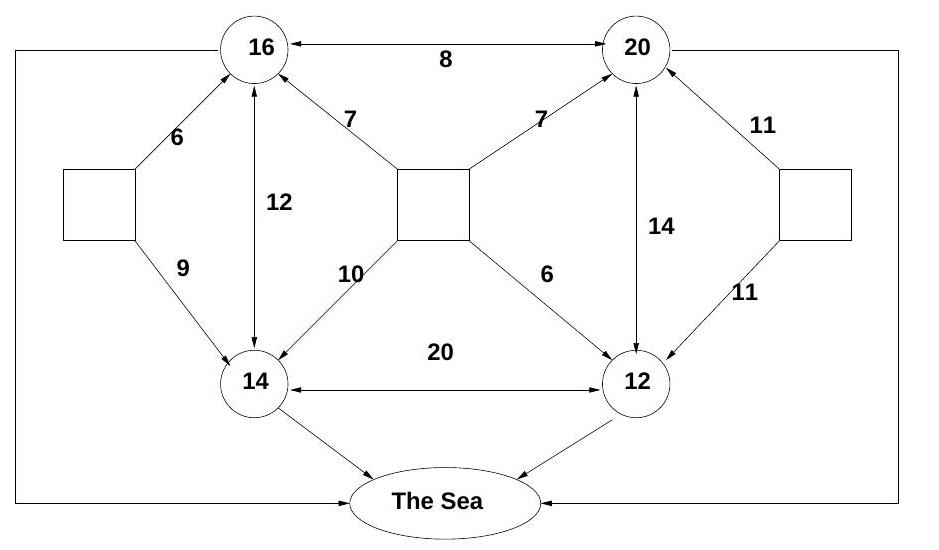
• Paper 2, Section I, H

  Optimization | Part IB, 2009

  The diagram shows a network of sewage treatment plants, shown as circles, connected by pipes. Some pipes (indicated by a line with an arrowhead at one end only) allow sewage to flow in one direction only, others (indicated by a line with an arrowhead at both ends) allow sewage to flow in either direction. The capacities of the pipes are shown. The system serves three towns, shown in the diagram as squares.

  Each sewage treatment plant can treat a limited amount of sewage, indicated by the number in the circle, and this may not be exceeded for fear of environmental damage. Treated sewage is pumped into the sea, but at any treatment plant incoming untreated sewage may be immediately pumped to another plant for treatment there.

  Find the maximum amount of sewage which can be handled by the system, and how this is assigned to each of the three towns.

  

  comment

Quantum Mechanics

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2009

  Write down the expressions for the probability density $\rho$ and the associated current density $j$ for a particle with wavefunction $\psi(x, t)$ moving in one dimension. If $\psi(x, t)$ obeys the time-dependent Schrödinger equation show that $\rho$ and $j$ satisfy

  $$\frac{\partial j}{\partial x}+\frac{\partial \rho}{\partial t}=0$$

  Give an interpretation of $\psi(x, t)$ in the case that

  $$\psi(x, t)=\left(e^{i k x}+R e^{-i k x}\right) e^{-i E t / \hbar}$$

  and show that $E=\frac{\hbar^{2} k^{2}}{2 m}$ and $\frac{\partial \rho}{\partial t}=0$.

  A particle of mass $m$ and energy $E>0$ moving in one dimension is incident from the left on a potential $V(x)$ given by

  $$V(x)=\left\{\begin{array}{rl} -V_{0} & 0<x<a \\ 0 & x<0, x>a \quad, \end{array}\right.$$

  where $V_{0}$ is a positive constant. What conditions must be imposed on the wavefunction at $x=0$ and $x=a$ ? Show that when $3 E=V_{0}$ the probability of transmission is

  $$\left[1+\frac{9}{16} \sin ^{2} \frac{a \sqrt{8 m E}}{\hbar}\right]^{-1}$$

  For what values of $a$ does this agree with the classical result?

  comment

Special Relativity

• Paper 2, Section I, C

  Special Relativity | Part IB, 2009

  Show that the two-dimensional Lorentz transformation relating $\left(c t^{\prime}, x^{\prime}\right)$ in frame $S^{\prime}$ to $(c t, x)$ in frame $S$, where $S^{\prime}$ moves relative to $S$ with speed $v$, can be written in the form

  $$\begin{gathered} x^{\prime}=x \cosh \phi-c t \sinh \phi \\ c t^{\prime}=-x \sinh \phi+c t \cosh \phi \end{gathered}$$

  where the hyperbolic angle $\phi$ associated with the transformation is given by $\tanh \phi=v / c$. Deduce that

  $$\begin{aligned} &x^{\prime}+c t^{\prime}=e^{-\phi}(x+c t) \\ &x^{\prime}-c t^{\prime}=e^{\phi}(x-c t) \end{aligned}$$

  Hence show that if the frame $S^{\prime \prime}$ moves with speed $v^{\prime}$ relative to $S^{\prime}$ and $\tanh \phi^{\prime}=v^{\prime} / c$, then the hyperbolic angle associated with the Lorentz transformation connecting $S^{\prime \prime}$ and $S$ is given by

  $$\phi^{\prime \prime}=\phi^{\prime}+\phi$$

  Hence find an expression for the speed of $S^{\prime \prime}$ as seen from $S$.

  comment

Statistics

• Paper 2, Section II, H

  Statistics | Part IB, 2009

  What does it mean to say that the random $d$-vector $X$ has a multivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$ ?

  Suppose that $X \sim N_{d}\left(0, \sigma^{2} I_{d}\right)$, and that for each $j=1, \ldots, J, A_{j}$ is a $d_{j} \times d$ matrix. Suppose further that

  $$A_{j} A_{i}^{T}=0$$

  for $j \neq i$. Prove that the random vectors $Y_{j} \equiv A_{j} X$ are independent, and that $Y \equiv\left(Y_{1}^{T}, \ldots, Y_{J}^{T}\right)^{T}$ has a multivariate normal distribution.

  [Hint: Random vectors are independent if their joint $M G F$ is the product of their individual MGFs.]

  If $Z_{1}, \ldots, Z_{n}$ is an independent sample from a univariate $N\left(\mu, \sigma^{2}\right)$ distribution, prove that the sample variance $S_{Z Z} \equiv(n-1)^{-1} \sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)^{2}$ and the sample mean $\bar{Z} \equiv$ $n^{-1} \sum_{i=1}^{n} Z_{i}$ are independent.

  comment